An Improved CNN-BILSTM Model for Power Load Prediction in Uncertain Power Systems
Abstract
1. Introduction
- We model the uncertain power system and establish a power load model that takes into account the changes in factors such as market demand, power generation costs, and supply and demand balance.
- We define feature vectors that effectively represent the power load changes.
- We design the CNN-BILSTM model, where the CNN module is used to extract high-dimensional feature vectors from uncertain power data and map them to a low-dimensional feature space.
- We further propose a Bidirectional Long Short-term Memory (LSTM) module to capture temporal dependencies. The forward LSTM module and the reverse LSTM module consider factors influencing the timing of forward and reverse power loads within the entire power load dataset, thereby enhancing model performance.
2. Related Work
3. System Model and Problem Definition
3.1. Uncertain Power Systems
- Renewable energy sources: The output of renewable energy sources such as wind and solar power can vary due to changes in weather conditions, cloud cover, or wind speed. This variability introduces uncertainty into the power generation forecast.
- Demand variability: Electricity demand fluctuates throughout the day and is influenced by factors such as weather, time of day, seasonality, and economic activity. Uncertainty in demand forecasts can arise from unexpected changes in these factors.
- Equipment failures: Unexpected failures or outages of power generation or transmission equipment, such as turbines, transformers, or transmission lines, can lead to sudden changes in power flow and system reliability.
- Market conditions: Uncertainty in market conditions, including fuel prices, regulatory changes, and electricity market dynamics, can affect investment decisions, generation planning, and power flow within the system.
- Environmental factors: Natural disasters, such as hurricanes, earthquakes, or wildfires, can damage power infrastructure and disrupt power supply, leading to uncertainty in power system operation and restoration efforts.
- Human factors: Operator errors, cyber-attacks, or sabotage can also introduce uncertainty into power system operation and security.
3.2. Problem Definition
4. Proposed Method
4.1. Overall Architecture of CNN-BILSTM Model
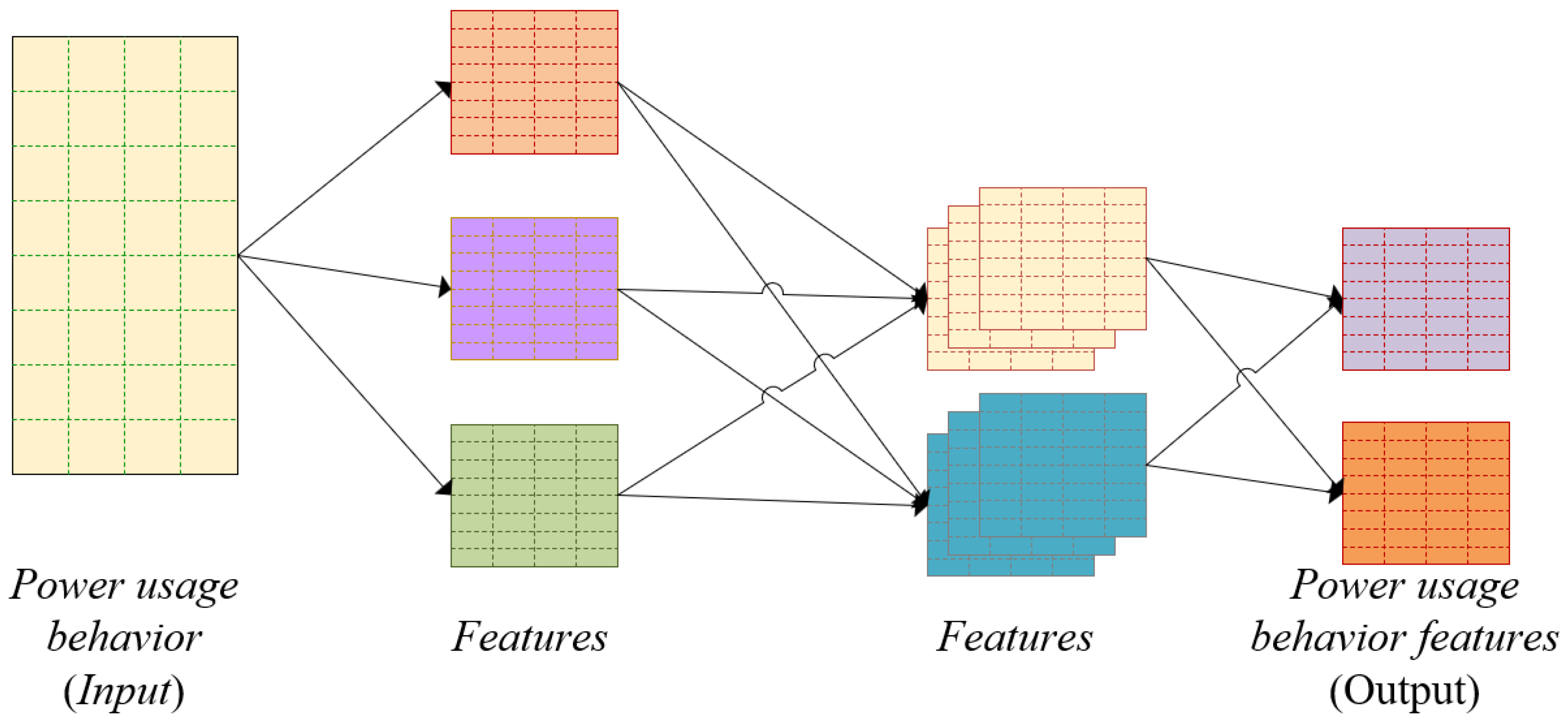
4.2. Convolutional Neural Network Module
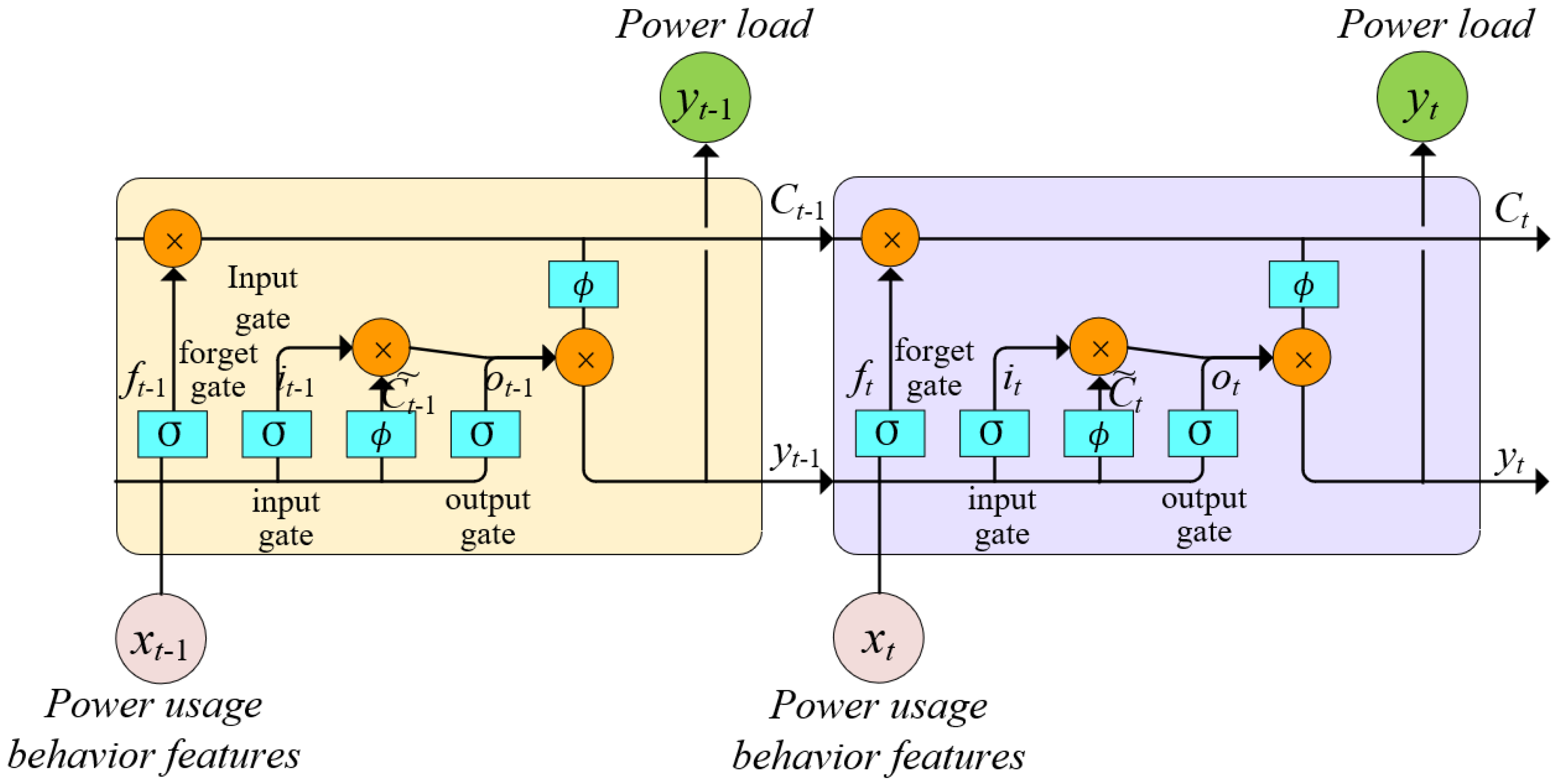
4.3. Long Short-Term Memory Module
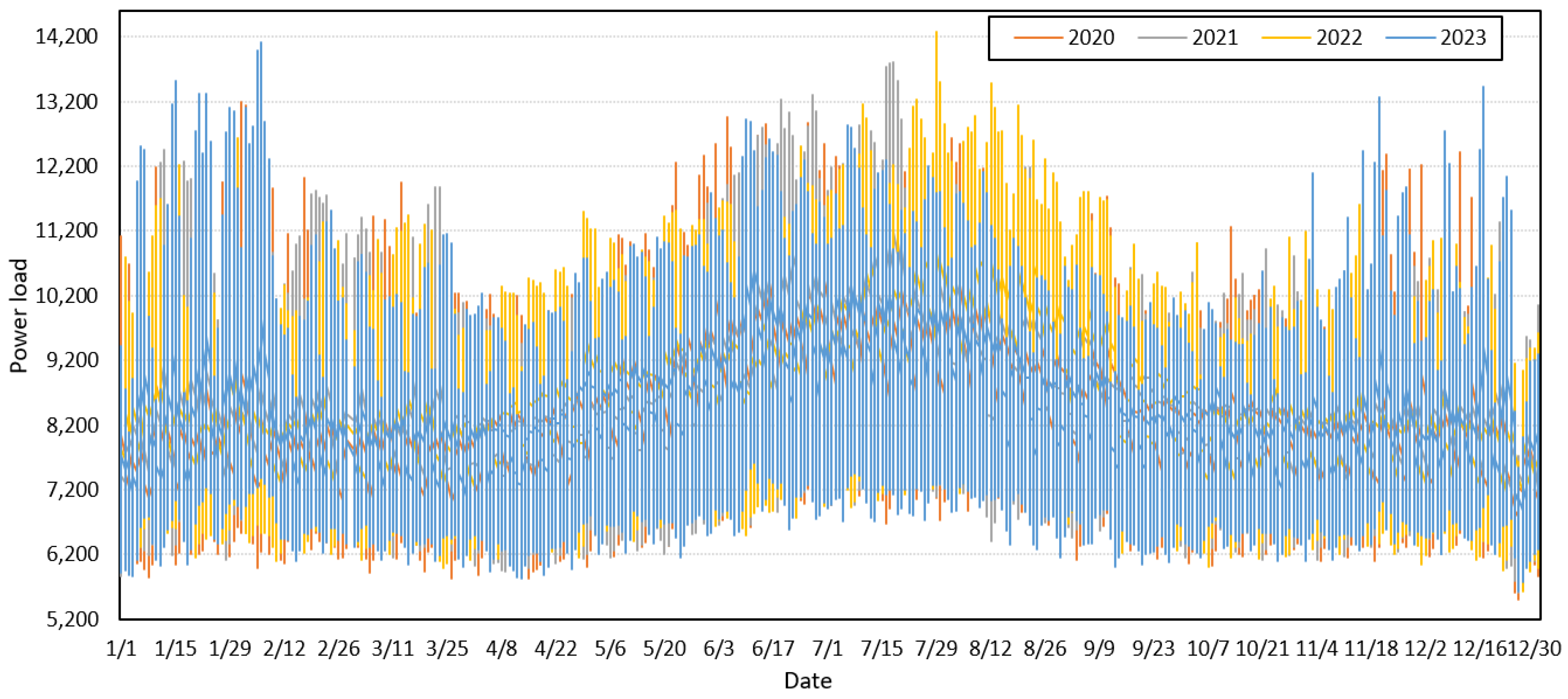
5. Experiments
5.1. Experimental Setup
5.2. Experimental Results
5.3. Ablation Experiments
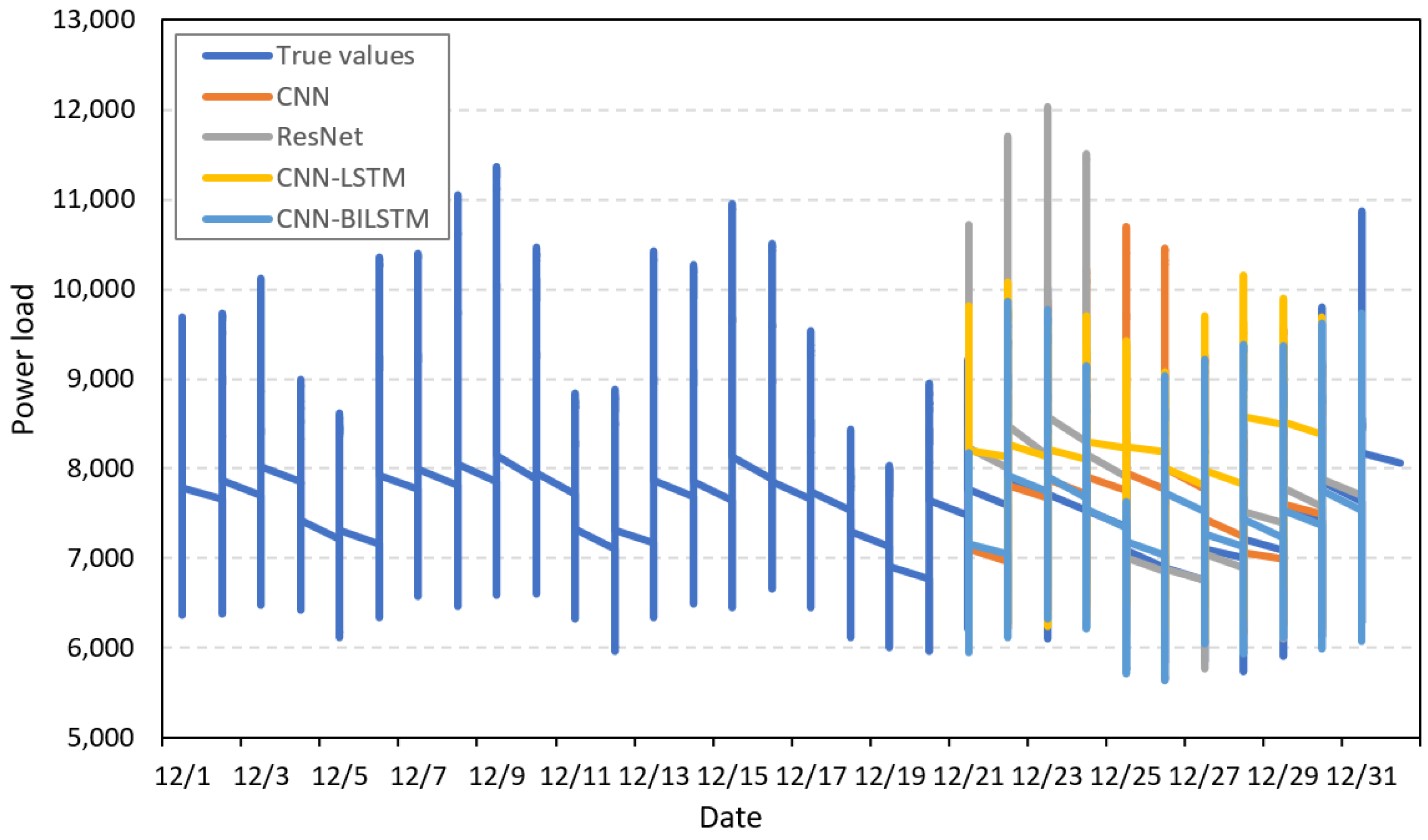
5.4. Prediction Accuracy Comparison
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dai, W.; Shi, B.; Li, T.; Goh, H.; Li, J. Power flow analysis considering solar road generation. Energy Rep. 2022, 8, 531–536. [Google Scholar] [CrossRef]
- Elgamal, M.; Korovkin, N.; Abdel Menaem, A.; Elmitwally, A. An algorithm for power flow analysis in isolated hybrid energy microgrid considering DG droop model and virtual impedance control loop. Sustain. Energy Grids Netw. 2022, 32, 100875. [Google Scholar] [CrossRef]
- Kumari, D.; Chattopadhyay, S.K.; Verma, A. Improvement of Power Flow Capability By Using An Alternative Power Flow Controller. IEEE Trans. Power Deliv. 2020, 35, 2353–2362. [Google Scholar] [CrossRef]
- Yue, Z.; Ding, Y.; Zhao, H.; Wang, Z. Ultra-high precise Stack-LSTM-CNN model of temperature-induced deflection of a cable-stayed bridge for detecting bridge state driven by monitoring data. Structures 2022, 45, 110–125. [Google Scholar] [CrossRef]
- Tang, C.Y.; Chen, P.T.; Jheng, J.H. Bidirectional Power Flow Control and Hybrid Charging Strategies for Three-Phase PV Power and Energy Storage Systems. IEEE Trans. Power Electron. 2021, 36, 12710–12720. [Google Scholar] [CrossRef]
- Lee, C.; An, J. LSTM-CNN model of drowsiness detection from multiple consciousness states acquired by EEG. Expert Syst. Appl. 2023, 213, 119032. [Google Scholar] [CrossRef]
- Lopez-Garcia, T.B.; Domínguez-Navarro, J.A. Power flow analysis via typed graph neural networks. Eng. Appl. Artif. Intell. 2023, 117, 105567. [Google Scholar] [CrossRef]
- Milano, F. Implicit Continuous Newton Method for Power Flow Analysis. IEEE Trans. Power Syst. 2019, 34, 3309–3311. [Google Scholar] [CrossRef]
- Khodaee, P.; Esfahanipour, A.; Mehtari Taheri, H. Forecasting turning points in stock price by applying a novel hybrid CNN-LSTM-ResNet model fed by 2D segmented images. Eng. Appl. Artif. Intell. 2022, 116, 105464. [Google Scholar] [CrossRef]
- Montoya, O.D.; Gil-González, W.; Garcés, A. A successive approximations method for power flow analysis in bipolar DC networks with asymmetric constant power terminals. Electr. Power Syst. Res. 2022, 211, 108264. [Google Scholar] [CrossRef]
- Portelinha, R.K.; Durce, C.C.; Tortelli, O.L.; Lourenço, E.M. Fast-decoupled power flow method for integrated analysis of transmission and distribution systems. Electr. Power Syst. Res. 2021, 196, 107215. [Google Scholar] [CrossRef]
- Chowdhury, B.H.; Taylor, C.W. Voltage stability analysis: VQ power flow simulation versus dynamic simulation. IEEE Trans. Power Syst. 2000, 15, 1354–1359. [Google Scholar] [CrossRef]
- Constante-Flores, G.E.; Illindala, M.S. Data-driven probabilistic power flow analysis for a distribution system with renewable energy sources using Monte Carlo simulation. IEEE Trans. Ind. Appl. 2018, 55, 174–181. [Google Scholar] [CrossRef]
- Fagundes, S.; Cardoso, F.; Stangler, E.; Neves, F.; Mezaroba, M. A detailed power flow analysis of the dual unified power quality conditioner (iUPQC) using power angle control (PAC). Electr. Power Syst. Res. 2021, 192, 106933. [Google Scholar] [CrossRef]
- Yoon, D.H.; Han, Y. Parallel power flow computation trends and applications: A review focusing on GPU. Energies 2020, 13, 2147. [Google Scholar] [CrossRef]
- Shekhar, A.; Soeiro, T.B.; Wu, Y.; Bauer, P. Optimal power flow control in parallel operating AC and DC distribution links. IEEE Trans. Ind. Electron. 2020, 68, 1695–1706. [Google Scholar] [CrossRef]
- Ahmadi, A.; Smith, M.C.; Collins, E.R.; Dargahi, V.; Jin, S. Fast Newton-Raphson power flow analysis based on sparse techniques and parallel processing. IEEE Trans. Power Syst. 2021, 37, 1695–1705. [Google Scholar] [CrossRef]
- Wu, X.W.; Zhu, L.F.; Wu, Z.M.; Ke, L.L. Vibrational power flow analysis of Timoshenko microbeams with a crack. Compos. Struct. 2022, 289, 115483. [Google Scholar] [CrossRef]
- Dalton, A.; Bekker, B.; Koivisto, M.J. Classified atmospheric states as operating scenarios in probabilistic power flow analysis for networks with high levels of wind power. Energy Rep. 2021, 7, 3775–3784. [Google Scholar] [CrossRef]
- Lu, K.D.; Zhou, L.; Wu, Z.G. Representation-learning-based CNN for intelligent attack localization and recovery of cyber-physical power systems. IEEE Trans. Neural Netw. Learn. Syst. 2024, 35, 6145–6155. [Google Scholar] [CrossRef]
- Aksan, F.; Li, Y.; Suresh, V.; Janik, P. CNN-LSTM vs. LSTM-CNN to Predict Power Flow Direction: A Case Study of the High-Voltage Subnet of Northeast Germany. Sensors 2023, 23, 901. [Google Scholar] [CrossRef]
- Li, Z.; Liu, H.; Zhao, J.; Bi, T.; Yang, Q. Fast power system event identification using enhanced LSTM network with renewable energy integration. IEEE Trans. Power Syst. 2021, 36, 4492–4502. [Google Scholar] [CrossRef]
- Yan, Z.; Xu, Y. Real-time optimal power flow: A lagrangian based deep reinforcement learning approach. IEEE Trans. Power Syst. 2020, 35, 3270–3273. [Google Scholar] [CrossRef]
- Sayed, A.R.; Wang, C.; Anis, H.I.; Bi, T. Feasibility constrained online calculation for real-time optimal power flow: A convex constrained deep reinforcement learning approach. IEEE Trans. Power Syst. 2022, 38, 5215–5227. [Google Scholar] [CrossRef]
- Putri, S.M.; Maizana, D.; Bahri, Z. Analysis of smart grid power flow system with Gauss-Seidel method. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2021; Volume 753, p. 012005. [Google Scholar]
- Chamim, A.N.N.; Putra, K.T.; Al Farisi, M.F. Power Flow Analysis of Electrical Network Systems Using Gauss-Seidel Method and Python. Emerg. Inf. Sci. Technol. 2023, 4, 28–36. [Google Scholar]
- Chen, Y.; Zhao, Y.; Ma, J. Fast decoupled multi-energy flow calculation for integrated energy system. J. Mod. Power Syst. Clean Energy 2020, 8, 951–960. [Google Scholar] [CrossRef]
- Coutinho de Oliveira, C.; Bonini Neto, A.; Alves, D.A.; Minussi, C.R.; Castro, C.A. Alternative Current Injection Newton and Fast Decoupled Power Flow. Energies 2023, 16, 2548. [Google Scholar] [CrossRef]
- Tang, K.; Dong, S.; Song, Y. Successive-intersection-approximation-based power flow method for integrated transmission and distribution networks. IEEE Trans. Power Syst. 2020, 35, 4836–4846. [Google Scholar] [CrossRef]
- Liu, Y.; Li, Z.; Fan, M. A Newton–Raphson-based sequential power flow algorithm for hybrid AC/DC microgrids. IEEE Trans. Ind. Appl. 2021, 58, 843–854. [Google Scholar] [CrossRef]
- Sun, W.; Zamani, M.; Zhang, H.T.; Li, Y. Probabilistic optimal power flow with correlated wind power uncertainty via Markov chain quasi-Monte-Carlo sampling. IEEE Trans. Ind. Inform. 2019, 15, 6058–6069. [Google Scholar] [CrossRef]
- Palahalli, H.; Maffezzoni, P.; Gruosso, G. Modeling photovoltaic generation uncertainties for monte carlo method based probabilistic load flow analysis of distribution network. In Proceedings of the 2020 55th International Universities Power Engineering Conference (UPEC), Online, 1–4 September 2020; pp. 1–6. [Google Scholar]
- Jabari, F.; Shamizadeh, M.; Mohammadi-Ivatloo, B. Probabilistic power flow analysis of distribution systems using Monte Carlo simulations. In Optimization of Power System Problems: Methods, Algorithms and MATLAB Codes; Springer: Berlin/Heidelberg, Germany, 2020; pp. 215–232. [Google Scholar]
- Ni, F.; Nguyen, P.H.; Cobben, J.F. Basis-adaptive sparse polynomial chaos expansion for probabilistic power flow. IEEE Trans. Power Syst. 2016, 32, 694–704. [Google Scholar] [CrossRef]
- Mühlpfordt, T.; Roald, L.; Hagenmeyer, V.; Faulwasser, T.; Misra, S. Chance-constrained AC optimal power flow: A polynomial chaos approach. IEEE Trans. Power Syst. 2019, 34, 4806–4816. [Google Scholar] [CrossRef]
- Scikit Learn. Sikit-Learn: Machine Learning in Python. 2024. Available online: https://scikit-learn.org (accessed on 1 January 2024).
- CSDN. Power System Load Forecasting Data Set. 2024. Available online: https://download.csdn.net/download/qq_25888559/28453108 (accessed on 1 January 2024).



| No. | Modules | Layers | Parameters | Vaules |
|---|---|---|---|---|
| 1 | CNN | Conv1D-1 | kernel size | 3 |
| 2 | CNN | Conv1D-1 | filters | 100 |
| 3 | CNN | Conv1D-2 | kernel size | 3 |
| 4 | CNN | Conv1D-2 | filters | 64 |
| 5 | CNN | MaxPooling1D-1 | pool size | 2 |
| 6 | CNN | MaxPooling1D-2 | pool size | 2 |
| 7 | LSTM | LSTM-1 | units | 32 |
| 8 | LSTM | LSTM-2 | units | 16 |
| 9 | Dense | Dense-1 | units | 128 |
| 10 | Dense | Dense-2 | units | 32 |
| 11 | Dense | Dense-3 | units | 2 |
| Methods | Accuracy | AUC | F1 Score |
|---|---|---|---|
| CNN module | 64.25% | 72.24% | 0.68 |
| CNN + LSTM modules | 68.18% | 75.73% | 0.71 |
| CNN + BILSTM + Huber Loss | 89.27% | 90.51% | 0.85 |
| CNN + BILSTM + Quantile Loss | 92.48% | 91.34% | 0.89 |
| CNN + BILSTM + Cross Entropy Loss | 92.87% | 93.01% | 0.90 |
| Methods | Accuracy | AUC | F1 Score |
|---|---|---|---|
| C4.5 | 68.36% ± 8.14% | 75.42% ± 9.53% | 0.70 |
| RF | 74.52% ± 7.73% | 80.16% ± 6.98% | 0.72 |
| XGBoost | 76.19% ± 7.49% | 83.58% ± 7.75% | 0.79 |
| CNN | 78.36% ± 3.44% | 88.74% ± 3.26% | 0.85 |
| ResNet | 86.83% ± 3.62% | 90.26% ± 3.92% | 0.89 |
| CNN-BILSTM | 92.15% ± 2.14% | 94.87% ± 2.13% | 0.95 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, C.; Zhang, Y.; Wu, F.; Tang, Z. An Improved CNN-BILSTM Model for Power Load Prediction in Uncertain Power Systems. Energies 2024, 17, 2312. https://doi.org/10.3390/en17102312
Tang C, Zhang Y, Wu F, Tang Z. An Improved CNN-BILSTM Model for Power Load Prediction in Uncertain Power Systems. Energies. 2024; 17(10):2312. https://doi.org/10.3390/en17102312
Chicago/Turabian StyleTang, Chao, Yufeng Zhang, Fan Wu, and Zhuo Tang. 2024. "An Improved CNN-BILSTM Model for Power Load Prediction in Uncertain Power Systems" Energies 17, no. 10: 2312. https://doi.org/10.3390/en17102312
APA StyleTang, C., Zhang, Y., Wu, F., & Tang, Z. (2024). An Improved CNN-BILSTM Model for Power Load Prediction in Uncertain Power Systems. Energies, 17(10), 2312. https://doi.org/10.3390/en17102312






