Improving the Efficiency of the Blow-Jet WEC

Abstract

Establishing a renewable marine energy industry demands the development of high-efficiency devices that capture as much energy as possible. The Blow-Jet is a wave energy converter mainly composed of a sloping conical channel in the shape of a brass tube, which concentrates the waves at its widest part and expels a jet of water at its narrow upper end through an orifice that can be turbined. The device has no moving parts and great flexibility in its placement. This research presents an improvement of its geometry, increasing efficiency by minimizing undesired hydrodynamic interactions. The performance of the Blow-Jet was characterized using 3D numerical modeling and laboratory tests in a wave flume. Sixteen geometric configurations of the Blow-Jet were numerically tested, and that showing the best performance was 3D printed and assessed experimentally. The twofold objective was to evaluate the performance of the new Blow-Jet geometry and to validate a numerical tool for further geometrical improvements of the device. The novel geometry is nearly 20% more efficient than the original.

1. Introduction

The undesirable environmental consequences of using fossil fuels have led to the search for renewable, clean sources for the production of electricity. The most common renewable energy generation systems are land-based, e.g., wind, solar, and hydraulic. Later, other sources captured the interest of scientists, such as tides, geothermal, saline gradient, biomass, ocean currents, ocean winds, and sea waves [1,2,3].

There is vast energy potential in ocean waves. Therefore, many wave energy converters (WECs) are being developed worldwide, although only a few have been tested in open sea conditions [4,5]. The classification of WEC devices can be, with regard to their location, grouped as [6]: near the coast, onshore, and offshore. They can also be grouped by size and orientation [7] or according to the principle used in their operation [8]: pressure differential [9,10], floating [11,12], overflow [13], and impact [14]. A further classification is based on their power take-off (PTO) system: linear generators [15,16,17,18], turbines [19,20,21], and hydraulic systems [22].

WECs are still in the early stages of development, compared to inland renewable energy technologies. There are some large-scale prototypes for WEC plants, but only a few have reached the marketing level. The current worldwide trend in WEC development is site-specific designs that aim to reduce the costs of the energy produced and its mechanical complexity [23,24]. Examples of such devices are Wavestar, Pelamis, Wavedragon, Oyster, and Mightywhale [1]. Since the conditions in any marine environment are highly unpredictable, the reliability, installation, and ease of maintenance of the device are critical factors for its technological development [23].

Most existing WEC devices are designed to operate in areas where waves have a high energy potential. As such waves are not often found on Mexican coasts, it is necessary to design new devices or adapt existing technologies to the local wave conditions.

Many WECs consist of moving parts that require frequent preventive and corrective maintenance as a result of the pounding of waves. This raises operational costs, so a design with the lesser possible moving parts is desirable.

At the Engineering Institute of the National University of Mexico (UNAM) a novel device with the name Blow-Jet was developed and tested, showing acceptable efficiency [25]. The Blow-Jet consists of a Tapchan (tapered channel) and a reservoir, inspired by the naturally occurring phenomenon of a marine geyser. The water flow catchment takes place in a channel of positive slope that narrows as it goes into a reservoir, placed above the mean sea level. The reservoir has three sections: a wide, submerged, or semi-submerged entrance; a compression chamber; and a discharge hole [25,26]. The main disadvantage of the Blow-Jet is its being unable to force the entire captured wave out, which means a loss in efficiency. This can be addressed by improving the design of the compression chamber.

In this work a geometric optimization of the Blow-Jet to improve its hydrodynamic behavior is proposed. In this paper, in Section 2, the performance of the Blow-Jet was numerically characterized (Flow 3D model), and various modifications to the basic design were proposed to maximize its efficiency (assessed as the water velocity increase between the incoming flow and the expelled jet). Subsequently, the most efficient design was tested in a wave flume to validate the numerical results, as shown in Section 3. The results are discussed in Section 4, and Section 5 shows the general conclusions.

2. Numerical Modeling

FLOW-3D software was used to perform the numerical exercises, as this compute 5th order Stokes waves that are suitable for this study. The software can be automatically tuned via several parameters and options which ensure the numerical stability [27,28,29] and is less expensive in runtime than physical experimentation [30,31]. This model can use cylindrical or Cartesian coordinates and the computational grid must be constructed specifically for the phenomenon under study. Table 1 presents the main parameters used in this research [31] (these are the parameters that are automatically set by the software and can be changed by the user).

Table 1. Main numerical parameters used in FLOW-3D.

Option	Setup	Parameter
Flow mode	Incompressible	icmprs = 0
Maximum permitted time step	fs−1	dtmax
Momentum advection	First-order, explicit scheme	iorder = 1, impadv = 0
Pressure solver	General minimal residual (GMRES)	igmres = 1, imp = 1
Time step control	Automatic	autot = 1
Turbulence	Laminar calculation	---
Viscosity	Newtonian fluid	ifvisc = 1
Viscous stress	Laminar	ifvis = 0
VOF advection	Split Lagrangian method	ifvof = 6

The momentum advection parameter for wave models is set to first order, which is suitable for this research work. In case of numerical diffusion appearing in the solution, the software automatically adds artificial viscosity or numerical viscosity. Additionally, we can refine the mesh in case of any numerical diffusion warning flags.

Flow3D has five turbulence models: the Prandtl mixing length model, the one-equation, the two-equation $k-\epsilon$, RNG model (renormalization group theory), and large eddy simulation (LES) model.

In this work, the laminar flow option (ifvis = 0) was used, as the initial configuration, indicating that no turbulence model was employed in the initial setup. This was because a regular wave with a flat bottom was used, and the “Allow fluid to enter at outflow boundary” option was selected to enable the wave to propagate outside the computational domain. Additionally, waves dampers were implemented to prevent reflection. These conditions correspond to laminar flow. These conditions may vary during the simulation as we can make changes during the simulation due to any warning flags that may arise, meaning that the initial configuration may change at the end of the simulation. The “No-slip or partial slip” option was established for the wall shear boundary condition.

In some cases, depending on the initial configuration, fatal error alerts or critical warning alerts may occur regarding the omega or epsilon factor. The simulations that presented a fatal error alert regarding the omega or epsilon factor are automatically stopped. To address this issue, the LES turbulence model is manually activated (ifvis = −1) and the simulation is started from the beginning. As one-equation models have limitations in shear flows, under predicting separation, and decaying turbulence. On the other hand, two-equation $k-\epsilon$ and $k-\omega$ models have limitations in situations such as no-slip walls, adverse pressure gradients, jet flows, and strong curvatures.

The default values for the maximum and minimum time step are 1.0 × 10³⁵ and 1 × 10⁻¹¹, respectively. However, for the simulations of the 16 models, an initial time step interval ranging from 1 × 10⁻⁵ to 1 × 10⁻⁸ was used.

The following known constants were also set in the model: acceleration due to gravity g = −9.81 m/s²; density and molecular viscosity of water at 20 °C: d = 1000 kg/m³ and µ = 0.001 kg/m/s, respectively.

2.1. Description and Numerical Modeling of the Original Blow-Jet

As stated before, the Blow-Jet consists of a tapered channel of circular section (see Figure 1).

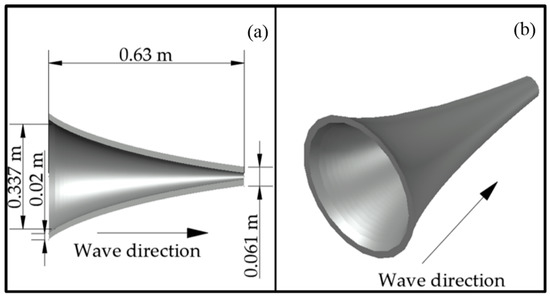
Figure 1. Longitudinal section with dimensions (a) and isometric view (b) of the Blow-Jet.

Equation (1) gave the dimensions of the numerically tested device (Figure 1). The wave characteristics and Blow-Jet placement correspond to those reported by [25] as these showed the greatest efficiency. The prototype scale is of the numerical model to the laboratory tests is 1:1; while the scale to the real size device is 1:20. The units of the equation which describes the shape of the Blow-jet are centimeters.

$${\mathrm{y}=1.37178\mathrm{x}}^{\raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$4$}\right.}$$

(1)

Table 2 shows the input data used in the numerical modeling. The wave parameters that showed the highest average values of velocity and pressure at the outlet of the device reported by Chávez [25] were taken. The submerged device portion is the section of the device that is in contact with the water under idle conditions.

Table 2. Settings and wave parameters for the Flow-3D model.

Parameter	Quantity	Unit
Time step	1 × 10−5	s
Simulation time	30	s
Wave height	8	cm
Mean fluid depth	70	cm
Fluid elevation	70	cm
Initial fluid elevation	70.1	cm
Wave period	1.2	s
Submerged device portion	16.85	cm
Inclination angle	10	Degrees

The 3D representation of the Blow-Jet was vectorized (its use extends from typography representation to three-dimensional modeling) with the same dimensions used by Chavez [25], with the exception of the wall thickness (changed to avoid model instability). To save computational time and make use of the axial symmetry of the device only half the domain was modeled.

To generate the most optimized grid possible, only constant cell sizes were set at the borders (boundaries). The FLOW3D software offers 10 different types of boundaries that can be assigned to each face (boundary, border) of the blocks and/or mesh. For this work, the following types of boundaries were used: “wave (WV)”, in which the wave parameters and solution method to be solved by the model were configured; “wall (W)”, considered as a rigid and impermeable boundary; “outflow (O)”, allows for the propagation of the fluid outside the computational domain and avoids possible reflection; and “symmetry (S)”, which maintained continuity between blocks. These boundaries are shown in the drawing area on the faces of each block and mesh with the respective letter. Then, to obtain the highest resolution around the device, a block-structured mesh was selected. Using the input parameters shown in Table 2, a 400 × 24 × 100 cm mesh, composed of six blocks was defined. The dimensions of the cells were chosen so that no cell is bigger than twice the size of its neighbor. The maximum cell resolution of the final grids was 0.5 cm for blocks shorter than 400 cm and 1 cm for the 400 cm long blocks. The resolution is assigned to the cells, which can be cubic or rectangular. Flow3D employs a technique called FAVOR (Fractional Area/Volume Obstacle Representation). This technique constructs the geometry by assembling solid geometric “objects” that combine to define the flow region for a simulation. The flow region is then embedded into the simulation by the preprocessor using this technique. The FAVOR method calculates the open area fractions on the cell faces, along with the open volume fraction, and reconstructs the geometry based on these parameters. To identify how well the computational grid defines the geometry, the FAVOR technique displays a window with the vectorized geometry, error tolerance, and possible inconsistencies of the geometry [27]. A minimum of four cells are required to correctly vectorize a volume. The selected cell size is small enough to avoid results dependency on it.

Figure 2 shows different views of the final mesh. In Figure 2a the position of the data recording points (sensors) is seen, while in Figure 2b,c the border type set for each block interface is presented.

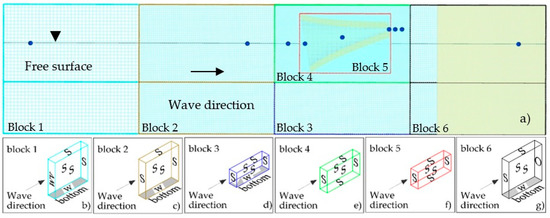
Figure 2. Views of the numerical grid used in Flow 3D. (a) Longitudinal view of the half-domain modeled showing the position of the data recording points (navy blue dots), free surface and wave damper; (b–g) an isometric view of Blocks 1, 2, 3, 4, 5, and 6, respectively. Additionally, the boundaries assigned to each of the faces that make up these blocks are displayed.

The cream-colored body located in block 6 was set as a wave damper, as suggested by [32]. Figure 2 represents in a general way the mesh configuration, the necessary measurement elements, and the parameters to perform the simulation. This figure corresponds to the configuration of the original Blow-Jet, and all simulations with the different models in this work have a similar configuration. The mesh dimensions, the number of blocks, cells, and resolution variations for each model are not significant.

At each data recording point, the flow velocity and pressure were stored. As an example, Figure 3 shows the time series of water velocity and pressure for the sensor located at the output of the device. These values correspond to the expelled jet that would be introduced into a turbine for electricity generation.

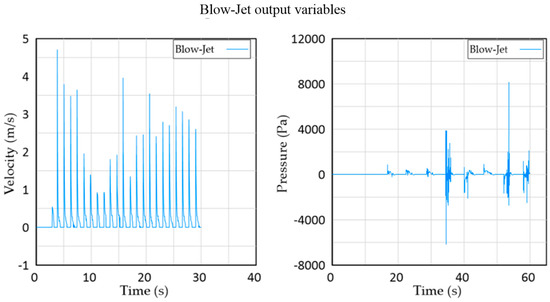
Figure 3. Water velocity (left) and pressure (right) at the Blow-Jet output.

One of the weaknesses of the Blow-Jet, as reported by [25], is the significant wave reflection at the entrance, and inside the device, which results in energy loss and a reduction in efficiency. The results obtained by Chávez are derived from laboratory tests. To facilitate the comparison between the 2010 experimental results and the present numerical data, it was carried out specifically regarding the maximum and mean velocities. The numerical modeling reproduced this phenomenon well in position and intensity, as seen in Figure 4.

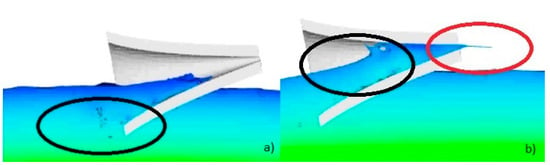
Figure 4. (a) Wave reflection at the inlet of the device (black ellipse); (b) wave breaking inside the device (black ellipse) and the jet at the outlet (red ellipse).

In Figure 4a the black ellipses indicate this wave reflection. This feature is one of the main points in improving the geometry of the existing device. In turn, the occurrence of this reflection in the numerical results is also evidence of its good performance. It is common in different fields, such as science, engineering, medicine, among others, to use numerical models and experimental, theoretical, and practical methods, which are based on assumptions that are considered more qualitatively than quantitatively. Figure 4b also evidences the production of the expelled jet from the output of the Blow-Jet.

2.2. Alternative Blow-Jet Geometries

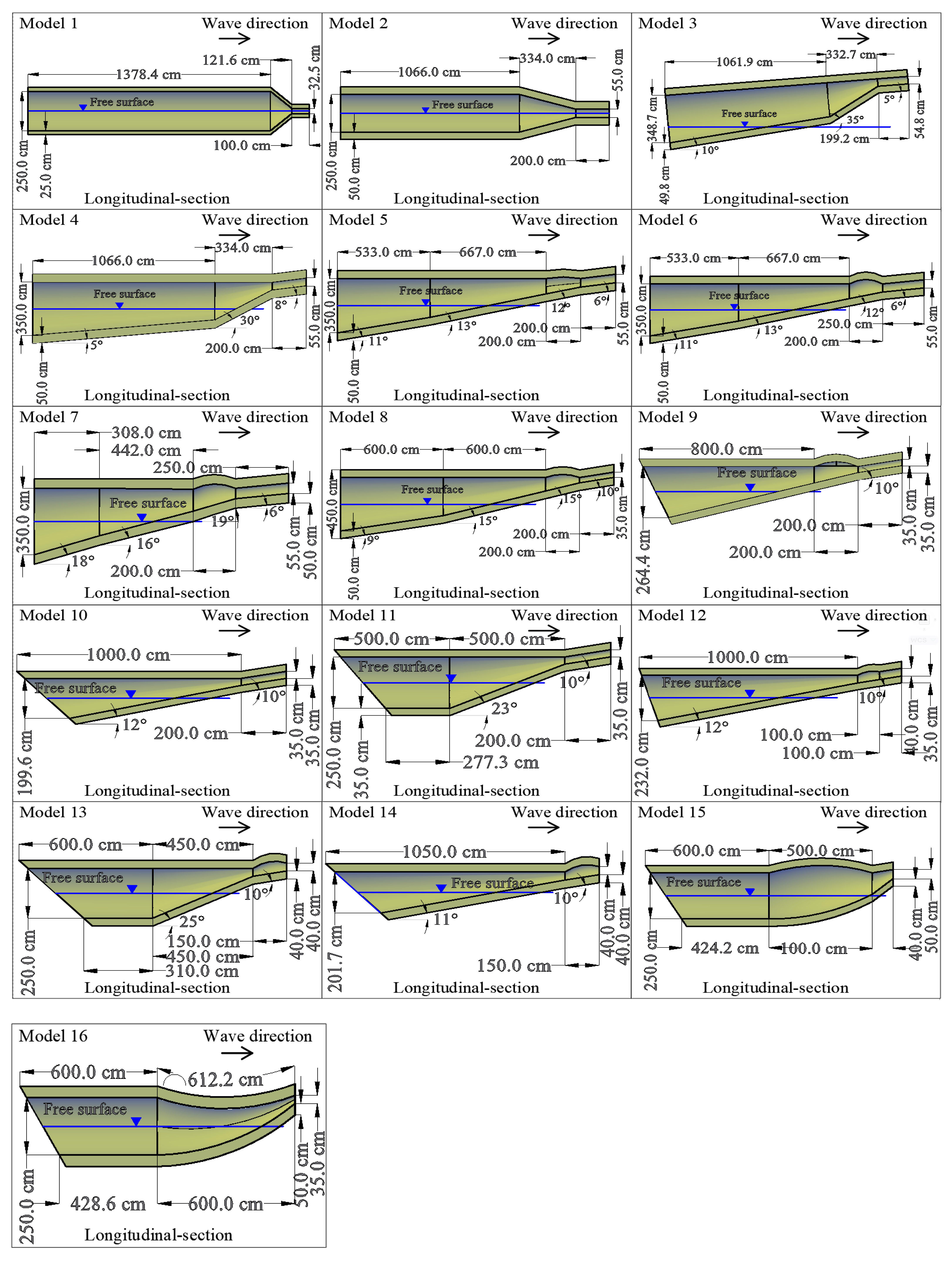
Sixteen geometries for the Blow-jet were proposed and numerically examined (sketches are presented in Appendix A). Based on the quantitative and qualitative analysis of the numerical results of each model and seeking possible causes for the observed deficiencies, changes in the device’s geometry were made to improve the performance. Some variables were set as fixed, such as the ratio of the input and output diameters which is always 6. In turn, the lengths of the devices are between one-third and one-fourth of the wavelength. The criteria used to ascertain that one geometry gave better performance than another were:

• Higher output velocities and pressures;
• Lower reflection at the entrance;
• No wave breaking inside the device.

All the devices tested had prototype dimensions (not at laboratory scale). Representative wave parameters for the Mexican coast were used, i.e., wave height of 2 m, wave period of 6 s, and still water depth of 10 m.

Figure 5 shows the water pressures at the device outlet for all the modeled geometries. Models 1, 2, 10, and 15 produce the highest values. It is worth noting that in models 1 and 2, the outlet was submerged. In turn, model 15 can be discarded as it only produced one pressure peak throughout the simulated time. Model 10 had the best performance, with a mean pressure of 119.7 Pa and with positive and negative peaks of irregular values.

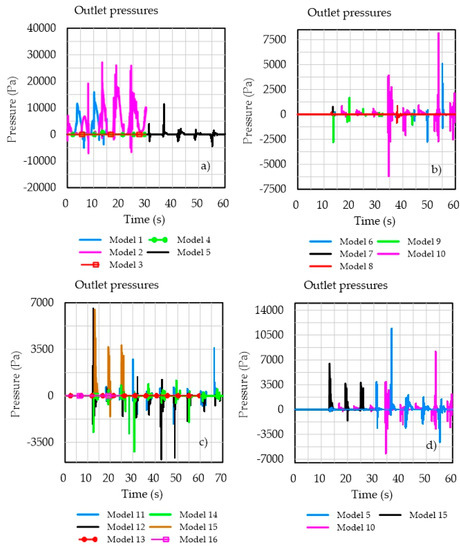
Figure 5. (a) The outlet pressure of the first 5 models, where the model with the highest-pressure values is highlighted in gray in the legend. In (b), the following 5 models are presented, also highlighting the best-performing one in gray. In (c), the last 6 models are shown, and in (d), the models with the highest values of (a–c) are presented, with the model with the highest outlet pressure values highlighted in yellow.

Figure 6 presents the velocities at the outlet for all the geometries. Models 5, 10, and 15 produced the highest values. The velocities of model 5 were less than 2.5 m/s and it had only one, very high, peak. Model 15 presents a regular occurrence of peaks of around 2.5 m/s alternating with gaps of null velocity. Model 10 produced an average velocity of 10 m/s with peaks of approximately 18.5 m/s.

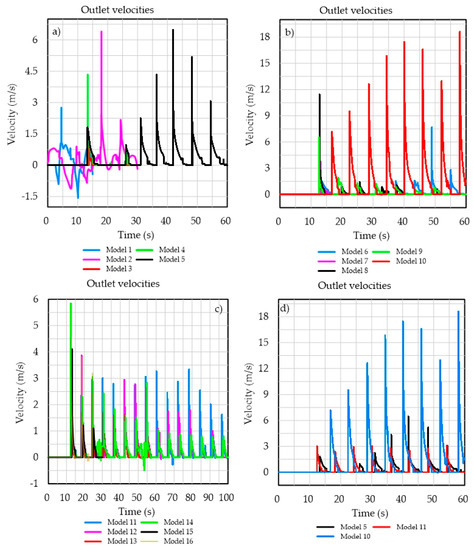
Figure 6. (a) The outlet velocity of models 1, 2, 3, 4, and 5; (b) models 6, 7, 8, 9, and 10; (c) models 11, 12, 13, 14, 15, and 16; (d) the models that exhibited the highest velocities in (a–c). The legends display the highest partial velocities in gray and the highest overall velocity in yellow.

There are also peaks in pressure for each wave period as it is an oscillatory motion; however, pressure is a scalar quantity and velocity is a vector quantity, so the software records these magnitudes differently. Probes in the numerical model record in any direction. Wave reflection cannot be completely eliminated even with activated attenuators. Depending on their position, some probes may register two values at the same time: one on the left side of the sensor and one on the right side. This occurs in scalar variables, and those quantities need to be separated for the statistical values to be representative.

In conclusion, model 10 had the highest average and point velocities and pressures. In addition, there was no reflection nor wave breaking inside the device, and the transit of the water towards the catchment area was rapid. The simulation showed adequate convergence. Therefore, model 10 was used for the experimental phase of this research. To assist in clarity, Figure 7 shows the velocity of the water jet and the pressure at the outlet of the device. Figure 8 is a snapshot of the simulation of model 10, showing the device full of water and the expelled jet.

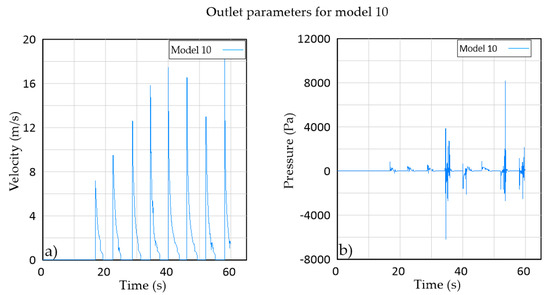
Figure 7. Water velocity showing the expelled peaks (a) and pressure at the outlet (b) for model 10.

Figure 8. Snapshots of model 10 during the numerical simulation. (a) When full of water, the device had minimized wave reflection, while the expelled water jet was maximum. (b) The emptying of the remaining water through the inlet diameter (larger diameter). (c) The transit of water inside the device.

3. Experimental Phase

3.1. Experimental Setup

An experimental program to reproduce and validate the numerical results was conducted. As with the numerical results, the variables of interest are the pressure and the water velocity at the outlet. The experiments were carried out in the wave flume of the Engineering Institute of the National Autonomous University of Mexico, which has dimensions of 37 m length, 0.8 m width, and 1.20 m height. The flume has a piston-type wave maker with an active wave absorption system. Representative wave parameters for the Mexican coast were used. These parameters are wave height (H) = 2 m, wave period (T) = 6 s, and the depth (d) was established at 10 m in order to be within the range of validity of second-order Stokes.

Model 10 was 3D-printed (Figure 9), in 1:20 scale, and instrumented with a Keller (London, UK) Druck PR-36X piezoresistive transmitter at the outlet. The velocity was recorded by an acoustic Doppler velocimeter (Vectrino, Rijeka, Croatia) and the water level by resistance wave gauges. The volume of the expelled jet was stored in a measuring probe, manually. The experimental setup is shown in Figure 10.

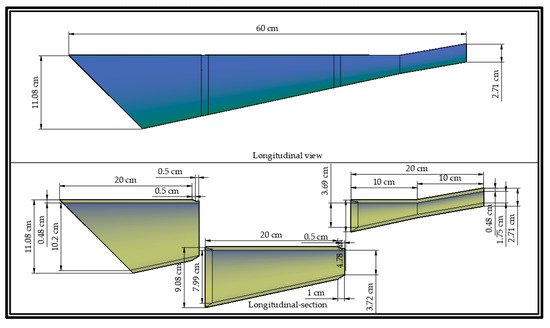
Figure 9. Longitudinal view of model 10 used in the laboratory tests (upper panel) and the various sections of this device (lower panel).

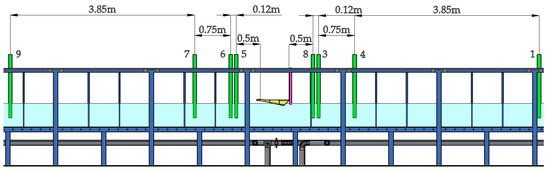
Figure 10. Experimental setup for the Blow-Jet tests.

Figure 11 shows aspects of the laboratory tests. Figure 11a shows the harness used to fix the device; in Figure 11b velocity measurements are being taken and the distance the jet reached is seen (blue circles) and the upper mounting of the device is shown in a yellow circle; and Figure 11c shows a pressure recording test. Velocity and pressure tests were conducted separately as the pressure transmitter blocks the output completely.

Figure 11. Images taken during the experimental tests. (a) Blow-Jet with its harness; (b) velocity test, showing the Blow-Jet output (yellow circle) and the distance reached by the jets (blue circles); (c) pressure recording test; and (d) panoramic view of the wave flume.

3.2. Experimental Methodology

A total of 26 tests were conducted, each repeated three times to record pressure, velocity, and the volume of the jet. Half of the tests were performed with regular waves and the other with irregular waves. The JONSWAP spectrum was used for irregular waves, while the 2nd-order Stokes theory was used for regular waves. Table 3 shows the test program.

Table 3. Laboratory tests performed.

Pressure, Velocity and Volume
Sensors	Test	Theory	H (m)	T (s)	d (m)	t (min)
8 level sensors 1 velocity sensor 1 pressure sensor	1	Stokes 2° order	0.10	1.34	0.5	30
	2	Stokes 2° order	0.10	1.34	0.5	30
	3	Stokes 2° order	0.12	1.40	0.5	30
	4	Stokes 2° order	0.12	1.60	0.5	30
	5	Stokes 2° order	0.12	1.80	0.5	30
	6	Stokes 2° order	0.12	2.00	0.5	30
	7	Stokes 2° order	0.10	2.00	0.5	30
	8	Stokes 2° order	0.10	1.60	0.5	30
	9	Stokes 2° order	0.10	1.80	0.5	30
	10	Stokes 2° order	0.10	2.24	0.5	30
	11	Stokes 2° order	0.10	2.68	0.5	30
	12	Stokes 2° order	0.12	2.24	0.5	30
	13	Stokes 2° order	0.12	2.68	0.5	30
	1	JONSWAP	0.10	1.34	0.5	30
	2	JONSWAP	0.10	1.34	0.5	30
	3	JONSWAP	0.12	1.40	0.5	30
	4	JONSWAP	0.12	1.60	0.5	30
	5	JONSWAP	0.12	1.80	0.5	30
	6	JONSWAP	0.12	2.00	0.5	30
	7	JONSWAP	0.10	2.00	0.5	30
	8	JONSWAP	0.10	1.60	0.5	30
	9	JONSWAP	0.10	1.80	0.5	30
	10	JONSWAP	0.10	2.24	0.5	30
	11	JONSWAP	0.10	2.68	0.5	30
	12	JONSWAP	0.12	2.24	0.5	30
	13	JONSWAP	0.12	2.68	0.5	30

3.3. Experimental Results

Figure 12 shows the pressures recorded at the outlet of the device for regular waves and irregular waves in the left and right boxes, respectively. For regular waves, the pressure is positively correlated to the wave period. The correlation is less clear for irregular waves, but the higher pressures correspond to the higher energy wave conditions.

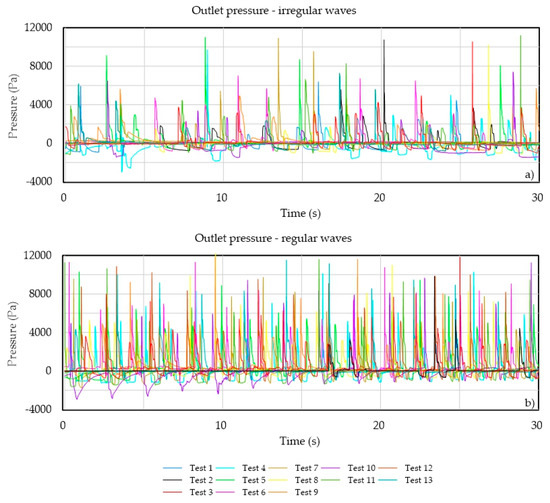
Figure 12. Water jet pressures at the outlet of the device under (a) regular waves and (b) irregular waves.

Figure 13 shows the velocities and flow rates averages of the water jet at the outlet of the device. The regular waves velocities range from 0.5 to 0.9 m/s, while for irregular waves they range from 0.12 to 0.5 m/s. The performance seems to be positively correlated to wave steepness.

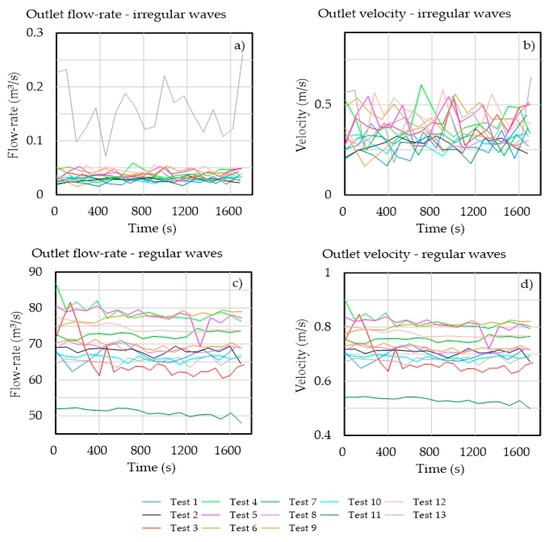
Figure 13. Velocity and flow rate averages of the water jet at the outlet of the device: (a,b) irregular waves and (c,d) regular waves.

4. Discussion

4.1. Comparison of Blow-Jet Hydrodynamic Performance

The results obtained from the numerical modeling for the original Blow-Jet and model 10 are compared in Figure 14. The comparison was made on a 1:1 prototype scale. The Froude condition was used to perform the hydrodynamic similarity; where gravity has a preponderance over viscous properties. Although the results in both are not as cyclical as expected, model 10 presents higher values.

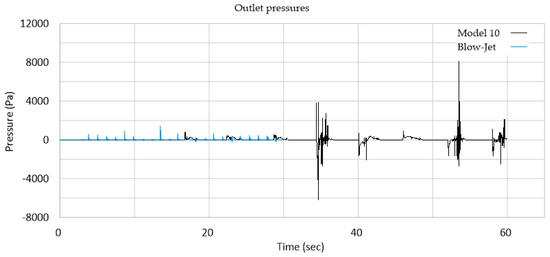
Figure 14. Outlet pressures for the original Blow-Jet and model 10.

The improved performance of model 10 is seen in the jet velocities, see Figure 15. Given that there will be times with no flux through the output, reaching higher velocities facilitates power generation. This can be aided by an inertial mechanical element (e.g., a flywheel). Therefore, it can be stated that the overall performance of model 10 is better than the original Blow-Jet.

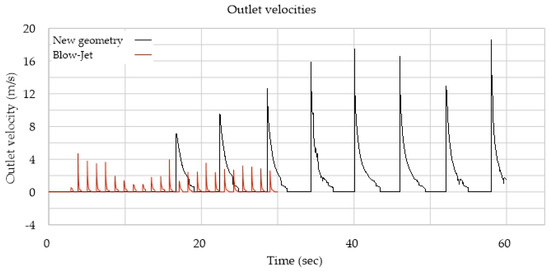
Figure 15. Water jet velocities at the outlet for the original Blow-Jet and model 10.

Table 4 presents the maximum outlet velocity (Vo max), average outlet velocity (Vo ave), maximum outlet pressure (Po max), and average outlet pressure obtained from the Blow-Jet and model 10 simulations.

Table 4. Velocities and pressures at the outlet of both devices in the numerical modeling.

Device	Vo max (m/s)	Vo ave (m/s)	Po max (Pa)	Po ave (Pa)
Original blow-Jet	4.7083	0.2184	1438.947	12.848
Model 10	18.5961	1.2229	8162.2822	119.741

4.2. Numerical Model Validation

Laboratory tests 1 and 2, under regular wave conditions (Table 3), were used for validation. The results of the numerical tests were scaled to a ratio of 20 to 1 and compared with the experimental data. To facilitate the comparison, the following adjustments were made: the maximum and minimum peaks were eliminated, the recording of the laboratory tests was shortened in time to match that of the numerical model, and the acquisition times of each piece of data was also matched to those of the numerical model, allowing the profiles to be compared. Figure 16, for example, shows the pressures at the outlet. A slight difference and phase shifts can be seen between the laboratory data and the Flow3D results; arguably due to the friction losses and vibration present in the laboratory tests. Nevertheless, a good correlation was found between both sets of data.

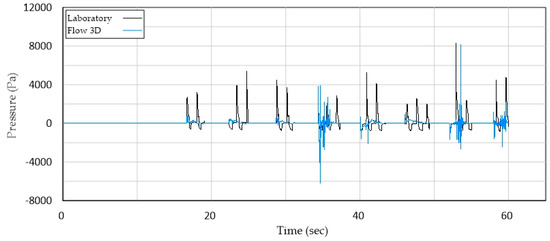
Figure 16. Laboratory and numerical model pressures.

The average (Po ave) and maximum (Po max) pressures at the outlet are given in Table 5. The maximum pressure in laboratory tests occurred at second 52.96, and for the numerical model, the maximum pressure occurred at second 53.56. The average pressure for both laboratory tests and the numerical model was determined using the bulk of the sample, from 0 to 60 s for the numerical model and from 0 to 1800 s for the laboratory tests.

Table 5. Average and maximum pressures at the outlet.

Analysis	Device	Po max (Pa)	Po ave (Pa)
Numeric model (FLOW-3D)	New geometry	8162.282	119.7418
Laboratory tests	New geometry	8320.820	111.2541

Figure 17 shows the comparison of numerical and experimental output velocities. The laboratory velocities were estimated as the ratio of jet volume to wave period. The experimental velocities are lower as they are average values. Furthermore, no phase shift is seen, as only the maximum value is valid because velocity increases and decreases are artificially distributed in time. Using this technique to estimate the velocity, information is lost at the peak of the signal. Even with the limitations mentioned, the numerical model represents the Blow-Jet performance sufficiently well, as seen in Table 6, where the average velocities are compared, and the values show the same order of magnitude. The difference between the experimental and numerical results (maximum and mean velocities and pressures at the outlet) is of 20%. Arguably, the difference is due to the oscillatory nature of the waves (including vibration during the experimental phase), uncertainty in the printing material roughness, and temporal inhomogeneity between the experimental and numerical records. Nevertheless, we can argue that both data are similar, and the simulations are valid.

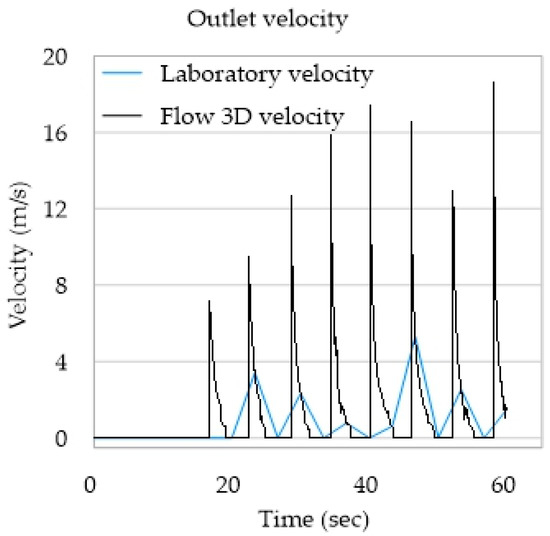
Figure 17. Laboratory and Flow 3D velocities at the outlet.

Table 6. Outlet velocity.

Analysis	Device	Vo ave (m/s)
Numerical model (FLOW-3D)	New geometry	0.73318
Laboratory tests	New geometry	0.707443

The comparison is based on the average velocity values, which have a coincidence rate above 80%. The average velocity was determined using raw data, without altering the sample size. Only the average velocity of the experimental phase was scaled. However, since the number of records and the duration of those records are not in the same order of magnitudes, a direct comparison of the trend lines is not significant.

4.3. Energy Production

To estimate the power production of the improved Blow-Jet, Table 7 shows the average and maximum power matrices for the small-scale and prototype models, considering the wave conditions tested in the laboratory. It is promising to see that the maximum power values are above 1 kW. The theoretical power [33] is determined using the maximum and average pressure and flow rate at the device’s outlet for both, the numerical and laboratory tests by Equation (2).

$$\mathrm{P}=\mathrm{p}\times \mathrm{Q}$$

(2)

Table 7. Average and maximum power (W) for various periods and wave heights of irregular wave.

Average Power Matrix (W), Irregular Waves
Laboratory Scale			Prototype Scale
Period (s)	Wave Height (m)		Period (s)	Wave Height (m)
	0.1	0.12		2	2.40
1.3	0.0008	N/A	6.0	28.66	N/A
1.4	N/A	0.0012	6.3	N/A	41.48
1.6	0.0003	0.0004	7.2	11.67	13.73
1.8	0.0006	0.0015	8.0	20.01	52.39
2	0.0004	0.0014	8.9	13.40	48.68
2.2	0.0002	0.0016	10.0	7.10	56.57
2.7	0.0002	0.0062	12.0	6.78	222.18
Maximum Power Matrix (W), Irregular Waves
Laboratory Scale			Prototype Scale
Period (s)	Wave Height (m)		Period (s)	Wave Height (m)
	0.1	0.12		2	2.40
1.3	0.0199	N/A	6.0	710.03	N/A
1.4	N/A	0.0339	6.3	N/A	1213.01
1.6	0.0172	0.0398	7.2	617.21	1424.52
1.8	0.0173	0.0311	8.0	619.11	1111.95
2	0.0201	0.0318	8.9	722.02	1137.05
2.2	0.0210	0.0406	10.0	752.40	1452.88
2.7	0.0346	0.1891	12.0	1238.44	6767.29

5. Conclusions

Technological development is usually an iterative process. Proven concepts need to be habitually tested and re-tested experimentally and numerically, even when close to the optimal or desirable performance. This is the case in the development of the Blow-Jet, a WEC that has been revisited twice and improved in the present work. The results of such numerical and experimental tests were presented.

The comparison of the numerical model and the experimental tests show that the average and maximum pressure values at the outlet of the device are computed with less than 10% of relative error. In turn, the velocities show less than a 5% error. These figures lead us to conclude that the numerical model results are valid and that further improvements can be performed only numerically. They also allow more robust scenarios to be designed, where spatial and physical parameters can easily be varied and quickly move between the validity ranges of the same model.

The geometry proposed here for the WEC (model 10) stems from reducing the reflection at the inlet, maximizing velocities and pressures at the outlet, and avoiding wave breaking inside the device. An additional aim was to reduce the size of the Blow-Jet. to give improved maneuverability over its predecessor. An extensive array of Blow-Jets must be installed together for this type of technology to attract investors.

Energy generation from renewable sources requires large farms to be profitable. Therefore, it is recommended that future work determine the minimum separation radii between devices to avoid reflection, refraction, diffraction, and even breakage, all of which would affect the overall performance of a Blow-Jet-based electric plant.

The present study is limited to unidirectional waves, the influence of wave direction and spreading will be investigated in the near future.