Optimisation of a Gas-Lifted System with Nonlinear Model Predictive Control
Abstract
1. Introduction
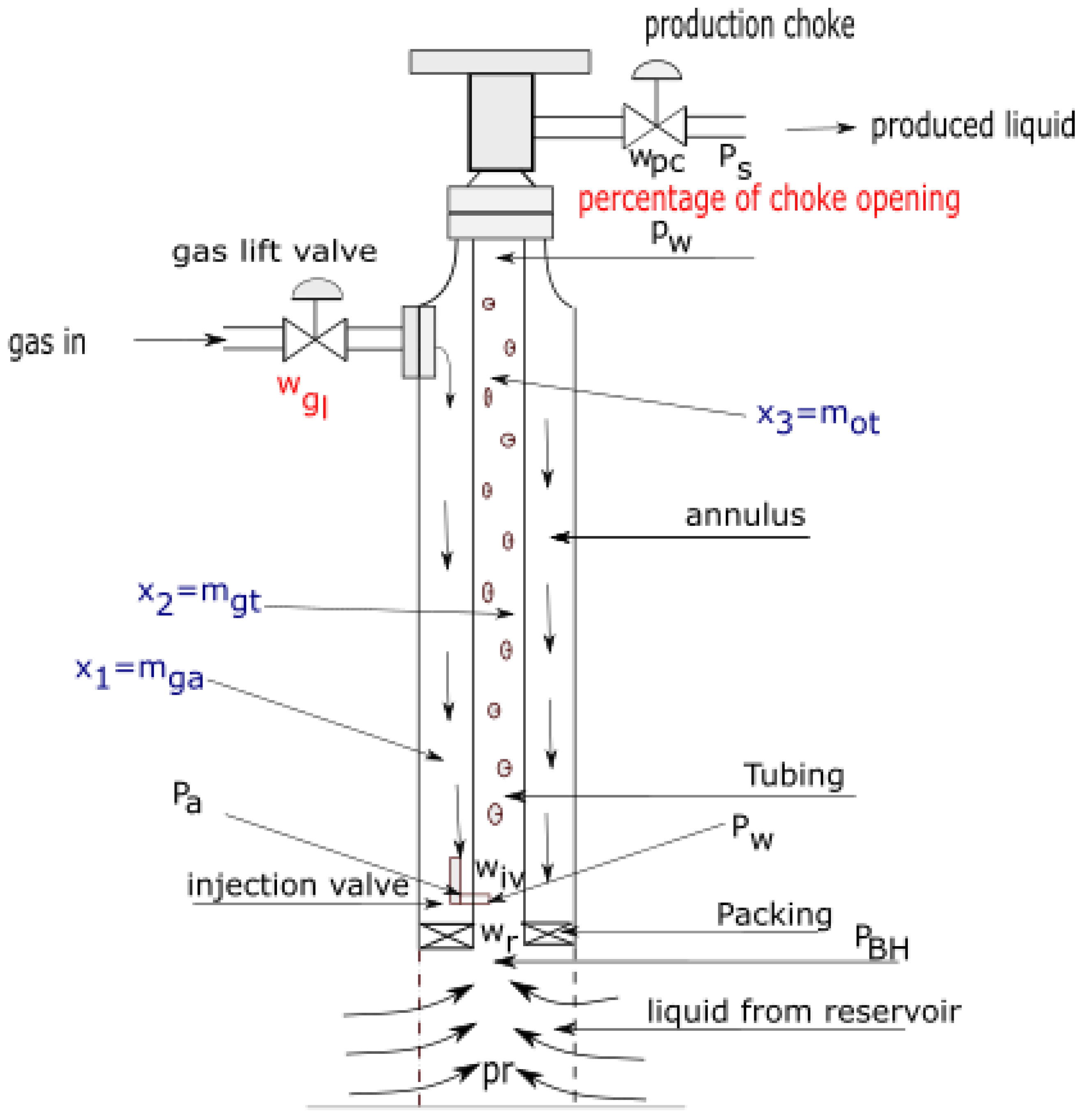
2. Gas-Lifted System: Models and Analysis
2.1. Gas-Lifted System Models
2.2. The Stable and Unstable Gas-Lifted System
2.3. Bifurcation
2.4. Linearised Gas-Lifted System
3. Terminal Equality-Constrained Nonlinear Model Predictive Control (NMPC) with Input Target and Control Zones
3.1. Recursive Feasibility
3.2. Convergence
4. Stabilisation of Gas-Lifted System Using Terminal Inequality Constrained NMPC with Input Target and Control Zones
4.1. Undisturbed Gas-Lifted Well Stabilization Using NMPC with Input within Bound: One Input Case
4.2. Undisturbed Gas-Lifted Well Stabilisation Using Terminal Equality Constrained NMPC with Input out of Bound: One Input Case
4.3. Disturbed Gas-Lifted Well Stabilisation Using NMPC with Input within Bound: One Input Case
4.4. Disturbed Gas-Lifted System Stabilisation Using Terminal Equality Constrained NMPC Having Input within Bound: Two Input Case
4.5. Compare with PI Controller
4.6. Comments on Validation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Khamehchi, E.; Mahdiani, M.R. Gas Allocation Optimization Methods in Artificial Gas Lift; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Fanchi, J.R.; Christiansen, R.L. Introduction to Petroleum Engineering; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Abu Bakar, A.I.; Ali Jabris, M.Z.; Abd Rahman, H.; Abdullaev, B.; Idris, K.N.; Kamis, A.A.; Yusop, Z.; Kok, J.C.; Kamaludin, M.F.; Zakaria, M.Z.; et al. CO2 Tracer Application to Supplement Gas Lift Optimisation Effort in Offshore Field Sarawak. In Proceedings of the SPE Asia Pacific Oil and Gas Conference and Exhibition, Brisbane, Australia, 23–25 October 2018. [Google Scholar]
- Khurshid, I.; Fujii, Y.; Choe, J. Analytical model to determine CO2 injection time in a reservoir for optimizing its storage and oil recovery: A reservoir compaction approach. J. Pet. Sci. Eng. 2015, 135, 240–245. [Google Scholar] [CrossRef]
- Khurshid, I.; Choe, J. An analytical model for dissolution of deposited asphaltene during CO2 injection from the porous media. Int. J. Oil Gas Coal Technol. 2018, 18, 338–352. [Google Scholar] [CrossRef]
- Mohd Khalil, M.I.; Chang, C.L.; Amran, A.; Kok, J.C. A Game Changer Data Acquisition Technology: Field Wide Gaslift Optimization through the Application of Welltracer Technology in a Mature Offshore Field. In Proceedings of the SPE Annual Technical Conference and Exhibition, Bali, Indonesia, 29–31 October 2019. [Google Scholar]
- Brown, K.E. Overview of artificial lift systems. J. Pet. Technol. 1982, 34, 2384–2396. [Google Scholar] [CrossRef]
- Plucenio, A.; Pagano, D.J.; Camponogara, E.; Traple, A.; Teixeira, A. Gas-lift optimization and control with nonlinear mpc. IFAC Proc. Vol. 2009, 42, 904–909. [Google Scholar] [CrossRef]
- Gas Lift Market Research. Available online: https://dataintelo.com/report/global-gas-lift-market/ (accessed on 16 March 2023).
- Hunt, J. Petroleum geochemistry and geology (textbook). In Petroleum Geochemistry and Geology (Textbook), 2nd ed.; WH Freeman Company: New York, NY, USA, 1995. [Google Scholar]
- Kak, A.; Meng, W.; Carnahan, N.F. Flow Assurance. In Encyclopedia of Maritime and Offshore Engineering; Wiley: Hoboken, NJ, USA, 2017; pp. 1–15. [Google Scholar]
- Jahanshahi, E. Control Solutions for Multiphase Flow: Linear and Nonlinear Approaches to Anti-Slug Control. Ph.D. Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 2013. [Google Scholar]
- Feng, J. Reliability Evaluation for a Subsea TO Shore Production System. Ph.D. Thesis, Universidade Federal do Rio de Janeiro, Rio de Janeiro, Brazil, 2017. [Google Scholar]
- Xu, Z.; Golan, M. Criteria for Operation Stability of Gas Lift; SPE paper no. 19362; Society of Petroleum Engineers: Richardson, TX, USA, 1989. [Google Scholar]
- Aamo, O.M.; Eikrem, G.O.; Siahaan, H.B.; Foss, B.A. Observer design for multiphase flow in vertical pipes with gas-lift—Theory and experiments. J. Process Control 2005, 15, 247–257. [Google Scholar] [CrossRef]
- Bin, H.; Golan, M. Gas-lift instability resulted production loss and its remedy by feedback control: Dynamical simulation results. In Proceedings of the SPE International Improved Oil Recovery Conference in Asia Pacific, Kuala Lumpur, Malaysia, 20–21 October 2003. [Google Scholar]
- Eikrem, G.O.; Foss, B.; Imsland, L.; Hu, B.; Golan, M. Stabilization of gas lifted wells. IFAC Proc. Vol. 2002, 35, 139–144. [Google Scholar] [CrossRef]
- Eikrem, G.O.; Aamo, O.M.; Foss, B.A. On instability in gas lift wells and schemes for stabilization by automatic control. SPE Prod. Oper. 2008, 23, 268–279. [Google Scholar] [CrossRef]
- Blick, E.; Boone, L. Stabilization of naturally flowing oil wells using feedback control. In Proceedings of the SPE California Regional Meeting, Oakland, CA, USA, 2–4 April 1986. [Google Scholar]
- Der Kinderen, W.; Dunham, C.; Poulisse, H. Real-time artificial lift optimization. In Proceedings of the Abu Dhabi International Petroleum Exhibition and Conference, Abu Dhabi, United Arab Emirates, 11 November 1998. [Google Scholar]
- Eikrem, G.O.; Imsland, L.; Foss, B. Stabilization of Gas Lifted Wells Based on State Estimation. IFAC Proc. Vol. 2004, 37, 323–328. [Google Scholar] [CrossRef]
- Scibilia, F.; Hovd, M.; Bitmead, R.R. Stabilization of gas-lift oil wells using topside measurements. IFAC Proc. Vol. 2008, 41, 13907–13912. [Google Scholar] [CrossRef]
- Jansen, B.; Dalsmo, M.; Nøkleberg, L.; Havre, K.; Kristiansen, V.; Lemetayer, P. Automatic control of unstable gas lifted wells. In Proceedings of the SPE Annual Technical Conference and Exhibition, Houston, TX, USA, 3–6 October 1999. [Google Scholar]
- Heath, J.A.; Kookos, I.K.; Perkins, J.D. Process control structure selection based on economics. IFAC Proc. Vol. 2012, 45, 93–100. [Google Scholar] [CrossRef]
- Jahanshahi, E.; Skogestad, S.; Hansen, H. Control structure design for stabilizing unstable gas-lift oil wells. IFAC Proc. Vol. 2012, 45, 93–100. [Google Scholar] [CrossRef]
- Shi, J.; Al-Durra, A.; Errouissi, R.; Boiko, I. Stabilization of artificial gas-lift process using nonlinear predictive generalized minimum variance control. J. Frankl. Inst. 2019, 356, 2031–2059. [Google Scholar] [CrossRef]
- Martin, P.A.; Odloak, D.; Kassab, F. Robust model predictive control of a pilot plant distillation column. Control Eng. Pract. 2013, 21, 231–241. [Google Scholar] [CrossRef]
- Capron, B.D.O.; Odloak, D. A robust LQR-MPC control strategy with input constraints and control zones. J. Process Control 2018, 64, 89–99. [Google Scholar] [CrossRef]
- Allgöwer, F.; Findeisen, R.; Nagy, Z.K. Nonlinear model predictive control: From theory to application. J. Chin. Inst. Chem. Eng. 2002, 35, 299–315. [Google Scholar]
- Diehl, F.C.; Almeida, C.S.; Anzai, T.K.; Gerevini, G.; Neto, S.S.; Von Meien, O.F.; Campos, M.C.; Farenzena, M.; Trierweiler, J.O. Oil production increase in unstable gas lift systems through nonlinear model predictive control. J. Process Control 2018, 69, 58–69. [Google Scholar] [CrossRef]
- Haaland, S.E. Simple and explicit formulas for the friction factor in turbulent pipe flow. J. Fluids Eng. 1983, 105, 89–90. [Google Scholar] [CrossRef]
- Rossiter, J.A. Model-Based Predictive Control: A Practical Approach; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Krishnamoorthy, D.; Foss, B.; Skogestad, S. Steady-state real-time optimization using transient measurements. Comput. Chem. Eng. 2018, 115, 34–45. [Google Scholar] [CrossRef]
- Nikoukhah, R. A new methodology for observer design and implementation. IEEE Trans. Autom. Control 1998, 43, 229–234. [Google Scholar] [CrossRef]
- Adukwu, O.; Odloak, D.; Junior, F.K. Stabilization of Artificial Gas Lift System Using Nonlinear Model Predictive Control with input Target and Control Zones. In Proceedings of the 2020 IEEE Congreso Bienal de Argentina (ARGENCON), Resistencia, Argentina, 1–4 December 2020; pp. 1–7. [Google Scholar]
- Simon, D. Optimal State Estimation: Kalman, H Infinity, and Nonlinear Approaches; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Rashid, K.; Demirel, S.; Couët, B. Gas-lift optimization with choke control using a mixed-integer nonlinear formulation. Ind. Eng. Chem. Res. 2011, 50, 2971–2980. [Google Scholar] [CrossRef]
- Klan, P.; Gorez, R. On aggressiveness of PI control. IFAC Proc. Vol. 2005, 38, 355–360. [Google Scholar] [CrossRef]

















Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Adukwu, O.; Odloak, D.; Kassab, F., Jr. Optimisation of a Gas-Lifted System with Nonlinear Model Predictive Control. Energies 2023, 16, 3082. https://doi.org/10.3390/en16073082
Adukwu O, Odloak D, Kassab F Jr. Optimisation of a Gas-Lifted System with Nonlinear Model Predictive Control. Energies. 2023; 16(7):3082. https://doi.org/10.3390/en16073082
Chicago/Turabian StyleAdukwu, Ojonugwa, Darci Odloak, and Fuad Kassab, Jr. 2023. "Optimisation of a Gas-Lifted System with Nonlinear Model Predictive Control" Energies 16, no. 7: 3082. https://doi.org/10.3390/en16073082
APA StyleAdukwu, O., Odloak, D., & Kassab, F., Jr. (2023). Optimisation of a Gas-Lifted System with Nonlinear Model Predictive Control. Energies, 16(7), 3082. https://doi.org/10.3390/en16073082






