Abstract
The predictions of turbulent burning velocity parameterizations for non-unity Lewis number flames have been assessed based on a single-step chemistry Direct Numerical Simulation (DNS) database of premixed Bunsen flames for different values of characteristic Lewis numbers ranging from 0.34 to 1.2. It has been found that the definition of the turbulent burning velocity is strongly dependent on the choice of projected flame brush area in the Bunsen burner configuration. The highest values of normalized turbulent burning velocity are obtained when the projected flame brush area is evaluated using the area of the isosurface of the Reynolds averaged reaction progress variable of 0.1 out of different options, namely the Favre averaged and Reynolds averaged isosurfaces of reaction progress variable of 0.5 and integral of the gradient of Favre and Reynolds averaged reaction progress variable. Because of the axisymmetric nature of the mean flame brush, the normalized turbulent burning velocity has been found to decrease as the burned gas side is approached, due to an increase in flame brush area with increasing radius. Most models for turbulent burning velocity provide comparable, reasonably accurate predictions for the unity Lewis number case when the projected flame brush area is evaluated using the isosurface of the Reynolds averaged reaction progress variable of 0.1. However, most of these parameterizations underpredict turbulent burning velocity values for Lewis numbers smaller than unity. A scaling relation has been utilized to extend these parameterizations for non-unity Lewis numbers. These revised parameterizations have been shown to be more successful than the original model expressions. These modified expressions also exhibit small values of L2-norm of the relative error with respect to experimental data from literature for different Lewis numbers, higher turbulence intensity and thermodynamic pressure levels.
1. Introduction
Due to threats of climate change, countries and industries are searching for cleaner and efficient ways of generating energy. Although renewable forms of energy exist, these have their own drawbacks, such as the intermittent generation of energy for wind and solar. Unless and until more efficient methods to store such energy are devised, it is very likely that combustion will remain the principal mode of energy production. Premixed combustion, in which reactants are homogenously mixed, is a good way to reduce the emission of pollutants as it limits the chances of incomplete combustion. Moreover, it is easier to control NOx emissions by optimizing between the peak temperature achieved and power produced. This can be done by either controlling the temperature or the composition of the reactants. The emission of greenhouse gases such as CO2 can also be reduced by using a premixed combustion of fuels such as hydrogen, ammonia or syngas. Net zero targets by governments can be achieved by the application of low/zero-carbon fuels such as biofuel, hydrogen and ammonia, as proposed by contemporary scenario plans [1].
The application of pure hydrogen enables combustion with the complete elimination of carbon-based greenhouse gas emission [1]. However, the thermochemistry of hydrogen combustion is significantly different from that of hydrocarbon fuels [2], and the presence of lighter chemical species induces significant effects of differential diffusion. This, in turn, impacts upon practical operational burner characteristics such as (i) variations in flame stability maps and (ii) susceptibility to premature combustion (knocking) and flashback. As most existing combustion devices are designed to operate based on hydrocarbon fuels, the switch from hydrocarbon to hydrogen fuel will happen gradually and, in the interim period, hydrogen is expected to be blended in fixed proportions with hydrocarbon fuel to enable a transitional reduction in greenhouse gas emissions. The presence of H2 in the fuel induces a significant amount of differential diffusion of heat and species due to the non-unity Lewis number. Thus, the non-unity Lewis number effects cannot be ignored in the premixed combustion of High-Hydrogen-Content (HHC) fuels.
It has been shown in several previous analytical [3,4,5,6], experimental [7,8,9,10] and computational [11,12,13,14,15,16,17,18] studies that the turbulent burning velocity in premixed turbulent flames increases with decreasing characteristic Lewis number. As turbulent burning velocity is one of the most important quantities in the modelling of turbulent premixed combustion [7,8,9,19,20,21,22], it is important to consider the modelling of in response to the variations of the characteristic Lewis number. However, a universal scaling law for the turbulent flame speed is yet to be reported [23] and is still a subject of current research. Bray and Cant [24] pointed out that the is proportional to the product of the flame brush thickness and the maximum of the flame surface density multiplied by the stretch factor . These quantities in turn depend on the turbulence structure and the thermophysical properties of the fuel. Often a quadratic scaling of turbulent burning velocity in terms of turbulence intensity is assumed [23]. However, upon onset of the hydro-dynamic instability, a sub-unity scaling exponent for turbulence intensity is reported [23]. Similarly, Kobayashi et al. [25] suggested a correlation of turbulent burning velocity in terms of pressure and turbulence intensity. Driscoll [26] argued that for an ideal geometry independent turbulent flame, would be expected to be a function of the normalized turbulence intensity and integral length scale as well as the turbulent Markstein number. Further, Driscoll [26] pointed out that for real flames, the wrinkling has a memory effect which will make the functional relationship more complicated. A variety of experimental and numerical data and empirical formulations are discussed in a review article [26]. A rather complex formulation based on measured turbulent burning velocities has been suggested by Filatyev et al. [27] which also provides a fit to the nonlinear bending observed for high turbulence intensities. An important ingredient for this formulation was to include the mean flow velocity and the burner width. The turbulent bending effect has been discussed by several authors, and the reader is referred to [28,29] for further information in this regard. Both the Markstein length and the thermophysical properties, related to the Lewis number of the flame, play an important role. In this respect, it is worth noting that most existing parameterizations of turbulent burning velocity [7,8,9,19,20,21,22] have been proposed for unity Lewis number conditions where the differential diffusion of heat and mass was ignored.
As reactants are composed of different gases with different Lewis numbers, it is difficult to estimate a characteristic mixture Lewis number. However, different methods of estimation of the characteristic Lewis number have been proposed, such as equating the Lewis number of the reactant with the least concentration [30,31], calculating it from measurements made of the heat release rate [8], by numerically estimating it from binary diffusion theory for mixtures [32] or by individually calculating the thermal conductivity and mass diffusivity based on the mole fraction of the constituent species [33]. Bechtold and Matalon [31] have suggested that the mixture Lewis number can be calculated as: where with for and being the equivalence ratio, Heaviside function and Zel’dovich number, respectively. Subscripts F and O are used for fuel and oxidizer, respectively. The present analysis employs the concept of characteristic Lewis number to analyse the effects of on the turbulent burning velocity using simple chemistry DNS data of Bunsen burner flames.
To date, most of the turbulent burning velocity parameterizations [7,8,9,19,20,21,22] have been proposed for unity Lewis number conditions and therefore disregard the effects of differential diffusion of heat and species. The performance and applicability of these parameterizations in the flames with the non-unity characteristic Lewis number are yet to be assessed in detail. The present analysis addresses this gap in the literature by considering a DNS database of turbulent premixed Bunsen burner flames with a non-unity characteristic Lewis number to assess the performance of existing parameterizations [7,8,9,19,20,21,22]. The turbulent burning velocity can be defined in terms of the volume-integral in the following manner [34]:
where is the reaction rate of reaction progress variable , is the unburned gas density and is the projected flame brush area in the direction of mean flame propagation. The evaluation and definition of gives rise to uncertainties to the evaluation of the turbulent burning velocity , and the impact of evaluation on will be assessed in this analysis by employing different methodologies to extract the projected flame surface area . In this respect, the main objectives of this analysis are:
- (a)
- To assess the performances of the existing parameterizations of turbulent burning velocity for turbulent premixed flames with characteristic Lewis numbers significantly different from unity.
- (b)
- To illustrate the impact of the projected flame brush surface area evaluation on turbulent burning velocity for turbulent Bunsen burner flames with different characteristic Lewis numbers.
The rest of the paper will be organized as follows. The mathematical background and numerical implementation pertaining to the current analysis are presented in Section 2 and Section 3 of this paper. The results will be presented in Section 4 of this paper, and finally, the main findings are summarized and conclusions are drawn in Section 5.
2. Mathematical Background
The present analysis deals with the integral quantities such as volume-integrated burning rate and flame surface area, which can be captured reasonably accurately by single-step chemistry. It was shown elsewhere [35,36] that the flame propagation statistics extracted from single-step chemistry DNS is qualitatively similar to that obtained for detailed chemistry DNS and the quantitative differences are of the same order of uncertainty associated with different definitions of reaction progress variable . Thus, a single-step chemistry has been considered in this analysis in the interest of computational economy and to identify the effects of the characteristic Lewis number in isolation. In the context of simple chemistry, the reactive scalar field can be described with the help of reaction progress variable and non-dimensional temperature , which are defined as:
where is the mass fraction of species based on which reaction progress variable is defined, the subscripts u and b are used to refer to the values in the unburned gas and burned gas, respectively, and is the adiabatic flame temperature. Accordingly, the reaction rate of the reaction progress variable is defined as:
In the context of Reynolds Averaged Navier–Stokes (RANS) simulations, the mean reaction rate can be modelled in the following manner for high values of Damköhler number (i.e., ) [37]:
Here, , and are the Reynolds averaged, Favre averaged and Favre fluctuation of a general quantity . In Equation (4), is the scalar dissipation rate based on Favre fluctuations of reaction progress variable, is the reaction progress variable diffusivity and is a thermochemical parameter with being the burning mode probability density function, and the subscript ‘Lam’ refers to the unstretched laminar flame quantities. It was discussed by Bray [37] that the assumption of any continuous function for is sufficient for the evaluation of . Although Equation (4) was originally proposed for flames, it was demonstrated subsequently by Chakraborty and Cant [17] that this relation holds in an order of magnitude sense for the flames with . However, the scalar dissipation rate is an unclosed quantity and based on the leading order balance of the terms of the transport equation of under for unity Lewis number conditions, Kolla et al. [22] proposed the following algebraic closure of scalar dissipation rate:
where , and are the model parameters, is the local Damköhler number, is the local Karlovitz number with and being the thermal flame thickness, turbulent kinetic energy and its dissipation rate, respectively. In Equation (5), is a thermochemical parameter [22] with being the velocity vector.
Equations (4) and (5) can be utilized to obtain the turbulent burning velocity using the Kolmogorov–Petrovski–Piskunov (KPP) theorem [38,39,40]:
where is the eddy kinematic viscosity with , and is the turbulent Schmidt number, which is of the order of unity. Equation (6) upon using Equations (4) and (5) yields the following expression for [22]:
where and are used and these values are understood to be taken at the leading edge of the flame brush. It has been shown elsewhere (Ref. [22]) that the predictions of Equation (7) compare well with experimental data [7,41,42,43] for for premixed flames with a characteristic Lewis number close to unity.
For the sake of completeness, it is useful to consider the other well-known parameterizations of [7,8,9,19,20,21,22]. Peters [19] proposed the following expression for based on the leading order balance of the strain rate, kinetic restoration and molecular dissipation of flame surface ratio transport equation in the context of the level-set method:
where is the Zel’dovich flame thickness with being the unburned gas thermal diffusivity. It is worth noting that Equation (8) is obtained as a positive meaningful root of a quadratic equation, and thus, it is not physically meaningful to modify any model parameters and length scales in isolation in this model expression.
Gülder [20] proposed a parameterization of based on a large volume of experimental findings in the following manner:
Zimont [21] also proposed a similar expression given by:
It is important to note that the parameterizations in Equations (7)–(10) are proposed for unity Lewis number conditions, and they do not explicitly account for non-unity Lewis number effects. Moreover, is implicitly assumed in these parameterizations, but this relation is only approximately valid for statistically planar unity Lewis number flames and is rendered invalid for non-unity Lewis number conditions.
Bradley [44] proposed a parameterization of including the non-unity Lewis number and stretch rate effects in the following manner based on experimental findings:
The model expressions provided above are summarised in Table 1 for convenience. For statistically planar flames in a canonical configuration, there is no ambiguity in terms of the evaluation of because it is the cross-section of the simulation domain [45]. It is important to appreciate that the experimental evaluations of and are not always straightforward [45]. It has been discussed recently that can be estimated accurately from DNS data using the following expression [45]:

Table 1.
Summary of normalized turbulent burning velocity model expressions.
However, the evaluation of gives rise to several possibilities. It is possible to evaluate in the following manner:
Another alternative expression for can be obtained as:
Experimental investigations often considered the area of and 0.5 isosurfaces for the evaluation of [25,41,46,47,48]:
Borrowing the same concept, could alternatively be calculated based on the area of and 0.5 isosurfaces as:
The implications of the assumptions of the evaluation of using Equations (12)–(16) and the performances of parameterizations based on Equations (7)–(11) will be assessed based on DNS data in Section 4 of this paper. It is worth noting that the turbulent burning velocity in Bunsen flames is often evaluated by using a conventional flame angle method (see Ref. [9] and references therein), which attempts to identify based on the contour of or in the evaluation of . This approach is equivalent to definitions given by Equations (15) and (16). However, the assumption of conical shape due to curvature at the flame tip and estimation of the flame angle based on the tangent to the or contour introduces additional uncertainties in experimental measurements.
3. Numerical Implementation
A DNS database of turbulent premixed Bunsen flames with characteristic Lewis numbers and 1.2 has been considered in this analysis. The simulations have been conducted using a well-known 3D compressible DNS code SENGA+ [49] where all the spatial derivatives for internal grid points are evaluated using a 10th-order central difference scheme, but the order of accuracy gradually drops to a one-sided 2nd-order scheme at the non-periodic boundaries [49]. An explicit 3rd-order low-storage Runge-Kutta scheme [50] is employed for the time-advancement using a generic single-step Arrhenius type irreversible reaction. For the purpose of an extensive parametric analysis in SENGA+, governing equations of mass, momentum, energy and reaction progress variable are solved in non-dimensional form which are provided elsewhere [51]. The simulation domain is taken to be a cube with each side of where is the diameter of the nozzle, and a schematic diagram of the computational domain is presented in Figure 1a. The normalized mean inflow velocity , normalized root-mean-square inlet velocity and normalized integral length scale of turbulence (i.e., and ) and the grid size along with inlet values of bulk Reynolds number , Damköhler number and Karlovitz number are listed in Table 2 where is the integral length scale of turbulence, and is the thermal flame thickness. The grid spacing is sufficient to resolve the thermal flame thickness and the Kolmogorov length scale for all cases considered here. The simulations have been carried out for different values of characteristic Lewis number of the mixture (i.e., , 0.6, 0.8, 1.0 and 1.2). For the purpose of isolating the effects of , the Zel’dovich number (=6.0) and heat release parameter (=4.5) are kept unaltered for all cases where and are the activation temperature, unburned gas temperature and adiabatic flame temperature, respectively. The Prandtl number and the ratio of specific heats assume standard values (i.e., and . All the cases in Table 2 nominally represent the flamelets regime combustion [52], and their position on Borghi–Peters diagram is shown in Figure 1b. The Lewis number 0.34 case is representative of a lean hydrogen–air mixture of equivalence ratio of 0.40. The Lewis number 0.6 and 0.8 cases are representative of hydrogen-blended methane–air mixtures (e.g., 20% and 10% (by volume) hydrogen blended methane–air flames with overall equivalence ratio of 0.6), and the Lewis number 1.2 case is representative of a hydrocarbon–air mixture involving a hydrocarbon fuel which is heavier than methane (e.g., ethylene–air mixture with equivalence ratio of 0.7) [9,10,33,53]. In the case, the inlet velocity was increased from to to avoid flashback, which led to an increase in [51].
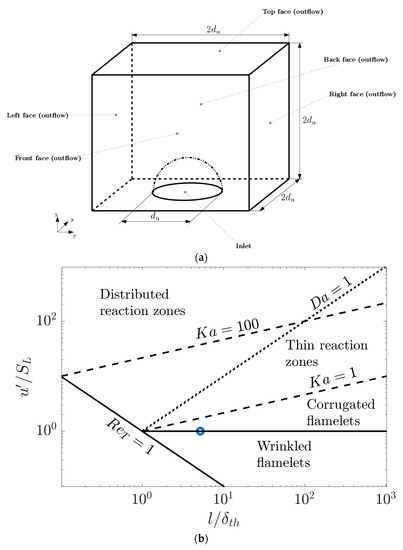
Figure 1.
(a) Schematic diagram of the computational domain; (b) position of the cases on Borghi–Peters diagram.

Table 2.
The turbulence inlet flow parameters for the considered cases.
A mean velocity distribution with a hyperbolic tangent-like profile is used for the inlet boundary condition. The digital filter-based method uses filtered random data in order to obtain realistic pseudo-turbulent velocity correlations [54]. In order to overcome the efficiency problems related to the generation of synthetic turbulent inflow data on large-sized distributed grids, several modifications have been implemented: (a) the Gaussian filter in temporal space in this process was substituted by an autoregressive AR1 process requiring only two time levels; (b) the two-dimensional filter kernel after (a) is replaced by the tensor product of two one dimensional filters, which reduces the cost of the filtering operation for a single grid point from to , where is the number of grid points related to the length of the filter in one direction; (c) identical random seeds for generating inflow data in buffer regions that overlap with neighbouring local domains are used, which avoids the necessity of message passing communications; (d) instead of filtering the inflow data for each local domain located in the inflow plane with its allocated CPU, the filtering is done by all available processors. These measures provide an efficient generation of inflow data which takes the order of 1% of the time required for advancing one time step.
All boundaries apart from the one containing the inlet are taken to be partially non-reflecting outflow and are specified using the Navier–Stokes Characteristic Boundary Conditions (NSCBC) technique [55]. The reacting scalars are initialized using an unstrained premixed laminar flame solution, which is specified as a function of radial distance from the centre of the inlet. The statistics in this analysis are recorded after at least two flowthrough times and two initial eddy turnover times. For the purpose of the evaluation of Reynolds/Favre averaged values (i.e., and ), the primitive variable is averaged in time and also in the azimuthal direction using at least 20 statistically independent snapshots for every case considered here. Further information on this database can be obtained from Refs. [51,56,57,58,59,60,61].
4. Results and Discussion
The instantaneous views of isourfaces (from the product side) coloured by local values of non-dimensional temperature for the cases considered here are shown in Figure 2. It can be seen from Figure 2 that the extent of flame wrinkling increases with decreasing , although the inlet turbulence intensity remains the same. Moreover, the flame wrinkles which are associated with a convex (concave) shape towards the reactants in the cases are associated with high (low) temperature values, and this tendency is particularly prevalent for the case. By contrast, high (low) temperature values are obtained where flame wrinkles are concave (convex) towards the reactants in the case. This behaviour is well-known and is consistent with several previous analyses [13,15,18]. The focusing of diffusion of fresh reactants into the reaction zone is stronger than the defocusing of heat in the flame surface elements which are convex towards the reactants in the cases with . This gives rise to the simultaneous presence of high values of reactant concentration and temperature at the convexly curved zones towards the reactants, which leads to further increase in reaction rate magnitude and temperature in these zones. Thus, these regions in the flames propagate faster than the corresponding unstretched planar flames. By contrast, defocusing of diffusion of fresh reactants into the reaction zone is stronger than the focusing of heat in the flame surface elements which are concave towards the reactants in the cases with . As a result, these zones in the cases are subjected to the simultaneous presence of low reactant concentration and low temperature, which reduces the propagation rate in these regions. This tendency strengthens with decreasing , and the combination of high flame propagation rates into the reactants for the convexly curved regions and low propagation rates at the concavely curved zones gives rise to increased flame wrinkling with decreasing for the cases with . In the case, the focusing of diffusion of fresh reactants into the reaction zone is weaker than the defocusing of heat in the flame surface elements which are convex towards the reactants. This acts to reduce both the reaction rate magnitude and temperature in the regions which are convex towards the reactants in the case. Just the opposite mechanism leads to high reaction rate magnitude and high temperature in the regions which are concave towards the reactants in the case. The combination of low flame propagation rates into the reactants for the convexly curved regions and high propagation rates at the concavely curved zones leads to reduced flame wrinkling in the case in comparison to the corresponding case.
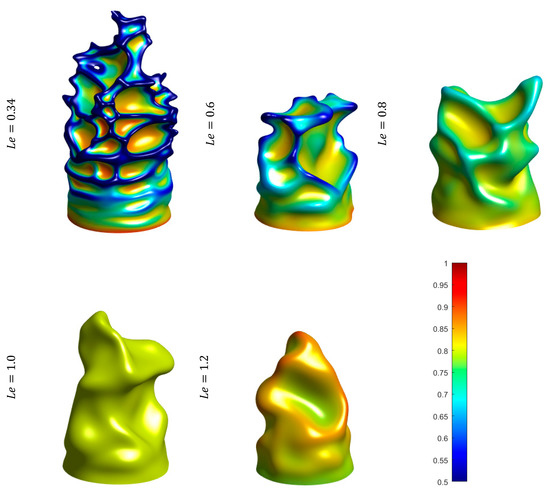
Figure 2.
Instantaneous isosurfaces of reaction progress variable c = 0.8 (seen from the burned gas side) coloured by non-dimensional temperature θ = (T − T0)/(Tad − T0) for Le = 0.34, 0.6, 0.8, 1.0, 1.2.
The increase in the extent of flame wrinkling with decreasing is reflected in the increases in with a decrease in when all flow parameters remained unchanged, which can be substantiated from Figure 3 where is evaluated for different choices of (i.e., , , , , and ). The values in Figure 3 show that and for all cases considered here irrespective of the characteristic Lewis number because the value of remains unchanged for a given case. It can further be seen from Figure 3 that the values of based on provided higher values than the corresponding definition based on irrespective of the value of .
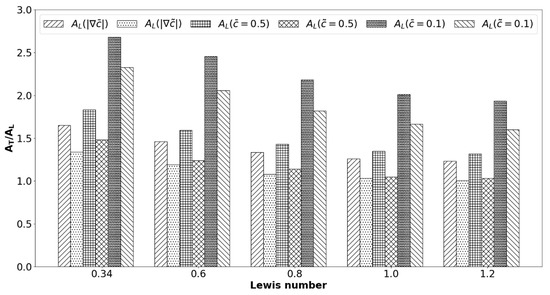
Figure 3.
Variations of for premixed turbulent Bunsen flame cases with , and for , , , , and .
The higher values of for smaller values of the Lewis number also leads to increases in with a decrease in . This can indeed be substantiated from Figure 4, which shows that for a given definition increases with decreasing Lewis number . The increasing trends of and are consistent with several previous analytical [3,4,5,6], experimental [7,8,9,10] and computational [11,12,13,14,15,16,17,18] analyses. Consistent with Figure 3, it can further be seen from Figure 4 that for is the smallest and for is the highest for a given case among the different choices of definitions. The higher values of for than for are consistent with previous experimental findings [25,46,47,48] for turbulent premixed Bunsen burner flames. The value of for was found to be 1.74 times that of the corresponding value for for Kobayashi’s experiments [25], whereas Tamadonfar and Gülder [46] reported a ratio of 2–3.6 for the values for and , and Smallwood et al. [47] reported a ratio of 1.2 to 1.5. The DNS data presented here closely correspond with the ratio reported by Smallwood et al. [47] based on their experimental data. Once again, Figure 4 suggests that based on yields higher values than the corresponding values based on irrespective of the value of .
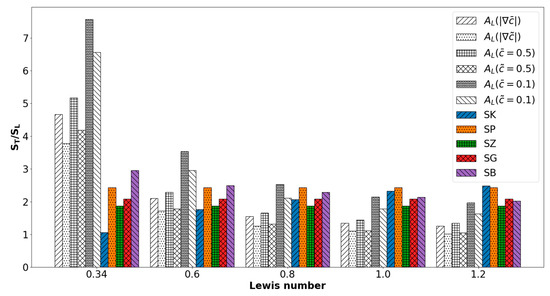
Figure 4.
Variations of for premixed turbulent Bunsen flame cases with , and for , , , , and along with the predictions of SK, SP, SG, SZ and SB models (see Table 1).
The values of for the cases considered here are shown in Figure 5, which shows that the ratio increases with decreasing . It is worth noting that the ratio is independent of , and thus, this quantity is independent of the method of evaluation of . A unity value of indicates the perfect validity of Damköhler’s first hypothesis [62]. It can be seen from Figure 5 that remains greater than unity (i.e., ) in the unity Lewis number Bunsen flame case (characterized by a global negative mean curvature), and the detailed physical explanations for this behaviour can be found elsewhere [59] and thus will not be repeated here. Figure 5 further suggests that increases significantly with decreasing for the sub-unity Lewis number (i.e., ) cases. The ratio signifies the ratio of consumption rate per unit area between turbulent and laminar flow conditions. Thus, the increasing trends of with decreasing are the manifestations of thermo-diffusive effects induced by the non-unity Lewis number. Under positively strained flames, the rate of reactants diffusion into the reaction zone dominates over the diffusion of heat out of this zone, which gives rise to an increase in with decreasing . This tendency strengthens further with decreasing and was reported in previous analyses [15,17,18]. By comparing Figure 3, Figure 4 and Figure 5, it becomes evident that the increase in is caused to a larger extent by the increase in than the increase in , and both effects together amplify each other.
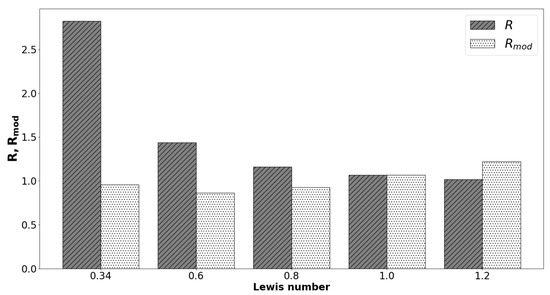
Figure 5.
Variations of and for premixed turbulent Bunsen flame cases with , and .
The flames become thermo-diffusively unstable for where high fuel concentration and high temperature values are found at the flame surface elements, which are convex towards the reactants (see Figure 2), and this combination locally augments the reaction and propagation rates much greater than the corresponding value for the same reaction progress variable in an unstretched planar flame. By contrast, the flame elements that are concave towards the reactants propagate slower than the corresponding unstretched planar flame due to the combination of low reactant concentration and temperature for (see Figure 2). The combination of high flame propagation rates at the convexly curved regions and relatively low flame propagation rates at negatively curved regions acts to increase the extent of flame wrinkling and makes the convexly curved regions stable. These mechanisms act to increase the flame surface area (see Figure 3) and the overall burning rate per unit flame surface area (as can be seen from the large value of in Figure 5) with a decrease in . As a consequence, turbulent burning velocity exhibits an increasing trend with decreasing (see Figure 4). The aforementioned mechanisms become more prominent when where is the threshold Lewis number under which cellular instability becomes triggered [51,63]. For the thermochemistry used here, the cellular instability is obtained for [51]. Thus, the case shows much higher values of , and than the rest of the cases considered here.
By considering Equation (4) and scaling using and , one gets: (see Ref. [17]) where is the generalized FSD [64]. Volume integrating both sides of yields: . It can be seen from Figure 5 that remains close to unity for all cases considered here, which is consistent with previous findings (i.e., ) [15,17,18] for the non-unity Lewis number flames. It is worth noting that based on leading edge theory, Lipatnikov and Chomiak [39] proposed a relation which suggests that . However, the numerical values of and remain comparable for and 1.2, but the values are significantly different for . Therefore, (or ) is not maintained for the case and thus will not be considered hereafter in this paper.
The predictions of different models for are compared to the normalized turbulent burning velocities obtained for different definitions of in Figure 4. The values used for and in the case of the SK model are listed in Table 3. It can be seen from Figure 4 that the models proposed by Kolla et al. [22], Peters [19], Gülder [20], Zimont [21] and Bradley [44] (Equations (7)–(11), alternatively SK, SP, SG, SZ and SB models in Table 1) yield comparable values to that of when is used in the unity Lewis number case, for which these models were originally designed and benchmarked. The quantitative agreement is the best for the model proposed by Gülder [20], Bradley [44] and Kolla et al. [22] (i.e., Equations (7), (9) and (11), alternatively SG, SB and SK models), and the models by Peters [19] and Zimont [21] (i.e., SP and SZ) overpredict and underpredict the magnitude of , respectively, when is used. All of these models overpredict when , , , and are used for the unity Lewis number case. It is worth noting that the predictions of the models proposed by Peters [19], Gülder [20] and Zimont [21] (Equations (8)–(11), alternatively SP, SG, SZ and SB models in Table 1) do not change for the non-unity Lewis number cases because and remain identical for all the cases considered here, and these model expressions do not account for the effects of . The prediction by the model proposed by Kolla et al. [22] varies with , and the magnitude of prediction by this model decreases with decreasing , due to the variation in and (see Table 3). The prediction of the model by Bradley [44] (i.e., Equation (11) or SB model) predicts an increase in the magnitude of with a decrease in for a given set of values of and , and the prediction of Equation (11) remains comparable to when is used for the cases with and 1.2 but overpredicts the values of when , , , and are used. However, the model by Bradley [44] (i.e., Equation (11) or SB model) underpredicts all possible definitions of considered here for the case. It is important to note that Equations (7) and (11) predict the unphysical zero value of for laminar conditions (i.e., ), and adding 1.0 on the right hand side of Equations (7) and (11) (i.e., SK and SB models) gives rise to overpredictions of when (or ) is used for the cases with and 1.2. This also does not affect the underpredictions of for the case.

Table 3.
Thermochemical parameters used in the model by Kolla et al. [22].
As the models of by Kolla et al. [22], Peters [19], Gülder [20] and Zimont [21] (Equations (7)–(10), alternatively SK, SP, SG and SZ models in Table 1) are originally proposed for unity Lewis number flames with an implicit assumption of , it is worth considering the performances of these models when the multiplier is used to account for non-unity Lewis number effects, as shown in Table 4, because assumes a value close to unity (see Figure 5). The expressions for the models by Peters [19], Gülder [20] and Zimont [21] in Table 4 (i.e., SPL, SGL and SZL models in Table 4) are modified in such a manner that for large values of (i.e., ), the expressions in Table 1 multiplied by are obtained, and the original expressions in Table 1 are recovered for . Moreover, these modifications ensure that is recovered for the laminar condition (i.e., ).

Table 4.
Summary of modified normalized turbulent burning velocity model expressions.
The predictions of the modified expressions for the models by Kolla et al. [22], Peters [19], Gülder [20] and Zimont [21] (SKL, SPL, SGL and SZL models in Table 4) are compared for non-unity Lewis number flames considered here in Figure 6. It can be seen from Figure 6 that the SGL models show a good agreement with when is used for most of the non-unity Lewis number flames but underpredicts for the case. The SPL model slightly overpredicts when is used for the and 0.8 cases but shows reasonable quantitative agreement with and cases. The values for are underpredicted for cases by the SKL model (see Table 4), although it shows good agreement for and . The SZL model expression shows good agreement with obtained from DNS data when is used for the and 1.2 cases, but is underpredicted for the case.
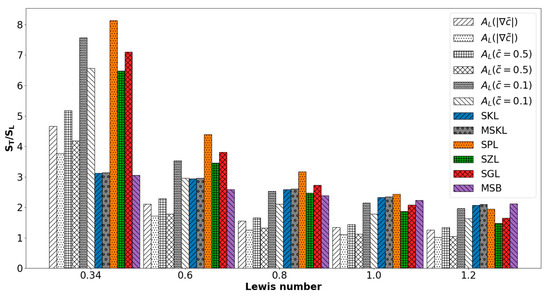
Figure 6.
Variations of for premixed turbulent Bunsen flame cases with , and for , , , , and along with the predictions of SKL, SPL, SGL, SZL, MSB and MSKL models (see Table 4).
A modified version of Kolla et al. [22] (i.e., SKL model) can be proposed in the following manner so that the expression for for can be reasonably predicted for non-unity Lewis number flames while satisfying for :
Equation (17) will henceforth be referred to as the MSKL model in this paper. The predictions of Equation (17) are also shown in Figure 6, which shows that the MSKL model offers comparable performance to that of the SKL model. Similar to Equation (17), the SB can be modified (henceforth referred to MSB model) in the following manner so that assumes a value of 1.0 for :
The prediction of the MSB model remains comparable to that of the SB model. The MSB predicts reasonably accurately when is used for the cases with and 1.2 but overpredicts the values of for other definitions of . Similar to the SB model, the MSB model also underpredicts all possible definitions of considered for the case considered here.
The -norm of the relative error values (where refers to the value of for the th case and ‘DNS’ and ‘Model’ superscripts are used for DNS and model expression values, respectively and is the total number of different cases considered here) of the model expressions of listed in Table 1 are shown in Figure 7, which shows that SK, SP, SG, SZ and SB models exhibit comparable , but values are high for definitions , , and . The corresponding values of the model expressions for listed in Table 4 are shown in Figure 8. A comparison between Figure 7 and Figure 8 reveals that the modified expressions in Table 4 significantly decrease the values when is used for the evaluation of .
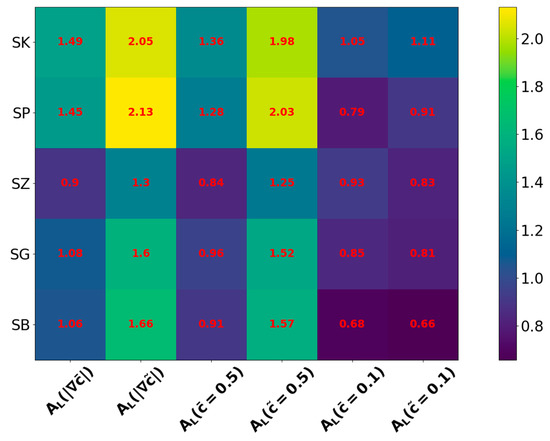
Figure 7.
Variations of for all premixed turbulent Bunsen flame cases for , , , , and for the predictions of SK, SP, SG, SZ and SB models (see Table 1).
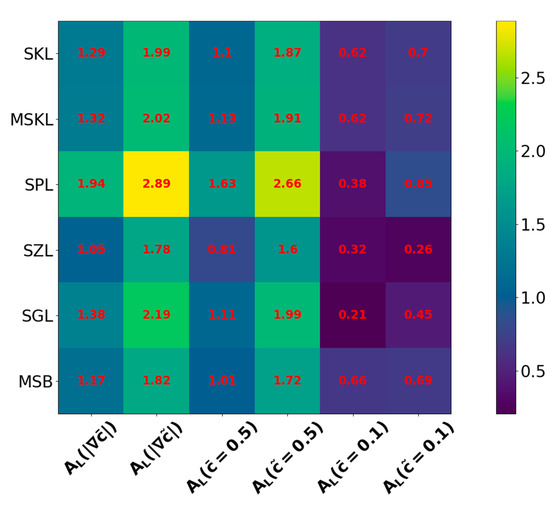
Figure 8.
Variations of for all premixed turbulent Bunsen flame cases for , , , , and for the predictions of SKL, SPL, SGL, SZL, MSB and MSKL models (see Table 4).
It is worth noting that the DNS database used for this analysis considers only a single modest value of turbulence intensity and a single pressure level. Therefore, it is worth considering the predictions of the model expressions summarized in Table 4 for experimental conditions for non-unity Lewis number conditions for different pressures and higher turbulence intensity, which were recently analysed by Lipatnikov et al. [10]. These experimental conditions by Lipatnikov et al. [10] are summarized in Table 5. The predictions of the model expressions in Table 4 are compared to values reported by Lipatnikov et al. [10] in Figure 9 and the corresponding -norm of relative error values (where refers to the value of for the th case and ‘Expt’ superscript is used for experimental values) are shown in Figure 10.

Table 5.
Summary of the experimental conditions from Lipatnikov et al. [10].
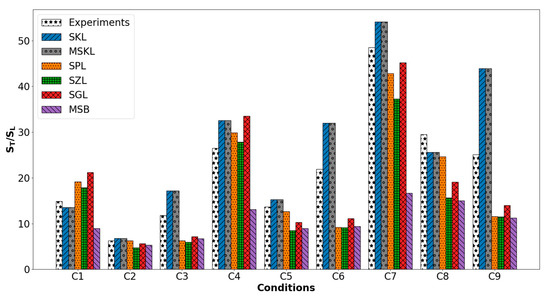
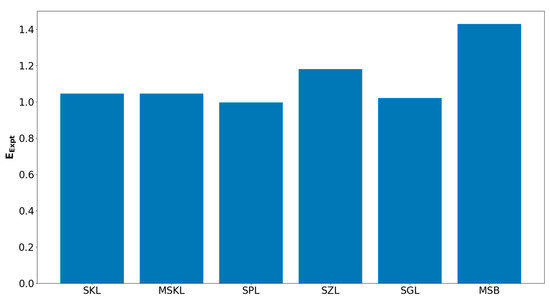
It can be seen from Figure 9 that the MSKL, SKL and SPL models predict values obtained from experimental conditions [10] reasonably well for conditions C1, C2, C5 and C8. The performances of the SGL and SZL models remain comparable to those of the MSKL, SKL and SPL models for C1 and C2 conditions, and the SGL model predicts the experimental value of satisfactorily for the C5 condition, but both SGL and SZL models underpredict values significantly for other cases. The MSKL and SKL model expressions overpredict values for C3, C4, C6, C7 and C9 conditions. Among these conditions, only under the C4 condition, the predictions of the SPL and SZL models remain comparable to those of the MSKL and SKL models and experimental value of , but in other conditions, the SPL, SGL and SZL models underpredict values. It can indeed be seen from Figure 10 that the SKL, SPL, SGL and MSKL model expressions yield relatively small values of . It is worth noting that the original model expressions by Kolla et al. [22], Peters [19], Gülder [20] and Zimont [21] (i.e., SK, SP, SG and SZ models) underpredict significantly for conditions C1, C2, C4, C5, C7 and C8 and return higher values of than the SPL, SGL and SZL models and thus are not explicitly shown in Figure 9 and Figure 10. The model MSB underpredicts for all the conditions considered in the experiment.
As is explained in Section 2, most models for turbulent burning velocity were developed for unity Lewis number conditions. As can be seen in Figure 4, while all these models do quite well for , most models used in the present work fail for non-unity Lewis numbers. The models are made to work for non-unity Lewis numbers by taking advantage of the scaling (i.e., ) that is observed in Figure 5, which shows that . However, this along with the assumptions in the closure equations is not a precise expression and could have led to the overshoot and undershoot of the predictions. It is worth noting that the experimental methodologies of the measurements of and the projected flame brush area are different from case to case and from the DNS-based methodologies. It has also been noted by Driscoll [26] that the parameterization of turbulent burning velocity might also be geometry dependent to some extent (note experiments in Ref. [10] were carried out for spherical flame kernels and not for Bunsen burner flames). These uncertainties may contribute to the discrepancies between model predictions and values obtained from DNS/experimental data. However, a careful comparison between Table 5 and Figure 9 reveals that several models provide reasonable predictions when the characteristic Lewis number remains close to unity. Moreover, it can be seen from Figure 10 that the newly proposed modifications to the existing parameterizations of turbulent burning velocity do reasonably well in an average sense, even for non-unity Lewis number flames.
Based on the results shown in Figure 4, Figure 7, Figure 8, Figure 9 and Figure 10, it seems that the SGL, SPL and SZL model expressions provide reasonable estimates of obtained from both DNS and experiments for a wide range of values of and different pressure levels, even though there are quantitative discrepancies for some cases. It is worth noting that the experimental methodologies of the measurements of and the projected flame brush area are different to the DNS-based methodologies. Furthermore, is approximately valid in a scaling sense, but it is not a precise expression. These uncertainties may contribute to the discrepancies between model predictions and values obtained from DNS/experimental data.
5. Conclusions
The statistical behaviour of the turbulent burning velocity has been analysed based on a Direct Numerical Simulation database of turbulent premixed Bunsen flames for different values of characteristic Lewis number ranging from 0.34 to 1.2. It has been found that the turbulent burning velocity normalized by the laminar burning velocity and the turbulent flame surface area normalized by the projected flame brush area for a given set of flow parameters increase with decreasing . Further, the value of depends strongly on the definition of the projected flame brush area , and six different alternatives (i.e., , , , and ) have been considered here. The variations of the numerical value of can be up to 50% depending on the definition of . It has been found that the highest values of and for a given Bunsen premixed flame case are obtained when the projected flame brush area is based on the area of isosurface, and the smallest value is obtained when is evaluated based on the volume-integration of . The choice of higher value of or for the evaluation of has been found to give rise to smaller values of and values in this configuration, and the quantitative variation has been found to be as large as 50% in the cases analysed here. This is found to be consistent with previous experimental findings [25,46,47,48] for turbulent premixed Bunsen flames. Moreover, it has been found that and values based on assume greater values than the corresponding values based on . The predictions of different models for [19,20,21,22,44] have been compared to the corresponding values obtained from DNS data. It has been found that most available parameterizations of provide comparable predictions when is evaluated based on the area of the isosurface. However, most of these models were originally proposed for the unity Lewis number [19,20,21,22], where Damköhler’s first hypothesis (i.e., ) [62] is implicitly assumed. However, Damköhler’s first hypothesis (i.e., ) is rendered invalid for the non-unity Lewis number flames, and the existing parameterizations tend to underpredict values for flames with , and this tendency strengthens with a decreasing Lewis number. It has been found that remains of the order of unity which has been justified using scaling arguments. This relation has been utilized to extend parameterizations of (which were originally proposed for the unity Lewis number) for non-unity Lewis number conditions while satisfying the limiting condition for . These revised parameterizations based on the models proposed by Peters [19], Gülder [20] and Zimont [21] have been found to be more successful than the other models in terms of predictions across the datasets considered when is evaluated based on the area of isosurface especially for flames compared to the original model expressions. The performances of these revised parameterizations have been assessed for a recent experimental dataset [10] for different values of . It has been found that the expressions, which provide satisfactory quantitative agreement with DNS data, also exhibit small values of -norm of the percentage error with respect to the experimental data [10]. However, the performance of these model parameterizations needs to be assessed for different flame configurations under higher turbulence intensity and also in the presence of detailed chemistry and transport, which will form the platform for further investigations.
Author Contributions
Conceptualization, N.C. and M.K.; methodology, V.M., M.H., N.C. and M.K.; software, V.M. and M.H.; formal analysis, V.M. and N.C.; resources, N.C. and M.K.; writing—original draft preparation, N.C.; writing—review and editing, V.M., N.C. and M.K.; visualization, V.M., N.C. and M.K.; supervision, N.C. and M.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by EPSRC grants (EP/R029369/1, EP/W026686/1).
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Acknowledgments
The authors are grateful to the Gauss Centre for Supercomputing (grant: pn69ga) for the computational support. Further, the present work is funded by dtec.bw—Digitalization and Technology Research Center of the Bundeswehr, Project MORE, which is gratefully acknowledged. dtec.bw is funded by the European Union–NextGenerationEU. N.C. and V.M. are grateful to EPSRC (EP/R029369/1, EP/W026686/1) and ARCHER2 for the financial and computational support. We acknowledge financial support by Universität der Bundeswehr München.
Conflicts of Interest
The authors declare no conflict of interest.
References
- A Strategic Framework for Hydrogen Energy in the UK. 2004. Available online: https://webarchive.nationalarchives.gov.uk/ukgwa/20090609003228/http://www.berr.gov.uk/files/file26737.pdf (accessed on 5 March 2023).
- Dixon-Lewis, G. Kinetic mechanism, structure and properties of premixed flames in hydrogen—oxygen—nitrogen mixtures. Phil. Trans. R. Soc. Lond. 1979, 292, 45–99. [Google Scholar]
- Sivashinsky, G.I. Diffusional-thermal theory of cellular flames. Combust. Sci. Technol. 1977, 16, 137–145. [Google Scholar] [CrossRef]
- Sivashinsky, G.I. Instabilities, Pattern Formation and Turbulence in Flames. Annu. Rev. Fluid Mech. 1983, 15, 179–199. [Google Scholar] [CrossRef]
- Libby, P.A.; Linan, A.; Williams, F.A. Strained premixed laminar flames with nonunity Lewis numbers. Combust. Sci. Technol. 1983, 34, 257–293. [Google Scholar] [CrossRef]
- Clavin, P.; Joulin, G. Premixed flames in large scale and high intensity turbulent flow. J. Phys. Lett. 1983, 44, L1–L12. [Google Scholar] [CrossRef]
- Abdel-Gayed, R.; Bradley, D.; Hamid, M.; Lawes, M. Lewis number effects on turbulent burning velocity. Proc. Combust. Inst. 1984, 20, 505–512. [Google Scholar] [CrossRef]
- Law, C.K.; Kwon, O.C. Effects of hydrocarbon substitution on atmospheric hydrogen–air flame propagation. Int. J. Hydrog. Energy 2004, 29, 876–879. [Google Scholar] [CrossRef]
- Muppala, S.R.; Aluri, N.K.; Dinkelacker, F.; Leipertz, A. Development of an algebraic reaction rate closure for the numerical calculation of turbulent premixed methane, ethylene, and propane/air flames for pressures up to 1.0 Mpa. Combust. Flame 2005, 140, 257–266. [Google Scholar] [CrossRef]
- Lipatnikov, A.N.; Chen, Y.-R.; Shy, S. An experimental study of the influence of Lewis number on turbulent flame speed at different pressures. Proc. Combust. Inst. 2022, 39. in press. [Google Scholar] [CrossRef]
- Ashurst, W.T.; Peters, N.; Smooke, M.D. Numerical simulation of turbulent flame structure with non-unity Lewis number. Combust. Sci. Technol. 1987, 53, 339–375. [Google Scholar] [CrossRef]
- Haworth, D.C.; Poinsot, T.J. Numerical simulations of Lewis number effects in turbulent premixed flames. J. Fluid Mech. 1992, 244, 405–436. [Google Scholar] [CrossRef]
- Rutland, C.; Trouve, A. Direct Simulations of premixed turbulent flames with nonunity Lewis numbers. Combust. Flame 1993, 94, 41–57. [Google Scholar] [CrossRef]
- Trouvé, A.; Poinsot, T. The evolution equation for flame surface density in turbulent premixed combustion. J. Fluid Mech. 1994, 278, 1–31. [Google Scholar] [CrossRef]
- Chakraborty, N.; Cant, R.S. Influence of Lewis number on curvature effects in turbulent premixed flame propagation in the thin reaction zones regime. Phys. Fluids 2005, 17, 105105. [Google Scholar] [CrossRef]
- Han, I.; Huh, K.Y. Roles of displacement speed on evolution of flame surface density for different turbulent intensities and Lewis numbers in turbulent premixed combustion. Combust. Flame 2008, 152, 194–205. [Google Scholar] [CrossRef]
- Chakraborty, N.; Cant, R. Effects of Lewis number on flame surface density transport in turbulent premixed combustion. Combust. Flame 2011, 158, 1768–1787. [Google Scholar] [CrossRef]
- Ozel-Erol, G.; Klein, M.; Chakraborty, N. Lewis Number Effects on Flame Speed Statistics in Spherical Turbulent Premixed Flames. Flow Turbul. Combust. 2021, 106, 1043–1063. [Google Scholar] [CrossRef]
- Peters, N. The turbulent burning velocity for large-scale and small-scale turbulence. J. Fluid Mech. 1999, 384, 107–132. [Google Scholar] [CrossRef]
- Gülder, O.L. Turbulent premixed flame propagation models for different combustion regimes. Proc. Combust. Inst. 1990, 23, 743–750. [Google Scholar] [CrossRef]
- Zimont, V.L. Gas premixed combustion at high turbulence: Turbulent flame closure combustion model. Exp. Therm. Fluid Sci. 2000, 21, 179–186. [Google Scholar] [CrossRef]
- Kolla, H.; Rogerson, J.; Chakraborty, N.; Swaminathan, N. Scalar dissipation rate and its modelling. Combust. Sci. Technol. 2009, 181, 518–535. [Google Scholar] [CrossRef]
- Creta, F.; Matalon, M. Propagation of wrinkled turbulent flames in the context of hydrodynamic theory. J. Fluid Mech. 2011, 680, 225–264. [Google Scholar] [CrossRef]
- Bray, K.N.C.; Cant, R.S. Some applications of Kolmogorov turbulence research in the field of combustion. Proc. R. Soc. Lond. A 1991, 434, 217–227. [Google Scholar]
- Kobayashi, H.; Kawazoe, H. Flame instability effects on the smallest wrinkling scale and burning velocity of high-pressure turbulent premixed flames. Proc. Combust. Inst. 2000, 28, 375–382. [Google Scholar] [CrossRef]
- Driscoll, J.F. Turbulent premixed combustion: Flamelet structure and its effect on turbulent burning velocities. Prog. Energy Combust. Sci. 2008, 34, 91–134. [Google Scholar] [CrossRef]
- Filatyev, S.A.; Driscoll, J.F.; Carter, C.D.; Donbar, J.M. Measured properties of turbulent premixed flames for model assessment, including burning velocities, stretch rates, and surface densities. Combust. Flame 2005, 141, 1–21. [Google Scholar] [CrossRef]
- Ahmed, U.; Chakraborty, N.; Klein, M. Insights into the Bending Effect in Premixed Turbulent Combustion Using the Flame Surface Density Transport. Combust. Sci. Technol. 2019, 191, 898–920. [Google Scholar] [CrossRef]
- Varma, A.R.; Ahmed, U.; Klein, M.; Chakraborty, N. Effects of turbulent length scale on the bending effect of turbulent burning velocity in premixed turbulent combustion. Combust. Flame 2021, 233, 111569. [Google Scholar] [CrossRef]
- Mizomoto, M.; Asaka, Y.; Ikai, S.; Law, C. Effects of preferential diffusion on the burning intensity of curved flames. Proc. Combust. Inst. 1984, 20, 1933–1940. [Google Scholar] [CrossRef]
- Bechtold, J.; Matalon, M. The Dependence of the Markstein length on stoichiometry. Combust. Flame 2001, 127, 1906–1913. [Google Scholar] [CrossRef]
- Clarke, A. Calculation and consideration of the Lewis number for explosion studies. Proc. Inst. Chem. Eng. Part B 2002, 80, 135–140. [Google Scholar] [CrossRef]
- Dinkelacker, F.; Manickam, B.; Muppala, S. Modelling and simulation of lean premixed turbulent methane/hydrogen/air flames with an effective Lewis number approach. Combust. Flame 2011, 158, 1742–1749. [Google Scholar] [CrossRef]
- Poinsot, T.; Veynante, D. Theoretical and Numerical Combustion, 1st ed.; R.T. Edwards Inc.: Philadelphia, PA, USA, 2001. [Google Scholar]
- Keil, F.B.; Amzehnhoff, M.; Ahmed, U.; Chakraborty, N.; Klein, M. Comparison of flame propagation statistics extracted from DNS based on simple and detailed chemistry Part 1: Fundamental flame turbulence interaction. Energies 2021, 14, 5548. [Google Scholar] [CrossRef]
- Keil, F.B.; Amzehnhoff, M.; Ahmed, U.; Chakraborty, N.; Klein, M. Comparison of flame propagation statistics extracted from DNS based on simple and detailed chemistry Part 2: Influence of choice of reaction progress variable. Energies 2021, 14, 5695. [Google Scholar] [CrossRef]
- Bray, K. Turbulent Flows with Premixed Reactants. In Turbulent Reacting Flows; Libby, P.A., Williams, F.A., Eds.; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 1980; pp. 115–183. [Google Scholar]
- Duclos, J.; Veynante, D.; Poinsot, T. A comparison of flamelet models for premixed turbulent combustion. Combust. Flame 1993, 95, 101–117. [Google Scholar] [CrossRef]
- Lipatnikov, A.N.; Chomiak, J. Turbulent flame speed and thickness: Phenomenology, evaluation and application in multi-dimensional simulations. Prog. Energy Combust. Sci. 2002, 28, 1–74. [Google Scholar] [CrossRef]
- Sabelnikov, V.A.; Lipatnikov, A.N. Speed selection for traveling-wave solutions to the diffusion-reaction equation with cubic reaction term and Burgers nonlinear convection. Phys. Rev. E 2014, 90, 033004. [Google Scholar] [CrossRef]
- Smith, K.; Gouldin, F. Experimental investigation of flow turbulence effects on premixed methane-air flames. Prog. Astro. Aero. 1978, 58, 37–54. [Google Scholar]
- Aldredge, R.; Vaezi, V.; Ronney, P. Premixed-flame propagation in turbulent Taylor–Couette flow. Combust. Flame 1998, 115, 395–405. [Google Scholar] [CrossRef]
- Savarianandam, V.R.; Lawn, C. Burning velocity of premixed turbulent flames in the weakly wrinkled regime. Combust. Flame 2006, 146, 1–18. [Google Scholar] [CrossRef]
- Bradley, D. How fast can we burn? Proc. Combust. Inst. 1992, 24, 247–262. [Google Scholar] [CrossRef]
- Klein, M.; Herbert, A.; Kosaka, H.; Böhm, B.; Dreizler, A.; Chakraborty, N.; Papapostolou, V.; Im, H.G.; Hasslberger, J. Evaluation of flame area based on detailed chemistry DNS of premixed turbulent hydrogen-air flames in different regimes of combustion. Flow Turbul. Combust. 2020, 104, 403–419. [Google Scholar] [CrossRef]
- Tamadonfar, P.; Gülder, Ö.L. Flame brush characteristics and burning velocities of premixed turbulent methane/air Bunsen flames. Combust. Flame 2014, 161, 3154–3165. [Google Scholar] [CrossRef]
- Smallwood, G.J.; Gülder, Ö.L.; Snelling, D.R.; Deschamps, B.M.; Gökalp, I. Characterization of flame front surfaces in turbulent premixed methane/air combustion. Combust. Flame 1995, 101, 461–470. [Google Scholar] [CrossRef]
- Jiang, L.; Shy, S.; Li, W.; Huang, H.; Nguyen, M. High-temperature, high-pressure burning velocities of expanding turbulent premixed flames and their comparison with Bunsen-type flames. Combust. Flame 2016, 172, 173–182. [Google Scholar] [CrossRef]
- Jenkins, K.W.; Cant, R.S. Direct numerical simulation of turbulent flame kernel. In Recent Advances in DNS and LES; Springer: Berlin/Heidelberg, Germany, 1999; pp. 191–202. [Google Scholar]
- Wray, A.A. Minimal Storage Time Advancement Schemes for Spectral Methods, Unpublished Report; NASA Ames Research Center: Mountain View, CA, USA, 1990. [Google Scholar]
- Rasool, R.; Chakraborty, N.; Klein, M. Effect of non-ambient pressure conditions and Lewis number variation on direct numerical simulation of turbulent Bunsen flames at low intensity. Combust. Flame 2021, 231, 111500. [Google Scholar] [CrossRef]
- Peters, N. Turbulent Combustion, Cambridge Monograph on Mechanics; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Kobayashi, H.; Tamura, T.; Maruta, K.; Niioka, T.; Williams, F.A. Burning velocity of turbulent premixed flames in a high-pressure environment. Proc. Combust. Inst. 1996, 26, 389–396. [Google Scholar] [CrossRef]
- Klein, M.; Sadiki, A.; Janicka, J. A digital filter based generation of inflow data for spatially developing direct numerical or large eddy simulations. J. Comput. Phys. 2003, 186, 652–665. [Google Scholar] [CrossRef]
- Poinsot TJ, A.; Lele, S.K. Boundary conditions for direct simulation of compressible viscous flows. J. Comp. Phys. 1992, 101, 104–129. [Google Scholar] [CrossRef]
- Klein, M.; Alwazzan, D.; Chakraborty, N. A Direct Numerical Simulation analysis of pressure variation in turbulent premixed Bunsen burner flames-Part 1: Scalar gradient and strain rate statistics. Comput. Fluids 2018, 173, 178–188. [Google Scholar] [CrossRef]
- Klein, M.; Alwazzan, D.; Chakraborty, N. A Direct Numerical Simulation analysis of pressure variation in turbulent premixed Bunsen burner flames-Part 2: Surface Density Function transport statistics. Comput. Fluids 2018, 173, 147–156. [Google Scholar] [CrossRef]
- Klein, M.; Nachtigal, H.; Hansinger, M.; Pfitzner, M.; Chakraborty, N. Flame curvature distribution in high pressure turbulent Bunsen premixed flames. Flow Turbul. Combust. 2018, 101, 1173–1187. [Google Scholar] [CrossRef]
- Chakraborty, N.; Alwazzan, D.; Klein, M.; Cant, R.S. On the validity of Damköhler’s first hypothesis in turbulent Bunsen burner flames: A computational analysis. Proc. Combust. Inst. 2019, 37, 2231–2239. [Google Scholar] [CrossRef]
- Rasool, R.; Chakraborty, N.; Klein, M. Algebraic Flame Surface Density modelling of high pressure turbulent premixed Bunsen flames. Flow Turbul. Combust. 2020, 106, 1313–1327. [Google Scholar] [CrossRef]
- Rasool, R.; Klein, M.; Chakraborty, N. Flame Surface Density based mean reaction rate closure for Reynolds Averaged Navier Stokes methodology in turbulent premixed Bunsen Flames with non-unity Lewis number. Combust. Flame 2022, 239, 111766. [Google Scholar] [CrossRef]
- Damköhler, G. Der Einfluss der Turbulenz auf die Flammengeschwindigkeit in Gasgemischen. Z. Elektrochem. Angewante Phys. Chem. 1940, 46, 601–626. [Google Scholar]
- Pelce, P.; Clavin, P. Influence of hydrodynamics and diffusion upon the stability limits of laminar premixed flames. J. Fluid Mech. 1982, 124, 219–237. [Google Scholar] [CrossRef]
- Boger, M.; Veynante, D.; Boughanem, H.; Trouvé, A. Direct Numerical Simulation analysis of flame surface density concept for Large Eddy Simulation of turbulent premixed combustion. Proc. Combust. Inst. 1998, 27, 917–925. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).