Abstract
The existing distribution networks were designed at a time when there was virtually no embedded generation. The design methods ensured the voltage at various parts of the network remained within the limits required by standards, and for the most part, this was very successfully achieved. As Distributed Energy Resources (DERs) started to grow, the rise in voltage due to injected currents and the local impedances started to push network voltages toward, and even above, the desired upper limits. Voltage limits are based on typical appliance requirements, and long-term over-voltages will ultimately result in unacceptably short appliance life spans. Distribution Static Compensators (dSTATCOMs) are shunt-connected devices that can improve low-voltage networks’ performance by injecting currents that do not transfer real power. The currents can be reactive, negative or zero sequence, or harmonic. System performance can be improved by reducing conduction loss, improving voltage profile and voltage balance, or reducing Total Harmonic Distortion (THD). To obtain these benefits, optimal sizes of dSTATCOMs need to be placed at optimal locations within the distribution network. This paper has considered seventy research articles published over the past years related to the optimal placement and sizing of dSTATCOMs. In this study, minimization of power losses, voltage profile improvement, loadablity factor, voltage sag mitigation, and reduction in annual operating costs are considered fitness functions that are subjected to multiple constraint sets. The optimization algorithms found in the literature are categorized into six methods: analytical methods, artificial neural network-based methods, sensitivity approaches, metaheuristic methods, a combination of metaheuristic and sensitivity analysis, and miscellaneous. This study also presents a comparison among distribution network types, load flow methods optimization tools, etc. Therefore, a comprehensive review of optimal allocation and sizing of dSTATCOMs in distribution networks is presented in this paper, and guidance for future research is also provided.
1. Introduction
Voltage drop becomes a significant issue in low voltage (LV) distribution networks. It will manifest at the feeders’ end, increasing the network’s power loss. Distribution networks incur 10–13% losses of the whole generated power due to low voltage and high current [1,2]. Reactive compensation or phase balancing devices can reduce Ohmic losses. Optimal capacitors can be used as reactive compensating shunt devices at optimal locations for voltage profile improvement and the minimization of losses [3]. However, capacitors cannot vary reactive power under variable load conditions [4]. Again, capacitors bring in resonance effect that will lead to voltage and current amplification and that will aggregate thermal degradation and equipment failure [5]. Custom power devices (CPDs) can be used as alternative solutions to capacitors by improving the power quality of the distribution networks. Some of the recently used CPDs are dynamic voltage restorers (DVRs) [6], static synchronous compensators (STATCOMs) [7], static VAR compensators (SVCs) [8], and unified PQ conditioners (UPQCs) [9]. Among all the CPDs, dSTATCOM is getting much attention nowadays due to its several functions such as reactive power compensation, power factor (PF) correction, and harmonic suppression [7,10,11,12]. This is a shunt voltage source converter that can supply or absorb reactive power [13]. Furthermore, STATCOM is used to improve power quality (voltage profile, voltage stability, power loss) in distribution networks [14,15,16]. One of the most attractive features of dSTATCOM is that it can be used in conjunction with photovoltaic systems. This will lead to the sustainable growth of renewables in the distribution network [17,18].
A dSTATCOM is a voltage source converter connected to a particular bus parallel to the network. It compensates for the inductive or capacitive reactive power or sequence power, depending on the needs of the power system [19]. It can also supply or sink active power if it is connected to a battery energy storage system (BESS) [20]. Only one article has considered integrating BESS with dSTATCOM [21]. A dSTATCOM consists of a DC link capacitor, a three-phase three-wire DC/AC voltage source converter (VSC), and a coupling transformer shown in Figure 1 connected in parallel between bus and bus [22,23]. The voltages of sending end bus and receiving end bus are and , and the angles of these buses are and , respectively. Resistance and reactance of the line between these two buses are and , respectively. and are the active and reactive power flowing from bus to bus , respectively. The current flowing through the line is , and is the dSTATCOM current. The hysteresis controller based on pulse width modulation (PWM) is used to control the VSC [24]. In [25], dSTATCOM is considered as three current sources connected to three controllable switches. These switches can be turned on and off to supply or absorb the required amount of reactive power. The state averaging technique is used to model VSC in dSTATCOM [26]. However, the benefits of dSTATCOMS are realized when they are placed in optimal locations and sizes. They cannot be placed in all bus locations, which makes them unnecessary and economically unviable. Therefore, an extensive search on the optimal allocation of dSTATCOMs is important to reduce power losses and cost, improve stability and load balancing, and moreover, enhance the power quality of the distribution network [27,28]. As a result, a growing interest in research is seen in the optimal placement and sizing of dSTATCOM. Figure 2 shows the number of publications from 2011 to 2023. 2011 has the highest number of articles so far, and 2023 shows an increasing trend of publications. Though there are approximately seventy articles found in the literature regarding optimal placement, only one article presents a literature review. Hence, there is an urge for a comprehensive survey to be performed on the existing literature. The main contributions of this paper are:
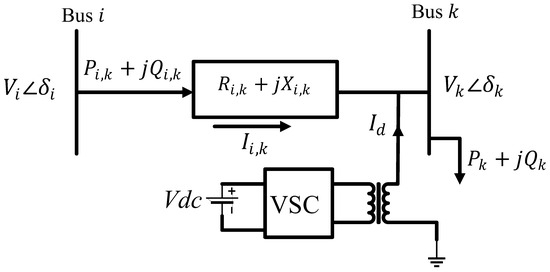
Figure 1.
dSTATCOM connected to the network.

Figure 2.
The number of publications from 2011 to 2023.
- Control systems for reactive power compensation have been identified and discussed;
- dSTATCOM is used in the distribution network to reduce power losses, energy losses, and operating costs and improve voltage profile and reliability. The importance of dSTATCOMs has been reported by pointing out the quantitative figures from the existing literature;
- A generalized approach has been undertaken for the optimization of dSTATCOM placement and sizing by considering different fitness functions and constraints;
- The algorithms used for optimization have been classified into six categories, which are briefly discussed;
- This paper also gives an insight into power flow methods, test systems, and optimization tools being used in the existing literature;
- A future research direction has been suggested.
2. Importance of the Optimal Placement of STATCOMs
With the increase in the high penetration of renewable energy sources to the grid, the network tends to operate closer to its technical limits. The power system faces many technical problems, as stated in [29,30,31].
- Power losses;
- Energy losses;
- Voltage violation;
- The need for network updates over time;
- Reliability.
These technical problems can be overcome to some extent by installing dSTATCOMs within the network. The benefits of optimal dSTATCOM placement are shown in Figure 3. The optimal solutions of locations, sizes, and number of dSTATCOMs can have both technical and economic advantages such as reactive power compensation, power factor correction, harmonic suppression, annual operating cost savings, network upgrade cost savings, etc. A literature survey shows the degree of improvement in these sectors in the following section.
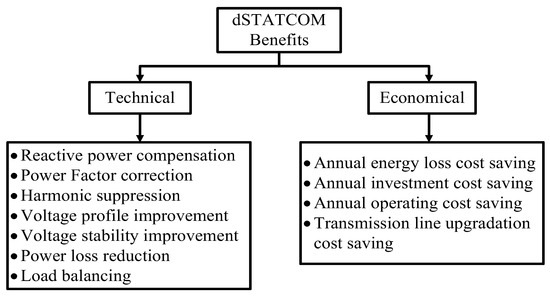
Figure 3.
Advantages of dSTATCOM placement.
2.1. Power Losses
The optimal placement and sizing of dSTATCOMs can significantly reduce power losses. After placing dSTATCOMs, 18.45%, 24.54%, and 27.66% reductions in power losses have been achieved for industrial, residential, and commercial loads, respectively [32]. Similarly, the Whale Optimization Algorithm (WOA) has been proposed to reduce the losses by 21.60%, 30.71%, and 22.03% for residential, commercial, and industrial loads [33]. The optimal solution proposed in [34] decreases the expected losses by 49.6591%. A reduction in power losses of 29.25% has been achieved by placing STATCOM using the BAT algorithm [35]. In [36], dSTATCOM has been placed with Distributed Generators (DGs) to minimize the losses by 87.67% using a fuzzy-based RAO-3 algorithm. Again, to minimize the power losses, a method combining particle swarm pptimization and the general algebraic modeling system has been proposed, and a 32.54% loss reduction has been achieved [37]. A combined algorithm called the firefly algorithm–sine–cosine acceleration coefficients–particle swarm optimization (FA-SCAC-PSO) has been proposed to minimize losses by 44.83% by installing dSTATCOMs [38]. A STATCOM has been placed optimally through an analytical solution to minimize the losses by 31.01% [39]. A Non-dominated Sorting Genetic Algorithm (NSGA-Ⅱ) has been proposed to minimize the losses by 27.15% after placing STATCOM [40].
2.2. Energy Losses
The authors in [41] proposed an analytical method to reduce energy losses by 6.396% after placing dSTATCOM in the optimal location. This paper considered the voltage unbalances in the distribution network and developed a method to reduce the unbalance between phases while reducing energy losses.
2.3. Annual Installation and Operating Cost
Articles [42,43] proposed a mixed-integer second-order cone programming (MI-SOCP) model and a stochastic mixed-integer convex (SMIC) model to minimize the annual operating cost by 14.71% and 29.25%, respectively. The estimated investment cost per STATCOM is found to be USD 9900.26. The optimal solution for the investment cost of STATCOM is USD 17182.21 [34]. A master–slave optimization method has been developed to estimate the annual operating cost of STATCOMs, which was found to be USD 77870.16 for meshed grid topology [44]. The annual operating cost consists of energy loss cost and investment cost. Similar results have been found in [45,46,47,48]; annual operation costs of USD 77,834.42, USD 77,685.48, USD 98,497.89, and USD 109,455.96 were found by applying the generalized normal distribution optimizer (GNDO), the discrete sine–cosine algorithm (DSCA), the discrete continuous vortex search algorithm (DCVSA), and the Chu and Beasley genetic algorithm–second order cone programming (CBGA-SOCP), respectively. The authors in [49] have proposed a discrete–continuous Chu–Beasley genetic algorithm (DC-CBGA) to calculate the expected operation cost of USD 108,196.458. An approximate mixed-integer convex and conic programming algorithm has been proposed to calculate the investment cost of USD 96,767.67 [50]. Annual cost savings of USD 27,776.97 has been reported in [37] after dSTATCOMs installation.
2.4. Voltage Profile Improvement
The voltage deviation index (VDI) is improved by 80.6594%, 85.43%, 70.5%, and 42.25% by placing STATCOMs at optimal locations within the network [34,35,40,51]. The minimum per unit (p.u.) voltage is increased from 0.902 to 0.981 by installing dSTATCOMs, which is an 8.64% increase in voltage profile [36]. Voltage is improved from 0.9131 p.u. to 0.9367 p.u by installing two dSTATCOMs in [52]. After dSTATCOM placement, the distribution network voltage has gone from 0.937 p.u. to 0.96 p.u. [38]. The network voltage profile improvement index (NVPII) is considered in [53] to evaluate the enhancement of voltage profile and is found to be 1.661, which indicates a good enhancement of voltage. dSTATCOM placement has improved the voltages from 0.8948 to 0.9767 p.u. [54]. The minimum voltage is 0.9046 p.u. without dSTATCOM, and after the installation of dSTATCOM, the voltage improved to 0.9305 p.u [39]. A 22.45% voltage improvement has been reported in [55].
2.5. Voltage Stability Improvement
The voltage stability index (VSI) is considered to show the stable operation of the network. The authors in [56] reported a 12.8% improvement in voltage stability. In [55], the VSI improved from 0.6610 p.u. to 0.7228 p.u. The minimum VSI is 0.6610 p.u, and after installing dSTATCOM, it increased to 0.9113 p.u [57]. For 100% load level, the VSI is reported to increase from 57.3865 to 64.4264 [58]. The authors in [40] have reported an increase in the VSI from 0.6951 p.u. to 0.768 p.u. to show the system’s stability improvement.
2.6. Total Harmonic Distortion (THD) Reduction
Total Harmonic Distortion (THD) is reduced by 1.15% after the optimal placement of multiple DGs and dSTATCOMs [59]. Authors have proposed a firefly algorithm (FA) to mitigate THD in all buses to meet the IEEE standard requirements [60,61].
3. Power Flow Analysis
The distribution network has a higher R/X ratio compared to the transmission line. Therefore, the optimum load flow solutions cannot be guaranteed by using the existing following algorithm [32]:
- Newton–Raphson method;
- Gauss–Seidal method;
- Fast decoupled method.
The existing literature has reported the backward/forward sweep (BFS) load flow analysis algorithm as the most efficient one to calculate voltages and power losses at each bus [22,33,39,40,51,62,63]. To solve load flow, a direct approach is adopted in [54,64] to find the voltages and power losses at each node of the network.
3.1. Problem Formulation
An optimization algorithm would need fitness function and associated constraints in a logical manner [65]. A fitness function could be single- or multi-objective, which will define the problems under consideration [66]. Single fitness functions will include the minimization of power losses, energy cost minimization, network voltage profile enhancement, voltage stability improvement, THD reduction, etc. Multi-objective fitness functions will have a combination of two or more single-objective functions. A general procedure and the most common objection functions found in the literature will be discussed as follows.
3.2. Fitness Function
The fitness function can be minimized or maximized depending on the criteria. When the associated constraints are applied, the fitness function is optimized by the algorithm [67,68].
The multi-objective fitness function containing all single-objective fitness functions is expressed in Equation (1).
where is the number of objective functions that will make a fitness function.
Network Power Losses: The fitness function is formulated to minimize the power losses of the electrical distribution network by the following equation [32,34,37,69,70]:
where
- is the total number of lines;
- is the current at line;
- is the resistance of line.
Total Harmonic Distortion (THD): The objective is to minimize the THD level of the whole system, and the fitness function is given as follows [59,60]:
- = number of buses;
- = amplitude of all harmonics;
- = fundamental component.
Voltage profile: The fitness function is expressed below [71], and the objective is to maximize the fitness function:
where
- = reference voltage;
- = voltage at bus.
Loadability factor: The objective is to maximize the equation by increasing the loadability factor () [51]:
where = apparent power at bus.
Voltage sag: The fitness function for calculating the total number of sags for all faults is given as follows [72]:
where
- = the number of voltage sags due to faults on buses;
- the bus fault rate;
- number of sags on faulted distribution lines;
- = number of sags on the faulted transformer.
Annual operating cost: The annual operating cost consists of two costs: annual energy loss cost and annual investment cost. The fitness function is expressed as follows [49]:
where
- = the average cost per ;
- = 365 days;
- = admittance matrix of and buses with angle ;
- = voltage at bus with angle ;
- = voltage at bus with angle ;
- = load flow evaluation time;
- = a set of periods;
- = a set of the number of buses;
- = annualized investment costs;
- = dSTATCOM lifespan;
- reactive power at th bus;
- = installation cost constant.
Voltage stability index: The voltage stability index (VSI) is used to indicate the stable operation of the distribution network, and it should be . The fitness function is calculated at each bus as follows [3,54,73,74,75]:
where
- = effective real power fed through bus ;
- is effective reactive power fed through bus ;
- line reactance between and bus;
- line resistance between and bus;
- voltage magnitude at th bus.
Reliability index: The distribution authorities should supply reliable electric power to its consumers. If there are any outages or disruptions, the index number helps the authorities to take decisions for future power system planning. The optimal placement and sizing of dSTATCOM can enhance the reliability of the system. To check the reliability of the system, there are different reliability indices such as the system average interruption duration index (SAIDI), the system average interruption frequency index (SAIFI), the customer average interruption frequency index (CAIFI), the customer average interruption duration index (CAIDI), energy not supplied (ENS), average energy not supplied (AENS), etc. [76,77,78,79,80]. The minimization of ENS denotes the improvement of system reliability [33,81,82]. The fitness function is expressed as follows:
3.3. Constraints
The fitness function should satisfy all the constraints within the optimization algorithm. If the algorithm does not satisfy all the given constraints, then the optimum solution would not be achieved, which will lead to malfunctioning performance. The constraints used in the literature are discussed below, and they are used as a combination set by the algorithm [33,34,83]:
Active and reactive power balance constraint: The consumed active and reactive power of the network should be equal to the generated power of the system [84].
where substation active and reactive power are denoted by and . Active and reactive line losses are denoted by and and active and reactive loads are and . Reactive power injected by the dSTATCOM is referred as , and denotes the dSTATCOM numbers.
Voltage constraint: The bus voltages should be within allowable limits, and the constraint is expressed as follows [34]:
where and are the minimum and maximum voltages at node.
Voltage angle constraint: The voltage angle () should vary between the minimum and maximum limit at any particular node [37].
dSTATCOM reactive power constraint: dSTATCOM can inject a certain amount of reactive power depending on its capacity [37]:
Line capacity: The apparent power passed through the line () should be less than the maximum allowable limit () [33]:
Thermal constraint: The current flowing through each line () must be less than the maximum allowable current () [85]:
Size constraint: For each dSTATCOM, there is a limitation in available sizes () [34]:
where and refer to the minimum and maximum dSTATCOM sizes.
Power factor (PF) constraint: The distribution network PF should be within allowable limits as follows [33]:
where the minimum and maximum power factors are denoted by and , respectively.
THD constraint: The THD should be limited to the allowable standard of the distribution network () [59]:
4. A Generalized Algorithm for Optimal Sizing and Placement of dSTATCOM
A generalized approach is followed in all optimization algorithms to solve the fitness function for dSTATCOMs sizing and locations, which is illustrated as follows:
- Step 1:
- read the network data such as line data, bus data, and load data;
- Step 2
- execute the load flow algorithm;
- Step 3:
- calculate bus voltages and power losses;
- Step 4:
- determine the optimization algorithm;
- Step 5:
- determine fitness function (single-/multi-objective) and define inputs of the chosen algorithm;
- Step 6:
- create the initial population;
- Step 7:
- compute fitness function;
- Step 8:
- check whether constraints are satisfied or not;
- Step 9:
- if not satisfied, go to step 6;
- Step 10:
- if constraints are satisfied, then the optimum solution is achieved.
The optimization procedure consisting of input data, fitness function, constraint, and output solution is shown in Figure 4.
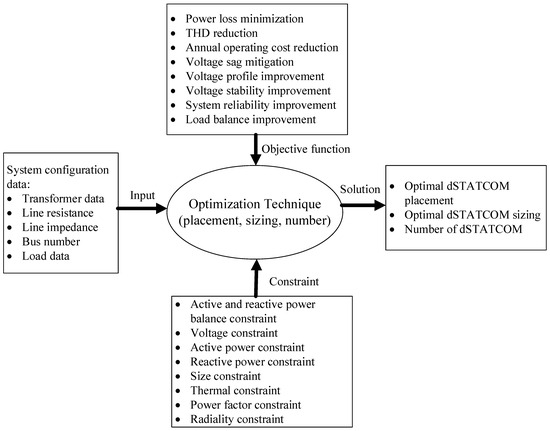
Figure 4.
A generalized optimization procedure for optimal placement and sizing of dSTATCOM.
5. Methods for the Optimal Placement and Sizing of dSTATCOM in Distribution Networks
The literature shows six major categories of methods and techniques being used for optimal sizing and placement of dSTATCOMs, as follows:
- Analytical methods;
- Artificial neural network-based methods;
- Sensitivity approaches;
- Metaheuristic methods;
- A combination of metaheuristic and sensitivity analysis;
- Miscellaneous.
5.1. Analytical Methods
The authors in [86] followed an exhaustive search technique to find the optimal location and size of dSTATCOM. The fitness function includes the minimization of voltages and enhancement of voltage. The proposed method computes the fitness function at each bus to find the minimum value. The proposed method is tested on the IEEE 33 bus network. The limitation of this article is that it is applicable to only one dSTATCOM placement in the distribution network.
In [23], an analytical method is proposed to find the optimal sizing and siting of DG and dSTATCOMs. The stability index and loss sensitivity factor (LSF) are considered in this article to minimize power losses and improve the voltage profile. The proposed method is tested on the IEEE 33 bus network. One of the limitations of analytical approaches is that they do not consider the complexity and nonlinearity of the optimization problem.
The optimal location of dSTATCOM is found by carrying out multiple analytical approaches in [87]. These techniques include the power loss index (PLI), the voltage profile index (VPI), the loss sensitivity factor (LSF), and the performance indicator (PI) to reduce the power losses and improve the voltage profile.
An exhaustive search is carried out for power loss minimization and voltage profile improvement by placing dSTATCOM in the optimal position. The proposed mathematical model calculates the injected reactive power by dSTATCOM and the corresponding power loss at every node of the IEEE 30 network [39]. Again, a similar approach is carried out in [52].
A methodology is developed in [41] to use voltage unbalance detection for optimal placement of a single dSTATCOM. The unbalance of voltages is detected from load flow analysis, and a dSTATCOM is placed on most higher unbalance terminals. However, the method requires a large amount of data to model the distribution network accurately.
5.2. Artificial Neural Network (ANN) Based Methods
In [53], the optimal incorporation of PV, the battery energy storage system (BESS), and dSTATCOM is determined by a fuzzified extended nondominant sorting genetic algorithm (E_NSGA II). Improvement in the voltage profile, environmental benefit, reliability of the network, and a reduction in costs are considered in the fitness function. The test is performed by the IEEE 69 network, and a comparison is made with the multi-objective genetic algorithm (MOGA) [88], strength-Pareto evolutionary algorithm (SPEA) [89], and multi-objective particle swarm optimization (MOPSO) [90]. The proposed methodology takes less computational time and preserves diversity among solutions than the others.
NSGA II is also used as an optimization method along with fuzzy decision-making (FDM) for dSTATCOM placement in [40]. The fitness function includes the VDI, VSI, and power loss. The proposed method is carried out on the IEEE 33 bus system and the Portuguese 94 bus real distribution network considering load uncertainty. The proposed method shows better performance than the immune algorithm (IA) [22] and bat algorithm (BA) [35] by improving the VDI, VSI, and annual cost savings.
A fuzzy-based RAO-3 algorithm is proposed to determine the optimal positioning and sizing of dSTATCOM [36]. The article seeks to mitigate the power loss, improve the power factor, and improve the voltage profile. Rao has proposed the RAO-3 population-based algorithm, which is named after him [91]. An IEEE 69 bus system is considered for implementing this algorithm and shows better performance than the two-stage fuzzy multi-objective method proposed in [92].
5.3. Metaheuristic Methods
An immune algorithm (IA) is proposed in [22] to search for the best location and size of dSTATCOM. The paper seeks to minimize loss and installation costs and enhance voltage and current profiles. The immune algorithm is inspired by the immune system of the human body and is applied to solve optimization problems [93]. The algorithm is tested on the IEEE 33 and 69 bus systems and shows a comparison between the genetic algorithm (GA) and the IA. The IA shows less convergence time, power loss, and installation cost, and has a smaller dSTATCOM size than the GA.
In [85], the differential evolution (DE) algorithm has been applied to optimally place dSTATCOM in the distribution network. The main contribution of the paper is to improve the voltage profile, minimize the power loss, minimize the energy loss and investment cost, and maximize the net saving. Differential evolution is a population-based metaheuristic method that has four stages: initialization of vectors known as chromosomes, mutation with different chromosomes, crossover, and selection [94]. Compensation through dSTATCOMs has been performed on IEEE 30 bus, IEEE 33, and IEEE 69 bus at light, medium, and peak load levels. The paper shows better cost reduction and less convergence time than the immune algorithm and gravitational search algorithm proposed in [22,95], respectively.
Optimal placement problems and reconfiguration are considered in [51] to reduce power loss and improve voltage profile and loadability. Multi-objective particle swarm optimization (MOPSO) is used to create a set of solutions and techniques for order performance by similarity to the ideal solution (TOPSIS), which is used to rank these solutions according to the weighting factors. The proposed methodology is tested on the IEEE 33 and 69 bus systems.
The bacterial foraging algorithm (BFA) requires a high convergence time with higher complexity in selecting parameters and is possibly stuck at local minima [96]. In order to avoid these drawbacks, an improved bacterial foraging algorithm (IBFA) is developed to improve voltage profile and stability and reduce power loss [56]. The difference between the BFA and IBFA is to consider two parameters, such as run time and cell-to-cell signaling mechanisms. The IBFA is tested on a 78-bus Quha feeder of Lachi and shows improvement in voltage profile and stability and a reduction in power losses than the conventional BFA.
A discrete continuous vortex search algorithm (DCVSA) is proposed to reduce the total power losses and annual investment cost of dSTATCOMs by placing them in optimal positions [47]. The VSA, a metaheuristic algorithm, is built upon the vortical demeanors of stirred fluids [97] An improvement of the VSA method is proposed to include the hybrid environment of the problem, named the DCVSA. Optimal sizes and locations are determined by the continuous and discrete codification, respectively. To validate the effectiveness of the algorithm, the IEEE 33 and 69 bus systems are used.
The optimal allocation problem of DG and dSTATCOM is solved by the grey wolf optimizer (GWO) under different load levels [98]. The purpose of this is to reduce power losses and improve voltage stability. The GWO is inspired by the hunting behavior and leadership hierarchy of grey wolves and consists of three main phases: tracking, encircling, and attacking the prey [99]. The proposed method is tested on the IEEE 85 bus system and shows an improvement in power loss reduction and voltage profile.
In [38], the firefly algorithm with the sine–cosine acceleration coefficient–particle swarm optimization (FA-SCAC-PSO) is proposed for the optimal placement of DG and dSTATCOM. The objectives considered in this paper are short circuit level (SCL), voltage deviation level (VDL), net saving level (NSL), environmental pollution reduction level (EPRL), and active power loss level (APLL). The proposed method is compared with other methods proposed in the literature, such as adaptive acceleration coefficient PSO (AAC-PSO) [100], autonomous particles groups for PSO (APG-PSO) [101], time-varying acceleration for PSO (TVA-PSO) [102], nonlinear dynamic acceleration coefficient PSO (NDAC-PSO) [103], and sine–cosine acceleration coefficient (SCAC-PSO) [104], and shows better performance in terms of loss and pollution reduction and improvement in voltage profile and cost saving.
The Whale Optimization Algorithm (WOA) is proposed in [33] to minimize the power loss and energy not supplied (ENS) and enhance voltage profile. The WOA mimics the metaphor of the hunting behavior of humpback whales, which includes fewer operators than evolutionary algorithms. This algorithm consists of three stages: recognizing and encircling the prey, the bubble net attacking method, and searching for prey [105]. The proposed algorithm is implemented on the IEEE 33 and 69 bus networks at residential, commercial, and industrial load levels. The article compares the results with the methods in [35,55,83,106,107] to show better performance in terms of loss reduction and enhancement of voltage profile.
In [48], the Chu and Beasley genetic algorithm (CBGA), along with second-order cone programming, is used to determine the optimal location and size of dSTATCOM, respectively. The algorithm seeks to minimize the annual energy loss costs and investment costs. The CBGA is an evolutionary-based metaheuristic algorithm consisting of three stages: selection, recombination, and mutation [108]. The proposed method is implemented on the IEEE 33 bus system.
The discrete–continuous version of the Chu–Beasley genetic algorithm (CBGA) is proposed, where the locations and sizings are determined by the discrete and continuous codification, respectively [49]. The fitness function consists of a reduction in the annual operating costs of dSTATCOM. The method is tested on the IEEE 33 bus network, both on radial and meshed configurations, which shows better performance than the genetic–convex model [48].
The authors in [44] have proposed a salp swarm algorithm (SSA) with backward/forward power flow as a master–slave approach to find the optimal sizing and siting of dSTATCOMs. The fitness function is associated with a reduction in annual energy loss costs and investment costs. The SSA mimics the behavior of forming a salp chain by gelatinous salps to have better locomotion in the deep ocean [109]. The IEEE 33 bus system is selected as a test feeder to check the effectiveness of the proposed method. One of the limitations of the paper is the application of the proposed method only on distribution feeders without voltage-controlled nodes. If there are multiple voltage-controlled sources, this method will not be applicable.
A generalized normal distribution optimizer (GNDO) along with a successive approximation power flow is proposed in [46] to reduce the annual operating costs of the networks after installing dSTATCOMs. The GNDO is inspired by Gaussian distribution theory to describe the physical and natural phenomena and follows two main steps: local and global exploration [110]. The two-stage optimization method is validated on the IEEE 33 bus network for both radial and meshed topology. A comparison is made with the SSA, and the GNDO demonstrates less operational cost than the SSA.
A population-based metaheuristic algorithm named the discrete sine–cosine algorithm (DSCA) is proposed in combination with the BONMIN solver in GAMS software [45]. This paper offers two stage processes: the master stage uses the DSCA to find the locations and the slave stage uses GAMS software to find the optimal sizes by using the locations found in the master stage. The DSCA uses trigonometric sine and cosine functions to explore and exploit the space vector by varying the amplitude over a number of iterations [111]. GAMS software is a versatile optimization tool to solve linear, nonlinear, and mixed-integer problems by taking lesser convergence time and offering an interface with MATLAB [112]. For these reasons, this software is used in [45] as an interface with MATLAB to find the optimal locations and sizes of dSTATCOMs. The proposed method is tested on the IEEE 33 bus system and shows better performance than the genetic convex algorithm [48] and the discrete Chu and Beasley genetic algorithm (DCBGA) [49].
5.4. Sensitivity Analysis
A sensitivity analysis is proposed for the optimal sizing of dSTATCOM [113]. The aim of the paper is to provide fast recovery of voltages at generator buses at abnormal conditions by injecting reactive power compensation through dSTATCOM. The proposed methodology is tested on 16 and 43 bus systems and considers different DGs, such as wind and solar. This method has reduced the number of dSTATCOM units required for the distribution network, which in turn reduces the costs.
In [59], the voltage stability index is used for solving the optimization problem of dSTATCOM allocation. This solves a multi-objective function consisting of power loss reduction, along with THD and voltage profile enhancement. In this article, a harmonic load flow analysis is used where nonlinear loads are considered as current injectors. The proposed method is carried out on the IEEE 34 bus system.
A two-stage sensitivity analysis is proposed in [114] for optimal sizing and siting of dSTATCOM. The total system loss sensitivity index is used for finding the optimal location, and load flow analysis performed by the Newton–Raphson method, which is used for the optimal sizing of dSTATCOM. The problem considers loss reduction as a fitness function. The proposed method is implemented in the IEEE 14 bus network.
5.5. Combination of Metaheuristic and Sensitivity Analysis
The authors in [54] have proposed a bacterial foraging algorithm (BFA), a population-based search algorithm, to determine the optimal placement and sizing of dSTATCOM, along with Distribution Generation (DG). The BFA is used in conjunction with the loss sensitivity factor (LSF). The fitness function includes power loss and operational cost reduction and voltage profile improvement. E. coli bacteria, which are located in human intestines, show foraging behavior, and the BFA is inspired by this mechanism [115]. The proposed method is tested on the IEEE 33 and 119 bus networks for different load models, showing a 19.45% greater reduction in power losses compared to the immune algorithm [22].
The artificial fish swarm optimization algorithm (AFSOA) along with the VSI is used to find the optimal sizing and location of dSTATCOM. The objective of the proposed algorithm is to reduce the system power losses. The AFSOA is based on the habitual behavior of fish such as preying, swarming, and following the local fish for food [116]. The simulations are carried out on the IEEE 33 and 69 bus systems.
The bat algorithm (BA) along with the VSI is proposed in [35] under multi-load levels. The curve fitting technique (CFT) is to determine the optimal size of dSTATCOM when the load changes. The fitness function considers the minimization of power loss. The BA is based on the finding of prey by bats by using a special sound called echolocation [117]. To check the validity of the proposed method, it is tested on the IEEE 33 and 69 bus networks. The results are compared with the BFA [54] and show better performance in terms of power loss reduction, annual cost saving, and voltage profile improvement. The same approach is adopted in [118]. The only difference is that it does not consider different load levels.
The BA is also used in [69] to determine the optimal sizing while the location of DG and dSTATCOM, which are determined by the LSF and VSI. A reduction in power loss is included as a single objective in the fitness function. The IEEE 34 and 85 bus systems are used for simulations.
The authors in [32] have proposed a combination of the Cuckoo Search Algorithm (CSA), a metaheuristic method and the loss sensitivity factor (LSF) for the optimal placement of dSTATCOM. The LSF is used to find the optimal locations and the CSA is used to find the optimal sizing. The paper seeks to minimize the power losses and enhance the voltage profile considering four load models: constant, residential, commercial, and industrial. The CSA is based on the metaphor of cuckoo birds laying eggs on the other bird’s nest and has two solution populations created through Levy flights and random walk [119,120]. The proposed method is validated on the IEEE 33 bus and IEEE 69 bus systems and shows better performance in terms of minimizing power loss and voltage profile improvement than the methods proposed in [22,54,121,122].
The VSI and LSF are used to determine the optimal locations of dSTATCOM and DG in [107], whereas the CSA is used to find the optimal size of DG and dSTATCOM. The parameters that are to be considered for fitness function are minimizing power loss and improvement of voltage profile. The proposed method is tested on the IEEE 33 and IEEE 136 bus systems for different load levels. The CSA performs better than other methods, such as the backtracking search algorithm (BSA) [123], quasi-oppositional teaching learning-based optimization (QOTLBO) [124], and BFA [54] in terms of computational time and power loss reduction and voltage and power factor improvement.
In [24], the optimal sizing and siting of dSTATCOM and DG are detected by the LSF and dwarf mongoose optimization (DMO) methods. The LSF is used to find the primary location and DMO is used to find the final optimum location. DMO is based on the restrictive behavior of hunting prey of dwarf mongoose [125]. DMO with the LSF seeks to minimize the power loss and operation cost and improve the voltage profile. The performance of the proposed method is compared with the dragonfly algorithm (DA) [126], shell game optimization (SGO), and salp swarm algorithm (SSA) [109].
5.6. Miscellaneous
A Monte Carlo simulation (MCS) is an iterative process, and the convergence time gets smaller with the increase in iteration number. There are two types of MCS: probabilistic and deterministic [127]. Probabilistic evolutionary methods, such as Latin hypercube sampling (LHS) and the k-means-based data clustering method (DCM), have been used to evaluate the objective function in the particle swarm optimization (PSO) algorithm [34]. The proposed method plays a significant role in mitigating power loss, improving the VDI, and decreasing dSTATCOM installation costs considering the uncertain nature of renewable energy sources (RESs). In this article, wind turbine (WT) and solar photovoltaic (PV) cells are considered, which are the algorithms applied to the IEEE 69 bust system. However, there is no proof of comparison of the results found from this method and other existing literature.
A mixed-integer second-order cone programming (MI-SOCP) is a deterministic convex optimization model proposed in [43]. This model aims to minimize the annual installation and operating costs of dSTATCOMs by finding the global optimum. The proposed method has reduced the cost by 13.71% compared to the vortex search algorithm (VSA) discussed in [47]. However, one of the limitations of the proposed strategy is the application to only radial distribution feeders.
In [128], a mixed-integer convex method has been proposed to reduce the annual operating cost of the network by optimally placing dSTATCOMs. The fitness function includes the annual energy loss cost of dSTATCOM placement, which is a convex function due to the resistances of distribution lines, and other investment costs can be approximated to the convex component due to the smaller sizes of dSTATCOM. Therefore, the proposed method can solve the fitness function in a convex environment. To check the validity, it is tested on the IEEE 33 bus system in both radial and meshed configurations. However, similar results have been found in [44] in terms of annual cost savings.
A decoupled optimization technique is proposed in [50] that involves mixed-integer convex optimization reformulation. This includes a mixed-integer quadratic programming (MIQP) model to detect the optimal locations and a second-order cone programming (SOCP) model to select optimal sizes. The objective is to reduce the annual energy loss cost and annual investment cost of dSTATCOM. Simulations are carried out on the IEEE 33 and the 69 bus systems, and a numerical comparison is presented. The decoupled method shows better results than the DCVSA [47].
The authors in [42] proposed a stochastic mixed-integer convex (SMIC) optimization technique by transforming a nonlinear problem into a convex one. The fitness function is a multi-objective function that includes a reduction in annual operating costs. The proposed methodology is tested on the IEEE 33, 69, and 89 bus systems.
6. Comprehensive Literature Review
A comprehensive literature survey of different research works based on dSTATCOM allocation has been summarized in Appendix A Table A1.
6.1. Distribution Network
Most of the research papers have used the IEEE 33 bus network as a test case scenario, which includes 48% of the total publications shown in Figure 5. The IEEE 69 has also been used in many articles, consisting of 15% of the total publications. Only 19% of them have used real distribution network data.
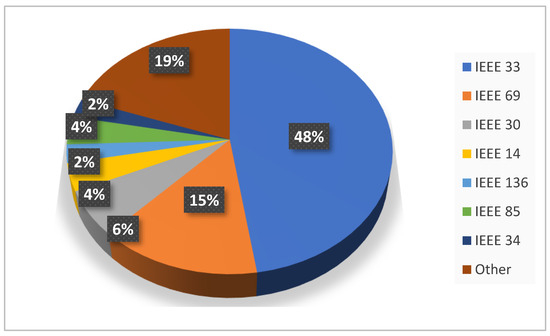
Figure 5.
Distribution network test system.
6.2. Load Flow Method
The backward/forward sweep method is one of the popular load flow methods used in the literature. Around 49% of the total publications have used the BFS as a load flow method, which is shown in Figure 6. A direct approach has been adopted in 16% of these publications. Another 13% have used successive approximation methods for load flow analysis.
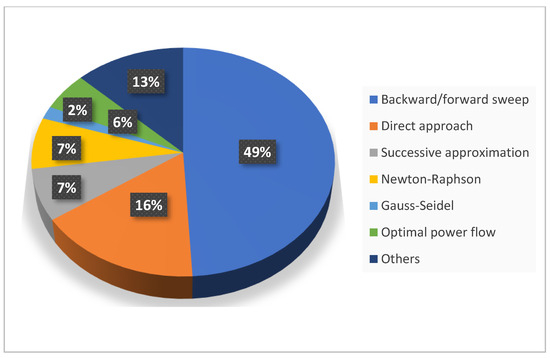
Figure 6.
Load flow methods used in research articles.
6.3. Optimization Methods
Figure 7 gives a complete set of algorithms being used in the publications, which fall under the six categories discussed earlier.
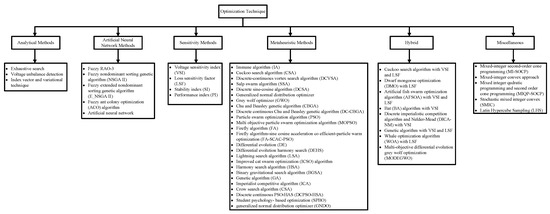
Figure 7.
Different algorithms used in the literature.
6.4. Optimization Tool
Most of the research articles have used MATLAB, which is a very powerful tool. MATLAB has been used for both load flow and optimization execution. However, there are other tools that have been used by the researchers for load flow and optimization procedures such as GAMS, DigSILENT, etc. In many publications, BONMIN and COUENNE solvers in GAMS have been to model mixed-integer nonlinear problems. The CVX tool in MATLAB has been used in some of the articles. The percentage of tools being used in the analysis has been shown in Figure 8.
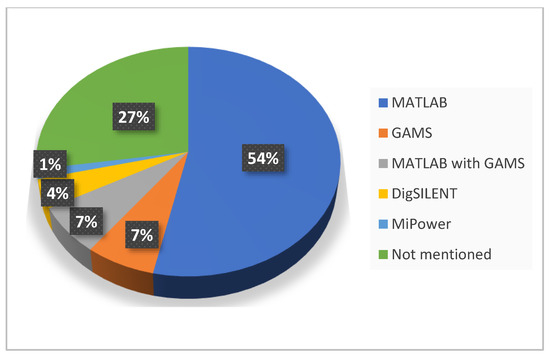
Figure 8.
The usage of software tools to solve placement problems.
7. Review Findings
This article considers the continual growth of interest in the optimal placement and sizing of dSTATCOM in distribution networks. After a comprehensive review, the following findings are reported here:
- The published research considers single- and multi-objective fitness functions. The optimization problem becomes complex if there are more objectives within the fitness function. Some of the latest literature has considered the convexification of the cost function. However, there is still scope for more research in handing these multi-objective cost functions and associated constraints;
- Though the implementation of analytical approaches for finding optimal allocation is simpler, easier, and has high precision in solutions that can be achieved, they are not suitable for solving multi-objective and multi-constrained nonlinear problems [66,129]. Metaheuristic methods can handle multi-objective problems and require fewer iterations. However, this comes with the problems of premature convergence, trapping at local optima, and giving unstable results, and shows less diversity among solutions. Hybrid metaheuristic methods can have a faster convergence rate than the single metaheuristic method and can solve mixed environment problems, such as discrete and continuous. Again, they require more setting parameters and skilled persons for coding;
- When an algorithm is used to solve an optimization problem, it is very difficult to understand the validity of the results. A comparison with other existing methods will give an idea of the efficiency, efficacy, and convergence rate of the proposed algorithm;
- From 2021 to 2023, interest has grown in using two-stage (master–slave) optimization techniques for the optimal placement and sizing of dSTATCOM. This technique has just considered annual operating cost minimization as a fitness function. However, loss reduction and voltage profile improvement should also be included within these two-stage approaches;
- Very few articles have reported on the control system or modulator used for the dSTATCOM VSC. As dSTATCOM is the main component of the placement problem, the controller should be described. Moreover, the new controllers suggested in recent literature might increase the performance of the optimization procedure;
- Most of the literature has considered dSTATCOMs without attached energy storage. It is recommended to use dSTATCOM with energy storage to increase the power quality and system reliability;
- There is very little work being performed on unbalanced networks. dSTATCOM can be a useful device to mitigate voltage unbalance in the distribution network. Therefore, voltage unbalance should be considered while performing placement problems;
- The distribution network can have a radial or meshed configuration. Some of the articles have considered both. However, it is useful to test the optimization methods on both networks to check the validity of the results, though the results will be slightly different for both configurations;
- Load variation or uncertainties is another factor that needs to be considered while performing placement and sizing problems; their position and sizing might change depending on load change;
- Voltage sag mitigation can be considered as an objective for fitness function;
- Another important factor of power systems is THD reduction, which has been neglected in the existing literature. THD reduction can be included as an objective of the fitness function to solve for optimal allocation of dSTATCOM;
- The power system should sustain the sustainable growth of renewable energy sources (RES). Another emerging load is electric vehicles (EVs). A combination of RES, BESS, EV, and dSTATCOM should be considered while performing the optimal placement and sizing problem.
8. Conclusions
This article presents a comprehensive literature review of the optimal placement and sizing of dSTATCOM in distribution networks. If dSTATCOMs are placed at optimal locations and with optimal sizes, then the power system obtains the benefits of loss reduction, voltage profile improvement, voltage stability improvement, THD reduction, annual energy loss cost reduction, and annual investment cost reduction. Moreover, it helps to avoid the cost of network upgrades. This paper discusses load flow methods used for the power flow solution. This review also gives an idea of the number of publications over the past years. A comparison is carried out among the existing literature in terms of power loss reduction, annual cost reduction, THD reduction, voltage profile improvement, and voltage stability improvement. Again, it also articulates different algorithms that fall under six categories discussed in the earlier portion of this paper. Analytical methods seem to be easier, but they do not consider the complexity and nonlinearities of multi-objective problems. Therefore, artificial neural networks, metaheuristics, or hybrid approaches are more appropriate for this multi-objective application due to their faster response. This paper presents a complete picture of the existing literature based on the optimal placement and sizing of dSTATCOMs.
Author Contributions
U.M.: conceptualization, formal analysis, methodology, resources, and writing–original draft; S.A.: administration, supervision, and writing—review and editing; P.W.: administration, supervision, and writing—review and editing. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| DER | Distributed energy resource |
| THD | Total harmonic distortion |
| LV | Low voltage |
| CPD | Custom power device |
| DVR | Dynamic voltage restorer |
| STATCOM | Static synchronous compensator |
| SVC | Static VAR compensator |
| UPQC | Unified PQ conditioner |
| PF | Power factor |
| BESS | Battery energy storage system |
| VSC | Voltage source converter |
| PWM | Pulse width modulation |
| WOA | Whale optimization algorithm |
| DG | Distributed generation |
| BAT | BA |
| PSO | Particle swarm optimization |
| FA | Firefly algorithm |
| SCAC | Sine–cosine acceleration coefficient |
| GA | Genetic algorithm |
| E_NSGA | Non-sorting genetic algorithm |
| MI | Mixed integer |
| SOCP | Second-order cone programming |
| SMIC | Stochastic mixed-integer convex |
| GNDO | Generalized normal distribution optimizer |
| DCVSA | Discrete–continuous vortex search algorithm |
| CBGA | Chu and Beasley genetic algorithm |
| NVPII | Network voltage profile improvement index |
| VSI | Voltage stability index |
| BFS | Backward/forward sweep |
| SAIDI | System average interruption duration index |
| SAIFI | System average interruption frequency index |
| CAIFI | Customer average interruption frequency index |
| CAIDI | Customer average interruption duration index |
| ENS | Energy not supplied |
| AENS | Average energy not supplied |
| PF | Power factor |
| ANN | Artificial neural network |
| PLI | Power loss index |
| LSF | Loss sensitivity factor |
| DICA-NM | Discrete imperialistic competition–Nelder–Mead |
| LSA | Lightning search algorithm |
| FVSI | Fast voltage sensitivity index |
| MODE | Multi-objective differential evolution |
| MOGA | Multi-objective genetic algorithm |
| SPEA | Strength-pareto evolutionary algorithm |
| MOPSO | Multi-objective particle swarm optimization |
| FDM | Fuzzy decision making |
| VDI | Voltage deviation index |
| IA | Immune algorithm |
| DE | Differential evolution |
| IBFA | Improved bacterial foraging algorithm |
| GWO | Grey wolf optimizer |
| SCL | Short circuit level |
| VDL | Voltage deviation level |
| NSL | Net saving level |
| EPRL | Environmental pollution reduction level |
| APLL | Active power loss level |
| AAC | Adaptive acceleration coefficient |
| APG | Autonomous particles groups |
| TVA | Time-varying acceleration |
| NDAC | Nonlinear dynamic acceleration coefficient PSO |
| WOA | Whale optimization algorithm |
| SSA | Salp swarm algorithm |
| AFSOA | Artificial fish swarm optimization algorithm |
| CFT | Curve fitting technique |
| CSA | Cuckoo search algorithm |
| BSA | Backtracking search algorithm |
| QOTLBO | Quasi-oppositional teaching learning-based optimization |
| DMO | Dwarf mongoose optimization |
| DA | Dragonfly algorithm |
| SGO | Shell game optimization |
| MCS | Monte Carlo simulation |
| LHS | Latin hypercube sampling |
| DCM | Data clustering method |
| WT | Wind turbine |
| MIQP | Mixed-integer quadratic programming |
| LSI | Loss sensitivity index |
| BGSA | Binary gravitation search algorithm |
| SI | Sensitivity index |
| ACO | Ant colony optimization |
| ICSO | Improved cat swarm optimization |
| HSA | Harmony search algorithm |
| VSF | Voltage sensitivity factor |
| MCSA | Modified crow search algorithm |
| COA | Coyote optimization algorithm |
Appendix A

Table A1.
Literature survey.
Table A1.
Literature survey.
| Reference | Year | Algorithm | Fitness Function | Constraints | Load Flow | Test Set | Solver | Contribution | Integration with other Device | Comparison with other Method |
|---|---|---|---|---|---|---|---|---|---|---|
| [129] | 2011 | DE | Multi-objective (power loss, voltage profile) | Voltage constraint, thermal constraint | Gauss–Seidel | IEEE 69 and Taiwan 83 | Network reconfiguration along with dSTATCOM allocation is considered to reduce losses and enhance the voltage profile | no | PSO | |
| [26] | 2011 | VSI, LSI, and GA | Multi-objective (power loss, voltage stability, reactive power) | Voltage constraint | Average model | Zanjan province of Iran | DIgSILENT | A compound voltage sensitivity index is introduced to find the optimal placement, and the GA is used to determine the optimal sizing | no | no |
| [25] | 2012 | ANN | Single objective (voltage sag) | IEEE 14 | MATLAB/Simulink | ANN uses post-fault voltage magnitude to find the locations of CPD and select an effective controller for voltage sag mitigation | no | DVR, UPQC | ||
| [72] | 2012 | BGSA | Multi-objective (voltage sag, reliability) | Voltage constraint, thermal constraint, power loss constraint | 47 bus system | Voltage sag is mitigated to improve the system reliability by short circuit analysis | No | no | ||
| [86] | 2013 | Exhaustive search technique | Multi-objective (power loss and voltage profile) | Power balance | Backward/forward power flow | IEEE 33 | Voltages and losses are calculated for each bus to place the STATCOM at the optimal position. Only one STATCOM can be placed | No | no | |
| [113] | 2013 | SI | Single objective (fast voltage recovery) | Nominal load flow | Radial 16 and 43 bus system | A sensitivity index is proposed to find the optimal sizing of dSTATCOM by ensuring fast recovery of voltage at generator buses | Wind, PV | no | ||
| [60] | 2013 | FA | Multi-objective (THD, voltage deviation, investment cost) | voltage constraint, reactive power constraint, | IEEE 16 | MATLAB | THD reduction is considered along with investment cost reduction. | GA, PSO | ||
| [22] | 2014 | IA | Multi-objective (power loss, installation cost voltage, and current profile) | Power balance constraint, thermal constraint, voltage constraint | Backward /forward sweep | IEEE 33 and IEEE 69 | MATLAB | Power loss reductions of 10.9% and 18% are achieved in IEEE 33 and 69 buses, respectively. Energy cost reductions of 10.89% and 18% are achieved in IEEE 33 and 69 buses, respectively. Shows better performance than the GA | no | GA |
| [130] | 2014 | SI | Multi-objective (voltage profile, power loss) | Voltage constraint, | Load flow is performed by compensating values for CP, CI, CZ | IEEE 33 | MATLAB | A sensitivity analysis is carried out to find the optimal location for dSTATCOM | no | no |
| [131] | 2014 | PSO | Multi-objective (power loss, voltage profile) | Voltage constraint, thermal constraint | Direct approach | IEEE 12 and IEEE 69 | MATLAB | The proposed method has reduced power loss and improved voltage profile | DG | Analytical method |
| [132] | 2015 | Fuzzy ACO | Multi-objective (power loss, voltage profile, load balancing) | Active power balance constraint, voltage constraint, thermal constraint, radiality constraint | Backward/forward sweep | IEEE 33 and Tai-Power 11.4 kV | MATLAB | Reconfiguration of the network is considered under different load levels | DG | ACO, fuzzy GA, fuzzy PSO |
| [35] | 2017 | VSI, BA, and CFT | Single objective (power loss) | active and reactive power balance constraints, voltage constraint, reactive power constraint, | Direct approach | IEEE 33, 69 | MATLAB | A hybrid approach consisting of the VSI and BAT is proposed to locate the optimal position and size of dSTATCOM considering different load levels. The CFT is used for optimal sizing per load level to obtain more accurate results | no | BFA |
| [39] | 2015 | Exhaustive search method | Multi-objective (power loss, voltage profile) | Voltage constraint, thermal constraint | Backward/forward sweep | IEEE 30 | The injected reactive power and corresponding power loss are calculated at each node | no | no | |
| [133] | 2015 | ICSO | Single objective (power loss) | Voltage constraint, radiality constraint | Newton–Raphson | IEEE 69 | Network reconfiguration is considered but is limited to radial networks. The algorithm has less convergence time | DG | PSO, CSO | |
| [134] | 2015 | HSA | Single objective (power loss) | Voltage constraint, active power balance constraint, reactive power constraint | Direct approach | IEEE 33 | MATLAB | Optimal allocation and sizing of dSTATCOM is performed by HSA by considering a single objective fitness function | no | IA |
| [121] | 2016 | Index vector and variational technique | Multi-objective (power loss, voltage profile, energy saving) | Active power loss constraint | Backward/forward sweep | IEEE 69 | MATLAB | The index vector is used for optimal placement and a variational technique is used to determine the optimal sizes of dSTATCOM where reconfiguration and load growth are considered | no | DE, fuzzy ACO |
| [135] | 2016 | DICA-NM, VSI | Multi-objective (power loss, voltage stability) | Voltage constraint, thermal constraint, reactive power constraint, active power constraint, thermal constraint | Backward/forward sweep | IEEE 30 | A hybrid approach is proposed and tested under light, medium, and peak loads | DG | no | |
| [136] | 2016 | GA | Multi-objective (loadability, energy loss cost, and investment cost) | Voltage constraint, active power constraint, reactive power constraint | Backward/forward sweep | IEEE 33 and IEEE 69 | Optimal allocation and selecting numbers and sizes of DG and dSTATCOM are performed by Pareto analysis. Loadability is considered | DG | no | |
| [59] | 2017 | VSI | Multi-objective (power loss, THD) | Voltage constraint, THD constraint | Backward/forward power flow | IEEE 34 | The optimization problem is solved by sensitivity analysis, and a reduction in losses and THD have been achieved | DG | no | |
| [114] | 2017 | LSI | Single objective (power loss) | Voltage constraint, voltage angle constraint | Newton–Raphson | IEEE 14 | MATLAB | A two-stage approach consisting of the LSI and Newton–Raphson load flow is used to locate the optimal solution | no | no |
| [118] | 2017 | VSF, BA | Single objective (power loss) | active and reactive power balance constraints, voltage constraint, reactive power constraint, | Backward/forward sweep | IEEE 33, 69 | MATLAB | A hybrid approach consisting of the VSF and BAT is proposed to locate the optimal position and size of dSTATCOM to improve the overall efficacy of the network | VSI, PSI, LSF, BFA | |
| [137] | 2017 | LSA | Multi-objective (power loss, voltage deviation, and VSI) | active and reactive power balance constraints, voltage constraint, active power constraint, reactive power constraint, | Backward/forward sweep | IEEE 33, 69 | MATLAB | The loads are varied with a step size of 1%. The CFT is used to determine the optimal sizing and the LSA is used for the optimal placement of dSTATCOM | DG | BFA, QOTLBO, BSA |
| [138] | 2017 | ICA | Multi-objective (power loss, voltage profile, load balancing, annual cost saving) | Voltage constraint, thermal constraint | Direct approach | IEEE 33 and IEEE 69 | MATLAB | Load uncertainty is considered | BFA, BA | |
| [15] | 2018 | LSF | Multi-objective (power loss, voltage profile) | Voltage constraint, active reactive power balance | Direct approach | IEEE 33 | MATLAB | Simultaneous placement of DG and dSTATCOM improves the overall network voltage profile and minimizes the active and reactive power losses | DG | no |
| [23] | 2018 | LSF and SI | Multi-objective (power loss, voltage profile) | Direct approach | IEEE 33 | An analytical approach is presented based on a stability index for the optimal placement and sizing of DG and dSTATCOM | DG | no | ||
| [40] | 2018 | NSGA II with FDM | Multi-objective (VDI, VSI, power loss) | Voltage constraint, reactive power constraint, thermal constraint | Backward/forward sweep | IEEE 33 and Portugese 94 bus system | MATLAB | NSGA II is used to solve multi-objective optimization problems, and FDM uses the Pareto front technique to determine the best solution considering load uncertainty | no | IA, BA |
| [139] | 2018 | DE | Multi-objective (power loss, zero sequence voltage unbalance, negative sequence voltage unbalance) | Active and reactive power balance constraints, voltage constraint | Backward/forward sweep | 25, 19 bus system | MATLAB | Negative and zero sequence voltage unbalance are considered while developing a 3-phase unbalanced dSTATCOM model | no | The method proposed in [140] |
| [141] | 2018 | SI | Multi-objective (power loss, voltage stability, voltage profile, energy loss cost) | Load flow based on KCL and KVL | UK 38 bus | MATLAB | A sensitivity index is proposed for the optimal placement and sizing under seasonal load growth for meshed networks only | no | FVSI, VSI, | |
| [142] | 2018 | MCSA | Multi-objective (power loss, voltage profile, pollution index, economic index) | Voltage constraint, power flow constraint | Backward/forward sweep | 51 bus real | MATLAB | Wind DG along with dSTATCOM shows better performance in terms of power loss minimization and voltage profile enhancement | DG | CSA, HSA, DE |
| [53] | 2018 | E_NSGA II | Multi-objective (improvement in voltage profile, environmental benefit, reliability of the network, and reduction in costs) | Voltage constraint, pf constraint, power flow constraint | Backward/forward sweep | IEEE 69 | MATLAB | The proposed method offers less convergence time and more diversity among solutions | PV, BESS | MOGA, SPEA, MOPSO |
| [51] | 2019 | MOPSO and TOPSIS | Multi-objective (power loss, voltage profile, loadability) | Active and reactive power balance constraints, voltage constraint, reactive power constraint, size constraint, thermal constraint | Backward/forward sweep | IEEE 33 and 69 | Loadbility is included along with power loss and voltage profile in the fitness function. Reconfiguration is considered | no | no | |
| [58] | 2019 | GWO | Multi-objective (power loss, voltage stability) | Active and reactive power balance constraints, voltage constraint, reactive power constraint, thermal constraint | Backward/forward power flow | IEEE 85 | The GWO is applied to solve allocation problems under multi-load levels | DG | no | |
| [57] | 2019 | VSI, LSF, and AFSOA | Single objective (power loss) | Voltage constraint, reactive power constraint | Backward/forward sweep | IEEE 33, 69 | MATLAB | The AFSOA is used to determine the optimal sizing and the VSI for finding the optimal location of dSTATCOM by reducing the losses and improving the voltage profile | DG | no |
| [143] | 2019 | GA | Single objective (power loss) | Voltage constraint, power balance constraint, thermal constraint | IEEE 37 | DG, dSTATCOM, and PHEV are placed with different static load models. The power factor is considered a system performance indicator | DG, PHEV | no | ||
| [144] | 2019 | EGWO | Single objective (power loss) | Active and reactive power balance constraint, voltage constraint, reactive power constraint, active power constraint, power factor constraint, thermal constraint | Backward/forward sweep | Egyptian network | MATLAB | The EGWO is an improved version of the GWO, which considers adaptive operators based on levy flight distribution. Load uncertainty is considered | DG | no |
| [98] | 2019 | GWO | Multi-objective (power loss, load balancing) | active power balance constraint, voltage constraint, reactive power constraint, radiality constraint | Direct approach | IEEE 33, IEEE 69, real-time 31 bus | The local solutions are determined by the index vector (IV), and the optimal solutions are found by the GWO. Reconfiguration of the network is also considered | no | GA, fuzzy GA | |
| [145] | 2019 | Analytical-COA | Multi-objective (power loss, voltage profile) | reactive power balance constraint, voltage constraint, reactive power constraint | IEEE 33, IEEE 69 | Sizing is determined by the analytical approach, where placement is performed by the COA | no | PSO, BA, IA, GA, hybrid GAM-PSO | ||
| [62] | 2020 | LSF, MODEGWO | Multi-objective (power loss, voltage deviation, allocation cost) | Active and reactive power balance constraint, voltage constraint, reactive power constraint | Backward/forward sweep | IEEE 33 | PV output uncertainties are estimated by Monte Carlo simulation methods, and different load levels are also considered | PV | NSGA II, MODEGWO | |
| [87] | 2020 | LSF, real power performance indicator (PI), voltage profile index (VPI), and power loss index (PLI) | Minimizing power loss and improving voltage profile | IEEE 14, IEEE 30 | DigSILENT PowerFactory | dSTATCOM is placed at the optimal position by using several analytical approaches. However, sizing is not considered here | no | no | ||
| [52] | 2020 | Exhaustive search method | Multi-objective (power loss, voltage profile) | Voltage constraint | Newton–Raphson | IEEE 33 | MiPower | Different load conditions with disturbance are considered while performing the exhaustive search | no | no |
| [146] | 2020 | LSF, WOA | Multi-objective (operating cost, power loss) | Active power balance constraint, voltage constraint, real power constraint, reactive power constraint | Backward/forward sweep | IEEE 33 and IEEE 136 | MATLAB | DG and dSTATCOM are placed simultaneously by combining the LSF and WOA | DG | BSA, BFA |
| [147] | 2020 | DEHSA | Multi-objective (power loss, system stability, operation cost) | Active and reactive power balance constraint, voltage constraint, reactive power constraint | Newton–Raphson | IEEE 30 | To find the global optima, mutation and cross-over stages are adopted. To enhance the diversity among the solutions, an opposition-based learning technique is also proposed | no | no | |
| [47] | 2021 | Discrete–continuous vortex search algorithm (DCVSA) | Multi-objective (energy loss cost and investment cost) | Active and reactive power balance constraints, voltage constraint, reactive power constraint, size constraint | Successive approximation power flow (SAPF) | IEEE 33 and 69 | MATLAB, GAMS with BONMIN and COUENNE solvers | The VSA is updated to apply in mixed environments, such as discrete and continuous. Reduction in annual energy losses is achieved by managing the amount of reactive power injection | no | no |
| [148] | 2021 | LSF and LSA-SM | Multi-objective (power loss, voltage deviation, and operational cost) | active and reactive power balance constraints, voltage constraint, active power constraint, reactive power constraint | Direct approach | IEEE 33 and 69 | MATLAB | The LSF is used for finding the optimal location and LSA-SM is used to find the optimal sizing of dSTATCOM | DG | LSA |
| [48] | 2021 | CBGA and SOCP | Multi-objective (annual energy loss cost and investment cost) | active and reactive power balance constraints, voltage constraint, reactive power constraint, size constraint | Optimal power flow (OPF) | IEEE 33 | GAMS | A master–slave two-stage algorithm is proposed to minimize the annual operating costs under different load levels | no | |
| [49] | 2021 | DC-CBGA | Multi-objective (annual energy loss cost and investment cost) | active and reactive power balance constraints, voltage constraint, reactive power constraint, size constraint | Successive approximation | IEEE 33 | GAMS | A mixed approach consisting of discrete–continuous codification is proposed for both radial and meshed configuration, and variations in loads are also considered | no | Genetix–Convex |
| [50] | 2021 | MIQP and SOCP | Multi-objective (annual energy loss cost and investment cost) | active and reactive power balance constraints, voltage constraint, reactive power constraint, size constraint | IEEE 33,69 | GAMS with BONMIN and COUENNE, CVX tool in MATLAB with Gurobi solver | The optimization methodology decouples the location and sizing problem. It only applies to radial configuration | No | DCVSA | |
| [41] | 2021 | Voltage unbalance detection | Single objective (energy losses) | active and reactive power balance constraints, voltage constraint, reactive power constraint, size constraint | Quasi-dynamic analysis | Four European distribution feeders | DIgSILENT | The proposed method takes voltage unbalances into consideration for the optimal placement of a single dSTATCOM | no | no |
| [69] | 2021 | VSI, LSF, BA | Single objective (power loss) | active and reactive power balance constraints, voltage constraint, reactive power constraint, active power constraint | Direct approach | IEEE 34, 85 | The VSI and LSF are used for the optimal allocation of dSTATCOM and DG, respectively, and the BAT is used for optimal sizing | DG | no | |
| [38] | 2021 | FA-SCAC-PSO | Multi-objective (APLL, VDL, SCL, NSL, EPRL) | active and reactive power balance constraints, voltage constraint, active power constraint, reactive power constraint, size constraint, thermal constraint | IEEE 33, 69, Algerian 205 bus | MATLAB | A hybrid algorithm consisting of three algorithms is proposed. Load uncertainty is considered | DG | PSO, SCAC-PSO, NDAC-PSO, AAC-PSO, APG-PSO, TVA-PSO | |
| [149] | 2021 | MSCA | Single objective (power loss) | Voltage constraint, thermal constraint, size constraint | IEEE 33, 69 | MATLAB | The traditional SCA is modified by introducing operational-based learning | no | no | |
| [33] | 2021 | WOA | Multi-objective (power loss, voltage profile, reliability) | active and reactive power balance constraints, voltage constraint, reactive power constraint, size constraint, thermal constraint, pf constraint | Backward/forward sweep | IEEE 33, Ahvaz 59 | The WOA shows high convergence speed and accuracy in determining the optimization problem. Variable load demands are considered | FPA, BA, GA, CSA, BFA | ||
| [43] | 2022 | Mixed-integer second-order cone programming (MI-SOCP) | Multi-objective (energy loss cost and investment cost) | active and reactive power balance constraints, voltage constraint, reactive power constraint, size constraint | Branch power flow | IEEE 33 | MATLAB with CVX and Gurobi solver | The MI-SOCP uses weighting factors to solve the multi-objective fitness function and find a global optimum and takes less computational time to converge | no | VSA |
| [44] | 2022 | Salp swarm algorithm (SSA) with backward/forward power flow | Multi-objective (annual energy loss cost and investment cost) | active and reactive power balance constraints, voltage constraint, reactive power constraint, size constraint | Backward/forward power flow | IEEE 33 | MATLAB, GAMS | A master–slave optimization approach containing the SSA and backward/forward sweep power flow considering different load levels is developed. The proposed method is tested on radial and meshed topology and is independent of network configuration | no | no |
| [128] | 2022 | A Mixed-integer convex approach | Multi-objective (annual energy loss cost and investment cost) | active and reactive power balance constraints, voltage constraint, reactive power constraint, size constraint | IEEE 33 | MATLAB, GAMS with BONMIN and COUENNE solvers, CVX tool with a Gorobi solver | A two-stage optimization method, including an exact nonlinear programming model and a mixed-integer convex model, is proposed to select the optimal siting and sizing of dSTATCOMs, irrespective of network configuration | no | SSA | |
| [36] | 2022 | Fuzzy base RAO-3 | Multi-objective (loss of power, voltage profile, PF) | reactive power constraint, active power constraint | Backward/forward sweep | IEEE 69 | MATLAB | The proposed methodology uses the RAO-3 algorithm to place EV, DG, and dSTATCOM simultaneously | EV, DG | Two-stage methodology |
| [150] | 2022 | DCPSO-HSA | Multi-objective (energy loss cost and investment cost) | active and reactive power balance constraints, voltage constraint, reactive power constraint, size constraint | Successive approximation | IEEE 33, 69 | MATLAB | A hybrid methodology is proposed to reduce the annual operating costs | no | GA-PSO, DCVSA |
| [73] | 2022 | SPBO | Multi-objective (power loss, voltage deviation, voltage stability, annual cost) | Voltage constraint | Backward/forward sweep | IEEE 33, 118 | MATLAB | Technological, economic, and environmental benefits are considered by four indices: RPLMI, BVVMI, SVSMI, and SACMI | DG | SOS, HHO |
| [45] | 2023 | Discrete sine–cosine algorithm (DCSA) with BONMIN solver using GAMS software | Multi-objective (annual energy loss cost and investment cost) | active and reactive power balance constraints, voltage constraint, reactive power constraint, size constraint | Optimal power flow (OPF) | IEEE 33 | MATLAB, GAMS with BONMIN | A master–slave optimization approach is adopted to find the global optimum point reduce the annual cost | no | The genetic convex algorithm, DCCBGA, SSA |
| [46] | 2023 | Generalized normal distribution optimizer (GNDO) with successive approximations of power flow | Multi-objective (annual energy loss cost and investment cost) | active and reactive power balance constraints, voltage constraint, reactive power constraint, size constraint | Optimal power flow (OPF) | IEEE 33 | MATLAB, GAMS | Discrete–continuous codification is used to model the GNDO method in radial and meshed configurations. The GNDO requires few parameters and is a much simpler implementation technique | no | SSA |
| [24] | 2023 | Dwarf mongoose optimization with LSF | Multi-objective (loss of power, operation cost, voltage profile) | active and reactive power balance constraints, voltage constraint, reactive power constraint | Backward/forward power flow | IEEE 30 | MATLAB | A hybrid optimization algorithm is proposed consisting of the LSF and DMO. Only one parameter needs to be tuned in the DMO | DG | DA, SGO, SSA |
| [42] | 2023 | SMIC | Multi-objective (annual energy loss cost and investment cost) | active and reactive power balance constraints, voltage constraint, reactive power constraint, size constraint | IEEE 33,69, 85 | GAMS with BONMIN and COUENNE, MATLAB with Gurobi and a CVX solver | The methodology solves the optimization problem by relaxing hyperbolic constraints and transforming a nonlinear model into a convex one | no | no | |
| [151] | 2023 | GNDO and successive approximation power flow | Multi-objective (annual energy loss cost and investment cost) | active and reactive power balance constraints, voltage constraint, reactive power constraint, active power constraint, size constraint | Successive approximation | IEEE 69, IEEE 33 | GAMS with BONMIN and COUENNE | A master–slave optimization method is proposed to determine the location and sizing of fixed-step capacitor banks and dSTATCOM in both radial and meshed networks | Capacitor banks | GA-PSO, VSA |
References
- Rohouma, W.; Balog, R.S.; Peerzada, A.A.; Begovic, M.M. D-STATCOM for harmonic mitigation in low voltage distribution network with high penetration of nonlinear loads. Renew. Energy 2020, 145, 1449–1464. [Google Scholar] [CrossRef]
- Paz-Rodríguez, A.; Castro-Ordoñez, J.F.; Montoya, O.D.; Giral-Ramírez, D.A. Optimal Integration of Photovoltaic Sources in Distribution Networks for Daily Energy Losses Minimization Using the Vortex Search Algorithm. Appl. Sci. 2021, 11, 4418. [Google Scholar] [CrossRef]
- Yuvaraj, T.; Devabalaji, K.R.; Srinivasan, S.; Prabaharan, N.; Hariharan, R.; Haes Alhelou, H.; Ashokkumar, B. Comparative analysis of various compensating devices in energy trading radial distribution system for voltage regulation and loss mitigation using Blockchain technology and Bat Algorithm. Energy Rep. 2021, 7, 8312–8321. [Google Scholar] [CrossRef]
- DİRİK, H.; GezegİN, C.; DİRİK, H.S. Reactive power compensation with hybrid compensator combining a synchronous motor and switched capacitors. Electr. Power Syst. Res. 2023, 216, 109010. [Google Scholar] [CrossRef]
- Jinn-Chang, W.; Hurng-Liahng, J.; Kuen-Der, W.; Shen, N.C. Power converter-based method for protecting three-phase power capacitor from harmonic destruction. IEEE Trans. Power Deliv. 2004, 19, 1434–1441. [Google Scholar] [CrossRef]
- HS, T.; Prakash, T.R.D. Reduction of power quality issues in micro-grid using fuzzy logic based DVR. Int. J. Appl. Eng. Res. 2018, 13, 9746–9751. [Google Scholar]
- Nafeh, A.A.; Heikal, A.; El-Sehiemy, R.A.; Salem, W.A. Intelligent fuzzy-based controllers for voltage stability enhancement of AC-DC micro-grid with D-STATCOM. Alex. Eng. J. 2022, 61, 2260–2293. [Google Scholar] [CrossRef]
- Loureiro, P.C.; Variz, A.M.; de Oliveira, L.W.; Oliveira, Â.R.; Pereira, J.L. ANN-based SVC tuning for voltage and harmonics control in microgrids. J. Control. Autom. Electr. Syst. 2017, 28, 114–122. [Google Scholar] [CrossRef]
- Alkahtani, A.A.; Alfalahi, S.T.Y.; Athamneh, A.A.; Al-Shetwi, A.Q.; Mansor, M.B.; Hannan, M.A.; Agelidis, V.G. Power Quality in Microgrids Including Supraharmonics: Issues, Standards, and Mitigations. IEEE Access 2020, 8, 127104–127122. [Google Scholar] [CrossRef]
- Chen, J.-H.; Tan, K.-H.; Lee, Y.-D. Intelligent Controlled DSTATCOM for Power Quality Enhancement. Energies 2022, 15, 4017. [Google Scholar] [CrossRef]
- Srinivas, M.; Hussain, I.; Singh, B. Combined LMS–LMF-Based Control Algorithm of DSTATCOM for Power Quality Enhancement in Distribution System. IEEE Trans. Ind. Electron. 2016, 63, 4160–4168. [Google Scholar] [CrossRef]
- Rezaeian-Marjani, S.; Talavat, V.; Galvani, S.; Habibinia, D. Probabilistic Assessment of DSTATCOM Operation in Distribution Systems Using Data Clustering Method. Electr. Power Compon. Syst. 2020, 48, 2063–2073. [Google Scholar] [CrossRef]
- Tuzikova, V.; Tlusty, J.; Muller, Z. A novel power losses reduction method based on a particle swarm optimization algorithm using STATCOM. Energies 2018, 11, 2851. [Google Scholar] [CrossRef]
- Pandu, S.B.; Sundarabalan, C.K.; Srinath, N.S.; Krishnan, T.S.; Priya, G.S.; Balasundar, C.; Sharma, J.; Soundarya, G.; Siano, P.; Alhelou, H.H. Power Quality Enhancement in Sensitive Local Distribution Grid Using Interval Type-II Fuzzy Logic Controlled DSTATCOM. IEEE Access 2021, 9, 59888–59899. [Google Scholar] [CrossRef]
- Iqbal, F.; Khan, M.T.; Siddiqui, A.S. Optimal placement of DG and DSTATCOM for loss reduction and voltage profile improvement. Alex. Eng. J. 2018, 57, 755–765. [Google Scholar] [CrossRef]
- Eid, A.; Kamel, S.; Zawbaa, H.M.; Dardeer, M. Improvement of active distribution systems with high penetration capacities of shunt reactive compensators and distributed generators using Bald Eagle Search. Ain Shams Eng. J. 2022, 13, 101792. [Google Scholar] [CrossRef]
- Isha, G.; Jagatheeswari, P. Optimal allocation of DSTATCOM and PV array in distribution system employing fuzzy-lightning search algorithm. Automatika 2021, 62, 339–352. [Google Scholar] [CrossRef]
- Singh, B.; Kandpal, M.; Hussain, I. Control of Grid Tied Smart PV-DSTATCOM System Using an Adaptive Technique. IEEE Trans. Smart Grid 2018, 9, 3986–3993. [Google Scholar] [CrossRef]
- Siddiqui, A.S.; Khan, M.T.; Iqbal, F. Determination of optimal location of TCSC and STATCOM for congestion management in deregulated power system. Int. J. Syst. Assur. Eng. Manag. 2017, 8, 110–117. [Google Scholar] [CrossRef]
- Repalle, B.M.; Rosalina, K.M.; Kumar, N.P. Fuzzy logic based optimal location and sizing of DSTATCOM in radial distribution systems. Int. J. Adv. Technol. Eng. Sci. 2014, 2, 122–129. [Google Scholar]
- Ghahremani, E.; Kamwa, I. Optimal allocation of STATCOM with energy storage to improve power system performance. In Proceedings of the 2014 IEEE PES T&D Conference and Exposition, Chicago, IL, USA, 14–17 April 2014; pp. 1–5. [Google Scholar]
- Taher, S.A.; Afsari, S.A. Optimal location and sizing of DSTATCOM in distribution systems by immune algorithm. Int. J. Electr. Power Energy Syst. 2014, 60, 34–44. [Google Scholar] [CrossRef]
- Weqar, B.; Khan, M.T.; Siddiqui, A.S. Optimal Placement of Distributed Generation and D-STATCOM in Radial Distribution Network. Smart Sci. 2018, 6, 125–133. [Google Scholar] [CrossRef]
- Raj, A.F.; Saravanan, A.G. An optimization approach for optimal location & size of DSTATCOM and DG. Appl. Energy 2023, 336, 120797. [Google Scholar]
- Tanti, D.; Verma, M.; Singh, B.; Mehrotra, O. Optimal placement of custom power devices in power system network to mitigate voltage sag under faults. Int. J. Power Electron. Drive Syst. 2012, 2, 267. [Google Scholar] [CrossRef]
- Samimi, A.; Golkar, M. A novel method for optimal placement of STATCOM in distribution networks using sensitivity analysis by DIgSILENT software. In Proceedings of the 2011 Asia-Pacific Power and Energy Engineering Conference, Wuhan, China, 25–28 March 2011; pp. 1–5. [Google Scholar]
- Kazmi, S.A.A.; Ameer Khan, U.; Ahmad, H.W.; Ali, S.; Shin, D.R. A Techno-Economic Centric Integrated Decision-Making Planning Approach for Optimal Assets Placement in Meshed Distribution Network Across the Load Growth. Energies 2020, 13, 1444. [Google Scholar] [CrossRef]
- Bagheri, M.; Nurmanova, V.; Abedinia, O.; Naderi, M.S. Enhancing Power Quality in Microgrids with a New Online Control Strategy for DSTATCOM Using Reinforcement Learning Algorithm. IEEE Access 2018, 6, 38986–38996. [Google Scholar] [CrossRef]
- Kefayat, M.; Ara, A.L.; Niaki, S.N. A hybrid of ant colony optimization and artificial bee colony algorithm for probabilistic optimal placement and sizing of distributed energy resources. Energy Convers. Manag. 2015, 92, 149–161. [Google Scholar] [CrossRef]
- Niknam, T.; Taheri, S.I.; Aghaei, J.; Tabatabaei, S.; Nayeripour, M. A modified honey bee mating optimization algorithm for multiobjective placement of renewable energy resources. Appl. Energy 2011, 88, 4817–4830. [Google Scholar] [CrossRef]
- Wang, D.T.-C.; Ochoa, L.F.; Harrison, G.P. DG impact on investment deferral: Network planning and security of supply. IEEE Trans. Power Syst. 2009, 25, 1134–1141. [Google Scholar] [CrossRef]
- Kaliaperumal Rukmani, D.; Thangaraj, Y.; Subramaniam, U.; Ramachandran, S.; Madurai Elavarasan, R.; Das, N.; Baringo, L.; Imran Abdul Rasheed, M. A New Approach to Optimal Location and Sizing of DSTATCOM in Radial Distribution Networks Using Bio-Inspired Cuckoo Search Algorithm. Energies 2020, 13, 4615. [Google Scholar] [CrossRef]
- Noori, A.; Zhang, Y.; Nouri, N.; Hajivand, M. Multi-Objective Optimal Placement and Sizing of Distribution Static Compensator in Radial Distribution Networks with Variable Residential, Commercial and Industrial Demands Considering Reliability. IEEE Access 2021, 9, 46911–46926. [Google Scholar] [CrossRef]
- Rezaeian-Marjani, S.; Galvani, S.; Talavat, V.; Farhadi-Kangarlu, M. Optimal allocation of D-STATCOM in distribution networks including correlated renewable energy sources. Int. J. Electr. Power Energy Syst. 2020, 122, 106178. [Google Scholar] [CrossRef]
- Yuvaraj, T.; Ravi, K.; Devabalaji, K.R. DSTATCOM allocation in distribution networks considering load variations using bat algorithm. Ain Shams Eng. J. 2017, 8, 391–403. [Google Scholar] [CrossRef]
- Mohanty, A.K.; Babu, P.S.; Salkuti, S.R. Fuzzy-Based Simultaneous Optimal Placement of Electric Vehicle Charging Stations, Distributed Generators, and DSTATCOM in a Distribution System. Energies 2022, 15, 8702. [Google Scholar] [CrossRef]
- Murty, V.V.S.N.; Kumar, A. Impact of D-STATCOM in distribution systems with load growth on stability margin enhancement and energy savings using PSO and GAMS. Int. Trans. Electr. Energy Syst. 2018, 28, e2624. [Google Scholar] [CrossRef]
- Zellagui, M.; Lasmari, A.; Settoul, S.; El-Sehiemy, R.A.; El-Bayeh, C.Z.; Chenni, R. Simultaneous allocation of photovoltaic DG and DSTATCOM for techno-economic and environmental benefits in electrical distribution systems at different loading conditions using novel hybrid optimization algorithms. Int. Trans. Electr. Energy Syst. 2021, 31, e12992. [Google Scholar] [CrossRef]
- Sanam, J.; Ganguly, S.; Panda, A.K. Placement of DSTATCOM in radial distribution systems for the compensation of reactive power. In Proceedings of the 2015 IEEE Innovative Smart Grid Technologies—Asia (ISGT ASIA), Bangkok, Thailand, 3–6 November 2015; pp. 1–6. [Google Scholar]
- Shahryari, E.; Shayeghi, H.; Moradzadeh, M. Probabilistic and multi-objective placement of D-STATCOM in distribution systems considering load uncertainty. Electr. Power Compon. Syst. 2018, 46, 27–42. [Google Scholar] [CrossRef]
- Fernández, G.; Martínez, A.; Galán, N.; Ballestín-Fuertes, J.; Muñoz-Cruzado-Alba, J.; López, P.; Stukelj, S.; Daridou, E.; Rezzonico, A.; Ioannidis, D. Optimal D-STATCOM Placement Tool for Low Voltage Grids. Energies 2021, 14, 4212. [Google Scholar] [CrossRef]
- Gil-González, W. Optimal Placement and Sizing of D-STATCOMs in Electrical Distribution Networks Using a Stochastic Mixed-Integer Convex Model. Electronics 2023, 12, 1565. [Google Scholar] [CrossRef]
- Montoya, O.D.; Garces, A.; Gil-González, W. Minimization of the distribution operating costs with D-STATCOMS: A mixed-integer conic model. Electr. Power Syst. Res. 2022, 212, 108346. [Google Scholar] [CrossRef]
- Mora-Burbano, J.A.; Fonseca-Díaz, C.D.; Montoya, O.D. Application of the SSA for Optimal Reactive Power Compensation in Radial and Meshed Distribution Using D-STATCOMs. Algorithms 2022, 15, 345. [Google Scholar] [CrossRef]
- Barreto-Parra, G.F.; Cortés-Caicedo, B.; Montoya, O.D. Optimal Integration of D-STATCOMs in Radial and Meshed Distribution Networks Using a MATLAB-GAMS Interface. Algorithms 2023, 16, 138. [Google Scholar] [CrossRef]
- García-Pineda, L.P.; Montoya, O.D. Optimal Reactive Power Compensation via D-STATCOMs in Electrical Distribution Systems by Applying the Generalized Normal Distribution Optimizer. Algorithms 2023, 16, 29. [Google Scholar] [CrossRef]
- Montoya, O.D.; Gil-González, W.; Hernández, J.C. Efficient Operative Cost Reduction in Distribution Grids Considering the Optimal Placement and Sizing of D-STATCOMs Using a Discrete-Continuous VSA. Appl. Sci. 2021, 11, 2175. [Google Scholar] [CrossRef]
- Montoya, O.D.; Chamorro, H.R.; Alvarado-Barrios, L.; Gil-González, W.; Orozco-Henao, C. Genetic-Convex Model for Dynamic Reactive Power Compensation in Distribution Networks Using D-STATCOMs. Appl. Sci. 2021, 11, 3353. [Google Scholar] [CrossRef]
- Castiblanco-Pérez, C.M.; Toro-Rodríguez, D.E.; Montoya, O.D.; Giral-Ramírez, D.A. Optimal Placement and Sizing of D-STATCOM in Radial and Meshed Distribution Networks Using a Discrete-Continuous Version of the Genetic Algorithm. Electronics 2021, 10, 1452. [Google Scholar] [CrossRef]
- Montoya, O.D.; Alvarado-Barrios, L.; Hernández, J.C. An Approximate Mixed-Integer Convex Model to Reduce Annual Operating Costs in Radial Distribution Networks Using STATCOMs. Electronics 2021, 10, 3102. [Google Scholar] [CrossRef]
- Rezaeian Marjani, S.; Talavat, V.; Galvani, S. Optimal allocation of D-STATCOM and reconfiguration in radial distribution network using MOPSO algorithm in TOPSIS framework. Int. Trans. Electr. Energy Syst. 2019, 29, e2723. [Google Scholar] [CrossRef]
- Magadum, R.B.; Chitragar, N.R.; Dodamani, S.N.; Gopikrishna, P. Impact on Voltage Stability with Integration of Multiple STATCOM at Different Loading Conditions. In Proceedings of the 2020 5th International Conference on Devices, Circuits and Systems (ICDCS), Coimbatore, India, 5–6 March 2020; pp. 321–325. [Google Scholar]
- Ghatak, S.R.; Sannigrahi, S.; Acharjee, P. Multi-Objective Approach for Strategic Incorporation of Solar Energy Source, Battery Storage System, and DSTATCOM in a Smart Grid Environment. IEEE Syst. J. 2018, 13, 3038–3049. [Google Scholar] [CrossRef]
- Devabalaji, K.; Ravi, K. Optimal size and siting of multiple DG and DSTATCOM in radial distribution system using bacterial foraging optimization algorithm. Ain Shams Eng. J. 2016, 7, 959–971. [Google Scholar] [CrossRef]
- Sirjani, R. Optimal placement and sizing of PV-STATCOM in power systems using empirical data and adaptive particle swarm optimization. Sustainability 2018, 10, 727. [Google Scholar] [CrossRef]
- Khan, B.; Redae, K.; Gidey, E.; Mahela, O.P.; Taha, I.B.M.; Hussien, M.G. Optimal integration of DSTATCOM using improved bacterial search algorithm for distribution network optimization. Alex. Eng. J. 2022, 61, 5539–5555. [Google Scholar] [CrossRef]
- Salkuti, S.R. Optimal location and sizing of DG and D-STATCOM in distribution networks. Indones. J. Electr. Eng. Comput. Sci. 2019, 16, 1107–1114. [Google Scholar]
- Mohamed, M.A.E.S.; Mohammed, A.A.E.; Abd Elhamed, A.M.; Hessean, M.E. Optimal Allocation of Photovoltaic Based and DSTATCOM in a Distribution Network under Multi Load Levels: Optimal Allocation of Photovoltaic Based and DSTATCOM in a Distribution Network under Multi Load Levels. Eur. J. Eng. Technol. Res. 2019, 4, 114–119. [Google Scholar] [CrossRef]
- Gupta, A.R. Effect of optimal allocation of multiple DG and D-STATCOM in radial distribution system for minimizing losses and THD. In Proceedings of the 2017 7th International Symposium on Embedded Computing and System Design (ISED), Durgapur, India, 18–20 December 2017; pp. 1–5. [Google Scholar]
- Farhoodnea, M.; Mohamed, A.; Shareef, H.; Zayandehroodi, H. Optimum D-STATCOM placement using firefly algorithm for power quality enhancement. In Proceedings of the 2013 IEEE 7th international power engineering and optimization conference (PEOCO), Langkawi, Malaysia, 3–4 June 2013; pp. 98–102. [Google Scholar]
- IEEE Std 519-2014 (Revision of IEEE Std 519-1992); IEEE Recommended Practice and Requirements for Harmonic Control in Electric Power Systems. IEEE: Piscataway, NJ, USA, 2014; pp. 1–29.
- Zhang, T.; Yu, L. Optimal allocation of DSTATCOM considering the uncertainty of photovoltaic systems. IEEJ Trans. Electr. Electron. Eng. 2020, 15, 355–363. [Google Scholar] [CrossRef]
- Elseify, M.A.; Kamel, S.; Nasrat, L.; Jurado, F. Multi-objective optimal allocation of multiple capacitors and distributed generators considering different load models using Lichtenberg and thermal exchange optimization techniques. Neural Comput. Appl. 2023, 35, 11867–11899. [Google Scholar] [CrossRef]
- Teng, J.-H. A direct approach for distribution system load flow solutions. IEEE Trans. Power Deliv. 2003, 18, 882–887. [Google Scholar] [CrossRef]
- Chaib, A.E.; Bouchekara, H.R.E.H.; Mehasni, R.; Abido, M.A. Optimal power flow with emission and non-smooth cost functions using backtracking search optimization algorithm. Int. J. Electr. Power Energy Syst. 2016, 81, 64–77. [Google Scholar] [CrossRef]
- Georgilakis, P.S.; Hatziargyriou, N.D. Optimal distributed generation placement in power distribution networks: Models, methods, and future research. IEEE Trans. Power Syst. 2013, 28, 3420–3428. [Google Scholar] [CrossRef]
- Ehsan, A.; Yang, Q. State-of-the-art techniques for modelling of uncertainties in active distribution network planning: A review. Appl. Energy 2019, 239, 1509–1523. [Google Scholar] [CrossRef]
- Li, Y.; Feng, B.; Wang, B.; Sun, S. Joint planning of distributed generations and energy storage in active distribution networks: A Bi-Level programming approach. Energy 2022, 245, 123226. [Google Scholar] [CrossRef]
- Salkuti, S.R. Optimal allocation of DG and D-STATCOM in a distribution system using evolutionary based Bat algorithm. Int. J. Adv. Comput. Sci. Appl. 2021, 12, 360–365. [Google Scholar] [CrossRef]
- Yang, N.-C.; Chang, Z.-H. Optimal Capacity and Location for STATCOM with Seasonal Wind Power Prediction Using C-Vine Copula. Mathematics 2023, 11, 2815. [Google Scholar] [CrossRef]
- Mumtahina, U.; Alakahoon, S.; Wolfs, P. Optimal d-STATCOM Placement using OpenDSS/Matlab. In Proceedings of the 2021 IEEE PES Innovative Smart Grid Technologies—Asia (ISGT Asia), Brisbane, Australia, 5–8 December 2021; pp. 1–5. [Google Scholar]
- Salman, N.; Mohamed, A.; Shareef, H. Reliability improvement in distribution systems by optimal placement of DSTATCOM using binary gravitational search algorithm. Przegląd Elektrotechniczny 2012, 88, 295–299. [Google Scholar]
- Dash, S.K.; Mishra, S.; Abdelaziz, A.Y.; Hong, J.; Geem, Z.W. Optimal Planning of Multitype DGs and D-STATCOMs in Power Distribution Network Using an Efficient Parameter Free Metaheuristic Algorithm. Energies 2022, 15, 3433. [Google Scholar] [CrossRef]
- Oda, E.S.; Hamed, A.M.A.E.; Ali, A.; Elbaset, A.A.; Sattar, M.A.E.; Ebeed, M. Stochastic Optimal Planning of Distribution System Considering Integrated Photovoltaic-Based DG and DSTATCOM Under Uncertainties of Loads and Solar Irradiance. IEEE Access 2021, 9, 26541–26555. [Google Scholar] [CrossRef]
- Sridhar, J.; Prakash, R. Multi-objective whale optimization based minimization of loss, maximization of voltage stability considering cost of DG for optimal sizing and placement of DG. Int. J. Electr. Comput. Eng. IJECE 2019, 9, 835–839. [Google Scholar] [CrossRef]
- Sekhar, P.C.; Deshpande, R.A.; Sankar, V. Evaluation and improvement of reliability indices of electrical power distribution system. In Proceedings of the 2016 National Power Systems Conference (NPSC), Bhubaneswar, India, 19–21 December 2016; pp. 1–6. [Google Scholar]
- Rodríguez-Montañés, M.; Rosendo-Macías, J.A.; Gómez-Expósito, A.; Tévar, G. Algebraic Framework for Outage Information Management in Distribution Networks. IEEE Trans. Power Syst. 2018, 33, 6806–6815. [Google Scholar] [CrossRef]
- Jamshid, S.; Abrar, M. Evaluation of Load Point and Customer Point Indices of a Distribution Generation System. In Proceedings of the 2020 International Youth Conference on Radio Electronics, Electrical and Power Engineering (REEPE), Moscow, Russia, 12–14 March 2020; pp. 1–5. [Google Scholar]
- Ghiasi, M.; Ghadimi, N.; Ahmadinia, E. An analytical methodology for reliability assessment and failure analysis in distributed power system. SN Appl. Sci. 2018, 1, 44. [Google Scholar] [CrossRef]
- Schuerger, R.; Arno, R.; Dowling, N. Why Existing Utility Metrics Do Not Work for Industrial Reliability Analysis. IEEE Trans. Ind. Appl. 2016, 52, 2801–2806. [Google Scholar] [CrossRef]
- Nowdeh, S.A.; Davoudkhani, I.F.; Moghaddam, M.H.; Najmi, E.S.; Abdelaziz, A.Y.; Ahmadi, A.; Razavi, S.-E.; Gandoman, F.H. Fuzzy multi-objective placement of renewable energy sources in distribution system with objective of loss reduction and reliability improvement using a novel hybrid method. Appl. Soft Comput. 2019, 77, 761–779. [Google Scholar] [CrossRef]
- Moghaddam, M.J.H.; Kalam, A.; Nowdeh, S.A.; Ahmadi, A.; Babanezhad, M.; Saha, S. Optimal sizing and energy management of stand-alone hybrid photovoltaic/wind system based on hydrogen storage considering LOEE and LOLE reliability indices using flower pollination algorithm. Renew. Energy 2019, 135, 1412–1434. [Google Scholar] [CrossRef]
- Abdelaziz, A.Y.; Ali, E.S.; Abd Elazim, S.M. Flower Pollination Algorithm and Loss Sensitivity Factors for optimal sizing and placement of capacitors in radial distribution systems. Int. J. Electr. Power Energy Syst. 2016, 78, 207–214. [Google Scholar] [CrossRef]
- Ali, E.S.; Abd Elazim, S.M.; Abdelaziz, A.Y. Improved Harmony Algorithm and Power Loss Index for optimal locations and sizing of capacitors in radial distribution systems. Int. J. Electr. Power Energy Syst. 2016, 80, 252–263. [Google Scholar] [CrossRef]
- Sanam, J. Optimization of planning cost of radial distribution networks at different loads with the optimal placement of distribution STATCOM using differential evolution algorithm. Soft Comput. 2020, 24, 13269–13284. [Google Scholar] [CrossRef]
- Hussain, S.M.S.; Subbaramiah, M. An analytical approach for optimal location of DSTATCOM in radial distribution system. In Proceedings of the 2013 International Conference on Energy Efficient Technologies for Sustainability, Nagercoil, India, 10–12 April 2013; pp. 1365–1369. [Google Scholar]
- Ismail, B.; Wahab, N.I.A.; Othman, M.L.; Radzi, M.A.M.; Vijayakumar, K.N.; Naain, M.M. Analytical approaches on optimal placement of STATCOM under contingency occasions. In Proceedings of the 2020 2nd International Conference on Smart Power & Internet Energy Systems (SPIES), Bangkok, Thailand, 15–18 September 2020; pp. 7–12. [Google Scholar]
- Murata, T.; Ishibuchi, H. MOGA: Multi-objective genetic algorithms. In Proceedings of the IEEE International Conference on Evolutionary Computation, Troyes, France, 25–27 October 2006; pp. 289–294. [Google Scholar]
- Zitzler, E.; Thiele, L. Multiobjective evolutionary algorithms: A comparative case study and the strength Pareto approach. IEEE Trans. Evol. Comput. 1999, 3, 257–271. [Google Scholar] [CrossRef]
- Abido, M. Multiobjective particle swarm optimization for environmental/economic dispatch problem. Electr. Power Syst. Res. 2009, 79, 1105–1113. [Google Scholar] [CrossRef]
- Rao, R. Rao algorithms: Three metaphor-less simple algorithms for solving optimization problems. Int. J. Ind. Eng. Comput. 2020, 11, 107–130. [Google Scholar] [CrossRef]
- Gampa, S.R.; Jasthi, K.; Goli, P.; Das, D.; Bansal, R. Grasshopper optimization algorithm based two stage fuzzy multiobjective approach for optimum sizing and placement of distributed generations, shunt capacitors and electric vehicle charging stations. J. Energy Storage 2020, 27, 101117. [Google Scholar] [CrossRef]
- Timmis, J.; Hone, A.; Stibor, T.; Clark, E. Theoretical advances in artificial immune systems. Theor. Comput. Sci. 2008, 403, 11–32. [Google Scholar] [CrossRef]
- Das, S.; Suganthan, P.N. Differential Evolution: A Survey of the State-of-the-Art. IEEE Trans. Evol. Comput. 2011, 15, 4–31. [Google Scholar] [CrossRef]
- Shuaib, Y.M.; Kalavathi, M.S.; Rajan, C.C.A. Optimal capacitor placement in radial distribution system using gravitational search algorithm. Int. J. Electr. Power Energy Syst. 2015, 64, 384–397. [Google Scholar] [CrossRef]
- Amjady, N.; Fatemi, H.; Zareipour, H. Solution of Optimal Power Flow Subject to Security Constraints by a New Improved Bacterial Foraging Method. IEEE Trans. Power Syst. 2012, 27, 1311–1323. [Google Scholar] [CrossRef]
- Doğan, B.; Ölmez, T. Vortex search algorithm for the analog active filter component selection problem. AEU-Int. J. Electron. Commun. 2015, 69, 1243–1253. [Google Scholar] [CrossRef]
- Selvaraj, G.; Rajangam, K. Multi-objective grey wolf optimizer algorithm for combination of network reconfiguration and D-STATCOM allocation in distribution system. Int. Trans. Electr. Energy Syst. 2019, 29, e12100. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Ziyu, T.; Dingxue, Z. A modified particle swarm optimization with an adaptive acceleration coefficients. In Proceedings of the 2009 Asia-Pacific Conference on Information Processing, Shenzhen, China, 18–19 July 2009; pp. 330–332. [Google Scholar]
- Mirjalili, S.; Lewis, A.; Sadiq, A.S. Autonomous particles groups for particle swarm optimization. Arab. J. Sci. Eng. 2014, 39, 4683–4697. [Google Scholar] [CrossRef]
- Ratnaweera, A.; Halgamuge, S.K.; Watson, H.C. Self-organizing hierarchical particle swarm optimizer with time-varying acceleration coefficients. IEEE Trans. Evol. Comput. 2004, 8, 240–255. [Google Scholar] [CrossRef]
- Chen, K.; Zhou, F.; Wang, Y.; Yin, L. An ameliorated particle swarm optimizer for solving numerical optimization problems. Appl. Soft Comput. 2018, 73, 482–496. [Google Scholar] [CrossRef]
- Chen, K.; Zhou, F.; Yin, L.; Wang, S.; Wang, Y.; Wan, F. A hybrid particle swarm optimizer with sine cosine acceleration coefficients. Inf. Sci. 2018, 422, 218–241. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Abul’Wafa, A.R. Optimal capacitor allocation in radial distribution systems for loss reduction: A two stage method. Electr. Power Syst. Res. 2013, 95, 168–174. [Google Scholar] [CrossRef]
- Yuvaraj, T.; Ravi, K. Multi-objective simultaneous DG and DSTATCOM allocation in radial distribution networks using cuckoo searching algorithm. Alex. Eng. J. 2018, 57, 2729–2742. [Google Scholar] [CrossRef]
- Momoh, J.A.; Reddy, S.S. Optimal location of FACTS for ATC enhancement. In Proceedings of the 2014 IEEE PES General Meeting|Conference & Exposition, National Harbor, MD, USA, 27–31 July 2014; pp. 1–5. [Google Scholar]
- Mirjalili, S.; Gandomi, A.H.; Mirjalili, S.Z.; Saremi, S.; Faris, H.; Mirjalili, S.M. Salp Swarm Algorithm: A bio-inspired optimizer for engineering design problems. Adv. Eng. Softw. 2017, 114, 163–191. [Google Scholar] [CrossRef]
- Zhang, Y.; Jin, Z.; Mirjalili, S. Generalized normal distribution optimization and its applications in parameter extraction of photovoltaic models. Energy Convers. Manag. 2020, 224, 113301. [Google Scholar] [CrossRef]
- Mahdad, B.; Srairi, K. A new interactive sine cosine algorithm for loading margin stability improvement under contingency. Electr. Eng. 2018, 100, 913–933. [Google Scholar] [CrossRef]
- Soroudi, A. Power System Optimization Modeling in GAMS; Springer: Berlin/Heidelberg, Germany, 2017; Volume 78. [Google Scholar]
- Aziz, T.; Mhaskar, U.; Saha, T.K.; Mithulananthan, N. An index for STATCOM placement to facilitate grid integration of DER. IEEE Trans. Sustain. Energy 2013, 4, 451–460. [Google Scholar] [CrossRef]
- Rao, V.S.; Rao, R.S. Optimal placement of STATCOM using two stage algorithm for enhancing power system static security. Energy Procedia 2017, 117, 575–582. [Google Scholar] [CrossRef]
- Panda, A.; Tripathy, M. Optimal power flow solution of wind integrated power system using modified bacteria foraging algorithm. Int. J. Electr. Power Energy Syst. 2014, 54, 306–314. [Google Scholar] [CrossRef]
- Luan, X.-Y.; Li, Z.-P.; Liu, T.-Z. A novel attribute reduction algorithm based on rough set and improved artificial fish swarm algorithm. Neurocomputing 2016, 174, 522–529. [Google Scholar] [CrossRef]
- Jaddi, N.S.; Abdullah, S.; Hamdan, A.R. Optimization of neural network model using modified bat-inspired algorithm. Appl. Soft Comput. 2015, 37, 71–86. [Google Scholar] [CrossRef]
- Yuvaraj, T.; Ravi, K.; Devabalaji, K. DSTATCOM allocation in the radial distribution networks with different stability indices using bat algorithm. Gazi Univ. J. Sci. 2017, 30, 314–328. [Google Scholar]
- Nguyen, T.T.; Nguyen, T.T. An improved cuckoo search algorithm for the problem of electric distribution network reconfiguration. Appl. Soft Comput. 2019, 84, 105720. [Google Scholar] [CrossRef]
- Yang, X.-S.; Deb, S. Cuckoo search: Recent advances and applications. Neural Comput. Appl. 2014, 24, 169–174. [Google Scholar] [CrossRef]
- Gupta, A.R.; Kumar, A. Energy Saving Using D-STATCOM Placement in Radial Distribution System under Reconfigured Network. Energy Procedia 2016, 90, 124–136. [Google Scholar] [CrossRef]
- Khorram-Nia, R.; Baziar, A.; Kavousi-Fard, A. A novel stochastic framework for the optimal placement and sizing of distribution static compensator. J. Intell. Learn. Syst. Appl. 2013, 5, 90–98. [Google Scholar] [CrossRef]
- El-Fergany, A. Optimal allocation of multi-type distributed generators using backtracking search optimization algorithm. Int. J. Electr. Power Energy Syst. 2015, 64, 1197–1205. [Google Scholar] [CrossRef]
- Sultana, S.; Roy, P.K. Multi-objective quasi-oppositional teaching learning based optimization for optimal location of distributed generator in radial distribution systems. Int. J. Electr. Power Energy Syst. 2014, 63, 534–545. [Google Scholar] [CrossRef]
- Agushaka, J.O.; Ezugwu, A.E.; Abualigah, L. Dwarf Mongoose Optimization Algorithm. Comput. Methods Appl. Mech. Eng. 2022, 391, 114570. [Google Scholar] [CrossRef]
- Babu, B.S. Adaptive Dragonfly Optimization Based Placement of Capacitor Banks for Voltage Stability Enhancement in Distribution Networks. Strateg. Plan. Energy Environ. 2021, 40, 25–38. [Google Scholar] [CrossRef]
- Martinez, J.A.; Guerra, G. A parallel Monte Carlo method for optimum allocation of distributed generation. IEEE Trans. Power Syst. 2014, 29, 2926–2933. [Google Scholar] [CrossRef]
- Garrido, V.M.; Montoya, O.D.; Medina-Quesada, Á.; Hernández, J.C. Optimal Reactive Power Compensation in Distribution Networks with Radial and Meshed Structures Using D-STATCOMs: A Mixed-Integer Convex Approach. Sensors 2022, 22, 8676. [Google Scholar] [CrossRef] [PubMed]
- Jazebi, S.; Hosseinian, S.H.; Vahidi, B. DSTATCOM allocation in distribution networks considering reconfiguration using differential evolution algorithm. Energy Convers. Manag. 2011, 52, 2777–2783. [Google Scholar] [CrossRef]
- Jain, A.; Gupta, A.; Kumar, A. An efficient method for D-STATCOM placement in radial distribution system. In Proceedings of the 2014 IEEE 6th India International Conference on Power Electronics (IICPE), Kurukshetra, India, 8–10 December 2014; pp. 1–6. [Google Scholar]
- Devi, S.; Geethanjali, M. Optimal location and sizing determination of Distributed Generation and DSTATCOM using Particle Swarm Optimization algorithm. Int. J. Electr. Power Energy Syst. 2014, 62, 562–570. [Google Scholar] [CrossRef]
- Tolabi, H.B.; Ali, M.H.; Rizwan, M. Simultaneous reconfiguration, optimal placement of DSTATCOM, and photovoltaic array in a distribution system based on fuzzy-ACO approach. IEEE Trans. Sustain. Energy 2014, 6, 210–218. [Google Scholar] [CrossRef]
- Kanwar, N.; Gupta, N.; Niazi, K.; Swarnkar, A. Improved cat swarm optimization for simultaneous allocation of DSTATCOM and DGs in distribution systems. J. Renew. Energy 2015, 2015, 1–10. [Google Scholar] [CrossRef]
- Yuvaraj, T.; Devabalaji, K.; Ravi, K. Optimal placement and sizing of DSTATCOM using harmony search algorithm. Energy Procedia 2015, 79, 759–765. [Google Scholar] [CrossRef]
- Chabok, B.S.; Ashouri, A. Optimal placement of D-STATCOMs into the radial distribution networks in the presence of distributed generations. Am. J. Electr. Electron. Eng. 2016, 4, 40–48. [Google Scholar]
- Karami, H.; Zaker, B.; Vahidi, B.; Gharehpetian, G.B. Optimal multi-objective number, locating, and sizing of distributed generations and distributed static compensators considering loadability using the genetic algorithm. Electr. Power Compon. Syst. 2016, 44, 2161–2171. [Google Scholar] [CrossRef]
- Thangaraj, Y.; Kuppan, R. Multi-objective simultaneous placement of DG and DSTATCOM using novel lightning search algorithm. J. Appl. Res. Technol. 2017, 15, 477–491. [Google Scholar] [CrossRef]
- Sedighizadeh, M.; Eisapour-Moarref, A. The imperialist competitive algorithm for optimal multi-objective location and sizing of DSTATCOM in distribution systems considering loads uncertainty. INAE Lett. 2017, 2, 83–95. [Google Scholar] [CrossRef]
- Samal, P.; Mohanty, S.; Ganguly, S. Modeling, optimal sizing, and allocation of DSTATCOM in unbalanced radial distribution systems using differential evolution algorithm. Int. J. Numer. Model. Electron. Netw. Devices Fields 2018, 31, e2351. [Google Scholar] [CrossRef]
- Samal, P.; Mohanty, S.; Ganguly, S. Effect of DSTATCOM allocation on the performance of an unbalanced radial distribution systems. In Proceedings of the 2016 IEEE International Conference on Engineering and Technology (ICETECH), Coimbatore, India, 17–18 March 2016; pp. 927–931. [Google Scholar]
- Gupta, A.R.; Kumar, A. Optimal placement of D-STATCOM using sensitivity approaches in mesh distribution system with time variant load models under load growth. Ain Shams Eng. J. 2018, 9, 783–799. [Google Scholar] [CrossRef]
- Sannigrahi, S.; Acharjee, P. Implementation of crow search algorithm for optimal allocation of DG and DSTATCOM in practical distribution system. In Proceedings of the 2018 International Conference on Power, Instrumentation, Control and Computing (PICC), Thrissur, India, 18–20 January 2018; pp. 1–6. [Google Scholar]
- Singh, B.; Singh, S. GA-based optimization for integration of DGs, STATCOM and PHEVs in distribution systems. Energy Rep. 2019, 5, 84–103. [Google Scholar] [CrossRef]
- Kamel, S.; Ramadan, A.; Ebeed, M.; Yu, J.; Xie, K.; Wu, T. Assessment integration of wind-based DG and DSTATCOM in Egyptian distribution grid considering load demand uncertainty. In Proceedings of the 2019 IEEE Innovative Smart Grid Technologies-Asia (ISGT Asia), Chengdu, China, 21–24 May 2019; pp. 1288–1293. [Google Scholar]
- Amin, A.; Kamel, S.; Selim, A.; Nasrat, L. Optimal placement of distribution static compensators in radial distribution systems using hybrid analytical-coyote optimization technique. In Proceedings of the 2019 21st International Middle East Power Systems Conference (MEPCON), Cairo, Egypt, 17–19 December 2019; pp. 982–987. [Google Scholar]
- Yuvaraj, T.; Devabalaji, K.; Thanikanti, S.B. Simultaneous allocation of DG and DSTATCOM using whale optimization algorithm. Iran. J. Sci. Technol. Trans. Electr. Eng. 2020, 44, 879–896. [Google Scholar] [CrossRef]
- Zhang, T.; Xu, X.; Li, Z.; Abu-Siada, A.; Guo, Y. Optimum location and parameter setting of STATCOM based on improved differential evolution harmony search algorithm. IEEE Access 2020, 8, 87810–87819. [Google Scholar] [CrossRef]
- Chinnaraj, S.G.R.; Kuppan, R. Optimal sizing and placement of multiple renewable distribution generation and DSTATCOM in radial distribution systems using hybrid lightning search algorithm-simplex method optimization algorithm. Comput. Intell. 2021, 37, 1673–1690. [Google Scholar] [CrossRef]
- Dash, S.K.; Mishra, S. Simultaneous optimal placement and sizing of D-STATCOMs using a modified sine cosine algorithm. In Advances in Intelligent Computing and Communication: Proceedings of ICAC 2020; Springer: Singapore, 2021; pp. 423–436. [Google Scholar]
- Grisales-Noreña, L.F.; Montoya, O.D.; Hernández, J.C.; Ramos-Paja, C.A.; Perea-Moreno, A.-J. A Discrete-Continuous PSO for the Optimal Integration of D-STATCOMs into Electrical Distribution Systems by Considering Annual Power Loss and Investment Costs. Mathematics 2022, 10, 2453. [Google Scholar] [CrossRef]
- Montoya, O.D.; Gil-González, W.; Hernández, J.C. Efficient Integration of Fixed-Step Capacitor Banks and D-STATCOMs in Radial and Meshed Distribution Networks Considering Daily Operation Curves. Energies 2023, 16, 3532. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).