Analysis of the DC-Link Voltage Ripple for the Three-Phase Voltage Source Converter under Nonlinear Output Current

Abstract

The dc-link voltage ripple plays an important role in dc capacitor design for three-phase voltage source converters (VSCs). However, the analytical models of the dc-link voltage ripple have rarely been reported for VSCs with nonlinear output current. This paper first derived the LOH voltages expressions in the dc-link. It reveals that each LOH component in ac current would induce two dc-link LOH voltages. Then the switching frequency harmonic voltages (SHVs) and their envelope expressions are formulated. Moreover, the proposed analytical models could be very much simplified when applied to special cases in the previous literature. Finally, an easy to design dc capacitor equation under nonlinear output current is also derived. Both simulation and experimental results validate the proposed method.

1. Introduction

Three-phase voltage source converters (VSCs) have been widely used in many industrial applications, such as uninterruptible power supply (UPS), active power filters (APFs), grid-tied inverters, etc., due to their flexible control and bidirectional energy flow. Therefore, the power stage of VSC, including the dc-link capacitor, needs to be designed carefully to realize high reliability and efficiency. The capacitor sizing aims at two issues: dc-link voltage ripple and capacitor power losses. As the power losses are related to dc-link current and capacitor equivalent series resistance (ESR), a lot of dc-link current analytical methods have been reported in [1,2,3,4,5,6]. Among them, Bierhoff et al. [1] derived the dc-link current spectrum of VSC under different modulation strategies. McGrath et al. [2] proposed a generalized method to determine the current harmonic spectrum of the dc-link for different VSC topologies. Sun et al. [3] derived the dc-link current spectrum expressions with considered the effect of the output ac current harmonics, which improves the accuracy of the dc-link current model. As the dc-link current spectrum needs complicated double Fourier integration, the RMS computational method is also widely used to analyze the dc-link current of VSC [4,5,6]. Moreover, a novel pulse width modulation strategy is proposed to reduce the dc-link current in [7] so that the dc capacitor power losses and temperature rise are suppressed.

On the other hand, the harmonic currents (including switching harmonics and its sideband components) in the dc-link are absorbed by the dc capacitor, resulting in the dc voltage ripple. Dahono et al. [8] derived and compared the RMS of dc-link current and voltage ripple with different modulation methods. Vujacic et al. [9,10] analyzed the time-domain waveform of the dc-link voltage ripple for the single-phase and three-phase VSC. Pei et al. [11] discussed the capacitor design method based on the dc-link voltage ripple. Furtherly, Vujacic et al. [12] established a general mathematical model of dc-link voltage ripple for two-level polyphase VSC and studied the influence of different phase numbers on the size of dc-link capacitors. Guo et al. [13] analyzed the dc-link voltage ripple of the three-phase VSC when considering the diode reverse recovery process. It is concluded that the voltage ripple error is only 2% when considering and not considering the diode reverse recovery process. So far, nearly all the dc-link voltage ripple study methods assume the sinusoidal output current [8,9,10,11,12,13]. Only a few papers discussed the dc-link voltage ripple under nonlinear ac output current. Kang et al. [14] analyzed the dc-link low order harmonic voltage under unbalanced ac output current (negative sequence, still at the fundamental frequency). It shows that the second harmonic voltage would occur when the ac current contains the fundamental negative sequence component. However, the switching harmonic voltages in dc-link are not discussed. Moreover, the analytical method cannot be used to analyze the dc-link voltage ripple for VSC under arbitrary low-order harmonic combinations in an ac current. Wang et al. [15,16] investigated the impacts of the LOH ac output currents on the dc-link current for single-phase H bridge inverter and three-phase VSC. Therein, the LOH and switching frequency harmonics RMS of the dc-link current are formulated individually. However, they also did not analyze the dc-link voltage. Yang et al. [17] divided the dc-link voltage ripple into LOH voltage and switching frequency harmonic voltage (SHV). In addition, they established its expressions for VSC under nonlinear output current. However, the dc-link SHV envelop expressions were not analyzed.

This paper is the extension of a conference paper [17] and shows a more detailed investigation of the dc-link voltage for VSCs under nonlinear output current. Therein, the dc-link SHV envelop expressions are successfully derived and verified by more simulation results. Moreover, the dc-link SHV models are formulated in a simpler way and show more experimental results. Moreover, the prior work [10,14] can be viewed as a special case of the proposed analytical method in this paper. This paper is organized as follows. In Section 2, the dc-link capacitor current models are established. Then, the general expressions of the dc-link LOH voltage and SHV are derived in Section 3. It is shown that each LOH in the ac current would induce two LOH voltages. Moreover, an easy to design dc-link capacitor equation under nonlinear output current is also derived. Finally, a thorough dc-link voltage ripple simulation and experimental results are performed under nonlinear output and validate the proposed computational methods.

2. Basic Analysis of DC-Link Circuit and Current

2.1. Basic Analysis of DC-Link Circuit

The typical circuit of a three-phase VSC is shown in Figure 1. The dc-link capacitor current is

$$i_{cap}=i_{DC}-i_{dc}$$

(1)

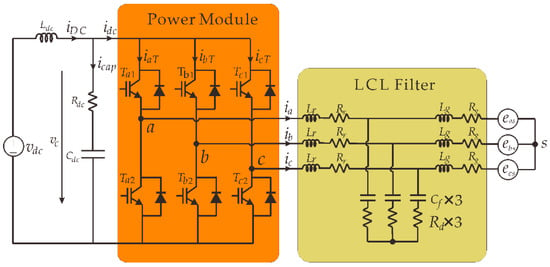
Figure 1. The typical three-phase VSC topology.

Due to the impedance frequency characteristic of the capacitor, the average capacitor current i_cap is zero. So, the dc component of i_dc is totally supplied by the dc front end current i_DC. In addition, almost all the dc-link harmonic currents should be absorbed by the dc-link capacitor. On the other hand, the dc-link current can be expressed as the sum of LOH current (i_dcLOH, including dc component I_dcAVG) and switch frequency harmonic current (SHC, i_dcSHC), then the dc-link capacitor current can be written as

$$i_{cap}=I_{dcAVG}-i_{dcLOH}-i_{dcSHC}$$

(2)

Therefore, the dc-link voltage ripple can be expressed as

$$\Delta v_c=\frac{1}{C_{dc}}{\displaystyle \int \left(I_{dcAVG}-i_{dcLOH}-i_{dcSHC}\right)}dt$$

(3)

Obviously, the dc-link voltage ripple is also divided by the LOH voltage (Δv_cLOH) and SHV (Δv_cSHV), and they are defined as

$$\Delta v_{cLOH}=\frac{1}{C_{dc}}{\displaystyle \int \left(I_{dcAVG}-i_{dcLOH}\right)}dt$$

(4)

$$\Delta v_{cSHV}=\frac{1}{C_{dc}}{\displaystyle \int \left(-i_{dcSHC}\right)}dt$$

(5)

Equations (4) and (5) are the basic model of dc-link voltage ripple. It will be fully investigated in the next section.

2.2. DC-Link Current Analysis

It is clear to see from (4) and (5) that the dc-link voltage ripple is dependent on the dc-link capacitor, dc current (I_dcAVG), dc-link LOH current (i_dcLOH), and dc-link SHC (i_dcSHC). As stated in Section 2.1, the dc-link current can be written as

$$i_{dc}=i_{dcLOH}+i_{dcSHC}$$

(6)

Integrating (6) over one switching period (T_s) results in

$$\frac{1}{T_s}{\displaystyle {\int }_{t_0}^{t_0+T_s}{i}_{dc}dt}=\frac{1}{T_s}{\displaystyle {\int }_{t_0}^{t_0+T_s}{i}_{dcLOH}dt}+\frac{1}{T_s}{\displaystyle {\int }_{t_0}^{t_0+T_s}{i}_{dcSHC}dt}$$

(7)

where t₀ is the starting time of integration, which can be any value. Since the switching frequency is much greater than the frequency of LOH, the i_dcLOH can be regarded as a constant in each switching period. The second term in (7) is zero, due to the fact that the charge and discharge of the dc-link capacitor with i_dcSHC over one switching period should be balanced. Therefore, the LOHs in the dc-link can be expressed as

$$i_{dcLOH}=\frac{1}{T_s}{\displaystyle {\int }_{t_0}^{t_0+T_s}{i}_{dc}dt}$$

(8)

From (6), the SHC in the dc-link is

$$i_{dcSHC}=i_{dc}-i_{dcLOH}$$

(9)

When switch T_x1 is on or off, the switching state S_x (x = a, b, c) equals 1 or 0, respectively. Then, the dc-link current can be written as the summation of the three-phase leg current, which equals each phase current multiplied by its switching state. Therefore,

$$i_{dc}=S_a{i}_a+S_b{i}_b+S_c{i}_c$$

(10)

By substituting (10) into (8), the LOH current in dc-link is expressed as

$$i_{dcLOH}=d_a{i}_a+d_b{i}_b+d_c{i}_c$$

(11)

where d_x (x = a, b, c) is the duty cycle and is defined as

$$d_x=\frac{1}{2}\left(1+v_{xref}+v_{com}\right)$$

(12)

where v_xref represents the reference signal and v_com is the common-mode signal. The different modulation strategies correspond to different v_com. As the sum of the three-phase current is zero, substituting (12) into (11) yields

$$i_{dcLOH}=v_{aref}{i}_a+v_{bref}{i}_b+v_{cref}{i}_c$$

(13)

In a three-phase VSC, the three-phase reference voltages are defined as

$$\{\begin{array}{l}{v}_{aref}=M\sin \left({\omega }_{1}t\right)\\ v_{bref}=M\sin \left({\omega }_{1}t-2\pi /3\right)\\ v_{cref}=M\sin \left({\omega }_{1}t+2\pi /3\right)\end{array}$$

(14)

where M represents the modulation index. Unlike the ac voltages, the three-phase current consists of a series of LOHs in applications like the APFs. Thus, the general three-phase current expressions are defined as

$$\{\begin{array}{l}{i}_a=I_k^{+}\sin \left(k{\omega }_{1}t-{\phi }_k^{+}\right)+I_n^{-}\sin \left(n{\omega }_{1}t-{\phi }_n^{-}\right)\\ i_b=I_k^{+}\sin \left(k{\omega }_{1}t-\frac{2\pi }{3}-{\phi }_k^{+}\right)+I_n^{-}\sin \left(n{\omega }_{1}t+\frac{2\pi }{3}-{\phi }_n^{-}\right)\\ i_c=I_k^{+}\sin \left(k{\omega }_{1}t+\frac{2\pi }{3}-{\phi }_k^{+}\right)+I_n^{-}\sin \left(n{\omega }_{1}t-\frac{2\pi }{3}-{\phi }_n^{-}\right)\end{array}$$

(15)

The superscript ‘+’ represents the positive sequence and ‘−’ represents the negative sequence. The superscript ‘k’ and ‘n’ are corresponding harmonic orders. φ is the phase angle difference between current and voltage. By substituting (15) and (14) into (13), then the dc-link LOH currents are

$$i_{dcLOH}=\frac{3}{4}M\left[{\displaystyle \sum _{k=1}{I}_k^{+}\cos \left[\left(k-1\right){\omega }_{1}t-{\phi }_k^{+}\right]-{\displaystyle \sum _{n=1}{I}_n^{-}\cos \left[\left(n+1\right){\omega }_{1}t-{\phi }_n^{-}\right]}}\right]$$

(16)

Herein, the dc current in dc-link current is obtained by setting k as 1 in (16)

$$I_{dcAVG}=\frac{3}{4}M{I}_1^{+}\cos {\phi }_1^{+}$$

(17)

Equations (9), (10), (16), and (17) are a complete set of generalized tools to obtain the dc current, LOH current, and SHC in dc-link. They are the foundation for dc-link voltage ripple.

3. DC-Link Voltage Ripple

3.1. The LOH Voltage in DC-Link

The LOH voltage ripple is defined as in (4). By substituting (16) and (17) into (4), the LOH voltage ripple can be obtained as

$$\Delta v_{cLOH}=-\frac{3M}{4{\omega }_1{C}_{dc}}\left[{\displaystyle \sum _{k=2}\frac{I_k^{+}}{k-1}\sin \left[\left(k-1\right){\omega }_{1}t-{\phi }_k^{+}\right]}-{\displaystyle \sum _{n=1}\frac{I_n^{-}}{n+1}\sin \left[\left(n+1\right){\omega }_{1}t-{\phi }_n^{-}\right]}\right]$$

(18)

Obviously, the LOH voltage has no relevance to the modulation strategy. As in (18), the kth positive sequence harmonic component in ac currents would induce (k − 1)th LOH voltage in dc-link; the nth negative sequence harmonic component in ac currents would induce (n + 1)th LOH voltage in dc-link. Therefore, if the harmonic order and phase angle in ac currents satisfy |k−n| = 2 and φ_k⁺ = φ_n⁻, then the (k − 1)th and (n + 1)th LOH voltage induced in the dc-link would cancel each other. By contrast, if the harmonic order and phase angle in ac currents satisfy |k − n| = 2 and |φ_k⁺ − φ_n⁻| = π, then the (k−1)th and (n + 1)th LOH voltage induced in the dc-link would reinforce each other. For example, the dc-link would occur 2nd and 6th harmonic voltages when ac currents consist of −1st and +7th harmonics.

3.2. The SHV in DC-Link

The SHV ripple is defined as in (5). As stated in Section 2.2, the average value of i_dcSHC over one switching period is zero whatever modulation strategy is used. It means that the initial and final values of the SHV in dc-link are the same. Therefore, the dc-link SHV pattern is the same for each switching period. On the other hand, the dc-link voltage period is π/3 with balanced and sinusoidal output ac current as shown in Figure 2a. Therefore, only one sector of a range of π/3 needs to be analyzed in this case. However, from Figure 2b–d, it is clear that the envelopes of dc-link SHV are quite different with different harmonic combinations in ac currents. Therefore, to consider all possible harmonic combinations in ac currents, the dc-link SHV analysis range should be extended to 2π. Figure 3 depicts the dc-link SHV over one switching period with whole sectors.

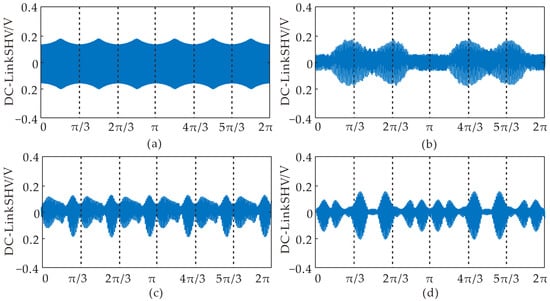
Figure 2. DC-link SHV when the ac port current consists of: (a) 1st; (b) 1st; (c) +7th; (d) −1th and +7th.

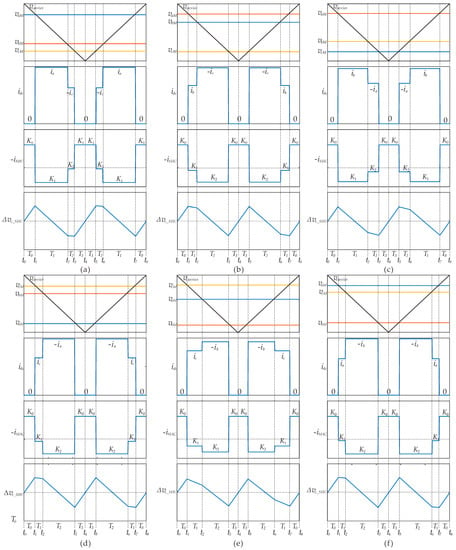
Figure 3. The SHV ripple in dc-link over one switching period: (a) Sector 1; (b) Sector 2; (c) Sector 3; (d) Sector 4; (e) Sector 5; (f) Sector 6.

It is clear that the dc-link SHV is symmetric with a half-switching cycle. Hence only the half-switching cycle needs to be analyzed. For each sector, a combination of Equations (5), (9), (10), and Figure 3 for the dc-link SHV over the half-switching period can be expressed as

$$\Delta v_{cSHC}=\frac{1}{C_{dc}}\{\begin{array}{l}{K}_0\left(t-t_0\right)if{t}_0\le t<t_1\\ K_1\left(t-t_1\right)+\Delta v_{1}if{t}_1\le t<t_2\\ K_2\left(t-t_2\right)+\Delta v_1+\Delta v_{2}if{t}_2\le t<t_3\\ K_0\left(t-t_3\right)-\Delta v_{1}if{t}_3\le t<t_4\end{array}$$

(19)

where

$$\{\begin{array}{l}\Delta v_1=K_0\left(t_1-t_0\right)=K_0{T}_0\\ \Delta v_2=K_1\left(t_2-t_1\right)=K_1{T}_1\end{array}$$

(20)

Then the maximum peak value of switching harmonic voltage over one switching period in dc-link can be written as

$${\left\{\Delta v_{cSHC}\right\}}_{\max }=\frac{1}{C_{dc}}\max \left(\left|\Delta v_1\right|,\left|\Delta v_1+\Delta v_2\right|\right)$$

(21)

It should be noted that the values of K₀, K₁, K₂, T₀, T₁, and T₂ vary with different sectors. The K_i (i = 0, 1, 2) actually equals to –i_dcSHC, and it can be calculated by Equations (9), (10), and (16). Their values are summarized in Table 1. With the above Equations (19)–(21), the SHV and its maximum peak value can be easily obtained. Unlike LOH voltage, the SHV pattern is dependent on the modulation strategy. For SVPWM, the v_com can be expressed as

$$v_{com}=-\frac{1}{2}\left[\max \left(v_{aref},v_{bref},v_{cref}\right)+\min \left(v_{aref},v_{bref},v_{cref}\right)\right]$$

(22)

Table 1. The values of K₀, K₁, K₂, T₀, T₁, and T₂ in different sectors with SVPWM.

Category	T0	T1	T2	K0	K1	K2
Sector 1	Ts × (1 − uaref − ucom)/8	Ts × (uaref − ubref)/4	Ts × (ubref − ucref)/4	idcLOH	idcLOH − ia	idcLOH + ic
Sector 2	Ts × (1 − ubref − ucom)/8	Ts × (ubref − uaref)/4	Ts × (uaref − ucref)/4	idcLOH	idcLOH − ib	idcLOH + ic
Sector 3	Ts × (1 − ubref − ucom)/8	Ts × (ubref − ucref)/4	Ts × (ucref − uaref)/4	idcLOH	idcLOH − ib	idcLOH + ia
Sector 4	Ts × (1 − ucref − ucom)/8	Ts × (ucref − ubref)/4	Ts × (ubref − uaref)/4	idcLOH	idcLOH − ic	idcLOH + ia
Sector 5	Ts × (1 − ucref − ucom)/8	Ts × (ucref − uaref)/4	Ts × (uaref − ubref)/4	idcLOH	idcLOH − ic	idcLOH + ib
Sector 6	Ts × (1 − uaref − ucom)/8	Ts × (uaref − ucref)/4	Ts × (ucref − ubref)/4	idcLOH	idcLOH − ia	idcLOH + ib

3.3. The DC-Link Voltage Ripple Evaluation

With given LOHs in output ac current, the dc-link LOH voltages and SHVs can be directly calculated by the Equations (18)–(20), respectively, and the envelope of SHVs is determined by (21). Then the theoretical total dc-link voltage ripple can be obtained by summing the results of (18) and (19). Figure 4 gives the flow chart of the dc-link voltage ripple for the VSC with nonlinear output current.

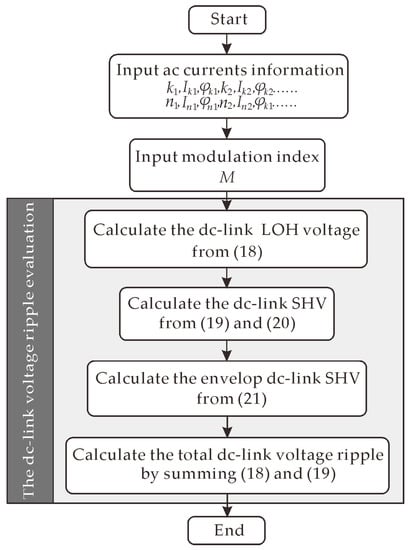
Figure 4. The flow chart of the dc-link voltage ripple with nonlinear output current.

3.4. Equations Compatibility with Special Cases

The proposed general dc-link voltage ripple model could be simplified when applied to special cases, such as a three-phase inverter with an unbalanced load, where both the 1st positive sequence and first negative sequence components exist in ac output current. In this case, the dc-link low order harmonic voltage is obtained by setting n = 1 in the second term of (18). The resulting peak voltage ripple (23) exactly matches the half of the peak-to-peak ripple (36) in [14].

$$\Delta v_{cLOH}=\frac{3M{I}_n^{-}}{8{\omega }_1{C}_{dc}}\sin \left[2{\omega }_{1}t-{\phi }_n^{-}\right]$$

(23)

As for the three-phase inverter with balanced ac current, only the first positive sequence component exists in ac output current. Therefore, the dc-link low order harmonic voltages are zero from (18). Only SHVs exist in dc-link, and they are directly determined by (19) and (20). Figure 5 depicts the envelopes of dc-link voltage ripple under different modulation indexes by (21), which are the same as Figure 4 in [10]. It should be noted that the definition of modulation ratio is V_m/(V_dc/2) in this paper and V_m/V_dc in [10]. V_m represents the amplitude of reference voltage.

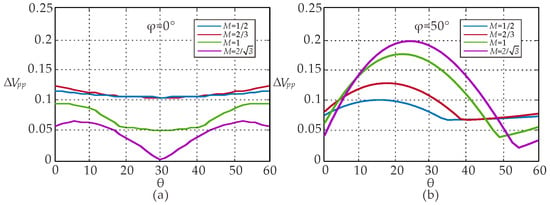
Figure 5. Normalized peak-to-peak dc-link voltage ripple amplitude ΔV_pp over the period [0, 60°] for different modulation indices, M = 1/2, 2/3, 1, and 2/$\sqrt{3}$, and output phase angles (a) φ = 0° and (b) φ = 50°.

3.5. Equations Simplification for Practical Design

With the given LOHs in ac currents, the dc-link LOH voltage and SHV can be obtained from Section 3.1 and Section 3.2. In the practical design, the voltage ripple in the worst case needs to be considered. It is impractical to obtain the maximum peak value of dc-link voltage ripple by directly using the (18) and (19)–(21), as the phase angles of each LOH ac current could have infinite possible combinations. Therefore, some simplifications are needed to facilitate the design practice.

Firstly, for the dc-link LOH voltage from (18), the maximum peak value of the LOH voltage ripple in the worst case can be obtained as

$${\left\{\Delta v_{cLOH}\right\}}_{\max }=\frac{3M}{4{\omega }_1{C}_{dc}}\left({\displaystyle \sum _{k=2}\frac{I_k^{+}}{k-1}+}{\displaystyle \sum _{n=1}\frac{I_n^{-}}{n+1}}\right)$$

(24)

Secondly, the dc-link SHV ripple has a quite complicated form in different sectors as stated in Section 3.2. Comparing Δv₁ and Δv₂ in different sectors with the maximum peak value of LOH voltage in (24), it is clear that the LOH voltage is the dominant component.

Therefore, the SHV can be reasonably neglected due to the integral time of SHV being far less than the LOH voltage integral time. If the dc-link voltage ripple requirement is given, then the capacitance of the dc-link capacitor can be easily obtained by (25).

$$C_{dc}=\frac{3M}{4{\omega }_1\Delta v_c}\left({\displaystyle \sum _{k=2}\frac{I_k^{+}}{k-1}+}{\displaystyle \sum _{n=1}\frac{I_n^{-}}{n+1}}\right)$$

(25)

4. Simulation and Experimental Results

To validate the proposed analytical method of the dc-link voltage ripple, both simulation and experiment are carried out under different LOH output current combinations.

4.1. Simulation Results

Circuit simulation of the VSC is performed by MATLAB/Simulink. Simulink parameters are: dc voltage is 400 V, the three-phase grid voltage is set at 240 V, and the switch frequency is 10 kHz. Therefore, the modulation index can be approximately calculated as 0.98. The LCL filter and dc-link capacitor parameters are listed in Table 2.

Table 2. System parameters.

Category	Part Number	Parameters
Grid side inductor Lg	Custom-made	200 uH, 30 Arms
Converter side inductor Lr	Custom-made	400 uH, 40 Arms
Filter capacitor Cf	MKP1847610354P4	10 uF
Damping resistor Rd	TEH100M1R00JE	1 Ω
DC-Link capacitor Cdc	450HXG120MFM	720 uF
IGBT modules	SKiiP 39AC126V2	1200 V

The following two groups of LOH ac currents were selected as the output: (1) I₁⁻ = 15A (φ₁⁻ = 0); (2) I₁⁻ = 10A (φ₁⁻ = 0), I₅⁻ = 10A (φ₅⁻ = 0). Figure 6 shows the simulation and computational results of the dc-link voltage ripple under the above two ac current conditions. From top to bottom are the total dc-link voltage the total dc-link voltage (including LOH voltage and SHV), the LOH voltage (second diagram), SHV ripple (third diagram), and FFT results of LOH voltage in dc-link. The computational results of LOH voltage and dc-link SHV envelop are calculated by (18) and (21), respectively. The theoretical total dc-link voltage ripple is calculated by summing the results of (18) and (19).

Figure 6. Simulation results of the total dc-link voltage ripple: (a) AC link currents contain −1st (15A, 0); (b) AC link currents contain −1st (10A, 0) and −5th (10A, 0).

Obviously, the simulation and computational results are matched well, which proves the correctness and effectiveness of the analytical method proposed in this paper. From Figure 6a, it can be seen that when the ac current contains the fundamental negative sequence component, the second harmonic voltage would occur in the dc-link. Similarly, Figure 6b shows that when the ac current contains both the fundamental negative sequence and the fifth negative sequence components, the secnd and sixth harmonic would occur in the dc-link. Moreover, since the integration time of SHV in the dc-link is much smaller than the LOH voltage integration time, the maximum value of the LOH voltage is much larger than the maximum value of SHV in the dc-link. Therefore, compared with the dc-link LOH voltage, the SHV in the dc-link can be ignored.

4.2. Experimental Results

The experimental setup is shown in Figure 7. It should be pointed out that the power module in the experimental setup is mounted on a heatsink and covered by a drive board, so it can not be seen in Figure 7. The graphic user interface shown in Figure 8 is used to control the grid-tied inverter output current. The PI paralleled with multiple PR controllers in a d-q reference frame were used to inject the desired multiple LOH currents into the grid. Therefore, the dc-link voltage ripple can be easily evaluated under a specific ac current. The switching and sample frequency are 10kHz, and all the experimental parameters are consistent with the simulation.

Figure 7. The flexible three-phase grid-tied VSC prototype.

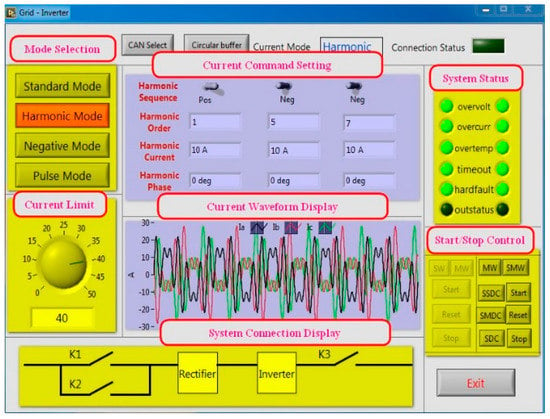
Figure 8. The graphical user interface for the experimental setup.

Figure 9a and Figure 10a show the experimental results of total dc-link voltage ripple when the ac currents consist of: (1) I₁⁻ = 15A (φ₁⁻ = 0); (2) I₁⁻ = 10A (φ₁⁻ = 0), I₅⁻ = 10A (φ₅⁻ = 0), respectively. The corresponding theoretical total dc-link voltages are shown in Figure 9b and Figure 10b, which are obtained by summing the results of (18) and (19). It should be noted that the output ac current conditions in Figure 9 and Figure 10 are the same as Figure 6. It is obvious that the computational, simulation, and experimental results are matched well. Figure 11 show the experimental and computational total dc-link voltage ripple results when ac current consist of I₁⁻ = 8A (φ₁⁻ = 0), I₅⁻ = 8A (φ₅⁻ = π), I₇⁺ = 8A (φ₇⁺ = 0). Again, they match well. It is interesting that the dc-link voltage ripple in Figure 10 increased significantly compared with Figure 9, due to the 6th harmonic voltages in dc-link produced by −5th and +7th harmonics in the ac current being reinforced by each other from (18).

Figure 9. Experimental and computational results of the dc-link voltage ripple when the ac currents contain −1st (10A, 0): (a) experimental results; (b) computational results.

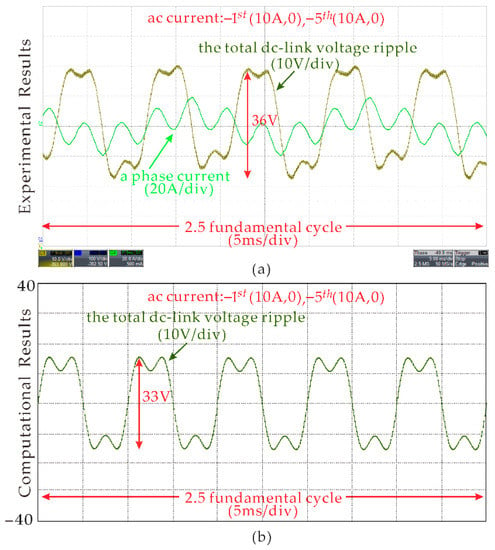
Figure 10. Experimental and computational results of the dc-link voltage ripple when the ac currents contain −1st (10A, 0) and −5th (10A, 0): (a) experimental results; (b) computational results.

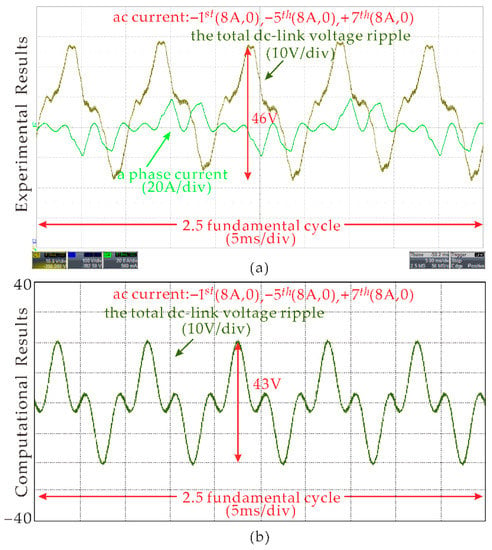
Figure 11. Experimental and computational results of the dc-link voltage ripple when the ac currents contain −1st (8A, 0), −5th (8A, π), and +7th (8A,0): (a) experimental results; (b) computational results.

5. Conclusions

This paper presents a general analytical model of the dc-link voltage ripple to facilitate the dc capacitor design for the three-phase VSCs under nonlinear output current. The dc-link voltage ripples are decomposed into LOH voltages and SHVs and formulated separately. It is interesting to discover that the dc-link LOH voltages would reinforce or cancel each other with different phase angles combinations in ac current. Moreover, the dc-link voltage ripple models in the previous literature could be easily obtained by applying specific cases to the proposed analytical models in this paper. Moreover, the maximum dc-link voltage ripple expression is also derived to accelerate dc capacitor design in the worst case. With the proposed method, the various unusual dc-link voltage ripple under arbitrary combinations of LOHs in the ac output current can be accurately evaluated in advance without amounts of simulations. The complete equation sets are demonstrated by both simulation and experimental results.