Optimization of Well Control during Gas Flooding Using the Deep-LSTM-Based Proxy Model: A Case Study in the Baoshaceng Reservoir, Tarim, China

Abstract

Gas flooding has proven to be a promising method of enhanced oil recovery (EOR) for mature water-flooding reservoirs. The determination of optimal well control parameters is an essential step for proper and economic development of underground hydrocarbon resources using gas injection. Generally, the optimization of well control parameters in gas flooding requires the use of compositional numerical simulation for forecasting the production dynamics, which is computationally expensive and time-consuming. This paper proposes the use of a deep long-short-term memory neural network (Deep-LSTM) as a proxy model for a compositional numerical simulator in order to accelerate the optimization speed. The Deep-LSTM model was integrated with the classical covariance matrix adaptive evolutionary (CMA-ES) algorithm to conduct well injection and production optimization in gas flooding. The proposed method was applied in the Baoshaceng reservoir of the Tarim oilfield, and shows comparable accuracy (with an error of less than 3%) but significantly improved efficiency (reduced computational duration of ~90%) against the conventional numerical simulation method.

1. Introduction

Gas flooding has proven to be a viable enhanced oil recovery (EOR) strategy for mature water-flooding reservoirs [1,2]. Previous laboratory and numerical simulation studies suggest that injected gas is favorable to oil swelling, oil viscosity reduction, and phase behavior, and thus tends to improve the ultimate oil recovery beyond the primary and secondary oil recovery stages. During the gas flooding process, gas channeling is a critical issue due to reservoir heterogeneity, inherent high oil/gas viscosity ratio and improper well control schedules (e.g., injection and production rates). The occurrence of gas channeling results in significant reductions in the sweep efficiency, ultimate recovery and economics of the gas injection EOR project. Therefore, to optimize the well control parameters prior to deploying a gas injection project is a vital step in order to increase gas flooding performance [3].

The optimal gas flooding control parameters can be determined using either core flooding experiments [4] or field-scale numerical simulations. Core flooding experiments are generally conducted on core samples, which are associated with significantly higher recovery factors than real reservoirs. Besides, the core flooding tests are incapable of simulating multiple injectors or multiple producers. The field-scale numerical simulation method integrates the numerical simulator with the optimization algorithm, and automatically finds the optimal well control parameters. For example, Chen et al. [5] combined the GA with numerical simulations to optimize water-alternating gas well control parameters. Liu et al. [6] used the genetic algorithm (GA) to optimize the injection and production of CO₂ flooding. A most significant issue associated with the conventional numerical simulation method is that hundreds or thousands of numerical simulation scenarios are required in order to derive reasonable near-optimal results. The exercise of such a number of numerical simulations is computationally expensive and time-consuming and thus results in relatively low efficiency of optimization runs.

In recent years, with the development of artificial intelligence technology, many scholars have introduced machine-learning methods to predict the production dynamics of oilfields. Chakra et al. [7] used a high-order neural network (HONN) to predict the cumulative oil production of the reservoir. Wang et al. [8] established a prediction model for shale oil reservoirs using a deep learning network (DNN) to replace the numerical model process. Gu et al. [9] proposed the use of an extreme gradient boosting decision tree model to construct a surrogate model for predicting water cut based on real production data. Wang et al. [10] established a proxy model for the production performance prediction of multi-stage fracturing horizontal wells of shale oil reservoirs based on the Deep Belief Network (DBN) model, and also obtained outstanding results using the trained DBN model as a proxy to optimize the fracturing design. Gang et al. [11] employed the Extra Trees algorithm to build up the final prediction model, which is used to optimize total fluid volume and proppant quality for high volume shale gas production. Huang et al. [12]. collected the actual development data in the field, and established a water-flooding reservoir development prediction model based on a long short-term memory artificial neural network (LSTM). Javadi et al. [13] combined the artificial neural network with GA to optimize well control parameters for gas flooding.

In view of the above research problems and experiences, this paper takes as its research background the optimization of injection and production parameters in the process of continuous gas flooding development in Tarim Baoshaceng reservoir. It proposes a gas flooding prediction model based on deep learning theory to replace the numerical simulation of gas injection development reservoirs, and to combine with the adaptive covariance matrix intelligent optimization algorithm (CMA-ES) to solve the built injection-production parameter optimization mathematical model, thus establishing rapid optimization method for a set of Baoshaceng reservoir gas flooding injection and production parameters. The development and adjustment of reservoir gas flooding injection–production parameters have important guiding significance.

2. Materials and Methods

2.1. Background of the Baoshaceng Reservoir

The Baoshaceng reservoir of the Tarim Oilfield is located in Shaya County, Aksu Prefecture, Xinjiang Province, China. The structure of the Baoshaceng reservoir includes nose-shaped uplifts that subside in the northwest direction and uplift in the southeast direction. The reservoir is characterized by a relatively large burial depth (5000–5023 m), high pressures (51.7–53.87 MPa) and high temperatures (111.5–115.9 °C). The average porosity and permeability are 13.67% and 98.68 × 10⁻³ μm², respectively. The porosity, permeability and pressure distributions are shown in Figure 1. The underground crude oil has an average density of 0.79 g/cm³, and average viscosity of 4.71 mPa·s.

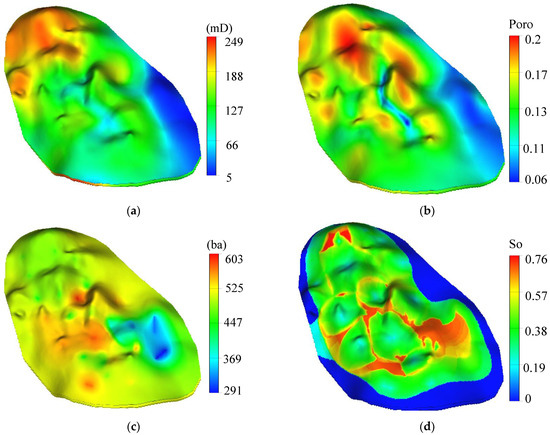
Figure 1. Basic properties of Baoshaceng reservoir: (a) Permeability distribution, (b) Porosity distribution, (c) Pressure distribution, (d) Oil saturation distribution.

The development of the Baoshaceng reservoir started with primary depletion in September 1998, which was followed by subsequent water flooding initiated in October 2002. Currently, the target reservoir has 12 water injectors, 4 gas injectors and 21 producers. The comprehensive water cut, formation pressure and oil recovery are 77.6%, 48.5 MPa and 33.24%, respectively. The injected gas type is the natural gas associated with a minimum miscible pressure of 45.2 MPa with the crude oil. Figure 1 shows the field map distribution of the Baoshaceng reservoir model, and Figure 2 the historical production dynamics of the Baoshaceng reservoir. The accuracy of history matching in the whole area is over 90%, indicating that this model can be used to predict reservoir development performance.

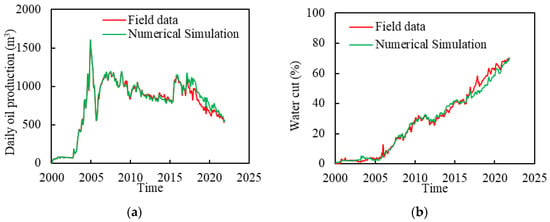
Figure 2. Production history of the Baoshaceng reservoir. (a) Daily oil production history fitting. (b) Water cut history fitting.

2.2. Sample Construction

To construct the data samples used for training the Deep-LSTM model, numerical simulations were conducted for 800 scenarios of injection and production parameter combinations. In this paper, the simulation scenarios were generated using the Latin hypercube sampling method [14]. Data was divided into the training set and test set, according to the distribution 8 to 2. The composite simulator ECLIPSE E300 was used for simulation. The number of effective grids in the H reservoir was 104,073, and the average running time was 30 min. Each scenario considered the well control parameters including (i) the initiating time of gas injection, gas injection rate and total gas injection volume of each gas injector, (ii) the water injection rate of each water injector and (iii) the liquid production rate of each producer. The well control parameter boundaries are given in Table 1. The upper and lower limits of the gas injection rate depend on the power of the on-site compressor, the water injection rate limit depends on the power of the on-site pump, and the upper and lower limits of the liquid production rate refer to the actual on-site data. All the data are based on the actual situation on site. However, in order to achieve a better optimization effect, the upper limit of the optimization variable was appropriately enlarged. The economic parameters involved in calculating the objective function are shown in Table 2. Gas injection costs, water injection costs, and water treatment costs are derived from the actual field data from the oil field. We referred to the literature for the value of the annual discount rate, and we assumed a reasonable value of 10 [10,15,16,17]. Numerical simulations were run on a production duration of 10 years and the net present value (NPV) was calculated based on the simulated injection and production data, which can be written as:

$$NPV={\displaystyle \sum }_{t=1}^{N_t}\left[\frac{1}{{\left(1+b\right)}^k}\left({\displaystyle \sum }_{i=1}^{N_P}{r}_{\mathrm{gp}}{q}_{\mathrm{gp}}^{i,k}+{\displaystyle \sum }_{i=1}^{N_P}{r}_{\mathrm{op}}{q}_{\mathrm{op}}^{i,k}-{\displaystyle \sum }_{i=1}^{N_{\mathrm{IW}}}{c}_{\mathrm{wi}}{q}_{\mathrm{wi}}^{i,k}-{\displaystyle \sum }_{i=1}^{N_{\mathrm{IG}}}{c}_{\mathrm{gi}}{q}_{\mathrm{gi}}^{i,k}-{\displaystyle \sum }_{i=1}^{N_P}{c}_{\mathrm{wp}}{q}_{\mathrm{wp}}^{i,k}\right)\right]$$

(1)

where $q_{\mathrm{op}}^{i,k}$ is the cumulative oil production of the ith well in the kth year; $q_{\mathrm{gp}}^{i,k}$ is the cumulative gas production of the ith well in the kth year; $q_{\mathrm{wp}}^{i,k}$ is the cumulative water production of the ith well in the kth year; $q_{\mathrm{w}i}^{i,k}$ is the accumulated water injection of the ith well in the kth year; $q_{\mathrm{g}i}^{i,k}$ is the cumulative gas injection of the ith well in the kth year; r_op is oil price; r_gp is gas price; c_wp is water treatment price; c_wi is water injection cost; c_gi is gas injection cost; N_t is evaluation time, years; b is the annual discount rate; N_IW is number of water injection wells; N_IG is number of gas injection wells; N_P is number of producer wells.

Table 1. Latin hypercube sampling upper and lower limits.

Parameters	Lower Sampling Limit	Upper Sampling Limit
Gas injection timing (days)	0	120
Gas injection rate (m3/d)	0	120,000
Total gas injection (108 m3)	0	4
Water injection rate (m3/d)	0	150
Liquid production rate (m3/d)	0	150

Table 2. Economic parameter value.

Parameters	Value
Gas injection cost (RMB/m3)	1.3
Water injection cost (RMB/m3)	30
Water treatment cost (RMB/m3)	10
Oil sale price (RMB/m3)	2800
Gas sale price (RMB/m3)	0.9
Annual discount rate	10

Since the orders of magnitude of the well control parameters are different, each well control parameter was normalized so that all the parameters are comparable at an equivalent order of magnitude. The normalization was achieved using the following formula [18]:

$$X_i=\frac{x_i-x_{min}}{x_{max}-x_{min}}$$

(2)

where X_i is the ith normalized data corresponding to the ith original data x_i; x_min and x_max are the upper and lower sampling boundaries, respectively.

It is worth noting that all calculations in this work were run on the following computer system configuration, as shown in Table 3:

Table 3. Computer system configuration and simulation environment.

Parameter	Type
RAM	16G
GPU	NVIDIA GTX 1060
CPU	Intel i7 10875H@2.30 GHz
Computer system	Windows10
Deep learning environment	TensorFlow

2.3. Development of the Deep-LSTM Proxy Model

2.3.1. Basics of the Deep-LSTM

Long Short-Term Memory (LSTM) networks are popular neural models that are used for learning and predicting long-term dependencies. An LSTM network typically consists of an input layer, a hidden layer and an output layer. The hidden layer, which is also referred to as the memory unit, controls the long-distance temporal information transmission. The memory unit consists of three gate calculation structures, namely the “input gate”, “forget gate” and “output gate” (Figure 3). The “input gate” is used for inputting and filtering new information. The “forget gate” is the most important controlling mechanism of an LSTM, discarding the useless information and retaining the useful information. The “output gate” enables the memory cell to output only information relevant to the current time step. These three gate structures perform operations such as matrix multiplication and nonlinear summation in the memory unit so that the memory information will not disappear in continuous iterations (i.e., the issue of gradient disappearance can be effectively resolved) [19,20,21].

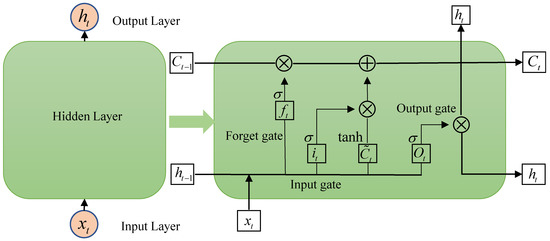
Figure 3. LSTM neural network memory unit structure.

Mathematically, the information input at the t-th time step passes through the input gate, and the input value in the memory unit and the candidate value of the hidden layer (i_t and C_th) are computed respectively as:

$$i_t=\sigma \left(W_i\times H_{t-1},X_t\right]+b_i)$$

(3)

$$C_{\mathrm{th}}=\tan h(W_c\times \left[H_{t-1},X_t\right]+b_c)$$

(4)

Then the input information passes through the forget gate, and the forgetting layer of the memory unit at the t time step is assigned as f_t:

$$f_t=\sigma \left(W_f\times \left[H_{t-1},X_t\right]+b_f\right)$$

(5)

At this time, the information of the hidden layer in the memory unit is updated to C_t:

$$C_t=f_t\times C_{t-1}+i_t\times C_{\mathrm{th}}$$

(6)

Finally, the information passes through the output gate. The value O_t of the output layer in the memory unit at the t-th time step and the final output value h_t are:

$$O_t=\sigma \left(W_o\times \left[H_{t-1},X_t\right]+b_o\right)$$

(7)

$$h_t=O_t\times \tan h\left(C_t\right)$$

(8)

Previous studies have shown that Deep-LSTM has stronger stability and higher accuracy than conventional LSTM [22,23]. Deep-LSTM can be considered as multiple LSTM network neurons stacked together to form a training unit, with the time series information output of the previous layer used as the time series information input of the next layer (Figure 4). The depth of the structure can build a hierarchical feature representation of the input data, thereby improving the efficiency of model training. Since the time series of Deep-LSTM is very complex, the number of training iterations is large, and problems of overfitting and data redundancy are prone to occur. Therefore, the dropout function is added to the network framework, and a certain amount of loss can proportionally occur during each iteration of training. The output of the LSTM structure at the current moment is passed into a fully connected dense layer to obtain the final output.

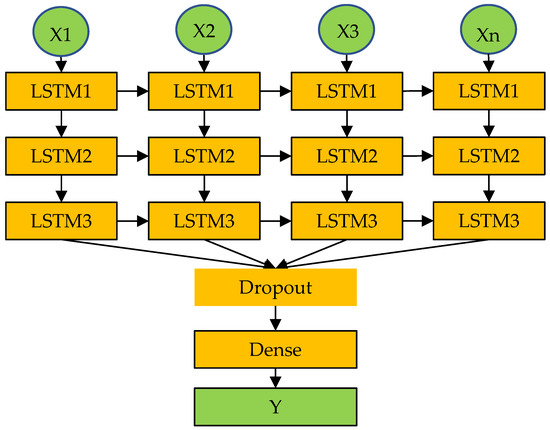
Figure 4. Deep-LSTM neural network memory architecture.

2.3.2. Construction of the Deep-LSTM Proxy Model

In this study, a 3-layer Deep-LSTM was constructed to develop the proxy model for predicting the gas flooding performance. The “return_sequences” line indicates whether to return the value of the hidden state of the last time step or the value of the hidden state of each time step in the output sequence. When “return_sequences” is “True”, it returns the value of the hidden state of each time step, when “return_sequences” is “False”, it returns the value of the hidden state of the last time step. In this study, the “return_sequences” of the first two layers of LSTM were set to “True”, and the “return_sequences” of the last layer of LSTM was set to “False”. The learning rate determines whether and when the objective function converges to a local minimum. Smaller learning rates tend to increase the risk of overfitting, while larger ones may slow convergence. Batch size affects the training accuracy and speed of the model, and its value may affect computer performance. If there are too many neurons, the calculation speed is slow and overfitting is easy; if there are too few neurons, the training accuracy will be affected. The loss value of the Dropout layer can effectively prevent overfitting, and if it is too large, it will lead to poor training accuracy. The Epoch value represents the number of times of training. If it is too small, it will underfit, and if it is too large, it will overfit. These hyperparameters affect each other, so there is an optimal combination for the model training. In the LSTM layer, the activation function of the neuron was set to be the linear rectification function (Relu). The optimizer used Adam [24,25]. The mean square error (MSE) and coefficient of determination (R²) were used to evaluate the accuracy of the proxy model.

The hyperparameters of the Deep-LSTM (e.g., the number of hidden layers, learning rate and training times, etc) may affect training efficiency and accuracy [26]. Therefore, this study used the Bayesian optimization to determine the optimal values of the hyperparameters. The details of the hyperparameter optimization process are given in references and therefore are not repeated in this paper [27,28,29,30]. The hyperparameters that were optimized and their ranges are given in Table 4.

Table 4. Bayesian Optimization Hyperparameters.

Parameters	Range	Optimal Parameters
Learning rate	0.0001~0.1	0.001
Batch size	20~100	32
The number of neurons in the first layer	10~200	24
The number of neurons in the second layer	10~200	48
The number of neurons in the third layer	10~200	60
Loss function value(Dropout)	0.05~0.5	0.2
Epoch	10~200	100

2.4. Optimization of the Well Control Parameters for Gas Flooding

The goal of well control parameter optimization is to find optimal values for injection and production parameters that maximize oil production or economics. For the continuous gas flooding problem, the optimization variables for each gas injection well include gas injection start time, gas injection rate, and total gas injection volume; the optimization variable for each water injection well is the water injection rate; the optimization variable for production wells is all production wells under certain constraints and liquid production rate under certain conditions (e.g., bottom hole pressure, BHP). For the production of constant fluid volume in every well, the optimization variables are:

$$x_g=\left[I_{t1},\cdots ,I_{ti},\cdots ,I_{tn},I_{vg1},\cdots ,I_{vgi},\cdots ,I_{vgn},I_{cg1},\cdots ,I_{cgi},\cdots ,I_{cgn}\right]$$

(9)

$$x_w=\left[I_{vw1},\cdots ,I_{vwi},\cdots ,I_{vwz}\right]$$

(10)

$$x_p=\left[P_{L1},\cdots ,P_{Li},\cdots ,P_{Lm}\right]$$

(11)

where x_g is the optimization variable for each gas injection well; x_w is the optimization variable for each water injection well; x_p is the optimization variable for each production well; I_ti is gas injection timing of the ith gas injection well; I_vg is gas injection rate of the ith gas injection well; I_cgi is the Cumulative gas injection of the ith gas injection well; I_vwi is the water injection rate of the ith water injection well; P_Li is the fluid production of the ith production well; z is the number of water injection wells; n is the number of gas injection wells; m number of producer wells.

In the actual production processes of different oil reservoirs, the injection and production systems have certain constraints. For example, the daily gas injection rate of the gas injection well depends on the actual gas injection capacity of the on-site compressor. In order to ensure that the numerical simulation results are within a reasonable range, it was necessary to add corresponding constraints to the optimization variables in the optimization mathematical model. The constraints for the well control optimization of gas flooding are summarized in Table 5.

Table 5. Mathematical Model Constraints.

Constraint Type	Constraint Variables	Constraint Expression
Inequality Boundary Condition Constraints	Gas injection timing	$I_{ti}^{min}\le I_{ti}\le I_{ti}^{max},i=1,2,\cdots n$
	Gas injection rate	$I_{\mathrm{vg}i}^{min}\le I_{\mathrm{vg}i}\le I_{\mathrm{vg}i}^{max},i=1,2,\cdots n$
	Total gas injection	$I_{\mathrm{cg}i}^{min}\le I_{\mathrm{cg}i}\le I_{\mathrm{cg}i}^{max},i=1,2,\cdots n$
	Liquid production rate	$P_{Li}^{min}\le P_{Li}\le P_{Li}^{max},i=1,2,\cdots m$
	Water injection speed	$I_{\mathrm{vw}i}^{min}\le I_{\mathrm{vw}i}\le I_{\mathrm{vw}i}^{max},i=1,2,\cdots z$

On the basis of the construction of the Deep-LSTM proxy model, we further combined the covariance matrix adaptive evolutionary algorithm (CMA-ES) with the Deep-LSTM model to optimize the injection and production parameters of hydrocarbon gas flooding in the Baoshaceng reservoir. The CMA-ES is a stochastic non-gradient algorithm that has strong global optimization ability [31,32]. The specific optimization process is shown in Figure 5 and is presented briefly as follows:

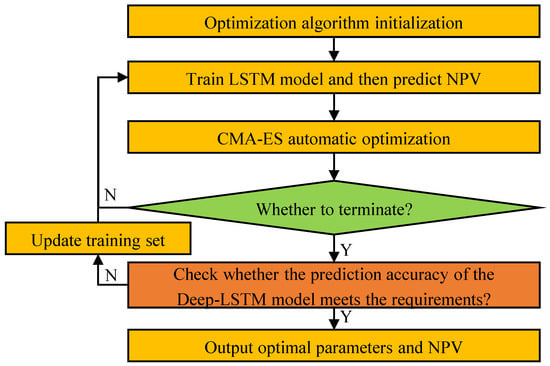
Figure 5. CMA-ES optimization process.

• Step 1: Initialize the optimization algorithm and the optimization variables;
• Step 2: Train the Deep-LSTM model and then predict NPV;
• Step 3: Automatic optimization of CMA-ES algorithm;
• Step 4: Determine whether the termination condition is reached;
• Step 5: If the prediction accuracy of the Deep-LSTM model meets the requirements, output optimal well control parameters and NPV; otherwise, repeat from Step 2 to Step 4 (e.g., update the training set, retrain the model, restart the optimization algorithm).

3. Results and Discussion

3.1. Development of the Proxy Model

Figure 6 shows the model accuracy’s dependence (in terms of the determination coefficient R²) on the number of samples at varying numbers of layers. It can be seen that for a given number of layers, the model accuracy shows a gradually increasing trend with the increase in the number of samples. However, when the number of samples is larger than approximately 800, increasing the number of samples results in a very limited elevation in the model accuracy. It can be also seen from Figure 6 that the number of layers exerts a profound effect on the model accuracy. For example, for a given number of samples of 800, the R² values of the single-, two-, three- and four-layer Deep-LSTM network are 0.967, 0.975, 0.989 and 0.986, respectively. By comparison, it can be found that the three-layer Deep-LSTM model has higher accuracy and stability than models with single, two and four layers. In this regard, the three-layer Deep-LSTM architecture was selected in this study.

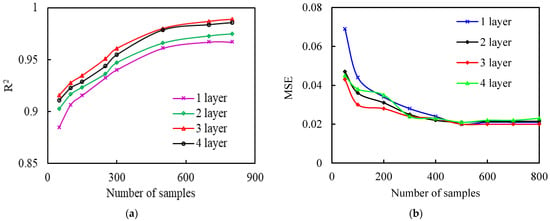
Figure 6. Comparison of (a) Effect of the number of samples and layers on the model accuracy and (b) Effect of the number of samples and layers on the model MSE.

With the aim of optimizing the Deep-LSTM architecture, the values of the hyperparameters were further optimized. The results showed that the optimal time step, single batch output, number of neurons in a single layer, dropout loss value and training round were 3, 32, 24, 48, 60, 0.2 and 100, respectively. Figure 7 depicts the scatter plot of predicted versus true NPVs with the optimized Deep-LSTM. It can be seen that the data points are located around the 45-degree line. The corresponding R² and MSE are 0.9954 and 0.018, respectively, indicating the relatively high accuracy of the model.

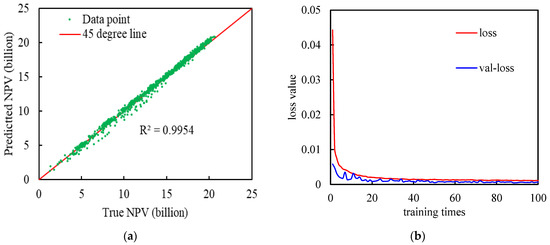
Figure 7. Comparison of (a)The cross plot of predicted versus true NPV based on the Deep-LSTM model (test set training effect) and (b) Loss function value changes during training.

In order to verify the reliability and superiority of the Deep-LSTM constructed in this study, the Deep-LSTM model was compared with the classic machine-learning algorithms XGBoost and FCNN. These two methods are the most commonly used machine-learning algorithms and have been widely utilized in the energy field [9,33]. Before comparison, the hyperparameters of XGBoost and FCNN were also optimized by the Bayesian optimization method. The training effects of different algorithm test sets are shown in Figure 8. Obviously, the training effect of the FCNN and XGBoost test set was not as good as Deep-LSTM. As can be seen from Table 6, comparing the accuracy and error of model predictions for different methods, the Deep-LSTM established in this paper is better than XGBoost and FCNN in terms of accuracy, robustness and generalization ability.

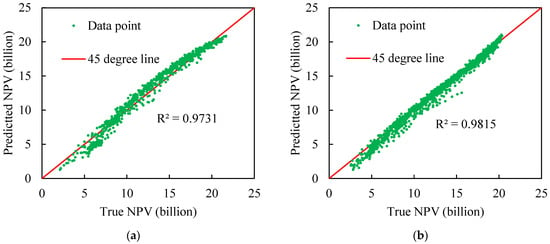
Figure 8. Test set training effect comparison (a) XGBoost model (b) FCNN model.

Table 6. Comparison of NPV Training Accuracy of Different Algorithms.

Method	MSE	R2
Deep-LSTM	0.018	0.9954
FCNN	0.059	0.9815
XGBoost	0.081	0.9731

3.2. Optimization of the Well Control Parameters

We used the CMA-ES optimization algorithm, set the maximum number of iterations to 600 and the number of populations to 20, calculated NPV based on the constructed Deep-LSTM model, and optimized the injection and production parameters for the H reservoir. As shown in Figure 9, Due to the randomness of the algorithm, the solid lines denote the average results for ten independent runs.

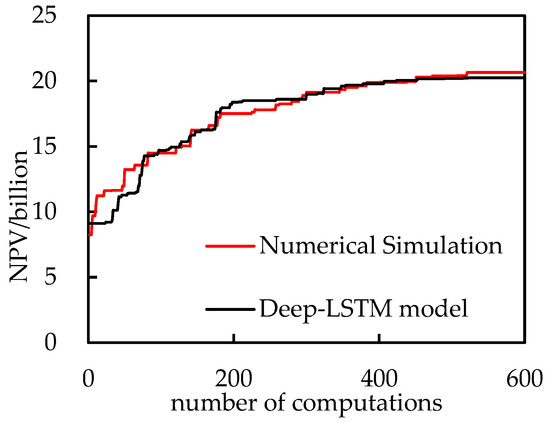
Figure 9. Comparing the process of optimizing NPV using different methods.

Table 7 is the comparison of the optimization results of four gas injection wells, Table 8 is the comparison of the optimization results of 12 water injection wells, and Table 9 is the comparison of the optimization results of 21 production wells.

Table 7. Comparison of optimization results of 4 gas injection wells.

Optimization Parameters	Optimization Variables	Numerical Simulation	Deep-LSTM Model
gas injection start time (days)	It1	3365	3482
	It2	1	1
	It3	3495	3330
	It4	1111	954
gas injection rate (m3/d)	Ivg1	51,681.95	63,797.47
	Ivg2	114,304.78	115,261.37
	Ivg3	95,569.58	88,207.42
	Ivg4	87,742.34	89,058.18
gas injection volume (m3)	Icg1	368,426.22	236,419.96
	Icg2	193,615,238.47	144,773,030.62
	Icg3	65,753,357.66	42,146,090.84
	Icg4	55,483,180.47	57,906,751.61

Table 8. Comparison of optimization results of 12 water injection wells.

Water Injection Rate (m3/d)	Ivw1	Ivw2	Ivw3	Ivw4	Ivw5	Ivw6
Numerical simulation	150.00	138.61	150.00	148.44	145.96	124.09
Deep-LSTM model	150.00	134.56	148.20	149.18	150.00	125.27
Water Injection Rate (m3/d)	Ivw7	Ivw8	Ivw9	Ivw10	Ivw11	Ivw12
Numerical simulation	100.54	65.26	56.00	98.66	140.36	142.38
Deep-LSTM model	136.31	77.60	65.32	91.25	146.33	1355.60

Table 9. Comparison of optimization results of 21 production wells.

Production Well Rate (m3/d)	P1	P2	P3	P4	P5	P6	P7	P8	P9	P10	P11
Numerical simulation	149	122.3	142	150.1	83.5	150.1	150.1	124.1	150.1	149.7	85.5
Deep-LSTM model	142.5	139	130.1	139	77	150.1	143.7	119	143.3	135	88.2
Production Well Rate (m3/d)	P12	P13	P14	P15	P16	P17	P18	P19	P20	P21
Numerical simulation	108.1	98	91.6	132.8	73.9	142.6	69.1	1	57.9	120.2
Deep-LSTM model	100.1	109.7	82.5	142.0	66.1	145	70	1	59	128.8

Figure 10 compares optimal results based on the Deep-LSTM proxy model and numerical simulations. It can be seen that the dynamics of both the optimal NPV and cumulative production based on Deep-LSTM model optimization exhibited a trend similar to that based on numerical simulation. As shown in Figure 11, the distribution of remaining oil and the fluid production rate of oil wells after optimization by different methods showed a similar pattern, which verifies the effectiveness of the method in this paper.

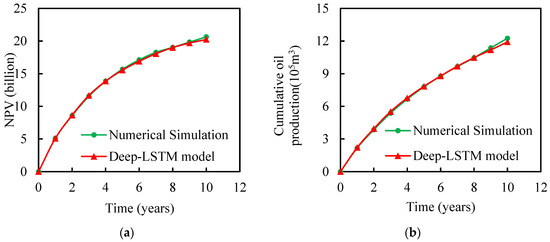
Figure 10. Comparison of (a) NPV and (b) cumulative oil production using different methods.

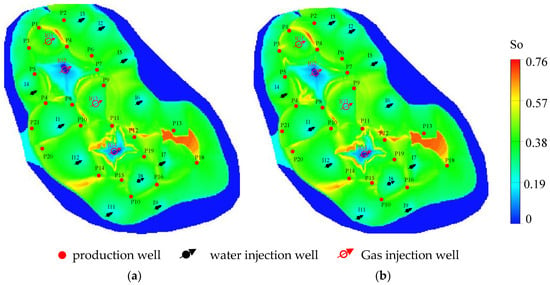
Figure 11. Comparison of oil saturation after well control optimization using (a) conventional numerical simulation and (b) the Deep-LSTM proxy model.

Table 10 compares optimization results based on the Deep-LSTM and conventional numerical simulation. It can be seen from the table that compared with the optimization results based on numerical simulation, the prediction error of NPV is 2.1%, and the prediction error of cumulative oil production is 3.5%. However, the optimization efficiency of the Deep-LSTM model was improved by more than 90%. In summary, the optimization method based on the Deep-LSTM model established in this paper significantly improved optimization efficiency while ensuring optimization accuracy, which proves the effectiveness and superiority of the optimization method based on the Deep-LSTM model. At the same time, the Deep-LSTM model we established in the optimization process has the characteristics of repeatable optimization.

Table 10. Comparison of optimization results of different methods.

Methods	NPV (Billion)	Cumulative Oil (105 m3)	CPU Time
Numerical simulation	20.65	12.25	345.38 h
Deep-LSTM	20.24	11.92	5 h 42 min
Error (%)	2.1	2.7	/

4. Conclusions

This study used Deep-LSTM to construct a proxy model, which was then used for optimizing well control parameters of the gas flooding EOR process. It is shown that the prediction accuracy of the Deep-LSTM model (in terms of R²) can reach 0.995. The constructed Deep-LSTM model was then integrated with the classical CMA-ES algorithm to establish a fast optimization method of the well control parameters for the gas flooding process. The method was applied to the Baoshaceng reservoir in Tarim Oilfield, showing comparable accuracy (with an error of less than 3%) but significantly improved efficiency (reduced computational duration of ~90%) against the conventional numerical simulation method. At the same time, the Deep-LSTM optimization model established in this paper has the advantage of repeated use, and can repeatedly and quickly calculate the optimization of injection and production parameters for the Baoshaceng reservoir, thereby providing effective technical support for on-site development decisions at the Baoshaceng reservoir.