Bidding Strategy for VPP and Economic Feasibility Study of the Optimal Sizing of Storage Systems to Face the Uncertainty of Solar Generation Modelled with IGDT

Abstract

Virtual power plants (VPP) emerge as a new participant that, in order to maximise their visibility and income, represents a group of distributed energy resources (DER) in the electricity market. However, this DER aggregation brings challenges, such as fluctuating renewable sources dependent on weather variables and guaranteeing power set points. One way to deal with these intermittencies is to incorporate the energy storage system (ESS) into the VPPs. Therefore, this paper presents a novel bidding strategy of VPP that includes modelling the uncertainty associated with solar generation using information gap decision theory (IGDT) and the optimal sizing of ESS systems so as to deal with solar generation fluctuations. Additionally, a study is carried out to determine the economic viability of this methodology in the short, medium and long terms using the return on investment (ROI).

1. Introduction

The electric power system is transforming due to the penetration of distributed energy resources (DER). One way to maximise their visibility in the market and income is through aggregation in a virtual power plant (VPP). VPP represents a variety of DER in different geographic locations on the market.

One of the fundamental issues in VPP is the uncertainties modelling. Modelling the uncertainties allows the operator to make decisions that guarantee that the power setpoints bid in electricity markets. Different modelling techniques are highlighted, including probabilistic methods that depend on historical information and probability density functions [1,2,3], and non-probabilistic methods that are used when information is absent. Once uncertainties are modelled, different decision methods arise, such as robust optimisation [4,5] and the information gap decision theory (IGDT) technique [6,7,8].

One of the disadvantages of making an optimal programming based on uncertainty modelling is that the decisions made by the operator can be risky or, on the contrary, conservative. The energy storage systems (ESS) can diminish the consequences of bad decisions or unexpected events, becoming an essential asset in the VPP. ESS can support the operation when the renewable generation forecasts mismatch the weather events and provide ancillary services such as voltage and frequency regulation. Studies such as those presented in [9,10,11] evaluate different penetration levels of renewable generation and size ESS by minimising their operating and investment cost. Additionally, other papers such as [12,13,14] reduced the costs of incorporating ESS and analysed this device’s cost benefit. However, these papers do not validate whether these investments are profitable in the short, medium or long term. Other authors studied the optimal location of the storage systems to guarantee technical support to the networks at the lowest possible cost [15,16,17].

On the other hand, some authors focus on optimally designing the control of battery units to reduce the peak electricity demand. In addition, they maximise the use of photovoltaic energy to charge the energy storage unit [18,19]. Moreover, in the literature, articles have been found that use the optimal sizing of ESS with objectives different from those previously presented. For example, ESS is used in [20,21] to guarantee power quality by taking advantage of its fast response ramp to supply power at times of shortage when compared to conventional generators. In addition, the incorporation of ESS guarantees power reliability on the consumer side, serving as a backup when there are contingencies in the electrical system [22]. The optimal sizing is used in [23] to ensure that the energy storage devices combined with other dispatchable generators provide an adequate regulation reserve. Publications [24,25,26] propose an ESS sizing strategy to perform voltage regulation, loss reduction and peak load shaving. Additionally, this kind of method applies to the unit commitment problem with a spinning reserve for a microgrid [27].

The scientific community proposed several test systems with optimal sizing strategies. In [28], Wong et al. presented a review with 110 references focused on storage systems classified according to the objective function, and [29] shows an overview of 271 papers related to the placement, sizing operation and power quality in storage systems. Researchers developed approaches in microgrids and distribution networks. None of them investigated the cost minimisation of storage systems in VPP. Nevertheless, in [30], Sadeghian et al. proposed a decision-making procedure to size and locate ESS systems within a VPP, including a study on investment risk management. In this case, the authors did not consider the uncertainties related to generators, only considered market price uncertainty and did not include an analysis of the economic feasibility of the proposed methodology.

Therefore, the main contributions of the current study are:

• An optimal bidding strategy of VPP that seeks to maximise the benefits of VPP and perform the optimal sizing of ESS to deal with fluctuations in solar generation.
• An analysis of the robustness and opportunity of solar uncertainty using IGDT for the VPP operator to make risk-averse or conservative decisions to maximise its benefits.
• An economic study using return on investment (ROI) to determine the feasibility of investing in ESS to compensate for the uncertainty of solar generation in the short, medium and long terms.

2. Proposed Methodology

The proposed methodology sought to determine what is more profitable for a VPP: making robust and optimistic decisions based on solar uncertainty modelling or compensating for possible generation fluctuations by incorporating storage systems. Therefore, we compared the profits in the RT market through a deterministic optimisation approach, with an optimal bidding strategy of a VPP modelling the solar uncertainty using IGDT and with the VPP bidding strategy considering the optimal size of batteries for dealing with fluctuations in solar generation. Section 2.1, Section 2.2, Section 2.3 describe the optimisation approaches. It is essential to highlight that the first two strategies were taken from [31].

2.1. Deterministic Approach: Bidding Strategy of VPP to Trade in Real-Time Market

The first approach considers the bidding strategy of a VPP, whose objective is to maximise profits in the RT market through a deterministic optimisation problem as described in Equations (1)–(14).

$$\underset{{\mathrm{P}}_{\mathrm{t},\mathrm{i}}^{\mathrm{RT}}{,\mathrm{P}}_{\mathrm{t},\mathrm{i}}^{\mathrm{PV}}{,\mathrm{P}}_{\mathrm{t},\mathrm{i}}^{\mathrm{W}}{,\mathrm{P}}_{\mathrm{t},\mathrm{i},\mathrm{b}}^{\mathrm{dis}}{,\mathrm{P}}_{\mathrm{t},\mathrm{i},\mathrm{b}}^{\mathrm{ch}}{,\mathrm{E}}_{\mathrm{b},\mathrm{t}}{,\mathrm{u}}_{\mathrm{t}}}{\max }{\displaystyle \sum }_{\mathrm{t}=\mathsf{\tau }}^{ {\Omega }^{\mathrm{T}}}{\mathsf{\lambda }}_{\mathrm{t}}^{\mathrm{RT}}{\mathrm{P}}_{\mathrm{t},\mathrm{i}}^{\mathrm{RT}}∆t$$

(1)

The objective function (1) is the revenue from the sale of energy to the real-time (RT) market. Equation (2) represents the active power balance, and Equation (3) the active power flow in line ij. Equations (4)–(8) are the operative limits of the distributed generators and the import and export power to the electricity market. Equations (9) and (10) represent the charge and discharge battery power, and Equations (11) and (12) represent the battery charge and discharge limit. Finally, Equation (13) shows the stored energy of the batteries for each period, and (14) represents the storage limit of batteries.

$${\mathrm{P}}_{\mathrm{t},\mathrm{i}}^{\mathrm{PV}}{+\mathrm{P}}_{\mathrm{t},\mathrm{i}}^{\mathrm{W}}{+\mathrm{P}}_{\mathrm{t},\mathrm{i},\mathrm{b}}^{\mathrm{dis}}-{\displaystyle \sum }_{\mathrm{ij}\in {\mathsf{\Omega }}_{\mathrm{ij}} \mathrm{i}\ne \mathrm{j}}{\mathrm{P}}_{\mathrm{t},\mathrm{ij}}=\widetilde{{ \mathrm{P}}_{\mathrm{t}}^{\mathrm{DA}}}{+\mathrm{P}}_{\mathrm{t}}^{\mathrm{RT}}{+\mathrm{P}}_{\mathrm{t}}^{\mathrm{d}}{+\mathrm{P}}_{\mathrm{t},\mathrm{i},\mathrm{b}}^{\mathrm{ch}}$$

(2)

$${\mathrm{P}}_{\mathrm{t},\mathrm{ij}}{=\mathrm{B}}_{\mathrm{ij}}·\left({\mathsf{\delta }}_{\mathrm{i},\mathrm{t}} {- \mathsf{\delta }}_{\mathrm{j},\mathrm{t}}\right)$$

(3)

$$\underset{\_}{{\mathrm{P}}_{\mathrm{t}}} \le { \mathrm{P}}_{\mathrm{t},\mathrm{ij}} \le \overline{{ \mathrm{P}}_{\mathrm{t}}}$$

(4)

$$0 \le { \mathrm{p}}_{\mathrm{t},\mathrm{i}}^{\mathrm{PV}} \le \overline{{ \mathrm{P}}_{\mathrm{t},\mathrm{i},\mathrm{d}}^{\mathrm{PV}}}$$

(5)

$$0 \le { \mathrm{P}}_{\mathrm{t},\mathrm{i},\mathrm{d}}^{\mathrm{w}} \le \overline{{ \mathrm{P}}_{\mathrm{t},\mathrm{i}}^{\mathrm{w}}}$$

(6)

$$\underset{\_}{{\mathrm{P}}_{\mathrm{t}}^{\mathrm{M}}} \le \widetilde{{ \mathrm{P}}_{\mathrm{t}}^{\mathrm{DA}}}{+\mathrm{P}}_{\mathrm{t}}^{\mathrm{RT}} \le \overline{{\mathrm{P}}_{\mathrm{t}}^{\mathrm{M}}}$$

(7)

$$\underset{\_}{{\mathrm{P}}_{\mathrm{t}}^{\mathrm{RT}}} \le { \mathrm{P}}_{\mathrm{t}}^{\mathrm{RT}} \le \overline{{ \mathrm{P}}_{\mathrm{t}}^{\mathrm{RT}}}$$

(8)

$$\widetilde{{\mathrm{P}}_{\mathrm{ch}}} = {\mathsf{\gamma }}_{\mathrm{s}}{\mathrm{x}}_{\mathrm{s}}\widetilde{{\mathrm{E}}_{\mathrm{b}}}$$

(9)

$$\widetilde{{\mathrm{P}}_{\mathrm{dis}}} = \frac{1}{{\mathsf{\gamma }}_{\mathrm{s}}}{\mathrm{x}}_{\mathrm{s}}\widetilde{{\mathrm{E}}_{\mathrm{b}}}$$

(10)

$$0 \le { \mathrm{P}}_{\mathrm{t},\mathrm{i},\mathrm{b}}^{\mathrm{ch}} \le \widetilde{{ \mathrm{P}}_{\mathrm{b}}^{\mathrm{ch}}}$$

(11)

$$0 \le { \mathrm{P}}_{\mathrm{t},\mathrm{i},\mathrm{b} }^{\mathrm{dis}}\le \widetilde{{\mathrm{P}}_{\mathrm{b}}^{\mathrm{dis}}}$$

(12)

$${\mathrm{E}}_{\mathrm{b},\mathrm{t}}{=\mathrm{E}}_{\mathrm{b},\mathrm{t}-1}+{\mathsf{\gamma }}_{\mathrm{s}}{ \mathrm{P}}_{\mathrm{t},\mathrm{i},\mathrm{b}}^{\mathrm{dis}} - \frac{1}{{\mathsf{\gamma }}_{\mathrm{s}}}{\mathrm{P}}_{\mathrm{t},\mathrm{i},\mathrm{b}}^{\mathrm{ch}}$$

(13)

$$\frac{\widetilde{{\mathrm{E}}_{\mathrm{b}}}}{2} \le { \mathrm{E}}_{\mathrm{b},\mathrm{t}} \le \widetilde{{\mathrm{E}}_{\mathrm{b}}}$$

(14)

2.2. An Optimisation Approach to Model Solar Generation Uncertainty with IGDT

This section presents an optimisation approach whose objective is the same as the deterministic approach described above, maximising VPP profits. The model includes the uncertainty associated with the fluctuation of solar irradiance. In the literature, different uncertainty modelling techniques are highlighted. If the historical information is incomplete, techniques such as IGDT are recommended, since they do not require any probability distribution assumption of the uncertain factors. Therefore, we decided to use this technique to model the uncertain parameter associated with solar generation in this paper. This formulation includes modelling the robustness and opportunity functions derived based on IGDT in order to analyse the conservative or risky decisions that the VPP operator can make. Section 2.2.1 and Section 2.2.2 present, respectively, robust and opportunistic optimisation approaches.

2.2.1. Robust Approach

The function $\widehat{\mathsf{\alpha }}\left(\mathrm{q},{\mathrm{r}}_{\mathrm{c}}\right)$ in Equation (15) represents the risk-averse strategy that seeks to be immune against losses or a low profit due to unfavourable deviations of the forecasted solar generation. Equations (15)–(19) describe the optimisation problem, where (16) is the revenue from the sale of energy to the real-time (RT) market. Equation (17) represents the expected maximum profit obtained in the deterministic approach. Meanwhile, Equation (18) defines the minimum revenue value that the VPP operator expects to obtain. Finally, the robust modelling of solar generation uncertainty with IGDT is in the inequality (19) and considers the effects of a decrease in solar generation power.

$$\widehat{\mathsf{\alpha }}\left(\mathrm{q},{\mathrm{r}}_{\mathrm{c}}\right)=\underset{{\mathsf{\alpha }}_{\mathrm{PV}},{\mathrm{P}}_{\mathrm{t}}^{\mathrm{RT}},{\mathrm{P}}_{\mathrm{t},\mathrm{i}}^{\mathrm{PV}}}{\max } {\mathsf{\alpha }}_{\mathrm{PV}}$$

(15)

$$\mathrm{B}={\displaystyle \sum }_{\mathrm{t}=\mathsf{\tau }}^{ {\Omega }^{\mathrm{T}}}{\mathsf{\lambda }}_{\mathrm{t}}^{\mathrm{RT}}{\mathrm{P}}_{\mathrm{t}}^{\mathrm{RT}}{∆}_{\mathrm{t}}$$

(16)

$${\mathrm{B}}_0= \underset{\mathrm{V}}{\max }{\displaystyle \sum }_{\mathrm{t}=\mathsf{\tau }}^{ {\Omega }^{\mathrm{T}}}{\mathsf{\lambda }}_{\mathrm{t}}^{\mathrm{RT}}{\mathrm{P}}_{\mathrm{t}}^{\mathrm{RT}}∆\mathrm{t}$$

(17)

$$\mathrm{B} \ge { \mathrm{B}}_{\mathrm{R}}{=\mathrm{B}}_0\left(1-\mathsf{\sigma }\right)$$

(18)

$$0 \le { \mathrm{p}}_{\mathrm{t},\mathrm{i}}^{\mathrm{PV}} \le { (1-\mathsf{\alpha }}_{\mathrm{PV}})·\overline{{\mathrm{P}}_{\mathrm{t},\mathrm{i}}^{\mathrm{PV}}}$$

(19)

2.2.2. Opportunistic Approach

The function $\widehat{\mathsf{\beta }}\left(\mathrm{q},{\mathrm{r}}_{\mathrm{c}}\right)$ in Equation (20) represents the risk-seeker strategy that analyses the unexpected behaviour of the solar generation from these favourable variations. Equations (20)–(24) describe the optimisation problem. Observe that Equation (21) is the revenue from the sale of energy to the real-time (RT) market. Equation (22) represents the expected maximum profit obtained in the deterministic approach. Equation (23) defines the maximum revenue value that the VPP operator expects to obtain. The opportunistic modelling of solar generation uncertainty with IGDT is in inequality (24) and considers the increment in the solar generation power.

$$\widehat{\mathsf{\beta }}\left(\mathrm{q},{\mathrm{r}}_{\mathrm{c}}\right)=\underset{{\mathsf{\alpha }}_{\mathrm{PV}},{\mathrm{P}}_{\mathrm{t}}^{\mathrm{RT}},{\mathrm{P}}_{\mathrm{t},\mathrm{i}}^{\mathrm{PV}}}{\min } {\mathsf{\alpha }}_{\mathrm{PV}}$$

(20)

$$\mathrm{B}={\displaystyle \sum }_{\mathrm{t}=\mathsf{\tau }}^{ {\Omega }^{\mathrm{T}}}{\mathsf{\lambda }}_{\mathrm{t}}^{\mathrm{RT}}{\mathrm{P}}_{\mathrm{t}}^{\mathrm{RT}}{∆}_{\mathrm{t}}$$

(21)

$$\mathrm{B} \ge { \mathrm{B}}_{\mathrm{R}}{=\mathrm{B}}_0\left(1+\mathsf{\sigma }\right)$$

(22)

$${\mathrm{B}}_0=\underset{\mathrm{V}}{ \max }{\displaystyle \sum }_{\mathrm{t}=\mathsf{\tau }}^{ {\Omega }^{\mathrm{T}}}{\mathsf{\lambda }}_{\mathrm{t}}^{\mathrm{RT}}{\mathrm{P}}_{\mathrm{t}}^{\mathrm{RT}}∆t$$

(23)

$$0 \le { \mathrm{p}}_{\mathrm{t},\mathrm{i}}^{\mathrm{PV}} \le { (1+\mathsf{\alpha }}_{\mathrm{PV}})·\overline{{\mathrm{P}}_{\mathrm{t},\mathrm{i}}^{\mathrm{PV}}}$$

(24)

2.3. An Optimal Approach to the Sizing Storage System to Deal with the Fluctuations

The last stage of the proposed methodology minimises the batteries’ storage capacity (25) while guaranteeing in (26) that the income obtained by the VPP is greater than or equal to the income obtained in the deterministic approach of stage 1. Likewise, Equation (27) defines the storage capacity limits. The energy stored in the batteries at each time t is presented in Equation (28) and is limited in (29). Subsequently, Equations (30) and (31) represent the charging and discharging power of the batteries, and their limits are in Equations (32) and (33). Meanwhile, Equations (34) and (35) guarantee that the battery cannot be charged and discharged simultaneously. The constraint related to the active power balance is included in Equation (36). The robust model of solar generation obtained in stage 2 is presented in (37). This restriction is fundamental in the optimisation approach since it represents the uncertainty of a reduced solar generation power that the ESS must compensate. The operational limits of wind generation are in the inequality (38). The limits on the energy that can be imported and exported from the RT market are in (39). Finally, Equation (40) sets the limits on how much energy the VPP can offer in the day-ahead (DA) and RT market during the same moment in time.

$$\underset{\mathrm{V}}{\min }{\displaystyle \sum }_{\mathrm{b} \in {\Omega }^{\mathrm{B}}}\widehat{{\mathrm{E}}_{\mathrm{b}}}$$

(25)

$${\displaystyle \sum }_{\mathrm{t} \in {\Omega }^{\mathrm{T}}}{\mathsf{\lambda }}_{\mathrm{t}}^{\mathrm{RT}}{\mathrm{P}}_{\mathrm{t},\mathrm{d}}^{\mathrm{RT}}{∆}_{\mathrm{t}}{=\mathrm{B}}_0$$

(26)

$$\widetilde{{\mathrm{E}}_{\mathrm{b}}^{\min }} \le \widehat{{\mathrm{E}}_{\mathrm{b}}} \le \widetilde{{\mathrm{E}}_{\mathrm{b}}^{\max }}$$

(27)

$${\mathrm{E}}_{\mathrm{b},\mathrm{t},\mathrm{d}}{=\mathrm{E}}_{\mathrm{b},\mathrm{t}-1}{+\mathsf{\gamma }}_{\mathrm{s}}{ \mathrm{P}}_{\mathrm{t},\mathrm{i},\mathrm{b}}^{\mathrm{ch}} - \frac{1}{{\mathsf{\gamma }}_{\mathrm{s}}}{\mathrm{P}}_{\mathrm{t},\mathrm{i},\mathrm{b}}^{\mathrm{dis}}$$

(28)

$$\frac{\widehat{{\mathrm{E}}_{\mathrm{b}}}}{2} \le { \mathrm{E}}_{\mathrm{b},\mathrm{t}} \le \widehat{{ \mathrm{E}}_{\mathrm{b}}}$$

(29)

$$\widetilde{{\mathrm{P}}_{\mathrm{ch}}}{=\mathsf{\gamma }}_{\mathrm{s}}{\mathrm{x}}_{\mathrm{s}}\widehat{{\mathrm{E}}_{\mathrm{b}}}$$

(30)

$$\widetilde{{\mathrm{P}}_{\mathrm{dis}} }=\frac{1}{{\mathsf{\gamma }}_{\mathrm{s}}}{\mathrm{x}}_{\mathrm{s}}\widehat{{\mathrm{E}}_{\mathrm{b}}}$$

(31)

$$0 \le { \mathrm{P}}_{\mathrm{t},\mathrm{i},\mathrm{b}}^{\mathrm{ch}} \le \widetilde{{\mathrm{P}}_{\mathrm{b}}^{\mathrm{ch}}}$$

(32)

$$0 \le { \mathrm{P}}_{\mathrm{t},\mathrm{i},\mathrm{b}}^{\mathrm{dis}} \le \widetilde{{ \mathrm{P}}_{\mathrm{b}}^{\mathrm{dis}}}$$

(33)

$${\mathrm{P}}_{\mathrm{t},\mathrm{i},\mathrm{b}}^{\mathrm{ch}} \le { \mathrm{M} \mathrm{u}}_{\mathrm{t}},\forall \mathrm{t} \in {\Omega }^{\mathrm{f}}, {\mathrm{u}}_{\mathrm{t}}\in \left\{0,1\right\}$$

(34)

$${\mathrm{P}}_{\mathrm{t},\mathrm{i},\mathrm{b} }^{\mathrm{dis}}\le { \mathrm{M}(1-\mathrm{u}}_{\mathrm{t}}),\forall \mathrm{t} \in {\Omega }^{\mathrm{t}}, {\mathrm{u}}_{\mathrm{t}}\in \left\{0,1\right\}$$

(35)

$${\mathrm{P}}_{\mathrm{t},\mathrm{i}}^{\mathrm{PV}}{+\mathrm{P}}_{\mathrm{t},\mathrm{i}}^{\mathrm{w}}{+\mathrm{P}}_{\mathrm{t},\mathrm{i}}^{\mathrm{b}}{=\mathrm{P}}_{\mathrm{t}}^{\mathrm{DA}}{+\mathrm{P}}_{\mathrm{t}}^{\mathrm{RT}}{+\mathrm{P}}_{\mathrm{t}}^{\mathrm{d}}$$

(36)

$$0 \le { \mathrm{p}}_{\mathrm{t},\mathrm{i}}^{\mathrm{PV}} \le \left({1-\mathsf{\alpha }}_{\mathrm{PV}}\right)·\widetilde{{\mathrm{P}}_{\mathrm{t},\mathrm{i},\mathrm{d}}^{\mathrm{PV}}}$$

(37)

$$0 \le { \mathrm{P}}_{\mathrm{t},\mathrm{i}}^{\mathrm{w}} \le \widetilde{{ \mathrm{P}}_{\mathrm{t},\mathrm{i}}^{\mathrm{w}}}$$

(38)

$$\underset{\_}{{\mathrm{P}}_{\mathrm{t}}^{\mathrm{RT}}} \le { \mathrm{P}}_{\mathrm{t}}^{\mathrm{RT}} \le \overline{{\mathrm{P}}_{\mathrm{t}}^{\mathrm{RT}}}$$

(39)

$$\underset{\_}{{\mathrm{P}}_{\mathrm{t}}^{\mathrm{M}}} \le { \mathrm{P}}_{\mathrm{t}}^{\mathrm{DA}}{+\mathrm{P}}_{\mathrm{t}}^{\mathrm{RT}} \le \overline{{ \mathrm{P}}_{\mathrm{t}}^{\mathrm{M}}}$$

(40)

3. Case Study

The market strategy was applied to the test system shown in Figure 1. The data and the deterministic optimisation result are taken from [32]. The VPP comprises photovoltaic panels, wind turbines, batteries and loads. Figure 2 shows the total demand curve, RT market price and wind and solar generation forecast. This analysis assumed that the only profile that changed during the year was solar generation. In the other cases, the study assumed the same daily profile throughout the year to quantify the actual effect of the uncertainty of solar generation. The market price data was taken from the New England system, corresponding to 18 January 2019. Finally, Table 1 shows the parameters of the batteries and Table 2 the parameters of the electrical system.

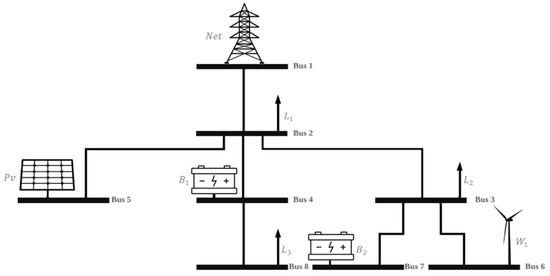
Figure 1. Test system. Taken from [31].

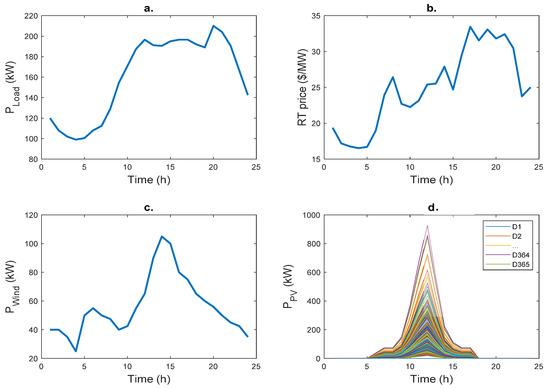
Figure 2. (a) Hourly demand curve, (b) RT market price, (c) wind turbine generation profile and (d) yearly PV generation profile aligned hourly.

Table 1. Storage system characteristics of the test system. Taken from [32].

Battery	SoC ini	SoC fin	SoC min	SoC max	Φb (p.u)	Eb_c(i) (kW)	Eb_d(i) (kW)
B1	0.5	0.5	0.5	1	0.4	62.5	50
B2	0.5	0.5	0.5	1	0.5	50	40

Table 2. Electrical system parameters of the test system. Taken from [32].

Parameter	Value
Floss	7.14%
∆t	1
Susceptance	0.419 S
Power limit	1500 kW

4. Results

To show the importance of the proposed methodology, Figure 3 shows the optimal dispatch obtained by VPP when it participates in the RT market using the deterministic approach proposed in (1)–(16). Under these conditions, the VPP buys in the DA market, takes advantage of the distributed sources’ maximum capacity, and sells in the RT market. The profit obtained by the VPP is USD 24,926 per year. This data will be essential for analysing the uncertainty of solar generation using IGDT since it is an input parameter in the optimisation problem described in Section 2.2.

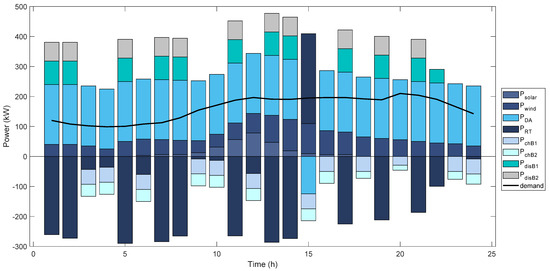
Figure 3. Optimal dispatch when the VPP participates in the RT market. Solar power (${\mathrm{P}}_{\mathrm{solar}}$), wind power (${\mathrm{P}}_{\mathrm{wind}}$), power traded in DA (${\mathrm{P}}_{\mathrm{DA}}$), power traded in RT (${\mathrm{P}}_{\mathrm{RT}}$), battery charging power 1 (${\mathrm{P}}_{\mathrm{chB}1}$) battery charging power 2 (${\mathrm{P}}_{\mathrm{chB}2})$, battery discharging power 1 (${\mathrm{P}}_{\mathrm{disB}1}$), battery discharging power (${\mathrm{P}}_{\mathrm{disB}2}$) and demand power (demand).

After defining the expected profits in the deterministic approach, the bidding strategy to quantify the effect of solar generation on VPP revenues is proposed. This strategy considers modelling the positive and negative impacts of solar fluctuations. Figure 4 and Table 3 show the behaviour of the uncertain parameter considering different cost targets. The blue line shows how much the solar generation forecast would have to change for the VPP to obtain greater profits than expected. On the contrary, the red line indicates how the uncertainty of the solar generation would negatively affect the expected profits. The VPP is immune to the negative variation on the solar generation when the expected revenue is less than USD 19,500. It is important to note that the profit obtained by the VPP is not influenced to a great extent by the solar uncertainty, since to obtain an additional 10% of profits, the solar generation would have to change by 78%.

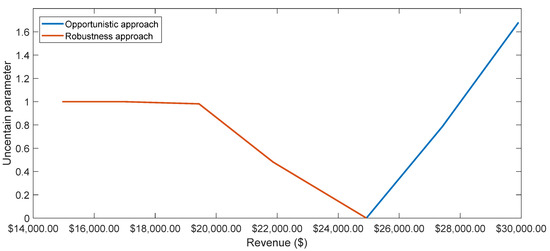
Figure 4. The effect of solar generation uncertainty on the target revenue.

Table 3. The effect of solar generation fluctuation on the target revenue.

Solar Uncertainty (UND)	Revenue Variation ($)	Revenue Variation (%)
1.68	29,911	20%
0.786	27,418	10%
0	24,926	0%
−0.481	21,866	−10%
−0.98	19,436	−20%
−1	17,007	−30%
−1	14,955	−40%

In the last stage of the proposed methodology, the VPP operator decides to guarantee the energy dispatch by increasing the installed storage capacity. The optimal sizing of the batteries to face fluctuations in the solar generation is presented in Table 4.

Table 4. Optimal sizing of the batteries when the solar generation forecast changes.

Battery	Case 1		Case 2		Case 3
	Initial Battery Sizing (kWh)	Capital Cost Energy Capacity (USD)	Battery Sizing to Compensate for the Decrease in the Solar Generation to 48.7% (kWh)	Capital Cost Energy Capacity (USD)	Battery Sizing to Compensate for the Decrease in the Solar Generation to 98% (kWh)	Capital Cost Energy Capacity (USD)
B1	250	59,000	572	134,992	750	177,000
B2	200	47,200	230	54,280	600	141,600

The calculated storage system’s capacity would deal with a decrease of 48.7% and 98% of solar generation. Table 4 and Figure 5 show that the batteries must increase their capacity to deal with the fluctuations. With a reduction in PV production of 48.7%, B1 must increase their capacity from 250 kWh to 572 kWh (more than double), and B2 must increase from 200 kWh to 230 kWh. In the case of a reduction of PV productions of 98%, B1 should increase from 250 kWh to 750 kWh (three times), and B2 should increase from 230 kWh to 600 kWh (more than three times). Additionally, the capital costs that the VPP would have to incur to guarantee this storage capacity are evaluated in the same table. This study assumed that the batteries were Li-ion and that the capital cost for the energy capacity would be USD 236/kWh, according to [33]. On the other hand, Figure 6 compares the optimal dispatches on day 1 when VPP bids in the RT market while considering the deterministic approach with when VPP considers increasing the capacity of the storage system to deal with solar generation uncertainty. If the amount of solar energy is reduced, the amount of charge and discharge energy in the batteries increases during each moment in time.

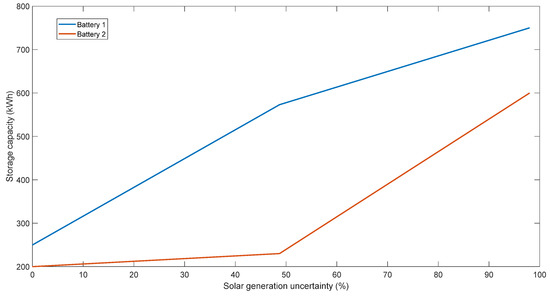
Figure 5. Solar generation uncertainty vs. storage capacity.

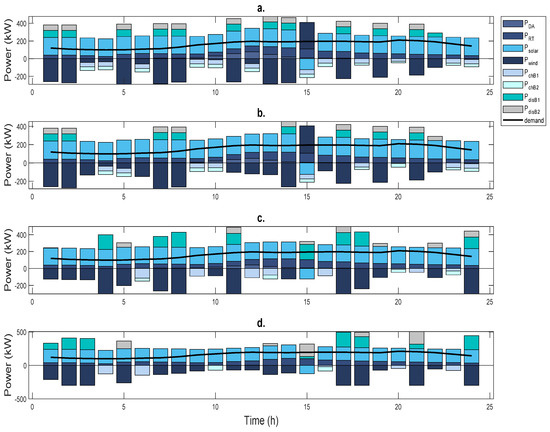
Figure 6. Comparison of optimal dispatches on day 1. (a) The VPP offers in the market in real time. (b) The VPP bids in the market in real time with a reduction in solar generation of 35.5%. VPP examples when increasing the storage capacity to compensate for the reduction of solar generation to (c) 48.1% and (d) 98%.

The return on investment (ROI) expected by the VPP when the storage capacity is increased to deal with the fluctuations of renewable sources is presented in Table 5. Table 6 presents the cost of including additional energy storage capacity to compensate for solar generation uncertainty. The decrease of 48.7% in solar generation causes a decrease in VPP income of 12.3%, equivalent to USD 3060 per year, when compared with the deterministic case. Suppose the goal is to guarantee the same income as the deterministic approach. In that case, the VPP should invest in an additional storage capacity of 352 kWh, increasing the capital cost by 78%, equivalent to USD 83,072. The VPP would recover the investment in 27 years, which makes the incorporation of the batteries unfeasible at the given prices. If the price of the batteries falls to USD 56/kWh, the ROI will be 6.44 years. In this case, the proposed methodology will also be unfeasible since the average number of annual cycles of B1 will be 400 and those of B2 will be 600. The cycle life would be 8.75 and 5.83 years, respectively, assuming that the number of cycles of a lithium battery at 80% deep discharge is 3500 [33]. This way, the investor would recover the investment when the battery life ends. For this methodology to be viable, the price of the storage kWh would need to fall to USD 30/kWh, so that the ROI would be 3.5 years.

Table 5. Costs for including additional energy storage capacity to compensate for solar generation uncertainty.

Battery	Additional Capacity Required	The Capital Cost Needed to Compensate for Solar Uncertainty of 48.7%		Additional Capacity Required	The Capital Cost Needed to Compensate for Solar Uncertainty of 98%
		The Capital Cost of Batteries per kWh = $236/kWh	The Capital Cost of Batteries per kWh = $56/kWh		The Capital Cost of Batteries per kWh = $236/kWh	The Capital Cost of Batteries per kWh = $56/kWh
B1	322	$75,992	$18,032	500	$118,000	$28,000
B2	30	$7080	$1680	600	$94,400	$22,400
B1 + B2	352	$83,072	$19,712	1100	$212,400	$50,400

Table 6. ROI analysis when the capital cost of batteries per kWh changes.

Capital Cost of Batteries per kWh	ROI When the Additional Capacity Is 352 kWh (Years)	ROI When the Additional Capacity Is 1100 kWh (Years)
$236/kWh	27	38.7
$56/kWh	6.44	9.18
$30/kWh	3.45	6

Finally, the decrease of 98% in solar generation causes a decrease in the VPP income of 22%, equivalent to USD 5490 per year, when compared with the deterministic case. VPP would have to invest USD 212,400 to offset this reduction in power generation, assuming a capital cost of USD 236/kWh. The investment will be recovered after 38 years, making it unviable. If the capital cost of storage were USD 56/kWh, the investment would be recovered in 9.18 years, and if the capital cost of storage were USD 30/kWh, the ROI would be six years. This way, we concluded that for VPP, it is better to obtain less income in the RT market than to incorporate the storage system so as to deal with the uncertainty of 98% of the solar panels.

5. Conclusions

In the present study, an analysis was carried out to determine what was more profitable for a VPP: make robust and optimistic decisions based on the modelling of solar uncertainty using IGDT or compensate for fluctuations in solar generation by incorporating storage systems.

A case study was implemented to validate the minimum storage capacity required to face adverse fluctuations in solar generation of 48.1% and 98%. We observed that the two storage systems had to double and triple the initial capacity. Although it was possible to compensate for fluctuations in solar generation, the capital costs of the ESS are high. Therefore, in the short term, it is more viable to use the supply strategy that is based on modelling uncertainties than to increase the storage capacity. It is expected that the storage systems will be cheaper in less than thirty years. In this way, the ROI could decrease from 27 to 3.5 years if the capital cost of the batteries per kWh falls from USD 236 to USD 30. Reaching such a low storage cost will allow its massive incorporation into the electrical system. Likewise, it will contribute to auxiliary energy services, such as the real-time compensation of power deviations, which will take advantage of its rapid generation ramps. In this way, the optimal battery sizing strategy for dealing with fluctuations in the proposed generation will be made viable in the long term.