Abstract
Unconventional oil and gas formations are abundant, have become an increasingly important part of the global energy supply, and are attracting increasing attention from the industry. Predicting key reservoir properties plays a significant role in both geological science and subsurface engineering workflows. With the advent of horizontal well drilling and multiple-stage hydraulic fracturing, the Montney Shale formation is one of the most promising and productive shale plays in Canada. However, very few academic papers discuss its in situ stress, reservoir pressure, and permeability, which are essential for the development of the Montney Shale. The objective of this study is to analyze the geo-stress, the pore pressure, and several key reservoir properties by using diagnostic fracture injection test (DFIT) data from the Montney Shale. One horizontal well from the Wapiti field has been analyzed with a set of DFIT data, and its results show that the general pressure and Gdp/dG responses from Well-A indicate a signature of height recession/transverse storage. In the study, the Tangent Line method, the Compliance method, and the Variable Compliance method have been applied to estimate the key reservoir properties. As a result, the Well-A DFIT analysis estimates that the closure pressure is ranging from 34.367 to 39.344 MPa, contributing to the stress gradient from 14.09 to 16.13 KPa/m for the formation. The pore pressure is ranging from 20.82 to 24.58 MPa, contributing to the pore pressure gradient from 8.54 to 10.07 KPa/m for the formation. The porosity is ranging from 3% to 6%. These reservoir properties are contoured cross the Montney Shale formation. Using the DFIT’s numerical simulation and history matching, the reservoir permeability is 0.024 md, fracture length is 13.44 m, and fracture geometries are analyzed by different models. Moreover, the physics behind the DFIT are analyzed and discussed in detail. For the first time, three different analysis methods have been applied to estimate a series of key reservoir properties for the case wells in the Montney Shale formation. This approach can not only reduce the potential prediction error caused by a single method application but also increase the persuasiveness of the assessment and save time, ensuring the efficient implementation of engineering operations. Given the significance of quantifying in situ stress and reservoir pore pressure in unconventional hydrocarbon exploration and development, this study could help the operator to quickly understand the stress regimes, the fracture geometry, and the formation properties of the Montney Shale formation in the Wapiti field. Furthermore, the interpreted results demonstrated in this paper are adding substantial business value to the asset, especially in terms of improving the hydraulic fracturing design and, thus, accelerating the cashflow from production.
1. Introduction
Unconventional hydrocarbon resources, including shale hydrocarbon, tight hydrocarbon, and coalbed methane, have become an increasingly essential part of the global oil and gas supply during the past decades [1,2]. Compared to conventional plays, unconventional formations have different transport properties at pore scale, such as extreme low permeability and the dispersion effect, which significantly affect hydrocarbon production [3]. Therefore, in the development of unconventional hydrocarbon exploration, predicting key reservoir properties, such as in situ stress and formation pore pressure, plays a significant role in both geological science and subsurface engineering workflows. Understanding pore pressure, closure pressure, and net pressure are important for the development of an unconventional reservoir [4,5,6,7]. While advanced drilling, completion, hydraulic fracturing, and reservoir stimulation technologies have become more mature recently, low- and extremely low-permeability formations can be developed more efficiently, which can potentially bring huge benefits to the global oil and gas industry [8]. However, there are very few academic publications discussing the geo-stress, pore pressure, net pressure, permeability, and corresponding DFIT applications in Canada’s Montney Shale, while few study were continued in the Wapiti Montney shale formation.
Multi-rate well testing is an efficient way to evaluate reservoir properties, such as pore pressure, permeability, reservoir boundary, etc., as well as near-wellbore properties such as skin factor and fracture weight length. Additionally, quantifying effective formation permeability and initial reservoir pressure accurately is essential for reservoir recovery evaluation and well performance optimization. The traditional methodologies, such as the extended leak-off test (XLOT) and pump-in and flow-back test (PIFB), have been widely used in the industry for stress evaluation during drilling. In the above approaches, the drilling mud is injected to create a tiny hydraulic fracture in a vertical open hole below a newly cemented casing [9]. However, the permeability of a shale-gas formation is extremely low; it may take several days, even weeks, to detect a pseudo-radial flow by conventional build-up tests, thus leading to low evaluation efficiency. Therefore, the diagnostic fracture injection test (DFIT) arises, which is an advanced and cost-effective technique to analyze stress regimes and reservoir properties compared to the traditional methods. Based on DFIT data, there are many remarkable publications attempting to formalize a method for in-suit stress prediction, which have been applied to many formations and fields globally. G-function has been firstly developed by Nolte [10,11,12]. Based on Nolte’s study, Castillo [13] interpreted the pressure vs. G-function plot with a straight line. However, Castillo’s method works less efficiently when many points of inflection occur, and, thus, an expected linearity relationship cannot be identified. Based on Castillo’s model, Barree et al. [13,14,15,16,17] developed a prevailing methodology, the Tangent Line method, to conquer the challenges of this unobvious issue. Furthermore, Barree’s team developed a series of G-function plots, displaying normal and non-ideal leak-off behaviors. Based on numerical simulation, McClure et al. [18,19] created the Compliance methodology to calculate minimum in situ stress or fracture closure pressure using DFIT data. Considering both the Tangent Line and the Compliance methods, Wang and Sharma [20,21,22,23] advanced this topic and developed the Variable Compliance method for closure pressure estimation.
This study focuses on the Montney Shale formation in the Wapiti field. Firstly, the governing equations of DFIT are compared and summarized. The closure press is estimated by the Tangent Line method. Most importantly, the Montney Shale DFIT data are interpreted to analyze geo-stress, pore pressure, and several key reservoir properties of the Montney Shale in the Wapiti field.
Given the significance of quantifying in situ stress and reservoir pore pressure in unconventional hydrocarbon exploration and development, this study could help the operator to understand the stress regimes, the fracture geometry, and the formation properties of the Montney Shale formation in the Wapiti field. Additionally, in the current “lower for longer” business climate, there are significant needs to unlock the full value of the engineering information in the data that we already own in the field, to optimize the hydraulic fracturing design and enhance the performance of shale resources.
2. Materials and Methods
Diagnostic fracture injection tests were developed by Halliburton, and its process is similar to the leak-off and formation integrity tests [6,12,15,16,24,25,26]. Before a full-scale hydraulic fracture stimulation, a small amount of fluid is pumped into a well at a constant rate to induce a small hydraulic fracture in the near-wellbore formation. Throughout the entire history of its application, DFIT has been initially used to determine the fluid efficiencies, leak-off coefficient, and closure pressure. Then, geo-scientists and engineers gradually found out the advantages of DFIT application for estimating additional important reservoir properties, such as pore pressure and permeability [27]; most recently, the pressure transient data provided by DFIT can even provide additional useful results, including induced fracture variability and connectivity [22]. In general, DFIT is a very practical and effective technique for calculating in situ stress, closure pressure (minimum in situ pressure), and other important reservoir properties, which facilitate operators to understand their reservoirs, optimize the well completion designs, enhance recovery, and consequently gain more value in shale and low-permeability formation [28].
Figure 1 shows a typical workflow diagram of pre-fracturing injection falloff diagnostic test. The point of instantaneous fracture closure splits the whole workflow into two distinct regions, the Before Closure (BC) pressure region and the After Closure (AC) pressure region [29,30]. Normally, the bottom-hole pressure can be directly metered by bottom-hole gauge or calculated from surface measurement plus hydrostatic pressure, in this project we use the calculation method since there is no available bottom-hole gauge pressure data in the test well. As shown in Figure 1, in Region of BC, the pressure behavior is more dominated by fracture geometrics. With a constant fluid injection rate (normally water), the bottom-hole pressure is building up to the leak-off point (LOP) where the first fracture has been created, while formation breakdown pressure (FBP) is the peak pressure during the whole injection process. The well is then shut in when FBP has been reached; the pressure consequently drops from the fracture propagation pressure (FPP) to the instantaneous shut-in pressure (ISIP) since no more fluid is injected into wellbore. The key point, fracture closure pressure, is defined as the pressure at which the planes of induced fractures come into contact and, therefore, the fracture is closed. Region of AC is more dominated by near wellbore formation properties and divided into linear flow and radial flow. If the hydraulic fracture length is relatively long, bilinear flow will exist in addition to linear and radial flow periods. More importantly, initial reservoir pressure and permeability can be estimated in this stage to evaluate the reservoir.
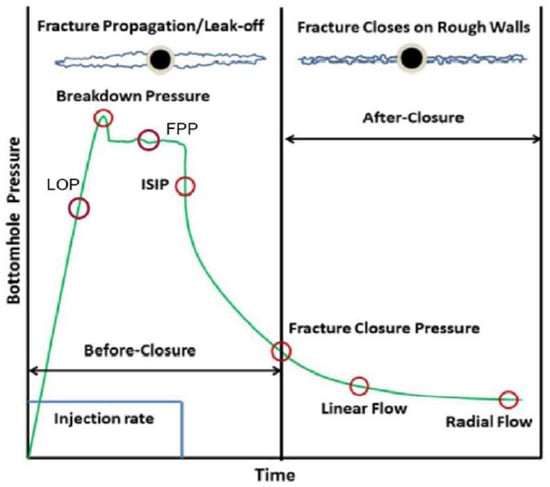
Figure 1.
Typical DFIT data and relevant physical phenomena in region of Before Closure and region of After Closure.
G-function, a useful time function to estimate in situ stress by pressure decline analysis, was firstly created by Nolte [10,11,12]. G-function is a classic and useful equation for fracture pressure as a function of dimensionless time, which is derived using the following assumptions: (1) normal leak-off behaviors, including a constant leak-off area, constant Carter leak-off theory, and constant stiffness; (2) the fluid properties and formation parameters are independent of pressure; (3) the spurt loss is neglected. Castillo [13] used the pressure vs. G-function plot with a straight line based on Nolte’s work, interpreted this plot and estimated that any variation from this straight line in the G-function plot is the minimum in situ stress (Fracture Closure Pressure), and its slope can be used to estimate the leak-off coefficient. However, the Straight Line method often fails when analyzing practical projects, because points of inflexion may obscure the linearity of the formation in the plot. Barree and Mukherjee [14,15] (2009, 1996) recognized this problem and solved it creatively by converting straight line to tangent line. Combining the Straight Line and Tangent Line methods together, closure pressure can be estimated more accurately and more reliably. The dimensionless time is given by:
depending on the leak-off level, the dimensionless leak-off equation can be summarized as:
(1) For high fluid efficiency,
(2) For low fluid efficiency,
vs. G-function is plotted for Straight Line method, and vs. G-function is plotted for Tangent Line method. The G-function equation can be written as
Additionally, Barree [14] (2009) developed a remarkable workflow to interpret the DFIT results. From that study, both normal leak-off and non-ideal leak-off behaviors are summarized in Figure 2.
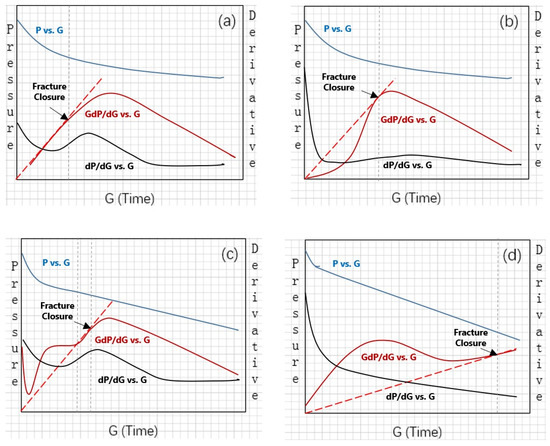
Figure 2.
Type of pressure vs. G-function, dP/dG vs. G-function, and GdP/dG vs. G-function trends: (a) normal leak-off behavior and (b) non-ideal leak-off behavior (I) that depicts a signature of height recession/transverse storage. (c) Non-ideal leak-off behavior (II) that depicts a signature of pressure-dependent leak-off behavior, which occurs when the fluid-loss rate varies significantly with the pressure-dependent permeability in a dual-porosity system (usually micro-cracks and natural fractures exist in these cases). (d) Non-ideal leak-off behavior (III) that demonstrates a signature of fracture tip extension, which occurs in low-permeability reservoirs.
The Compliance method developed by McClure et al. [18,19] is based on numerical simulation, assuming that the fracture stiffness starts to increase as the fracture walls come into contact, resulting in a concave-up trend on the plot of GdP/dG. Consequently, the fracture stiffness continues to increase as well. Therefore, Compliance method explains that the minimum in situ stress should be picked at the point where the GdP/dG trend starts to depart from the expected linearity on the G-plot, resulting in a higher value of pressure in comparison to the minimum in situ stress estimated by the Tangent Line method.
Remarkably, Wang and Sharma [20,21,22,23] present a novel approach to estimate the minimum in situ pressure and important reservoir/fracture parameters by numerical simulation, called Variable Compliance method. The Variable Compliance method addresses that fracture closure is a dynamic process instead of an isolated point. In other words, the fracture closes gradually from the boundary to the center, and the fracture stiffness is not constant anymore. Consequently, the results of closure pressure determination by Variable Compliance method often show an average value between Tangent Line and Compliance methods.
The identification of fracture closure time by different methodologies (Tangent Line, Compliance, and Variable Compliance methods) is the key point of dividing Before Closure and After Closure regimes, analyzing the closure pressure, and, consequently, evaluating the reservoir pore pressure and permeability based on the pressure transient analysis. Numbers of outstanding studies were performed on this topic, suggesting that Pseudolinear, bilinear, and Pseudoradial flows occurred in the After Closure regime [12,14,31]. The reservoir pressure (pore pressure) and permeability can be estimated by After Closure analysis, and relevant equations are summarized as below.
Pseudolinear flow regime shows a linear relationship between bottom-hole pressure and , and the reservoir stimulation coefficient can be estimated by the equation of
Here, we assume that,
Pseudoradial flow regime shows a linear relationship between bottom-hole pressure and , and the pore pressure and permeability can be estimated as
Here, we assume that,
where pw(t) is the bottom-hole pressure at t time, MPa. pi is the initial reservoir pressure, MPa. is the cumulative injection fluid volume, m3. h is the formation thickness, m. μ is the fluid viscosity, mPa.s. φ is the porosity, %. Ct is the formation compressibility. is the fracture half length, m. k is reservoir permeability. ∆t is the testing duration. KL is the slope between ∆P and time in Pseudolinear flow regime, while KR is the slope between ∆P and time in Pseudoradial flow regime.
3. Results
3.1. Background of Montney Shale Formation
3.1.1. General Information of Montney
The Montney Formation is a sedimentary wedge that was deposited on the western margin of the exposed North American craton during the earliest Triassic time, 232–245 MYA [32]. The entire Montney Formation stretches over about 142,450 square meters from NE British Columbia to NW Alberta, and it is deposited in a forearc extensional Arcuate Depositional basin called the Peace River Basin that developed on the Western Margin of the Pangaea supercontinent. A stable continental shelf and shoreline prevailed throughout the Montney deposition, in a westward-deepening and open-shelf marine environment. Desert conditions prevailed on the Pangea supercontinent. Windblown silt from the desert was transported and deposited into the Peace River Basin, and sediments were reworked by marine processes, including waves, currents, and gravity, as shown in Figure 3a.
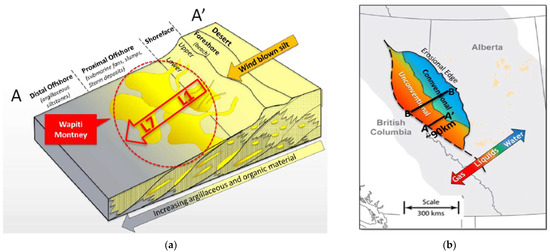
Figure 3.
(a) Depositional environment of Montney Formation; (b) Montney conventional vs. unconventional plays.
3.1.2. Development of Wapiti Field
The Montney Sequence can be divided into two different development areas: the eastern part, where depositional system is dominated by shoreface deposits, treated as a conventional fairway; the western part, dominated by distal ones and treated as an unconventional fairway (Figure 3b). The unconventional Montney is part of a basin-centered hydrocarbon system, which has no free water, relatively low porosity, and low permeability compared to a conventional resource.
Initial drilling targeted the conventional Montney plays. Benefitting from the development of horizontal well drilling and multiple stages of hydraulic fracturing, more drilling activities began targeting the upper Montney in NE British Colombia in 2005. Currently, drilling activities have targeted the Montney liquid-rich gas and oil areas along the fairway that follows the over-pressure edge and extends east from Dawson in British Columbia, across into Alberta, and down through the Wapiti, Kakwa, and Karr fields, as presented in Figure 4.
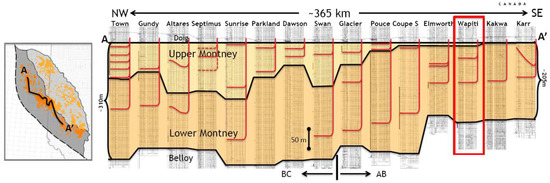
Figure 4.
The Montney production fields from north to south in unconventional development area.
3.1.3. Summaries of Key Reservoir Parameters
In Figure 5, stratigraphically, the Montney unconformably overlies the Permian Belly formation and is abruptly overlain by the Triassic Doig source rock in most of the Wapiti field. The top of the Wapiti Montney ranges from 2200 to 2900 meters in true vertical depth from the surface. The formation average thickness is over 200 meters, and intervals consist of shale, siltstone, and fine-grained sandstones. Due to the over-pressurized nature, the porosity and permeability are low, ranging from 3.0–6.0% and 0.005–0.05 mD, respectively. More reservoir information is summarized in Table 1. Additionally, five key engineering parameters are shown by the statistical histogram in Figure 6.
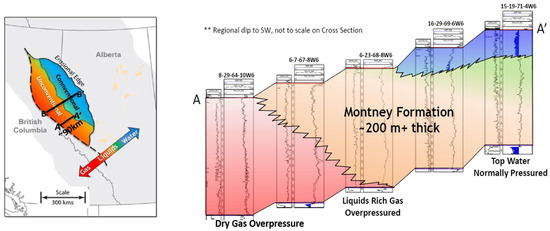
Figure 5.
The Wapiti production fields from west to east in unconventional development area.

Table 1.
Wapiti Montney reservoir properties.
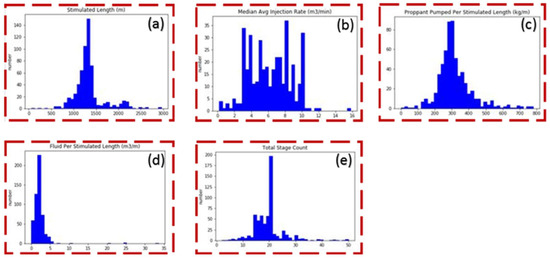
Figure 6.
Wapiti Montney engineering information: (a) stimulated length (m); (b) injection rate (m3/min); (c) proppant per SL (kg /m); (d) fluid per SL (m3/min); (e) total stage count.
3.2. Application of Diagnostic Fracture Injection Tests
3.2.1. Selection of Experimental Well
The Montney tight reservoir is one of the most promising and productive unconventional plays in Canada. However, few academic papers discuss its fracture closure pressure, pore pressure, and permeability, which are essential for the development of the Montney Shale. Therefore, in this study, one horizontal gas well (Well-A) targeting the Montney Shale has been selected in this study. The DFIT was conducted in the toe of Well-A, and the DFIT analysis is conducted using data from the DFIT test. This well is in the Wapiti field, and its horizontal interval is treated by slick water into around 24 stages along its 2285-meter horizontal interval. The average perf TVD of this well is 2439 meters. The cumulative gas and liquid condensate produced from this well to date are approximately 32,516,000 m3 and 342.60 m3, respectively, and this well is predicted to be economically viable based on the predicted EUR, operating cost, and capital investment.
3.2.2. DFIT Data Analysis and Interpretation
As discussed above, a DFIT is performed at a wellsite to understand the closure pressure and the pore pressure of the formation. Figure 6 shows the pump schedule and pressure response as a function of time for the performed DFIT. To create a micro-fracture downhole, water is injected into the wellbore for approximately 10 min, with an average injection rate of 0.41 m3/min, and the total injected volume is about 4.0 m3. After 10 min, pump is shut down and the surface pressure is monitored and recorded for 10 days. It should be noted that the pressure in Figure 7 refers to the surface pressure.
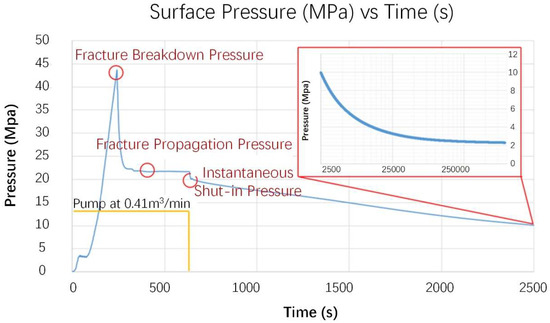
Figure 7.
Well-A DFIT pressure and pump schedule. The inserted images show pressure vs. time in semi-log plot.
As demonstrated in Figure 7, at the bottom-hole condition, the fracture breakdown pressure is 66 MPa at the point where the pressure reaches its peak during the injection period. Following the peak, the fracture propagation pressure is picked at 44 MPa, as it shows a flat trend. In general, the leak-off pressure is read at the point where the pressure deviates from the expected linear relationship. However, in this test, the leak-off pressure is not obvious.
To estimate the closure pressure and the pore pressure of the formation, the DFIT data presented above are analyzed by the pressure and GdP/dG vs. G-function plot and the BHP and vs. the square root of time plot, as shown in Figure 8a,b. The G-function and the square root of time plots deliver the same message, while it is easier to interpret time by the second plot. There are noises in the GdP/dG response after the closure time, which is commonly observed in the DFIT analysis. In this study, the data noises are smoothed by the Butterworth filter, after which the filtered signals become clean and explicit, demonstrated by the red line in Figure 8a,b. The general GdP/dG response from the Well-A DFIT presents a characteristic concave upward trend, indicating a signature of pressure–loss–acceleration behavior, which results from height recession and/or transverse storage mechanisms.
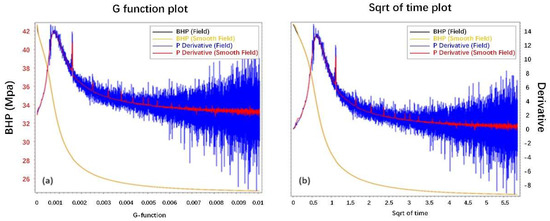
Figure 8.
Well-A DFIT data in (a) G-function and (b) square root of time plots.
After the pump was shut down, an instantaneous shut-in pressure of 42 MPa is captured from the data, and this ISIP can be verified in the following G-Plot analysis, as shown in Figure 7. The pressure response was recorded for 10 days, with a minimum pressure of 2.32 MPa, as shown in the inserted semi-log plot in Figure 9.
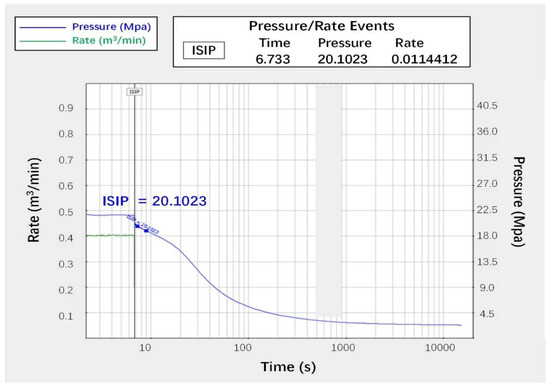
Figure 9.
Surface pressure and rate changing for 10 days after pump shut down.
3.2.3. Results Discussion
As shown in Figure 2b, height recession and transverse storage are the two main mechanisms contributing to the pressure–loss–acceleration signature. However, they are two different mechanisms from the perspective of physics. The height recession mechanism occurs when an induced fracture grows into overlying and/or underlying formations during a DFIT, causing increasing stiffness and, thus, accelerating the pressure drop rate. On the other hand, the transverse storage mechanism takes place when fluid, expelled from transverse fractures after the pump is shut down, enters the induced fracture and contributes to the increasing leak-off rate and accelerated GdP/dG. Besides these two mechanisms, McClure [18,19] states that fracture closure is a dynamic process; thus, the concave upward trend is actually an indication that two fracture planes come into contact, so stiffness is increased. It is difficult to confirm which mechanism results into the discrepancy without further supporting data, but the methodology to determine the closure pressure of a concave-up trend is consistent. Figure 8 shows closure pressure determination by the Tangent Line method, the Compliance method, and the Variable Compliance method, as depicted by the red, blue, and green dashed lines, respectively. The Compliance method suggests that fracture closure pressure is determined when the GdP/dG response starts to deviate from the expected linearity, while the Variable Compliance method is an average result of the Tangent Line method and the Compliance method. Therefore, the Compliance method shows an upper bound, while the Tangent method suggests a lower bound of closure pressure estimations. The closure pressure in this DFIT is estimated to be 34.367 MPa, contributing to a stress gradient of 14.09 kpa/m, by the Tangent method; 39.344 MPa contributing to 16.13 kpa/m, by the Compliance method; and 37.163 MPa contributing to 15.23 kpa/m, by the Variable Compliance method. The true ISIP is extrapolated to 42.3 MPa when the square root of time reaches to zero, compared to the estimated ISIP of 42 MPa from the pump schedule presented above. This minor difference between the extrapolated ISIP and the estimated ISIP suggests that the fracture complexity and wellbore tortuosity in Well-A is insignificant. A net pressure of 5.137 MPa is determined and applied to the fracture geometry estimation, which is discussed in the following simulation section. As a result, the Well-A DFIT analysis estimates that the closure pressure ranges from 34.367 to 39.344 MPa, contributing to the stress gradient of 14.09–16.13 KPa/m for the formation.
As shown in Figure 10, the closure pressure point has been identified by the plot of G*dP/dG vs. G-time, by drawing a line from the origin to the tangent to G*dP/dG [14]. The closure pressure by the Tangent method in this DFIT is estimated to be 34.367 MPa, contributing to a stress gradient of 14.09 kpa/m. The true ISIP is extrapolated to 42.3 MPa when the square root of time reaches zero, compared to the estimated ISIP of 42 MPa from the pump schedule presented above. This minor difference between the extrapolated ISIP and the estimated ISIP suggests that the fracture complexity and wellbore tortuosity in Well-A are insignificant.
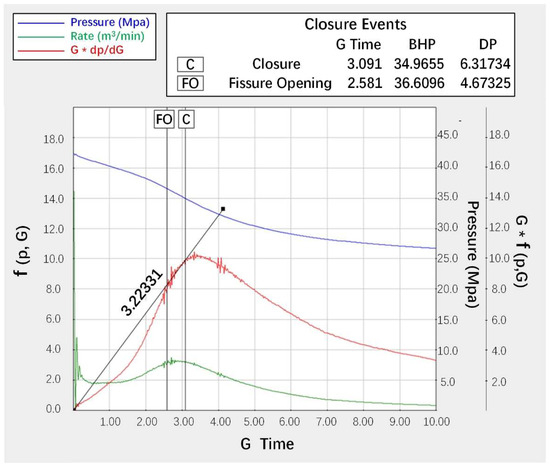
Figure 10.
Closure pressure determination by the Tangent method using filtered filed DFIT data.
In addition, the derivative pressure-pattern reading from well-A’s G-function analysis plot shows a behavior of non-ideal leak-off type I, which depicts a signature of a height recession/transverse storage characteristic, as shown in Figure 2b above. Normally, we could not identify which mechanisms are playing a dominant role in this situation immediately; however, based on the seismic data interpretation of neighborhood wells in the Wapiti field, the height recession is more likely to contribute to the pressure–loss–acceleration signature. Height recession mechanism occurs when an induced fracture grows into overlying and/or underlying formations during a DFIT, causing increased stiffness and, thus, an accelerated pressure drop rate.
After the fracture closure time, the reservoir flow starts to dominate the process, and the pore pressure is estimated by pressure transient analysis. The adjacent reservoir fluid first flows in the induced fracture by a 1D flowing pattern, resulting in the linear flow regime, as implied by the slope of −0.5 on the pressure derivative plot. Later, the fracture starts to deplete the fluid further into the reservoir by a 2D flowing pattern, contributing to the radial flow regime, measured by a slope of −1 on the pressure derivative plot. Both flow regimes are observed in the Well-A DFIT, as shown by the red (linear) and green lines (radial) in Figure 11. Based on the plot, the linear flow regime starts from 34 min, and the radial flow regime starts from 58 min. To estimate the pore pressure, the pressure data in the linear flow regime are regressed linearly in a log–log plot of pressure vs. inverse of square root of time, as shown in Figure 12, and the pressure data in the radial flow regime are regressed linearly in Horner plot, as shown in the inserted image in Figure 12. The pore pressure is determined by the intercept of the y-axis and regressed straight line for both methods. In general, the pore pressure by the radial flow regime shows an upper bound estimation, and the linear flow gives a lower bound estimation. As demonstrated in Figure 12, the pore pressure of Well-A by the radial flow regime is estimated to be 24.58 MPa, contributing to the pore pressure gradient of 10.07 KPa/m; the pore pressure of Well-A by the linear flow regime is estimated to be 20.82 MPa, resulting in the pore pressure gradient of 8.54 KPa/m. As a result, the Well-A DFIT analysis estimates that the pore pressure ranges from 20.82 to 24.58 MPa, contributing to the pore pressure gradient from 8.54 to 10.07 KPa/m for the formation.
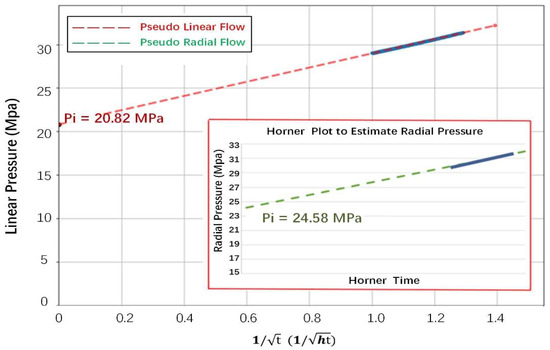
Figure 11.
Before Closure (BC) and After Closure (AC) analyses by pressure derivative log–log plot. Signatures of linear and radial flow regimes are slopes of −0.5 and −1, respectively, after the fracture closure time.
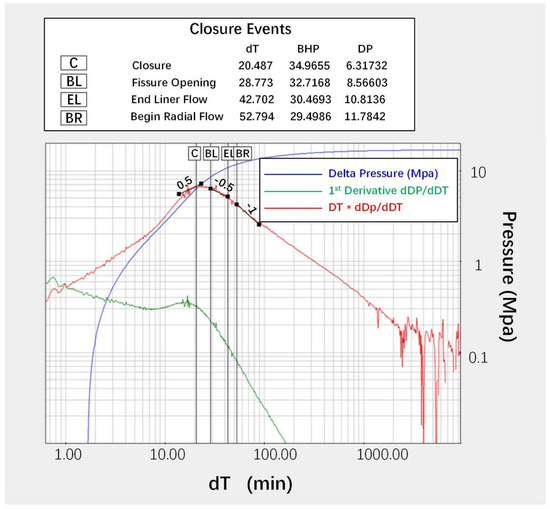
Figure 12.
Pore pressure is estimated by pressure transient analysis. The main image shows pore pressure determination by linear flow regime, and the inserted image shows pore pressure determination by radial flow regime.
In the After Closure time regime, the reservoir flow gradually replaces the fracture flow, and it starts to dominate the flowing process. The pore pressure and important reservoir properties can be estimated in this stage. Both flow regimes are observed in the Well-A DFIT, as shown by the red (linear) and green lines (radial) in Figure 11. Based on the plot, the linear flow regime starts from 34 min, and the radial flow regime starts from 58 min. To estimate the pore pressure, the pressure data in the linear flow regime are regressed linearly in a log–log plot of pressure vs. inverse of square root of time, as shown in Figure 12, and the pressure data in the radial flow regime are regressed linearly in Horner plot, as shown in the inserted image in Figure 12. The pore pressure is determined by the intercept of the y-axis and regressed straight line for both methods. In general, pore pressure by the radial flow regime shows an upper bound estimation, and linear flow gives a lower bound estimation. As demonstrated in Figure 12, the pore pressure of Well-A by the radial flow regime is estimated to be 24.58 MPa, contributing to the pore pressure gradient of 10.07 KPa/m; the pore pressure of Well-A by the linear flow regime is estimated to be 20.82 MPa, resulting in the pore pressure gradient of 8.54 KPa/m. As a result, the Well-A DFIT analysis estimates that the pore pressure ranges from 20.82 to 24.58 MPa, contributing to the pore pressure gradient from 8.54 to 10.07 KPa/m for the formation.
3.2.4. DFIT Numerical Simulation
In the development stage of Canada’s Wapiti field, understanding the pore pressure and fracture closure pressure are important to estimate the reservoir net pressure, identify the flow regime, calibrate the hydraulic fracture model, and perform the DFIT numerical simulation for unconventional developed activities. In the numerical simulation part, the Variable Compliance method [23] is used to calculate pore pressure, reservoir permeability, and fracture geometry. The net Pressure is defined by
where is the fracture stiffness, is the average fracture width, and is the minimum principal stress (fracture closure pressure). Assuming it is a problem of one dimensionless leak-off into a semi-infinite reservoir condition, the differential form of the mass balance can be written as
At the surface of the fracture, both the leak-off rate into the reservoir and Darcy’s law are based on the material balance equation. So the boundary condition for the above equation can be written as
The initial conditions for the governing equations are
where ISIP is instantaneous shut-in pressure, and P0 is the initial reservoir pressure. Then, we gain Sf by different fracture geometries, as presented in Table 2.

Table 2.
Expression to calculate the Sf by three different fracture geometries [23].
Where hf is the fracture height, is the fracture half-length, Rf is the fracture radius, and E’ is the plane strain for Young’s modulus.
By inputting the rock properties and fracture parameters into the simulator, DFIT numerical simulations are performed to match the historical pressure and GdP/dG data from the Well-A DFIT. The input parameters include porosity, viscosity, Poisson’s ratio, injection volume, total compressibility, Young’s modulus, and wellbore storage coefficient. Figure 13 demonstrates that the simulated pressure and its derivative matches with the Well-A field DFIT data very well. The reservoir permeability for the Wapiti Montney Formation is about 0.024 mD. The fracture geometry simulation is performed based on the material balance, the net pressure calculation by Equation (11), and the fracture geometry calculation from Table 2. With an assumption of a 15 m fracture height, the simulation results of fracture geometry are summarized in Table 3. It should be noted that the simulation results are consistent with the estimations from our reservoir and petrophysics studies.
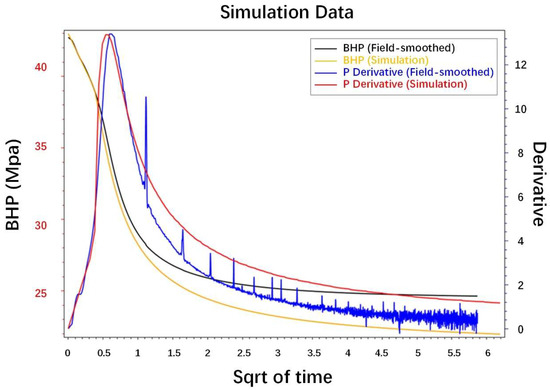
Figure 13.
Bottom hole pressure field-smoothed vs. simulation results; pressure derivative field-smoothed vs. simulation results.

Table 3.
Fracture geometry estimation by numerical simulation.
4. Conclusions
In the development of unconventional hydrocarbon exploration, predicting key reservoir properties, such as in situ stress and formation pore pressure, plays a significant role in both geological science and subsurface engineering workflows. The objective of this study is to analyze the key reservoir properties by using diagnostic fracture injection test data from the Montney Shale. One horizontal well from the Wapiti field has been selected to perform DFIT. In the Before Closure regime, the Tangent Line method is used to identify the fracture closure time, and then the closure pressure and stress gradient are estimated by further data analysis. In the After Closure regime, the pore pressure is analyzed by pressure transient analysis. The results from this DFIT analysis are encouraging and insightful, which can significantly help the operator to improve the understanding of the Wapiti field. Furthermore, the interpreted results demonstrated in this paper add substantial business value to the asset, especially in terms of improving the hydraulic fracturing design and, thus, accelerating the cashflow from production. From this article, the following conclusions can be made:
- The general pressure Gdp/dG responses’ results for Well-A show a signature of pressure-dependent leak-off behavior, which occurs when the fluid-loss rate varies significantly with the pressure-dependent permeability in a dual-porosity system. A characteristic height recession/transverse storage trend has been identified.
- The net pressure of DFIT on Well-A in the Wapiti Montney formation is about 5.137 MPa, based on the determined fracture closure pressure.
- Based on DFIT data, the closure pressure is estimated to be 34.367 MPa, contributing to a stress gradient of 14.09 kpa/m; 39.344 MPa contributing to 16.13 kpa/m by the Compliance method; and 37.163 MPa contributing to 15.23 kpa/m by the Variable Compliance method.
- Based on the pressure transient analysis, the pore pressure ranges from 20.82 to 24.58 MPa, which is equivalent to a pore pressure gradient of 8.54 to 10.07 KPa/m for the Wapiti Montney formation.
- Using the DFIT’s numerical simulation and history matching, the reservoir permeability is 0.024 md, fracture length is 13.44 m, and fracture geometries analyzed by different models are summarized in Table 3.
In the future, DFIT analysis using multiple methodologies should be applied in more horizontal wells. Moreover, new advanced technologies, such as data mining and machine learning, can be used to increase the diversity of this work strategy, to improve the accuracy of key reservoir parameters and production forecasts.
Author Contributions
Conceptualization, G.L. and Y.Z.; methodology, Y.L.; data curation and validation, Y.L; writing—original draft preparation, L.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Key R&D Program, Complex Oil and Gas Intelligent Drilling Theory and Method, grant number 2019YFA0708300”, The Project of The State Key Laboratory of Shale Oil and Gas Enrichment Mechanisms and effective development, grant number 10010099-19-ZC0607-0042” and the Sinopec Fundamental Program of Science & Technology, grant number P21073-1-1”.
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
Not applicable.
Acknowledgments
The authors would like to thank all the contributors from the Sinopec International Petroleum E&P Corporation and Sinopec Research Institute of Petroleum Engineering. The authors would also like to thank the supports from China University of Petroleum and Yangtze University. Particularly, the authors appreciate the contributions from Zhe Wang, from Engineering Physics, Tsinghua University for reviewing this paper.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| A | Fracture surface area |
| C | A constant relevant to leak-off coefficient and comprehensive compressibility |
| C | Closure |
| Carter’s leak-off coefficient | |
| Total compressibility | |
| Plane strain for Young’s modulus | |
| h | Formation thickness |
| Fracture height | |
| Linear flow regime | |
| Radial flow regime | |
| k | Permeability |
| Reservoir initial pressure | |
| Net pressure | |
| Bottom hole pressure at generic time | |
| Minimum principal stress | |
| Fracture stiffness | |
| t | Generic time |
| Shut-in time | |
| Pumping time | |
| Dimensionless time in G-function | |
| Cumulative pumped fluid volume | |
| Average fracture width | |
| Fracture half-length | |
| φ | Formation porosity |
| μ | Fluid viscosity |
| AC | After Closure |
| BC | Before Closure |
| DFIT | Diagnostic fracture injection tests |
| BL | End linear flow |
| BR | Begin radial flow |
| FBP | Formation breakdown pressure |
| FO | Fissure opening |
| FPP | Fracture propagation pressure |
| ISIP | Instantaneous shut-in pressure |
| LOP | Leak-off point |
References
- Liao, L.; Zeng, Y.; Liang, Y. Data Mining: A Novel Strategy for Production Forecast in Tight Hydrocarbon Resource in Canada by Random Forest Analysis. Presented at the International Petroleum Technology Conference and Exhibition, Dhahran, Kingdom of Saudi Arabia, 13–15 January 2020. SPE-20344-MS. [Google Scholar]
- Liang, Y.; Liao, L.; Guo, Y. A Big Data Study: Correlations between EUR and Petrophysics/Engineering/Production Parameters in Shale Formations by Data Regression and Interpolation Analysis. Presented at the SPE Hydraulic Fracturing Technology Conference and Exhibition, The Woodlands, TX, USA, 5–7 February 2019; SPE-194381-MS. p. 30. [Google Scholar]
- Liang, Y.; Ning, Y.; Liao, L.; Yuan, B. Chapter Fourteen—Special Focus on Produced Water in Oil and Gas Fields: Origin, Management, and Reinjection Practice; Yuan, B., Wood, D.A.., Eds.; Formation Damage During Improved Oil Recovery; Gulf Professional Publishing: Woburn, MA, USA, 2018; pp. 515–586. [Google Scholar] [CrossRef]
- Liang, Y.; Wen, B.; Hesse, M.A.; DiCarlo, D. Effect of Dispersion on Solute Convection in Porous Media. Geophys. Res. Lett. 2018, 45, 9690–9698. [Google Scholar] [CrossRef]
- Geng, L. Application status and development suggestions of big data technology in petroleum engineering. Pet. Drill. Tech. 2021, 49, 72–78. [Google Scholar]
- Potocki, D.J. Understanding Induced Fracture Complexity in Different Geological Settings Using DFIT Net Fracture Pressure. Presented at the SPE Canadian Unconventional Resources Conference, Calgary, AB, Canada, 30 October–1 November 2012; SPE-I62814-MS. p. 19. [Google Scholar]
- Wallace, J.; Kabir, C.S.; Cipolla, C. Multiphysics Investigation of Diagnostic Fracture Injection Tests in Unconventional Reservoirs. Presented at the SPE Hydraulic Fracturing Technology Conference, The Woodlands, TX, USA, 4–6 February 2014; SPE-168620-MS. p. 20. [Google Scholar]
- Wu, P.; Aguilera, R. Uncertainty Analysis of Shale Gas Simulation: Consideration of Basic Petrophysical Properties. Presented at the SPE Unconventional Resources Conference-Canada, Calgary, AB, Canada, 5–7 November 2013. SPE-167236-MS. [Google Scholar]
- Chen, K.; Zhu, S.; Zou, M. Research on development evaluation well drilling modes for exploration and development integration in Weixinan Sag. Pet. Drill. Tech. 2021; 49, pp. 42–49. [Google Scholar]
- Nolte, K.G. Determination of Proppant and Fluid Schedules from Fracturing-Pressure Decline. SPE Prod. Eng. 1986, 1, 255–265. [Google Scholar] [CrossRef]
- Nolte, K.G. A General Analysis of Fracturing Pressure Decline with Application to Three Models. SPE Form. Eval. 1986, 1, 571–583. [Google Scholar] [CrossRef]
- Nolte, K.G. Determination of Fracture Parameters from Fracturing Pressure Decline. Presented at the SPE Annual Technical Conference and Exhibition, Las Vegas, NV, USA, 23–26 September 1979; SPE-8341-MS. p. 16. [Google Scholar]
- Castillo, J.L. Modified Fracture Pressure Decline Analysis Including Pressure-Dependent Leakoff. Presented at the Low Permeability Reservoirs Symposium, Denver, CO, USA, 18–19 May 1987; SPE-16417-MS. p. 9. [Google Scholar]
- Barree, R.D.; Barree, V.L.; Craig, D. Holistic Fracture Diagnostics: Consistent Interpretation of Prefrac Injection Tests Using Multiple Analysis Methods. SPE Prod. Oper. 2009, 24, 396–406. [Google Scholar] [CrossRef]
- Barree, R.D.; Miskimins, J.; Gilbert, J. Diagnostic Fracture Injection Tests: Common Mistakes, Misfires, and Misdiagnoses. SPE Prod. Oper. 2015, 30, 84–98. [Google Scholar] [CrossRef]
- Barree, R.D.; Barree, V.L.; Craig, D. Holistic Fracture Diagnostics. Presented Rocky Mountain Oil & Gas Symposium, Denver, CO, USA, 16–18 April 2007. SPE-107877-MS. [Google Scholar]
- Barree, R.D.; Mukherjee, H. Determination of Pressure Dependent Leakoff and Its Effect on Fracture Geometry. Presented at the SPE Annual Technical Conference and Exhibition, Denver, CO, USA, 6–9 October 1996; SPE-36424-MS. p. 10. [Google Scholar]
- McClure, M.W.; Jung, H.; Cramer, D.D.; Shanna, M.M. The Fracture-Compliance Method for Picking Closure Pressure from Diagnostic Fracture-Injection Tests (see associated supplementary discussion/reply). SPE J. 2016, 21, 1321–1339. [Google Scholar] [CrossRef]
- McClure, M.W.; Blyton, C.A.J.; Jung, H.; Sharma, M.M. The Effect of Changing Fracture Compliance on Pressure Transient Behavior During Diagnostic Fracture Injection Tests. Presented at the SPE Annual Technical Conference and Exhibition, Amsterdam, The Netherlands, 27–29 October 2014; SPE-170956-MS. p. 23. [Google Scholar]
- Wang., H.; Sharma, M.M. A Rapid Injection Flow-Back Test RIFT to Estimate In-Situ Stress and Pore Pressure in a Single Test. Presented at the SPE Hydraulic Fracturing Technology Conference and Exhibition, The Woodlands, TX, USA, 4–6 February 2020. SPE-199732-MS. [Google Scholar]
- Wang., H.; Sharma, M.M. A Novel Approach for Estimating Formation Permeability and Revisit After-Closure Analysis from DFIT. Presented at the SPE Hydraulic Fracturing Technology Conference and Exhibition, The Woodlands, TX, USA, 5–7 February 2019; SPE-194344-MS. p. 32. [Google Scholar]
- Wang, H.; Sharma, M.M. Estimating Unpropped Fracture Conductivity and Compliance from Diagnostic Fracture Injection Tests. Presented at the SPE Hydraulic Fracturing Technology Conference and Exhibition, The Woodlands, TX, USA, 23–25 January 2018; SPE-189844-MS. p. 28. [Google Scholar]
- Wang, H.; Sharma, M.M. New Variable Compliance Method for Estimating In-Situ Stress and Leak-Off from DFIT Data. Presented at the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 9–11 October 2017; SPE-187348-MS. p. 40. [Google Scholar]
- Craig, D.P. New Type Curve Analysis Removes Limitations of Conventional After-Closure Analysis of DFIT Data. Presented at the SPE Unconventional Resources Conference, The Woodlands, TX, USA, 1–3 April 2014; SPE-168988-MS. p. 11. [Google Scholar]
- Craig, D.P.; Blasingame, T.A. Application of a New Fracture-Injection/Falloff Model Accounting for Propagating, Dilated, and Closing Hydraulic Fractures. Presented at the SPE Gas Technology Symposium, Calgary, AB, Canada, 15–17 May 2006; p. 17. [Google Scholar]
- Soliman, M.Y.; Craig, D.P.; Bartko, K.M.; Rahim, Z.; Adams, D.M. Post-Closure Analysis to Determine Formation Permeability, Reservoir Pressure, Residual Fracture Properties. Presented at the SPE Middle East Oil and Gas Show and Conference, Manama, Bahrain, 15–18 March 2005; SPE-93419-MS. p. 15. [Google Scholar]
- Soliman, M.Y.; Kabir, C.S. Testing unconventional formations. J. Pet. Sci. Eng. 2012, 92–93, 102–109. [Google Scholar] [CrossRef]
- Wang, H. What Factors Control Shale Gas Production Decline Trend: A Comprehensive Analysis and Investigation. SPE J. 2016, 22, 562–581. [Google Scholar] [CrossRef]
- Chipperfield, S.T. After-Closure Analysis To Identify Naturally Fractured Reservoirs. SPE Res. Eval. Eng. 2006, 9, 50–60. [Google Scholar] [CrossRef]
- Mayerhofer, M.J.; Ehlig-Economides, C.A.; Economides, M.J. Pressure Transient Analysis of Fracture Calibration Tests. J. Pet. Technol. 1995, 47, 229–234. [Google Scholar] [CrossRef]
- Liu, G.; Ehlig-Economides, C. Comprehensive Global Model for Before-Closure Analysis of an Injection Falloff Fracture Calibration Test. Presented at the SPE Annual Technical Conference and Exhibition, Houston, TX, USA, 28–30 September 2015; SPE-I74906-MS. p. 29. [Google Scholar]
- Kuppe, F.; Haysom, S.; Nevokshonoff, G. Liquids Rich Unconventional Montney: The Geology and the Forecast. Presented at the SPE Canadian Unconventional Resources Conference, Calgary, AB, Canada, 30 October–1 November 2012. SPE-162824-MS. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).