Abstract
In this work, three raised expanded metal meshes (EMMs) differing in mesh size were tested experimentally with regard to their flow and transport properties. Empirical equations for the Nusselt number and Fanning friction factor were developed. Alongside the experiments, simple computational fluid dynamics (CFD) models were used to simulate the pressure drop and heat transfer coefficients within EMMs. Finally, the Performance Efficiency Criterion (PEC) was applied to compare EMMs with other reactor packings.
1. Introduction
The design and optimization of structured reactors’ performance are crucial for environmental catalytic processes such as the catalytic combustion of volatile organic compounds (VOCs) or the selective catalytic reduction (SCR) of nitrogen oxides (NOx). It is highly desirable to ensure a large surface-area-to-volume ratio and high heat and mass transfer rates to maximize the catalyst consumption and, at the same time, low flow resistance to reduce pumping costs [1,2]. Although significant progress in catalysis has been made, there is still a need to intensify the heat/mass transfer for catalytic reactors to ensure the overall process rate of faster reaction kinetics is not limited.
An effective technique to improve the rate of heat transfer to fluid flowing in a duct, as well as the rate of mass transfer of reagents to the catalyst surface, is the enhancement of fluid mixing. It can be obtained by applying a certain type of catalyst support, which provides some disarray in the flow. However, it would result in an increase in pressure drop. In order to keep the flow resistance at a minimum level, the mixing flow should exist in a region very close to the wall surface of the catalyst carrier.
Many different reactor fillings have been proposed to achieve the above phenomenon. Short-channel structures, which are short monoliths, are the simplest example due to the possibility of modifying their geometry (the ratio of the channel diameter to its length), as well as their arrangement in the reactor (alternating and/or with gaps) [3,4,5,6]. Solid foams ensure mixing flow, thus enhancing heat/mass transfer and low flow resistance, due to their stochastic structure [7,8,9,10,11,12,13]. The geometry of periodic open cellular structures is, in some sense, the combination of a foam matrix and a monolith structure, hence they are expected to enable fluid mixing [14,15].
Meshes, called also screens or grids, have been used for years to control fluid motion, thus it is possible to influence the direction, speed, or turbulence intensity of the flow [16,17]. Kołodziej et al. [18] investigated knitted and woven wire gauzes because of their wire arrangement. It was proven that gauzes enhance heat/mass transfer with a slight increase in flow resistance. In comparison with other available catalyst supports, gauze seems to be more efficient [7,19,20,21,22].
The expanded metal mesh (EMM) is a metal foil that is simultaneously slit and stretched longitudinally into a network of diamond- or hexagonal-shaped holes of uniform size, shape, and regularity [16,17,23]. It comes in four basic types: Raised (or standard), flattened, Gridwalk, and architectural (or decorative) meshes. EMM’s applications include energy absorption, construction, protection–decoration, flow control, filtration, biomechanics, and electrochemical applications [17,24]. Expanded metal meshes are produced from a solid sheet or a plate. Carbon, aluminum, or stainless steel and different alloys including copper, nickel, silver, titanium, etc., can be used as materials. No metal is lost in the expanding process. After the process of cutting and plastic deformation, the area of the EMM is up to 12 times larger and its weight is reduced by 80% per square meter in comparison with the original sheet or plate [17,25]. The final product is much stiffer and more durable and has solid joints and no seams or welds. Because it is made from a solid sheet of metal, it can never untangle. Even if cut at one or more points, the remaining strand intersections continue to hold.
The flow behavior and its impact on heat transfer and flow resistance around expanded meshes have been studied by several researchers. Saini and Saini [26] experimentally investigated the turbulent flow in an artificially roughened rectangular duct with a large aspect ratio with an expanded metal mesh as the roughness element. The authors concluded that the use of an expanded metal mesh on the absorber plate of a solar air-heater duct brings the enhancement of heat transfer, depending on the system and operating parameters. The correlations for the Nusselt number and friction factor for the system were also developed. Oshinowo and Kuhn [17] performed an experimental study of the turbulent flow in a low-turbulence wind tunnel with expanded metal screens. The characteristics of mean velocity, pressure drop, and turbulence of expanded metal sheets were shown. Mustaffar et al. [24] experimentally and numerically tested the melting of the phase-change material (PCM) via a raised aluminum expanded metal mesh. It was shown that the presence of expanded metal meshes increased the PCM’s effective thermal conductivity, resulting in a reduction in melting time. Mallick and Thombre [27] evaluated the performance of the passive direct methanol fuel cell (DMFC) and compared it with different combinations of supporting plates and an expanded metal mesh current collector (EMCC). It was found that better results were achieved for the passive DMFC with EMCC, which also facilitates a better distribution of the fuel on the anode catalyst layer and increases the operating temperature. Lafmejani et al. [25] experimentally and numerically studied the application of expanded metal meshes as flow plates in polymer electrolyte membrane (PEM) water electrolysis cells. It was shown, in particular, that the expanded metal grid behaves as a porous medium although there is a local flow of mixing. The authors measured the pressure loss under different orientations and velocities and found the dependence of measured parameters on the flow direction and size of the pores.
In this work, the internal fluid flow and heat transfer performance of raised expanded metal meshes differing in mesh openings was investigated experimentally and numerically. The effect of mesh geometry and dimensions on flow friction and heat-transfer characteristics in expanded metal grids was analyzed. New empirical equations of Fanning friction factors and Nusselt numbers were developed based on the experimental data. The results achieved for expanded metal screens were compared with packed bed, monolith, and woven wire gauzes in relation to the heat/mass transfer and flow resistance.
2. Materials and Methods
2.1. Expanded Meshes Characterization
Three types of expanded meshes made of stainless steel were tested. Figure 1 shows the structures of the expanded meshes, while Figure 2 and Table 1 present the mesh characterization. The specific surface area (Sv) and the void fraction (ε) were determined based on scans from microtomography, while the other parameters were measured.

Figure 1.
Photos of single expanded meshes (A–C).
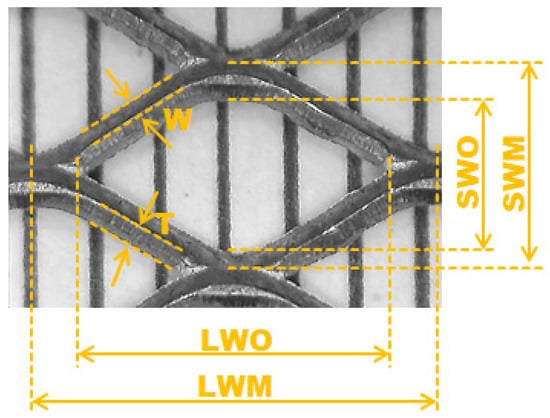
Figure 2.
Mesh characterization.

Table 1.
Geometrical parameters of expanded meshes.
2.2. Experimental Procedure
The experimental apparatus applied for the pressure difference (A) and heat convection (B) measurements is shown schematically in Figure 3. A square reactor (30 × 30 mm) was employed to carry out the flow resistance experiments. Sheets of expanded meshes were placed inside the reactor without separating gaps. Table 1 shows the bed length L of the sheets. The pressure drop was measured using the Recknagel micromanometer and water U-tube manometer. The flow resistance experiments were performed for gas velocities u0 of 0.07 ÷ 4 m/s at room temperature and ambient pressure.
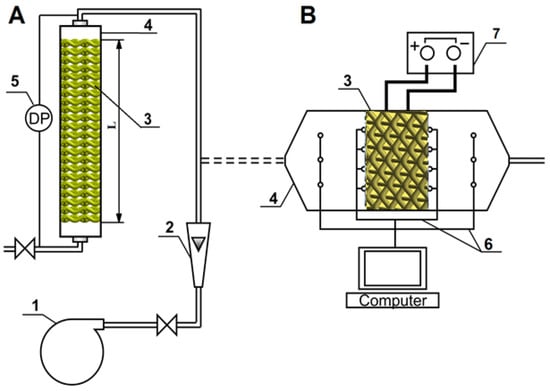
Figure 3.
Experimental apparatus for pressure drop (A) and heat transfer (B) measurements: 1—blower; 2—flowmeter; 3—wire gauze; 4—test reactor; 5—manometer; 6—thermocouples; 7—electric current.
A test reactor with a rectangular cross-section (45 × 30 mm) was used to perform the heat transfer experiments. A single expanded mesh was placed inside the reactor and heated by an electric current flowing directly through it. The inlet and outlet temperatures of the flowing air and mesh surface were measured with K-type thermocouples: Three thermocouples each at the reactor’s inlet and outlet and four on the mesh surface on the inlet and outlet sides. Special composite glue that secured good heat conduction and no electric conduction was used to attach the thermocouples to the wire surface. The setup was connected to a computer data-acquisition system. Experiments were conducted with various superficial velocities of air u0 entering the test section (0.2 ÷ 3 m/s).
2.3. Numerical Simulation
2.3.1. Computational Domain and Mesh Generation
The commercial code ANSYS FLUENT 21.2, based on the finite volume method, was employed as a CFD tool. The geometry models were created to simplify the meshing procedure. The domain was discretized with a high-quality mesh and tetrahedral cells in the core of the domain, while 5 prism layers were implemented near the mesh surface to collect the heat exchange between the mesh wall and the fluid. The detailed computational domain for mesh type B is shown in Figure 4.
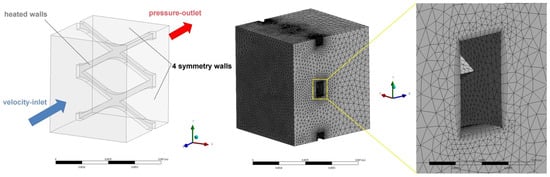
Figure 4.
Computational domain for mesh type B with boundary conditions (left) and numerical grid (right).
The sensitivity analysis of the base size of the cells applied in the core of the domain, as well as on the heated wall, was carried out for each mesh type. Table 2 shows the variation of the unit pressure drop ΔP/L and Nusselt number Nu for u0 = 1 m/s with respect to the number of elements for mesh type B. Finally, the fine grid was chosen for mesh type B, as well as for other meshes.

Table 2.
Grid independency results for mesh type B.
2.3.2. Governing Equations
The continuity, momentum, and energy equations for the fluid phase are as follows:
where ρ is the density, xi is the Cartesian coordinates, and ui is the velocity components.
where p is the static pressure and τij is the stress tensor.
where cp is the specific heat, k is the thermal conductivity, and T is the temperature.
2.3.3. Boundary Conditions
All simulations were performed for the following boundary conditions:
- Velocity-inlet condition with a uniform value and a static temperature equal to 300 K was defined at the inlet.
- Pressure-outlet condition with zero-gauge pressure was defined at the outlet.
- Constant heat flux and no-slip conditions were imposed on the mesh surface.
- Symmetry condition on the four side boundaries of the computational domain.
2.3.4. Numerical Assumptions
The operation conditions for the simulation are as follows:
- The air is defined as an ideal gas.
- The flow is in the steady state and laminar due to the maximum value of the Reynolds number, which is nearly 1100 for the arrangement with mesh type B.
- The physical properties of the fluid phase are temperature dependent because of its variations in the simulations.
- The radiative effects were not considered.
2.3.5. Computational Methodology
- A commercially available CFD code, ANSYS FLUENT 21.2, was employed to simulate the fluid flow and heat transfer. The simulation procedure was:
- The pressure–velocity coupling formulation was handled with a coupled algorithm.
- The second-order upwind schemes of discretization were adopted for the momentum and energy equations.
- The residual limit was set to 1 × 10−3 for the continuity and momentum equations and 1 × 10−6 for the energy equation.
3. Results and Discussion
3.1. Flow Resistance
According to Saini and Saini [26], the Fanning friction factor f is calculated based on the pressure loss across the channel and air velocity, defined by the Darcy–Weisbach equation:
and presented as a function of the Reynolds number Re defined with the hydraulic diameter Dh = 4ε/Sv and the interstitial fluid velocity u0 = u/ε:
Figure 5 shows the flow resistance characteristics derived from experiments and numerical modeling for all three expanded meshes tested. It is noticeable for all EMMs that the higher the superficial gas velocity, the greater the unit pressure drop (Figure 5 left). The discrepancies in the unit pressure drop between different EMMs also increased. It should be noted that mesh type B indicates the lowest flow resistance, while mesh type C has the highest one. The comparison of experimental and numerical results indicates good agreement; the average relative error ey is approximately 17.4%, 5.7%, and 18.2% for mesh types A, B, and C, respectively. The Fanning friction factor (Figure 5 right) for all meshes studied decreases when the Reynolds number increases, becoming flatter and flatter. However, the lower the Reynolds number, the smaller the discrepancies between meshes types. Computational simulations confirm this trend.
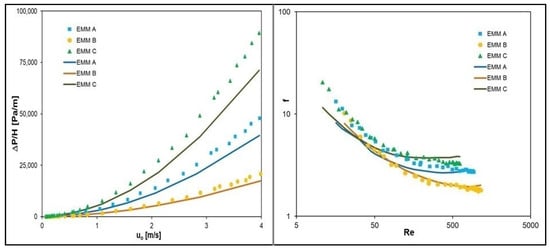
Figure 5.
Flow resistance characteristics derived from experiments (points) and modeling (lines): (left)—unit pressure drop vs. superficial gas velocity; (right)—Fanning friction factor vs. Reynolds number.
The available literature relating to the expanded mesh does not propose correlations describing the flow resistance. Therefore, new formulae were developed (see Table 3) in the form of the Ergun [28] model:
where A and B differ for meshes. The fit of the developed equations to the experimental data is shown in Figure 6.

Table 3.
Correlations for Fanning friction factors of expanded metal meshes.
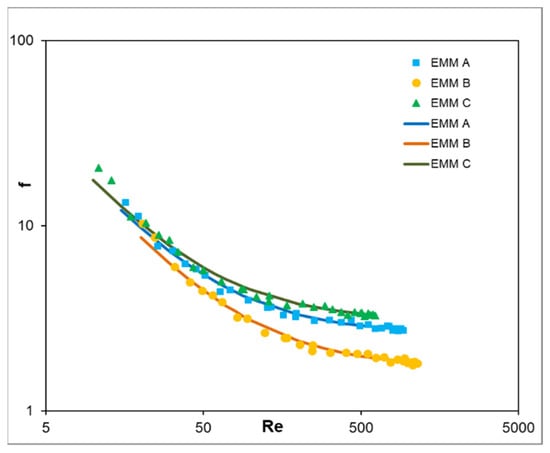
Figure 6.
Comparison of Fanning friction factor derived from experiments (points) and calculated by correlations from Table 3 (lines).
3.2. Heat Transfer
The Nusselt number Nu calculated from the heat transfer coefficient h is used to evaluate the heat transfer characteristic:
where ΔT is the logarithmic mean temperature difference between the mesh wall and the air at the inlet and outlet sides. The Nusselt number Nu is presented as a function of the Reynolds number Re.
Figure 7 presents the heat transfer results derived from experimental data and computational simulations for all EMMs tested. It is visible for all meshes that the higher the superficial gas velocity, the greater the heat transfer coefficients (Figure 7 left). It should be noted that mesh type B indicates the most intense heat transfer, while the heat transfer characteristics for mesh types A and C are located close together. Similar results were achieved using CFD modeling. The comparison of experimental and numerical results indicates that CFD modelling is able to predict the heat transfer of expanded metal meshes with reasonable accuracy (the average relative error ey is approximately 10.1%, 22.3%, and 14.7 for mesh types A, B, and C, respectively).
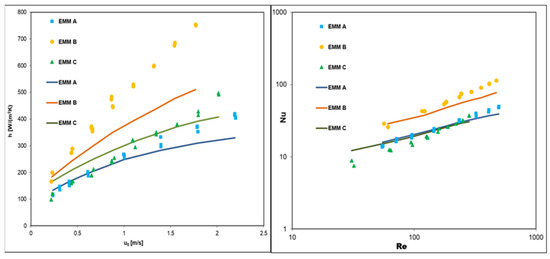
Figure 7.
Heat transfer characteristics derived from experiments (points) and modeling (lines): left—heat transfer coefficient vs. superficial gas velocity; right—Nusselt number vs. Reynolds number.
The available literature relating to the expanded mesh does not propose correlations describing the heat transfer. Therefore, new formulae were developed (see Table 4) in the form:
where A and B differ for meshes. The fit of the developed equations to the experimental data is presented in Figure 8.

Table 4.
Correlations for Nusselt numbers of expanded metal meshes.
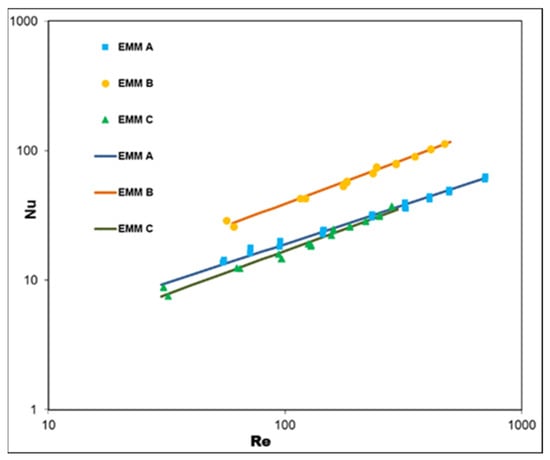
Figure 8.
Comparison of Nusselt number derived from experiments (points) and calculated by correlations from Table 4 (lines).
3.3. Comparison of Different Catalyst Supports
The comparison of expanded metal meshes with other reactors’ internals, such as the monolith, packed bed, or woven-wire gauze, is presented in Figure 9. The data on the specific surface area and void fraction of the compared packings are collated in Table 5.
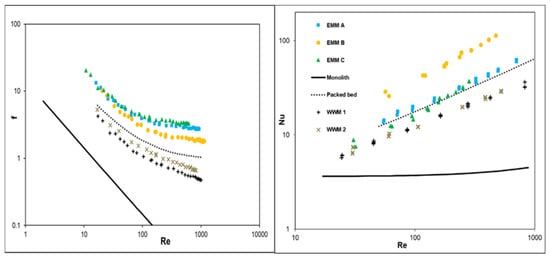
Figure 9.
Comparison of flow resistance (left) and heat transfer (right) of different reactor packings.

Table 5.
Comparison of expanded meshes with other catalyst carriers.
As can be seen from Figure 9, expanded meshes display higher flow resistance than the packed bed, but also more intense heat transfer, especially EMM type B. The lowest values of Fanning friction factors and Nusselt numbers are achieved for the monolith. However, it is not clear which reactor’s internal structure is the most efficient as a catalyst support. One of the meaningful ways to find the best solution for a given catalytic process is to use the Performance Efficiency Criterion (PEC) (Figure 10), which expresses the trade-off of the mass transfer intensity vs. the flow resistance [8,13]:
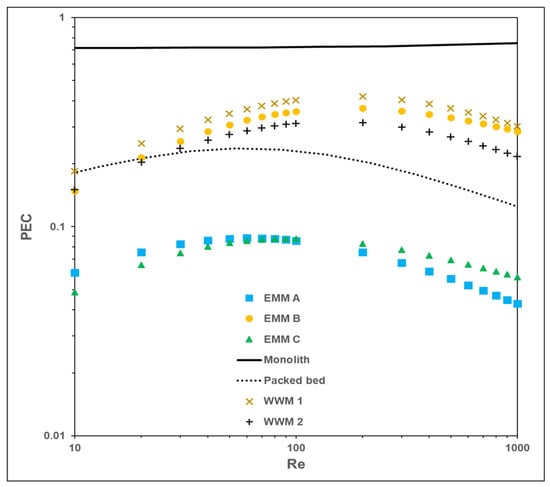
Figure 10.
Comparison of Performance Efficiency Criterion of different reactor packings.
The air–methane mixture was the tested reaction [13]. The Chilton–Colburn analogy [30] was applied to calculate the mass transfer coefficients:
Due to the highest PEC values, the monolith is the most beneficial catalyst support for the reaction mentioned. Although mesh type B indicates the highest flow resistance, its PEC values are comparable with that of wire gauzes because of the much more intense heat transfer. Mesh types A and C are not suitable for methane combustion due to their high flow resistance and, hence, low PEC values.
4. Conclusions
New formulae to evaluate the heat transfer and flow resistance characteristics of expanded metal meshes were developed. Fanning friction factors and Nusselt numbers were described by three equations dependent on the mesh type. The dimensions of meshes have an impact on the flow and transport characteristics; mesh type B seems to have the most desirable geometry.
Simple CFD models of expanded metal meshes were used to simulate the pressure drop and heat transfer coefficients. Numerical results agree well with experimental data. CFD modelling could be employed as a rapid and effective tool to predict the flow and transport properties of EMMs.
The comparison of expanded metal meshes with the monolith, packed bed, and woven-wire gauzes showed that their flow and transport characteristics are higher than other reactor internals. The Performance Efficiency Criterion (PEC) indicated that EMM type B and wire gauzes can be applied as catalyst carriers for methane oxidation.
Author Contributions
Conceptualization, M.I. and P.J.J.; methodology, A.G. and M.I.; software, M.I. and M.K.; validation, A.G. and P.J.J.; formal analysis, M.I., M.K. and A.G.; investigation, B.L., K.S. and M.S.; writing—original draft preparation, M.I.; writing—review and editing, A.K. and A.G.; visualization, M.I., M.S. and K.S.; supervision, A.G., A.K. and P.J.J.; funding acquisition, P.J.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Centre for Research and Development, LIDER/204/L-6/14/NCBR/2015.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Nomenclature
| A, B | constants |
| cp | specific heat, J·kg−1·K−1 |
| Dp | grain diameter, mm |
| Dh | hydraulic diameter, mm |
| d | wire diameter, mm |
| ey | average relative error, % |
| F | surface area, m2 |
| f | Fanning friction factor, |
| h | heat transfer coefficient, W∙m−2∙K−1 |
| k | thermal conductivity, W∙m−1∙K−1 |
| L | bed length, m |
| Nu | Nusselt number |
| ΔP | pressure drop, Pa |
| Pr | Prandtl number |
| p | static pressure, Pa |
| q | heat flux, W·m−2 |
| Re | Reynolds number |
| S | sheet thickness, mm |
| Sc | Schmidt number |
| Sh | Sherwood number |
| Sv | specific surface area, m2∙m−3 |
| T | temperature, K |
| T | strand thickness, mm |
| ui, uj | velocity component |
| u0 | superficial (approach) velocity, m∙s−1 |
| W | strand width, mm |
| xi, xj | Cartesian coordinate |
| ε | porosity |
| µ | viscosity, Pa∙s |
| ρ | density, kg∙m−3 |
| τij | stress tensor |
References
- Tang, H.-Y.; Erickson, P.; Yoon, H.C.; Liao, C.-H. Comparison of steam and autothermal reforming of methanol using a packed-bed low-cost copper catalyst. Int. J. Hydrogen Energy 2009, 34, 7656–7665. [Google Scholar] [CrossRef]
- Yang, J.; Wang, Q.; Zeng, M.; Nakayama, A. Computational study of forced convective heat transfer in structured packed beds with spherical or ellipsoidal particles. Chem. Eng. Sci. 2010, 65, 726–738. [Google Scholar] [CrossRef]
- Kołodziej, A.; Łojewska, J.; Łojewski, T.; Iwaniszyn, M. Short-channel structures of triangular cross-section. Int. J. Heat Mass Transf. 2011, 54, 3291–3295. [Google Scholar] [CrossRef]
- Kołodziej, A.; Łojewska, J.; Ochońska, J.; Łojewski, T. Short-channel structured reactor: Experiments versus previous theoretical design. Chem. Eng. Process.-Process Intensif. 2011, 50, 869–876. [Google Scholar] [CrossRef]
- Iwaniszyn, M.; Ochońska, J.; Jodłowski, P.J.; Knapik, A.; Łojewska, J.; Janowska-Renkas, E.; Kołodziej, A. Short-channel structured reactor as a catalytic afterburner. Top. Catal. 2013, 56, 273–278. [Google Scholar] [CrossRef]
- Iwaniszyn, M.; Ochońska, J.; Jodłowski, P.J.; Łojewska, J.; Matuszek-Chmurowska, A.; Kołodziej, A. Microstructured reactor as a pre-turbo catalytic converter. Top. Catal. 2013, 56, 384–389. [Google Scholar] [CrossRef][Green Version]
- Jodłowski, P.J.; Kryca, J.; Rogulska, A.; Gil, B.; Iwaniszyn, M.; Łojewska, J.; Kołodziej, A. New method of determination of intrinsic kinetic and mass transport parameters from typical catalyst activity tests: Problem of mass transfer resistance and diffusional limitation of reaction rate. Chem. Eng. J. 2017, 162, 322–331. [Google Scholar] [CrossRef]
- Giani, L.; Groppi, G.; Tronconi, E. Mass-Transfer Characterization of Metallic Foams as Supports for Structured Catalysts. Ind. Eng. Chem. Res. 2005, 44, 4993–5002. [Google Scholar] [CrossRef]
- Peng, W.; Xu, M.; Li, X.; Huai, X.; Liu, Z.; Wang, H. CFD study on thermal transport in open-cell metal foams with and without a washcoat: Effective thermal conductivity and gas-solid interfacial heat transfer. Chem. Eng. Sci. 2017, 161, 92–108. [Google Scholar] [CrossRef]
- Bianchi, G.; Schwieger, W.; Freund, H. Assessment of Periodic Open Cellular Structures for Enhanced Heat conduction in Catalytic Fixed-Bed Reactors. Adv. Eng. Mater. 2016, 18, 608–614. [Google Scholar] [CrossRef]
- Kumar, P.; Topin, F. Simultaneous determination of intrinsic solid phase conductivity and effective thermal conductivity of Kelvin like foams. Appl. Therm. Eng. 2014, 71, 536–547. [Google Scholar] [CrossRef]
- Bracconi, M.; Ambrosetti, M.; Maestri, M.; Groppi, G.; Tronconi, E. A systematic procedure for the virtual reconstruction of open-cell foams. Chem. Eng. J. 2017, 315, 608–620. [Google Scholar] [CrossRef]
- Gancarczyk, A.; Iwaniszyn, M.; Piątek, M.; Korpyś, M.; Sindera, K.; Jodłowski, P.J.; Łojewska, J.; Kołodziej, A. Catalytic Combustion of Low-Concentration methane on Structured Catalyst Supports. Ind. Eng. Chem. Res. 2018, 57, 10281–10291. [Google Scholar] [CrossRef]
- Busse, C.; Freud, H.; Schwieger, W. Intensification of heat transfer in catalytic reactors by additively manufactured periodic open cellular structures (POCS). Chem. Eng. Process.-Process Intensif. 2018, 124, 199–214. [Google Scholar] [CrossRef]
- Klumpp, M.; Inayat, A.; Schwerdtfeger, J.; Korner, C.; Singer, R.F.; Freund, H.; Schwieger, W. Periodic open cellular structures with ideal cubic cell geometry: Effect of porosity and cell orientation on pressure drop behavior. Chem. Eng. J. 2014, 242, 364–378. [Google Scholar] [CrossRef]
- Oshinowo, L.; Kuhn, D.C.S. Turbulence Decay Behind Expanded Metal Screens. Can. J. Chem. Eng. 2000, 78, 1032–1039. [Google Scholar] [CrossRef]
- Smith, D.; Graciano, C.; Martínez, G. Expanded metal: A review of manufacturing, applications and structural performance. Thin-Walled Struct. 2021, 160, 107371. [Google Scholar] [CrossRef]
- Kołodziej, A.; Łojewska, J. Mass transfer for woven and knitted wire gauze substrates: Experiments and modelling. Catal. Today 2009, 147S, S120–S124. [Google Scholar] [CrossRef]
- Ahlström-Silversand, A.F.; Odenbrand, C.U.I. Modelling catalytic combustion of carbon monoxide and hydrocarbons over catalytically active wire meshes. Chem. Eng. J. 1999, 73, 205–216. [Google Scholar] [CrossRef]
- Lyubovsky, M.; Karim, H.; Menacherry, P.; Boorse, S.; LaPierre, R.; Pfefferle, W.C.; Roychoudhury, S. Complete and partial catalytic oxidation of methane over substrates with enhanced transport properties. Catal. Today 2003, 83, 183–197. [Google Scholar] [CrossRef]
- Porsin, A.V.; Kulikov, A.V.; Dalyuk, I.K.; Rogozhnikov, V.N.; Kochergin, V.I. Catalytic reactor with metal gauze catalysts for combustion of liquid fuel. Chem. Eng. J. 2015, 282, 233–240. [Google Scholar] [CrossRef]
- Jodłowski, P.J.; Kuterasiński, Ł.; Jędrzejczyk, R.J.; Chlebda, D.; Gancarczyk, A.; Basąg, S.; Chmielarz, Ł. DeNOx Abatement Modelling over Sonically Prepared Copper USY and ZSM5 Structured Catalysts. Catalysts 2017, 7, 205. [Google Scholar] [CrossRef]
- Zalosh, R. Deflagration suppression using expanded metal mesh and polymer foams. J. Loss Prev. Process Ind. 2007, 20, 659–663. [Google Scholar] [CrossRef]
- Mustaffar, A.; Harvey, A.; Reay, D. Melting of phase change material assisted by expanded metal mesh. Appl. Therm. Eng. 2015, 90, 1052–1060. [Google Scholar] [CrossRef]
- Lafmejani, S.S.; Müller, M.; Olesen, A.C.; Kær, S.K. Experimental and numerical study of flow in expanded metal plate for water electrolysis applications. J. Power Sources 2018, 397, 334–342. [Google Scholar] [CrossRef]
- Saini, R.P.; Saini, J.S. Heat transfer and friction factor correlations for artificially roughened ducts with expanded metal mesh as roughness element. Int. J. Heat Mass Transf. 1997, 40, 973–986. [Google Scholar] [CrossRef]
- Mallick, R.K.; Thombre, S.B. Performance of passive DMFC with expanded metal mesh current collectors. Electrochim. Acta 2017, 243, 299–309. [Google Scholar] [CrossRef]
- Ergun, S. Fluid flow through packed columns. Chem. Eng. Prog. 1952, 48, 89–94. [Google Scholar]
- Iwaniszyn, M.; Sindera, K.; Gancarczyk, A.; Korpyś, M.; Jędrzejczyk, R.J.; Kołodziej, A.; Jodłowski, P.J. Experimental and CFD investigation of heat transfer and flow resistance in woven wire gauzes. Chem. Eng. Process.-Process Intensif. 2021, 163, 108364. [Google Scholar] [CrossRef]
- Chilton, T.H.; Colburn, A.P. Mass transfer (absorption) coefficients prediction from data on heat transfer and fluid friction. Ind. Eng. Chem. 1934, 26, 1183–1187. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).