Optimization of Magnetic Gear Patterns Based on Taguchi Method Combined with Genetic Algorithm

Abstract

Magnetic gears (MGs) have gained increasing attention due to their sound performance in high torque density and low friction loss. Aiming to maximize the torque density, topology design has been a popular issue in recent years. However, studies on the optimization comparisons of a general MG topology pattern are very limited. This paper proposes a Taguchi-method-based optimization method for a general MG topology pattern, which can cover most of the common types of radially magnetized concentric-surface-mounted MGs (RMCSM-MGs). The Taguchi method is introduced to evaluate the influence of each parameter in MGs. Moreover, the parameter value range is re-examined based on the sensitivity analysis results. The genetic algorithm (GA) method is adopted to optimize the topology pattern in the study.

1. Introduction

Wind power generation has become more and more popular in industrial production and daily life due to its clean and inexhaustible advantages over traditional coal-fired power [1]. Gearboxes are widely used in wind power generation systems. Components of different speeds can be made to run at certain speed ratios by connecting them through gearboxes. Mechanical gears, which are currently widely used in industry, suffer from the following problems: loud noise, high manufacturing and installation accuracy requirements, high friction loss, etc., [2]. In recent years, due to the development of rare earth materials, magnetic gears (MGs) are expected to replace mechanical gears [3]. Abundant research and experiments have indicated that the transmission torque of MGs can reach up to 100 kNm/m³ [4]. In addition, MGs have the advantages of physical isolation, lower maintenance costs, and inherent overload protection [5].

The main material required for MGs is rare-earth permanent magnets (PMs), which are expensive. Hence, there is an increasing concern regarding saving PM material without sacrificing the torque density. There have been several longitudinal studies involving optimizing the MG topology to save resources and costs. To meet application requirements, studies on the topology design of radially magnetized concentric-surface-mounted MGs (RMCSM-MGs) have become popular in recent years. It is well-known that RMCSM-MGs are commonly made of three layers. Traditional RMCSM-MGs have PMs embedded in the inner layer and outer layer, while the middle layer is made of ferrite material. Another kind of MG with competitive performance is the triple-PM-excited MGs, which have PMs embedded in each layer. The torque per unit PM volume among the six basic topologies of triple-PM-excited MGs is compared in [6]. However, the six types of topologies have the same outer rotor structure and modulation ring structure. Only the topology of the inner rotor is changed during the comparison. In [7], the author attempted to propose a pattern design for the triple-PM-excited MGs. However, the unipolar permanent magnetic–ferrite array and the air–ferrite array of the inner rotor and modulation ring are not considered in this pattern. Moreover, optimization of the PM and ferrite distribution is mostly ignored in the literature; the assumption that PM and ferrite are equally distributed is taken by default, without any explanation.

Research on this subject has been mostly restricted to individually optimizing each type of MG, which may cost an amount of time. This paper aims to optimize and comprehensively compare the topology of common RMCSM-MGs. Therefore, a topology pattern was designed, which could cover most of the common types of RMCSM-MGs. In previous studies, authors often needed to optimize once for each MG structure [8,9,10]. By resorting to pattern design, optimization must be performed only once [11,12]. The optimization method used in this article is the genetic algorithm (GA). Local convergence, the so-called “premature phenomenon”, is a problem that has always plagued researchers. Common solutions include increasing the probability of mutation, increasing diversity, and reducing the probability of selecting excellent chromosomes [13]. However, these approaches may result in a higher amount of computation. In this paper, the Taguchi method is employed to obtain a near-optimal value, which can help to determine the appropriate initial values and ranges in GA optimization [14,15,16]. The Taguchi method has been widely used in the field of industrial engineering. To name a few applications, the parameters of the Jiles–Atherton hysteresis model are optimized using Taguchi’s method in [17], and the author of [18] blended the Taguchi orthogonal array (OA) concept into the design of the linear antenna array. In [19], the Taguchi method is employed to optimize the material of multiple layers of dielectric thin films in the photonic radiative cooler. Many other applications of the Taguchi method were reviewed in [20,21,22], among other studies.

2. General Pattern Design

The RMCSM-MG is mainly composed of three rings. The inner and the outer ring can rotate, so they are named rotors. The middle ring is stationary, and is named the modulation ring. It is worth noting that the PMs of the RMCSM-MG are magnetized in radial directions. As shown in Figure 1, the rotors may be designed as a bipolar PM array, unipolar PM array, or bipolar PM–ferrite array [23]. As presented in Figure 2, the modulation ring may be created as a ferrite–air array, ferrite–PM array, or ferrite–PM–air array [23]. Hence, there are 27 possible topologies of RMGSM-MG, which are discussed in this study. The intuitive approach is to separately optimize each of the 27 types, but this requires a lot of computation. In this article, we design a pattern to cover these 27 special structural types. This can greatly reduce the amount of computation.

Figure 1. Three kinds of rotor arrays: (a) bipolar PM array (b) unipolar PM array (c) bipolar PM–ferrite array [23].

Figure 2. Three kinds of modulation arrays: (a) ferrite–air array (b) ferrite–PM array (c) ferrite–PM–air array [23].

The configuration of the RMCSM-MG pattern is shown in Figure 3. It is well-known that the working principle of MGs obeys the modulation effect [24], and the proposed RMGSM-MG pattern in this article is no exception. Figure 4 is a partially enlarged drawing of the RMGSM-MG pattern in Figure 3. The red and blue segments represent the S and N pole PMs made from NdFeB material, respectively. The magnetization directions are marked in the figure. The grey segments are ferrite pieces made of M19_24G material. The flux path of both inner and outer rotor PM poles before modulation is shown. After modulation, the inner rotor flux path has the same pole pair number as that of the outer rotor. Similarly, the outer rotor can be modulated to match the PM pole pair of the inner rotor. Thus, they can transmit torque steadily between each rotor at any different rotational speed. For this reason, the pole pair number of each layer can be summarized by the following equations:

$$\begin{array}{cc}{p}_o=\left|p_i-m\right|& \end{array}or\begin{array}{cc}& p_i=\left|p_o-m\right|\end{array}$$

(1)

where p_i and p_o represent the inner and outer pole pair numbers, respectively. The quantity m represents the segment of modulation ferrite.

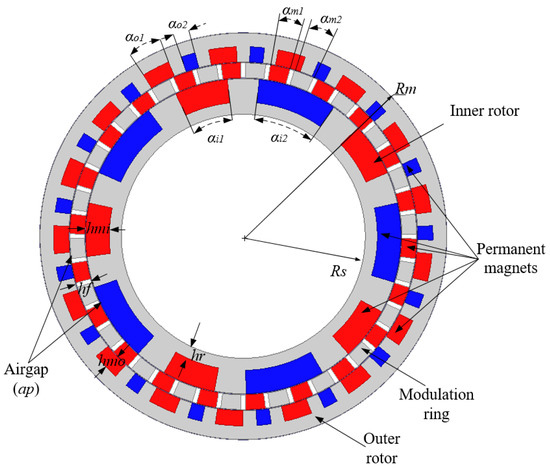
Figure 3. Configuration of RMCSM-MG pattern.

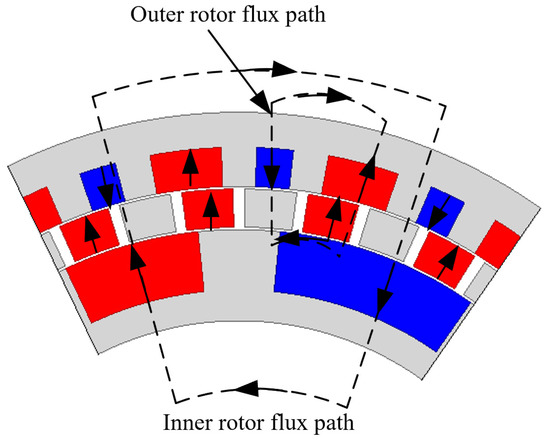
Figure 4. Flux path of inner and outer rotor PM poles before modulation.

The parameters of the RMCSM-MG pattern are shown in Table 1. As shown in Figure 3, the innermost radius, R_s = 60 mm, and the outermost radius, R_m = 105 mm, are also constant to keep the total volume of the MG invariable. For each layer, the distribution of PM and ferrite segments is re-examined by setting the expansion angles as variables. It can be deduced that the PM and ferrite arrays shown in Figure 1 and Figure 2 are particular cases included in the general pattern. For instance, Figure 1a shows the rotor arrays when α_i1 = α_i2 or α_o1 = α_o2. Figure 1b shows the case when α_i1 = 180°/p_i, α_i2 = 0 or α_o1 = 180°/p_o, α_o2 = 0.

Table 1. Main parameters of the pattern of RMCSM-MG.

Symbol	Meaning	Value
pi	inner rotor pole pair number	5
po	outer rotor pole pair number	17
m	modulation ferrite segments	22
ag	airgap length	0.5 mm
lg	axial length	65 mm
hmi	inner layer height	variable
hf	middle layer height	variable
hmo	outer layer height	variable
hr	inner rotor height	variable
Rs	innermost radius	60 mm
Rm	outermost radius	105 mm
αi1	angle of inner layer S pole	variable
αi2	angle of inner layer N pole	variable
αm1	angle of middle layer S pole	variable
αm2	angle of middle layer ferrite pole	variable
αo1	angle of outer layer S pole	variable
αo2	angle of outer layer N pole	variable
μr	relative permibility	1.044
Hc	magnetic coercivity	−8.38 × 105 A/m

3. Sensitivity Analysis and Optimization

By employing a Taguchi-method-based sensitivity analysis, it is possible to discover a near-optimal solution. In this study, the value range in the optimization is refined according to the near-optimal solution. It is well-known that each parameter will be given an upper boundary and lower boundary in a random search optimization algorithm [25,26,27]. In the Taguchi method, each parameter is evaluated on several specific levels [18].

Parameters to be optimized are listed in Table 1. Assume X represents the array of parameters, and C(X) represents the torque per unit PM volume, which can be expressed as follows:

$$C(X)=T(X)/V_{PM}(X)$$

(2)

where T(X) is the average electromagnetic torque of the inner rotor and outer rotor in one rotation period, and V_PM(X) is the total volume of the PM pieces. The optimization criterion of this study is to maximize C(X). It is worth noting that the unit of C(X) is kNm/m³.

Some linear constraints are also added to ensure that the geometry is logical:

$$\{\begin{array}{c}{\alpha }_{i1}+{\alpha }_{i2}\le \frac{360°}{p_i}\\ {\alpha }_{m1}+{\alpha }_{m2}\le \frac{360°}{n_s}\\ {\alpha }_{o1}+{\alpha }_{02}\le \frac{360°}{p_o}\\ hf+hmi+hmo+hr<Rm-Rs-2·ap\end{array}$$

(3)

Furthermore, another constraint is added to ensure a high stability of the MG, which is presented as:

$$T_r\left(X\right)\le 4\begin{array}{cc}& (\mathrm{Nm})\end{array}$$

(4)

where T_r(X) is the average torque ripple of the inner rotor and outer rotor. This value is designed as 2% of the common torque density of RMCSM-MG [24]. In this study, the torque and torque ripple values were measured using the finite element method (FEM) [27]. The 2D FEM solver adopted in this study is Ansys Maxwell 16.0.

This section is divided into subheadings as follows.

3.1. Taguchi Orthogonal Array Analysis of Objective Function

In the Taguchi sensitivity analysis, each parameter is designed with three levels as shown in Table 2 [23]. The L27 Taguchi Orthogonal Array (TOA) is applied in the analysis. A total of 27 experiments are involved in L27 TOA, and each experiment examines the parameters in a specific combination of levels. Level combinations, experimental results, and the resultant cost values are listed in Table 3. It is worth noting that L1, L2, and L3 are the abbreviations of level 1, level 2, and level 3, respectively.

Table 2. Parameter level design.

	X1 (hmi)	X2 (hf)	X3 (hmo)	X4 (hr)	X5 (αi1)
Level 1	4 mm	4 mm	4 mm	4 mm	18°
Level 2	8 mm	8 mm	8 mm	8 mm	24°
Level 3	12 mm	12 mm	12 mm	12 mm	36°
	X1 (hmi)	X2 (hf)	X3 (hmo)	X4 (hr)	X5 (αi1)
Level 1	18°	60°/17	60°/17	60°/22	60°/22
Level 2	24°	120°/17	120°/17	120°/22	120°/22
Level 3	36°	180°/17	180°/17	180°/22	180°/22

Table 3. L27 Taguchi orthogonal array and experimental results for objective function.

No.	X1	X2	X3	X4	X5	X6	X7	X8	X9	X10	C(X)
1	L1	L1	L1	L1	L1	L1	L1	L1	L1	L1	47.39
2	L1	L1	L1	L1	L2	L2	L2	L2	L2	L2	69.29
3	L1	L1	L1	L1	L3	L3	L3	L3	L3	L3	112.18
4	L1	L2	L2	L2	L1	L1	L1	L2	L2	L2	37.28
5	L1	L2	L2	L2	L2	L2	L2	L3	L3	L3	60.19
6	L1	L2	L2	L2	L3	L3	L3	L1	L1	L1	80.14
7	L1	L3	L3	L3	L1	L1	L1	L3	L3	L3	29.13
8	L1	L3	L3	L3	L2	L2	L2	L1	L1	L1	45.86
9	L1	L3	L3	L3	L3	L3	L3	L2	L2	L2	83.24
10	L2	L1	L2	L3	L1	L2	L3	L1	L2	L3	112.43
11	L2	L1	L2	L3	L2	L3	L1	L2	L3	L1	13.08
12	L2	L1	L2	L3	L3	L1	L2	L3	L1	L2	71.91
13	L2	L2	L3	L1	L1	L2	L3	L2	L3	L1	39.62
14	L2	L2	L3	L1	L2	L3	L1	L3	L1	L2	56.42
15	L2	L2	L3	L1	L3	L1	L2	L1	L2	L3	61.95
16	L2	L3	L1	L2	L1	L2	L3	L3	L1	L2	108.48
17	L2	L3	L1	L2	L2	L3	L1	L1	L2	L3	27.85
18	L2	L3	L1	L2	L3	L1	L2	L2	L3	L1	44.07
19	L3	L1	L3	L2	L1	L3	L2	L1	L3	L2	51.76
20	L3	L1	L3	L2	L2	L1	L3	L2	L1	L3	53.78
21	L3	L1	L3	L2	L3	L2	L1	L3	L2	L1	23.84
22	L3	L2	L1	L3	L1	L3	L2	L2	L1	L3	82.40
23	L3	L2	L1	L3	L2	L1	L3	L3	L2	L1	68.20
24	L3	L2	L1	L3	L3	L2	L1	L1	L3	L2	35.61
25	L3	L3	L2	L1	L1	L3	L2	L3	L2	L1	32.28
26	L3	L3	L2	L1	L2	L1	L3	L1	L3	L2	83.49
27	L3	L3	L2	L1	L3	L2	L1	L2	L1	L3	35.15

Then we need to evaluate the average effect of the parameters. This index is the average of the experimental results for one parameter at a certain level. For example, the average effect of X1 at L1 is calculated using the following equation:

$$m_{\mathrm{X}1,\mathrm{L}1}=\frac{1}{9}{\displaystyle \sum _{n=1}^{9}C(n)}$$

(5)

where C(n) represents the results of the nth experiment. Using the same method, we obtained the results shown in Table 4.

Table 4. Average analysis results.

	X1	X2	X3	X4	X5	X6	X7	X8	X9	X10
L1	62.74	61.74	66.16	59.75	60.08	50.90	33.97	60.71	64.61	43.83
L2	59.53	57.97	58.43	51.62	53.12	58.93	57.74	50.87	57.37	66.38
L3	51.83	54.39	49.51	60.20	60.89	51.94	82.39	62.51	52.12	63.89

Suppose the array element [X1, L1] represents the value in column X1 and row L1. The value represents how much the value of L1 of parameter X1 may influence the cost value. The larger the value, the greater the effect. Therefore, we can extract the most influential level for each parameter. The results illustrate that the parameter combination [L1, L1, L1, L3, L3, L2, L3, L3, L1, L2] is the near-optimal solution. Then, an improved value range is obtained around the near-optimal solution, as shown in Table 5. Considering the actual situation in manufacturing, the lower boundaries of h_mi, h_f and h_mo are set to 4 mm.

Table 5. Original and improved parameter value range.

Parameter	Original Value Range	Improved Value Range
X1(hmi)	[4 mm, 20 mm]	[4 mm, 8 mm]
X2(hf)	[4 mm, 20 mm]	[4 mm, 8 mm]
X3(hmo)	[4 mm, 20 mm]	[4 mm, 8 mm]
X4(hr)	[4 mm, 20 mm]	[8 mm, 16 mm]
X5(αi1)	[0°, 36°]	[30°, 42°]
X6(αi2)	[0°, 36°]	[24°, 36°]
X7(αo1)	[0°, 18°]	[120°/17, 240°/17]
X8(αo2)	[0°, 18°]	[120°/17, 240°/17]
X9(αm1)	[0°, 18°]	[0°/22, 120°/22]
X10(αm2)	[0°, 18°]	[60°/22, 180°/22]

3.2. Sensitivity Analysis and Linear Interpolation Fitting of Torque Ripple Function

To deal with the requirements of the constraint function (4), initially, a study of the sensitivity of each parameter to the constraint function T_r(X) was conducted. Moreover, the most influential parameters were selected to perform the linear interpolation fitting of T_r(X) [28]. Therefore, the value that fulfills the fitting can be considered to be approximately satisfied with the constraint function.

In this study, the parameters are further divided into three levels within the improved value ranges in Table 5. The new level design is shown in Table 6. Then, the L27 TOA, using the parameter level design shown in Table 7, was conducted to obtain the results for T_r(X). Subsequently, the analysis of variance (ANOVA) technique was employed to obtain the influence of each parameter [14]. For instance, the sum of the square of the parameter X1 SS_X1 is governed by the formula:

$$S{S}_{\mathrm{X}1}={\left(t{m}_{\mathrm{X}1,\mathrm{L}1}-tm\right)}^2+{\left(t{m}_{\mathrm{X}1,\mathrm{L}2}-tm\right)}^2+{\left(t{m}_{\mathrm{X}1,\mathrm{L}3}-tm\right)}^2$$

(6)

where tm represents the total average T_r(X) value of all experiments. The values tm_X1,L1, tm_X1,L2, and tm_X1,L3 represent the average T_r(X) values of parameter X1 in level 1, level 2, and level 3, respectively. The ANOVA results are shown in Table 7. The SS value represents the degree of sensitivity. The larger the value, the more obvious the influence of this parameter on torque ripple. Table 7 also includes the percentage of influence of each parameter. It can be seen that the parameters X5, X6, X7, and X8 are the four most effective factors on T_r(X). In order to reduce the level of computation, all parameters except for X5, X6, X7, and X8 were ignored in the linear interpolation fitting.

Table 6. Parameter level design of torque ripple function.

	X1 (hmi)	X2 (hf)	X3 (hmo)	X4 (hr)	X5 (αi1)
Level 1	4 mm	4 mm	4 mm	8 mm	30°
Level 2	6 mm	6 mm	6 mm	12 mm	36°
Level 3	8 mm	8 mm	8 mm	16 mm	42°
	X6 (αi2)	X7 (αo1)	X8 (αo2)	X9 (αm1)	X10 (αm2)
Level 1	24°	120°/17	120°/17	0°/22	60°/22
Level 2	30°	180°/17	180°/17	60°/22	120°/22
Level 3	36°	240°/17	240°/17	120°/22	180°/22

Table 7. Average analysis results.

	X1	X2	X3	X4	X5	X6	X7	X8	X9	X10
SS	0.04	0.11	0.25	0.03	1.77	1.87	1.74	1.68	0.68	0.81
PC(%)	0.44	1.22	2.78	0.33	19.7	20.8	19.4	18.7	7.57	9.02

The α_i1 and α_i2 for the inner layer and the α_o1 and α_o2 for the outer layer were discussed during fitting. In the sampling process, 20 groups of experimental results of the average torque ripple versus (α_i1, α_i2) and (α_o1, α_o2) were obtained. All the parameter values are randomly generated from the improved value range. After the linear interpolation fitting, the curve of the average torque ripple versus (α_i1, α_i2) and (α_o1, α_o2) can be achieved, the results of which are shown in Figure 5 and Figure 6. The results in Figure 5 show that the torque ripple fulfils the constraint in all (α_i1, α_i2) evaluations. It is worth noting that, by introducing the interpolation fitting, the torque ripple may become negative, which is unnatural. Therefore, these values are modified to zero in this study. From the data in Figure 6, a polynomial fitting can be achieved to satisfy the constraint function in (4). The polynomial fitting result is as follows:

$${\alpha }_{o2}+0.001{\alpha }_{o1}^3-0.056{\alpha }_{o1}^2+1.625{\alpha }_{o1}^{}-21.73>0$$

(7)

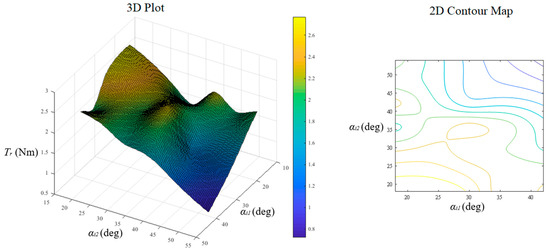
Figure 5. Torque ripple versus α_i1 and α_i2.

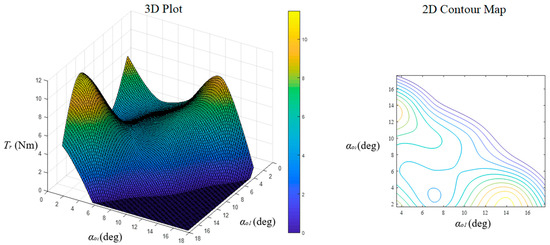
Figure 6. Torque ripple versus α_o1 and α_o2.

3.3. Establishing Optimization

The last step was to establish optimization by combining the sensitivity analysis results. In this study, we used the GA optimization method refined by the improved value ranges and constraint functions.

The crossover probability was set as 0.7 and the mutation probability was set as 0.15 [29]. The maximum optimization generation G_max was set as 40, where each generation contained 60 individuals. The convergence condition is as follows:

$$\begin{array}{l}\left|C^i(x)-C^{i-1}(x)\right|\le 0.1\\ i=1,2,\dots ,G_{\max }\end{array}$$

(8)

where Cⁱ(x) represents the best solution of the objective function in the ith generation. The optimization is supposed to finish when it attains the convergence condition or reaches the maximum generation.

3.4. Optimization Results Discussions

Without a sensitivity analysis, optimization is performed within a given original value range which may be very costly in terms of time and computational resources. Indeed, the optimization results always fall into local optimality when using the original value range. Therefore, the study of a sensitivity analysis based on the Taguchi method, and the linear interpolation fitting of the torque ripple constraint, is essential. According to the analysis results, the GA optimization is refined with a more precise value range (Table 5) and constraint function (7).

Figure 7 shows the cost value variation in each generation of the refined optimization process. The optimization converges after 11 generations. The configuration and torque performance of both the optimized model and original model are shown in Figure 8 and Figure 9, respectively. The average torque of the inner rotor and outer rotor increases by about 47% after optimization. However, the torque ripple increases by about 17% after optimization but still satisfies the constraint in (4). The average torque per unit PM volume before and after optimization is about 163.72 kNm/m³ and 225.41 kNm/m³, respectively. The average torque per unit PM volume increases by about 38%.

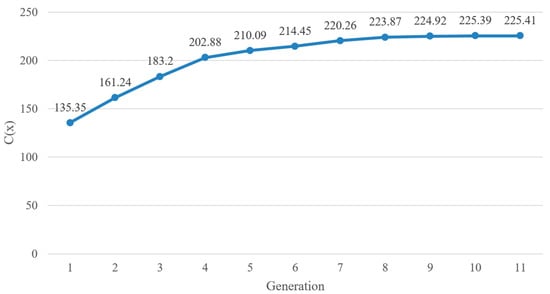
Figure 7. Cost value variation in each generation.

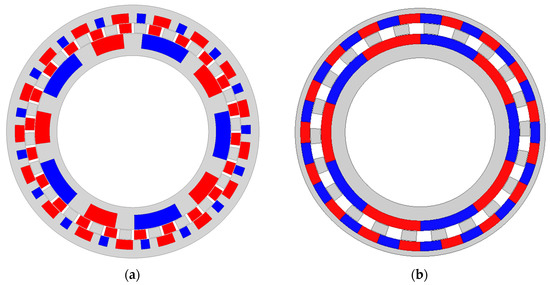
Figure 8. (a) Configuration of the original model. (b) Configuration of the optimized model.

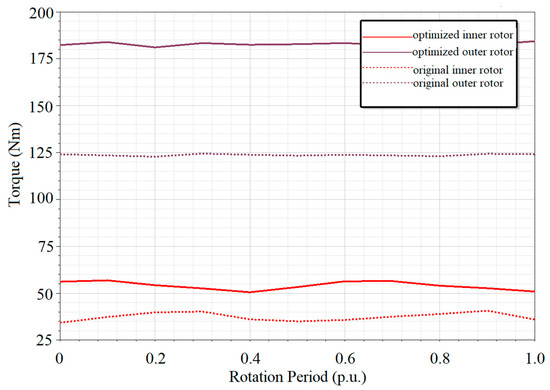
Figure 9. Torque performance of the optimized and original model.

Detailed optimized parameter values are shown in Table 8.

Table 8. Parameters of the original model and optimized model.

Parameter	Original Model	Optimized Model
X1 (hmi)	11.54 mm	7.9 mm
X2 (hf)	7.31 mm	8.0 mm
X3 (hmo)	7.49 mm	7.4 mm
X4 (hr)	5.95 mm	11.3 mm
X5 (αi1)	19.5 deg	35.8 deg
X6 (αi2)	28.8 deg	36.1 deg
X7 (αo1)	8.5 deg	10.4 deg
X8 (αo2)	4.3 deg	10.6 deg
X9 (αm1)	6.6 deg	0.0 deg
X10 (αm2)	6.7 deg	8.2 deg

4. Conclusions

The present study makes several noteworthy contributions towards optimizing a general topology pattern for RMCSM-MG. This pattern can cover most of the common types of MGs. The objective is to discover the MG topology with the highest torque per PM volume. Moreover, the torque ripple should be kept within a reasonable range. To discover the optimal topology, the GA optimization method was conducted. In order to reduce the possibility of local convergence and increase the computational cost, the parameter value range was refined using a sensitivity analysis based on the Taguchi method and interpolation fitting. The optimization converges after 11 generations. After optimization, the average torque increases by about 47%, and the average torque per PM volume increases by about 38%.