Identification of Generators’ Economic Withholding Behavior Based on a SCAD-Logit Model in Electricity Spot Market

Abstract

The effective identification of the economic withholding behavior of the generators can help ensure the fair operation of the electricity market. A SCAD-logit model is proposed to improve the performance of the logit model for the massive data of electricity market. First, a social network analysis method is used to construct an equity relationship graph of the generators to obtain a set of key monitoring generators. An indicator system for identifying the economic withholding behavior of the generators is constructed based on structure conduct performance (SCP) theory. The indicators are screened by the smoothed clipped absolute deviation (SCAD) penalty regression method to reduce the collinearity and improve identification efficiency. Then, a SCAD-logit model is established to identify the economic withholding of key monitoring generators, so that the boundary contributions of each indicator to the economic withholding behavior are obtained. The confusion matrix, ROC curve, and AUC values are used to evaluate the model’s performance. Finally, the model is applied to the electricity spot market, and the method can identify the generators that exercise economic withholding behavior with a correct rate of 96.83%. Indicators such as market share, quotation fluctuation degree, high quotation index, and volume price index can be used as important indicators for identifying the economic withholding behavior.

1. Introduction

At present, China’s electricity spot market has entered into trial operation, which is a critical period for the development of the electricity market. During trial operations, imperfect trading rules lead to market power abuse [1,2], and economic withholding is a prominent form [3]. Economic withholding refers to the behavior of generators wherein they declare a high price so that part of their power generation capacity does not win the bid, thereby raising the market-clearing price and making generators or their affiliates ally to obtain high profits. Economic withholding can seriously affect the safety, stability, and healthy development of the electricity spot market. Around the world, electricity market prices in California and Spain have soared due to economic withholding [4,5]. Therefore, it is urgent to quickly and effectively identify the economic withholding behavior of generators.

The abuse of market power includes many forms; however, current research does not distinguish them. Ref. [6] created the local market power index that measures market power abuse based on market concentration, transmission constraints, and demand–supply ratio. Ref. [7] reviewed the measurement indicators of market power abuse. Ref. [8] established an indicator system to evaluate the multilevel market power abuse. These studies measure and assess the market’s abuse of market power by constructing indicators; however, there are many forms of market power abuse, such as economic withholding, physical withholding, and collusion bidding, and each form has a unique way of being exercised. Therefore, as market participants become more proficient in market rules, it is necessary to provide different identification methods for different forms of market power abuses, and ensure the fair operation of the market.

In research on the economic withholding behavior of generators, Ref. [9] analyzed the internal mechanism of economic withholding behavior from the perspective of the relationship between electricity spot prices and generation failures. Ref. [10] analyzed the incentive effect of a unified marginal clearing price mechanism on economic withholding based on the Cournot game model of generators. Ref. [11] studied the economic withholding behavior that would lead to more generators being more profitable in the market. Ref. [12] discussed the conditions under which economic withholding occurs and the resulting market impact by determining whether the supply will decrease during periods of high demand. Ref. [13] used a two-stage market liquidation method to alleviate economic withholding behavior. The aforementioned papers analyzed the exercise conditions and consequences of economic withholding behavior, focusing on a theoretical analysis, and did not monitor and identify economic withholding. Refs. [14,15] proposed a withholding capability return index and a distortion–withheld index to monitor and identify the economic withholding behavior of generators, respectively. Ref. [16] used the distortion–withheld index to explore the potential ability for economic withholding in the market. Ref. [17] used two dynamic withholding indicators to identify the possibility of generators exercising economic withholding. Ref. [18] proposed a capacity collusion index to monitor economic withholding behavior in power trading from a preventive perspective. These papers monitored and identified economic withholdings; however, the proposed indicators required the individual identification of all generators.

This paper uses Social network analysis (SNA) to narrow the scope of identification. SNA is a structural analysis method developed based on graph theory that studies the political, social, or economic structure between objects from the perspective of the relationship. Ref. [19] used economy, distance, carbon emissions, and other factors to build a spatial relationship network and analyzed the synergy of carbon emission networks between cities. In [20], the SNA method was shown to be an effective tool for monitoring market power in the electricity market. This paper constructs a graph about the equity relationship between generators, and based on the SNA method, the key monitoring generators are obtained, and the scope of identification is narrowed.

The logit model can identify market power abuse, such as economic withholding, in multiple fields. Ref. [21] constructed an identification model of listed financial risks of the companies based on a logit model. Ref. [22] constructed a multivariate binary logit Early Warning Model for systemic banking crises. Compared with other identification methods, the logit model can provide model explanations and obtain the impact size of various indicators [23]. The transaction data of the electricity spot market are complex and high-dimensional. This study combines variable selection methods to improve the performance of the logit model. In existing research, variable selection methods primarily include the shrinkage method, dimensionality reduction method, and smoothly clipped absolute deviation (SCAD) penalty regression method [24]. This paper adopts the SCAD penalty regression method, which can remove variables with similar characteristics, thereby eliminating the collinearity between indicators and reducing the data dimension [25].

In this paper, a method to identify the economic withholding behaviors of generators is proposed. First, the key monitoring generators are obtained through the SNA method, and the structure conduct performance (SCP) theory is used to construct an economic withholding indicator system. Then, the indicators are screened by the SCAD penalty regression method, and a SCAD-logit model is established to identify the economic withholding of generators. Finally, the confusion matrix, receiver operating characteristic (ROC) curve, and area under curve (AUC) values are used to evaluate the performance of the model.

2. Key Monitoring Generators

In some regions of China, there are a few power generation groups that have large market shares and hold multiple power plants [26]. Several power generation groups often form an interest alliance, and generators belonging to interest alliances are more likely to carry out economic withholding behavior. Moreover, it is more difficult for generators outside the interest alliance to exercise economic withholding behavior. Therefore, the focus is on the market behavior of the generators within the interest alliance.

First, an equity relationship graph $G(V,N)$ of the generators is constructed. V is the vertices set representing the generators; N is the edges set representing equity relationship between the generators. The weight $m_{ih}$ of the edge between generator i and generator h is defined as

$$m_{ih}=({\beta }_i+{\beta }_h){\displaystyle \sum _{a=1}^A{z}^a{g}_i^a{g}_h^a}$$

(1)

where $1<i\le h<Z$, Z is the total number of generators; ${\beta }_i$ and ${\beta }_h$ are the installed capacity of generator i and generator h, respectively; $z^a$ is the market share of power generation group a in the power generation market, $1\le a\le A$, where A is the total number of power generation groups; and $g_i^a$, $g_h^a$ are the shareholding ratios of generator i and generator h, respectively, in power generation group a. The weight of the equity relationship among generation groups is the product of the sum of the total shareholding ratios of all power generation groups in the market and the sum of installed capacity.

Second, cohesive subgroups analysis is used in $G(V,N)$ [27], and the $G(V,N)$ is divided into multiple subgraphs, and V is divided into subsets $V_f(f=1,2,\cdots ,F)$. In $V_f(f=1,2,\cdots ,F)$, there is a connected edge between all generators.

Third, the intermediate central potential ${\phi }_f$ of the generator subset $V_f$ is calculated, that is, the closeness degree of the generator subset $V_f$ [28]. The calculation formula for ${\phi }_f$ is as follows:

$${\phi }_f=\frac{{\displaystyle \sum _{i\in f}({\delta }_{f,\max }-{\delta }_{f,i})}}{{\tau }_f-1}$$

(2)

where ${\delta }_{f,i}$ is the betweenness centrality of generator i in the generator subset $V_f$, which can measure the closeness of generator i with other generators in the set; ${\delta }_{f,\max }$ is the maximum betweenness centrality of the generators in the set; ${\tau }_f$ is the number of generators in the set; and ${\delta }_{f,i}$ can be obtained using the following equation:

$${\delta }_{f,i}=\frac{2{\displaystyle \sum _{h\in f}{\displaystyle \sum _{v\in f}\frac{{\eta }_{hv}(i)}{{\eta }_{hv}}}}}{{\tau }_f^2-3{\tau }_f+1}$$

(3)

where ${\eta }_{hv}$ is the number of edges directly connected between generator h and generator v, and ${\eta }_{hv}(i)$ is the edges connected by the generator i between generator h and generator v.

Finally, according to the magnitude of the intermediate central potential ${\phi }_f$, the generator subset $V_f$ can be obtained. The generator subsets whose intermediate central potential exceeds the threshold are selected. The key monitoring generator $V^{*}$ is the union of the obtained generator subsets.

3. Indicator System for Identifying Generators’ Economic Withholding Behavior

Based on the SCP theory in industrial economics [29], an indicator system for identifying economic withholding behavior of the generators is constructed. In SCP theory, there is a causal relationship between market structure, behavior, and performance. To obtain the ideal market performance, it is necessary to adopt active government control, improve market structure, and regulate market behavior.

Therefore, based on the SCP theory, an indicator system for identifying economic withholding behavior of the generators is divided into three aspects: market structure, bidding strategy, and clearing result. As an established factor, the market structure reflects the characteristics of the region, determines the bidding strategy of market participants, and ultimately affects the result of market clearing. The indicator system is illustrated in Figure 1.

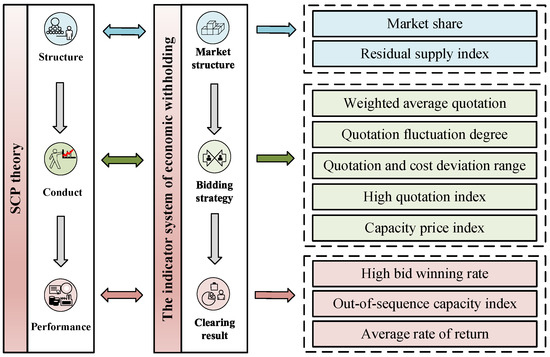
Figure 1. An indicator system for identify economic withholding behavior of the generators.

3.1. Market Structure Indicators

Market structure indicators primarily reflect the market position of market entities. Two indicators are selected: market share and residual supply index.

(1)

Market share

This indicator refers to the declared capacity of generator divided by the total declared capacity. The calculation formula is as follows:

$$S_{i,t}^{}=\frac{q_{i,t}}{q_t}\times 100\%$$

(4)

where $q_{i,t}$ is the declared capacity, and $q_t$ is the total declared capacity.

This indicator reflects the generator size. Regardless of grid congestion, as the market share of a generator increases, its conditions for using economic withholding to raise the clearing price improve [30].

(2)

Residual supply index

This indicator refers to the percentage of the difference between the total declared capacity on the market and the declared capacity of individual generators in the total market demand. The calculation is as follows:

$$I_{i,t}^{RS}=\frac{q_t-q_{i,t}}{D_t}\times 100\%$$

(5)

where $D_t$ is the total market demand at time t.

This indicator measures the position of the generator in the market. When the remaining supply index of a generator is less than 100%, it indicates that the generator is in a critical position [31]. In the case of inelastic demand prices, to meet market demand, the generator will be used for output, even if it declares a high price.

3.2. Bidding Strategy Indicators

The bidding strategy indicator reflects the bidding strategy formed by the generator during the quotation period, based on the maximization of revenue. The selected indicators are weighted average quotation, quotation fluctuation degree, quotation and cost deviation range, high quotation index, and capacity price index.

(1)

Weighted average quotation

The weighted average quotation refers to the product of the price and the capacity in the declaration curve of a generator divided by the total declared capacity [32]. The formula is as follows:

$${\overline{P}}_{i,t}=\frac{{\displaystyle \sum _{w=1}^{d_{i,t}}{P}_{i,t,w}{Q}_{i,t,w}}}{{\displaystyle \sum _{w=1}^{d_{i,t}}{Q}_{i,t,w}}}$$

(6)

where $P_{i,t,w}$ is the w-segment price quoted; $Q_{i,t,w}$ is the declared volume of the w-segment quoted price quoted, which corresponds to $P_{i,t,w}$; and $d_{i,t}$ is the total number of quotations.

The weighted average quotation reflects the quotation of the generator. If the generator exercises economic withholding behavior, the quotation sequence of this generator will generally be much higher than the market average. This indicator can be used to determine whether the generator has abnormal quotations and analyze whether the market is controlled by economic withholding.

(2)

Quotation fluctuation degree

The quotation fluctuation degree is the ratio of the weighted standard deviation of the quotation to the weighted average quotation [33]. The formula is as follows:

$${\tilde{Q}}_{i,t}=\frac{\sqrt{{\displaystyle \sum _{w=1}^d{Q}_{i,t,w}{(P_{i,t,w}-{\overline{P}}_{i,t})}^2}}}{{\overline{P}}_{i,t}}$$

(7)

The degree of quotation fluctuation can reflect changes in the generator quotes. The economic withholding behavior of generators will avoid supervision by the regulatory authorities as much as possible, so that only part of the capacity is quoted at a high price. By contrast, the other capacity quotes are normal or even lower than the market average. At this time, the average quotation of the generator may be normal, but the volatility of the quotation will increase accordingly. As the quotation volatility of generators increases, the quotation strategies adopted in different quotation segments will become more variable, and the possibility of raising the price through economic withholding will increase.

(3)

Quotation and cost deviation range

The quotation and cost deviation range is the difference between the highest quotation and marginal cost. The formula is as follows:

$$R_{i,t}={\tilde{P}}_{i,t}-C_{i,t}$$

(8)

where in Equation (8), ${\tilde{P}}_{i,t}$ is the highest quotation; and $C_{i,t}$ is the marginal cost.

This indicator reflects the difference between the highest quotation and marginal cost, which can measure the possibility of deliberately raising the quotation to exercise economic withholding behavior.

(4)

High quotation index

The high price index refers to the sum of the product of the price and the capacity in the high-price-declaration segment of the generator declaration sequence. The formula is as follows:

$$W_{i,t}={\displaystyle \sum _{w=\underset{\_}{w}}^{\overline{w}}{P}_{i,t,w}{Q}_{i,t,w}}$$

(9)

$$P_{i,t,\underset{\_}{w}-1}\le C<P_{i,t,\underset{\_}{w}}$$

(10)

$${\displaystyle \sum _{w=1}^{\overline{w}-1}{Q}_{i,t,w}}<90\%{\displaystyle \sum _{w=1}^d{Q}_{i,t,w}}\le {\displaystyle \sum _{w=1}^{\overline{w}}{Q}_{i,t,w}}$$

(11)

where C is the average power generation cost, which is usually replaced by the average on-grid price of the previous year. In fact, taking a value near the average power generation cost will not significantly impact the high quotation index. Equations (10) and (11) are the constraint conditions of $\underset{\_}{w}$ and $\overline{w}$, respectively. At time t, we take the declaration section $\underset{\_}{w}$ for generator i in the market. The declared electricity price of the section $\underset{\_}{w}$ is greater than the average power generation cost, and the sum of the declared capacity of the section $\underset{\_}{w}$ and its previous sections is less than 90% of the available capacity.

The normal operation reserve of a power system is approximately 90%. Therefore, when the load exceeds the first 90% of the declared capacity and enters the last 10% of the remaining capacity range, it indicates that the load supply is tight. At this time, the electricity spot market begins to fall short of demand and transforms into an imperfectly competitive market. Risky psychology will drive the generator to report a high price in the final declared capacity. Therefore, even if the generator reports a high price in the final remaining capacity range, it can be considered reasonable [34]. A diagram of the price declaration interval for generators is shown in Figure 2.

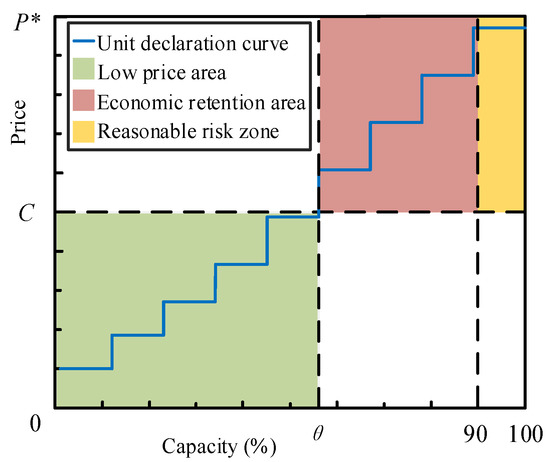
Figure 2. Diagram of the price declaration interval for generators.

In Figure 2, P* is the upper limit of the market price and $\theta$ is the value of the intersection of the quotation curve and the average power generation cost mapped to the horizontal axis.

If the high price declared in the last 10% of the remaining capacity range is not considered an economic withholding behavior, then

$$90\%{\displaystyle \sum _{w=1}^d{Q}_{i,t,w}}<{\displaystyle \sum _{w=1}^{\overline{w}}{Q}_{i,t,w}}$$

(12)

In this case, the declared capacity with respect to $\overline{w}$ needs to be revised as follows:

$$90\%{\displaystyle \sum _{w=1}^d{Q}_{i,t,w}}-{\displaystyle \sum _{w=1}^{\overline{w}-1}{Q}_{i,t,w}}$$

(13)

As the high quotation index increases, so does the possibility that the generator will exercise economic withholding behavior to raise the market-clearing price during the bidding period. However, this indicator ignores the high price of the last 10% of the capacity, which may give some generators a chance to take advantage, i.e., take the risk of reporting a high price in the last segment of the capacity and reporting a high price or not reporting a high price in the other quotation segments. Therefore, the volume price index is chosen as a supplement.

(5)

Capacity price index

This indicator is the weighted sum of the segment capacity in the generator quote data [35]. The calculation formula is as follows:

$$E_{i,t}={\displaystyle \sum _{w=1}^d\left[{\left(\frac{P_{i,t,w}}{C}\right)}^3\left(\frac{Q_{i,t,w}}{Q_{i,t,Avail}}\right)\times 100\right]}$$

(14)

where $Q_{i,t,Avail}$ is the available capacity.

Suppose that the capacity price index of the generator is large. In this case, the quotation is mostly high range. There is suspicion of raising the clearing price through economic withholding behavior.

3.3. Clearance Result Indicators

The clearance result indicators reflect the results of generator bidding and are an important basis for measuring the high profitability of generators. Three indicators are selected: high bid-winning rate, out-of-sequence capacity index, and average return rate.

(1)

High bid-winning rate

This indicator reflects the ratio of the high price quantity that has won the bid for the declared quantity of electricity. The calculation formula is as follows:

$$B_{i,t}=\frac{Q{h}_{i,t}}{Q{c}_{i,t}}$$

(15)

where $Q{h}_{i,t}$ is the electricity that generator i declared as high price and won the bid with at time t, where a price higher than the market average is still selected as the high price; and $Q{c}_{i,t}$ is the declared electricity.

The high bid-winning rate reflects the fact that generators have raised their prices of declared capacity. Regarding the identification of generator economic withholding behavior, as this indicator decreases, the behavior of part of the generator’s capacity to quote high prices and raise the clearing price becomes more obvious, and the generator is more likely to exercise economic withholding behavior.

(2)

Out-of-sequence capacity index

This indicator is the ratio of the out-of-sequence capacity of the generator to the actual declared capacity divided by the ratio of the unsuccessful capacity of the system to the capacity of participating in the quotation [36]. The calculation formula is as follows:

$$U_{i,t}=\frac{Q_{i,t}^{\mathrm{OC}}}{q_{i,t}}\times \frac{q_t}{q_t-(D_t-Q_t^{\mathrm{nbid}})}\times 100$$

(16)

where $Q_{i,t}^{\mathrm{OC}}$ is the unsuccessful power; and $Q_t^{\mathrm{nbid}}$ is the sum of the fixed output of generators that have not participated in the quotation at time t.

In an ideal electricity spot market, the out-of-sequence capacity index should be 100. Suppose that the out-of-sequence capacity index of a generator in a certain period of time is high, especially when it is higher than 100. In this case, the quotation of the generator may be high. This generator should attract the attention of the market supervision department.

(3)

Average rate of return

The average rate of return is the ratio of the overall revenue to the number of generators. The calculation formula is as follows:

$$H_{i,t}=\frac{{\displaystyle \sum _{i=1}^L{\widehat{B}}_{i,t}{Q}_{i,t}}}{L_i}$$

(17)

where ${\widehat{B}}_{i,t}$ is the bid-winning rate of generator, $Q_{i,t}$ is the bid-winning capacity, and $L_i$ is the number of generators in the generator set where generator i is located.

The average rate of return is used to measure the overall profitability of the generator subset. As the average rate of return grows larger, the more the generator subset as a whole becomes more profitable, and the possibility of the generators in the subset exercising economic withholding behavior increases.

3.4. Indicator System Architecture

The aforementioned indicators are combined to obtain a system of identifying indicators for the economic withholding of generators. An indicator system for identifying economic withholding behavior of the generators is listed in Table 1.

Table 1. An indicator system for identifying economic withholding behavior of the generators.

Irregularities	First Level Indicator	Secondary Indicators	Indicator Symbol
The economic withholding	Market structure indicators	Market share	$S_{i,t}$
		Residual supply index	$I_{i,t}^{\mathrm{RS}}$
	Bidding strategy indicators	Weighted average quotation	${\overline{P}}_{i,t}$
		Quotation fluctuation degree	${\tilde{Q}}_{i,t}$
		Quotation and cost deviation range	$R_{i,t}$
		High quotation index	$W_{i,t}$
		Capacity price index	$E_{i,t}$
	Clearance result indicators	High bid winning rate	$B_{i,t}$
		Out-of-sequence capacity index	$U_{i,t}$
		Average rate of return	$H_{i,t}$

4. Variable Selection and Model Construction

Multiple indicators are prone to dimensionality disasters, excessive calculations, and multi-collinearity during the identification process. Therefore, reducing the data dimension and removing collinearity can enhance the performance of the model.

First, the logit discrete choice model is constructed, and the SCAD penalty regression method is used to filter the indicators. Variable selection can reduce the impact of data dimensions and the collinearity [37]. Second, the SCAD-logit model is used to identify the economic withholding behavior of generators. Finally, the confusion matrix, ROC curve, and AUC values are used to evaluate the model’s performance.

4.1. Logit Discrete Choice Model

Regarding the identification results of generators, there are two behaviors: exercise and non-exercise of economic withholding. A logit discrete choice model is used to make the binary selection for generators.

A binary logit discrete choice model is established that introduces a latent variable $y_i^{\ast }$ and satisfies the following relationship:

$$\begin{array}{ll}{y}_i^{\ast }& ={\beta }_0+{\displaystyle \sum _{j=1}^J{x}_{ij}{\beta }_j}+{\epsilon }_i\\ & ={\beta }_0+\beta {\mathit{x}}_i+{\epsilon }_i\end{array}$$

(18)

where $i=1,2,\dots ,n$; $j=1,2,\dots ,J$; $x_{ij}$ is explanatory variables; ${\beta }_0$ and ${\beta }_j$ are regression coefficients; ${\epsilon }_i$ are random error terms; and the distribution function [38] is $P({\epsilon }_i\le z)=e^z/(1+e^z)$. To simplify the subsequent formula expression, we assume ${\mathit{x}}_i$ to be the indicator vector of the generator i, and $\beta$ to be the coefficient vector.

$y_i$ is a categorical variable that represents the exercise and non-exercise of economic withholding. The formula is as follows:

$$y_i=\{\begin{array}{c}0 y_i^{\ast }<0\\ 1 y_i^{\ast }\ge 0\end{array}$$

(19)

The probabilities of the generator i being judged as two types of results are as follows:

$$\begin{array}{ll}P(y_i=1)& =P(y_i^{\ast }\ge 0)\\ & =P({\epsilon }_i\ge -{\beta }_0-\beta {\mathit{x}}_i)\\ & =\frac{e^{({\beta }_0+\beta {\mathit{x}}_i)}}{1+e^{({\beta }_0+\beta {\mathit{x}}_i)}}\end{array}$$

(20)

$$\begin{array}{ll}P(y_i=0)& =1-P(y_i=1)\\ & =\frac{1}{1+e^{({\beta }_0+\beta {\mathit{x}}_i)}}\end{array}$$

(21)

The binary logit discrete choice model [39] is constructed as follows:

$$\begin{array}{ll}L[e^{({\beta }_0+\beta {\mathit{x}}_i)}]& =\ln \frac{P(y_i=1)}{P(y_i=0)}\\ & ={\beta }_0+\beta {\mathit{x}}_i\end{array}$$

(22)

4.2. SCAD-Logit Model

The SCAD penalty regression method [40] solves the multi-collinearity problem based on the idea of penalty. It can compress a smaller regression coefficient to 0 and is an approximate unbiased estimate method. It compensates for the lack of a Lasso variable selection method, which always has biased estimates and unstable results [41].

First, the log-likelihood function of the discrete choice model of (22) is as follows:

$$\begin{array}{ll}\log L({\beta }_0,\beta )& =\log {\displaystyle \prod _{i=1}^n{p}_i}\\ & ={\displaystyle \sum _{i=1}^n\log [P{(y_i=0)}^{1-y_i}P{(y_i=1)}^{y_i}]}\\ & ={\displaystyle \sum _{i=1}^n[y_i({\beta }_0+\beta {\mathit{x}}_i)-\log (1+e^{{\beta }_0+\beta {\mathit{x}}_i})]}\end{array}$$

(23)

where $p_i$ is the categorical variable probability of generator i.

Next, we combine Equation (23) and the SCAD penalty regression method to eliminate multi-collinearity and perform variable selection. According to ref [42], the aforementioned formula is considered negative, and the penalty function $p_{\lambda }({\beta }_j)$ is added to transform it into a Lagrange’s equation:

$$\widehat{\beta }=\underset{\beta }{\arg \min }[-\log L({\beta }_0,\beta )+{\displaystyle \sum _{j=1}^J{p}_{\lambda }({\beta }_j)}]$$

(24)

where $\lambda$ is the adjustment parameter, which aims to weigh the model fitting effects and the number of variables used. A suitable $\lambda$ prevents the model from falling into overfitting and enables variable selection. Generally, as the value of $\lambda$ decreases, the punishment is weaker and more variables tend to be used; as the value of $\lambda$ increases, the punishment is stronger and fewer variables are used. The penalty function $p_{\lambda }({\beta }_j)$ is defined as follows:

$$p_{\lambda }({\beta }_j)=\{\begin{array}{cc}\lambda \left|{\beta }_j\right|,& \left|{\beta }_j\right|\le \lambda \\ -\frac{{\left|{\beta }_j\right|}^2-2a\lambda \left|{\beta }_j\right|+{\lambda }^2}{2(a-1)},& \lambda <\left|{\beta }_j\right|\le a\lambda \\ \frac{(a+1){\lambda }^2}{2},& \left|{\beta }_j\right|>a\lambda \end{array}$$

(25)

where a is a constant and $a>2$. The derivative form of the aforementioned equation is as follows:

$${p^{\prime }}_{\lambda }({\beta }_j)=\lambda \left[I(\left|{\beta }_j\right|\le \lambda )+\frac{{(a\lambda -\left|{\beta }_j\right|)}_{+}}{(a-1)\lambda }I(\left|{\beta }_j\right|>\lambda )\right]\mathrm{sgn}({\beta }_j)$$

(26)

where $I(\cdot )$ is a characteristic function, $\mathrm{sgn}(\cdot )$ is a signum function, and ${(a\lambda -\left|{\beta }_j\right|)}_{+}=\max (0,a\lambda -\left|{\beta }_j\right|)$.

It can be seen from Equation (25) that when $\left|{\beta }_j\right|\le \lambda$, $\left|{p^{\prime }}_{\lambda }({\beta }_j)\right|=\lambda$, the SCAD penalty function penalizes the coefficient; when $\lambda <\left|{\beta }_j\right|\le a\lambda$, $\left|{p^{\prime }}_{\lambda }({\beta }_j)\right|=\lambda (0+\frac{{(a\lambda -\left|{\beta }_j\right|)}_{+}}{(a-1)\lambda })=\frac{{(a\lambda -\left|{\beta }_j\right|)}_{+}}{a-1}<\lambda$, which indicates that the penalty of the SCAD penalty function on the coefficient is weakened; and when $\left|{\beta }_j\right|>a\lambda$, ${p^{\prime }}_{\lambda }({\beta }_j)=0$, the SCAD penalty function cancels the penalty for the coefficient.

The choice of the penalty parameter $\lambda$ is an important part of the SCAD penalty regression method. In this paper, the K-fold cross-validation method is selected to determine $\lambda$.

The candidate set of $\lambda$ is determined, N different values of $\lambda$ are considered, and the candidate set $\mathsf{\Gamma }=({\lambda }_1,{\lambda }_2,\cdots ,{\lambda }_N)$ is obtained. The indicator data are divided into K subsets. Each time, the K−1 subsets are used as the training set, and the remaining subsets are used as the test set. In this way, there are K divisions and trainings. For the c-th division, ${\omega }_c$ is the training set and ${\psi }_c$ is the test set. We use different ${\lambda }_{\delta }(\delta =1,2,\cdots ,N)$ to perform regression analysis on the training set data and obtain the regression coefficient $\widehat{\beta }({\lambda }_{\delta })$. The obtained regression coefficient is substituted into the test set, and the value of the loss function is obtained using the following equation:

$$s_c={\displaystyle \sum _{i\in {\psi }_c}\left\{\log [1+e^{{\beta }_0+\widehat{\beta }({\lambda }_{\delta }){\mathit{x}}_i}]-y_i[{\beta }_0+\widehat{\beta }({\lambda }_{\delta }){\mathit{x}}_i]\right\}}$$

(27)

The loss function $s_c$ under different partitions is added to obtain the statistic $S_V({\lambda }_{\delta })$, and ${\lambda }_{\delta }$ is selected to minimize $S_V({\lambda }_{\delta })$ as an adjustment parameter. The equation is as follows:

$$S_V({\lambda }_{\delta })={\displaystyle \sum _{c=1}^K{s}_c}$$

(28)

In summary, based on Equation (24), the cross-validation method is used to calculate the statistics, and indicator screening is then realized. Then, according to the screening results of the SCAD penalty regression method and the binary logit model, a SCAD-logit model for the identifying economic withholding behavior of the generators is constructed. The SCAD-logit model is as follows:

$$L[P(y_i=1)]={\tilde{\beta }}_0+\tilde{\beta }{\tilde{\mathit{x}}}_i$$

(29)

where ${\tilde{\beta }}_0$ and $\tilde{\beta }$ are the indicator coefficients obtained after estimation; ${\tilde{\mathit{x}}}_i$ are the indicators obtained after screening. According to the aforementioned model, it is possible to identify whether the generator exercises economic withholding behavior and to conduct an indicator significance test.

4.3. Performance Evaluation

In this study, the confusion matrix, ROC curve, and AUC value are used to evaluate the performance of the SCAD-logit model.

(1)

Confusion matrix

The confusion matrix is a standard format used for model accuracy evaluation, as shown in Table 2.

Table 2. Confusion matrix of SCAD-logit model.

Category of Real Behavior	Category of Identify Behavior
	0	1
0	TN	FP
1	FN	TP

The SCAD-logit model is a two-classification model. Under the generator economic withholding identification task, there are four different combinations of the identify behavior and the real behavior. TP in Table 2 indicates that the real behavior is 1, and the identify behavior is 1, which means that the generator has successfully identified the economic withholding behavior. TN means that the real behavior is 0, and the identify behavior is 0; that is, it has successfully identified that the generator has not exercised economic withholding behavior. FP means that the real behavior is 0, and the identify behavior is 1, which means that the generator that has not exercised economic withholding is mistakenly identified as exercising economic withholding. FN indicates that the real behavior is 1, the identify behavior is 0, and the generator that is about to exercise economic withholding is mistakenly identified as not exercising economic withholding. The first two, TP and TN, indicate successful model identification and positively affect the supervision of the electricity spot market; the latter two, FP and FN, indicate misidentification. There is no positive effect on the supervision of the electricity spot market, and excessive supervision increases market risks.

(2)

ROC curve

The ROC curve is generally used to evaluate model identification ability as a coordinate schema analysis tool.

The two main indicators in the ROC curve are the true positive rate and the false positive rate, also called sensitivity and specificity. Generally, the false positive rate is the abscissa, and the true positive rate is its ordinate. The true positive rate formula is TP/(TP + FN), and the false-positive rate is TN/(FP + TN). For model evaluation, it is natural to expect that a high true positive rate and low false positive rate indicate success. Therefore, if the model identification ability is good, the ROC curve is close to the upper-left corner.

(3)

AUC value

The AUC value represents the area under the ROC curve. As an application of the evaluation model, its value range is between 0 and 1. Because the ROC curve is closer to the upper-left corner, the ideal value of AUC is 1, and the closer it is to 1, the better is the model identification effect [43].

4.4. SCAD-Logit Model’s Process

The SNA method is used to screen the generators to obtain a set of key monitoring generators. An indicator system for identifying economic withholding behavior is constructed using SCP theory, combined with the SCAD penalty regression method and logit discrete selection model to identify the economic withholding behavior of generators. The specific process is shown in Figure 3 and proceeds as follows:

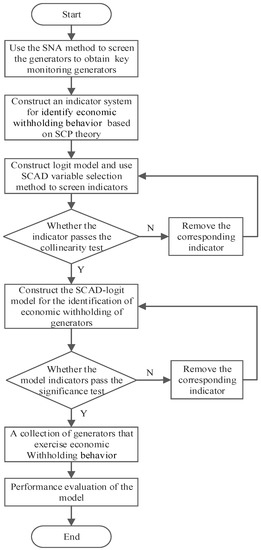
Figure 3. Flow chart of identifying the economic withholding behavior of generators.

(1)

The SNA method is used to construct an equity relationship graph $G(V,N)$ with the generator as the vertex and the equity relationship of the generators as the edge. Then, the cohesive subgroup analysis method and intermediate central potential indicator screening are used to obtain the key monitoring generators.

(2)

According to the SCP theory, an indicator system for economic withholding behavior is constructed from three aspects: market structure, bidding strategy, and clearing results.

(3)

The generator sample set and test set are constructed, the indicators values of the key monitoring generators are calculated, and dimensionless processing of the indicators data is performed. Then, the logit discrete selection model is established. The SCAD penalty regression method and collinearity test are used to select indicators and eliminate collinearity indicators.

(4)

Indicators that pass the collinearity test are selected and the SCAD-logit model is established to identify the economic withholding based on the sample set data. Then, a significance test of each indicator in the model is carried out to verify its explanatory effect on the identification of economic withholding behavior. If the significance test is not passed, the corresponding indicators are eliminated; otherwise, we proceed to the next step.

(5)

The SCAD-logit model is used to identify the test set data and obtain generators that exercise economic withholding behavior.

(6)

The confusion matrix, ROC curve, and AUC value are used to evaluate the model’s performance.

5. Case Analysis

In this section, the data of the electricity spot market are selected and the 3-day transaction data of 216 generators are employed as the identification objective.

5.1. Key Monitoring Generators Selection

Based on the equity structure information of 216 generators, the equity data are calculated using Equation (1) to obtain the adjacency matrix M and normalize it. The results are shown in Table 3.

Table 3. Data of adjacency matrix M.

Serial Number of Generators	1	2	3	4	……	216
1	1.000	0.851	0.694	0.383	……	0.887
2	0.851	1.000	0.783	0.376	……	0.007
……	……	……	……	……	……	……
88	0.304	0.926	0.167	0.554	……	0.574
89	0.415	0.854	0.661	0.836	……	0.421
……	……	……	……	……	……	……
215	0.467	0.152	0.881	0.027	……	0.513
216	0.887	0.007	0.904	0.903	……	1.000

M is the adjacency matrix constructed by the weight of the equity relationship of the generators. The data of adjacency matrix M in Table 3 are imported into the Ucinet software. The equity relationship between generators is visualized to generate a graph $G(V,N)$ for the equity analysis. Figure 4 is a schematic diagram of part of the graph $G(V,N)$. The equity relationship data of the generator are shown in Table A2.

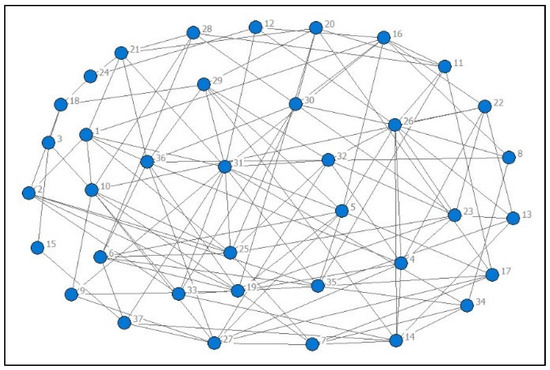
Figure 4. Graph of equity analysis (partial).

The SNA method is used to conduct cohesive subgroup analysis on the generator equity analysis network and obtain multiple generator subsets $V_f(f=1,2,\cdots ,F)$. Based on Equations (2) and (3), the intermediate central potential of the generator is calculated. The resulting fleet is sorted according to the magnitude of the intermediate central potential. The lower quartile of the intermediate central potential ${\phi }_f$ is used as the threshold. Generators larger than the threshold are selected. The union of the obtained generators is the key monitoring generators $V^{*}$. A total of 168 key monitoring generators are screened.

5.2. Indicators Selection

Based on the obtained 168 monitoring generators, the data from 96 clearings per day are selected as the experiment cycle. The indicators listed in the indicator system to identify economic withholding behavior based on transaction data in the selected electricity spot market are calculated. Then, min-max dimensionless processing is performed on the generator indicator data as the basic data for subsequent indicator selection. The proportion of the sample set that exercises economic withholding behavior and the part that does not exercise it is considerably uneven in the sample data. A total of 500 samples are randomly selected from the exercise and non-exercise economic withholding behavior. The indicator data are shown in Table A1.

The 10-fold cross-validation method is used based on the SCAD penalty regression method. Different mean square errors are obtained from different $\lambda$ values as the basis. Specific results as shown in Figure 5.

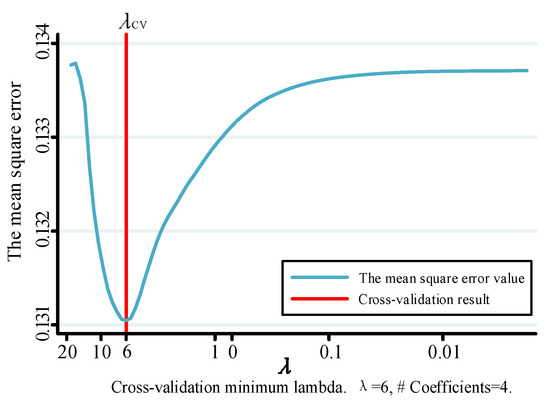
Figure 5. Cross-validation effect chart.

In Figure 5, the vertical and horizontal coordinates represent the mean square error and $\lambda$ values, respectively. The mean square error changes with changes of $\lambda$. When $\lambda =6$, the error is the smallest, and there are four indicators whose coefficients are not 0.

To show the process of indicator selection more intuitively, the effect diagram of the change in each indicator coefficient with the penalty parameter is shown in Figure 6.

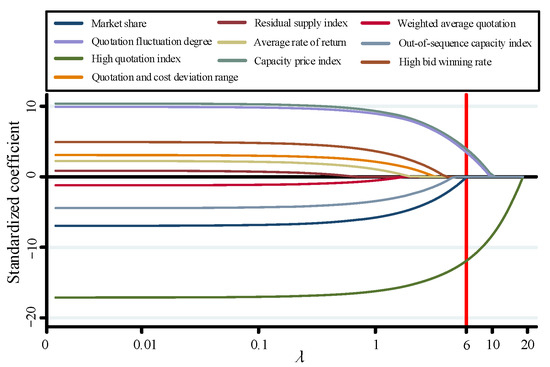
Figure 6. Effect diagram of change in indicators with the value of λ.

In Figure 6, the ordinate is the indicators coefficient, the abscissa is the value of $\lambda$, and the red vertical line is the cross-validation result, that is, $\lambda =6$. The indicators change dynamically with $\lambda$. When $\lambda$ is 0, the penalty function $p_{\lambda }({\beta }_j)$ is the smallest, and all indicators have not been filtered out; as $\lambda$ increases, the indicator coefficients gradually approach zero and finally stabilize at zero, thus satisfying the expected purpose of indicator selection.

The indicator selection results are obtained, and a collinearity test is carried out among the indicators. The results are listed in Table 4.

Table 4. Indicator selection results and collinearity test.

Indicators	Variance Inflation Factor	Tolerance
Quotation fluctuation degree	1.02	0.983
Market share	1.01	0.986
High quotation index	1.01	0.993
Capacity price index	1.00	0.997

If the selected indicator variance inflation factor is greater than 10 or the tolerance is less than 0.1, it indicates collinearity between the indicators. From the results of the collinearity test in Table 5, the variance inflation factors of the quotation fluctuation degree, market share, high quotation index, and capacity price index are all less than 10, and the tolerance of all is greater than 0.1; hence, there is no collinearity in the selected indicators.

Table 5. SCAD-logit model estimation results.

Indicators	Coefficients	Wald	Significance
Quotation fluctuation degree	3.718	58.64	0.00
Market share	2.739	31.30	0.00
High quotation index	52.233	25.68	0.00
Capacity price index	2.625	35.23	0.00
Constant	−6.223	105.87	0.00

In summary, the selected indicators are the quotation fluctuation degree, market share, high quotation index, and capacity price index. The economic withholding behavior identification model is constructed based on the four indicators obtained.

5.3. Identification Results

Based on the results of indicator selection, the SCAD-logit model is established using the quotation fluctuation degree, market share, high quotation index, and capacity price index, and the significance of the model is tested. The estimated results are presented in Table 5.

Table 5 shows that the quotation fluctuation degree, market share, high quotation index, and capacity price index all passed the significance test at a significance level of 0.05. The four indicators in the model all have a significant linear relationship with economic withholding and prove that the built model can have a good effect on identifying the economic withholding behavior. The SCAD-logit model for economic withholding identification of generators is as follows:

$$\begin{array}{ll}L[P(y_i=1)]& ={\tilde{\beta }}_0+\tilde{\beta }{\tilde{\mathit{x}}}_i\\ & =-6.223+3.718{\tilde{Q}}_{i,t}+2.739S_{i,t}\\ & +52.233W_{i,t}+2.625E_{i,t}\end{array}$$

(30)

The obtained model shows that the quotation fluctuation degree, market share, high quotation index, and capacity price index all positively impact the economic withholding behavior of generators. The obtained indicator is consistent with the behavioral mechanism of the economic withholding of generators. As the aforementioned four indicators increase, the more favorable factors for the economic withholding behavior of generators become, and the possibility of withholding increases.

The coefficient of the high quotation index is the largest, among the regression coefficients of the obtained model, indicating that it has the largest contribution to the identification of generator economic withholding behavior. Under the condition that the electricity spot market adopts the unified clearing of the marginal electricity price, it is reasonable for the generator to declare a high price for a part of the electricity to benefit itself. Similarly, the degree of quotation fluctuation also has a greater marginal contribution to economic withholding. During the quotation period, generators need to adopt various quotation strategies to raise the market-clearing price, so the monitoring quotation fluctuation degree is positive for economic withholding behavior. The last two indicators, the marginal contribution of market share and capacity price index, are smaller than the high quotation index and quotation fluctuation degree. However, they also positively impact economic withholding behavior, which cannot be ignored.

Therefore, the power market supervision department can monitor the degree of quotation fluctuation, market share, high quotation index, and capacity price index. Moreover, the regression coefficients of the aforementioned four indicators are all positive; that is, all have a positive impact on economic withholding behavior. Therefore, economic withholding can be effectively controlled by suppressing the corresponding generator indicators.

Based on the established model, to identify a certain transaction process from 168 generators in the electricity spot market in the region, the probability of economic withholding behavior of the generators is as follows:

$$\begin{array}{ll}P(y_i=1)& =\frac{1}{1+e^{-({\tilde{\beta }}_0+\tilde{\beta }{\tilde{\mathit{x}}}_{i,t})}}\\ & =\frac{1}{1+e^{-(-6.223+3.718{\tilde{Q}}_{i,t}+2.739S_{i,t}+52.233W_{i,t}+2.625E_{i,t})}}\end{array}$$

(31)

This case assumes that when the probability of economic withholding behavior of the generator is $P(y_i=1)\ge 0.5$, the generator is considered to exercise economic withholding behavior; otherwise, the generator is not considered to exercise economic withholding behavior. The identification results of economic withholding of generators are shown in Table 6. More indicator data and identification results are shown in Table A3.

Table 6. Identification results of economic withholding of generators.

Identification Category	0	1
Number of generators	162	6

The indicator data of the six generators are analyzed, and the relevant data are shown in Table 7.

Table 7. Indicator data for generators that exercise economic withholding behavior.

Serial Number of Generators	Quotation Fluctuation Degree	Market Share	High Quotation Index	Capacity Price Index
1	0.786	0.406	0.822	0.479
2	0.985	0.667	0.436	0.266
3	0.739	0.880	0.046	0.975
4	0.707	0.800	0.046	0.715
5	0.942	0.903	0.039	0.803
6	0.927	0.418	0.043	0.973

The impact of the four indicators on economic withholding behavior is further analyzed. Further analyze the changes in the economic withholding probability. The results are shown in Figure 7.

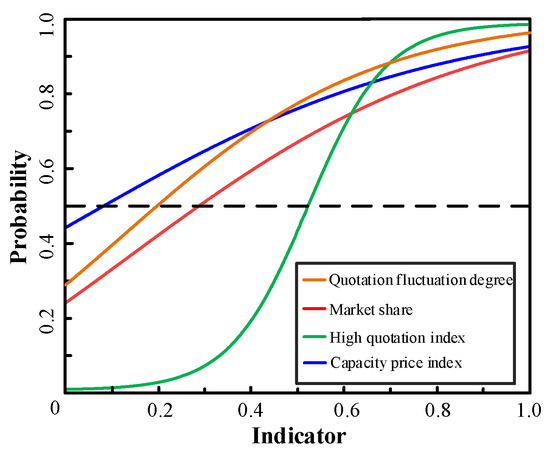
Figure 7. Impact of various indicators on the economic withholding probability of generators.

Figure 7 shows that the degree of quotation fluctuation, market share, high quotation index, and capacity price index have an important impact on the economic withholding probability. The probability increases with the dynamic changes in various indicators until it reaches a peak. The slope of the curve in descending order is the high quotation index, quotation fluctuation degree, market share, and capacity price index, and the marginal contributions also increase sequentially, when the probability is 0.5, which is consistent with the results obtained from the aforementioned model analysis.

5.4. Performance Results of the Model

To evaluate the performance of the SCAD-logit model, it is compared with the ordinary logit model, and Lasso-logit. The aforementioned sample set is used, 70% of which is randomly selected as the training set, and the remaining 30% is used as the test set. The aforementioned model is run 100 times. The overall correct rate, mean, and standard deviation of the FP and FN errors in the confusion matrix are calculated. The results of the performance evaluation of the model are presented in Table 8.

Table 8. Results of performance evaluation.

Evaluation Item		SCAD-Logit Model		Ordinary Logit Model		Lasso-Logit Model
		Training Set	Testing Set	Training Set	Testing Set	Training Set	Testing Set
overall correct rate	mean	0.9683	0.9675	0.9543	0.9538	0.9586	0.9574
	standard deviation	0.001	0.0014	0.0165	0.0196	0.0127	0.0143
FP	mean	0.0356	0.0354	0.0534	0.0514	0.0437	0.0476
	standard deviation	0.0021	0.0015	0.0227	0.0247	0.0138	0.0146
FN	mean	0.0278	0.0314	0.0347	0.0386	0.0293	0.0349
	standard deviation	0.0007	0.0012	0.0152	0.0214	0.0085	0.0128

Table 8 shows that for the evaluation results of the overall correct rate, FP, and FN, the results of the SCAD-logit model are better for both the training set and the testing set. The overall correct rate is higher, and the error rates of FP and FN are lower. At the same time, the standard deviation of the SCAD-logit model is also smaller, indicating that the SCAD-logit model is better than the ordinary logit model and Lasso-logit model in terms of stability.

The ROC curve is compared to verify the effectiveness of the model. The results are shown in Figure 8.

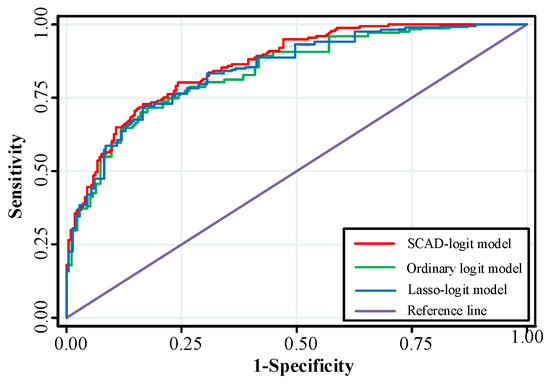
Figure 8. ROC curves.

Figure 8 shows that the model performance of the SCAD-logit model is better, because its ROC curve is closer to the upper left corner of the graph. Next, we calculate the area under the ROC curve and the AUC value. The results are listed in Table 9.

Table 9. AUC values.

Model	AUC Value
SCAD-logit model	0.9274
Ordinary logit model	0.8489
Lasso-logit model	0.8837

When the AUC value of the model increases, the performance of the model and accuracy are improved. Table 9 shows that the performance of the SCAD-logit model is better, as it is 9.25% higher than that of the ordinary logit model and 4.96% higher than that of the Lasso-logit model.

Based on the aforementioned analysis, the performance of the SCAD-logit model is superior to that of ordinary logit model and Lasso-logit model, and the result is consistent with that of a previous study. The SCAD-logit model uses the SCAD penalty regression method to compress some collinearity indicators coefficients to 0. The interference of some weakly correlated indicators on the model is avoided, thereby improving the performance of the model.

This method can identify the generators with economic withholding behavior. After excluding the generators that exercise economic withholding, then recalculating the quotation fluctuation degree, the high quotation index and the capacity price index. The quotation fluctuation degree ${\tilde{Q}}_{i,t}$ is reduced by an average of 6.7%, the high quotation index $W_{i,t}$ is reduced by an average of 19.4%, the capacity price index $E_{i,t}$ is reduced by an average of 8.2%. Therefore, the method can regulate the market order, make the market run fairly and justly, and prevent the electricity price from overflowing the upper limit. Market players can compete fairly and consumer property losses are avoided.

6. Conclusions

As the pilot electricity spot market has increased in recent years, market data have gradually become high-dimensional and complex. This study uses the SNA method to screen generators, based on the SCP theory, to construct an indicator system for identifying economic withholding behavior; it integrates the SCAD penalty regression method into the logit discrete choice model; and proposes a SCAD-logit identification method based on economic withholding behavior of generators. The main conclusions are as follows:

(1)

Facing complex and high-dimensional data in the electricity spot market, the SNA method can use cohesive subgroup analysis and intermediate central potential to screen out key generators, narrowing the search scope for data analysis and daily supervision. The SCAD penalty regression method can filter and obtain important identification indicators of economic withholding from various indicators, such as market share, quotation fluctuation degree, high quotation index, and capacity price index. Moreover, the collinearity and weakly related indicators are eliminated, thereby reducing the data dimension and the supervision cost of market managers.

(2)

The identification method is used in the electricity spot market, and the generators that exercise economic withholding are identified with a correct rate of 96.83%.

(3)

The SCAD-logit model clearly shows the contribution of each indicator to the identification of economic withholding behavior. Furthermore, effective control of economic withholding can be achieved by restricting relevant indicators.

Electricity markets around the world have great differences in market structure, bidding strategy and clearing mechanism. Therefore, when using this method, it is necessary to modify the indicator system to identify economic withholding behavior of the generators according to local characteristics. Moreover, with the further development of the electricity market, the economic withholding behavior of generators will become more concealed and challenging to be monitored. Other factors need to be considered according to the particularity of the region, such as network structure and congestion transmission congestions, profit margins of the generation groups and strategic biddings, etc.