Abstract
A new optimization technique is proposed for solving optimization problems having single and multiple objectives, with objective functions such as generation cost, loss, and severity value. This algorithm was developed to satisfy the constraints, such as OPF constraints, and practical constraints, such as ram rate limits. Single and multi-objective optimization problems were implemented with the proposed hybrid fruit fly-based artificial bee colony (HFABC) algorithm and the non-dominated sorting hybrid fruit fly-based artificial bee colony (NSHFABC) algorithm. HFABC is a hybrid model of the fruit fly and ABC algorithms. Selecting the user choice-based solution from the Pareto set by the proposed NSHFABC algorithm is performed by a fuzzy decision-based mechanism. The proposed HFABC method for single-objective optimization was analyzed using the Himmelblau test function, Booth’s test function, and IEEE 30 and IEEE 118 bus standard test systems. The proposed NSHFABC method for multi-objective optimization was analyzed using Schaffer1, Schaffer2, and Kursawe test functions, and the IEEE 30 bus test system. The obtained results of the proposed methods were compared with the existing literature.
1. Introduction
Recently, the operation, control, and management of power systems have become more complicated and difficult. The system severity value should be minimized to improve power system security and to avoid line overloading, bus voltage limit violations, and finally, line outage conditions. The transmission of bulk power and the difference in the loading pattern from the originally planned pattern affect the complexity of the power monitoring system. Hence, to secure and stabilize the operation of a power system, optimal power flow (OPF) performs a crucial role.
Optimization of the considered objective functions, such as generation cost, transmission loss, and severity value minimization, is the first target of the OPF problem. Recently, many heuristic optimization techniques have been proposed to solve the problems in power systems, such as the cost of power generation, transmission power loss, and severity value minimization. A hybrid fruit fly algorithm was previously utilized for solving multi-objective optimization in the presence of practical constraints, including the ramp rate limit and prohibited operating zone [1]. A hybrid cuckoo search algorithm was analyzed and used to converge the problem [2]. Using the firefly algorithm, the OPF solution was analyzed for cost, loss, and emission objective functions that were not optimized optimally [3]. To improve power system security, a multi-objective multi-population ant colony algorithm was used [4]. A dynamic population-based ABC algorithm was used for solving the OPF problem. The results were compared to the NSGA-II and multi-objective ABC methods [5]. The linear OPF method was used to linearize AC load flow equations to optimize generator dispatch. This LOPF method is seven times faster than the existing methods [6]. To test the TLBO algorithm in this article, multi-objective OPF problems were solved. Standard 9-bus and 26-bus systems were used to test the performance of the proposed method. Cost, power loss, and voltage deviation minimization functions were used to optimize the power system problems. The results were compared with those of a mixed-integer PSO algorithm [7]. The fruit fly algorithm for solving the engineering optimization problem proves that the convergence of the optimal problem is less than that of the ABC algorithm [8]. For this purpose, a knowledge-guided MOFOA was proposed for simultaneously minimizing the cost and the makespan. This non-dominated sorting approach has been used to optimize multi-objective problems [9]. In this improved fruit fly method for solving engineering design problems, the results were compared with existing GA, PSO, and DSLC-FOA methods [10]. The basic MGWO was modified using a reproduction operator and by adding the two-archive concept. It was then used to solve the multi-objective reactive power dispatch problem [11]. This hybrid multi-objective genetic algorithm was used to reduce the computational cost of OPF calculations [12]. The artificial bee colony with firefly (ABC-FF) algorithm was used for solving the optimal reactive dispatch problem [13] and the novel quasi-oppositional modified Jaya (QOMJaya) algorithm was used for solving the multi-objective OPF problems [14]. The sine–cosine algorithm was used for solving the OPF problems [15] and the multi-objective spotted hyena optimizer was used for solving multi-objective optimization problems [16]. The firefly algorithm was proposed for solving optimization problems [17]. The moth swarm algorithm was used for solving the OPF problem [18]. Convexified multi-objective models for optimal power flow were used to minimize the objective functions [19]. The performance of the tree seed algorithm used to solve the OPF problem was tested using two standard test systems [20]. A heuristic Fuzzy Adaptive Heterogeneous Comprehensive-Learning Particle Swarm Optimization algorithm was used to derive optimal reactive power dispatch solutions [21] and the Shuffled Frog Leaping optimization technique was used to solve the OPF problem with the incorporation of FACTS controllers [22]. Authors have described different optimization techniques, such as PSO, ABC, and NSGA-II, to solve multi-objective optimization problems in different applications [23,24,25,26,27,28]. For solving the single-objective optimization problem, the social spider optimization algorithm was used [29]. The PSO algorithm was used for solving the OPF problems with and without FACTS controllers [30].
In the above literature, several single and multi-objective optimization algorithms have been described. In the current study, the authors did not consider practical constraints, or the severity of the function under abnormal conditions, such as line outage conditions. We hybridized the considered algorithms to enhance the potential of the proposed algorithm. In this paper, we propose a novel hybrid fruit fly-based artificial bee colony (HFABC) algorithm to optimize the objective parameters. In the past, multi-objective optimization problems were solved using the weighted sum and the constraint method. In this study, a non-dominated sorting hybrid fruit fly-based artificial bee colony (NSHFABC) algorithm is proposed. The proposed algorithm was used for solving different standard test functions, in addition to the standard electrical IEEE 30 bus system. The optimal result obtained from the proposed method was compared with the existing literature results.
In this paper, Section 2 and Section 3 describe the problem formulation and objective functions, respectively. Section 4 describes the proposed HFABC algorithm, Section 5 describes the multi-objective control strategy, and Section 6 presents results and analysis for single and multi-objective optimization problem solutions.
2. Problem Formulation
The problem formulation of a multi-objective OPF consists of two components, namely, the objective function and the constraints, such as equality, inequality, and the ramp rate limit [1].
Ramp Rate Limit
Here, generator ramp rate limits are considered because, in a thermal power plant, the generator power output cannot change by more than a certain amount:
where is the power generation of the ith unit in the previous hour. and are the down and up ramp rate limits of the ith unit, respectively.
3. Objective Functions
In this paper, the main aim is to individually and simultaneously minimize the objectives. We consider the three objective functions to be generation fuel cost, transmission power loss, and severity value minimization. The considered objective functions are described as follows.
3.1. Generation Fuel Cost Minimization
The generation fuel cost quadratic expression is .
The total fuel cost of generation for all generator units can be mathematically expressed as:
where , , and are the coefficients of cost for the ith unit.
3.2. Transmission Loss Minimization
This objective can be written as:
where is the real power loss in the ith line. is the conduction of the line between buses and ; and are the magnitude and angle of voltage of the mth and nth buses, respectively.
3.3. Severity Value Minimization
Minimization of the bus voltages limits the violations under contingency conditions and enhances system security. Here, to increase the protection of the electrical power system, the value of the system severity function must be minimized.
The severity function can be written as:
where , are the lines and buses, respectively. and are the apparent powers of the ith line. and are the nominal and present voltage values, respectively. and are two coefficients.
4. Hybrid Fruit Fly-Based Artificial Bee Colony (HFABC)
By combining the ABC and fruit fly algorithms, the advantages of the ABC and fruit fly techniques can be inherited. The main drawback of the ABC algorithm is the untimely convergence in the search period. As a result, the desired accuracy of the optimal value may not be achieved. By hybridizing with the fruit fly algorithm, this problem can be overcome and the accuracy of the optimal value can be improved. Both the artificial bee colony and fruit fly algorithms are worth discovering in the search space. HFABC was developed to take advantage of the benefits of both the ABC and fruit fly algorithms. HFABC begins with the initial population and updates the solution by employing bees in the ABC, and then follows the mechanism of fruit fly optimization.
The proposed HFABC algorithm has five phases; initialization, the employed bee phase, the Osphersis foraging phase, the vision foraging phase, and stopping criteria.
- Step-1: Initialization
Start with a random selection using the following equation:
where λ is [0, 1], N represents the food sources, and D is the dimensionality.
- Step-2: Employed bee phase
Initially, the solution of the employed bee is copied to the new candidate solution . The solution is updated using Equation (5):
where is a random number between [−1, 1], and is taken as unity.
- Step-3: Osphersis foraging phase
Around the current fruit fly location, the population of food sources is generated randomly as Δ (randomly initialized swarm location), where the generated food sources are given by:
These food sources are within a radius of 1. The dynamically searched radius can be altered for the optimal solution with the iteration number, which is given by:
- Step-4: Vision foraging phase
The fruit fly follows a greedy selection procedure in which discovery of the best food source having a low value of fitness is given by:
where is superior to the current location. If it is the best position, then the new position location is updated; otherwise, there will be no change.
- Step-5: Stop Off Criteria
Stop the process when the number of generations equals the set iteration count; else, go to Step-2 and repeat until the set iteration count is reached.
5. Multi-Objective Control Strategy
To solve the multi-objective problem, the proposed non-dominated sorting hybrid fruit fly-based artificial bee colony (NSHFABC) algorithm was implemented. The steps for the proposed NSHFABC are detailed in the flow chart depicted in Figure 1. The non-dominated sorting and fuzzy decision-making process is given in [2].
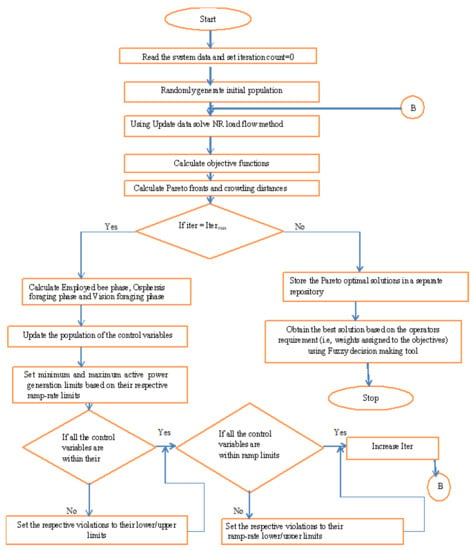
Figure 1.
Flow chart of the proposed strategy.
Decision Variables
The IEEE 30 bus test system was contemplated for testing the potency of the proposed algorithms. The considered system has 41 transmission lines and 18 control variables, namely 6 active power generators, 6 generator voltage magnitudes, 2 shunt compensators, and 4 tap setting transformers.
6. Results and Analysis
The obtained results of the Himmelblau function, Booth’s function, and the power system standard IEEE 30 bus and IEEE 118 bus test systems for single-objective optimization, and SCH1, SCH2, and IEEE 30 bus systems for multi-objective optimization, were used to validate the proposed methods. For the test system, individual single objectives were used for optimization by implementing the proposed HFABC, and multi-objective optimization was simultaneously implemented using the proposed NSHFABC algorithms. The input parameters for the test examples are tabulated in Table 1.

Table 1.
Input parameters for test examples.
6.1. Single-Objective Optimization
6.1.1. Himmelblau Test Function
Initially, the proposed HFABC algorithm was applied to the Himmelblau test function, and then applied to Booth’s function, as described in Section 6.1.2, to test the effectiveness of the proposed method.
The Himmelblau function equation is expressed as:
For the Himmelblau function, solutions are obtained using the existing genetic algorithm (GA), particle swarm optimization (PSO), artificial bee colony (ABC), and the proposed hybrid fruit fly-based artificial bee colony (HFABC) techniques. A comparison of the optimal solution for the Himmelblau function is shown in Table 2. Table 2 shows that the proposed method results in a superior solution in comparison to that of the existing methods, and the values of parameters (x1, x2) obtained using the proposed HFABC method are improved compared to those of the existing GA, PSO, and ABC methods. The function value is also lower. The computing time in the proposed HFABC method is 0.4326 s, whereas that in the existing PSO and ABC algorithms is 4.1726 and 2.5948 s, respectively; these values are greater than those of the proposed method. From Table 2, the function values for GA, PSO, ABC, and HFABC are 1.000 × 10−3, 0.004287118, 8.2451 × 10−4, and 2.0229 × 10−6, respectively. It is evident that the proposed method function value is minimized effectively. The standard deviation is 1.7288, and 0.788 for the ABC and the proposed HFABC methods, respectively. For the Himmelblau function, the x1 and x2 values are 3.0 and 2.0, respectively. The proposed method variable values are exactly the same as those of the standard test function values. From the above statistical analysis, it is concluded that the proposed method is better than those of the existing literature.

Table 2.
Comparison of the optimal solution for the Himmelblau function.
The convergence characteristic of the Himmelblau test function is depicted in Figure 2, which shows its iteration starts at a good function value and the rate of convergence is faster for the proposed method than that of the existing literature. This indicates that the proposed HFABC is superior to the existing method.
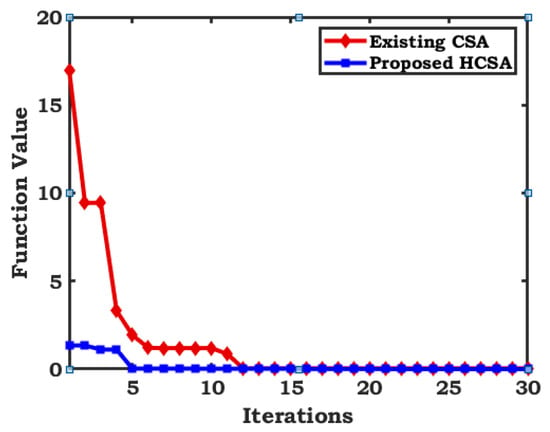
Figure 2.
Convergence characteristic of the Himmelblau function.
6.1.2. Booth’s Test Function
The second example considered is Booth’s function. The Booth function equation is given by:
The solution for the function was obtained by the existing PSO, CSA, and ABC methods, and the proposed HFABC method. The optimal solutions obtained by the various methods for Booth’s function are depicted in Table 3.

Table 3.
Comparison of the optimal solution for Booth’s function.
From Table 3, it is observed that the function values are 0.00029, 0.00020, 2.9285 × 10−7, and 1.6234 × 10−12, for PSO, CSA, ABC, and HFABC, respectively. The standard deviation is 0.086 and 0.035 for the ABC and proposed HFABC methods, respectively. The computation times are 8.23299, 6.9547, 2.12912, and 0.5297 s, respectively, for PSO, CSA, ABC, and HFABC. From these statistical analyses, the proposed method yields a better value compared to that of the existing methods.
From Figure 3, it is noticed that the proposed HFABC provides a better value and convergence occurs in fewer iterations in comparison to the existing ABC method.
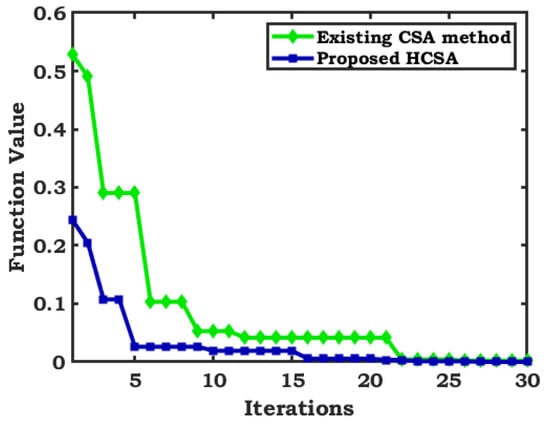
Figure 3.
Convergence characteristic of Booth’s function.
6.1.3. Electrical IEEE 30 Bus Test System
This system was contemplated for validating the proposed HFABC technique. The system data were taken from [32,33,34].
In this analysis, the considered objectives were solved using the proposed method with two cases: Case-A, without consideration of the ramp rate limit; and Case-B, with consideration of the ramp rate limit.
The summary of the test results is tabulated in Table 4. It is seen that, for the generation fuel cost minimization, Case-A yields lower values compared to Case-B; this is because of the ramp rate limit. Similarly, transmission loss and severity values are also increased with the ramp rate limit. The restriction of ramp rate limits on power generation leads to the rescheduling of the generators by changing their generation values. Hence, the total generation, power loss, and severity of the system is varied.

Table 4.
Comparison of the OPF solution for the IEEE 30 bus system.
The proposed method results are corroborated with the current literature methods and presented in Table 5. The proposed HFABC technique is superior compared to the existing methods.

Table 5.
Variations in OPF results for generation fuel cost, transmission power loss, and severity objectives for Case-A.
6.1.4. Electrical IEEE 118 Bus Test System
To validate the proposed method, the IEEE 118 bus system was taken into consideration. This system has 77 control variables and comprises 54 generators, 9 tap changing transformers, 186 transmission lines, and 14 VAR compensators. A comparison of the generation cost and total power loss obtained by the proposed method and different existing optimization methods is tabulated in Table 6. The proposed method is superior in comparison to existing methods. As per the simulation results, the computational time of the proposed method is 50 s, and the number of iterations to converge the control parameters is 30. Generator voltage profiles are better compared to those of the existing literature.

Table 6.
Validation of the proposed method with the literature for the IEEE 118 bus system.
6.2. Multi-Objective Optimization
The proposed non-dominated sorting hybrid fruit fly artificial bee colony (NSHFABC) method was utilized for the multi-objective optimization problem solutions. To validate the implementation of the proposed NSHFABC method, standard test functions, such as the Schaffer1, Schaffer2, and Kursawe functions, and the IEEE 30 bus system, were considered. In this problem, weights were taken equally for each objective function. In this research, for the multi-objective function minimization, and weights of all the considered functions were taken equally, at 50%, for the adapted setting for the proposed NSHFABC.
6.2.1. Schaffer1 (SCH1) function
The first multi-objective test function considered was the Schaffer function (SCH1). This is given by:
The multi-objective total generated Pareto front, best Pareto front, and selected Pareto fronts are shown in Figure 4 for the SCH1 function.
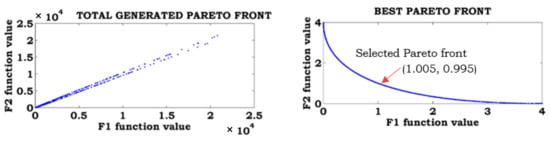
Figure 4.
Multi-objective Pareto front solutions for the SCH1 function.
From Figure 4, the best solution for the given objective functions by implementing the fuzzy decision tool for the first function is 1.005 and for the second function is 0.995.
6.2.2. Schaffer2 (SCH2) Function
Similar to the SCH1 analysis, the proposed method was analyzed for the Schaffer2 function (SCH2). The SCH2 function is given by:
The proposed method was analyzed with the SCH2 function, considering equal weights for the objectives. The total generated Pareto front, best Pareto front, and selected Pareto fronts are shown in Figure 5. From this figure, the best solution for the SCH2 function is 0, 1.
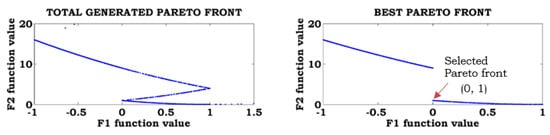
Figure 5.
Multi-objective Pareto front solutions for the SCH2 function.
6.2.3. Kursawe Function
The third example considered was the Kursawe function. The Kursawe function is given by:
The proposed method was applied to the Kursawe function, considering equal weights for the objectives. The total Pareto front, best Pareto front, and marked selected Pareto fronts are shown in Figure 6. From this figure, the best solution for the Kursawe function is −14.644, −11.379.
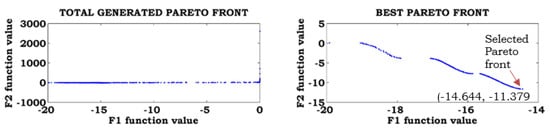
Figure 6.
Pareto front solutions for the Kursawe function.
6.2.4. IEEE 30 Bus Test Systems
To extend the effectiveness of the proposed NSHFABC method, the IEEE 30 bus test system was considered, with and without ramp rate limits, for different objective function combinations, as follows:
- Case-4: Cost–Loss combination
- Case-5: Cost–Severity combination
- Case-6: Loss–Severity combination
- Case-7: Cost–Loss–Severity combination
Optimal decision variables using multi-objective optimization for the IEEE 30 bus system are given in Table 7. It is shown that the combination of objective function values is increased by considering the ramp rate limit, compared to without the ramp rate limit. Validations of the proposed NSHFABC OPF results are given in Table 8. These data show that the cost and losses are lower in the proposed method compared with those of the existing methods.

Table 7.
Multi-objective OPF results for all the considered cases.

Table 8.
Comparison of the existing and proposed methods for Case-4.
The total Pareto generated front, best Pareto front, and preferred Pareto front are based on the user requirements obtained from the fuzzy decision approach for different combinations of the objective functions without consideration of ramp rate limits (Case-A) and with consideration of ramp rate limits (Case-B), as shown in Figure 7, Figure 8, Figure 9, Figure 10, Figure 11 and Figure 12. To show the effects of ramp rate limits on the total generated solutions, the best Pareto and preferred Pareto fronts for equal weights of the objective functions are shown in separate figures. From these figures, it can be noted that the function values are increased by considering ramp rate limits, compared to without consideration of ramp rate limits.
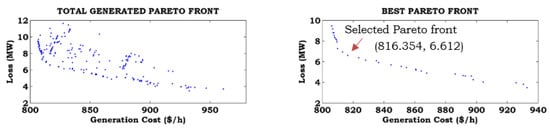
Figure 7.
Best Pareto optimal solution for Case-4 combined with Case-A.
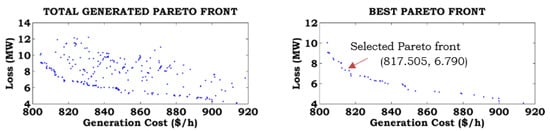
Figure 8.
Best Pareto optimal solution for Case-4 combined with Case-B.
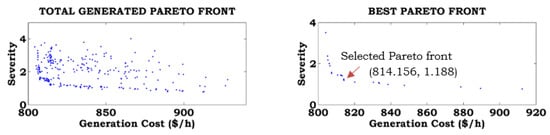
Figure 9.
Best Pareto optimal solution for Case-5 combined with Case-A.
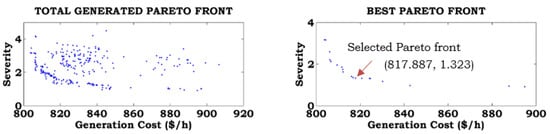
Figure 10.
Best Pareto optimal solution for Case-5 combined with Case-B.
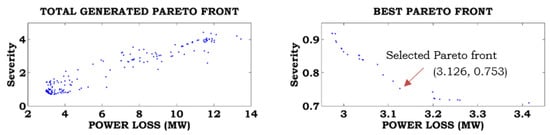
Figure 11.
Best Pareto optimal solution for Case-6 combined with Case-A.
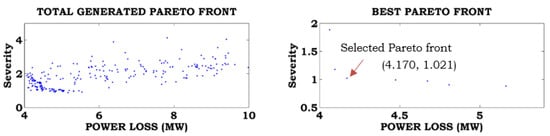
Figure 12.
Best Pareto optimal solution for Case-6 combined with Case-B.
7. Conclusions
In this study, a novel non-dominated sorting hybrid fruit fly-based artificial bee colony (NSHFABC) algorithm was designed for solving multi-objective optimization problems considering equality, inequality, ramp rate limits, and power system security constraints. To validate the proposed methods, standard test functions, such as the Himmelblau test function, Booth’s test function, the Schaffer1 (SCH1) function, the Schaffer2 (SCH2) function, the Kursawe function, and the standard IEEE 30 bus system, were tested. The Himmelblau function value using the proposed method was 2.0229 × 10−6, and the time taken to reach the optimal value was 0.4326 s; this compares to the time of the existing method of 4.6052 s. The Booth function value was 1.6234 × 10−12 and the time to reach the optimal value was 0.5297 s. The IEEE 30 bus system generation cost was 800.212 USD/h and 802.922 USD/h without and with ramp limits, respectively. Similarly, the severity values were 1.304 and 1.534 without and with ramp rate limit constraints, respectively. The multi-objective optimal power flow problem was solved as a multi-objective and multi-constrained optimization problem, where the cost, loss, and severity value were minimized. The obtained results show the Pareto optimal front obtained by NSHFABC was better than that of the existing literature. It was also observed that the proposed method can handle ramp rate limit constraints. The result shows that the proposed method is superior to the those presented in the existing literature.
Author Contributions
Conceptualization, B.M.; Formal analysis, V.P.P.; Methodology, R.S.; Validation, K.P.; Writing—original draft, V.K.R.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| OPF | Optimal power flow |
| ABC | Artificial bee colony |
| HFABC | Hybrid fruit fly-based artificial bee colony |
| NSHFAB | Non-dominated sorting hybrid fruit fly-based artificial bee colony |
| TLBO | Teaching learning-based optimization |
| DG | Distributed generation |
| ABC-FF | Artificial bee colony with firefly |
| QOMJaya | Quasi-oppositional modified Jaya |
| TSA | Tree seed algorithm |
| PSO | Particle swarm optimization |
| FACTS | Flexible alternating current transmission system |
| CSA | Cuckoo search algorithm |
| DSLC-FOA | Diminishing step and logistic chaos- fruit fly optimization algorithm |
References
- Balasubbareddy, M. Multi-objective optimization in the presence of ramp-rate limits using non-dominated sorting hybrid fruit fly algorithm. Ain Shams Eng. J. 2016, 7, 895–905. [Google Scholar] [CrossRef][Green Version]
- Balasubbareddy, M.; Sivanagaraju, S.; Suresh, C.V. Multi-objective optimization in the presence of practical constraints using non-dominated sorting hybrid cuckoo search algorithm. Eng. Sci. Technol. Int. J. 2015, 18, 603–615. [Google Scholar] [CrossRef][Green Version]
- Chen, G.; Yi, X.; Zhang, Z.; Wang, H. Applications of multi-objective dimension-based firefly algorithm to optimize the power losses, emission, and cost in power systems. Appl. Soft Comput. 2018, 68, 322–342. [Google Scholar] [CrossRef]
- Zhou, J.; Wang, C.; Li, Y.; Wang, P.; Li, C.; Lu, P.; Mo, L. A multi-objective multi-population ant colony optimization for economic emission dispatch considering power system security. Appl. Math. Model. 2017, 45, 684–704. [Google Scholar] [CrossRef]
- Ding, M.; Chen, H.; Lin, N.; Jing, S.; Liu, F.; Liang, X.; Liu, W. Dynamic population artificial bee colony algorithm for multi-objective optimal power flow. Saudi J. Biol. Sci. 2017, 24, 703–710. [Google Scholar] [CrossRef]
- Horsch, J.; Ronellenfitsch, H.; Witthaut, D.; Brown, T. Linear optimal power flow using cycle flows. Electr. Power Syst. Res. 2018, 158, 126–135. [Google Scholar] [CrossRef]
- Sahu, S.; Barisal, A.K.; Kaudi, A. Multi-objective optimal power flow with DG placement using TLBO and MIPSO: A comparative study. Energy Procedia 2017, 117, 236–243. [Google Scholar] [CrossRef]
- Wu, L.; Liu, Q.; Tian, X.; Zhang, J.; Xiao, W. A new improved fruit fly optimization algorithm IAFOA and its application to solve engineering optimization problems. Knowl. -Based Syst. 2018, 144, 153–173. [Google Scholar] [CrossRef]
- Wang, L.; Zheng, X. A knowledge-guided multi-objective fruit fly optimization algorithm for the multi-skill resource-constrained project scheduling problem. Swarm Evol. Comput. 2018, 38, 54–63. [Google Scholar] [CrossRef]
- Du, T.-S.; Ke, X.-T.; Liao, J.-G.; Shen, Y.-J. DSLC-FOA: Improved fruit fly optimization algorithm for application to structural engineering design optimization problems. Appl. Math. Model. 2018, 55, 314–339. [Google Scholar] [CrossRef]
- Nuaekaew, K.; Artrit, P.; Pholdee, N.; Bureerat, S. Optimal reactive power dispatch problem using a two-archive multi-objective grey wolf optimizer. Expert Syst. Appl. 2017, 87, 79–89. [Google Scholar] [CrossRef]
- Morshed, M.J.; Hmida, J.B.; Fekih, A. A probabilistic multi-objective approach for power flow optimization in hybrid wind-PV-PEV systems. Appl. Energy 2018, 211, 1136–1149. [Google Scholar] [CrossRef]
- Shareefa, S.K.M.; Rao, R.S. Optimal reactive power dispatch under unbalanced conditions using hybrid swarm intelligence. Comput. Electr. Eng. 2018, 69, 183–193. [Google Scholar] [CrossRef]
- Warid, W.; Hizam, H.; Mariun, N.; Wahab, N.I.A. A novel quasi-oppositional modified Jaya algorithm for multi-objective optimal power flow solution. Appl. Soft Comput. 2018, 65, 360–373. [Google Scholar] [CrossRef]
- Attia, A.F.; El Sehiemya, R.A.; Hasanien, H.M. Optimal power flow solution in power systems using a novel Sine-Cosine algorithm. Int. J. Electr. Power Energy Syst. 2018, 99, 331–343. [Google Scholar] [CrossRef]
- Dhiman, G.; Kumar, V. Multi-objective spotted hyena optimizer: A Multi-objective optimization algorithm for engineering problems. Knowl. -Based Syst. 2018, 150, 175–197. [Google Scholar] [CrossRef]
- Lv, L.; Zhao, J. The Firefly Algorithm with Gaussian Disturbance and Local Search. J. Signal Process. Syst. 2018, 90, 1123–1131. [Google Scholar] [CrossRef]
- Mohamed, A.-A.A.; Mohamed, Y.S.; EI-Gaafary, A.A.M.; Hemeida, A.M. Optimal power flow using moth swarm algorithm. Electr. Power Syst. Res. 2017, 142, 190–206. [Google Scholar] [CrossRef]
- Davoodi, E.; Babaei, E.; Mohammadi-ivatloo, B. An efficient covexified SDP model for multi-objective optimal power flow. Int. J. Electr. Power Energy Syst. 2018, 102, 254–264. [Google Scholar] [CrossRef]
- El-Fergany, A.A.; Hasanien, H.M. Tree-Seed Algorithm for Solving Optimal Power Flow Problem in Large-Scale Power Systems Incorporating Validations and Comparisons. Appl. Soft Comput. J. 2018, 64, 307–316. [Google Scholar] [CrossRef]
- Naderi, E.; Narimani, H.; Fathi, M.; Narimani, M.R. A Novel Fuzzy Adaptive Configuration of Particle Swarm Optimization to Solve Large-Scale Optimal Reactive Power Dispatch. Appl. Soft Comput. J. 2017, 53, 441–456. [Google Scholar] [CrossRef]
- Sedighizadeh, M.; Sarvi, M.; Naderi, E. Multi-Objective Optimal Power Flow with FACTS Devices Using Shuffled Frog Leaping Algorithm. Int. Rev. Electr. Eng. 2011, 6, 1794–1801. [Google Scholar]
- Wei, J.; Zhang, Y.; Wang, J.; Caob, X.; Khan, M.A. Multi-period planning of multi-energy microgrid with multi-type uncertainties using chance constrained information gap decision method. Appl. Energy 2020, 260, 114188. [Google Scholar] [CrossRef]
- Khan, A.; Hizam, H.; Abdul-Wahab, N.I.; Othman, M.L. Solution of Optimal Power Flow Using Non-Dominated Sorting Multi Objective-Based Hybrid Firefly and Particle Swarm Optimization Algorithm. Energies 2020, 13, 4265. [Google Scholar] [CrossRef]
- Yang, N.-C.; Mehmood, D.; Lai, K.-Y. Multi-Objective Artificial Bee Colony Algorithm with Minimum Manhattan Distance for Passive Power Filter Optimization Problems. Mathematics 2021, 9, 3187. [Google Scholar] [CrossRef]
- Subramanian, S.; Sankaralingam, C.; Elavarasan, R.M.; Vijayaraghavan, R.R.; Raju, K.; Mihet-Popa, L. An Evaluation on Wind Energy Potential Using Multi-Objective Optimization Based Non-Dominated Sorting Genetic Algorithm III. Sustainability 2021, 13, 410. [Google Scholar] [CrossRef]
- Tong, Z.; Xin, J.; Ling, C. Many-Objective Hybrid Optimization Method for Impeller Profile Design of Low Specific Speed Centrifugal Pump in District Energy Systems. Sustainability 2021, 13, 10537. [Google Scholar] [CrossRef]
- Islam, M.Z.; Wahab, N.I.A.; Veerasamy, V.; Hizam, H.; Mailah, N.F.; Guerrero, J.M.; Nasir, M.N.M. A Harris Hawks Optimization Based Single- and Multi-Objective Optimal Power Flow Considering Environmental Emission. Sustainability 2020, 12, 5248. [Google Scholar] [CrossRef]
- Nguyen, T.T. A high performance social spider optimization algorithm for optimal power flow solution with single objective optimization. Energy 2019, 171, 218–240. [Google Scholar] [CrossRef]
- Naderi, E.; Pourakbari-Kasmaei, M.; Abdi, H. An efficient particle swarm optimization algorithm to solve optimal power flow problem integrated with FACTS devices. Appl. Soft Comput. 2019, 80, 243–262. [Google Scholar] [CrossRef]
- Suresh, C.V.; Sivanagaraju, S. Analysis and effect of multi-fuel and practical constraints on economic load dispatch in the presence of Unified Power Flow Controller using UDTPSO. Ain Shams Eng. J. 2015, 6, 803–817. [Google Scholar] [CrossRef][Green Version]
- Abido, M.A. Optimal power flow using Tabu search algorithm. Electr. Power Compon. Syst. 2002, 30, 469–483. [Google Scholar] [CrossRef]
- Arul, R.; Ravi, G.; Velsami, S. Non-convex economic dispatch with heuristic load patterns, valve point loading effect, prohibited operating zones, ramp-rate limits, and spinning reserve constraints using harmony search algorithm. Electr. Eng. 2013, 95, 53–61. [Google Scholar] [CrossRef]
- Zhu, J.; Momoh, J.A. Multi-area power systems economic dispatch using nonlinear convex network flow programming. Electr. Power Syst. Res. 2001, 59, 13–20. [Google Scholar] [CrossRef]
- Niknam, T.; Narimani, M.R.; Aghaei, J.; Azizipanah-Abarghooee, R. Improved particle swarm optimisation for multi-objective optimal power flow considering the cost, loss, emission and voltage stability index. IET Gener. Transm. Distrib. 2012, 6, 515–527. [Google Scholar] [CrossRef]
- Chaib, A.E.; Bouchekara, H.; Mehasni, R.; Abido, M.A. Optimal power flow with emission and non-smooth cost functions using backtracking search optimization algorithm. Int. J. Electr. Power Energy Syst. 2016, 81, 64–77. [Google Scholar] [CrossRef]
- Naderi, E.; Kasmaei, M.P.; Cerna, F.V.; Lehtonen, M. A novel hybrid selfadaptive heuristic algorithm to handle single and multi-objective optimal power flow problems. Int. J. Electr. Power Energy Syst. 2021, 125, 106492. [Google Scholar] [CrossRef]
- Roy, P.K.; Ghoshal, S.P.; Thakur, S.S. Optimal power flow using biogeography based optimization. Int. J. Power Energy Convers. 2010, 2, 216–249. [Google Scholar] [CrossRef]
- Kumari, M.S.; Maheswarapu, S. Enhanced Genetic Algorithm based computation technique for multi-objective Optimal Power Flow solution. Electr. Power Energy Syst. 2010, 32, 736–742. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).