Abstract
The analytical hierarchy process (AHP) was utilized to determine the optimal location on which to install flat-plate solar thermal collectors for residential buildings in a number of cities in Iran under diverse climatic conditions. The payback period of investment (IPBP) was chosen as one of the decision criteria, while payback periods of energy and greenhouse gas emissions (EPBP and GGEPBP), being two recently introduced concepts, were also taken into account to provide a broader insight from the energy, economic, and environmental (3E) benefits of the system. The novelty of this work is proposing a method to find places with the greatest potential to install flat-plate solar collectors. It was performed using AHP as a systematic decision-making tool, and based on energy, environmental, and economic criteria, which are the key aspects of an energy system. Codes developed in the MATLAB software were employed to determine the values for different investigated cities. According to the results, Yazd, located in the center of the country, was found to be the best place to install the system. This city enjoys EPBP, IPBP, and GGEPBP scores of 2.47, 3.37, and 0.71 years, respectively. The collector area for this city was also found to be 109.8 m2. Yazd gained a score of 26.5 out of 100. With scores of 24.4, 18.6, 15.9, and 14.6 out of 100, Tehran, Bandar Abbas, Rasht, and Tabriz were found to be the second, third, fourth, and fifth priorities for utilizing the system, respectively.
1. Introduction
The depletion of natural oil resources and their impact on climate change are an undeniable facts [1]. Hot–arid climate countries, such as Iran, are consistently improving their utilization of renewable energy technologies in residential buildings [2]. In this post-pandemic world, much of the energy demand is based on building air-circulation and ventilation [3]. As such, the use of solar thermal collectors for hot water and cleaning could be realized by understanding the optimal performance and determining a suitable location for higher heat transfer [4]. The harnessing of solar energy for residential buildings has gained great importance in the supply of heating and cooling energy, as well as electricity, in both small and large scales [5,6,7].
One of the most common technologies used to harness solar irradiation and its conversion into thermal energy is solar thermal collectors for solar heating applications [8]. Due to their low cost, simple design, and the easy installation of flat-panel solar collectors compared to other forms of solar hot water technologies, their use in buildings (residential and commercial) is being explored in hot–arid countries such as Iran [9]. It is pertinent to discuss the various research literature on the simulation and evaluation of the performance of flat-plate solar collectors [10]. A review summary is presented in Table 1, in which each study is introduced and two research gap questions are investigated.

Table 1.
Investigations on various works in the literature identifying the knowledge gap and the novelty of this work compared to the conducted research in this field.
Table 1 shows that, in spite of the valuable reported research studies in this field, two items have not been addressed yet, which could be considered a gap in the research works in this area, that is:
- Only the return of investment has been taken into account, and the parameters that show the return of energy or greenhouse gas emissions have not been considered in evaluating the system.
- A systematic decision-making approach has not been employed to answer the question of, among a number of candidate locations utilizing flat-plate solar collectors, which one gains the most energy, economic, and environmental (3E) benefits?
Considering the success in employing the decision-making method for finding the best place to install different energy systems, including solar stills [25], coolers [26], and nanofluid-based photovoltaic thermal systems [27], the present research study is conducted to specifically contributes to determining solar thermal collectors’ optimal locations in residential buildings, addressing the two knowledge gaps as follows:
- There has been no study in the past in which a systematic approach was employed to determine the optimal installation of flat-plate solar collectors or building-integrated photovoltaic thermal (BIPV/T) systems among a number of cities. In other words, a systematic decision-making approach has never been employed to determine the best city for the installation of flat-plate solar collectors or BIPV/T systems among a number of candidate cities.
- Payback periods of energy and greenhouse gas emissions are considered in addition to the payback period of investment for the evaluation of the system. This leads to having one dimensionless characteristic from each 3E aspect to evaluate the potential of utilizing flat-plate solar collectors.
- The analytical hierarchy process (AHP) decision-making approach was employed to determine the best place among a number of candidate cities to utilize flat-plate solar collectors. Tehran, Tabriz, Rasht, Yazd, and Bandar Abbas, as the larger cities in Iran with diverse climatic conditions, were chosen as the candidate cities, and a flat-plate solar collector is assumed to provide a sufficient heating load for them. As shown in Figure 1, a flat-plate collector consists of glass and absorbent and insulating parts. Sunlight passes through the glass and hits the absorber plate, where it converts the solar energy into heat energy, causing fluid to heat up. The gained thermal energy is utilized for providing domestic hot water and space heating purposes.
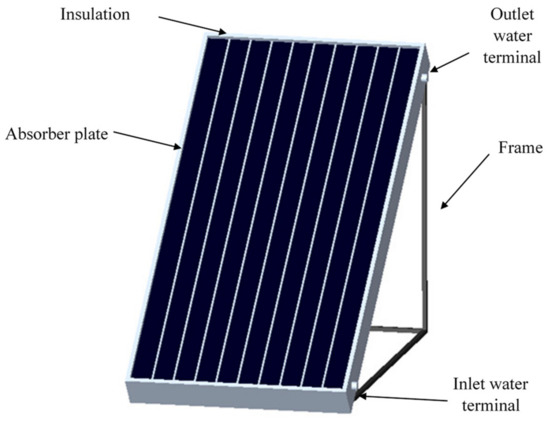 Figure 1. Schematic of the investigated flat-plate solar collector.
Figure 1. Schematic of the investigated flat-plate solar collector.
2. Methodology
2.1. The Building
In this study, a residential building was considered as the investigated case. It has a plan which is illustrated in Figure 2. This residential building was introduced in [28], and for more information about this building, that paper is referred to. The building is the representative of the most common type of building in the country from both the material and area viewpoints.
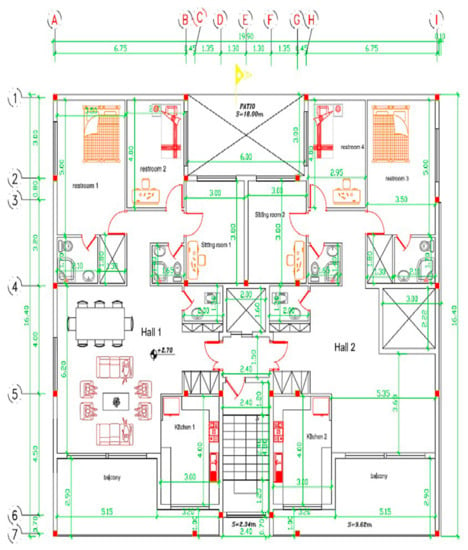
Figure 2.
Schematic diagram of the benchmark residential building [28].
2.2. The Cities
Tehran, Rasht, Yazd, Tabriz, and Bandar Abbas, five of the larger cities in Iran with diverse climatic conditions, were selected as the investigated cities in this study. The most important climatic parameters for them are presented in Table 2.

Table 2.
The most important climatic parameters of the five investigated cities [28].
The profiles for domestic hot water and space heating loads were determined for the investigated buildings, and the full details are reported elsewhere in [28].
3. Methodology
In this section, an explanation of the methodology utilized to simulate the performance of the system, as well as details about obtaining payback periods of energy, investment, and greenhouse gas emissions, are provided.
3.1. Mathematical Modeling of Flat Plate Solar Thermal Collector
The mathematical modeling approach implemented in the system is dependent on the specification of the collector’s input parameters and required heating load for the case study cities, based on their local temperatures. The amount of heat transferred to the liquid in a flat collector is obtained from Equation (1).
where is the transferred heat to the liquid; heat removal factor and collector area are shown by and , respectively. is the irradiance, is the overall loss coefficient, and are the symbols used for the outlet and inlet fluid temperatures. is the multiplication of the transmissivity of glass in the absorptivity of the plate. A reasonable approximation for is presented in Equation (2):
The coefficient 1.01 on the right-hand side of Equation (2) was suggested by Duffie and Beckman [29]. This is a practical value for most of the commercialized collectors. It is for single-cover glass types [30].
is also determined by multiplying the flow factor by the collector efficiency factor. The two latter indicated parameters are indicated by and , respectively:
Equations (4) and (5) calculate and , respectively.
In Equations (4) and (5), and are the tube outside diameter and spacing, respectively. is the standard fin efficiency, which is calculated from Equation (6); is the tube inside diameter; the heat transfer coefficient inside the tube is indicated by ; is the flow rate; and is specific heat.
where is also calculated from Equation (7):
In Equation (7), thermal conductivity and thickness of plate are shown by and .
In order to obtain the , the thermal resistance model was used. Based on this methodology, a flat-plate collector is composed of different layers, as shown in Figure 3 which include glass, a collector plate, and a collector back layer. In addition, there is thermal resistance between each layer and between the glass and ambient air, as well as the collector back and ambient air.
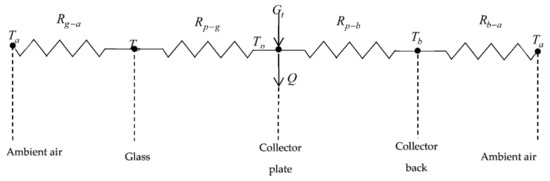
Figure 3.
Equivalent thermal resistive diagram between the plates of the collector.
In the employed approach, i.e., the thermal resistance method, the system was investigated under the steady-state condition. The heat transfer from collector plate to glass was determined by Equation (8):
where is the collector plate temperature and is the glass temperature. is also the thermal resistance between glass and collector plate, which is obtained from Equation (9).
In Equation (9), and are the convection and radiation heat transfer coefficients between the collector plate and glass, which are found using Equations (10) and (13), respectively [31].
In Equations (11) and (12), is the Nusselt number, is the collector slope, is the Rayleigh number, is the Gravitational constant, is the volumetric coefficient of expansion, is the Prandtl number, is the Kinetic viscosity, and is the absorber-to-glass cover distance. Moreover, in Equation (13), is the Stefan–Boltzmann coefficient, which is , and represents the emissivity.
Similar to Equation (8), the heat transfer coefficient from glass to ambient is computed from Equation (14):
In Equation (14), denotes thermal resistance between glass and ambient air , which is obtained from Equation (15):
In which:
In Equation (17), represents the wind velocity.
In order to obtain the top thermal resistance, which is another parameter in the modeling and indicated by , the calculated thermal resistance between the collector plate and glass and the thermal resistance between the glass and ambient air were added together as shown in Equation (18):
Finally, as shown in (19), to obtain the overall heat loss coefficient , three parameters were added together, which are the coefficients for:
- Bottom heat loss ,
- Top heat loss ,
- Edge loss .
should be found based on a trial-and-error process for and . In that process, for the determination of , in the first step, and are guessed, and with these assumed values, is obtained according to the given governing equations until the outcome of Equations (8) and (14) are close enough to each other. More details about modeling the flat-plate solar collector are also found in [32], and that reference is introduced for that purpose.
3.2. Calculation Method of Payback Periods
The payback periods of energy, greenhouse gas emissions, and investment are dimensionless, meaningful decision criteria to judge the installation of flat-plate solar collectors in major cities in Iran. In addition, these three criteria are employed to find the optimal location to install flat-plate thermal collectors.
In Iran, the government has a plan to install renewable energy systems, such as flat-plate solar collectors for households, as a way, in part, to utilize more renewable energy technologies. They will install the system for a building for free, and the investment is then returned by the obtained profit via fuel saving. The payback period is taken into account as the most important factor for policymakers in the Iranian government. For that reason, the payback period is considered in this investigation. The payback period methods have also been extensively employed for different renewable energy systems, which shows the great popularity of them. The references [33,34] are provided as examples of a research and review studies with regard to this topic, respectively.
3.2.1. Payback Period of Energy
Based on the definition, payback period of energy (EPBP) is defined as the energy footprint of solar collectors divided by the yearly energy savings caused by the solar collectors, as shown in Equation (23) [10]:
3.2.2. Payback Period of Investment
The number of years it takes to return an investment is called the payback period of investment, briefly, IPBP. An investment is made for buying flat-plate solar collectors with an area of AC. In this study, the employed flat-plate solar collector is simulated using the model introduced in [2]. Therefore, and by following the methodology presented in [35] and the information in [2], the initial purchase price of a collector can be determined using Equation (24) as a function of its area:
In this study, the present value (worth) (PW) method is employed, which expresses that the value of an amount of money that is paid or gained is different from its time of origin due to inflation (i) and discount (d) rates. is paid at the beginning of interval. Therefore, the PW of that is equal to the amount of payment, i.e., . This means:
In addition, another imposed cost to the system is the operating and maintenance cost (CO&M). CO&M is assumed to be 2% of , which increases by the inflation rate of iO&M in subsequent years. Consequently, the present value of payments for operating and maintenance after N years is:
The expenses for the initial purchase price of the collector and the operating and maintenance cost will be made up by the income from saving natural gas. Following the same fashion as the operating and maintenance cost, the present value of the income gained by saving natural gas, whose value in the first year is CNG, is obtained through Equation (27):
The payback period of investment for the investigated system (IPBP) is the period where the summation of and is covered by . Consequently, IPBP is determined by solving Equation (28):
It is worth mentioning that, as completely discussed in [6], Iran is a country with a special economic condition. In Iran, the price of buying components is on the international scale because they are imported from other countries. However, due to the very low dollar exchange rate and the imposition of strong subsidies by the government, the price of electricity and natural gas is too far from the international tariffs. Therefore, if the values for the country were utilized, they would be quite different from the international values. For this reason, and similar to the previous studies of the research team, reported in [6], for the sake of providing a better insight compared to international levels, the value for the United States, i.e., 0.3362 USD.m−3 is utilized as the natural gas tariff. , and are also considered to be 2.00, 2.00, and 1.50%, respectively.
3.2.3. Greenhouse Gas Emissions Payback Period
In the absence of a flat-plate solar collector system, the heat required to meet the heating demand is supplied by a fossil fuel system (such as a hot water coil). As a result, the system usage prevents the release of some carbon dioxide emissions into the environment. The environmental benefit of such an installation can be evaluated using a parameter called the payback period of greenhouse gas emission (GGEPBP). It is obtained from Equation (29):
In Equation (29), denotes the amount of carbon dioxide emissions released between the material extraction stage and the consumer delivery stage. also represents the annual heat covered by the flat-plate solar collector system. is also the amount of carbon dioxide emissions (CDE) from the combustion of natural gas, which is considered 0.185 kg.(kWh)−1 [36].
3.3. Decision-Making Approach
The analytical hierarchy process (AHP) is a method for ranking a number of alternatives. Initially in AHP, the alternatives, that is, the criteria that are involved in decision-making and the sub-criteria for each criterion (if any), are defined. Then, using the pairwise comparison made by experts—first the alternatives, then the sub-criteria—the criteria are evaluated, and the results for different cases in the matrix form. Each matrix is called a matrix of pairwise comparisons. Comparisons are made by taking advantage of the scale suggested by Saaty [37]. In the suggested scale, equal importance is shown by providing the number 1 to the made pairwise comparison. If the alternative “X” is superior to the alternative “Y”, a number greater than 1 is assigned to the made pairwise comparison. The number could be between 1 and 9, which is of extremely high importance. The importance of “Y” to “X” is the inverse value of the assigned number to the importance of “X” to “Y”.
There are a variety of decision-making approaches, such as the TOPSIS and LINMAP methods. AHP has some great advantages compared to these. For example, it considers the relative importance of different decision criteria. In addition, it has the capability of defining sub-criteria in addition to the criteria. The ability to work with criteria that are not numbers is another big advantage of AHP in comparison to other methods, such as TIPSIS and LINMAP [38].
As it was indicated in the introduction, in this study, a decision-making approach was employed to find the optimal location to install systems among the five cities. For this purpose, AHP, as one of the more popular and widely used decision-making tools, was chosen, while EPBP, IPBP, and GGEPBP, were selected as the decision criteria. Table 3 shows the values of the made comparisons of the decision criteria with respect to the goal of decision making, which ranks the representative cities with regard to the installation of flat-plate solar collectors. Based on the experts’ judgment, and as indicated in Table 3, IPBP is the most important decision criterion, while, after that, GGEPBP is in second place. EPBP is in the third rank, whose importance is close to that of GGEPBP. The full details of the AHP process are detailed by the present study team in [37].

Table 3.
Matrix showing the pairwise comparison of decision criteria.
4. Results and Discussion
A structure consisting of five parts was chosen to present the results of this study. First, in Section 4.1, Section 4.2, Section 4.3, Section 4.4, the values of AC, EPBP, IPBP, and GGEPBP are provided for the investigated cities and compared with one other, respectively. Then, in Section 4.5, an optimal location analysis for the installation of the system is conducted using the AHP method among the five cities.
4.1. Model Validation
The model used for the simulation of system performance is very well known, and it has been validated several times before in several research works. However, it is validated again here to ensure there was no mistake incurred by the authors.
Validation was performed using the experimental data reported in the study of Alvarez et al. [39]. Figure 4a,b demonstrate the comparisons for the mean plate and fluid temperatures. There were only 1.55% and 1.59% errors between simulation and experiment results in the average for the mean plate and fluid temperatures. Consequently, the employed simulation has been verified.
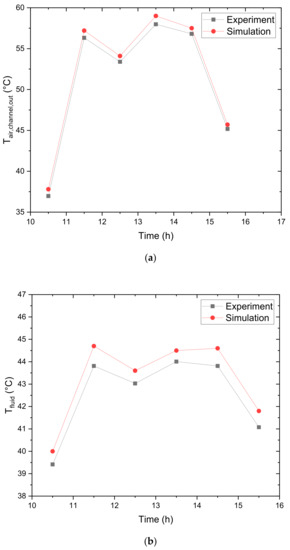
Figure 4.
Comparison of the simulation results with the experimental data reported in the study of Alvarez et al. [39] for mean temperature of (a) plate and (b) fluid.
4.2. The Area of Solar Thermal Collectors
As observed in Figure 5, with a value of 85.8 m2, Bandar Abbas has the lowest area among the cities due to a minimum heating load. After that, Yazd and Tehran are in the next places, in that order. For these two cities, the values of the collector areas are significantly close. The required collector area for Yazd is 109.8 m2, while for Tehran, it is only 4.3 m2 higher, i.e., 114.1 m2. In Rasht, the installed area of the solar collectors was found to be 130.1 m2. The highest value found for a collector area among the five investigated cities was in Tabriz: It is 174.2 m2, which is almost two times (exactly 2.03 times) larger than Bandar Abbas.
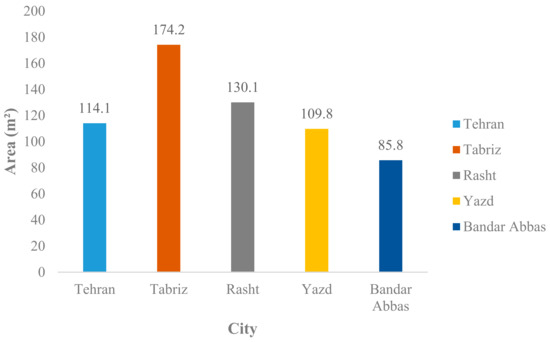
Figure 5.
The area of solar collectors in different cities.
4.3. Payback Period of Energy
The values of EPBP for the five cities are presented in Figure 6. According to Figure 6, it is demonstrated that the EPBP for all the cities is within an acceptable range of two to four years. Based on the obtained results, the best conditions for EPBP were observed to be in Tehran. In this city, the EPBP is 2.42 years. As with the collector areas, the EPBPs for Tehran and Yazd are close together, such that the value in Yazd is only 0.05 years longer, i.e., 2.47 years. Bandar Abbas is in the third rank from this viewpoint, where its EPBP is 2.81 years. The EPBP for Tabriz is also 0.22 years longer, i.e., 3.03 years. Finally, with a value of 3.29 years, Rasht was found to be the worst place among the five investigated cities from an EPBP aspect.
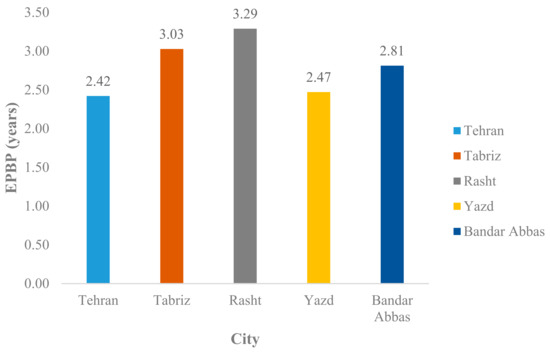
Figure 6.
The values of EPBP in different cities.
4.4. Payback Period of Investment
As indicated in Figure 7, investment in the system is returned in a range of around 2.80 to 4.20 years, which shows that the plan is economically justifiable. In this case, the trend is dependent on the collector area; Bandar Abbas, which is the city with the minimum collector area, has the lowest IPBP. After that, Yazd and Tehran have IPBP values of 3.37 and 3.49 years, respectively. The IPBP for Rasht is 3.66 years, and Tabriz has the worst IPBP among the cities with 4.20 years.
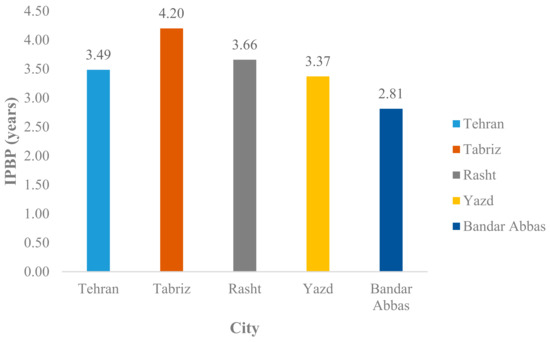
Figure 7.
The values of IPBP in different cities.
4.5. Payback Period of Greenhouse Gas Emissions
In this case, as found in Figure 8, all the cities benefited from GGEPBP values below one year, which reveals the high efficiency of installation in the system from an environmental point of view. The ranks are similar to the EPBP case. However, the differences are closer. For instance, the difference between Yazd and Tabriz, the cities in the second and third ranks, is 0.56 years for EBPB, which is reduced to almost one-third here (0.16 years). With 0.69 and 0.94 years, Tehran and Rasht have the best and worst GGEPBP values among the five investigated cities, respectively.
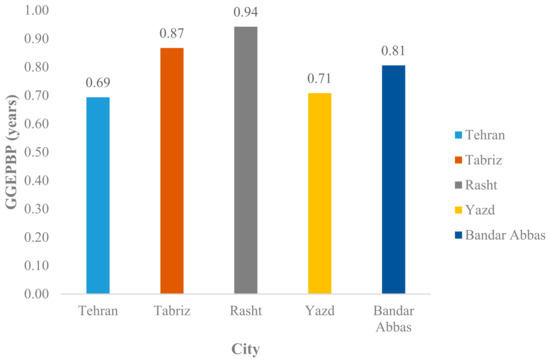
Figure 8.
The values of GGEPBP in different cities.
4.6. Optimal Location Analysis to Install the Solar Thermal Collector System
In AHP, each alternative gains a score out of 100, and each one that has the highest score among the others is selected as the foremost item. The scores of the alternatives are introduced in Figure 9, where Yazd is found to be the best location to install the system. This city gains a score of 26.5 out of 100. For this city, despite none of the decision criteria having the best value, all of them are at a good level. For example, the EPBP is 2.47 years, which is the second-best rank among the cities. In addition, the IPBP for Yazd is 3.37 years, which is the second most favorable value observed among the alternatives. Not only are EPBP and IPBP in the second rank for Yazd, with a value of 0.71 years, the GGEPBP of this city also has the second-best value among the cases.
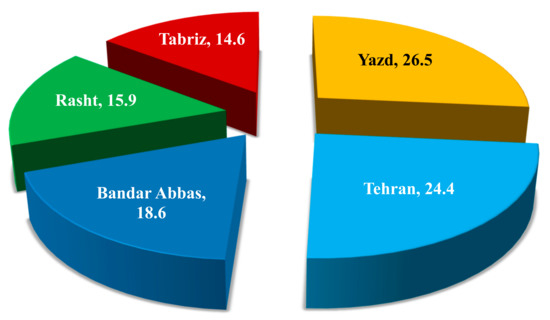
Figure 9.
The final scores of different cities for installation of the system.
Tehran, which is the nearest city to Yazd from with regard to all three mentioned aspects, is found to be in the second rank of decision-making. Tehran has a score of 24.4 out of 100, which is 2.1 points below Yazd. Bandar Abbas is in the third rank with a score of 18.6. The main advantage of Bandar Abbas compared to Rasht and Tabriz is a much lower heating demand, which leads it to having a better IPBP compared to them. For the same reason, i.e., a lower IPBP compared to Tabriz, Rasht was chosen as the next priority, and Tabriz, which has the highest heating demand and IPBP among the alternatives, was selected as the last item in the list of cities. Furthermore, as observed, the proposed approach is general, and it could be applied for any other set of the cities in Iran, or in other countries of the world.
5. Conclusions
The current research work was conducted to answer the question, “Among the representative cities of the diverse climatic conditions of Iran, which one is the best place to install a flat-plate solar collector on a residential building?” Payback periods of energy, investment, and greenhouse gas emissions (EPBP, IPBP, and GGEPBP) were selected as the decision criteria, and, by taking advantage of the analytical hierarchy process (AHP) as a systematic decision-making tool, the optimal location/city was chosen among representative cities of five different climatic conditions of Iran, namely, Tehran, Tabriz, Rasht, Bandar Abbas, and Yazd. Proposing a method to determine the place with the highest potential to utilize flat-plate solar collectors was taken into account as the innovation of this work. It was performed using AHP as a systematic decision-making tool and based on the energy, environmental, and economic criteria, which are the key aspects of an energy system. The results demonstrated that, by gaining a score of 26.5 out of 100, Yazd is the best place for utilizing this system. The values of EPBP, IPBP, and GGEPBP for this city are 2.47, 3.37, and 0.71 years, respectively. Tehran, Bandar Abbas, Rasht, and Tabriz were in the second, third, fourth, and fifth ranks, respectively. They gained scores of 24.4, 18.6, 15.9, and 14.6 out of 100, respectively.
Author Contributions
Data curation, S.J.; investigation, S.J., A.S., S.H., F.P.; methodology, A.S., S.H., F.P.; project administration, A.S., S.H., F.P.; resources, A.S., S.H., F.P.; software, S.J.; supervision, A.S., S.H., F.P.; validation, A.S., S.H., F.P.; writing—original draft, A.S. and S.J.; writing—review & editing, S.H. and F.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data sharing not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| List of symbols | |
| Area of the collector (m2) | |
| AHC | Annual heat Covered by the flat plate solar collector (KWh) |
| Cost | |
| CDE | Carbon Dioxide Emission |
| Tube outside diameter | |
| Discount rate (%) | |
| Energy (J) | |
| EPBP | Energy Pay Back Period |
| The factor for efficiency of the collector | |
| Standard efficiency of the fin | |
| Heat removal factor | |
| Flow factor | |
| Gravitational constant | |
| Irradiance (W.m−2) | |
| GGEPBP | Payback period of greenhouse gas emissions |
| The coefficient for heat transfer (W.K−1.m−2) | |
| Inflation rate (%) | |
| IPBP | Payback period of investment (Years) |
| IPP | Initial purchase price ($) |
| Thermal conductivity (W.m−1.K−1) | |
| Absorber to glass cover distance | |
| Nusselt number | |
| Mass flow rate (kg.s−1) | |
| Prandtl number | |
| Present value (worth) | |
| Heat flow (W) | |
| R | Resistance (m2.K.W−1) |
| Ra | Rayleigh number |
| Wind velocity (m.s−1) | |
| Temperature (K) | |
| Overall thermal transmittance (W.m−2.K−1) | |
| Tube spacing (m) | |
| Greek symbol | |
| Absorptivity | |
| Volumetric coefficient of expansion | |
| Collector slope | |
| ) | |
| Emissivity | |
| Kinetic viscosity | |
| Stefan Boltzmann coefficient (W.m−2.K−4) | |
| Transmissivity | |
| Subscripts | |
| Ambient | |
| Bottom | |
| Convection | |
| Edge of the glass | |
| Glass | |
| Inlet | |
| Natural gas | |
| Outlet | |
| Operating and Maintenance | |
| Plate | |
| Radiation | |
| Top | |
| Abbreviations | |
| AHP | Analytical Hierarchy Process |
References
- Álvarez-Sánchez, F.; Flores-Prieto, J.; García-Valladares, O. Annual Thermal Performance of an Industrial Hybrid Direct–Indirect Solar Air Heating System for Drying Applications in Morelos-México. Energies 2021, 14, 5417. [Google Scholar] [CrossRef]
- Sohani, A.; Hoseinzadeh, S.; Berenjkar, K. Experimental analysis of innovative designs for solar still desalination technologies; An in-depth technical and economic assessment. J. Energy Storage 2021, 33, 101862. [Google Scholar] [CrossRef]
- Mostafizur, R.M.; Rasul, M.G.; Nabi, M.N. Energy and Exergy Analyses of a Flat Plate Solar Collector Using Various Nanofluids: An Analytical Approach. Energies 2021, 14, 4305. [Google Scholar] [CrossRef]
- Eismann, R.; Hummel, S.; Giovannetti, F. A Thermal-Hydraulic Model for the Stagnation of Solar Thermal Systems with Flat-Plate Collector Arrays. Energies 2021, 14, 733. [Google Scholar] [CrossRef]
- Shahverdian, M.H.; Sohani, A.; Sayyaadi, H.; Samiezadeh, S.; Doranehgard, M.H.; Karimi, N.; Li, L.K.B. A dynamic multi-objective optimization procedure for water cooling of a photovoltaic module. Sustain. Energy Technol. Assess. 2021, 45, 101111. [Google Scholar] [CrossRef]
- Sohani, A.; Dehnavi, A.; Sayyaadi, H.; Hoseinzadeh, S.; Goodarzi, E.; Garcia, D.A.; Groppi, D. The real-time dynamic multi-objective optimization of a building integrated photovoltaic thermal (BIPV/T) system enhanced by phase change materials. J. Energy Storage 2022, 46, 103777. [Google Scholar] [CrossRef]
- Sohani, A.; Sayyaadi, H. Employing genetic programming to find the best correlation to predict temperature of solar photovoltaic panels. Energy Convers. Manag. 2020, 224, 113291. [Google Scholar] [CrossRef]
- Kuczynski, W.; Kaminski, K.; Znaczko, P.; Chamier-Gliszczynski, N.; Piatkowski, P. On the Correlation between the Geometrical Features and Thermal Efficiency of Flat-Plate Solar Collectors. Energies 2021, 14, 261. [Google Scholar] [CrossRef]
- Alvi, J.Z.; Feng, Y.; Wang, Q.; Imran, M.; Khan, L.A.; Pei, G. Effect of Phase Change Material Storage on the Dynamic Performance of a Direct Vapor Generation Solar Organic Rankine Cycle System. Energies 2020, 13, 5904. [Google Scholar] [CrossRef]
- Zukowski, M.; Radzajewska, P. A New Method to Determine the Annual Energy Output of Liquid-Based Solar Collectors. Energies 2019, 12, 4586. [Google Scholar] [CrossRef] [Green Version]
- Shamshirgaran, S.; Khalaji Assadi, M.; Al-Kayiem, H.H.; Viswanatha Sharma, K. Energetic and exergetic performance of a solar flat-plate collector working with Cu nanofluid. J. Sol. Energy Eng. 2018, 140, 031002. [Google Scholar] [CrossRef]
- Kumaresan, G.; Santosh, R.; Raju, G.; Velraj, R. Experimental and numerical investigation of solar flat plate cooking unit for domestic applications. Energy 2018, 157, 436–447. [Google Scholar] [CrossRef]
- Mortazavi, A.; Ameri, M. Conventional and advanced exergy analysis of solar flat plate air collectors. Energy 2018, 142, 277–288. [Google Scholar] [CrossRef]
- García, A.; Herrero-Martin, R.; Solano, J.; Pérez-García, J. The role of insert devices on enhancing heat transfer in a flat-plate solar water collector. Appl. Therm. Eng. 2018, 132, 479–489. [Google Scholar] [CrossRef]
- Amraoui, M.A.; Aliane, K. Three-dimensional analysis of air flow in a flat plate solar collector. Period. Polytech. Mech. Eng. 2018, 62, 126–135. [Google Scholar] [CrossRef] [Green Version]
- Hashim, W.M.; Shomran, A.T.; Jurmut, H.A.; Gaaz, T.S.; Kadhum, A.A.H.; Al-Amiery, A.A. Case study on solar water heating for flat plate collector. Case Stud. Therm. Eng. 2018, 12, 666–671. [Google Scholar] [CrossRef]
- Karki, S.; Haapala, K.R.; Fronk, B.M. Technical and economic feasibility of solar flat-plate collector thermal energy systems for small and medium manufacturers. Appl. Energy 2019, 254, 113649. [Google Scholar] [CrossRef]
- Carmona, M.; Palacio, M. Thermal modelling of a flat plate solar collector with latent heat storage validated with experimental data in outdoor conditions. Sol. Energy 2019, 177, 620–633. [Google Scholar] [CrossRef]
- Garcia, R.P.; del Rio Oliveira, S.; Scalon, V.L. Thermal efficiency experimental evaluation of solar flat plate collectors when introducing convective barriers. Sol. Energy 2019, 182, 278–285. [Google Scholar] [CrossRef]
- Diez, F.; Navas-Gracia, L.; Martínez-Rodríguez, A.; Correa-Guimaraes, A.; Chico-Santamarta, L. Modelling of a flat-plate solar collector using artificial neural networks for different working fluid (water) flow rates. Sol. Energy 2019, 188, 1320–1331. [Google Scholar] [CrossRef]
- Toapanta, L.F.; Anthony Xavier, A.; Quitiaquez Sarzosa, W. CFD Analysis of a solar flat plate collector with different cross sections. Enfoque UTE 2020, 11, 95–108. [Google Scholar]
- Hussein, O.A.; Habib, K.; Muhsan, A.S.; Saidur, R.; Alawi, O.A.; Ibrahim, T.K. Thermal performance enhancement of a flat plate solar collector using hybrid nanofluid. Sol. Energy 2020, 204, 208–222. [Google Scholar] [CrossRef]
- Verma, S.K.; Sharma, K.; Gupta, N.K.; Soni, P.; Upadhyay, N. Performance comparison of innovative spiral shaped solar collector design with conventional flat plate solar collector. Energy 2020, 194, 116853. [Google Scholar] [CrossRef]
- Stalin, P.M.J.; Arjunan, T.; Matheswaran, M.; Dolli, H.; Sadanandam, N. Energy, economic and environmental investigation of a flat plate solar collector with CeO2/water nanofluid. J. Therm. Anal. Calorim. 2020, 139, 3219–3233. [Google Scholar] [CrossRef]
- Jafari, S.; Aghel, M.; Sohani, A.; Hoseinzadeh, S. Geographical Preference for Installation of Solar Still Water Desalination Technologies in Iran: An Analytical Hierarchy Process (AHP)-Based Answer. Water 2022, 14, 265. [Google Scholar] [CrossRef]
- Balyani, H.H.; Sohani, A.; Sayyaadi, H.; Karami, R. Acquiring the best cooling strategy based on thermal comfort and 3E analyses for small scale residential buildings at diverse climatic conditions. Int. J. Refrig. 2015, 57, 112–137. [Google Scholar] [CrossRef]
- Sohani, A.; Shahverdian, M.H.; Sayyaadi, H.; Samiezadeh, S.; Doranehgard, M.H.; Nizetic, S.; Karimi, N. Selecting the best nanofluid type for A photovoltaic thermal (PV/T) system based on reliability, efficiency, energy, economic, and environmental criteria. J. Taiwan Inst. Chem. Eng. 2021, 124, 351–358. [Google Scholar] [CrossRef]
- Moghadam, R.S.; Sayyaadi, H.; Hosseinzade, H. Sizing a solar dish Stirling micro-CHP system for residential application in diverse climatic conditions based on 3E analysis. Energy Convers. Manag. 2013, 75, 348–365. [Google Scholar] [CrossRef]
- Duffie, J.A.; Beckman, W.A.; Blair, N. Solar Engineering of Thermal Processes, Photovoltaics and Wind; John Wiley & Sons: Hoboken, NJ, USA, 2020. [Google Scholar]
- Sayigh, A.M.; Nasser, S.H. Comparing a way to calculate the heat loss coefficient of solar flat plate collector. J. Teknol. Energi 2012, 1, 11–21. [Google Scholar]
- Bergman, T.L.; Lavine, A.S.; Incropera, F.P.; DeWitt, D.P. Introduction to Heat Transfer; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Kalogirou, S.A. Solar Energy Engineering: Processes and Systems; Academic Press: Cambridge, MA, USA, 2013. [Google Scholar]
- Wang, W.; Liu, Y.; Wu, X.; Xu, Y.; Yu, W.; Zhao, C.; Zhong, Y. Environmental assessments and economic performance of BAPV and BIPV systems in Shanghai. Energy Build. 2016, 130, 98–106. [Google Scholar] [CrossRef]
- Peng, J.; Lu, L.; Yang, H. Review on life cycle assessment of energy payback and greenhouse gas emission of solar photovoltaic systems. Renew. Sustain. Energy Rev. 2013, 19, 255–274. [Google Scholar] [CrossRef]
- Sohani, A.; Sayyaadi, H. Design and retrofit optimization of the cellulose evaporative cooling pad systems at diverse climatic conditions. Appl. Therm. Eng. 2017, 123, 1396–1418. [Google Scholar] [CrossRef]
- Sohani, A.; Rezapour, S.; Sayyaadi, H. Comprehensive performance evaluation and demands’ sensitivity analysis of different optimum sizing strategies for a combined cooling, heating, and power system. J. Clean. Prod. 2021, 279, 123225. [Google Scholar] [CrossRef]
- Saaty, T.L. A scaling method for priorities in hierarchical structures. J. Math. Psychol. 1977, 15, 234–281. [Google Scholar] [CrossRef]
- Sohani, A.; Delfani, F.; Fassadi Chimeh, A.; Hoseinzadeh, S.; Panchal, H. A conceptual optimum design for a high-efficiency solar-assisted desalination system based on economic, exergy, energy, and environmental (4E) criteria. Sustain. Energy Technol. Assess. 2022, 52, 102053. [Google Scholar] [CrossRef]
- Alvarez, A.; Cabeza, O.; Muñiz, M.C.; Varela, L.M. Experimental and numerical investigation of a flat-plate solar collector. Energy 2010, 35, 3707–3716. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).