Design and Flow Analysis of an Adjustable Check Valve by Means of CFD Method

Abstract

The article presents results of research on an adjustable check valve. In particular, the article deals with improvement of flow characteristics and reduction in pressure losses of an existing valve design. The subject of the research was the valve body in the form of a steel block intended for mounting a typical cartridge valve insert. Two variants of the valve body were analysed: a standard one, which is currently in production, and the proposed new solution, in which the geometry was modified based on the results of CFD simulations. The main research task was to properly shape and arrange holes and flow channels inside the body, between the cartridge valve and the connecting plate. Using CFD analyses, a solution for minimising the flow resistance was sought and then the method of modifying flow channels geometry was developed. The CFD simulation results showed a significant reduction in pressure loss, up to 40%. The obtained simulation results were verified on a test bench using a prototype of the proposed valve block. A high degree of consistency in the results of CFD simulations and laboratory experiments was achieved. The relative difference between simulation and experimental results in the entire considered range of the flow rate did not exceed $6.0$%.

1. Introduction

Check valves are key components of hydraulic control systems. Design solutions in the form of cartridge-type inserts are becoming increasingly more popular as they allow the designer to create the housing according to individual needs and their own idea. Flow channels and seats for mounting inserts inside the housing can be made by casting or directly drilled by machining. Cast housings are usually made of cast iron or less commonly aluminium alloys. The most popular cast iron housings, in which the individual flow channels are created in the casting technology, are mainly used in large-scale production due to the relatively low cost per unit. Cast iron housings also have other advantages, such as the possibility of making flow channels with more advanced geometry and thus allowing lower flow resistance or more compact design. However, the high costs of necessary instrumentation and technological preparation make the low-volume production in such a case unprofitable. Therefore, steel housings are most often made in piece and small-lot production and also for operating at higher pressures due to better strength parameters. In this case, the flow channels are made by machining, usually using the drilling or milling operations. Thus, the flow channels are typically in the form of connected circular holes, turned chamfers and milled spaces. With this processing method, it is difficult to obtain the complex geometry of the flow channels with a quality close to that of a cast housing. However, it is possible to improve flow characteristics of the valve by modifying geometry of the flow channels inside the steel housing, based on the results of simulation tests carried out using the CFD method.

The problem of check valve flow analysis can be found in many significant publications. They are mainly related to the issues of CFD flow modelling or optimisation to reduce flow losses. Pauly [1] noted that check valves cause major pressure losses in over 30 percent of hydraulic systems. He recommended paying more attention to the parameters and positioning of valves of this type. Analysis of a poppet valve behaviour by means of CFD dynamic simulation was carried out by Gomez et al. [2]. The authors noted the possibility of dynamic characteristic enhancement by altering fluid viscosity and studied the effect of poppet angle on pressure. Furthermore, Jin et al. [3] studied the continuously-adjusted cam-driven valve opening, Woldemariam et al. [4] optimised a micro turbine valve, and Ye et al. [5] obtained transient flow characteristic of a high-pressure check valve in a hydrogen system. Research of a switching valve with innovative poppet head geometry was carried out by Filo et al. [6]. The proposed modifications allowed the operating range of the valve to be significantly increased. Development of an innovative proportional poppet-type valve for a water hydraulic system designed with the help of CFD simulations was published by Park [7], an interesting comparison of swing and tiling check valves designed for high-temperature compressible fluids was provided by Gao et al. [8], while Qian et al. analysed dynamic flow characteristics of a globe valve [9].

At present, numerical flow analyses concern a wide range of valve types, working with different fluids under various operating conditions. Scuro et al. conducted research on a three-dimensional model of a directly-operated safety relief valve using ANSYS-CFX software [10], while Wang et al. investigated cavitating flow in a control valve with a perforated cage in ANSYS-Fluent [11]. There are also publications on the CFD analyses involving extreme operating conditions, such as turbulent compressible flow through a multi-stage high pressure reducing valve conducted by Chen et al. [12], or thermal fluid-structure analysis of fast pressure relief valve under severe nuclear accident by Zhang et al. [13], as well as modelling the flow of a specific fluid, like liquefied natural gas, through a cryogenic valve carried out by Zhen-hao et al. [14]. The most recent research on check valves is mainly related to CFD analysis, which can be combined with dynamic mesh modelling [15], liquid interactions with channel walls using the $FSI$ technique [16] or advanced mesh refinement [17].

This article deals with the improvement in an existing design of an adjustable check valve. The principle of the valve operation ensures that the flow in one direction takes place through the pressure acting directly on the valve poppet against the spring force, while in the opposite direction the flow is opened by a hydraulic control signal applied to the pilot piston.

2. Working Principle of an Adjustable Check Valve

The subject of the analysis is an adjustable check valve containing a standard insert designed for the cartridge type installation. Design of the valve insert in a cross-sectional view is shown in Figure 1. It consists of a sleeve-shaped housing (1) with a movable poppet (3) inside. The housing is closed with a plug (2) which simultaneously constitutes a tensioner for a spring (4). Movement of the spring is assisted by a guide bar (5). Sealing rings (6,7) ensure tightness and provide the possibility to install the cartridge in a valve block. The cartridge is designed for the maximum operating pressure of $p_{max}=35$ MPa and the nominal flow rate $Q_{nom}=60$ dm${}^3$ min${}^{-1}$. It is possible to operate at higher flow rate, however at the cost of significant increase in pressure losses. The maximum analysed flow rate after applying the proposed modifications to the valve geometry was $Q_{max}=160$ dm${}^3$ min${}^{-1}$.

Figure 1. Cross-sectional view of a cartridge valve: (1) housing, (2) plug, (3) poppet, (4) spring, (5) spring guide bar, (6,7) sealing rings and (A and B) connection channels.

The complete adjustable check valve with a cartridge insert installed inside a body is shown in Figure 2. The valve consists of a body (1), a cartridge valve (2), a pilot piston (3) and a covering plate (4). The body is in the form of a steel block, and all necessary holes and flow channels are made by means of turning and drilling operations. The valve ports conform to ISO 5781 standard for sub-plate mounting.

Figure 2. Cross-sectional view of a complete adjustable check valve: (1) valve body, (2) cartridge valve, (3) pilot piston, (4) covering plate and (A, B, X) connection ports.

In the default design of the valve block (designated as version I), channels A and B are circular in cross section as shown in Figure 3a. It can be observed that there is a step change in the flow cross section and a sudden deflection of the fluid stream at the inlet of the flow channel to the poppet chamber. Therefore, the idea arose to shape the channel geometry in such a way as to modify the direction of the fluid stream and limit its deflection. However, the possibilities of shaping the geometry of the channels in a body made by means of traditional machining methods are strongly limited for technological reasons. Initial analyses showed that it is feasible to increase areas of both flow channels by performing additional drilling operations inclined to the main axis of the channel at $\alpha$ and $\beta$ angles, respectively. Figure 3b shows the cross sections illustrating the proposed modifications to the channel geometry, which is called version $II$. Due to the limitations resulting from the valve block geometry and its manufacturing technology, the permissible range of both $\alpha$ and $\beta$ angles was defined as $⟨{70}^{\circ }{90}^{\circ }⟩$. The modifications made are expected to cause changes in jet angles and thus affect flow characteristics, without unduly compromising the strength of the valve body.

Figure 3. Cross section of valve body channels: (a) version I: default design and (b) version $II$: proposed geometrical modification of flow channels.

3. CFD Flow Analysis

First, discrete fluid models were created based on the valve geometry and taking into account mesh quality factors, then turbulence model and boundary conditions were assigned and the planned simulations were carried out.

3.1. Discrete Model and Assessment of Mesh Quality

CFD analysis requires a discrete flow path model. Therefore, in the first step, a series of fluid geometric models corresponding to both analysed variants of the valve body geometry were built. The models were created in the Creo system using geometric Boolean operations, using 3D models of the housings and the check valve cartridge. Due to the lack of axial or planar symmetry in the housing geometry, it was necessary to analyse the turbulent flow in the fully 3D domain.

The meshing process and further analyses were carried out in the ANSYS/Fluent system. Irregular elements were used to create mesh, including prisms at the boundaries and tetrahedrons in the bulk flow. A pressure-based solver with the segregated algorithm was used to achieve the pressure–velocity coupling. The absolute values of both mass and momentum residuals were assumed to be less than ${10}^{-4}$. The mesh independence was assessed in preliminary studies, based on the default valve design (version I) and actual pressure loss data provided by the valve manufacturer. For nominal flow rate $Q_{nom}=60$ dm${}^3$ min${}^{-1}$, the kinematic viscosity of the fluid $\nu =41\times {10}^{-6}$ m${}^2$ s${}^{-1}$, temperature $t=50$ °C and the catalogue value of pressure losses in the $A-B$ direction is $\Delta p_{A-B}=0.60$ MPa, while in the opposite direction $\Delta p_{B-A}=0.59$ MPa. The tests included carrying out set of steady-state simulations using standard $k-\epsilon$ method. Pressure loss value was determined according to ISO 4411 standard [18]. Starting from element sizes recommended in ANSYS documentation [19], the technique of progressive mesh refinement in the poppet and valve seat areas was applied. This resulted in increasing the number of elements, but also reducing the difference between the simulation results and the manufacturer’s data. The obtained pressure loss and the percentage difference from the catalogue data ($A-B$ direction) are presented in Figure 4.

Figure 4. Mesh independence simulation results: (1) pressure loss from CFD simulation, (2) catalogue data, (3) relative percentage error and ($c1$ …$c8$) test case.

Based on the results of preliminary simulations, the model with 350,800 cells and over 120,000 nodes (test case $c5$) was accepted for further research. The obtained mesh is characterised by the following parameters: value of the orthogonal quality not less than $0.71$, skewness below $0.50$ and the maximum aspect ratio below $8.70$. A discrete model of the modified valve (version $II$) was created in an analogous way, yielding 382,600 cells and nearly 133,000 nodes. Figure 5 shows mesh models of fully opened valves (versions I and $II$, respectively) with a maximum poppet displacement $x_g=3.1$ mm.

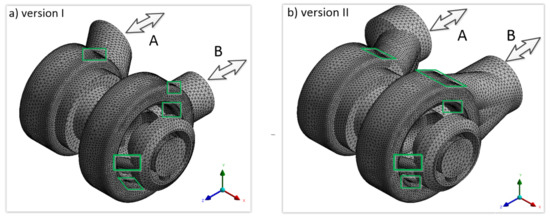
Figure 5. Meshed models of flow paths with refined areas denoted: (a) version I and (b) version $II$.

In order to confirm the final design, additional simulations with both lower and higher number of cells were carried out on the valve model in version $II$. The simulations were conducted for the nominal flow rate $Q=60$ dm${}^3$ min${}^{-1}$ and the minimum considered flow rate $Q=20$ dm${}^3$ min${}^{-1}$. The results shown in Figure 6 indicate that both doubling (C) and tripling (D) the number of elements related to the accepted final design (B) did not cause any significant changes in the resulting pressure loss, regardless the flow rate. For comparison, the result with the lower number of elements (A) was also presented, in which the obtained pressure drop was 5–10% higher.

Figure 6. Mesh independence test of the final version $II$ valve design: (A…D) mesh size case.

3.2. Turbulence Model

The first step in defining the turbulence model was to determine the range of the Reynolds number. Considering the poppet gap geometry, fluid kinematic viscosity $\nu =41\times {10}^{-6}$ m${}^2$ s${}^{-1}$ and flow rate range Q = 20–160 dm${}^3$ min${}^{-1}$, the Reynolds number values vary from $Re=1.5\times {10}^3$ to $Re=1.8\times {10}^4$. ANSYS/Fluent by default offers a wide range of turbulence models of $k-\epsilon$ and $k-\omega$ types, including $Standardk-\epsilon$, $RNGk-\epsilon$, $Realizablek-\epsilon$ and $Standardk-\omega$, $SSTk-\omega$. According to the literature ([2,19,20,21,22,23,24]), models of $k-\omega$ type describe the wall flow more accurately, while the $k-\epsilon$ ones are more often used to determine the bulk flow. Therefore, $k-\epsilon$ was selected for further research. During further simulations, results obtained with the use of individual variants of the $k-\epsilon$ model with the flow rate $Q_{nom}=60$ dm${}^3$ min${}^{-1}$ were compared. The comparison results are shown in Table 1.

Table 1. Turbulence model comparison.

	$Standard\mathit{k}-\mathit{\epsilon }$	$RNGk-\mathit{\epsilon }$	$Realizablek-\mathit{\epsilon }$
Simulated pressure drop (MPa)	0.6217	0.6208	0.6211
Catalogue pressure drop (MPa)	0.600	0.600	0.600
Relative error (%)	3.62	3.47	3.52
Relative computation time (%)	100	109	111

The accuracy obtained in all tested variants was similar. The difference between the highest and the lowest value did not exceed $0.15$%. At the same time, the calculation time of the $Standardk-\epsilon$ model was shorter by approximately 10%. Due to large number of planned simulations, it was decided to choose the fastest $Standardk-\epsilon$ model for further research. Turbulence factors, including k, kinetic energy of the turbulence, and $\epsilon$, kinetic energy dissipation, were computed on the basis of transport Equations (1) and (2). The specificity of turbulence is determined by Intensity I, Length scale ℓ and turbulent viscosity ${\mu }_t$ parameters which can be calculated using Equations (3)–(5), respectively:

$$\frac{\partial \left(\rho k\right)}{\partial t}+\frac{\partial \left(\rho k{u}_i\right)}{\partial x_i}=\frac{\partial }{\partial x_j}\left[\left(\mu +\frac{{\mu }_t}{{\sigma }_k}\right)\frac{\partial k}{\partial x_j}\right]+G_k+G_b-\rho \epsilon -Y_M+s_k,$$

(1)

$$\frac{\partial \left(\rho \epsilon \right)}{\partial t}+\frac{\partial \left(\rho \epsilon u_i\right)}{\partial x_i}=\frac{\partial }{\partial x_j}\left[\left(\mu +\frac{{\mu }_t}{{\sigma }_k}\right)\frac{\partial \epsilon }{\partial x_j}\right]+C_{1\epsilon }\frac{\epsilon }{k}\left(G_k+C_{3\epsilon }{G}_b\right)-C_{2\epsilon }\rho \frac{{\epsilon }^2}{k}+s_{\epsilon }.$$

(2)

$$I=0.16·{Re}^{-0.125},$$

(3)

$$\ell =0.07·D_H,$$

(4)

$${\mu }_t=\rho ·C_{\mu }·k^2·{\epsilon }^{-1},$$

(5)

where $G_k$ is increase in kinetic energy of turbulence; $G_b$ and $Y_M$ stand for energy generated by the buoyancy phenomenon and the fluid compressibility, respectively; $D_H$ is relevant hydraulic diameter; $Re$ is Reynolds number; and $\rho$ is fluid density. The remaining model constants were defined using values recommended by ANSYS [19]: $s_k=1.00$, $s_{\epsilon }=1.30$, $C_{1\epsilon }=1.44$, $C_{2\epsilon }=1.92$, $C_{\mu }=0.09$. The main parameters of the simulation model are presented in Table 2.

Table 2. Simulation model parameters.

Kinematic Viscosity	Density	Temperature	Turbulence Intensity	Length Scale	Min inlet Flow Rate	Max inlet Flow Rate	Outlet Pressure
$\nu$	$\rho$	T	I	ℓ	$Q_{min}$	$Q_{max}$	$p_{ret}$
$41\times {10}^{-6}$ m${}^2$ s${}^{-1}$	870 kg m${}^{-3}$	50.0 °C	4.7–6.4%	0.84 mm	20.0 dm${}^3$ min${}^{-1}$	160.0 dm${}^3$ min${}^{-1}$	0.1 MPa

Boundary conditions included average fluid velocity at the inlet and pressure at the outlet. The Boundary Conditions/Velocity Specification Method option was used to set the velocity magnitude as normal to the boundary. The Outlet condition was used to define the outlet pressure value $p_{ret}=0.1$ MPa in the Gauge Pressure option.

3.3. Plan and Results of CFD Simulations

Simulation tests were carried out for both directions of flow through the valve: $A-B$ and $B-A$. The flow in the $B-A$ direction is possible after the poppet is overdriven with the pilot spool. It was assumed that the valve is fully open, which indicates that the poppet position $x_g=3.1$ mm. The simulations were performed sequentially for the volumetric flow rate from $Q=20$ dm${}^3$ min${}^{-1}$ to $Q=160$ dm${}^3$ min${}^{-1}$ every 20 dm${}^3$ min${}^{-1}$.

Figure 7 and Figure 8 show the simulation results in the plane of the longitudinal section of the version I valve at the maximum considered flow rate $Q=160$ dm${}^3$ min${}^{-1}$. The results include velocity and pressure distributions, respectively. It arises from Figure 7 that the maximum obtained fluid velocities in both directions are similar and amount to 78 m s^‒1.

Figure 7. Velocity distribution in the longitudinal section plane, version I valve, $Q=160$ dm${}^3$ min${}^{-1}$, $x_g=3.1$ mm: (a) $A-B$ flow direction and (b) $B-A$ flow direction.

Figure 8. Pressure distribution in the longitudinal section plane, version I valve, $Q=160$ dm${}^3$ min${}^{-1}$, $x_g=3.1$ mm: (a) $A-B$ flow direction and (b) $B-A$ flow direction.

The pressure loss on the valve version I, calculated as the difference between the mean inlet and outlet pressure, was $3.21$ MPa for the $A-B$ direction (Figure 8a) and $3.16$ MPa for the $B-A$ direction (Figure 8b). Figure 9 shows a comparison of $CFD$ analysis results obtained for the $A-B$ direction and catalogue data, which were determined experimentally by the manufacturer. As can be seen from the diagram, the relative difference between the catalogue data and $CFD$ results did not exceed $6.0$% in the whole considered flow rate range.

Figure 9. Comparison of the $CFD$ analysis results with the experimental curve: (1) experimental (catalogue) curve, (2) $CFD$ simulation results and (3) relative percentage difference.

In order to determine the values of the $\alpha$ and $\beta$ angles (see Figure 3), a series of simulations was performed on the valve block models with modified geometry of the flow channels. The velocity and pressure distributions were determined for both $\alpha$ and $\beta$ angles in the range of 90 to 70${}^{\circ }$. The obtained results showed that changing both angles from 90${}^{\circ }$ to 78${}^{\circ }$ resulted in a progressive decrease in the maximum velocity of the fluid, compared to the initial version I. For $\alpha =\beta =78$${}^{\circ }$ (version $II$), the maximum speed decreased by 24% and 32% for the $A-B$ and $B-A$ directions, respectively. At the same time, the pressure loss was reduced by approximately 40%. Attempts to further effect a reduction in the angle values did not improve the flow parameters significantly, and moreover could lead to technological difficulties in the valve block production. The velocity and pressure distributions of version $II$ valve obtained for $Q=160$ dm${}^3$ min${}^{-1}$ and $x_g=3.1$ mm are shown in Figure 10 and Figure 11.

Figure 10. Velocity distribution in the longitudinal section plane, version $II$ valve, $Q=160$ dm${}^3$ min${}^{-1}$, $x_g=3.1$ mm: (a) $A-B$ flow direction and (b) $B-A$ flow direction.

Figure 11. Pressure distribution in the longitudinal section plane, version $II$ valve, $Q=160$ dm${}^3$ min${}^{-1}$, $x_g=3.1$ mm: (a) $A-B$ flow direction and (b) $B-A$ flow direction.

Analysis of the pressure distribution in the $A-B$ direction also revealed that the drainage channel of the poppet chamber was connected too close to the valve seat. This resulted in an incomplete relief due to the residual pressure remaining in the poppet chamber. As shown in Figure 12a, in the case of flow rate $Q=160$ dm${}^3$ min${}^{-1}$, the residual pressure was close to $0.45$ MPa. Drilling an additional drainage channel from under the poppet chamber, shown in Figure 12b, reduced the residual pressure to less than $0.10$ MPa. This operation did not reduce the total pressure loss; however, it significantly decreased the valve opening force.

Figure 12. Pressure distribution in the version $II$ valve, $A-B$ flow direction, $Q=160$ dm${}^3$ min${}^{-1}$, $x_g=3.1$ mm: (a) standard poppet chamber drainage and (b) with additional drainage channel.

4. Determination of Flow Characteristics

The results of $CFD$ simulations obtained for the I and $II$ valve versions in the entire flow rate range are presented in Table 3, while the resulting flow characteristics are shown in Figure 13 and Figure 14, respectively. The results indicate that in both cases a significant reduction in pressure loss was achieved, averaging $33.9$% for the $A-B$ flow direction and $37.7$% for the opposite one.

Table 3. Pressure loss determined by $CFD$ simulations for valve versions I and $II$.

	Direction and Version	Flow Rate Q (dm${}^3$ min${}^{-1}$)								Mean Decrease (%)
		20	40	60	80	100	120	140	160
Pressureloss $\Delta p$ (MPa)	$A-B$, ver. I	0.08	0.25	0.62	0.90	1.33	1.90	2.60	3.30	33.91
	$A-B$, ver. $II$	0.07	0.20	0.39	0.57	0.81	1.16	1.47	1.87
	$B-A$, ver. I	0.15	0.29	0.55	0.85	1.20	1.81	2.50	3.23	37.73
	$B-A$, ver. $II$	0.10	0.25	0.38	0.52	0.72	0.95	1.28	1.65

Figure 13. Flow characteristics in the $A-B$ direction based on the $CFD$ analysis results: (1) version I and (2) version $II$.

Figure 14. Flow characteristics in the $B-A$ direction based on the $CFD$ analysis results: (1) version I and (2) version $II$.

The obtained results of CFD simulation were next used to determine the flow coefficient of the poppet gap ${\mu }_g$. The coefficient values were calculated based on the equation of volumetric flow rate through a throttling gap (6) of the version $II$ valve.

$$Q={\mu }_g·A_g·\sqrt{\frac{2·\Delta p}{\rho }},$$

(6)

thus

$${\mu }_g=\frac{1}{A_g}·\sqrt{\frac{\rho }{2·\Delta p}}·Q.$$

(7)

The cross-sectional area of the gap for $x_g=3.1$ mm is constant and amounts to $A_g=74.6$ mm2, while its fluid density is $\rho =870$ kg m${}^{-3}$. The obtained values of the ${\mu }_g$ coefficients in both directions as functions of the volumetric flow rate Q and their approximations by the polynomial function of the second order are shown in Figure 15. The formulas of approximating functions, assuming that Q is expressed in (dm${}^3$ min${}^{-1}$), are presented in Equation (8). The justification of correctness of the approximating function selection is proven by the values of correlation coefficients. In the $A-B$ direction, the residual sum of squares is $RS{S}_{A-B}=2.42\times {10}^{-4}$ and the correlation coefficient is $R_{A-B}=0.996$, while in the $B-A$ direction they are $RS{S}_{B-A}=2.01\times {10}^{-4}$ and $R_{B-A}=0.998$, respectively.

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & {\mu }_{gA-B}\left(Q\right)=3.059\times {10}^{-1}+3.025\times {10}^{-3}Q-9.667\times {10}^{-6}{Q}^2,\hfill \\ \hfill & {\mu }_{gB-A}\left(Q\right)=1.952\times {10}^{-1}+5.381\times {10}^{-3}Q-1.860\times {10}^{-5}{Q}^2.\hfill \end{array}\end{array}$$

(8)

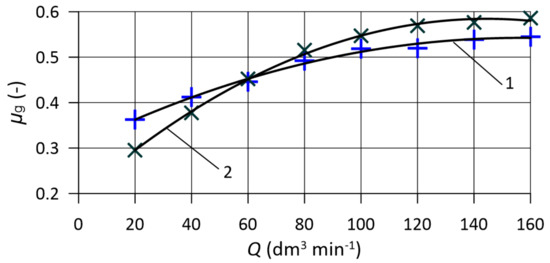
Figure 15. Flow coefficient of the version $II$ valve: (1) $A-B$ flow direction and (2) $B-A$ flow direction.

In the considered flow rate range, the flow coefficient value varies from $0.30$ to $0.59$. The mean values calculated for both flow directions are similar: ${\mu }_{gmeanA-B}=0.48$ and ${\mu }_{gmeanB-A}=0.49$.

5. Laboratory Experiments

The obtained results of simulations were verified experimentally on a test bench, which was designed according to the scheme in Figure 16. The test bench with the mounted valve in version I is shown in Figure 17.

Figure 16. Test bench scheme: (1) variable delivery pump, (2) relief valve, (3) control valve, (4) adjustable check valve, (5) throttle valve, (6) filter, (7 and 8) pressure transducer, (9) flow meter, (10) temperature gauge and (11) DAQ system.

Figure 17. Version I valve on the test bench: (1) valve body block, (2) cartridge valve insert, (3) mounting plate, (4 and 5) pressure transducers and (A and B) connection ports.

The test bench data acquisition system included two pressure sensors and a flow meter. The output signal of all sensors was 0–10 V. The used Kracht TM flow meter had a measuring range Q = 0.5–200 dm${}^3$ min${}^{-1}$ and the accuracy class $\pm 0.5$%. Both pressure sensors were Trafag NAT type with a measuring range of 0 to 10 MPa and the accuracy class $\pm 0.2$%. The measured data samples were acquired by a PC with a 16-bit National Instrument $DAQ$ card. A sampling frequency of 100Hz was used in all measurements.

At the beginning of each experiment, the flow direction was set by over-driving the control valve, then the pump was set a minimum flow rate. After starting the measurement, the flow rate was progressively increased to the maximum value, approximately 160 dm${}^3$ min${}^{-1}$, and then gradually decreased to zero again. The pressure drop was calculated as the difference between the readings of pressure sensors.

The comparison of experimental results with the approximated curves obtained from the CFD simulations for version I valve in the $A-B$ and $B-A$ direction is shown in Figure 18 and Figure 19, respectively. In the $B-A$ direction, the X port was given a pressure signal $p=10$ MPa. The analogous results for the version $II$ valve are presented in Figure 20 and Figure 21.

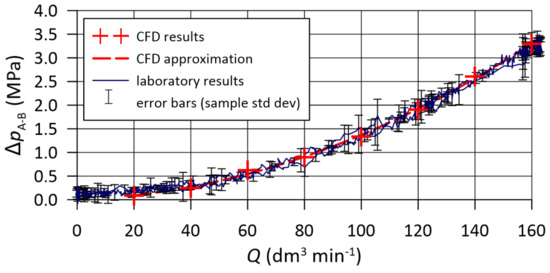
Figure 18. Results of laboratory experiments compared to theoretical curve based on $CFD$ simulations obtained for version I valve and $A-B$ flow direction.

Figure 19. Results of laboratory experiments compared to theoretical curve based on $CFD$ simulations obtained for version I valve and $B-A$ flow direction.

Figure 20. Results of laboratory experiments compared to theoretical curve based on $CFD$ simulations obtained for version $II$ valve and $A-B$ flow direction.

Figure 21. Results of laboratory experiments compared to theoretical curve based on $CFD$ simulations obtained for version $II$ valve and $B-A$ flow direction.

The figures show the results obtained during laboratory experiments as well as $CFD$ simulations and approximations of $CFD$ curves. Additionally, error bars in the form of a standard deviation of the samples were added. The error bars are shown for every fifth sample on a scale of 2 for better visibility. It arises from the figures that a high level of compliance was achieved. The results obtained from CFD analysis do not differ from laboratory experiments by more than $6.0$% for low flow rates, up to 40 dm${}^3$ min${}^{-1}$ and by $4.0$% for the rest of the considered range.

6. Conclusions

The article presents a proposal of pressure loss reduction in an adjustable check valve by means of geometrical modifications of flow channels. When analysing the default valve block design, a step change in the flow cross section and a sudden deflection of the fluid stream at the inlets of both flow channels to the poppet chamber were noticed. Therefore, the idea to shape the channel geometry in such a way as to profile the fluid stream more properly and reduce its deflection was arisen. Due to geometric and technological limitations, it was decided to drill additional holes at an angle to the main axes of the channels, which was feasible with the use of a modern $CNC$ machine tool. The inclination angles of the holes were determined on the basis of the $CFD$ simulation results. The introduced modifications resulted in a decrease of maximum fluid flow velocity by approximately 30% for the $A-B$ direction, as arises from the comparison between Figure 7a and Figure 10a. Similarly, pressure loss has been decreased by 30–40%, which leads to a significant reduction in total energy consumption and thus makes the valve more environmentally friendly. Then, based on the obtained results, the flow coefficient through the valve gap ${\mu }_g$ was determined. It has been shown that the coefficient value strongly depends on the flow rate, varying in the range from $0.3$ to $0.58$. The determined flow characteristics were verified experimentally on a test bench. High compliance of the $CFD$ analysis results with the laboratory tests was obtained. The maximum relative error did not exceed $6.0$% for low flow rates, $Q\le 40$ dm${}^3$ min${}^{-1}$ and $4.0$% for $Q>40$ dm${}^3$ min${}^{-1}$.

The proposed method of valve design improvement is particularly useful in the context of the possibility of processing on modern $CNC$ machines. This enables a significant reduction in pressure loss across the valve, compared to the commonly used valve blocks made with the machining on conventional machine tools. The resulting characteristics of the improved valve are similar to those achieved by the valves with cast blocks.