Abstract
Granulated chelates are innovative fertilizers that are highly effective and versatile, and they ensure the best start-up effect for plants. The final properties of granules are influenced by the method of their preparation and the used substances. The diameters of the obtained granules, their size range, and the final costs of the produced fertilizer are of great importance. The paper describes granules that were produced using an agglomeration of ZnIDHA in a fluidized bed with the aid of an aqueous solution of this substance with a high dry matter content. The aim of the study was to evaluate the effect of surfactant addition to the solution on the evolution of granule size distribution during the process carried out in a batch mode and to access the possibility of describing the process dynamics using population balance approach. A sieve analysis was performed in order to determine the size of the granulate, and numerical calculations were performed to determine the value of the constant aggregation rate. Based on experimental studies, it can be seen that the increase in the diameters of granules is mainly caused by the agglomeration process, and to a lesser extent by the coating process. The addition of surfactant increased the median size of the granules in the initial granulation stage, and also lowered the surface tension. This in turn enables a lower spraying pressure to be used. A comparison of different aggregation kernels constituting an integral part of the population balance model proved that the physically motivated equipartition kinetic energy kernel performs best in this case. Moreover, the computational results show an increase in the aggregation rate when the surfactant additive is used and confirm that population balance allows the extraction of physical information about the granulation.
1. Introduction
Granulation is the process of producing grains (granules), or enlarging existing solid particles [1]. Its main goal is to obtain a convenient and acceptable final form of a product for users [2]. Granulation, understood as the controlled agglomeration of powders with a high degree of dispersion, is a technique that is implemented in various ways. It can be divided into wet and dry granulation [3]. The most important difference between them is that in the case of wet granulation, it is necessary to apply an additional substance-granulating liquid [4,5]. The phenomenon of agglomeration occurs in the widely used wet granulation. The increase in grain size can be regulated by coating the grains with a layer of solution. The process involves the spraying of a liquid binder onto small particles that are mixed in, e.g., drums, a fluidized bed, mixers with high-speed mixing apparatus, or similar devices [6]. The factors that influence the combination of particles are surface tension, capillary pressure, and viscosity. In order to fix the formed bonds, drying or sintering is used in subsequent steps [7].
Fluid bed granulation, combined with the simultaneous spraying of a drying solution, is another known and commonly used method of obtaining granules. It is used in various industries, such as the food, pharmaceutical [5,8,9], fertilizer, and chemical industries [3,10]. In the chemical industry, the formed granules of fertilizers enable special properties regarding the rate of their dissolution to be obtained. This influences the innovativeness of the produced fertilizers, broadens the spectrum of their application, and minimizes their negative impact on the environment. Fertilizers in the form of granules enable the fertilizer to be applied with seeds. This ensures a better initial plant growth, as well as the plants’ uniformity, and also creates good conditions for their future growth and development. Moreover, innovations concern solutions that slow down and control the release of nutrients. The release of minerals from fertilizers is controlled physically and chemically. An important aspect of creating these types of fertilizers is their conditioning, i.e., covering them with a special coating that ensures the gradual and controlled release of ingredients. The time of operation of such a fertilizer depends on the type of material from which the coating is made, as well as the number of applied layers and their thickness and climatic conditions, such as temperature, soil moisture, and its pH.
As a result of the granulation process, solid particles with specific physicochemical properties, such as density, porosity, solubility, and grain size, can be obtained [11,12]. The equipment, process parameters, and the substance itself have an impact on the obtained effect. This method of obtaining granules involves the use of a bed consisting of solid particles suspended in a stream of hot air, in which the solution for drying is sprayed with the help of nozzles. The substances used to bind the particles into granules or agglomerates are the so-called binding solutions, which are chemically different chemical compounds when compared to granular particles. On the other hand, the binding solution may be a solution of a chemical substance with the same chemical composition as the substance that makes the fluidized bed. As a result of water evaporation, a drop may become so sticky that it will stick to solid particles. After the evaporation of most of the water, larger particles are formed, as they connect to each other by means of liquid bridges [13]. In the meantime, the particles may be further enlarged by agglomeration, granulation, or by being coated. The process that is antagonistic to the growth of granules is crushing, abrasion as a result of turbulent air flow, the collision of particles, or poorly selected drying parameters [14]. The drying process, as well as granulation on a fluidized bed, can be carried out periodically or continuously.
Chemical engineering uses mathematical models to simulate different processes, such as polymerization, granulation, etc. The development of granulation processes via drum, pan, or fluidized bed granulation is a multiscale operation [15]. Modeling of the fluidization process is a common and important practice used by many scientists in order to optimize the process parameters [16,17]. Przywara et al. [18] conducted experimental studies to determine the effect of the binder spray rate, binder composition, feed powder flow rate, pan inclination angle, and angular velocity on the distribution of the granule particle diameter, mechanical stability, and humidity. The fertilizer was made using a continuous granulator. An increase in the binder flow rate to feed rate, binder concentration, and the inclination angle of the pan resulted in an increase in the mean size of the granules. The obtained experimental results constitute the basis for the future mathematical modeling of the pan granulation process [18]. Fluid bed granulation is a process that is more complex to describe than pan granulation.
The most widely used and successful method for the analysis and quantitative prediction of the granulation processes is the approach based on population balance modeling [19,20,21,22,23]. The population balance equation (PBE), which is based on the law of conservation of mass, is a mathematical description of how the particle size distribution evolves [24]. It not only allows the change of particle size distribution during the granulation to be predicted, but also the mechanisms that play the most important role in the process under study to be understood. Different numerical methods, such as the method of successive approximations, Laplace transform, the method of moments and weighted residuals, and Monte Carlo simulation can be used to solve the PBE [22]. Another very efficient, yet relatively simple, approach was proposed by Hounslow [25], who formulated a discretized model in which particle sizes are divided into classes using geometric discretization, and in which the balance equation is applied to each class. The Hounslow discrete population balance (DPB) model is used in this study.
Earlier studies investigated the influence of drying parameters, such as drying temperature or solution spraying pressure, on granulation kinetics, or other features that characterize these types of processes [26]. The aim of this paper is to investigate the effect of adding surfactant to a ZnIDHA fertilizer solution on the drying and granulation process on a fluidized bed. Along with the analysis of experimental data, the possibility of describing the evolution of the particles using population balance was analyzed. In particular, the impact of using different types of so-called aggregation kernels in the model was evaluated and discussed.
In today’s agriculture, it is increasingly important to use specialized and properly selected fertilizers in order to increase the efficiency of agricultural production, while maintaining the appropriate quality of crops and soil. They should be characterized by a high concentration of the nutrient and its high availability to plants. In the literature, the use of surfactants in liquid fertilizers [27] and the high effectiveness of preventive foliar fertilization [28] is reported. Additionally, attention should be paid to the significant effect of fertilization of crops with agents containing high concentrations of Zn and the high availability of this important micronutrient in agricultural products. The experiment described in this study involves a fertilizer that meets these criteria [29,30,31].
2. Materials and Methods
2.1. Experimental Setup and Procedure
The agglomeration of ZnIDHA (D, L-Aspartic acid, N-(1,2 dicarboxyethyl) disodium salt of Zn), produced by PPC ADOB, was carried out using an aqueous solution of this substance with a high dry matter content. The liquid phase was fed by a pump to the fluidized bed using a nozzle to which an aqueous solution and compressed air were supplied separately in order to atomize the solution.
In the discussed experiment, a conical vertical granulator was used. It was applied as a batch granulator according to Figure 1. The diameter in the place of the fluidized bed was 1.3 m, and the height was equal to 11 m. The solution for drying was fed with the use of a metering pump, which adjusts the load to the given flow. The liquid phase was distributed to five separate liquid flow meters, and then flowed to the nozzle where it was sprayed with compressed air. The nozzles were located inside the fluidized bed just above the gas distributor, the task of which was to properly distribute the gas inside the system. The drying air flowed in co-current with the sprayed solution.
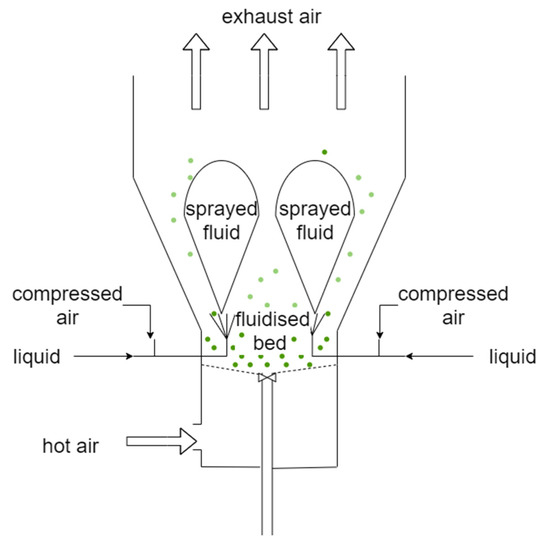
Figure 1.
Scheme of the agglomeration process on the fluidized bed in the used apparatus.
Figure 2 shows a schematic diagram of the test installation with the orientation points of the measuring equipment, fan and filters, that is:
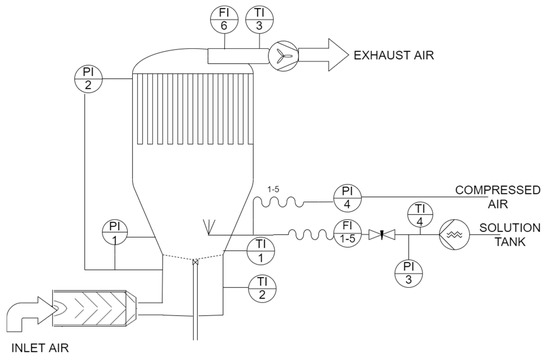
Figure 2.
Schematic diagram of the installation.
- TI—temperature sensors (TI 1—temperature of the fluidized bed; TI 2—temperature of the inlet air; TI 3—temperature of the exhaust air),
- PI—pressure measurement or the measurement of pressure drop,
- FI—process air flow sensor (FI 6) or liquid flow sensor (FI 1–5).
Before the experiment, the installation was heated until stable inlet and outlet air temperatures were established. After each experiment, the granulator was emptied thoroughly and prepared for a new test. The experiments were performed for the previously determined drying parameters: a drying temperature of 116 °C (±2 °C)—this value was kept constant by the burner—a spraying air pressure of 2.0 bar, a liquid pressure of 0.5 bar, a flow of drying solution of 40 l/h (±2 L/h) per nozzle, an initial charge that forms the fluidized bed of 20 kg (±2 kg) of granules, and a process air flow of 10.800 m3/h (±100 m3/h). The density of the fertilizer solution = 1270 kg/m3, and DM = 0.35. At the appropriate time of the test, a solution with the addition of polyglucoside surfactants (Agnique PG8105, Basf) and betains (C12-14-alkyldimethyl) at a total amount not exceeding 3.5% (V/V) of the final solution was prepared.
After the initial test conditions were obtained, sampling from the fluidized bed with the use of a sampler inserted into the bed layer and placed above the gas distributor was started. The sampling interval was 2.5 min, and the total duration of the experiment was 20 min. The mixture of particles was analyzed with regards to particle size ranges using sieving analysis. This analysis was conducted with a Retsch AS 200 analyzer using a vibration amplitude of 60% (digital, 1–100%; 0–3 mm). Based on the relevant standards [32,33], the specific and bulk densities of the obtained granulate were measured (the results are given in Table 1) [32,33].

Table 1.
Density of the used and obtained material.
2.2. Population Balance Modeling
The general form of a population balance equation for a well-mixed batch system can be written as [34,35]:
where n(L) is the population density based on the total number of particles in the bed, G is the growth rate of particles, and B and D are the birth and death rates, respectively.
Generally, the granulation process consists of different competing mechanisms [7]. The particle growth can be either due to the coating and solidification of the successive layers of solution or slurry on the seed particles, or due to agglomeration (aggregation) of particles, which results from the addition of a liquid binder. The liquid binder can also be a source of nuclei droplets of spray that dry before hitting the solid particles and become the smallest particles present in the bed. Other important phenomena are attrition and breakage, the contribution of which to the granulation process depends on the hydrodynamic conditions prevailing in the apparatus. For the sake of simplifying the complexity of the model, it was assumed in this study that nucleation, attrition, and particle breakage can be neglected. Consequently, the birth and death rates (i.e., B and D) are only attributable to agglomeration, while the growth rate G, which is associated with layering, is assumed to be size independent. Furthermore, the particles are assumed to be spherical.
Due to the high bed temperature, fast drying of the spray is assumed, and therefore, temperature and humidity do not appear in the model. The growth rate, which depends on the spray inflow to the system, is, thus, expressed as [35]:
where Xsl is the moisture fraction in the slurry and Φ is the effective spray inflow volumetric rate, which is defined as the ratio of the fresh fertilizer spray rate and the material density of the solid particles .
The agglomeration is described following the model proposed by Hulburt et al. [36], which is expressed in relation to the particle size L, and given by [25]:
where λ is the variable of integration and β(L,λ) is the coalescence kernel. In this study, the particle size is represented by its diameter dp.
The population density n(L) is defined as the ratio between the number of the particles in the differential neighborhood around L to the size of the neighborhood [25], namely:
To formulate a discretized population balance (DPB)—suitable for numerical simulations—it is necessary to use the number of the particles instead of the density function. When the nucleation is neglected, the discrete form for a batch process can be written as follows [26]:
The overall rate of change in the number of particles due to aggregation can be calculated as follows:
whereas the rate of change in the number of particles in the ith interval due to their growth is as follows:
In the above formulas, Ni is the number of particles in the ith interval, r is the ratio of the upper bound Li+1 and lower bound Li of this interval, and the parameter r is defined as follows [34]:
The coalescence (aggregation) kernel β, present in Equations (3) and (4), contains information about the probability of forming new aggregates. It generally depends on the time, and also the size of the particles, and is defined as the product of two contributions [37]:
where β0(t) is the aggregation rate constant and β*(Lx,Ly) is the particle-size dependent part. The success of using population balances to model granulation processes depends on the proper choice of kernel. Many different kernel dependencies with regards to time and particle size have been proposed and analyzed [38]. They can be divided into empirical and physic-based kernels.
The simplest coalescence kernel is based on the assumption that the influence of the size of the particles can be neglected, which in turn gives a so-called random (also referred to as a volume-independent) kernel with the following form [25]:
Another frequently used empirical kernel is the one proposed by Kapur [39], which is defined as follows:
where a and b are empirical constants.
The physically motivated equipartition kinetic energy (EKE) kernel assumes that particles collide as a consequence of their random velocity component, and also that the random components result in an equal distribution of the particles’ kinetic energy [40]:
A similar assumption as for the EKE kernel underlies the Brownian motion kernel [41]:
The value of the aggregation rate constant β0(t) is affected by the aggregation efficiency and the collision rate. The collision rate depends on the particle velocity, granulation temperature, and particle concentration distribution in the granulation zone. Therefore, a theoretical description of its time dependency is difficult. Typically, it is assumed that the aggregation rate constant is time-independent and averaged over the entire bed [37]. However, sometime dependent expressions for β0 are reported in the literature. Adetayo and co-authors [20] proposed a sequential kernel, according to which the granulation process can be divided into stages, with different kernel values being applied for each stage. When the aggregation rate constant is a continuous function of time, it typically has the linear form [40,41]:
where βA and βB are parameters that are estimated by fitting techniques.
In the framework of this study, three different agglomeration kernels were considered in order to describe the dynamics of the agglomeration process, namely the simplest random kernel and the EKE and Brownian kernels. In all cases, the aggregation rate constant β0(t) was assumed to be constant in time. Therefore, given the mathematical form of the kernels adopted, as well as the fact that the values of the parameters present in the expression for the growth constant are known, only the aggregation rate constant β0 had to be estimated from the experimental data. The parameter estimation was performed in Matlab software by minimizing the sum of square residuals between the simulated and experimental data. The fitting procedure was implemented with the use of fminsearch (with an embedded ode15s solver), which was implemented for the resolution of in order to solve the DPB equation at each iteration of the optimization function.
3. Results and Discussion
To evaluate the influence of adding the surfactants to the solution of fertilizer on the granulation process of the ZnIDHA, the size distribution of the granules initially present in the bed was determined using sieve analysis and compared with the size distribution obtained after 20 min from the start of the process. Figure 3a,b show the particle size evolution for the test performed without the surfactant, while Figure 3c,d illustrate the change in particle size distribution obtained over a time period of 20 min for the case in which the solution of fertilizer sprayed into the fluidized bed was enriched with the surfactant. The rapid increase in granule diameters indicates that agglomeration is the dominant mechanism here, with coating having a weaker effect on diameter growth.
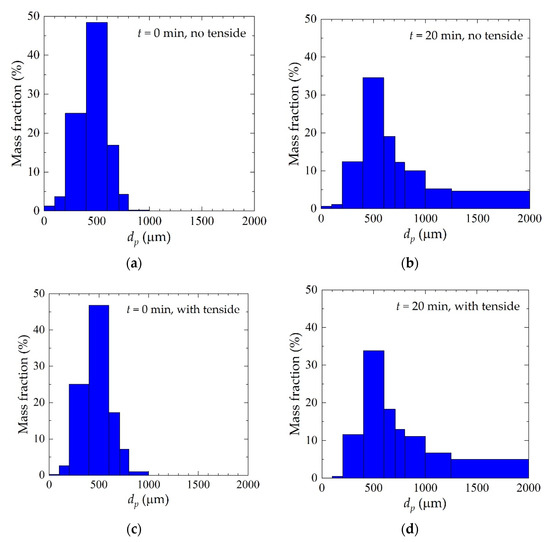
Figure 3.
Experimental mass-based histograms of particle size distribution: (a) initial particle size distribution for the test without surfactant addition; (b) particle size distribution after t = 20 min for the test without surfactant addition; (c) initial particle size distribution for the test with surfactant addition; (d) particle size distribution after t = 20 min for the test with surfactant addition.
The domination of the agglomeration mechanism is directly related to the size of the fluidized bed, which is likely to generate the collisions of particles. In addition, the movement of the particles is due to the location of the nozzles inside the bed. Moreover, the determining factor of agglomeration is the presence of a high concentration of dry matter and the administration of a relatively high flow and weight of the binding solution during the experiment.
At first sight, the particle size distributions obtained from the tests performed with and without tenside appear to be nearly identical. Nevertheless, the determination of the median particle diameter dp50 shown in Figure 4 reveals significant differences in the evolution of the granule size distribution. The strong influence of the surfactant additive is particularly evident in the early stage of the batch granulation process, i.e., up to t = 10 min, where the rate of growth in median diameter is much higher for the test performed with the additive.
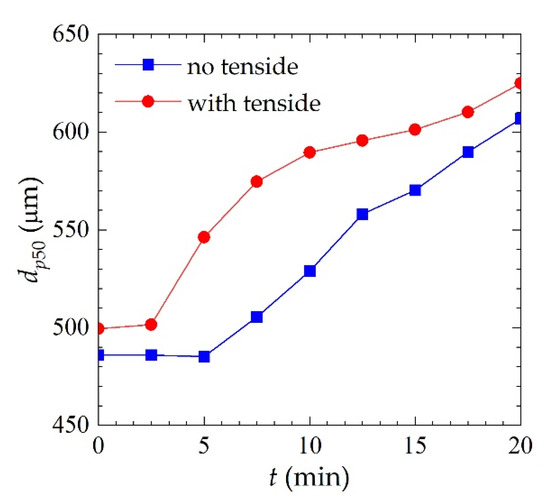
Figure 4.
Temporal evolution of the median particle diameter dp50.
The addition of the surfactant reduces the surface tension, and thus, it contributes to the reduction of the diameter of a single drop. Taking this into account in the tested process, we can predict the possibility of lowering the spraying pressure in relation to the parameters of the process of drying without the addition of the surfactant. At the same time, it is necessary to consider the possibility that the addition of the surfactant may affect the final stage of water evaporation from a single drop of the solution. In such a case, there can be a longer-lasting sticky surface of the granule, which will increase the ability of another solid particle sticking to it. In general, the fertilizer obtained in the experiment does not contain large amounts of respirable fractions, which is a great advantage of this method when compared to spray drying. At the same time, the achieved size and narrow size range of the granules will have a positive effect on both the application of the product and the water solubility in the preparation of the fertilizer solution for spraying. In addition, the obtained bulk densities for the product with the addition of the surfactant indicate the possibility of rational packaging management for the final product (within the range of 0.2–0.8 mm). The mechanism described above is reflected in the characteristic sigmoidal shape of the curves shown in Figure 4, and in the considerable initial lag that is observed for the test run without an additive. According to earlier studies [42,43] on batch granulation, the particle growth profiles strongly and nonlinearly depend on the particle morphology and binder-to-solid ratio. In particular, particles reported as referred as to “smooth” tend [42,43] to agglomerate faster than “rough” particles. Here, an analogous effect is clearly evoked by a longer-lasting sticky and more plastic surface of the granule produced in the presence of surfactant.
In the second step, the obtained data were compared in terms of the aggregation rate constant β0, which is a measure of the frequency of successful “sticking” after two granules collide. The EKE kernel (Figure 5) was taken as the baseline because it is generally accepted as the most suitable for fluid bed granulation. For comparison purposes, calculations were also performed using the simplest size-independent random kernel and the Brownian kernel.
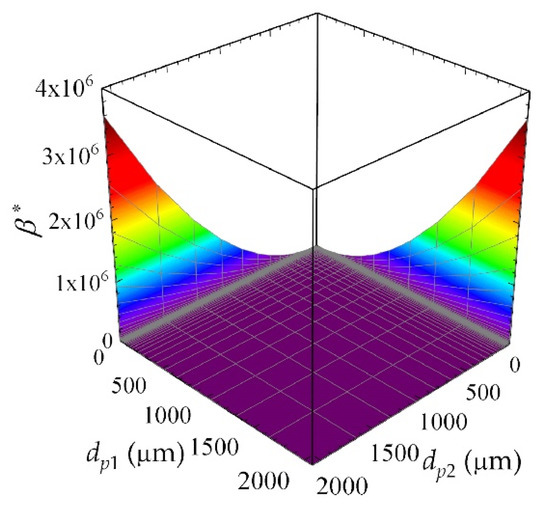
Figure 5.
3D representation of the particle size dependent part β*(dp1, dp2) of the equipartition kinetic energy (EKE) kernel.
Figure 6 shows the mass density distributions q3 calculated with the best fitted β0 values, namely β0 = 1.890 × 10−12 for the test performed without the addition of the surfactant (Figure 6a) and β0 = 2.497 × 10−12 (Figure 6b) for the test performed with the addition of the surfactant. The results obtained indicate much better efficiency (also in terms of the aggregation rate) of the granulation process, in which the solution of fertilizer was enriched with surfactant (~32% higher value of β0).
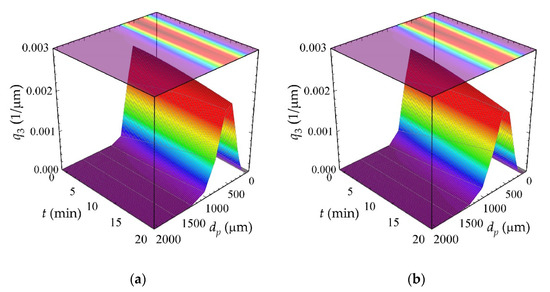
Figure 6.
Mass density distribution q3 simulated with the EKE kernel: (a) test without tenside; (b) test with tenside.
The values of β0 fitted to the DPB combined with different kernels are shown in Table 2. In all cases, the values of the aggregation rate obtained for the case with tenside additive are about ~32–33% higher than the values obtained when the additive was not added to the fertilizer solution. It has to be underlined that the different order of magnitude of the optimal value of β0 found for each model is due to their different mathematical forms. In any case, the predictions obtained with all the adopted models, shown in Figure 7 and Figure 8, respectively, for the tests performed without and with additive, are very similar, with the EKE kernel performing slightly better, especially after some time from the start of the process, i.e., at t = 20 min (Figure 7c and Figure 8c). This finding is consistent with previous studies of Honslow [40], which indicate that the EKE kernel is most suitable for fluidized bed granulation. Furthermore, as also indicated in the above cited work, the results presented in Table 2 confirm that despite its rather simple nature, PBE allows for the extraction of physical information about the granulation rate.

Table 2.
Aggregation rate constants β0 obtained using different kernels.
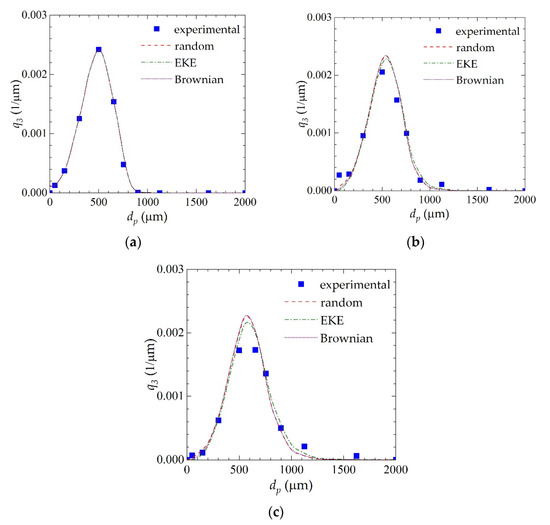
Figure 7.
Measured and simulated mass density distribution q3 for the test without tenside: (a) t = 0 min; (b) t = 10 min; (c) t = 20 min.
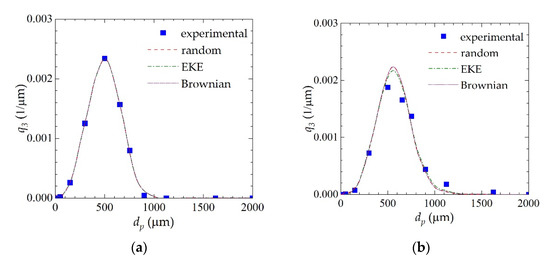
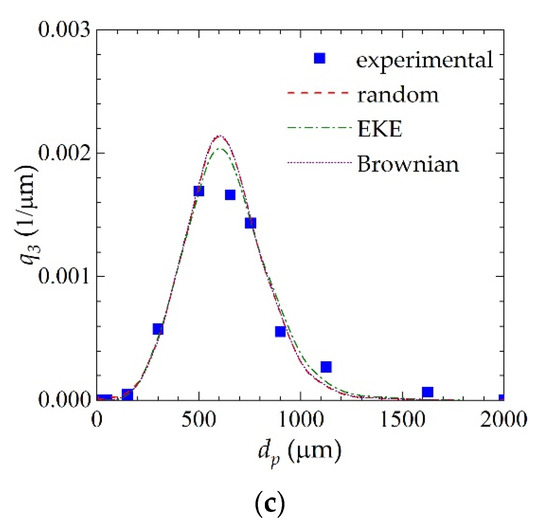
Figure 8.
Measured and simulated mass density distribution q3 for the test with tenside: (a) t = 0 min; (b) t = 10 min; (c) t = 20 min.
4. Conclusions
Granulation is a difficult and demanding process, but provides benefits in many application areas. One of them is agriculture, and more precisely, aspects related to the technology of producing fertilizers. The paper investigated the course of the wet granulation process carried out in a fluidized bed. In particular, the growth behavior of ZnIDHA fertilizer granules with and without surfactant was investigated for the first time. The experimental work performed and the fitting of the model contributes to a better understanding of the granulation of this fertilizer, which consequently may contribute to the development of methodology that will permit to easier control the process under study.
It was shown that the dominant mechanism is agglomeration, which is directly related to the selected granulation method—the operation parameters of the fluidized bed and the generated turbulent flow. The influence of tenside addition into the solution sprayed into the bed on the course of the process was determined. The reduction of surface tension influenced the breakdown of individual droplets and the evaporation of the water present in the system. Thanks to the applied method, it was possible to obtain a fertilizer that has much better properties than the fertilizer obtained with the use of the classic spray method. Properties such as the bulk density and particle size distribution of granules obtained using tests run with and without surfactant addition were determined and compared. Knowledge of these parameters and their appropriate values are of great importance with regard to packaging, transport, and storage of products. In order for the granulation process to be controllable and for its optimization or intensification to be possible, it is necessary to use appropriate mathematical models. The data obtained from the conducted experimental research allowed for the determination of an empirical aggregation kernel, which when employed within the population balance equation enables the process dynamics to be predicted. Given that model predictive control is nowadays an attractive approach to automation of industrial processes, ensuring a reliable and sustainable operation of enterprises, a consistent quality of products, and a better performance of the fluidization process, further investigation toward improving the mathematical tools is essential.
Author Contributions
Conceptualization, B.M., M.O., K.B. and S.W.; methodology, K.B. and B.M.; software, K.B. and D.B. validation, B.M., M.O., K.B., S.W., A.K., M.M., D.B., B.G. and R.O.; investigation, B.M., M.O., K.B., S.W., A.K., M.M., D.B., B.G. and R.O.; writing—original draft preparation, B.M., M.O., K.B., S.W. and A.K.; writing—review and editing, B.M., M.O., K.B., S.W. and A.K.; project administration, B.M. All authors have read and agreed to the published version of the manuscript.
Funding
The APC was funded by PCC Adob.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Acknowledgments
The research was carried out as part of an implementation PhD project (Ministry of Science and Higher Education, Poland).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Litster, J.D.; Ennis, B.J. The Science and Engineering of Granulation Process; Particle Technology Series; Springer Science & Business Media: New York, NY, USA, 2004; Volume 15. [Google Scholar]
- Kwiatek, J.; Siuda, R.; Gluba, T.; Olejnik, T.P.; Obraniak, A.; Marszałek-Gubiec, A.; Pietrasik, T. Granulation of limestone powder with selected binding liquids. Przem. Chem. 2018, 97, 1542–1548. [Google Scholar]
- Xu, J.; Yang, S.; Ren, Q.; Yang, G. Investigation of granulation calcined under the eutectic temperature in the fluidized bed. Constr. Build. Mater. 2021, 302, 124169. [Google Scholar] [CrossRef]
- Yohe, G.R. Binding materials used in making pellets and briquets. Ind. Miner. 1964, 19. Available online: https://www.ideals.illinois.edu/bitstream/handle/2142/43127/bindingmaterials19yohe.pdf?sequence=2 (accessed on 14 July 2021).
- Ficzere, M.; Meszaros, L.A.; Madarasz, L.; Novak, M.; Nagy, Z.K.; Galata, D.L. Indirect monitoring of ultralow dose API content in continuous wet granulation and tableting by machine vision. Int. J. Pharm. 2021, 607, 121008. [Google Scholar] [CrossRef]
- Chen, J.; Yang, H.; Xu, C.-M.; Cheng, J.-G.; Lu, Y.-W. Preparation of ZrO2 microspheres by spray granulation. Powder Technol. 2021, 385, 234–241. [Google Scholar] [CrossRef]
- Iveson, S.M.; Litster, J.D.; Hapgood, K.; Ennis, B.J. Nucleation, growth and breakage phenomena in agitated wet granulation processes: A review. Powder Technol. 2001, 117, 3–39. [Google Scholar] [CrossRef]
- Quatrini, E.; Li, X.; Mba, D.; Costantino, F. Fault diagnosis of a granulator operating under time-varying conditions using canonical variate analysis. Energies 2020, 13, 4427. [Google Scholar] [CrossRef]
- Fulop, G.; Domokos, A.; Galata, D.; Szabo, E.; Gyurkes, M.; Szabo, B.; Farkas, A.; Madarasz, L.; Demuth, B.; Lender, T.; et al. Integrated twin-screw wet granulation, continuous vibrational fluid drying and milling: A fully continuous powder to granule line. Int. J. Pharm. 2021, 594, 120126. [Google Scholar] [CrossRef]
- Maksakov, A.; Palis, S. Koopman-based data-driven control for continuous fluidized bed spray granulation with screen-mill-cycle. J. Process Control 2021, 103, 48–54. [Google Scholar] [CrossRef]
- Turchiuli, C.; Eloualia, Z.; El Mansouri, N.; Dumoulin, E. Fluidised bed agglomeration: Agglomerates shape and end-use properties. Powder Technol. 2005, 157, 168–175. [Google Scholar] [CrossRef]
- Soldati, R.; Zanelli, C.G.; Cavani, G.; Battaglioli, L.; Guarini, G.; Melandri, C.; Piancastelli, A.; Dondi, M. Powder rheology and compaction behavior of novel micro-granulates for ceramic tiles. Powder Technol. 2020, 374, 111–120. [Google Scholar] [CrossRef]
- Fries, L.; Dosta, M.; Antonyuk, S.; Palzer, S. Moisture distribution in fluidized beds with liquid injection. Chem. Eng. Technol. 2011, 34, 1076–1084. [Google Scholar] [CrossRef]
- Iveson, S.M.; Wauters, P.A.L.; Forres, S.; Litster, J.D.; Meesters, G.M.H.; Scarlett, B. Growth regime map for liquid-bound granules: Further development and experimental validation. Powder Technol. 2001, 117, 83–97. [Google Scholar] [CrossRef]
- Rao, N.N. Simulations for Modelling of Population Balance Equations of Particulate Processes Using Discrete Particle Model (dpm). Ph.D. Thesis, Otto-von-Guericke Universität, Magdeburg, Germany, 2009. [Google Scholar]
- Bück, A.; Dürr, R.; Schmidt, M.; Tsotsas, E. Model predictive control of continuous layering granulation in fluidised beds with internal product classification. J. Process Control 2016, 45, 65–75. [Google Scholar] [CrossRef]
- Neugebauer, C.; Diez, E.; Bück, A.; Palis, S.; Heinrich, S.; Kienle, A. On the dynamics and control of continuous fluidized bed layering granulation with screen-mill-cycle. Powder Technol. 2019, 354, 765–778. [Google Scholar] [CrossRef]
- Przywara, M.; Dürr, R.; Otto, E.; Kienle, A.; Antos, D. Process behavior and product quality in fertilizer manufacturing using continuous hopper transfer pan granulation—Experimental investigations. Processes 2021, 9, 1439. [Google Scholar] [CrossRef]
- Adetayo, A.A.; Litster, J.D.; Pratsinis, S.E.; Ennis, B.J. Population balance modelling of drum granulation of materials with wide size distribution. Powder Technol. 1995, 82, 37–49. [Google Scholar] [CrossRef]
- Heinrich, S.; Peglow, M.; Ihlow, M.; Henneberg, M.; Mörl, L. Analysis of start-up process in continuous fluidized bed spray granulation by population balance modelling. Chem. Eng. Sci. 2002, 57, 4369–4390. [Google Scholar] [CrossRef]
- Drechsler, J.; Peglow, M.; Heinrich, S.; Ihlow, M.; Mörl, L. Investigating the dynamic behavior of fluidized bed spray granulation processes applay numerical simulation tools. Chem. Eng. Sci. 2005, 60, 3817–3833. [Google Scholar] [CrossRef]
- Kumar, J.; Warnecke, G.; Peglow, M.; Heinrich, S. Comparison of numerical method for solving population balance equations incorporating aggregation and breakage. Powder Technol. 2009, 189, 218–229. [Google Scholar] [CrossRef]
- Golovin, I.; Strenzke, G.; Dürr, R.; Palis, S.; Bück, A.; Tsotsas, E.; Kienle, A. Parameter identification for continuous fluidized bed spray agglomeration. Processes 2018, 6, 246. [Google Scholar] [CrossRef] [Green Version]
- Ramkrishna, D. Population Balances; Academic Press: Cambridge, MA, USA, 2000. [Google Scholar]
- Hounslow, M.J. A discretized population balance for continuous systems at steady state. AIChE J. 1990, 36, 106–116. [Google Scholar] [CrossRef]
- Dacanal, G.C.; Menegalli, F.C. Experimental study and optimization of the agglomeration of acerola powder in a conical fluid bed. Powder Technol. 2009, 188, 187–194. [Google Scholar] [CrossRef]
- Stevens, P.J. Formulation of sprays to improve the efficacy of foliar fertilisers. N. Z. J. For. Sci. 1994, 24, 27–34. [Google Scholar]
- Wang, X.Z.; Liu, D.Y.; Zhang, W.; Wang, C.J.; Cakmak, I.; Zou, C.Q. An effective strategy to improve grain zinc concention of winter wheat, Aphids prevention and farmers’ income. Field Crop. Res. 2015, 184, 74–79. [Google Scholar] [CrossRef]
- Prom-u-thai, C.; Rerkasem, B.; Yazici, A.; Cakmak, I. Zinc priming promotes seed germination and seedling vigor of rice. J. Plant Nutr. Soil Sci. 2012, 175, 482–488. [Google Scholar] [CrossRef]
- Sawan, Z.M.; Hafez, S.A.; Basyony, A.E. Effect of phosphorus fertilization and foliar application of chelated zinc and calcium on seed, protein and oil yields and oil properties of cotton. J. Agric. Sci. 2001, 136, 191–198. [Google Scholar] [CrossRef]
- Niewiadomska, A.; Sulewska, H.; Wolna-Maruwka, A.; Ratajczak, K.; Waraczewska, Z.; Budka, A. The influence of bio-stimulants and foliar fertilizers on yield, plant features, and the level of soil biochemical activity in white lupine (Lupinus albus L.) cultivation. Agronomy 2020, 10, 150. [Google Scholar] [CrossRef] [Green Version]
- ISO. PN-EN ISO7837-2000; ISO: Geneva, Switzerland, 2011. [Google Scholar]
- ISO. PN-EN ISO 845:2000; ISO: Geneva, Switzerland, 2000. [Google Scholar]
- Hounslow, M.J.; Ryall, R.L.; Marshall, V.R. A discretized population balance for nucleation, growth, and aggregation. AIChE J. 1988, 34, 1821–1832. [Google Scholar] [CrossRef]
- Vreman, A.W.; Van Lare, C.E.; Hounslow, M.J. A basic population balance model for fluid bed spray granulation. Chem. Eng. Sci. 2009, 64, 4389–4398. [Google Scholar] [CrossRef] [Green Version]
- Hulburt, H.M.; Katz, S. Some problems in particle technology: A statistical mechanical formulation. Chem. Eng. Sci. 1964, 19, 555–574. [Google Scholar] [CrossRef]
- Cronin, K.; Ortiz, F.J.; Ring, D.; Zhang, F. A new-time dependent rate constant of coalescence kernel for modelling of fluidized bed granulation. Powder Technol. 2021, 379, 321–334. [Google Scholar] [CrossRef]
- Liu, L.X.; Litster, J.D. Population balance modelling of granulation with a physically based coalescence kernel. Chem. Eng. Sci. 2002, 57, 2183–2791. [Google Scholar] [CrossRef]
- Kapur, P.C. Kinetics of granulation by non-random coalescence mechanism. Chem. Eng. Sci. 1972, 27, 1863–1869. [Google Scholar] [CrossRef]
- Hounslow, M.J. The population balance as a tool for understanding particle rate processes. KONA Powder Part. J. 1998, 16, 179–193. [Google Scholar] [CrossRef] [Green Version]
- Hounslow, M.J.; Peterson, J.M.K.; Instone, T. Tracer studies of high-shear granulation: II. Population balance modeling. AIChE J. 2001, 47, 1984–1999. [Google Scholar] [CrossRef]
- Rajniak, P.; Sepanek, F.; Dhanasekharan, K.; Fan, R.; Mancinelli, C.; Chern, R.T. A combined experimental and computational study of wet granulation in a Wuster fluid bed granulator. Powder Technol. 2009, 189, 190–201. [Google Scholar] [CrossRef]
- Štěpánek, F.; Rajniak, R.; Mancinelli, C.; Chern, R.T.; Ramachandran, R. Distribution and accessibility of binder in wet granules. Powder Technol. 2009, 189, 376–384. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).