Abstract
In recent years, as photovoltaic (PV) power generation has rapidly increased on a global scale, there is a growing need for a highly accurate power generation forecasting model that is easy to implement for a wide range of electric utilities. Against this background, this study proposes a PV power forecasting model based on the generalized additive model (GAM) and compares its forecasting accuracy with four popular machine learning methods: k-nearest neighbor, artificial neural networks, support vector regression, and random forest. The empirical analysis provides an intuitive interpretation of the multidimensional smooth trends estimated by the GAM as tensor product splines and confirms the validity of the proposed modeling structure. The effectiveness of GAM is particularly evident in trend completion for missing data, where it is able to flexibly express the tangled trend structure inherent in time series data, and thus has an advantage not only in interpretability but also in improving forecast accuracy.
1. Introduction
PV power generation forecasting is indispensable for electric utilities. Based on the forecast of demand and renewable energy generation, power producers and retailers submit their generation and procurement plans for the next day or hour to the system operator. Forecast errors in PV generation can lead to losses in the form of imbalance charges (penalties imposed for supply–demand mismatch). Therefore, accurate forecasting of PV power generation has become an essential issue for the economical business operation of electric utilities. In particular, in recent years, many countries around the world have adopted PV power generation as a clean energy source to address global warming, and the need for PV power generation forecasting has been increasing each year. For example, in Japan, the feed-in tariff (FIT) system has provided incentives for the introduction of PV power generation, and many small-scale businesses have recently entered the PV power generation business [1]. This trend of increasing (or diversifying) the number of players is similar in other countries, although there are minor differences in the systems. Against this background, there is a need for a forecasting method that is not only highly accurate but also easy to implement and interpret by a wide range of practitioners, including small businesses.
For PV power forecasting, many previous studies have proposed various forecasting methods, which are very diverse in terms of the forecasting variables used, time granularity and forecast horizon, and algorithms. There are also various survey studies [2,3,4,5,6,7,8]. This study focuses on publicly available weather forecast information and its application to PV forecasting methods for more general electric utilities, but even if we focus on such a target, many machine learning (ML)-based models have been proposed, such as artificial neural networks (ANN) [9] and support vector regression (SVR) [10], and ML has become a mainstream approach.
Recent ML-based forecasting methods that focus on using publicly available weather data include Maitanova et al. [11], which applies a special architecture of an artificial recurrent neural network (RNN) called long short-term memory (LSTM). In the context of comparing forecast accuracy in ML methods, there have been many empirical studies, especially in the last few years. For example, Mohammed and Aung [12] compared seven ML methods, such as k-nearest neighbor (kNN) [13], decision tree, gradient boosting, and random forests (RF) [14]. Additionally, Das et al. [15] proposed a PV power prediction using SVR and compared it with ANN. Rosato et al. [16] proposed three techniques based on neural and fuzzy neural networks. Khandakar et al. [17] proposed an ANN-based prediction model to explore effective feature selection techniques. Nespoli et al. [18] also dealt with ANN-based forecasting methods, where a comparison was made between the historical dataset alone and a hybrid approach combining weather forecast. Abdel-Nasser and Mahmoud [19] proposed a model using LSTM and compared it with multiple linear regression and NN, among others. These previous studies have empirically shown that ML methods are superior in terms of forecast error reduction, but most forecasting methods using ML have challenges, such as high computational load and difficulty in interpretation, which is a well-known drawback in general.
In electric utility practice, the ease of interpretation is often the most important factor in building consensus and ensuring the reliability of the model [20]. Ease of implementation and computational tractability are also important factors, as well as accuracy. It is emphasized that these points have often been overlooked in recent research. Motivated by these practical needs, this study proposes a forecasting model based on the generalized additive model (GAM) [21], a statistical approach, rather than ML. In particular, we demonstrate that GAM-based PV forecasting models are easy to handle for a wide range of electric utilities, including new entrants, and compare our methodology with ML-based PV forecasting models.
The GAM-based PV forecasting models in this study generalize our previous studies [1,22] for the case of multidimensional tensor product spline functions. Note that these previous studies effectively modeled the smooth trend inherent in the seasonal (and in seasonal and hourly) [22] direction of PV power generation using a univariate or a bivariate tensor product spline function. In addition, note that another study using GAM for PV forecasting [23] aimed to improve the algorithm for capturing nonlinear dependencies in ensemble learning, one of the ML methods, but is slightly different from our interest. We would like to pursue ease of implementation and interpretation for practitioners; that is, our focus is more on application methods rather than on algorithm development.
Another issue of interest in this study is a “comprehensive and comparative analysis.” Although previous studies [1,22] have shown the effectiveness of GAM-based forecasting models in the context of interpretability and robustness, it has not been sufficiently verified, in the context of comparison between multiple models, how much better the forecasting accuracy of the GAM-based model is. In this study, we demonstrate the accuracy and practicability of GAM-based PV forecasting models in comparison with other regression models and several ML models. In addition, this study deals with data for both types of PV generation; that is, area-wide PV power generation in the grid area and an individual PV panel. In particular, for the latter dataset, we extend the models of previous studies [1,22] by utilizing a three-dimensional (3D) tensor product spline function. To the best of our knowledge, this is the first attempt to apply 3D tensor product spline functions not only for PV forecasting, but also for energy time series forecasting.
In the empirical analysis, we verify the reliability of the models from the structural aspect by visualizing the smooth trends estimated using tensor product spline functions for the proposed GAM-based PV forecasting models and provide reasonable interpretations of the estimated trends. Then, we conduct a comprehensive and comparative analysis with ML methods, such as kNN, ANN, SVR, and RF, to verify the accuracy of the forecasts. Overall, we conclude that the GAM-based model with multidimensional tensor product spline functions is superior in terms of interpretability, robustness, low computational load, and prediction accuracy. However, depending on the sample period (“in-sample period” for model estimation or “out-of-sample period” for accuracy validation.) and prediction error indices (MAE or RMSE), ML methods outperform in some cases, and additional empirical analysis leads to interesting insights into the conditions under which GAM-based models have advantages.
This paper is organized as follows: Section 2 introduces the GAM method and builds a forecasting model using tensor product spline functions. Section 3 provides an overview of the ML methods that this study compares. Section 4 presents an empirical analysis using actual data, provides an interpretation of the estimated multidimensional smooth trends, and analyzes the forecast errors from various aspects. Finally, Section 5 concludes the paper.
2. PV Power Forecasting Models based on GAM
In the following sections, we first construct an area-wide PV power generation forecast model, and then construct a forecasting model for individual PV panels.
2.1. Area-Wide PV Power Generation Forecasting Model
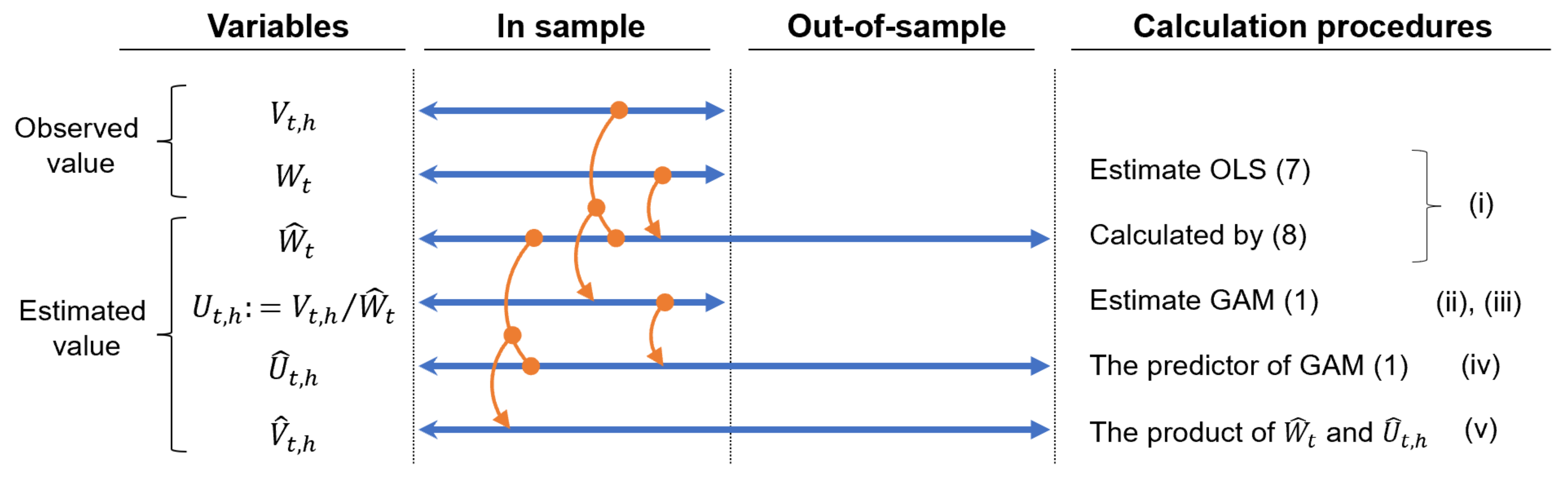
To forecast area-wide power generation, it is necessary to consider its yearly increasing trend; that is, the installed capacity of PV power generation is increasing year by year. To this end, our forecasting model is constructed by first adjusting the yearly trend of increasing capacity to derive a unit power generation. The total procedure is described as follows (note that the main variables used in these models can be found in the nomenclature at the end of this paper and the intuitive relationship between data preparation and the flow of model estimation is shown in Figure 1):
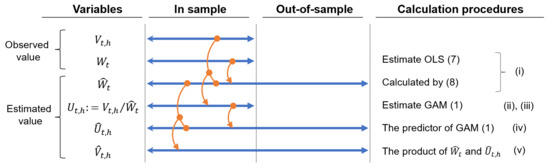
Figure 1.
Estimation procedures and data periods in the area-wide PV power generation forecasting model. Note: In our empirical analysis, we use the in-sample period from 1 April 2016, to 31 December 2017, and the out-of-sample period from 1 January to 31 December 2018 (as described in Section 4.1). When using the ML methods introduced in Section 3, the only difference is that each ML model is adopted instead of GAM (1) in steps (iii) and (iv), and the other steps are the same.
- (i)
- Using the actual areawide PV power generation capacity (observed no more frequently than monthly), the daily increasing trend is estimated using a linear model. As a result, the daily forecast value of PV power generation capacity is obtained as (see Appendix A).
- (ii)
- The unit power generation is obtained by dividing the measured hourly area-wide PV power generation by (i.e., ).
- (iii)
- For a GAM is built with calendar information, general weather conditions forecast, and maximum/minimum temperature forecast as explanatory variables.
- (iv)
- The out-of-sample forecast unit power generation is obtained by substituting the explanatory variables observed in the estimated GAM forecast formula (predictor part of the GAM).
- (v)
- The out-of-sample forecast power generation is obtained as the product of the forecast PV power capacity and the forecast unit power generation .
In the following, we apply GAM for unit power generation by using temperature and general (descriptive) weather forecasts. (Note that another possible method is to use solar radiation forecasting, but this method is not used in our area-wide PV forecast model because the solar radiation data are not available in many countries [24], and it is difficult to handle local fluctuations that depend on the observation points).
where is the tensor product spline function to be estimated by applying GAM, which is the 2D time trend that smoothly connects in the direction of both the date and hour (see Appendix B for an overview of the tensor product spline function and the smoothing mechanism). Note that the “snowy” term is only included in the model for snowy areas, which in this study are referred to Hokkaido, Tohoku, and Hokuriku, out of the nine target areas. The tensor product spline function provides smoothing conditions in two orthogonal directions (see [25] and Appendix B). This ensures robustness and makes it possible to incorporate multiple explanatory variables even with small sample sizes.
Note that and denote the maximum and minimum “temperature forecast deviations”, respectively, and they are obtained by applying GAM as follows:
We estimate the yearly cyclical trends as the spline functions in (2) and in (1), using yearly cyclical dummy variables . In this study, the starting point of the cyclical dummy variables is January 1, days are allocated in order from 1 to 365 (366 for leap years). To make the notation more concise, we denote and as and
Note that we select the cyclic cubic spline function [25] in the direction of for and . In this way, each spline function is given as a function that is smoothly continuous (the value and the first and second derivative values are all connected) not only throughout the domain of definition, but also at the beginning and end of the domain of definition. (See [26] for a detailed description and formulas of “basis functions” to apply to similar models with annual periodicity.)
2.2. Individual PV Power Generation Forecasting Model
In this section, we develop a model for forecasting the power generation of individual PV panels. In this study, we assume that solar radiation forecasts are available in the same region where the individual PV panels are located, and use this information in the model (note that in Japan, 5 km mesh solar radiation forecasts by the Japan Meteorological Agency (JMA) are widely distributed through the Japan Meteorological Business Support Center [27]). First, we propose the following forecast model “M3” for PV power generation at date time .
where is the forecast solar radiation, is the residual term, is the 3D tensor product spline function estimated by GAM (3), and is denoted by .
Next, we construct three alternative models, M0–M2, for comparison to make sure that the nonlinear conditions in 3D directions in M3 contribute to the improvement of explanatory power and robustness.
where s and s correspond to the regression coefficients and intercepts, respectively, when each model is viewed as a linear regression equation for solar radiation. Note that these values are constant for the entire period in M0, constant under a specific month and time in M1 (where is a dummy variable that is set to if the target time of the sample corresponds to and otherwise), and variables depending on the date and hour in M2. In fact, and are defined by 2D tensor product spline functions (where denotes ) with smoothing conditions in the date/hour direction.
In other words, M1 is synonymous with constructing a linear regression model for each hour of the month. M2 is the same type of model as the method described in Section 2.1 in which 2D tensor product spline functions express the regression coefficient and constant terms change smoothly in the date and hour directions. M2 is a more granular model than M1 in that the estimated parameters vary from day to day, and M3 is a more refined model in incorporating nonlinearity in the direction of solar radiation to M2.
3. Machine Learning Methods to Be Compared
To validate the accuracy of the GAM-based forecasting model proposed in the previous section, we also perform forecasts using multiple ML methods. Next, we introduce four popular ML algorithms, kNN, ANN, SVR, and RF, to perform similar forecasts to the previous section using the “caret” package [28] (short for classification and regression training). We also compare the forecast accuracy of our proposed methods using GAMs with these ML techniques.
A brief explanation of these four ML methods is given below.
- k-nearest neighbor (kNN): kNN [13] is one of the simplest yet effective ML algorithms [29]. kNN can be used for classification and regression problems. The main idea is to use the proximity of features to predict the value of new data points. When used for classification problems, the classification of an object is determined by the votes of its neighboring groups of objects (i.e., the most common class in the nearest neighbor groups is assigned to the object). kNN regression, on the other hand, uses the average of the values of the nearest neighbors, or the inverse distance weighted average of the nearest neighbors as the expected result. The kNN algorithm measures the distance between the numerical target parameters and a set of parameters in the dataset, usually the Euclidean distance (which is also used by caret’s “knn”). Other distances, such as the Manhattan distance, can also be used. kNN methods have the challenge of being sensitive to the local structure of the data.
- Artificial Neural Networks (ANN): ANN [9] is “a mathematical model or computational model based on biological neural networks; in other words, it is an emulation of a biological neural system” [30]. The perceptron is the starting point for the neural-network formation procedure. Simply put, the input is received by the perceptron, where it is multiplied by a series of weights and then passed to the activation function of choice (linear, logistic, hyperbolic tangent, or ReLU) to produce the output. A neural network consists of a multilayer perceptron model, which consists of a cascade of perceptron layers: an input layer, a hidden layer, and an output layer. Data are received in the input layer, and the final output is generated in the output layer. The hidden layer, as is commonly known, is located between the input and output layers, where transient computations occur.
- Support vector machine (SVM)/support vector regression (SVR): SVM is considered “one of the most robust and accurate methods among all well-known algorithms” [31]. When used for classification problems, SVMs learn the boundary that most boldly separates a given training sample (maximizing the margin, which is the distance between the boundary and the data). The unique feature of SVM is that it can be combined with the kernel method [32], which is a method for nonlinear data analysis. That is, by using a method that maps data to a finite (or infinite) dimensional feature space using a kernel function and performs linear separation on that feature space, it is possible to apply this method to nonlinear classification problems. When SVM is used for regression, known as support vector regression (SVR), as originally proposed in [10], some properties of the SVM classifier are inherited. That is, the problem is solved in such a way that the error and the weights (regression coefficients) of the mapping functions are minimized simultaneously (see [33] for the formula). This prevents overlearning in a manner similar to ridge regression [34]. SVR has a structure similar to that of kernel ridge regression (KRR), but it is unique in that a loss function called “(linear) ε-insensitive loss functions” (see, e.g., “Figure 1” of [35]) is used to evaluate the prediction error. In this respect, it differs from KRR, which has squared error loss as its loss function [36].
- Random Forest (RF): RF [14] is an ensemble model that combines several prediction models called “decision trees.” It is called “forest” because it consists of a large number of decision trees, and “random” because the decision trees (classification trees or regression trees) are constructed using (which is given in advance) sorts of randomly chosen explanatory variables instead of all explanatory variables. In random forest regression, when new data are given, each generated regression tree predicts the output of the individual prediction, and they are averaged to output the final prediction [14]. The random forest regressor has advantages in that it can solve complex problems on a variety of datasets using different functions and find and unbiased estimate the generalization error; however, it can be overfitted for some datasets and add noisy classification/regression tasks [37].
The caret package, which is used in this study, has been developed to facilitate the use of various ML algorithms [38], which is a very useful tool because it allows the user to manipulate the creation of forecast models, tuning of hyperparameters, and forecasting using the created models. The parameters to be tuned for each of the four methods in the caret package are presented in Appendix C. In caret, the default number of hyperparameters to be tuned (how many ways to evaluate for each hyperparameter) is four, but this number is set to 10 for more precise tuning and to avoid underestimating the prediction accuracy of ML methods as much as possible. We also make all the explanatory variables (including periods) used in the ML models perfectly consistent with those in the GAM.
4. Empirical Analysis
In this section, we present an empirical analysis using observation data from Japan and perform a comprehensive and comparative study between our proposed methods and the ML algorithms explained in the previous section.
4.1. Area-Wide PV Power Generation Forecasting Model
First, we demonstrate the empirical accuracy of the area-wide PV power generation forecasting models constructed in Section 2.1. We estimate each model using in-sample period data from 1 April 2016, to 31 December 2017, and we verify the forecast errors using out-of-sample data from 1 January 1 to 31 December 2018, in nine different power areas. For forecasting area-wide PV power generation, the following observed data are used:
- PV power generation volume (MW): published by nine electricity power companies (e.g., data for the Tokyo area was downloaded from [39])
- PV power capacity (MW): month-end results published by the Ministry of Economy, Trade and Industry [40]
- Weather condition dummy , max (min) temperature () (°C): forecast values (of one major city in each of the nine areas) announced by the JMA on the previous morning [41]
4.1.1. Estimated Trend
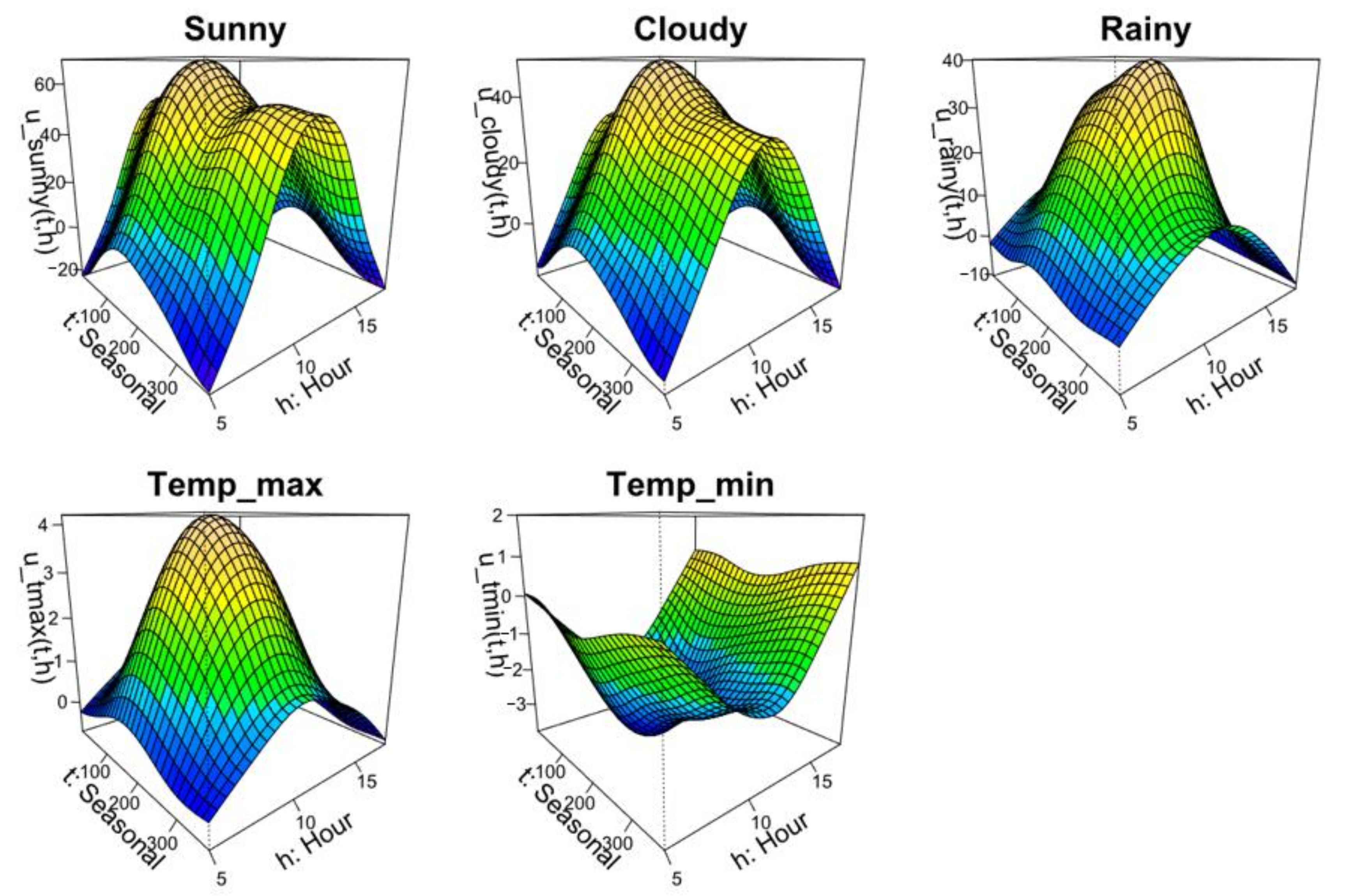
Figure 2 shows the estimated trends (2D tensor product splines in GAM(1)) for the Tokyo area (See Appendix D for estimated trends in all nine areas). It can be confirmed that power generation is greater in the order of sunny, cloudy, and rainy weather. The estimated trend of sunny weather declines in the summer, which reflects the technical fact that PV power generation decreases in efficiency during summer due to high temperatures. The significant decline in the rainy trend in winter is consistent with extreme darkening because the weather tends to change into sleets or snow. While the maximum temperature contributes to increasing power generation, the minimum temperature contributes to decreasing power generation, and this could be interpreted as under a fixed maximum temperature. The lower the minimum temperature (usually recorded around early dawn), the larger the solar radiation during the day (to raise the temperature). For this reason, there is a negative correlation between the minimum temperature and PV power generation.
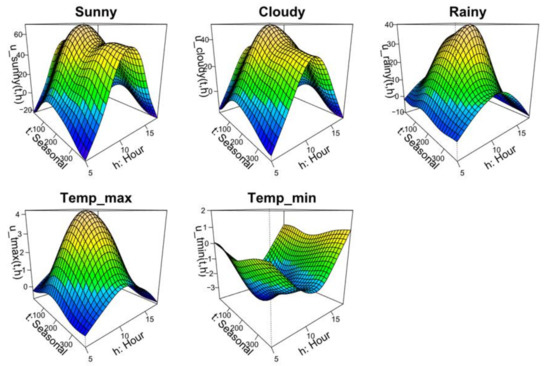
Figure 2.
Estimated trends for areawide PV power generation model (example of Tokyo area). Note: The unit of vertical axis for “Sunny,” “Cloudy” and “Rainy” is (%), and that for “Temp_max” and “Temp_min” is (%/°C). “Seasonal” denotes a yearly cyclical dummy variable (see Section 2.1), and “Hour” denotes the time (o’clock).
4.1.2. Comparison of Forecast Accuracy
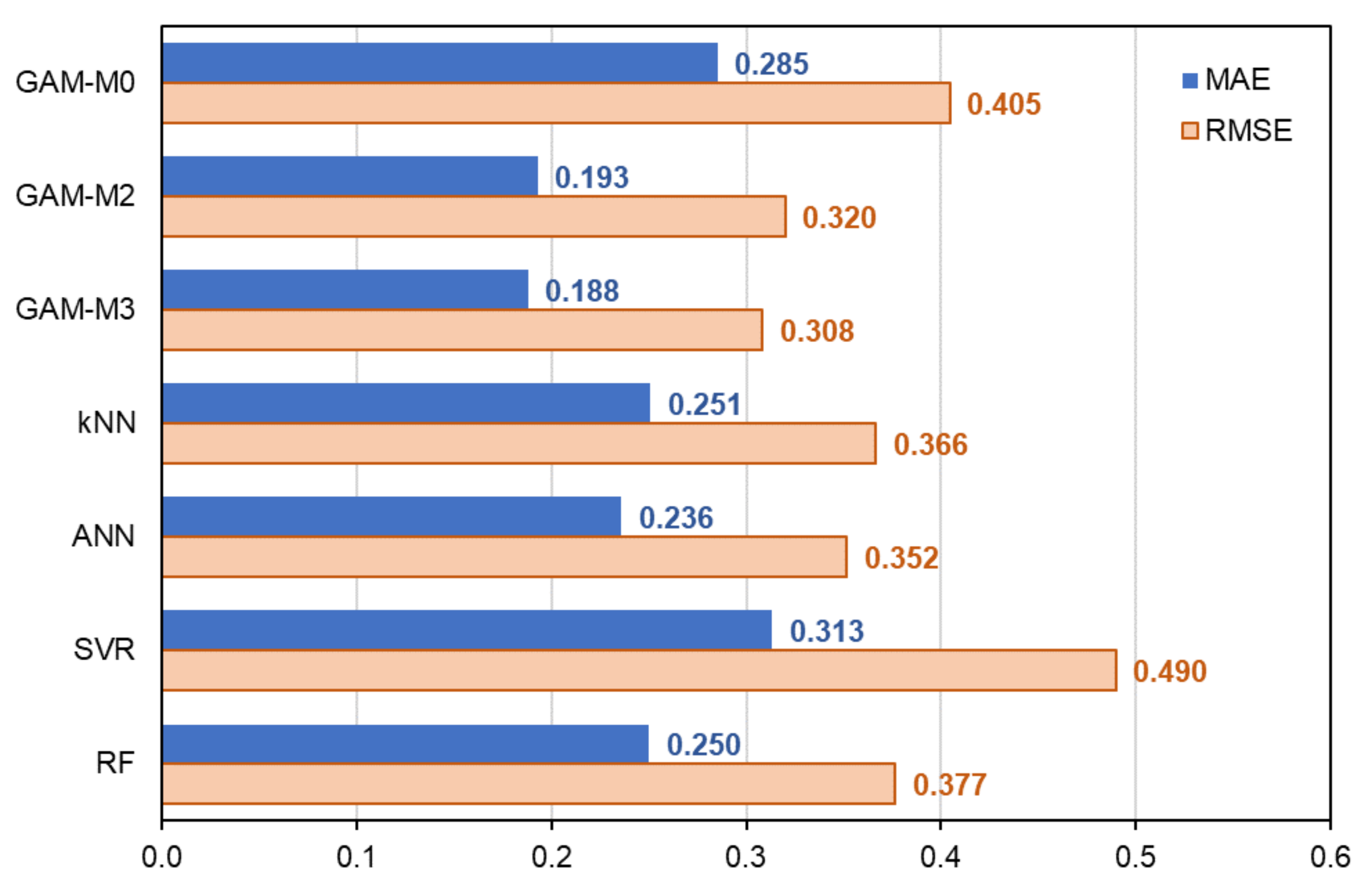
In this section, in order to compare and verify the forecasting accuracy of the four ML methods, Table 1 shows the R-squared (RSQ), mean absolute error (MAE), and root mean square error (RMSE) for each of the nine areas by in-sample and out-of-sample periods, respectively (see e.g., [42] for out-of-sample R-squared statistic). The computation time (in seconds) required for model estimation is also shown. Note that this simulation was run on a system with an Intel Core i9 CPU running at 3.10 GHz with 32 GB RAM (Windows 10), and this is also the case for the computation time in the empirical result in Section 4.2.2 shown later.

Table 1.
Forecasting accuracy and computation time of each method for PV power generation for nine areas.
As the table shows, GAM has the best accuracy indices (RSQ, MAE, and RMSE) among the five models in the out-of-sample period for all area cases. In terms of computation time, GAM is the second shortest after kNN, which is more than an order of magnitude shorter than that of the other three ML methods. Note that the computation time for each ML method includes the time required for tuning the hyperparameters by cross-validation (see Appendix C). However, GAM also performs similar calculations in that it uses cross-validation to find the optimal smoothing parameters (see Appendix B). In addition, it should be noted that we performed parallel computation (which is allowed for the caret package) on 28 cores in this study; the time required for tuning the four ML methods is approximately 1/28th of the original time for a simple calculation [43].
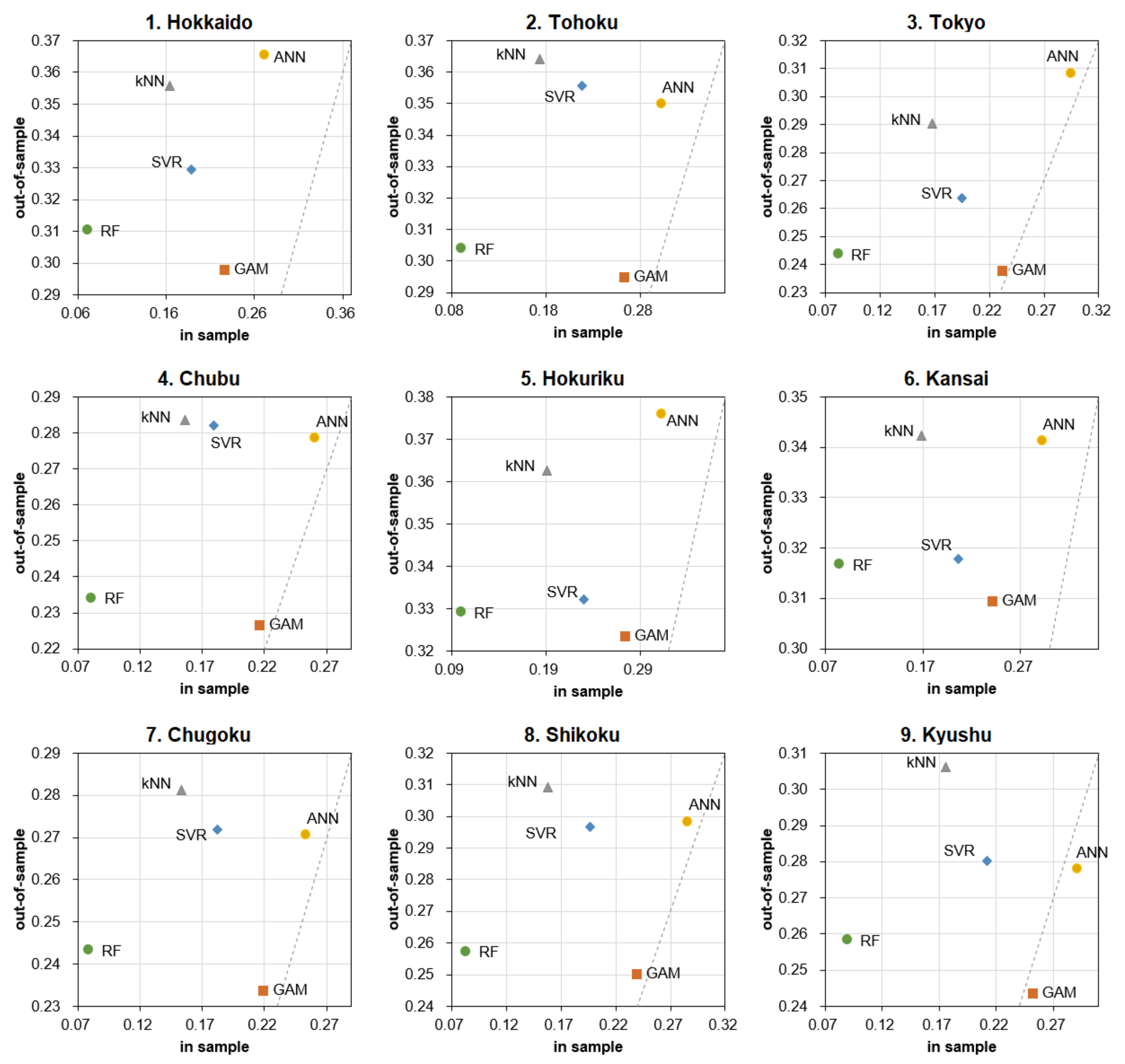
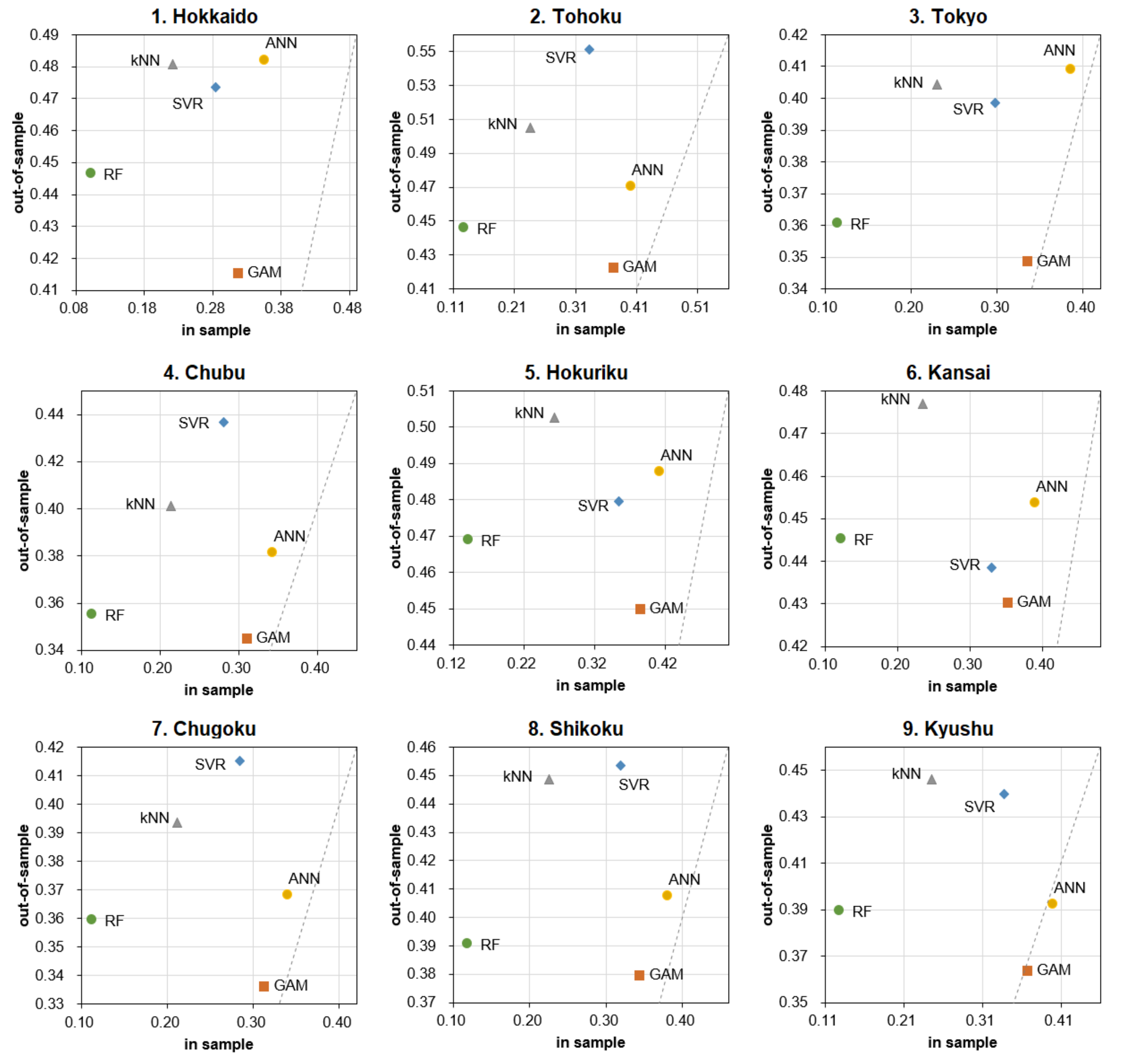
Next, in order to make a comparison between methods for both in-sample and out-of-sample forecast errors easier to understand, these are shown in Figure 3 (MAE) and Figure 4 (RMSE) as scatter plots by nine areas. The dashed lines in each graph represent straight lines where the values of the vertical and horizontal axes are equal (i.e., a 45-degree line). As the graphs show, GAM has the smallest out-of-sample forecast error in all cases, and the model is relatively robust in that it does not deviate significantly from the dashed line (i.e., it has the same level of accuracy in the out-of-sample as in-sample). The same is true for ANN in that it does not deviate from the 45-degree line, but it is still inferior to GAM in terms of out-of-sample prediction accuracy (in any case) because of the relatively poor fit of the original model (large in-sample prediction error).

Figure 3.
MAE of each method on PV power generation in nine areas.
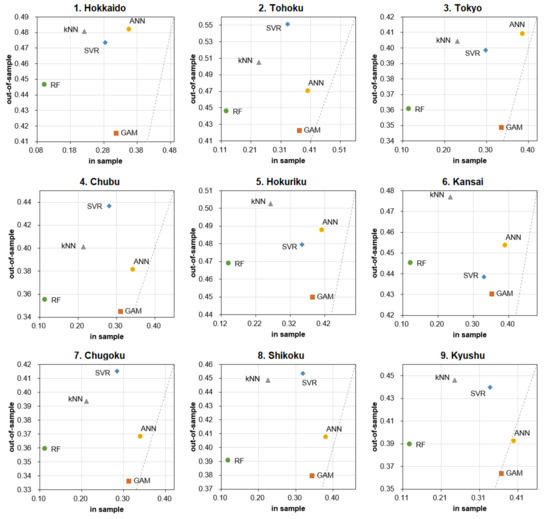
Figure 4.
RMSE of each method on PV power generation in nine areas.
Characteristically, the in-sample forecast errors of RF are minimal in all cases but the out-of-sample errors are larger than GAM. As explained in Section 3, this result reflects the fact that RF regression is prone to overlearning (the fitting image of RF regression is intuitive in the graph in “Section 2” of [44]). However, note that RF is relatively more accurate than the other ML methods even in terms of out-of-sample prediction error; if the sample size in the in-sample period had been sufficiently large, it is possible that the out-of-sample forecast error would have been even smaller. Additionally, although RF showed the longest computation time, it may be possible to reduce the computation time significantly by using a GPU environment instead of a CPU, since parallel computation is possible for the calculation of each decision tree, but such an investigation is left for future work (the same consideration also applies to the empirical results in Section 4.2.2).
4.2. Individual PV Power Generation Forecasting Model
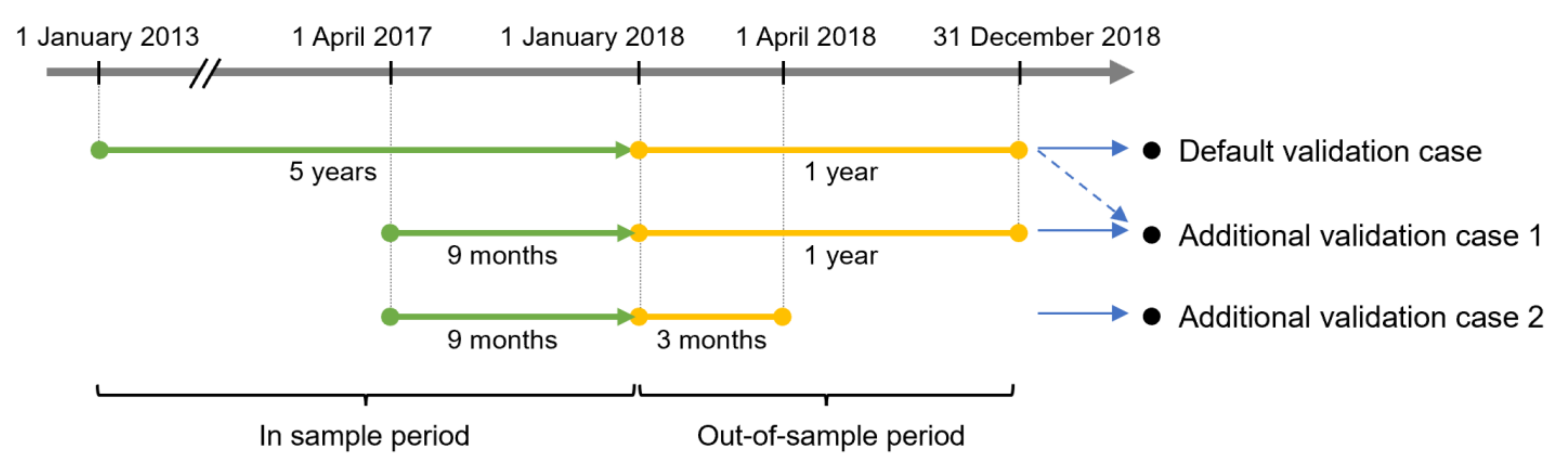
In this section, we present an empirical analysis of the individual PV power generation models constructed in Section 2.2. We estimate each model using in-sample period data from 1 January 2013, to 31 December 2017, and we verify the forecast errors using out-of-sample data from 1 January to 31 December 2018. Note that only when we conduct additional empirical analysis in the second half of Section 4.2.2 will we conduct forecast error analysis when varying the in-sample or out-of-sample period, which will be defined again at that time (note that they are also summarized in Figure 5 in advance). For the forecast of individual PV power generation, the following observed data are used:
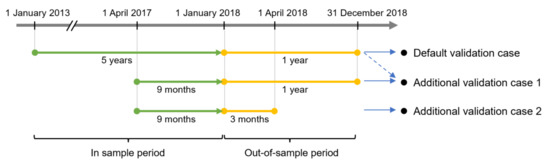
Figure 5.
The relationship between in-sample and out-of-sample periods of each validation case for the individual PV power generation forecasting model. Note: “Default validation case” corresponds to Figure 6 and Figure 7 and Table 1; “Additional validation case 1” corresponds to Figure 8 and Figure A2; “Additional validation case 2” corresponds to Figure 9.
- PV power generation volume (MW): measured value of the household’s solar power system (with the permission of the owner, we use the data of a private roof-mounted power system in Hiroshima city, Japan).
- Solar radiation (MJ/m2): Measured solar radiation in Hiroshima City as published by the JMA [45].
For solar radiation , this study uses actual measured values that are available free of charge for the purpose of comparison among models, considering that there is no essential difference in whether to use forecast values or measured values in the comparison between models. Incidentally, weather forecasts of the JMA have been reported to be effective in forecasting electricity time series up to about one week ahead [46], and it may be possible to compare models under different forecast horizons, but such analysis is a future issue.
4.2.1. Estimated Trend
Figure 6 shows the trend estimated for M3’s 3D tensor product spline function in GAM (3) by hour . The surface on the 2D coordinates of the date and solar radiation at each hour changes gradually with the hour. It should be noted that the slope of the PV generation with respect to the solar radiation tends to decrease (and even diminish with solar radiation) from spring to early summer, when the solar radiation is large at each time. This reflects the technical characteristics of PV panels, where the power generation efficiency decreases as the temperature (solar radiation) increases.
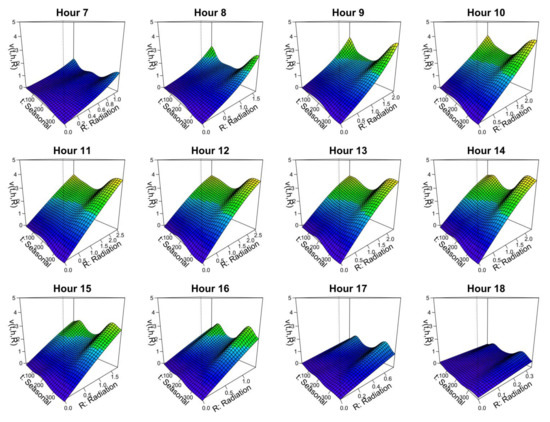
Figure 6.
Trend estimation results for the M3 model (estimated from 5 years of in-sample data). Note: The units of vertical axis and “Radiation” axis are (MW) and (MJ/m2), respectively. “Seasonal” denotes a yearly cyclical dummy variable (see Section 2.1).
4.2.2. Comparison of Forecast Accuracy
Table 2 shows the results of the comparison of the forecast error and computation time for each model. The results are discussed from two perspectives: the comparison between statistical models (M0-M3) and the comparison between GAM (M3) and ML methods, which are shown in the following two subsections.

Table 2.
Forecasting accuracy and computation time of each method for individual PV power generation.
Comparison of Forecast Accuracy among Statistical Models
In this section, we analyze the results in terms of comparison between the statistical models (M0 to M3). Since this study is the first attempt to apply 3D tensor product spline functions to energy time series data forecasting, it would be interesting to examine the effect of adding smoothing (nonlinear) conditions in multiple directions on the accuracy.
First, as seen in Table 2, the overall forecast accuracy is generally the highest for M3 for both in-sample and out-of-sample, while M0, which assumes a constant linear regression equation for the whole year, is significantly less accurate than the other models. The MAE and RMSE of M1 are better than M2 (comparable to M3) in the in-sample, but worse than M2 in the out-of-sample. This can be interpreted as M1 building a different linear model for each month and time, which makes it less robust than M2 and M3, where smoothing conditions are imposed in the date direction.
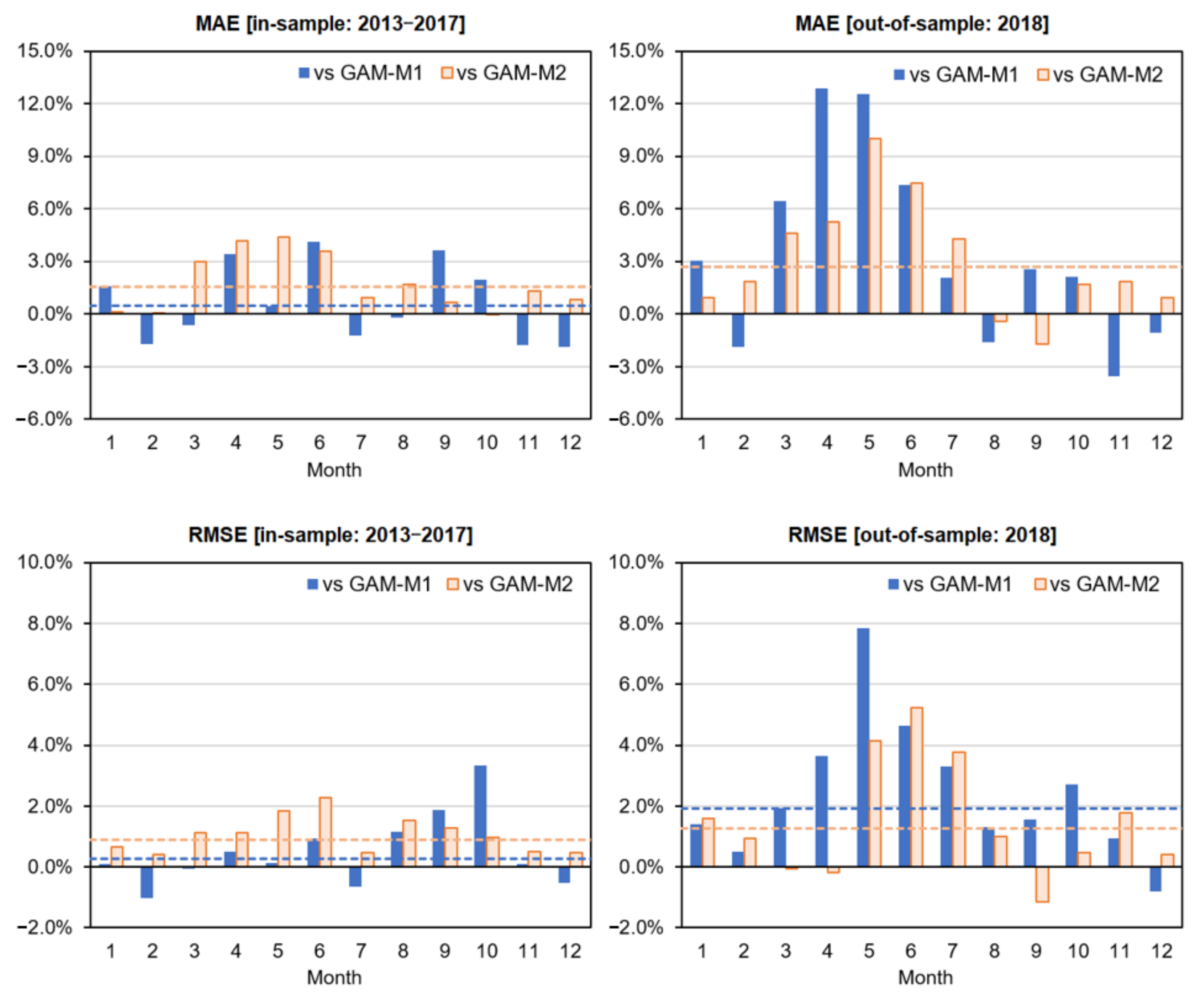
Next, to obtain a more detailed understanding of the effect of incorporating the nonlinearity between PV generation and solar radiation in the M3 model, we compare the prediction errors between models on a monthly basis. Figure 7 plots the relative error increments for the MAE (or RMSE) of both M1 and M2 relative to the MAE (or RMSE) of M3 by month (e.g., MAE, ). It can be seen that the relative errors (MAE and RMSE) of M1 and M2, both of which are linear models with respect to solar radiation, are particularly large during the spring and early summer months in the out-of-sample period. This is consistent with the fact that the slope of M3 diminished in relation to the solar radiation during the same period when the solar radiation increased, as is confirmed in Figure 6. This means that the nonlinearity that exists between PV generation and solar radiation during the same period was modeled relatively robustly in M3. In addition, although the forecast errors of M1 did not differ significantly from M3 during the in-sample period, the error increased for the out-of-sample period. This result also suggests that M1, which does not have a smoothing condition, had an undesirable (excessive) model fitting by month.
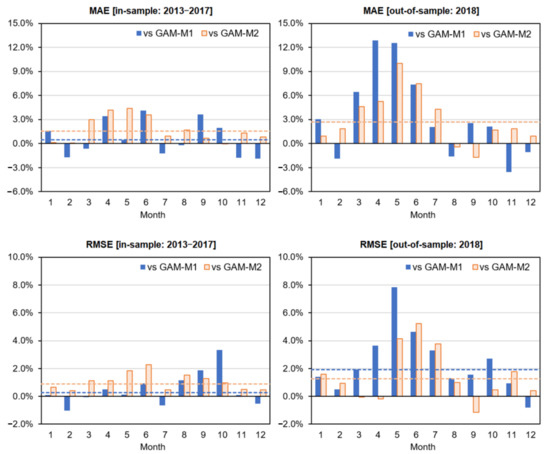
Figure 7.
Monthly relative forecast error (MAE and RMSE) of M1 and M2 with respect to M3. Note: The dashed line is the relative increment of the forecast error to M3 over the period (the out-of-sample MAEs overlap the two because they are equal). This is “Default validation case” in Figure 5.
Comparison of Forecasting Accuracy between GAM and ML Methods
Next, in this section, we compare the prediction accuracies of GAM and ML. As seen in the previous section, M3 was the model with the highest forecast accuracy among the GAMs (including linear models), so we omitted the M0–M2 models and dealt only with the M3 model (in this section, the term “GAM” refers solely to M3).
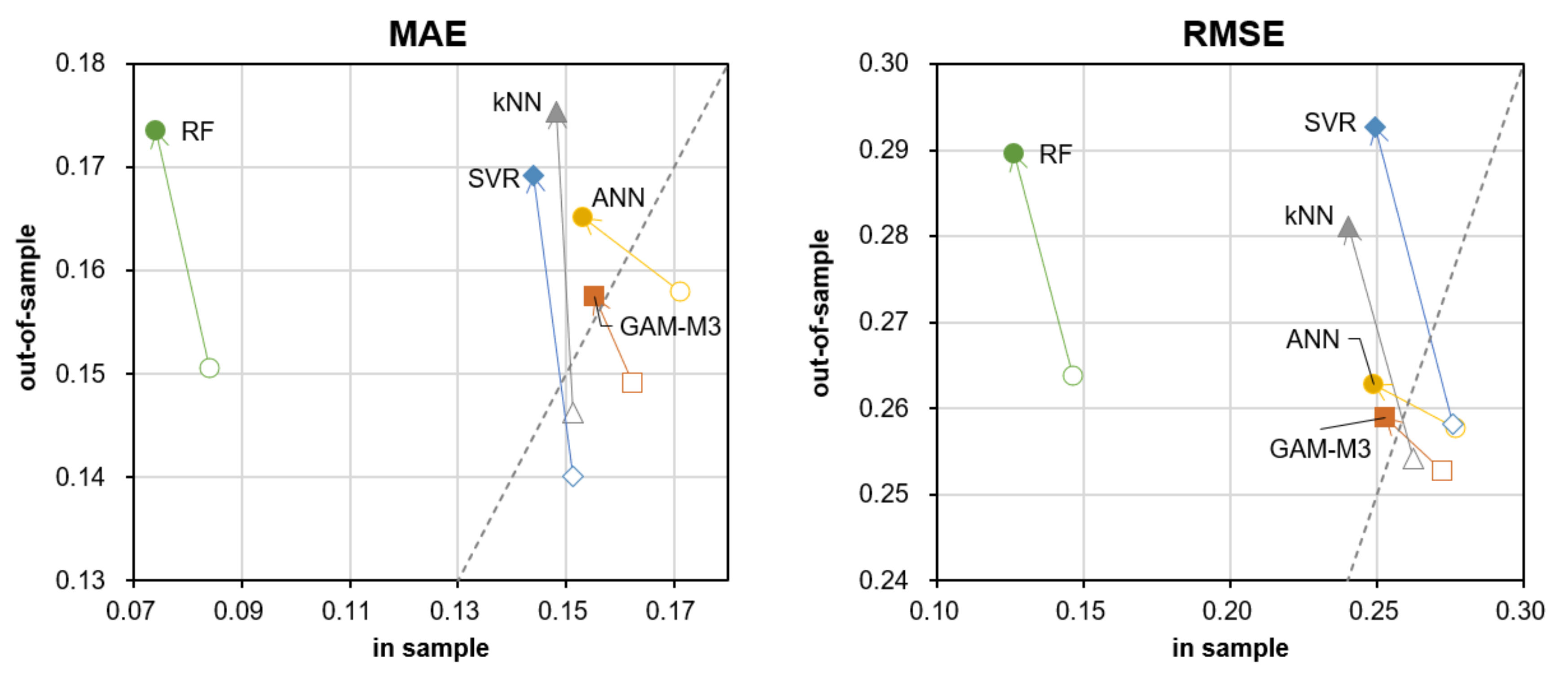
As can be seen in Table 2, in the comparison between GAM and the four ML methods, RF has the best fit in the in-sample, which is the same result as that of the area-wide PV generation model in Section 4.1.2. On the other hand, in terms of out-of-sample forecast errors, SVR is the best for MAE, and GAM is the best for RSQ and RMSE; the reason why SVR is the best for MAE is presumably because the objective function of SVR is close to MAE minimization. As mentioned in Section 3, SVR uses linear ε-insensitive loss functions (as shown in “Figure 1” of [35]), but because ε is relatively small, SVR can be said to approximately minimize the MAE.
In any case, it is true that GAM is a highly superior model overall in terms of computation time and ease of interpretation with intuitive visualization. However, it should be noted that when compared with the forecast accuracy results of the area-wide PV power generation model examined in Section 4.1.2, the results in this section seem to indicate that the superiority of GAM may not be so clear (at least, it is inferior to SVR and kNN in MAE).
One of the reasons for this may be the following: the area-wide PV generation model had a large number of incorporated explanatory variables, even though the period of the data used was relatively short (about a year and a half). That is, in the GAM, the “model structure”—which is based on rational human reasoning—was able to be taught in advance such that the sensitivities of the various explanatory variables (weather conditions and temperatures) each have a daily smooth yearly cyclical trend, along with a smooth trend in the orthogonal time direction. On the other hand, the individual PV model is a relatively simple model that only estimates a smooth trend in the three directions, which means that the ML methods (without prior knowledge of the existence of the multi-dimensional smooth trends) were able to estimate it reasonably effectively. In other words, when the modeling practitioner recognizes or detects the existence of a global model structure that is difficult to learn from the data alone, a statistical model, such as GAM, has an advantage in that it is relatively easy to describe it in the formulation to facilitate accurate forecasts.
To make this consideration more credible, in the following, we will assume a case where the in-sample period is short (a missing period is intentionally created), and an experiment to see how the accuracy of each forecasting method changes in that case. Below, we separately calculate the case where the in-sample period is from 1 April to 31 December 2017 (9 months), and plot in Figure 8 how the forecast error for out-of-sample (2018) changes from the original case where the in-sample period is 1 January 2013 to 31 December 2017 (5 years); the latter is already calculated in Table 2. In other words, the newly estimated model here contains missing data from January to March.
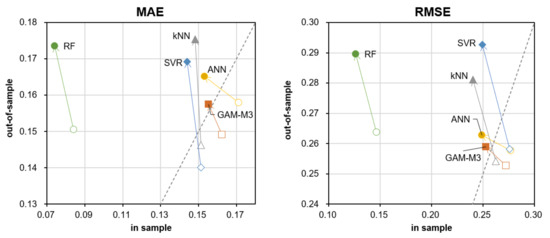
Figure 8.
MAE and RMSE of each method on individual PV power generation (change in forecast error by method when the in-sample period is shortened). Note: White dots represent the 5-year in-sample period (corresponding to values in Table 2), and color-filled dots represent the 9-month in-sample period. Out-samples were both 2018 (i.e., this is “Additional validation case 1” in Figure 5).
As can be seen from the graphs, when the in-sample period is shortened, the in-sample forecast error (MAE or RMSE) becomes smaller, but the out-of-sample forecast error becomes larger, which is common to all forecasting methods. This result is consistent with the intuition that the shorter the period, the better the fit of each model, but the less robust it will tend to be. More interestingly, while kNN, SVR, and RF significantly deteriorated the out-of-sample accuracy (when missing periods were included), GAM and ANN did not, and were relatively robust in trend completion for missing values. As a result, GAM had the smallest MAE and RMSE for the 9-month case. The reason for the robustness of the ANN suggests that some trend completion may have occurred in the hidden layer. On the other hand, kNN, SVR, and RF are unsuitable for trend estimation (especially extrapolation) that complements missing periods.
In the following, in order to make the performance comparison of trend completion clearer, using the estimated model based on nine months of in-sample data from 1 April to 31 December 2017, we compare the forecast errors measured from the following three months of out-of-sample data (1 January to 31 March 2018) in Figure 9. Note that in practice, insufficient historical data is common, especially for new entrants. This result clearly shows that the prediction errors of kNN, SVR, and RF by extrapolation are relatively large. In particular, the extremely poor prediction error of SVR may be due to the radial basis function (RBF) kernel used, which is also called a local kernel and is suitable for interpolation but not for extrapolation (see “Figure 8” in [47]). It has also been proposed that SVR methods can be improved by combining them with polynomial kernels (global kernels) [47], but the improvement of ML algorithms is beyond the scope of this study.
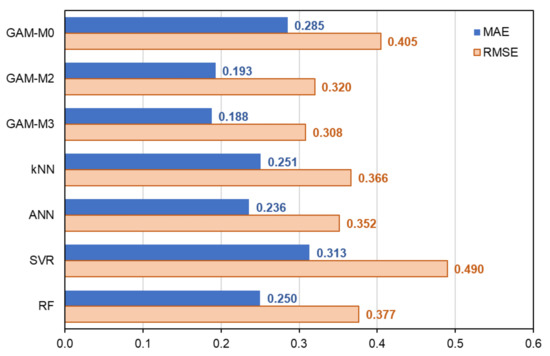
Figure 9.
Comparison of forecast errors for the next three months when the model is estimated from nine months of data. Note: The in-sample period is 9 months, from 1 April to 31 December 2017; the out-of-sample period is 3 months, from 1 January to 31 March 2018 (i.e., this is “Additional validation case 2” in Figure 5). The reason for the absence of GAM-M1 is that model estimation is not possible because of the lack of in-sample data for the same month.
For reference, Figure A2 in Appendix E shows the trend of the 3D tensor product spline function estimated from nine months of in-sample data from 1 April to 31 December 2017. It can be seen that even though there is no data for January–March, the shape is almost the same as in Figure 6, which uses data for five full years, and smooth trend estimation in the solar radiation and hour directions is achieved. This result also confirms the robustness of our GAM-based model.
5. Conclusions
This study proposed and validated a GAM-based model with multidimensional tensor product splines to support the forecasting of PV power generation in practice. In summary, our contribution lies in the following points:
- We constructed different GAM-based forecasting models for area-wide PV power generation and individual PV power generation, and demonstrated the effectiveness of the models by visualizing the estimated trends and providing reasonable interpretations.
- For the individual PV power generation model, we constructed a new forecasting model using 3D tensor product splines and demonstrated its effectiveness. We quantitatively demonstrated that the robustness and forecasting accuracy of the model increased when smoothing (nonlinear) conditions were incorporated in three directions by comparing it with linear models.
- By comparing the proposed GAM-based models with other popular ML methods, such as kNN, ANN, SVR, and RF for each PV power model, it was shown that the GAM-based models have advantages in terms of computational speed and forecast error minimization. Specifically, we have shown that the GAM-based model is highly effective for global nonlinear trend completion.
In general, ML has been reported to be superior to statistical models in terms of predictability. However, this study showed that our forecasting approach using GAM may have several advantages over ML methods, such as interpretability, robustness, computational load, and forecasting accuracy. Moreover, when the existence of a smooth (periodic) trend is inferred in advance, the GAM may capture the structure and provide better forecasting accuracy. For example, in this study, the 2D tensor product spline model was formulated in advance that the coefficients of each variable of weather and temperature should have smoothly connected trends in the seasonal and time directions, respectively. The 3D model was described as having a smooth trend in the directions of seasonal, time, and solar radiation. In addition, the cyclic cubic spline function was used to incorporate the condition that the seasonal trends are connected at the start and end points of the yearly cycle.
A statistical model, such as GAM, has various advantages in practical use, such as ease of reflecting the model designer’s prior knowledge, understanding the results intuitively, and explaining them to others. In particular, it has the advantage that the recognized global model structure can be formulated (taught) in advance, which makes it easier to build a reasonable and robust model compared to ML methods that recognize patterns from data only. Therefore, the descriptiveness of the model (with high interpretability) is an important factor that potentially contributes to an improvement in accuracy. In conclusion, it may be fair to say that our GAM-based models with multi-dimensional tensor product splines provide a promising forecast approach for practitioners that require model tractability, reliability, and forecasting accuracy in the PV business.
Author Contributions
Conceptualization, Y.Y.; methodology, T.M.; software, T.M.; validation, T.M.; data curation, T.M.; writing—original draft preparation, T.M.; writing—review and editing, Y.Y.; visualization, T.M.; supervision, Y.Y.; project administration, Y.Y.; funding acquisition, T.M. and Y.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded by a Grant-in-Aid for Scientific Research (A) 20H00285, Grant-in-Aid for Challenging Research (Exploratory) 19K22024, and Grant-in-Aid for Young Scientists 21K14374 from the Japan Society for the Promotion of Science (JSPS).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Please contact the authors.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| measured PV power generation volume at date , hour | |
| installed PV power capacity at date , hour | |
| unit power generation at date , hour | |
| dummy variables, which are 1 if the forecast general weather condition at date hour is the same as the suffix’s weather condition, or 0 otherwise | |
| yearly cyclical dummy variables | |
| , | previous day’s maximum or minimum temperature forecast at date |
| , | maximum or minimum temperature forecast deviation at date (observed temperature forecast minus its trend) |
| 2D tensor product spline functions estimated by the GAM of the area-wide PV power forecast model ( denote ) | |
| univariate spline functions estimated by the GAM of the temperature trend model ( denote ) | |
| residual terms with the average of 0 | |
| forecast solar radiation at date , hour | |
| , | coefficients and constant terms for the individual PV power generation models when each model is viewed as a linear regression equation for solar radiation (constant for M0 and M1, or variables defined by 2D tensor product spline function for M2) |
| 3D tensor product spline functions estimated by the GAM of the individual PV power forecast model ( denote ) |
Appendix A. Installed Capacity Trend Estimation for Area PV Generation Forecasting
The area-wide PV power capacity is modeled by the following ordinary least squares regression (OLS):
where and are the coefficient and intercept, respectively, estimated by the OLS (A1), is the (annualized) daily dummy variable representing the number of years that have passed, and is the residual term. Using this equation, the forecast capacity can be obtained as follows.
Note that the original observed capacity is monthly data with some missing values, but the forecast value can be obtained as daily granularity data because we use the daily dummy .
Appendix B. Smoothing Spline Functions
The univariate smoothing spline function is estimated as the function that minimizes the penalized residual sum of squares (PRSS), given by
In (A3), the first term measures the approximation of the data, and the second term (penalty term) adds penalties according to the magnitude of the curvature of the function. In this study, we construct the GAM using the R package “mgcv” [48] to obtain a series of smoothing spline functions, where the smoothing parameter is calculated using a general cross-validation criterion.
When estimating the 2D (3D) tensor product spline function (), the following penalty term () is included in the PRSS that should be minimized [25]:
Thus, the tensor product spline function can incorporate independent smoothing conditions for each variable (direction). Previous studies that applied 2D tensor product splines to different energy time series data include [49,50], where the tensor product spline functions are used for pricing weather derivatives for risk hedging rather than for forecasting models.
Appendix C. Hyperparameters to be Tuned for the Caret Package
The four ML methods in this study are automatically tuned by the caret package, and the hyperparameters to be tuned for each method are listed in Table A1 [51]. For details of the parameters, please refer to the references of each package. (Note that in the caret package, epsilon in the “ε-insensitive loss functions” of SVM (SVR) is not tuned, and the default value of 0.1 is used.)

Table A1.
Hyperparameters to be tuned in the four ML methods used in this study.
Table A1.
Hyperparameters to be tuned in the four ML methods used in this study.
| Model | Method Value | Package | Tuning Parameters | |
|---|---|---|---|---|
| kNN | knn | caret [28] | k | Number of neighbors considered |
| ANN | nnet | nnet [52] | decay | The parameter for weight decay |
| size | Number of units in the hidden layer | |||
| SVM (SVR) | svmRadial | kernlab [53] | sigma | The inverse kernel width used by the Gaussian kernel |
| C | The cost regularization parameter, which controls the smoothness | |||
| RF | rf | randomForest [54] | mtry | Number of variables randomly sampled as candidates at each split |
In the caret package, the parameter “tuneLength” (set to 4 by default) allows the user to select the number of tunings (how many different scenarios of each hyperparameter are compared and verified) for the target hyperparameters. In this study, by setting this parameter to 10, we tuned 10 scenarios for “knn” and “rf,” and 100 scenarios for “nnet” and “svmRadial”. For the evaluation method of the tuning, we adopted caret’s default method of 10-fold cross-validation (i.e., cross-validation was performed by dividing the training data into 10 equal parts).
Appendix D. Estimated Trends for Areawide PV Power Generation Model
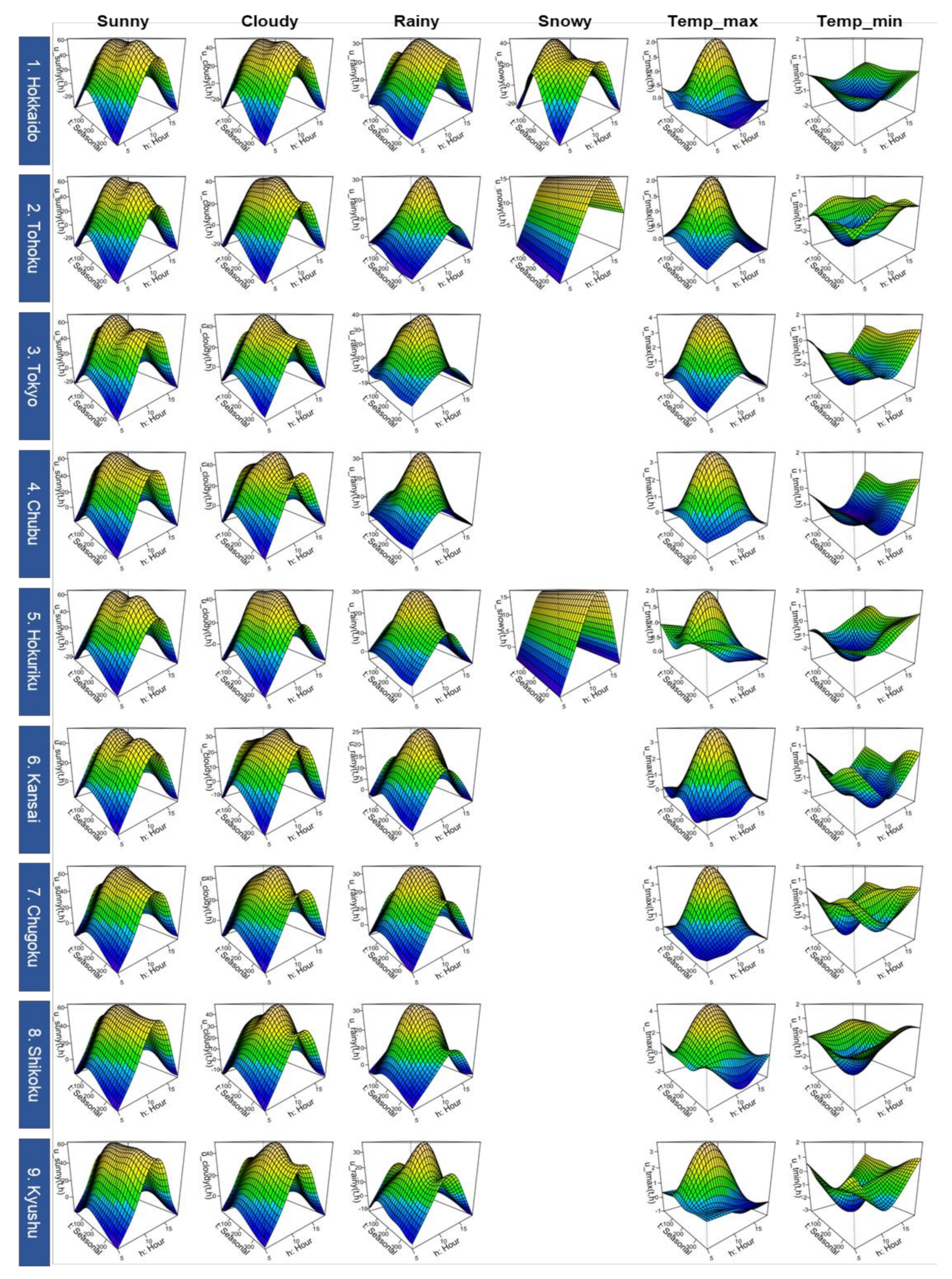
As shown in Figure A1, the estimated trends of the 2D tensor product spline functions for each of the nine areas are generally similar in shape, although there are some differences among the areas (the interpretation of the trend shapes described in Section 4.1.1 is common to all areas). If we look at the details, we can see that in Hokkaido, an area of high latitude, power generation is relatively level throughout the seasons (e.g., the decline of the rainy trend in winters is relatively small), and the seasonal trend of snow is extracted relatively clearly. The reason why Tohoku and Hokuriku, which are other snowfall areas, do not have such seasonal snowy trends, is perhaps because the sample sizes of snowy weather of these areas were not large enough.
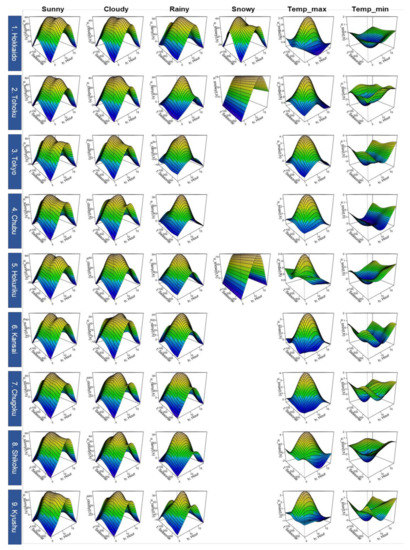
Figure A1.
Estimated trends for areawide PV power generation model (all nine areas). Note: The unit of vertical axis for “Sunny,” “Cloudy,” “Rainy” and “Snowy” is (%), and that for “Temp_max” and “Temp_min” is (%/°C). “Seasonal” denotes a yearly cyclical dummy variable (see Section 2.1), and “Hour” denotes the time (o’clock).
Figure A1.
Estimated trends for areawide PV power generation model (all nine areas). Note: The unit of vertical axis for “Sunny,” “Cloudy,” “Rainy” and “Snowy” is (%), and that for “Temp_max” and “Temp_min” is (%/°C). “Seasonal” denotes a yearly cyclical dummy variable (see Section 2.1), and “Hour” denotes the time (o’clock).
Appendix E. Trend Estimation Results for the M3 Model (Estimated from 9 Months of In-Sample Data)
The estimation results of the 3D tensor product spline function of the individual PV power generation model for the in-sample period from 1 April to 31 December 2017 are shown in Figure A2. All graphs have almost the same shape as the estimation results when the in-sample period is five years from 2013 to 2017 (Figure 6), indicating that the 3D tensor product spline function is highly robust.
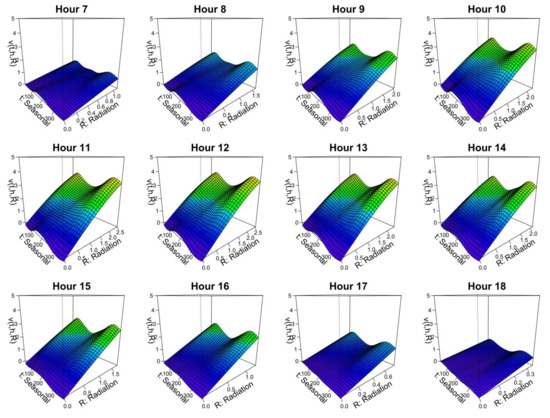
Figure A2.
Trend estimation results for the M3 model (estimated from 9 months of in-sample data). Note: The units of vertical axis and “Radiation” axis are (MW) and (MJ/m2), respectively. “Seasonal” denotes a yearly cyclical dummy variable (see Section 2.1).
Figure A2.
Trend estimation results for the M3 model (estimated from 9 months of in-sample data). Note: The units of vertical axis and “Radiation” axis are (MW) and (MJ/m2), respectively. “Seasonal” denotes a yearly cyclical dummy variable (see Section 2.1).
References
- Matsumoto, T.; Yamada, Y. Prediction method for solar power business based on forecasted general weather conditions and periodic trends by weather. Trans. Mater. Res. Soc. Jpn. 2019, 62, 1–22. (In Japanese) [Google Scholar] [CrossRef]
- Antonanzas, J.; Osorio, N.; Escobar, R.; Urraca, R.; Martinez-de-Pison, F.J.; Antonanzas-Torres, F. Review of photovoltaic power forecasting. Sol. Energy 2016, 136, 78–111. [Google Scholar] [CrossRef]
- Pelland, S.; Remund, J.; Kleissl, J.; Oozeki, T. Photovoltaic and Solar Forecasting: State of the Art; Report PVPS T14-10; International Energy Agency: Paris, France, 2013. [Google Scholar]
- Kato, T. Development of forecasting method of photovoltaic power output. J. IEEJ 2017, 137, 101–104. (In Japanese) [Google Scholar] [CrossRef]
- Raza, M.Q.; Nadarajah, M.N.; Ekanayake, C. On recent advances in PV output power forecast. Sol. Energy 2016, 136, 125–144. [Google Scholar] [CrossRef]
- Mosavi, A.; Salimi, M.; Faizollahzadeh Ardabili, S.; Rabczuk, T.; Shamshirband, S.; Varkonyi-Koczy, A.R. State of the art of machine learning models in energy systems, a systematic review. Energies 2019, 12, 1301. [Google Scholar] [CrossRef] [Green Version]
- Das, U.K.; Tey, K.S.; Seyedmahmoudian, M.; Mekhilef, S.; Idris, M.Y.I.; Van Deventer, W.; Horan, B.; Stojcevski, A. Forecasting of photovoltaic power generation and model optimization: A review. Renew. Sustain. Energy Rev. 2018, 81, 912–928. [Google Scholar] [CrossRef]
- Sobri, S.; Koohi-Kamali, S.; Rahim, N.A. Solar photovoltaic generation forecasting methods: A review. Energy Convers. Manag. 2018, 156, 459–497. [Google Scholar] [CrossRef]
- Ripley, B.D. Pattern Recognition and Neural Networks; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Drucker, H.; Burges, C.C.; Kaufman, L.; Smola, A.J.; Vapnik, V.N. Support vector regression machines. In Advances in Neural Information Processing Systems 9, NIPS 1997; MIT Press: Cambridge, MA, USA, 1996; pp. 155–161. [Google Scholar]
- Maitanova, N.; Telle, J.S.; Hanke, B.; Grottke, M.; Schmidt, T.; Maydell, K.V.; Agert, C. A machine learning approach to low-cost photovoltaic power prediction based on publicly available weather reports. Energies 2020, 13, 735. [Google Scholar] [CrossRef] [Green Version]
- Mohammed, A.A.; Aung, Z. Ensemble learning approach for probabilistic forecasting of solar power generation. Energies 2016, 9, 1017. [Google Scholar] [CrossRef]
- Altman, N.S. An introduction to kernel and nearest-neighbor nonparametric regression. Am. Stat. 1992, 46, 175–185. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Das, U.K.; Tey, K.S.; Seyedmahmoudian, M.; Idris, M.Y.I.; Mekhilef, S.; Horan, B.; Stojcevski, A. SVR-based model to forecast PV power generation under different weather conditions. Energies 2017, 10, 876. [Google Scholar] [CrossRef]
- Rosato, A.; Altilio, R.; Araneo, R.; Panella, M. Prediction in photovoltaic power by neural networks. Energies 2017, 10, 1003. [Google Scholar] [CrossRef] [Green Version]
- Khandakar, A.; Chowdhury, M.E.H.; Khoda Kazi, M.; Benhmed, K.; Touati, F.; Al-Hitmi, M.; Gonzales, J.S. Machine learning based photovoltaics (PV) power prediction using different environmental parameters of Qatar. Energies 2019, 12, 2782. [Google Scholar] [CrossRef] [Green Version]
- Nespoli, A.; Ogliari, E.; Leva, S.; Massi Pavan, A.; Mellit, A.; Lughi, V.; Dolara, A. Day-ahead photovoltaic forecasting: A comparison of the most effective techniques. Energies 2019, 12, 1621. [Google Scholar] [CrossRef] [Green Version]
- Abdel-Nasser, M.; Mahmoud, K. Accurate photovoltaic power forecasting models using deep LSTM-RNN. Neural Comput. Appl. 2019, 31, 2727–2740. [Google Scholar] [CrossRef]
- Matsumoto, T. Forecast Based Risk Management for Electricity Trading Market. Ph.D. Thesis, University of Tsukuba, Tokyo, Japan, 2020. [Google Scholar]
- Hastie, T.; Tibshirani, R. Generalized Additive Models; Chapman and Hall: London, UK, 1990. [Google Scholar]
- Matsumoto, T.; Yamada, Y. Construction of forecast model for power demand and PV power generation using tensor product spline function. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2021; Volume 812, p. 012001. [Google Scholar]
- Sundararajan, A.; Ollis, B. Regression and generalized additive model to enhance the performance of photovoltaic power ensemble predictors. IEEE Access 2021, 9, 111899–111914. [Google Scholar] [CrossRef]
- Gadiwala, M.S.; Usman, A.; Akhtar, M.; Jamil, K. Empirical models for the estimation of global solar radiation with sunshine hours on horizontal surface in various cities of Pakistan. Pak. J. Meteorol. 2013, 9, 43–55. [Google Scholar]
- Wood, S.N. Generalized Additive Models: An Introduction with R; Chapman and Hall: London, UK, 2017. [Google Scholar]
- Matsumoto, T.; Yamada, Y. Customized yet Standardized temperature derivatives: A non-parametric approach with suitable basis selection for ensuring robustness. Energies 2021, 14, 3351. [Google Scholar] [CrossRef]
- Japan Meteorological Business Support Center. Available online: http://www.jmbsc.or.jp/jp/online/file/f-online10200.html (accessed on 26 October 2021).
- Kuhn, M.; Wing, J.; Weston, S.; Williams, A.; Keefer, C.; Engelhardt, A.; Cooper, T.; Mayer, Z.; Kenkel, B.; Benesty, M.; et al. Package Caret. Available online: https://cran.r-project.org/web/packages/caret/caret.pdf (accessed on 26 October 2021).
- Cherkassky, V.; Mulier, F.M. Learning from Data: Concepts, Theory, and Methods; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Singh, Y.; Chauhan, A.S. Neural networks in data mining. J. Theor. Appl. Inf. Technol. 2009, 5, 37–42. [Google Scholar] [CrossRef]
- Wu, X.; Kumar, V.; Quinlan, J.R.; Ghosh, J.; Yang, Q.; Motoda, H.; McLachlan, G.; Ng, A.; Liu, B.; Yu, P.; et al. Top 10 algorithms in data mining. Knowl. Inf. Syst. 2008, 14, 1–37. [Google Scholar] [CrossRef] [Green Version]
- Aizerman, M. Theoretical foundations of the potential function method in pattern recognition learning. Autom. Remote Control 1964, 25, 821–837. [Google Scholar]
- Friedman, J.; Hastie, T.; Tibshirani, R. The Elements of Statistical Learning; Springer Series in Statistics: New York, NY, USA, 2001; Volume 1, Available online: https://web.stanford.edu/~hastie/ElemStatLearn/printings/ESLII_print12_toc.pdf (accessed on 26 October 2021).
- Marquardt, D.W.; Snee, R.D. Ridge regression in practice. Am. Stat. 1975, 29, 3–20. [Google Scholar]
- Smola, A.J.; Schölkopf, B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef] [Green Version]
- Scikit-learn. Kernel Ridge Regression. 2018. Available online: http://scikit-learn.org/stable/modules/kernel_ridge.html (accessed on 26 October 2021).
- Dutta, A.; Dureja, A.; Abrol, S.; Dureja, A. Prediction of ticket prices for public transport using linear regression and random forest regression methods: A practical approach using machine learning. In International Conference on Recent Developments in Science, Engineering and Technology; Springer: Singapore, 2019; pp. 140–150. [Google Scholar]
- Kuhn, M. Building predictive models in R using the caret package. J. Stat. Softw. 2008, 28, 1–26. [Google Scholar] [CrossRef] [Green Version]
- Tokyo Electric Power Co. “Announcement of Area Supply and Demand Results”. Available online: https://www.tepco.co.jp/forecast/html/area_data-j.html (accessed on 26 October 2021).
- Ministry of Economy, Trade and Industry. “Feed-In Tariff (FIT) Program Information Release Website”. Available online: https://www.fit-portal.go.jp/PublicInfoSummary (accessed on 26 October 2021).
- Changes in Weather Forecast. Available online: http://weather-transition.gger.jp/ (accessed on 26 October 2021).
- Campbell, J.Y.; Thompson, S.B. Predicting excess stock returns out of sample: Can anything beat the historical average? Rev. Financ. Stud. 2008, 21, 1509–1531. [Google Scholar] [CrossRef] [Green Version]
- Kuhn, M. Parallel Processing. Available online: https://topepo.github.io/caret/parallel-processing.html (accessed on 27 September 2021).
- Kaggle, mlcourse.ai. Open Machine Learning Course by OpenDataScience. Available online: https://www.kaggle.com/kashnitsky/topic-5-ensembles-part-2-random-forest (accessed on 26 October 2021).
- Japan Meteorological Agency “Historical Weather Data Download”. Available online: https://www.data.jma.go.jp/gmd/risk/obsdl/ (accessed on 26 October 2021).
- Takuji, M.; Misao, E. One-week-ahead electricity price forecasting using weather forecasts, and its application to arbitrage in the forward market: An empirical study of the Japan electric power exchange. J. Energy Mark. 2021, 14, 1–26. [Google Scholar]
- Smits, G.F.; Jordaan, E.M. Improved SVM regression using mixtures of kernels. In Proceedings of the 2002 International Joint Conference on Neural Networks, Honolulu, HI, USA, 12–17 May 2002; IJCNN’02 Cat. No. 02CH37290. IEEE: New York, NY, USA, 2002; Volume 3, pp. 2785–2790. [Google Scholar]
- Wood, S.N. 2019 Package “mgcv”. Available online: https://cran.r-project.org/web/packages/mgcv/mgcv.pdf (accessed on 15 October 2020).
- Matsumoto, T.; Yamada, Y. Simultaneous hedging strategy for price and volume risks in electricity businesses using energy and weather derivatives. Energy Econ. 2021, 95, 105101. [Google Scholar] [CrossRef]
- Matsumoto, T.; Yamada, Y. Cross hedging using prediction error weather derivatives for loss of solar output prediction errors in electricity market. Asia-Pac. Financ. Mark. 2018, 26, 211–227. [Google Scholar] [CrossRef]
- Kuhn, M. The Caret Package. J. Stat. Softw. 2009, 28. Available online: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.216.2142&rep=rep1&type=pdf (accessed on 26 October 2021).
- Ripley, B.; Venables, W.; Ripley, M.B. Package ‘nnet’. R Package Version. 2016. Available online: https://cran.r-project.org/web/packages/nnet/nnet.pdf (accessed on 26 October 2021).
- Karatzoglou, A.; Smola, A.; Hornik, K.; Karatzoglou, M.A. Package ‘Kernlab’. CRAN R Project. 2019. Available online: https://cran.r-project.org/web/packages/kernlab/kernlab.pdf (accessed on 26 October 2021).
- Breiman, L.; Cutler, A. Package ‘RandomForest’; University of California, Berkeley: Berkeley, CA, USA, 2018; Available online: https://cran.r-project.org/web/packages/randomForest/randomForest.pdf (accessed on 26 October 2021).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).