Abstract
The paper describes the cascaded voltage and current control for a bidirectional DC/DC converter in Dual Active Bridge (DAB) topology. The typical DAB converter circuit was extended by additional current filters, which allow it to operate in application fields with high requirements on current ripples. The core concept of the presented solution is usage of the modified Single Phase Shift (SPS) modulation, which allows to compensate for the DC-bias current occurring in dynamic states and provides a settling time of half switching cycle during transients. Its features were utilized to build a simplified dynamic model of the converter. The linear Proportional-Integral (PI) controllers are used in both voltage and current control loops. Based on the developed dynamic models, the tuning rules for both controllers were derived. In both cases, a number of the tuned parameters were reduced from two to one (which can present a great practical value for application engineers). The proposed solutions are validated based on a laboratory prototype. An important part of the experiments was devoted to non-linear effects occurring near the current limitation boundary of the system. The paper ends with a brief discussion regarding the future research directions.
1. Introduction
The Dual Active Bridge (DAB) topology for DC/DC converter was proposed in the late 1980s [1]. It provides a great operational flexibility in comparison with concurrent converter topologies [2], which has led to the constantly rising popularity of this solution over the past decade in many application fields [3]. The most important features of DAB converters are galvanic isolation, bidirectional power flow, and versatile voltage control range (both buck and boost functionality).
Many different control strategies were proposed for the DABs [3]. The most popular are the Single Phase Shift (SPS), the Extended Phase Shift (EPS), the Dual Phase Shift (DPS), and the Triple Phase Shift (TPS) modulation schemes. The SPS modulation is the most simple one, whereas the concurrent solutions provide higher system efficiency in exchange for a rising complexity of the implementation. An analysis presented here focuses mainly on the system dynamics and not the efficiency optimization, hence the SPS modulation was chosen for simplicity. Nevertheless, information regarding the extend-ability of the presented results on other modulation schemes is provided too (see Section 4).
In [4] a single Proportional-Integral (PI) linear controller was proposed for a closed loop voltage control of the DAB. It was tuned based on the dynamical model created with a harmonic modeling technique. The load step performance of the control loop was additionally improved with a feed-forward term.
The solutions presented in [5,6] both use an additional internal current control loop (also based on the linear PI controller). As explained in [5], such an additional loop can improve the dynamic performance of the control system. Unfortunately, incorporating the current feedback for the DAB converter control is not an obvious task, as the output current contains a great amount of higher harmonics and its DC component is not directly measurable. The authors of [5] solved this problem by adding an additional current averaging circuit. In [6] the sampled transformer current is used as a feedback signal. An impact of the current values in sampling instants on the output voltage dynamics is then described using transfer functions obtained using the small-signal averaging technique. The transfer functions are then used for controller tuning and stability analysis purposes.
In [7] a deadbeat current controller was used for the inner current control loop instead. It is based on the transformer current measurement in the middle of the switching period. This solution provides a current settling time within one switching period.
Literature reports also voltage control schemes based on algorithms other than linear PI control [8,9,10]. The model predictive controller was proposed in [8,9] and the sliding-mode controller in [10]. All these works provide a comparison of the proposed solutions with the PI controller-based algorithms. Unfortunately, it is either not defined which exact solution was used for the comparison [8,9] or it is hard to asses if the PI controllers where really well-tuned for the comparison [10], as they were tuned for the start-up performance and comparison was made based on the load step performance.
All the above mentioned voltage control solutions are dedicated for a basic DAB converter topology without any additional current filters. Nevertheless, it is an intrinsic feature of the DAB topology that the output current can exhibit a great amount of harmonic components depending on the load type [11]. Such a high level of harmonic content is often unacceptable in application fields with strict requirements on current ripples such as battery charging/discharging or automotive converters. In the case of industrial products intended for such applications there may be a need to suppress these current harmonics. It can be achieved using additional current filters, in particular LC filter topology with a parallel damping inductor path [12].
The presence of the current filters must be considered during a voltage control system design but this topic is rarely described in the literature. To the best of the authors’ knowledge, the reference [11] is the only work providing an experimentally tested voltage control solution for a DAB converter with current filters. This is a very comprehensive work providing a complex analysis regarding the system losses modeling and reduction by means of choosing an optimal modulation scheme and hardware design. Even though the closed loop voltage control was proposed and analyzed, it clearly was not the main focus of the author. Tuning of the controllers is described very briefly and the solution lacks the transient DC-bias current cancellation, which indirectly limits the bandwidth of the control system.
An occurrence of the DC-bias current in transformer windings during the dynamic operation of DAB converters is a well-known and widely described phenomenon [13]. It is often referred to as one of the most important problems to be solved, in order to reach an industrial quality of the converter design. It can lead to a severe fault of the converter if the system is not properly over-sized (and over-sizing is obviously undesired in case of commercial products). This issue was described for the first time in 2010 [14], and since then many algorithmic-based solutions for the DC-bias cancellation were proposed. Description of these algorithms, as well as detailed comparison of their features, can be found in [13].
The ambition of this paper is to provide a voltage control algorithm, which could meet the requirements of an industrial quality product. In the authors’ opinion, such a solution should consider the usage of current filters and transient DC-bias cancellation algorithm. It should also be simple and robust. The proposed solution uses the cascaded voltage and current control systems based on linear PI controllers. A Dual Rising Edge Shift (DRES) algorithm [13] is used for cancellation of the transient DC-bias current. This algorithm provides a very important feature, i.e., settling time within a half of switching cycle. It should be understood in such a way that the transient process after changing the power flow occurs only during the first half of the switching period. After that current waveforms in transformer windings, as well as at the converter’s input and output are the same as during the steady-state operation. This feature allows to develop a novel dynamic model of the DAB converter. This model is extremely simple with regard to a state of the art solution, i.e., the small-signal averaging technique. It also provides a linear transfer function in the whole operating range (which is not the case for the small-signal based model, as it is linearized around a particular operation point [5]). An important part of the proposed solution is the PI controller tuning. The developed rules provide robust control loop performance and allows to reduce the number of degrees of freedom for controller tuning from two to one. It means that the dynamics of each control loop can be adjusted by means of only one parameter, which is an important practical advantage. Additionally, an operation of the voltage control near the system limits was explored, which is crucial in terms of an industrial application.
2. Materials and Methods
Schematic of the DAB converter with additional current filters is shown in Figure 1. Q1, …, Q8 are transistor switches of the MOSFET type; are current filter elements (it is worth mentioning that the capacitors also fulfill a role of DC-link capacitors for the H-brides); and are input (primary-side) and output (secondary-side) buffer capacitors (F); is additional inductance connected in series with primary-side transformer winding (H).
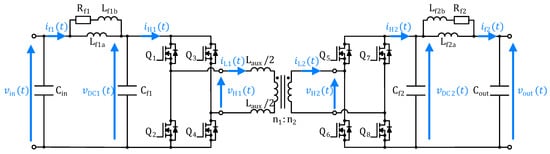
Figure 1.
Schematic of the DAB converter with current filters.
The following naming convention is used for the signals: and are input (primary-side) and output (secondary-side) converter voltages (V); and are input (primary-side) and output (secondary-side) filter currents (A); and are DC-link voltages of primary- and secondary-side H-bridges (V); and are currents on DC side of primary- and secondary-side H-bridges (A); and are primary- and secondary-side transformer currents (A); and are AC voltages of primary- and secondary-side H-bridges (V).
The parameters of the system analyzed in this paper are summarized in Table A1 (see Appendix A).
2.1. Modulation Scheme
The solution described here is based on some particular variant of the SPS modulation, i.e., the Double-Sided Single Phase Shift (DSSPS) modulation. The steady-state characteristics of this modulation scheme are the same as for the classical SPS modulation [15]. Both H-bridges are controlled with a constant duty ratio of 50% and the converter is controlled by means of the phase shift between them. Here, the phase shift is expressed in unit of normalized time, which is relative to the switching period:
where is normalized time; t is absolute time (s); is switching period (s). With such a definition, the value of corresponds to an angular phase shift of .
As derived in [15], with such a modulation scheme the value of phase shift should be limited to the range of . An average output current (i.e., averaged over one switching period) can be then expressed as:
where the subscript denotes the average value; is the base current (A), is the equivalent circuit inductance (H); is the transformer turns ratio; and are the number of turns at the primary and secondary transformer sides.
Equation (2), which describes a relationship between the control variable and average output current, is nonlinear. This function is strictly monotonic in the feasible control variable range (i.e., ) and because of that it can be inverted. Hence, the phase shift value providing a reference value of the average output current can be calculated as:
where the subscript denotes the reference value. The Equation (6) describes a control law used in the proposed solution (see current the control loop described in Section 2.2), which provides a linear relationship between the reference output current value and its average value in steady-state.
The DSSPS modulation scheme differs from the classical SPS algorithm during dynamic converter operation. According to the SPS modulation described in [15] the primary-side AC voltage waveform remains stationary in time, whereas only the secondary-side voltage waveform is being shifted accordingly during the phase shift transition. On the other hand, the double-sided variant used in this paper assumes that both primary- and secondary-side voltage waveforms are shifted symmetrically to the center of the switching period [13].
It is a well-known fact that usage of the same modulation scheme in steady-state and for dynamic operation introduces a so-called transient DC-bias current in transformer windings [13]. This undesired current component deteriorates system performance in means of efficiency and dynamic performance, i.e., settling time after the phase shift transition. In order to avoid it, the modulation scheme used here is complemented with the Dual Rising Edge Shift (DRES) algorithm [13], which allows to cancel the transient DC-bias current component. It is accomplished by an appropriate time shift of the rising edges for both primary- and secondary-side AC voltage waveforms. Equations allowing to calculate the time instants of consecutive switching operations are rewritten here for the readers’ convenience:
where is a correction time; is a change of phase shift value between the current and the previous switching cycle; and k is a number of the switching cycle, in which the calculated control values are applied.
The function of the used modulation scheme during the transition of the phase shift value is demonstrated in Figure 2. In the first switching cycle, the phase shift value equals and in the second cycle it changes to . AC voltage waveforms generated by both bridges are shown in Figure 2a,b. The first plot presents an operation of the basis DSSPS modulation without additional corrective shift of the rising edges during transient operation, i.e., the corrective time in Equations (7) and (8) is set to zero. On the second plot, the rising voltage edges are appropriately shifted by an amount of , which is indicated with red arrows.
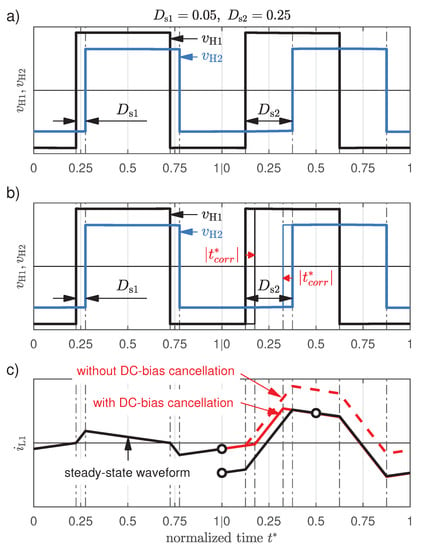
Figure 2.
Exemplary waveforms explaining the used modulation scheme during transition of the phase shift value: (a) AC voltages when a basic Double-Sided Single Phase Shift (DSSPS) modulation is applied, (b) AC voltage waveforms when the Dual Rising Edge Shift (DRES) algorithm for DC-bias cancellation is additionally applied, and (c) transformer current waveforms.
Transformer current waveforms are shown in Figure 2c. The steady-state waveform (solid black line) describes the current signal shape, which should be expected during a static converter operation. It can be clearly seen that it exhibits a discontinuity, which is a reason for the DC-bias occurrence (for a more detailed explanation please refer to [13]). It can also be observed that the current signal obtained using the basis DSSPS modulation (dashed red line) is shifted relative to the target steady-state waveform (an amount of this offset is called the DC-bias). Applying the DRES correction algorithm causes the resulting current waveform (solid red line) to converge to the steady-state one. This algorithm is designed in such a way that the transient state lasts no longer than half of the switching cycle [13]. It assures that the waveforms of the transformer currents and , as well as the DC-side bridge currents and are the same as in the steady-state in the second half of each switching cycle (even during dynamic converter operation). This is a very important feature of this modulation scheme, which plays a fundamental role in the presented closed loop control system.
2.2. Current Control Loop
Schematic of the proposed current control loop is shown in Figure 3. The control algorithm is realized in a discrete-time domain in a microcontroller. The controlled variable is the filter current at the converter’s output (see in Figure 1). It is sampled with a frequency equal to the switching frequency . Hence, there exists a time delay of one sample in the control loop (represented as the block in Figure 3).
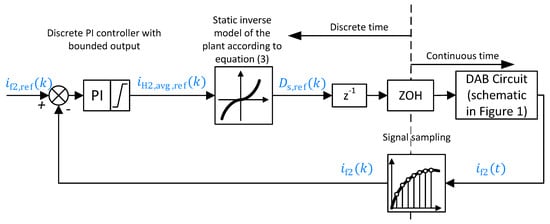
Figure 3.
Schematic of the current control loop.
The applied phase shift value does not change during a control cycle, which was modeled as a Zero Order Hold (ZOH) element. The reference phase shift value is calculated based on the reference average value for the secondary-side bridge output current . The calculation is carried out according to Equation (6), which allows compensating for the non-linear static characteristic of the plant (see Equation (2)).
The signal plays the role of the control variable and it is calculated by a discrete-time equivalent of the linear PI controller with limited output. For discretization, the bilinear transform was used [16]. Choosing the appropriate limitation values for the controller output requires a special attention. On the one hand, the signal should be limited in such a way, that calculation of the ’static inverse function’ (Equation (6)) gives a real number, i.e., the value under the square root must not be negative. Hence, the maximal value for the average output current in the k-th control cycle equals:
On the other hand, it is not the case that the output current of DAB should always be limited to the maximally achievable value. In general, there may be a need to additionally limit the current according to specification of the device. Hence, the authors propose to evaluate the Equation (13) in each control cycle and use this value as the controller output limitation only then, if it results in an absolute value lower than the maximal current due to the converter’s specification:
where is the actual maximal controller output limitation; is the actual minimal controller output limitation; is the maximal output current value according to the converter’s specification (A). The same limitation values are used for the voltage controller described in the next section.
It should be emphasized that the value is not only a pure mathematical limitation, but it also describes an absolute maximal current, which can be achieved at the DAB output in steady-state [15]. It is important to point out that the only variable in Equation (13) which can change over time is the input bridge DC voltage . It means that the achievable output current range is proportional to the input voltage so it can dynamically change.
In the case of the discrete-time control systems, it is normally the case that the control loop as a whole is a mixed-domain system. It means that a control algorithm is realized in the discrete-time domain, whereas the plant is a physical circuit, which is a continuous-time system. In order to tune the parameters of the controller, the dynamics of the control loop should be modeled using an equivalent transfer function in either the z (discrete-time) or s (continuous-time) domain.
The dynamic model presented here is created in the continuous-time domain. It is based on an observation that dynamics of the core DAB circuit (i.e., the relationship between the controller output and average current at the DC side of the secondary-side bridge) can be approximated with a time delay. It should be emphasized that it is possible only because of the used modulation scheme with DRES compensation (see Section 2.1) and the static inverse function (Equation (6)). It greatly reduces the complexity of system modeling in comparison with the state-of-the-art solution, i.e., the small-signal averaging technique.
The proposed approximation is going to be explained based on simulation results, which were obtained with a numerical converter model created in PLECS software [17] (the DAB parameters are listed in Table A1). The results are shown in Figure 4. In the simulated scenario output signal of the controller (black), there is a step function which changes value from 0 A to 15 A at the beginning of the second control cycle presented on the plot, i.e., at . The phase shift needed to achieve the average current value of 15 A in the steady-state is calculated with Equation (6) but it is applied first during the third control cycle, i.e., , because of the unity sample delay due to the discrete-time control realization. Hence, the current at the DC side of the secondary-side bridge (gray) remains unchanged during the first and second control cycles. As already mentioned in Section 2.1, thanks to the DRES algorithm, the transient process lasts only for the first half of the control cycle, whereas in the second half of the cycle the current signal reaches a steady-state. The authors propose to approximate this current signal with its average value calculated in each half cycle (blue signal in Figure 4). The dynamic relationship between the controller output signal (the reference value) and this averaged current signal (the result) can then be described as a time delay of 1.75 control periods. Such a delayed signal is shown in red in Figure 4.
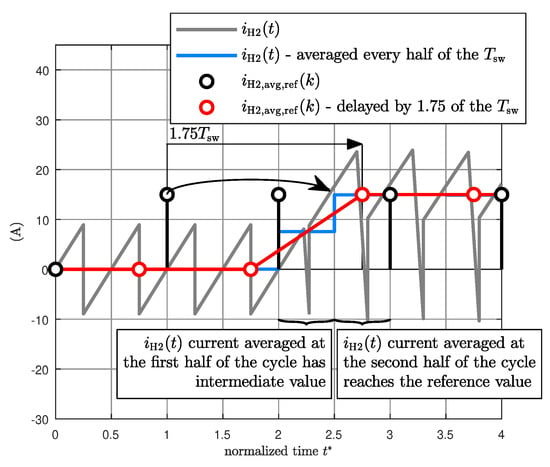
Figure 4.
Exemplary simulation results illustrating the proposed modelling method.
The dynamics of the filter current depends on both the current transferred through the DAB converter and output voltage and can be described in the s domain as follows [11]:
where is the transfer function of the low-pass current filter. Hence, the whole current control loop can be modeled according to the diagram shown in Figure 5. Since the controller can directly influence only the current transferred through the core DAB circuit , the output voltage signal should be treated as a disturbance.
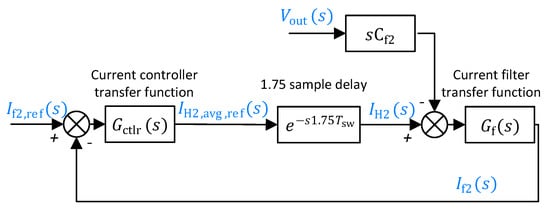
Figure 5.
Schematic of the continuous-time equivalent model for the current control loop in s domain.
The control loop dynamics can then finally be described using the transfer functions as follows:
where is the closed-loop system transfer function; is the disturbance transfer function; is the open-loop system transfer function; is the transfer function of the controller; is the proportional gain of the controller; is the integral time of the controller (s); is the transfer function of the controlled plant.
The proposed controller parameter tuning method is based on a notion of the gain margin [18]:
where is the complex frequency response of the transfer function for which the gain margin is calculated; is the gain margin cutoff frequency, i.e., a frequency resulting in phase lag of the frequency response equal to (rad/s); is the gain margin.
In the proposed tuning process the integral time is chosen arbitrary and then the proportional gain is calculated in such a way that the open-loop transfer function of the system (Equation (21)) exhibits the required gain margin value. The authors propose to choose the integral time of the controller in such a way that the decade containing the controller corner frequency (Equation (28)) is separated by at least one whole decade from the one containing the gain margin cutoff frequency (Equation (24)) calculated for a frequency response of the plant . In the next paragraphs, we explain why such a tuning rule was chosen.
Firstly, let us define how to calculate the proportional gain of the controller based on the chosen integral time and the requested gain margin value .
The calculation algorithm consists of two steps:
- Step 1: Proportional gain of the controller is set to unity () and the integral time is set to the requested value (). For such a case the Bode plots of the open-loop frequency response are drawn. Based on that, the gain margin cutoff frequency is determined according to Equation (24) and a gain margin for the unity gain is calculated as:
- Step 2: Based on the calculated gain margin value it can be determined how to set the controller gain in order to achieve the requested gain margin of the open-loop system as follows:
Exemplary characteristics of the current control system tuned according to this procedure are shown in Figure 6. A set of six characteristics for different input data values is presented. For each case, the requested gain margin value was exemplary chosen as . On the other hand, the requested integral time values are varied between s and s. Bode plots for the amplitude and phase of the open-loop system frequency responses are shown in Figure 6a,c respectively. The red solid lines represent the characteristics of the PI controller for different parameter values.
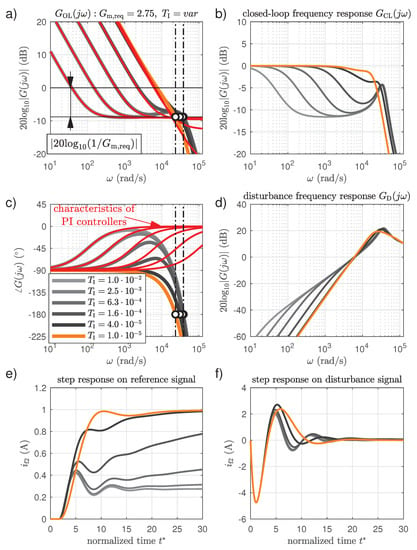
Figure 6.
The current control loop characteristics at constant gain margin of and for various controller integral time values: (a,c) amplitude and phase Bode plots of the open-loop system frequency response, (b) amplitude Bode plot of the closed-loop system frequency response, (d) amplitude Bode plot of the disturbance frequency response of the system, (e) response of the system on a unit step of the reference signal, (f) response of the system on a unit step of the disturbance signal.
It is important to point out that the maximal phase lag which can be introduced by the controller equals and varying of the integral time influences a frequency range where this phase lag is applied. Let us define the corner frequency of the PI controller as:
It is a very characteristic point, as it lies in the middle of the phase transition zone of the controller, i.e., between the phase lag values of and . It is important to observe that this transition zone has a width of approximately two decades at logarithmic frequency scale. It can then be approximately assumed that the controller introduces a phase lag of for frequencies lying one decade below the corner frequency and introduces no phase lag for frequencies lying one decade above this corner frequency.
It can also be observed that changing the integral time value in the descending direction introduces more phase lag to the open-loop system characteristics. As a result, the gain margin cutoff frequency values become slightly lower (see the white dots in Figure 6c), but this influence is relatively small because of the steep phase characteristics of the plant in this frequency range introduced by the time delay element (see Equation (23)).
As the requested gain margin values are constant for all the six characteristics, the points indicating the gain margin on amplitude characteristics of the open-loop system must then lie relatively near to each other (see the white dots in Figure 6a). It should also be emphasized that the PI controller exhibits amplifying features only in a limited frequency range, i.e., for frequencies lower than the corner frequency (Equation (28)). For frequencies higher than that threshold the controller gain is constant. As a result, shifting of the corner frequency of the controller into the higher values (and holding the constant gain margin value at the same time) allows to greatly increase the open-loop system gain in a pass-band of the control system. This effect can clearly be seen in Figure 6a. Maximizing the gain of the open-loop system in the possibly wide frequency range is desirable [19], as it brings frequency responses of the closed-loop system toward the unity and of the disturbance towards zero, which can be expressed mathematically as:
The positive effect that the rising of the controller corner frequency has on the closed-loop and disturbance characteristics of the system can be clearly observed by inspecting the amplitude frequency responses plotted in Figure 6b,d. The bandwidth of the closed-loop system rises, as well as an attenuation of the disturbances in low-frequency range. Finally, this effect can also be observed in the step responses on the reference signal (Figure 6e) and on the disturbance signal (Figure 6f). These responses were determined using the ’step()’ function in MATLAB software [20].
The above discussion allows to formulate a conclusion that for a given gain margin value, rising of the controller corner frequency has positive effects on system dynamics. On the other hand, at some point this effect saturates, as the controller phase lag equals in the whole relevant frequency range. The same applies to the amplitude characteristics of the open-loop system, as at some point the whole relevant part of these characteristics is amplified by the falling arm of the PI controller amplitude characteristics, and a further increase of the corner frequency has no relevant impact on the system behavior. It is then not important which exact value of the integral time is chosen, as long it assures that the relevant frequency band of the system lies meaningfully below the corner frequency of the controller. The already mentioned tuning rule (i.e., the controller corner frequency (Equation (28)) is separated by at least one whole decade from the one containing the gain margin cutoff frequency (Equation (24)) calculated for a frequency response of the plant ), which meets this requirement, since the transition zone of the controller ends approximately one decade below its corner frequency on the logarithmic frequency scale. In the presented case, the gain margin cutoff frequency calculated for the plant equals rad/s, i.e., it lies in the decade . According to the formulated rule of thumb the corner frequency should then not be smaller than rad/s (which corresponds to ).
Since there exist a rule on how to choose the integral time, the only parameter left to tune is the proportional gain of the controller. It can be chosen based on the requested gain margin value. This value should be chosen by a system designer based on the desirable characteristics of the reference step response. It can be done based on the system characteristics plotted in Figure 7. There is again a set of six different characteristics, but this time the integral time of the controller is constant and set to the previously calculated value of .
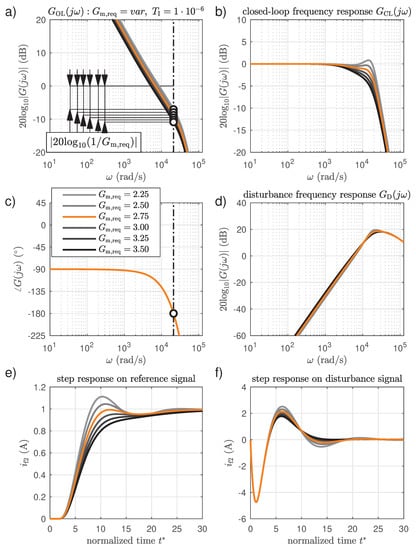
Figure 7.
The current control loop characteristics at constant integral time of and for various gain margin values: (a,c) amplitude and phase Bode plots of the open-loop system frequency response, (b) amplitude Bode plot of the closed-loop system frequency response, (d) amplitude Bode plot of the disturbance frequency response of the system, (e) response of the system on a unit step of the reference signal, (f) response of the system on a unit step of the disturbance signal.
On the other hand, the requested gain margin is varied between the values of 2.25 and 3.50 (see the legend in Figure 7c). Since the integral time is constant, varying of the controller gain has no influence on the phase characteristics of the open-loop system frequency response. However, it has an influence on the amplitude characteristics plotted in Figure 7a. Changing of the gain margin value impacts the amplitude characteristics of the closed-loop system shown in Figure 7b. This in turn changes a character of the step responses on the reference signal (see Figure 7e). On the other hand, an impact on the disturbance rejection possibilities of the control system (see Figure 7d,f) is not significant. A choice of the particular gain margin value should be made by the system designer based on his expertise. In the presented case, the authors propose to chose a value of , which results in a possibly fast step response on the reference signal but without any overshoot (this value corresponds to the orange curves in Figure 7). Nevertheless, the other value can be chosen too, if the designer desires a faster (lower gain margin) or less oscillatory (higher gain margin) character of the response.
To sum up, the final parameter values for the current controller presented in this paper are as follows:
2.3. Voltage Control Loop
For the voltage control purposes, an additional outer control loop was introduced to the control system. The schematic of the resulting control structure is shown in Figure 8. The voltage controller regulates voltage measured directly at the output capacitor (see in Figure 1). The voltage controller is realized in the same way as the current controller, i.e., it is a discrete-time equivalent of a linear PI controller with bounded output. The output signal of the voltage controller is the reference value of the output filter current . This signal is a reference value for the inner current control loop. Its value is limited by the voltage controller to the feasible output current range in steady-state, i.e., it is limited to the same range as the current controller according to Equations (14) and (15).
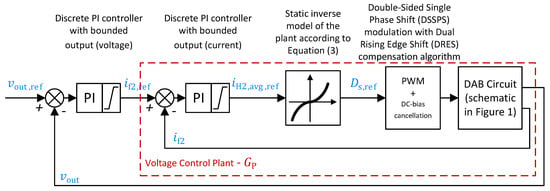
Figure 8.
Schematic of the cascaded voltage and current control system.
In order to tune the parameters of the voltage controller, the dynamics of the control loop should be modeled first. This loop consists of the voltage controller and the inner control loop for the current and output capacitor (see the outer circuit schematic in Figure 9).
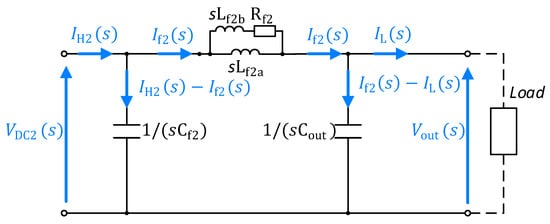
Figure 9.
Outer circuit schematic.
The voltage controller can influence only the filter current signal (indirectly by setting the reference value of this current for the inner control loop). Hence, the load current signal should be treated as the disturbance for the voltage control system. The model of the voltage control loop should also contain the dynamics of the inner control loop for the current. These dynamics can be described using the closed-loop (Equation (19)) and disturbance (Equation (20)) transfer functions for the current control system. As the closed form analytical formulas for these functions are relatively complex, the authors decided to approximate them with the following equivalent functions for the simplicity:
where is an approximation of the closed-loop transfer function for the current control system ; is an approximation of the disturbance transfer function for the current control system . The system poles exhibiting a slightly oscillating character were replaced by a series connection of the first order elements. It is a well-known technique that is used to simplify an analysis [19]. The exact structure of the approximating transfer functions was found by inspection and the parameter values were found with an engineering approach, i.e., trial and error followed by a visual evaluation of the Bode plots of the original and approximating functions. Bode plots of the corresponding frequency responses are shown in Figure 10. The original functions calculated for the current controller parameters (Equations (31)–(33)) according to equations (Equations (18)–(23)) are drawn with black color. The characteristics of the equivalent functions Equations (34) and (35) are drawn with orange color.
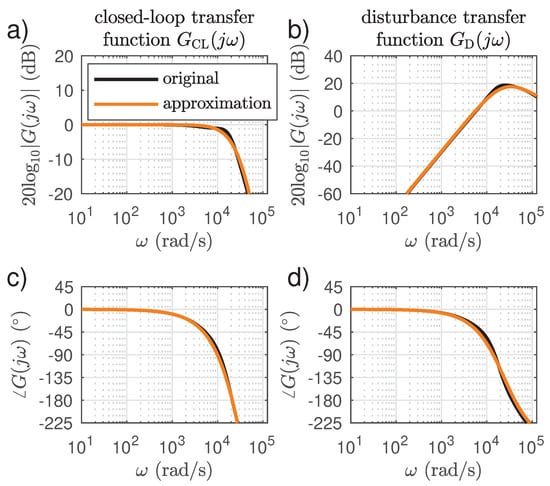
Figure 10.
Comparison of the Bode diagrams for the approximated and original frequency responses of the current control system: (a,c) amplitude and phase characteristics of the closed-loop frequency responses, (b,d) amplitude and phase characteristics of the disturbance frequency responses.
The block diagram illustrating the signal flow in the system is shown in Figure 11a. The output voltage signal is a result of integration of the capacitor current, i.e., (). The filter current signal is a sum of the current control loop responses on the reference signal (calculated by the voltage controller) and on the disturbance signal (output voltage). In order to describe the voltage control system dynamics using the standard notions of the plant, open-loop, closed-loop, and disturbance transfer functions [18], this diagram should be converted to a different form. In the schematic shown in Figure 11b the order of summation nodes was changed and the integration block was doubled to create an additional parallel path. The part marked with a dashed line can then be replaced with an equivalent transfer function . It results in the final diagram shown in Figure 11c, which can be described with the following transfer functions:
where is the closed-loop system transfer function; is the disturbance transfer function; is the open-loop system transfer function; is the transfer function of the controller; is the proportional gain of the controller; is the integral time of the controller (s); is the transfer function of the controlled plant; is the equivalent transfer function according to Figure 11b.
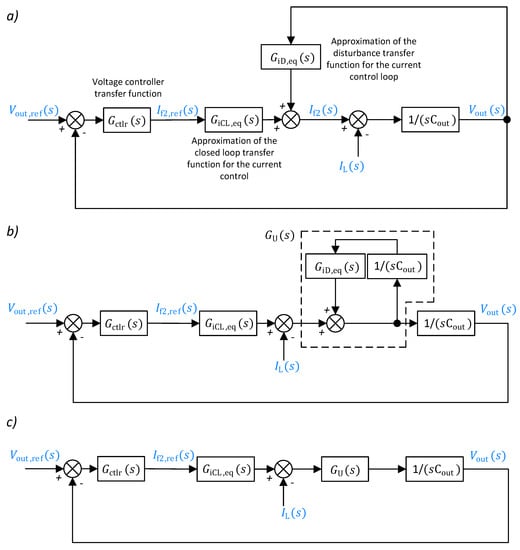
Figure 11.
Block diagram of the voltage control loop: (a) diagram illustrating the real signal flow in the system, (b,c) consecutive stages of the diagram transformation.
The proposed tuning method for a voltage controller based on a notion of phase margin is defined as follows [18]:
where is the phase margin cutoff frequency (rad/s), i.e., a frequency for which the amplitude of the frequency response equals unity; is the phase margin (). The proposed method is designed in order to achieve a high control loop robustness. Hence, for a given integral time value of the controller the proportional gain value is chosen in such a way that the phase margin calculated for the open-loop system frequency response is maximized.
The calculation algorithm consists of three steps:
- Step 1: Proportional gain of the controller is set to unity () and the integral time is set to the requested value (). For such a case the Bode plots of the open-loop frequency response are drawn. Based on that it is found for which frequency the phase of the drawn response is maximal:
- Step 2: An aim of the algorithm is to find such a proportional gain value, that the phase margin cutoff frequency (Equation (43)) for the resulting open-loop system equals the value (Equation (45)), as it assures the possibly maximal phase margin value. In order to do so, an amplitude of the open-loop frequency response for the unity gain should be read from the drawn characteristic at the frequency (Equation (45)):
- Step 3: Based on that, the proportional gain value can be calculated in such a way that the frequency response gain for the requested frequency equals unity, assuring that the phase margin calculation point lies exactly at the maximum of the phase characteristic:which ends the calculation procedure.
When such an algorithm is applied, there is only one parameter of the controller to be tuned, i.e., the integral time value (because the proportional gain value for the given value of integral time is determined by the above mentioned algorithm). Again, it is a decision of the designer which exact value to choose. It can be done based on system characteristics drawn for many different candidate values for the integral time, as exemplary illustrated in Figure 12. The phase margin cutoff frequency points for each characteristic are marked with white dots at phase plots of the open-loop system frequency response (see Figure 12c). It can be clearly seen that these points lie at frequencies of the possibly maximal phase margin values, as requested.
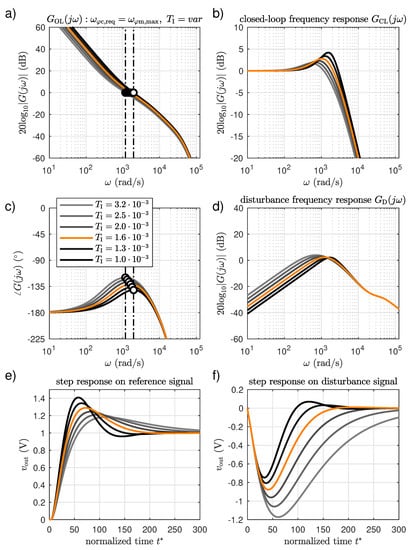
Figure 12.
The voltage control loop characteristics for various integral time values between s and s and for proportional gain calculated to maximize the open-loop system phase margin: (a,c) amplitude and phase Bode plots of the open-loop system frequency response, (b) amplitude Bode plot of the closed-loop system frequency response, (d) amplitude Bode plot of the disturbance frequency response of the system, (e) response of the system on a unit step of the reference signal, (f) response of the system on a unit step of the disturbance signal.
The final value of the integral time can be chosen based on the system step response on the disturbance signal and some common sense of the system robustness. The response on the reference signal step is of a lesser importance, as an overshoot can be eliminated with an additional pre-filter (as described later in this section) and the main task of the voltage regulatory system is to hold a constant output voltage value in various load conditions. The authors propose to choose an initial integral time value for the tuning, which provides a possibly fast attenuation of the disturbance step response with no overshoot. In the presented case it results in a value of s, which corresponds to the orange curves in Figure 12. As will be shown later in the course of this paper, the chosen value assures a proper behavior of a real control system in its linear operating range, but there are some negative effects occurring near the operational limits of the converter. The authors chose this integral time value as a starting point for the tuning of the experimental prototype with a full awareness of these issues. The reason is to demonstrate to the readers what can happen if the dynamics of this control loop is set to high. To sum up, the chosen set of the voltage controller parameters equals:
The last missing part of the proposed control system, is to add a pre-filter for the reference voltage signal. It allows to reduce an amount of overshoot in the reference step response of the system. After inspection of the closed-loop transfer function (Equation (37)) it appears that it exhibits only one zero, which equals to a zero of the controller (Equation (41)). The pre-filter was designed to compensate this zero. Hence, it has a stucture of a first order system with the time constant equal to the integral time of the voltage controller:
In order to finally validate the proposed dynamic models and parameter sets for both controllers, numerical models of the presented current and voltage control systems were created in PLECS software [17]. The models contain all the parasitic elements listed in Table A1 and allow to fully simulate the system dynamics, i.e., the results produced with these models can serve as a reference for the results obtained with the greatly simplified analytical models proposed in this paper. Hence, step responses on the reference and the disturbance signals were generated using the simulation models and then they were compared with those obtained with analytical ones. It should be emphasized that for this comparison both numerical and analytical models are supplemented with the pre-filter of the reference voltage signal (Equation (50)). It should also be mentioned that the control algorithm implemented in the simulation model is exactly the same as the one implemented in the laboratory prototype. However, stimulation of the control system was chosen in such a way that both controllers work in their linear operational region. The results are shown in Figure 13.
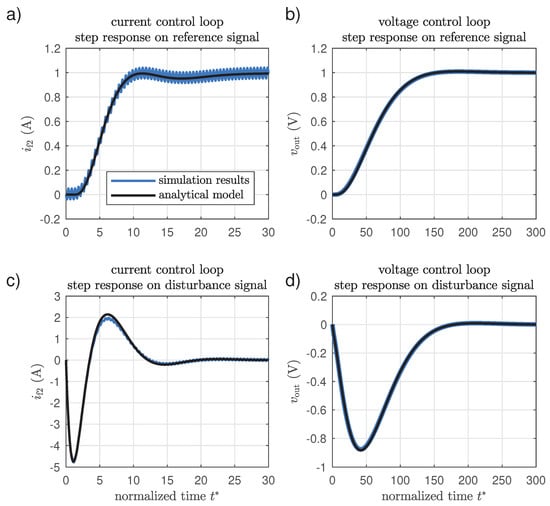
Figure 13.
Comparison of the control system responses obtained with numerical simulation model and analytical models presented in this paper: (a) current control loop, step response on reference signal, (b) voltage control loop, step response on reference signal, (c) current control loop, step response on disturbance signal, (d) voltage control loop, step response on disturbance signal.
The matching between the result obtained with both models is very good, especially taking into consideration the amount of simplifying assumptions made in the course of the analytical models derivation.
3. Results
This section describes the experimental tests of the proposed voltage control system, which were conducted with a laboratory prototype of the DAB converter with additional current filters. The circuit of the prototype converter corresponds to a circuit schematic shown in Figure 1. This prototype was constructed within a bigger research task, i.e., the research project founded by The National Center for Research and Development under Agreement number TECHMATSTRATEG1/346922/4/NCBR/2017. Within this task, many different power electronic converters were constructed and installed together in one rack, as shown in Figure 14. It allows to realize various test scenarios, where different power converters supply each other in various configurations, which can be changed via relays.

Figure 14.
View of the rack, in which the DAB converter and active rectifier are installed.
In the scenario used for the tests presented here, the DAB converter is supplied at the input side from an active rectifier, which regulates a constant DC voltage. The output side of the DAB converter is connected to a passive resistive load via a relay.
In order to allow an easy installation in the rack, the converter was built in a case made of aluminum profiles, as shown in the detailed view at the bottom left of the Figure 15. Within the research project a modular control interface was designed (see the bottom right of the Figure 15). It consists of various Printed Circuit Boards (PCB), which are re-configurable to provide different functionalities (in terms of the number of analog inputs, PWM and relay outputs, etc.) in order to cover different needs of each power converter in the rack. The interface is controlled with a dual-core microcontroller TMS320F28379D from Texas InstrumentsTM, which is mounted on the so-called controlCARD [21]. Both H-bridges were built based on the SiC-based MOSFET power modules CCS050M12CM2 from CREETM [22], which are mounted on the heatsink shown in the top right of the Figure 15. The modules are supplied via gate driver boards CGD15FB45P1 from CREETM [23], which are soldered on the top of power modules. The gate driver boards are connected with the DC-link capacitors (see and in Figure 1) using copper plates. The AC sides of the H-bridges are connected via transformer and auxiliary inductors, which are marked in Figure 15 as well.
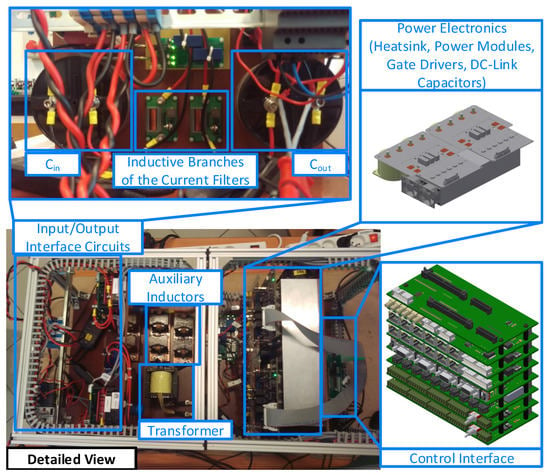
Figure 15.
Laboratory prototype of the Dual Active Bridge (DAB) converter with current current filters.
The inductive branches of the current filters (see inductors and resistors in Figure 1) are made in the form of PCBs, as shown at the top left of the Figure 15. The buffer capacitors and can be found in the same photograph as well.
The measurement results presented in this section were obtained with the MSO58 oscilloscope from TektronixTM using the P5205A and TCP0030A probes. All the tests were conducted at the same input voltage value, which is regulated by the active rectifier at 670 V. Similarly, the same load value of 16 was used in each test, and an amount of output current and power was changed by the setting of different voltage values at the DAB converter output. Each test lasts 400 ms and consists of the following phases:
- Phase 0: (first 40 ms) converter is in-active and PWM signals are not generated;
- Phase 1: (110 ms) the control algorithm and PWM generation are activated in the same time, the voltage reference value is set to the final value, the load is switched off;
- Phase 2: (155 ms) the load is rapidly switched on via relay;
- Phase 3: (95 ms) the load is rapidly switched off via relay.
The additional current limitation value for both controllers is set according to device specification (see Table A1) at value and an output of the controllers is limited according to Equations (14) and (15).
The first test was carried out for a reference output voltage value of and for the controller parameters set according to Equations (31)–(33) and Equations (48) and (49). The results are shown in Figure 16. The measured value of the input voltage signal (violet color) equals 674 V as opposed to its reference value of 670 V. This voltage is controlled by the active rectifier and this 4 V discrepancy is most likely caused by a measurement offset of the voltage transducer used by the active rectifier for the control feedback.
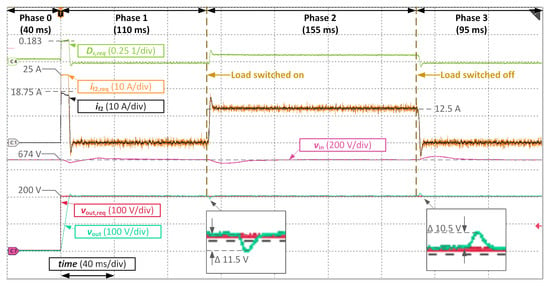
Figure 16.
Experimental results for controllers tuned according to parameters (31)–(33) and (48), (49): reference voltage value for the active rectifier , reference output voltage value for the DAB converter , additional current limitation , resistive load .
At the beginning of the Phase 1, the PWMs and control algorithm are being activated. It can be seen that the voltage controller output is saturated, as the reference value of the filter current (orange color) is set to its maximal value of 25 A. The interesting fact is that the measured filter current signal (black color) does not reach the reference value in this state. It is caused by the fact that the output of the current controller is saturated as well. It can be found out based on the control law (6) that at the input voltage value of 674 V, the required phase shift value calculated to achieve the 25 A equals (see the green colored signal in Figure 16). It can also be observed that after applying a load to the active rectifier, its output voltage value slightly drops, which results in a rise of the phase shift signal value according to Equation (6). It is important to point out that the value of the phase shift calculated with this equation actually results in the reference value of the average current for the core DAB circuit and it is consistent with the filter current value only in a steady-state. After inspection of the output DAB circuit shown in Figure 9 it becomes clear that the capacitors and create a current divider. When the output voltage rises, both these capacitors need to be charged. Since an average value of the DC-side current of the secondary H-bridge is saturated at 25 A and part of this current must charge the DC-link capacitor , only the rest of it can flow thorough the sensor measuring signal into the output capacitor . As the capacitance ratio of these two capacitors equals (see system parameters in Table A1), the current should be divided between these two circuits with approximately same ratio, i.e., 3:1. It means that in this saturated control state the measured value of the filter current signal cannot exceed the 75% of its reference value (in the analyzed case this boundary current value equals 18.75 A).
Based on the results shown in Figure 16, it can be seen that the voltage control system works properly. After reaching the reference value of 200 V, the output voltage signal is regulated at the constant value even during rapid load changes. At the beginning of the Phase 2 the 16 load is applied, which results in a 12.5 A load current during the steady-state operation. It can be observed that the filter current signal properly follows its reference value during the transient. After applying the load, the input voltage signal value slightly drops because of the limited bandwidth of the voltage control system implemented in the active rectifier supplying the DAB. Similar conclusions can be made during the load drop at the beginning of the Phase 3. The current control system works properly and there is a slight input voltage rise during the transient. The output voltage value of the DAB converter also drops and rises during the transients by the values 11.5 V and 10.5 V, respectively (see the zoomed parts in Figure 16). It should be mentioned that the fluctuations of the input voltage caused by the limited performance of the active rectifier control system actually have some positive effects from the experimental point of view. The reason is that it allows to produce relatively harsh conditions for testing the presented control system of the DAB converter (especially at the system limits, as will be shown later in this paper).
The presented test results proved the validity of the proposed voltage control system and tuning methods. Nevertheless, the load step test was carried out only in the linear operational range of the converter. The discussion regarding the limited filter current value at the beginning of Phase 1 proved that the control system exhibits some non-linearities, which arise at high current values. Hence, it is interesting to prove if the presented system can work properly if the load current exceeds the already mentioned boundary of the 75% of the maximal current. It means that the reference value for the output voltage should be increased to a value resulting in the load current higher than 18.75 A. With a load of 16 , this current would be achieved at a voltage of 300 V. Hence, for the next test the reference voltage value at the DAB output should be set to a value higher than that threshold. The value of was chosen, which should result in the load current of approximately 20.3 A. The results of this test are shown in Figure 17.
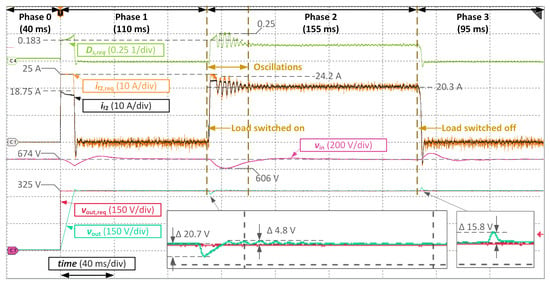
Figure 17.
Experimental results for controllers tuned according to parameters (Equations(Equations (31)–(33)) and Equations (48) and (49): reference voltage value for the active rectifier , reference output voltage value for the DAB converter , additional current limitation , resistive load .
The majority of the results are very similar to those from the previous test (see Figure 16 for comparison). The main difference in the system behavior can be observed at the beginning of Phase 2. The response of the control system becomes oscillatory, which is also clearly visible in all the relevant control signals. After a short while the oscillations fade away and the system enters a steady-state. The reason for this behavior is the fact that for some duration, the control system operates in the proximity of the maximal current, where its characteristics are not linear anymore. Let us analyze this oscillating phase in details. After applying the load, the input voltage drops to the value of 606 V. Substituting it to the Equation (13) results in the maximal possible value of the transmitted current of . It can be seen during the oscillation phase, the output signal of the voltage controller repeatedly bounces back and forth to this value. The current controller exhibits similar behavior, i.e., its output repeatedly reaches the saturation limit value of . In this state, the output circuit of the DAB converter (see Figure 9) can be approximately seen as a current divider with two paths: the DC-link capacitor and an RC branch built of the output capacitor and the load resistor. As already discussed, the existence of such a current divider introduces a non-linearity to the control system, if the current transmitted thorough the core DAB circuit reaches its limit. In particular, this non-linearity is a control dead-zone for the voltage controller, since above some threshold current value further rising of the voltage controller’s output has no effect on the system, because the current controller is already saturated.
As soon as the input voltage signal value is brought by the active rectifier back to it’s reference value, the maximal DAB current rises according to the Equation (13). As a result, the control system operates further from the current limitation value than before and reaches an equilibrium state. Based on the above discussion there are two conclusions. Firstly, the control system characteristics change, if the DAB converter is operated near it’s output current limit and a control dead-zone is introduced into the voltage control loop. Secondly, the voltage controller tuned to work well in the linear operating range of the converter can possibly fail to operate properly in this state and the voltage control system can behave improperly.
During the presented test, there was only a short time duration when the converter operated near the saturation limits of the controllers. Thus, it should be tested how the system behaves, if it is constantly operated near this boundary. Hence, the next test was carried out for an even higher value of the reference output voltage, i.e., , which increases the predicted load current value in steady-state to 21.9 A. The results are shown in Figure 18.
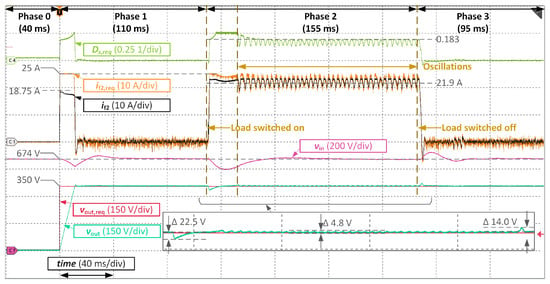
Figure 18.
Experimental results for controllers tuned according to parameters (Equations (31)–(33)) and Equations (48) and (49): reference voltage value for the active rectifier , reference output voltage value for the DAB converter , additional current limitation , resistive load .
It can be clearly seen that the load current value is close enough to its limit to bring the control system into oscillations during the whole Phase 2 duration. The system retains stability first after the load change at the beginning of Phase 3.
In order to improve the system behavior, the voltage controller should be re-tuned for the reduced dynamics. Thanks to the tuning rule derived in Section 2.3, it is a straightforward task, as there is only one parameter of the controller to choose (i.e., the integral time value) and the second one (i.e., the proportional gain) is determined by means of the tuning rule. The new voltage controller parameters were determined based on the characteristics shown in Figure 12. Among the analyzed parameter sets, the one resulting with the slowest dynamics was chosen (corresponding to characteristics drawn with the lightest shade of gray, i.e., for ), resulting in the following set of the voltage controller parameters:
In order to prove the proposed parameter set, the test for the output voltage value of was repeated with the voltage controller parameters changed to Equations (51)–(53). All the remaining parameters, e.g., current controller parameters, limitation values, etc., remained unchanged. The results of this test are shown in Figure 19.
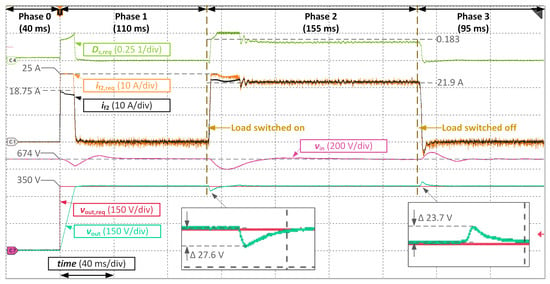
Figure 19.
Experimental results for voltage controller tuned with reduced dynamics: reference voltage value for the active rectifier , reference output voltage value for the DAB converter , additional current limitation , resistive load .
It can be clearly seen that re-tuning of the voltage controller for reduced dynamics improved the behavior of the system in Phase 2 of the test. There are no oscillations anymore and the output voltage is properly regulated at the reference value, even during the load steps. It proves an utilitarian value of the proposed tuning rules, as they allow a straightforward re-tuning of the controllers, if the real systems exhibits some unmodelled behavior.
On the other hand, it should be pointed out that reducing the voltage controller dynamics has a negative impact on the system performance in the linear operating range. It can be predicted based on the disturbance step responses drawn in Figure 12f. In order to illustrate this effect, a test in the linear operating range, i.e., the test for the reference output voltage value of , should be repeated with changed voltage controller parameters according to Equations (51)–(53). The results of this test are shown in Figure 20.
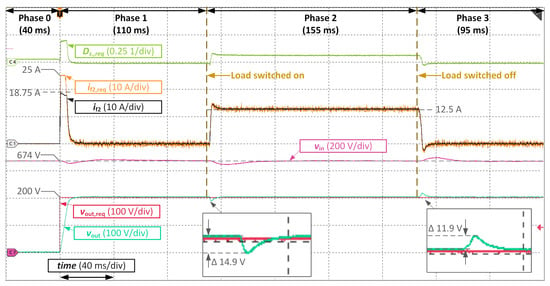
Figure 20.
Experimental results for voltage controller tuned with reduced dynamics: reference voltage value for the active rectifier , reference output voltage value for the DAB converter , additional current limitation , resistive load .
It can be observed that the voltage fluctuations during the load steps (see the zoomed parts of the Figure 20) are greater than their counterparts obtained with the voltage controller tuned for higher dynamics (compared with results shown in Figure 16). During the load step at the beginning of Phase 2, the voltage drop rose from 11.5 V to 14.9 V. The voltage rise during the load drop at the beginning of Phase 3 rose from 10.5 V to 11.9 V. As expected, re-tuning of the voltage controller for reduced dynamics deteriorated the system performance in the linear operational region of the plant, but in exchange it allowed a proper operation of the voltage control system near the current limitation of the converter.
4. Discussion
It is important to emphasize that the solution presented here was developed for the sake of industrial applications. This is a reason why the current filters were added, because they allow to apply the presented converter topology in application fields with high requirements on current ripples.
This is also a reason why the possibly simple controllers were used, i.e., linear PI controllers. Even though the various complex control schemes are known from the scientific literature, e.g., state feedback control, fuzzy logic, model predictive control, etc., these are normally not the first choice for industrial products. Application engineers usually prefer solutions, which are as simple as possible and just sufficient enough for a given task. The more sophisticated solutions are usually considered first when the simple ones do not perform at the required level. Hence, in the authors’ opinion it makes sense for a given application, to at first develop a control based on linear controllers and try to achieve a possibly good performance with them. Afterwards, this solution can serve as a reference for comparison with the more sophisticated algorithms. However, it is hard to make comparisons, if the reference is not well defined and tested under harsh conditions, which can be met in the real application field. This paper has an ambition to fill this gap for the DAB converters with current filters.
A very important part of the presented solution is usage of the extended modulation scheme. It has two important features: DC-bias current cancellation in dynamic states and settling time within the first half of the switching cycle. Based on these two features it was possible to greatly simplify a modelling process of the converter dynamics. It should be emphasized that the used modulation scheme was developed based on the SPS modulation, which is possibly the most simple one. It has some important drawbacks, such as an extremely low converter efficiency in some operational areas. The literature reports more complex modulation schemes, e.g., EPS, DPS, or TPS [3], which allow to overcome this issue. Hence, it is hard to claim a full industrial maturity of the presented solution if it uses such a basic modulation scheme. For this reason it is important to discuss its extend-ability for the more performative modulation algorithms. Since the presented modelling process is based on the fact that the current waveforms settle within a half switching cycle, it can be used with every modulation scheme possessing this feature. Thus, in the authors’ opinion their next natural research step should be an adaptation of the more complex modulation schemes to the solution presented here. In order to do so, these algorithms should be complemented by the following features: double-sided modulation and DC-bias cancellation basing on the corrective shift of the possibly earliest voltage edges occurring in a given switching cycle. When these two premises are met, the modulation scheme can be applied to the solution presented in this paper without any further changes.
It should also be mentioned that an important part of the presented material was an illustration of some stability issues, which can occur near the current limitation boundary of the converter. The authors hope to encourage other scientists to also test their solutions in the proximity of the system limits, as this is a true experimental verification of an applicability of the algorithm in the industrial field (where it is important to be able to utilize the whole specified operational range of the device). The presented way to overcome the stability problems has some obvious drawbacks, as it requires a re-tuning of the voltage controller, which in result deteriorates the system performance in the linear operational range. Nevertheless, it is relatively simple and straightforward to apply thanks to the developed tuning rules. It is obvious that this solution needs further improvements allowing it to avoid a reduction of the system performance in the linear operating range, but it was out of the scope of this paper and it is going to be a subject of for future research studies by the authors.
The analyzed converter topology, i.e., DAB circuit with additional current filters, is rarely treated in the scientific literature. To the best of the authors knowledge, there is only one work describing an experimentally verified voltage control system for such a converter topology [11]. It should be emphasized that none of the solutions presented in [4,5,6,7,8,9,10] can be applied to the voltage control of the DAB converter with current filters, at least not directly in the form provided in these publications. Hence, according to the authors’ knowledge the solution presented in [11] is so far the only published alternative to the algorithm described in this paper. Since the control system proposed in [11] uses cascaded voltage and current loops, as well as linear PI controllers, it may seem similar to the solution presented here. Hence, the differences between these two concepts, as well as the contributions of the presented work are emphasized below in the point-by-point manner:
- The inner current control loop proposed in [11] uses the input filter current signal as the feedback, whereas the solution presented here uses the output filter current signal instead. Usage of the output current signal has some important advantage. In both solutions the voltage controller calculates at its output the reference value for the output filter current. Hence, in [11] this reference value needs to be further converted to the corresponding reference current value at the input of the converter (since this is the actual controlled signal). This calculation facilitates the value of the so-called voltage conversion ratio, which requires a direct measurement of the DC-link voltage of the secondary-side H-bridge (see in Figure 1). On the other hand, the main task of the voltage control system is to regulate the voltage at the converter’s output, i.e., the signal . It would then require three voltage sensors to perform this task (the third sensor is needed to measure the DC-link voltage of the primary-side H-bridge , which is also needed for the voltage conversion ratio calculation). The author of [11] solved this problem by using the DC-link voltage signal as the feedback in the voltage control loop instead of the . Nevertheless, these two signals are equal only during the steady-state operation, which in consequence must deteriorate the voltage control performance during transients, especially the load changes (which is the most important test case for the voltage regulatory system). The solution presented here does not posses this drawback. The measurement of the DC-link voltage of the secondary-side H-bridge is not needed and there is a possibility to directly measure and control the output voltage signal without increasing the number of the voltage sensors above two (the second sensor is needed to measure the DC-link voltage of the primary-side H-bridge for the current limitation purposes, see Equations (13)–(15) as reference);
- The solution presented in [11] does not offer any DC-bias current cancellation algorithm. As already mentioned in the introductory section, the presence of this feature is very important to achieve the industrial quality of the controlled converter. The solution presented here does offer this functionality, which is clearly an advantage;
- In [11] there are moving average filters introduced in feedback signal paths of both current and voltage control loops. It introduces a delay of 10 switching periods, which greatly deteriorates an effective bandwidth of the voltage control system. In the presented solution there is no such additional filters and the sampling rate of the controller equals the switching frequency, which increases the dynamic performance of the system;
- The presented solution facilitates the modified modulation scheme and its features were used to develop a novel modeling method for the converter’s dynamics. This method is very simple and straightforward, especially when compared to the small-signal averaging method applied in [11]. This method is one of the most important contributions of this paper;
- Thanks to the above-mentioned modeling method, it was possible to develop a linear model of the converter dynamics in the s-domain, which is valid in the whole operational range of the converter (i.e., no linearization around an operational point is needed). Based on that, it was possible to develop some straightforward tuning rules for both current and voltage control loops. In each case it was possible to reduce the tuning process of the controller parameters to a single degree of freedom. The tuning process of each controller is then reduced to a choice of the desired trade-off between the dynamics of the system responses and robustness. It has great practical importance, as no model is perfect and it is often the case that the system designed based on simulations needs to be further re-tuned, as the experimental results normally differ from the theoretical ones. This is obvious, as in a real system there are always some parameter tolerances, measurement noises, and some characteristics which could not be perfectly modeled. The presented tuning rules are very convenient to use in such situations and they are the second important contribution of this paper;
- The last important contribution is an experimental illustration of the non-linear effects, which can occur if the system is operated near its current limitation. It demonstrates that sometimes an effective control system can not be designed by simply optimizing the simulated responses, as the robustness is also a very important feature and its required level is often very hard to predict theoretically. Hence, the presented results proved an usefulness of having some one dimensional tuning rules rather than a single set of parameters, which were derived based on some performance indexes and using the simulation or analytical tools.
Author Contributions
Conceptualization, M.G.; methodology, M.G.; software, M.G.; validation, M.G.; formal analysis, M.G.; investigation, M.G.; resources, L.M.G. and A.K.; data curation, M.G.; writing—original draft preparation, M.G.; writing—review and editing, L.M.G. and A.K.; visualization, M.G.; supervision, L.M.G. and A.K.; project administration, A.K.; funding acquisition, L.M.G. and A.K. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by The National Center for Research and Development under Agreement number TECHMATSTRATEG1/346922/4/NCBR/2017 for project “Technologies of semiconductor materials for high power and high frequency electronics”.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available in article.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AC | Alternating Current |
| DAB | Dual Active Bridge |
| DC | Direct Current |
| DPS | Dual Phase Shift (modulation) |
| DRES | Dual Rising Edge Shift (algorithm) |
| DSSPS | Double-Sided Single Phase Shift (modulation) |
| EPS | Extended Phase Shift (modulation) |
| PCB | Printed Circuit Board |
| PWM | Pulse Width Modulation |
| SST | Solid State Transformer |
| SPS | Single Phase Shift (modulation) |
| TPS | Triple Phase Shift (modulation) |
| ZOH | Zero Order Hold |
Appendix A

Table A1.
System Parameters.
Table A1.
System Parameters.
| Name | Symbol | Value | Unit |
|---|---|---|---|
| Input voltage range | V | ||
| Output voltage range | V | ||
| Output current range | A | ||
| Switching frequency | 40 | kHz | |
| Drain-source on-state resistance of MOSFETs | 25 | m | |
| Equivalent circuit inductance | H | ||
| Auxiliary inductance in series with primary transformer winding | H | ||
| Transformer turns ratio | − | ||
| Transformer magnetizing inductance | mH | ||
| Leakage inductance of primary transformer winding | H | ||
| Leakage inductance of secondary transformer winding | H | ||
| Resistance of primary transformer winding | m | ||
| Resistance of secondary transformer winding | m | ||
| Current filters’ parameters | 200 | F | |
| 165 | m | ||
| H | |||
| H | |||
| Capacitance of input and output capacitors | 600 | F |
References
- De Doncker, R.W.; Divan, D.M.; Kheraluwala, M.H. A three-phase soft-switched high power density DC/DC converter for high power applications. In Proceedings of the Conference Record of the 1988 IEEE Industry Applications Society Annual Meeting, Pittsburgh, PA, USA, 2–7 October 1988; pp. 796–805. [Google Scholar] [CrossRef]
- Zhao, B.; Song, Q.; Liu, W.; Sun, Y. Overview of Dual-Active-Bridge Isolated Bidirectional DC–DC Converter for High-Frequency-Link Power-Conversion System. IEEE Trans. Power Electron. 2014, 29, 4091–4106. [Google Scholar] [CrossRef]
- Hou, N.; Li, Y.W. Overview and Comparison of Modulation and Control Strategies for a Nonresonant Single-Phase Dual-Active-Bridge DC-DC Converter. IEEE Trans. Power Electron. 2020, 35, 3148–3172. [Google Scholar] [CrossRef]
- Segaran, D.S. Dynamic Modelling and Control of Dual Active Bridge Bi-Directional DC-DC Converters for Smart Grid Applications. Ph.D. Thesis, School of Electrical and Computer Engineering (SECE), RMIT University, Melbourne, Australia, 2006. Available online: https://core.ac.uk/download/pdf/15628024.pdf (accessed on 19 April 2021).
- Pan, Y.; Yang, Y.; He, J.; Sangwongwanich, A.; Zhang, C.; Liu, Y.; Blaabjerg, F. A Dual-Loop Control to Ensure Fast and Stable Fault-Tolerant Operation of Series Resonant DAB Converters. IEEE Trans. Power Electron. 2020, 35, 10994–11012. [Google Scholar] [CrossRef]
- Demetriades, G.D.; Nee, H. Dynamic modeling of the Dual-Active Bridge topology for high-power applications. In Proceedings of the 2008 IEEE Power Electronics Specialists Conference, Rhodes, Greece, 15–19 June 2008; pp. 457–464. [Google Scholar] [CrossRef]
- Wei, S.; Zhao, Z.; Li, K.; Yuan, L.; Wen, W. Deadbeat Current Controller for Bidirectional Dual-Active-Bridge Converter Using an Enhanced SPS Modulation Method. IEEE Trans. Power Electron. 2021, 36, 1274–1279. [Google Scholar] [CrossRef]
- Gao, G.; Lei, W.; Cui, Y.; Li, K.; Hu, X.; Xu, J.; Lv, G. Model Predictive Control of Dual Active Bridge Converter Based on the Lookup Table Method. In Proceedings of the 2019 IEEE 10th International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Xi’an, China, 3–6 June 2019; pp. 183–186. [Google Scholar] [CrossRef]
- Chen, L.; Shao, S.; Xiao, Q.; Tarisciotti, L.; Wheeler, P.W.; Dragičević, T. Model Predictive Control for Dual-Active-Bridge Converters Supplying Pulsed Power Loads in Naval DC Micro-Grids. IEEE Trans. Power Electron. 2020, 35, 1957–1966. [Google Scholar] [CrossRef]
- Li, K.; Yang, Y.; Tan, S.; Hui, R.S. Sliding-Mode-Based Direct Power Control of Dual-Active-Bridge DC-DC Converters. In Proceedings of the 2019 IEEE Applied Power Electronics Conference and Exposition (APEC), Anaheim, CA, USA, 17–21 March 2019; pp. 188–192. [Google Scholar] [CrossRef]
- Krismer, F. Modelling and Optimization of Bidirectional Dual Active Bridge DC-DC Converter Topologies. Ph.D. Thesis, Department of Information Technology and Electrical Engineering, ETH Zuerich, Zuerich, Switzerland, 2010. Available online: https://www.pes-publications.ee.ethz.ch/uploads/tx_ethpublications/Krismer_2011_03_17_Modeling_and_Optimization_of_Bidirectional_Dual_Active_Bridge_DC-DC_Converter_Topologies.pdf (accessed on 19 April 2021).
- Erickson, R.W.; Maksimovic, D. Input Filter Design. In Fundamentals of Power Electronics; Kluwer Academic Publishers: New York, NY, USA, 2004; pp. 377–408. [Google Scholar]
- Gierczynski, M.; Grzesiak, L.M.; Kaszewski, A. A Dual Rising Edge Shift Algorithm for Eliminating the Transient DC-bias Current in Transformer for a Dual Active Bridge Converter. Energies 2021, 14, 4264. [Google Scholar] [CrossRef]
- Han, S.; Munuswamy, I.; Divan, D. Preventing transformer saturation in bi-directional dual active bridge buck-boost DC/DC converters. In Proceedings of the 2010 IEEE Energy Conversion Congress and Exposition, Atlanta, GA, USA, 12–16 September 2010; pp. 1450–1457. [Google Scholar] [CrossRef]
- Everts, J. Modelling and Optimization of Bidirectional Dual Active Bridge AC-DC Converter Topologies. Ph.D. Thesis, Faculty of Engineering Science, KU Leuven, Leuven, Belgium, 2014. Available online: https://limo.libis.be/primo-explore/fulldisplay?docid=LIRIAS1731206&context=L&vid=Lirias&search_scope=Lirias&tab=default_tab&lang=en_US&fromSitemap=1 (accessed on 19 April 2021).
- Ogata, K.; Maksimovic, D. Design of Discrete-Time Control Systems by Conventional Methods. In Discrete-Time Control Systems, 2nd ed.; Prentice-Hall International: Englewood Cliffs, NJ, USA, 1995; pp. 173–292. [Google Scholar]
- PLECS|Plexim. Available online: https://www.plexim.com/products/plecs (accessed on 10 March 2021).
- Aestrom, K.J.; Murray, R.M. Frequency Domain Analysis. In Feedback Systems: An introduction for Sciencists and Engineers; Version v2.10b; Princeton University Press: Princeton, NJ, USA, 2009; pp. 267–292. [Google Scholar]
- Kessler, C. Ueber die Vorausberechnung optimal abgestimmter Regelkreise Teil III. Die optimale Einstellung des Reglers nach dem Betragsoptimum. Regelungstechnik 1955, 3, 40–49. [Google Scholar]
- MATLAB. Available online: http://www.mathworks.com/products/matlab.html (accessed on 10 March 2021).
- Delfino TMS320F28379 Control CARD. Available online: https://www.ti.com/lit/ug/sprui76a/sprui76a.pdf?ts=1623674671939&ref_url=https%253A%252F%252Fwww.ti.com%252Ftool%252FTMDSDOCK28379D (accessed on 15 June 2021).
- Cree CCS050M12CM MOSFET Power Modules. Available online: https://www.wolfspeed.com/media/downloads/189/CCS050M12CM2.pdf (accessed on 15 June 2021).
- Gate Driver for 1200V SiC MOSFET Power Module. Available online: https://www.wolfspeed.com/media/downloads/836/CGD15FB45P1.pdf (accessed on 15 June 2021).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).