Abstract
Due to the addition of the drag reducer in refined oil pipelines for increasing the pipeline throughput as well as reducing energy consumption, the classical method based on the Darcy-Weisbach Formula for precise pressure loss calculation presents a large error. Additionally, the way to accurately calculate the pressure loss of the refined oil pipeline with the drag reducer is in urgent need. The accurate pressure loss value can be used as the input parameter of pump scheduling or batch scheduling models of refined oil pipelines, which can ensure the safe operation of the pipeline system, achieving the goal of energy-saving and cost reduction. This paper proposes the data-driven modeling of pressure loss for multi-batch refined oil pipelines with the drag reducer in high accuracy. The multi-batch sequential transportation process and the differences in the physical properties between different kinds of refined oil in the pipelines are taken into account. By analyzing the changes of the drag reduction rate over time and the autocorrelation of the pressure loss sequence data, the sequential time effect of the drag reducer on calculating pressure loss is considered and therefore, the long short-term memory (LSTM) network is utilized. The neural network structure with two LSTM layers is designed. Moreover, the input features of the proposed model are naturally inherited from the Darcy-Weisbach Formula and on adaptation to the multi-batch sequential transportation process in refined oil pipelines, using the particle swarm optimization (PSO) algorithm for network hyperparameter tuning. Case studies show that the proposed data-driven model based on the LSTM network is valid and capable of considering the multi-batch sequential transportation process. Furthermore, the proposed model outperforms the models based on the Darcy-Weisbach Formula and multilayer perceptron (MLP) from previous studies in accuracy. The MAPEs of the proposed model of pipelines with the drag reducer are all less than 4.7% and the best performance on the testing data is 1.3627%, which can provide the calculation results of pressure loss in high accuracy. The results also indicate that the model’s capturing sequential effect of the drag reducer from the input data set contributed to improving the calculation accuracy and generalization ability.
1. Introduction
The pipeline transportation is one of the major ways in the petroleum industry. Pressure loss exists during the flow of refined oil that is transported in the pipeline, which can cause safety concerns [1,2]. Additionally, it will cause a large amount of pump energy waste along the pipelines and high oil transportation costs [3]. Nowadays, oil pipeline operators generally choose to mix oil with the drag reducer to reduce pressure loss [3,4,5], achieving the goal of delivery volume increment, saving pump energy consumption, and reducing operating costs. Nevertheless, the existence of the drag reducer can make a large error when calculating the pressure loss with the classical formula [6]. Moreover, the modeling of pressure loss in refined oil pipelines is of vital importance in industrial production activities, which directly affects the formulation of the pumping and oil delivery batch schedules [7]. Therefore, the accurate calculation of the pressure loss of refined oil pipelines containing drag reducers is conducive to formulating the oil delivery batch and pumping schedules, which ensure a safer operation of the pipeline system and better economic efficiency, achieving the goals of industrial energy saving, cost-saving, and promoting the process of carbon neutrality [7,8,9].
According to the theory of continuum mechanics, the classical method for calculating the pressure loss in refined oil pipelines depends on the Darcy-Weisbach Formula shown in Equation (1), which is widely used in the industrial scene [10]. Among all the parameters in the Darcy-Weisbach Formula, the Fanning friction factor is the most decisive one and is determined by the Reynolds number Re (shown in Equation (3)). Therefore, the accurate calculation of is of vital importance for the accurate calculation of the pressure loss. Previous researchers have made much effort in accurately calculating the Fanning friction factor of oil pipelines (shown in Table 1). For refined oil pipelines without the drag reducer, as refined oil is a Newtonian fluid, the Fanning friction factor directly follows the Prandtl-Karman law [6] in Equation (2). By solving the Prandtl-Karman law, the Fanning friction factor is determined and the pressure loss in the pipelines can be calculated according to the given operating conditions. However, the situation became complicated for pipelines with the drag reducer mixed with oil. Additionally, the earlier study performed by Virk [11] conducted comprehensive experiments of Newtonian fluids on drag reduction and illustrated the physical mechanism of drag reduction using the evidence concerned with data correlation and analysis (as there is a relationship between the drag reduction rate and pressure loss, by obtaining the drag reduction rate, the pressure loss is also obtained [12]). Moreover, Virk proposed the trend of maximum drag reduction asymptote for the Fanning friction factor, which was the foundation of many later researchers on this topic (theoretically, the value of the Fanning friction factor of refined oil is between the value calculated by the Prandtl-Karman law and the one related to Virk’s maximum drag reduction). In [5], the authors investigated various factors which affected the drag reduction rate in crude oil pipelines with the drag reducer. The results indicated that the drag reduction rate increased with the temperature, oil flowrate, pipe roughness, as well as the drag reducer concentration. The same authors proposed a general model derived from Virk’s model and established a model, in the next year in [13], for calculating the drag reduction rate in crude oil pipelines, in which various operating parameters were comprehensively analyzed. Although crude oil is a non-Newtonian fluid and follows the theory of Dodge and Metzner [14] who analyzed the turbulent flow of non-Newtonian systems, the form of the Dodge and Metzner correlation is similar to the Prandtl-Karman Law for Newtonian fluids [13] and the results in [13], which showed a good agreement with the experimental data.
Compared to the theoretical and semi-empirical models above, empirical models can fit the data robustly as they are often based on statistical and big data techniques [15,16]. Karami et al. [15] performed the experiments and analyzed the drag reduction rate in the pipeline by applying response surface methodology to historical data. As was noted in [15], more than 95% of the variation in the model could be described using the Reynolds number and concentration () of drag reducer. Therefore, a power relation was developed based on and , which yielded a simpler model to calculate the Fanning friction factor efficiently and both simplicity and accuracy were better compared to the model in [13]. With the development of the theory of artificial intelligence techniques and computational power, deep learning has become a powerful modeling tool that allows models composed of multiple hidden layers to learn representations of data with multiple levels of the abstraction of the relationship between the input and output, thus solving complex and nonlinear problems [17,18,19,20]. In [21], the authors presented multilayer perception (MLP) models for the prediction of the drag reduction rate in crude oil pipelines as well as compared it with other existing mathematical models, and the results stated the ability of the MLP model. The authors of [22] studied the feasibility of the Levenberg-Marquardt algorithm combined with the imperialist competitive computational method to predict the drag reduction rate in crude oil pipelines and provided an MLP-based formulation to estimate the drag reduction rate.


Table 1.
Evolution of the calculation method of the Fanning friction factor for the pipeline containing the drag reducer.
Table 1.
Evolution of the calculation method of the Fanning friction factor for the pipeline containing the drag reducer.
| Calculation Methods | Applicable Conditions |
|---|---|
| Prandtl-Karman Law [6] | Newtonian fluid; turbulence flow; without drag reducer in the pipeline |
| Virk’s maximum drag reduction [11] | Newtonian fluid; turbulence flow; with drag reducer in the pipeline |
| General law of drag reduction [11] | Newtonian fluid; turbulence flow; with drag reducer in the pipeline |
| Karami’s method of calculating drag reduction for crude oil [13] | Non-Newtonian fluid; turbulence flow; with drag reducer in the pipeline |
| Karami’s method of calculating drag reduction for crude oil [15] | Non-Newtonian fluid; turbulence flow; with drag reducer in the pipeline |
| Zabihi’s method of calculating drag reduction for crude oil [21] | Non-Newtonian fluid; turbulence flow; with drag reducer in the pipeline |
| Moayedi’s method of calculating drag reduction for crude oil [22] | Non-Newtonian fluid; turbulence flow; with drag reducer in the pipeline |
However, little previous literature has been concerned with the sequential effect of drag reduction such as the dispersing effect, which influenced the accuracy of calculating the pressure loss. Cao et al. [23] developed a modified equation for the prediction of the drag reduction rate and effectively promoted the application effect of the drag reducer in short distance pipelines. However, the disadvantage of the model in [23] was quite clear: The model was limited to the pipelines used case by case and the exact operational conditions (e.g., temperature, oil viscosity, concentration of the drag reducer) should be rigorously satisfied. From what was found from the data analysis in Section 2.2.3 and Appendix A, the effect of drag reducer on the pressure loss in the refined oil pipeline has something to do with the time sequence. In other words, when calculating the pressure loss with the drag reducer in the pipeline, if the relationship within the sequential data can be captured, the model can obtain temporal information indicating the effect of the time sequence of drag reduction and there will be better performance on the model’s accuracy. Recurrent neural networks (RNNs) are connectionist models that capture the dynamics of sequences via cycles in the network of neurons [24] and are used in domains such as speech recognition, handwriting recognition, polyphonic music modeling, etc. [25,26]. However, the memory produced from the recurrent connections can be severely limited by the algorithms employed for training RNNs. Additionally, the models related to RNNs so far have been subjected to the problem of exploding or vanishing gradients during the training process, resulting in the network failing to learn long-term sequential dependencies in data [27]. By introducing gate functions into the cell structure, the long short-term memory (LSTM) network could handle the problem of long-term dependencies well [28].
In this paper, the data-driven modeling of pressure loss in multi-batch refined oil pipelines with drag reducer using the LSTM network is proposed. The pressure loss given by the proposed model can be used as the input parameter of pump scheduling or batch scheduling models of refined oil pipelines, which is one of the main motivations of this research. Case studies using operational data on the production scene are performed to validate as well as illustrate the advantage of the proposed model compared to the models in previous papers. The main contributions of this paper are listed as follows:
- The data-driven modeling of pressure loss in multi-batch refined oil pipelines with drag reducer using the LSTM network is proposed, using the particle swarm optimization (PSO) algorithm for network hyperparameter tuning. The structure of the neural network model is designed and the input features of the proposed model are naturally inherited from the classical model and on adaptation to the multi-batch pipeline characteristics, which makes the proposed neural network model more easily interpreted and understood;
- Different from the studies in previous works which only considered a single kind of fluid in the pipeline, the multi-batch sequential transportation process and the differences in the physical properties between different kinds of refined oil in the pipelines are considered. The network input feature “the length ratio of gasoline and diesel” is chosen to describe the pressure loss change in refined oil pipelines during the multi-batch sequential transportation process;
- The sequential time effect of the drag reducer such as the dispersing effect that captures the sequential information of calculating the pressure loss is considered, which is paid scarce attention to in previous works. Different from the model of previous works that added an amendment to the formula, the time effect is captured and reflected by the LSTM module in the proposed model with high accuracy.
The rest of the paper is organized as follows. Section 2 introduces the general framework of the modeling of pressure loss in multi-batch refined oil pipelines with drag reducer using the LSTM network. Additionally, it illustrates the training process of the proposed model using the LSTM network, from data pre-processing to hyperparameter tuning and network parameters updating. In Section 3, case studies using operational data on the production scene are conducted to demonstrate the effectiveness as well as illustrate the advantage of the proposed model compared to the models in previous papers. Finally, conclusions are drawn in Section 4.
2. Methodology
2.1. Modeling of Pressure Loss in Multi-Batch Refined Oil Pipelines Using Methods in Previous Literature
In previous literature, whether there is a drag reducer in the pipelines or not, the calculation of pressure loss can be characterized by the Darcy-Weisbach Formula in [10], whose form is as follows:
where is the pressure loss in the refined oil pipeline (Pa), is the Darcy friction coefficient which is four times the Fanning friction factor (, dimensionless), is the length of the pipeline (m), is the gravitational acceleration (m/s2), is the mean flow velocity (m/s), is the diameter of the pipeline (m), and is the flowrate of the pipeline (m3/s).
For the pipelines without the drag reducer, the Fanning friction factor follows the Prandtl-Karman law in [6], whose form is:
where is the Fanning friction factor and is the Reynolds number that has the form:
in which is oil viscosity (m2/s).
For the pipelines with the drag reducer, Virk [11] proposed the Virk’s maximum drag reduction formula:
which could give the limit of the effect of the drag reducer on the pressure loss and be used to validate the proposed model. However, its result was sometimes far from the real value and could only be used as a reference value. To seek a more accurate method for calculating the Fanning friction factor, the model in [15] is one of the models with the highest accuracy and can be used as a comparison with our proposed model to present its progressiveness. The model in [15] is as follows:
In [21,22], the multilayer perceptron (MLP) models are utilized to calculate the drag reduction using two hidden layers with different numbers of neurons, respectively. A general transfer function for the MLP network with input is:
where and are the weight matrices of the hidden and output layers, respectively, is a bias vector in the hidden layer, is a bias vector in the output layer, and stands for the activation function.
The formulas for pipelines with the drag reducer from the previous literature are mainly for crude oil. According to [13], crude oil is a non-Newtonian fluid and follows the theory of Dodge and Metzner [14], which is similar to the Prandtl-Karman Law for Newtonian fluids. Therefore, the formula for crude oil can be used by the refined oil formula for reference.
2.2. Modeling of Pressure Loss in Multi-Batch Refined Oil Pipelines with Drag Reducer Using the LSTM Network
2.2.1. The Theory of LSTM Cells
The classical RNNs comprise hidden layers between the input layer and output layer [29]. By replacing hidden neurons with LSTM cells, the training process becomes more stable, which makes the LSTM popular. The structure of the LSTM network most commonly used was originally proposed in [30], which modified the original LSTM network from [31]. The concrete description of LSTM is as follows.
Figure 1 shows a detailed structure of a LSTM cell. The gating unit is introduced into the network to control the influence of the previous time information on the current information in order for the model to have the so-called “long short-term memory”, which is suitable for nonlinear sequential problems. Different from the classical RNNs [32], in the LSTM network, the neurons in the hidden layer are replaced by memory units with the mechanism of three gates: Input gate, output gate, and forgetting gate. The input of the model includes , which is the sequential input at time , the hidden state at time , , and the cell state at time , . The output contains the cell state at time , and the hidden state at time , , in which and , respectively contain the long-term and short-term memory information. By controlling the input gate, forgetting gate, and memory gate, the information passes through the LSTM cells. The sigmoid activation function acts on the input in the input gate, limiting the variables in the range [0, 1] to realize the control of . Moreover, a hyperbolic tangent (tanh) activation function is present in the input gate for blocking the input. The usage of the forgetting gate is to selectively forget some information from the cell state from the last moment , which is expressed in the control of by (see Equation (8)). The output gate is used to decide which parts of the filtered cell state are going to be the output. The calculation formulas are as follows [24]:
where , , represent the calculated results of the input gate, forgetting gate, and output gate, respectively, and represent the weight matrix and offset term of the corresponding gate, respectively, and is the sigmoid activation function. In the LSTM model, the output of the cell state and hidden state at time t is determined by the output gate and cell state, which is filtered through the tanh activation function. The formulas are as follows [24]:
where is the blocking input value acting on the result of the input gate at time t, tanh is the hyperbolic tangent activation function, and represents the pointwise multiplication of the vector.
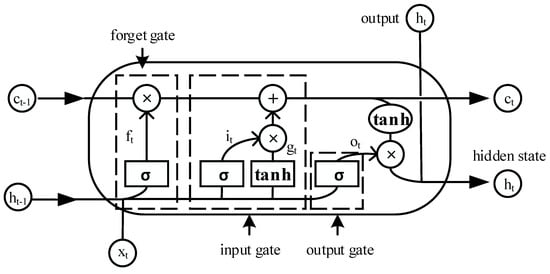
Figure 1.
The detailed structure of a LSTM cell.
2.2.2. The Proposed Model Using the LSTM Network
Referring to classical RNNs, Figure 2 shows the folded structure of a LSTM layer which consists of LSTM cells. It should be emphasized that the LSTM layer at each time has the same number of LSTM cells. At a certain time, the LSTM cells are parallel to each other without any connection. Additionally, the information transference of LSTM cells between two neighboring times reflects on the recurrent connection of the proceeding LSTM cells (i.e., the transference of cell state and hidden state through time), which is capable of capturing the temporal coupling characteristic from the data. The number of LSTM cells at each time should be chosen in advance by the experience of the researcher or optimization algorithm, which corresponds to the model’s ability of abstraction.
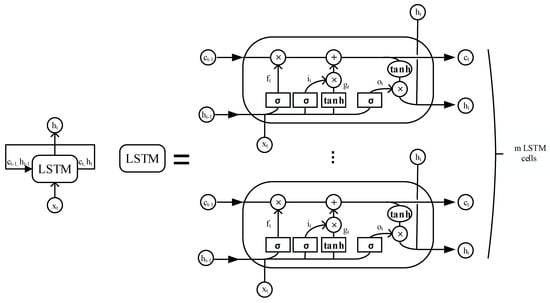
Figure 2.
Folded structure of a LSTM layer.
Before constructing the whole neural network model, representative features influencing the pressure loss need to be carefully chosen. It needs to be re-affirmed here that the research object in this paper is multi-batch refined oil pipelines. Therefore, the multi-batch sequential transportation process, which is displayed in Figure 3, should be taken into consideration. The assumption of the multi-batch sequential transportation process is derived from [7].
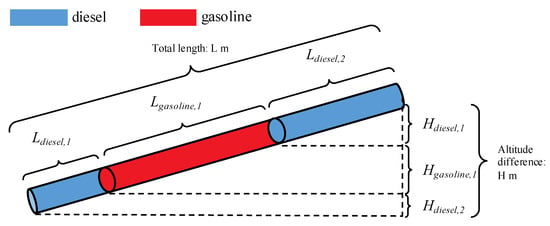
Figure 3.
Sketch map for a multi-batch refined oil pipeline.
This paper particularly considers two kinds of refined oil: Diesel and gasoline. For refined oil pipelines that contain other oil types, the same thought as the one presented here still works. If there is no drag reducer and both gasoline and diesel are in the pipeline, according to the Darcy-Weisbach Formula, the following formula for calculating the pressure loss in a pipeline can be obtained.
where , , are the Fanning friction factor, density, and total length of a certain refined oil in the pipeline, respectively. Define , then considering and the fact that the diameter of the pipeline remains unchanged, substitute into Formula (9) to get:
If the pipeline has the altitude difference, the pressure should consider its effect and the formula for the pressure loss will be added as one more term:
where is an additional term representing the pressure loss caused by the altitude difference. Suppose the altitude difference of a pipeline is , then is calculated as follows:
where and are the total length in height (the total height demonstrated in Figure 3). A trick is presented, whereby, when writing the computer program for calculating the , if the result is extremely large, then the will be artificially set to 100, which will cause little influence on the result. Additionally, the can be defined as the proportion of the length of gasoline in the length of the whole pipeline (both definitions work). As the Fanning friction factor is determined by the Reynolds number of the oil (see Equation (2)), it can be expressed by a function with the arguments and : . Therefore, the pressure loss is the function of the flowrate and the length ratio of diesel and gasoline in the pipeline, which can reflect the pipeline’s steady-state. In light of the analysis above, the flowrate and the volume ratio of diesel and gasoline in the pipeline are chosen to be the two input features of the model, while the output is the pressure loss. The structure of the neural network model is designed and the input feature is naturally inherited from the Darcy-Weisbach Formula and on adaptation to the multi-batch pipeline characteristics. In this situation, it can be imagined that the data-driven model will attain high accuracy compared to the derivation of the Darcy-Weisbach Formula. If the pipeline contains the drag reducer, the pressure loss can be calculated using the proposed model, given the sequence of flowrate and the length ratio of gasoline and diesel in the pipeline. The relationship between the input and output of the model is as follows:
where refers to the proposed model, is the vector of pressure loss in the pipeline, is the vector of flowrate in the pipeline, and is the vector of length ratio of diesel and gasoline in the pipeline. The length of the vector is which refers to the time length of the sequence.
Based on the hidden layers with LSTM cells, the proposed structure for the modeling of pressure loss in multi-batch refined oil pipelines with drag reducer is shown in Figure 4. In this paper, the size of the hidden state and cell state (these two are instinctively equal) is set to 1 and the number of LSTM layers is set to 2. There are several hyperparameters to be chosen in advance using the PSO algorithm: The length of time sequence, the number of LSTM cells at each time (the number is the same at each time), the number of neurons in the forward fully connected layer, the maximum number of training epochs, and the initial learning rate. It is clear in the unfolded structure of the model that the output of LSTM cells at each time (, which is a vector containing all the output of LSTM cells at certain time t) is fed into a deep neural network, respectively, which helps the model perceive a deeper abstraction of the input data. The final calculated values at each time are given by these deep neural networks, which no longer have the time coupling connection as LSTM.
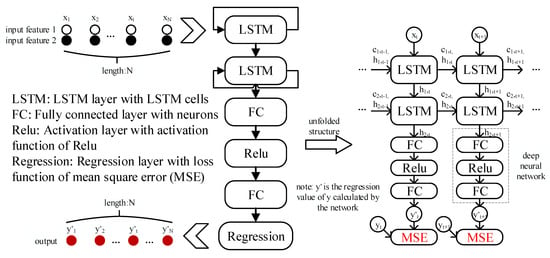
Figure 4.
Structure of the data–driven model for calculating the pressure loss.
2.2.3. Training the Proposed Model
Before training the model, the pre-processing work on the historical data of the pipeline pressure loss gathered from the production scene is of vital importance. As the data are directly extracted from the supervisory control and data acquisition (SCADA) system, the outliers exist and will influence the performance of the data-driven model. There are several techniques in processing the raw data, such as data cleaning [33] and data normalization [34]. To clean the dirty data from the data sets, the violin chart and box line chart are both used. The violin chart is used to observe the data distribution, while the box line chart is used to observe the outliers, and the two are combined to determine which values are outliers and should be refilled (see Appendix A for detailed information of the data cleaning procedure). Although the box line chart can reflect the range of the majority of data points, the outliers cannot all be refilled, since some special operational situations exist. Under this circumstance, the violin chart can serve as the reference, in which the distribution information can tell us whether the outliers in the box line chart should be refilled or not (i.e., if the probability density of the outliers is not negligible, they should be taken into consideration). The comparison between before and after the refill of outliers for Case 2 in Section 3 is shown in Figure 5 and Figure 6 and gives an example of how the raw data are cleaned, which is the effect of the utilization of box line and violin charts, as well as the outlier detection and refill technique. After the cleaning of raw data, for a common procedure of machine learning, the data are often divided into three parts: Training data, validation data, and testing data. The proportion of each data set depends on the scale of the raw data set, and in this paper, the proportion of 6:1:1 for training data, validation data, and testing data is chosen. The data normalization technique is required when there are big differences in the ranges of different features and the detailed formulas are shown in Appendix B. In this paper, the two input features of the three data sets are normalized by the mean and variance of the training data set.
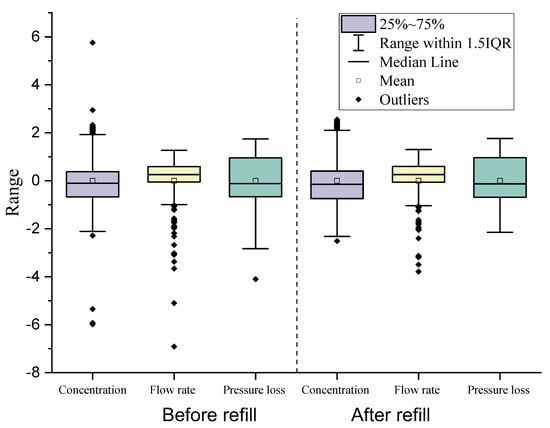
Figure 5.
Box line plots before and after the refill of the outliers of Pipeline No. 4 (normalized). As the units of the two input parameters and one output parameter are different, in order to present them in one figure, the data sets before and after the refill are normalized. In fact, the normalization process is done after the data have been divided into training data, validation data, and testing data. The situation is the same in Figure 6.
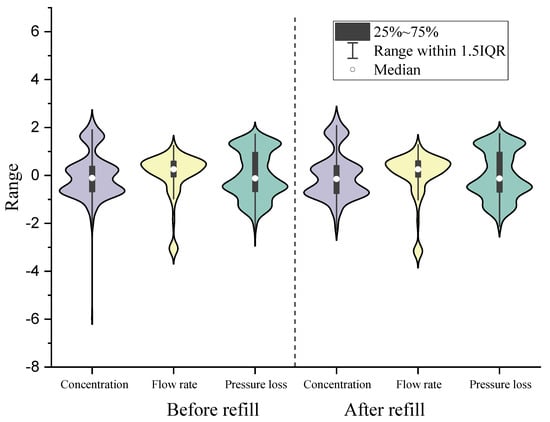
Figure 6.
Violin plots before and after the refill of outliers of Pipeline No. 4 (normalized).
As is shown in Figure 7, the data are firstly cleaned, then divided into three data sets. Thereafter, the divided data sets are normalized right after the division. As there are various hyperparameters to be tuned, the PSO algorithm is applied to search for a better combination of the parameters. When initializing the particle swarm, each particle is given five dimensions, which refer to the five tunable hyperparameters. The algorithm for training the proposed neural network is ADAM [35], which is straightforward to implement and computationally efficient. It is worth mentioning that in the program, the random number seed should be executed to help reproduce the training performance with the obtained hyperparameters. After training the proposed network, the testing data are devoted to evaluate the performance of the trained network. The formulas for updating the velocity and position of each particle can be found in [36]. Up to the maximum iteration, the algorithm reaches an end and the five hyperparameters of the global best particle are obtained. The trained model with the optimized hyperparameters can be used to calculate the pressure loss given with a pretty small mean square error, which shows a good generalization of the model. The next section will validate and show the advantage of the proposed model compared to the previous ones.
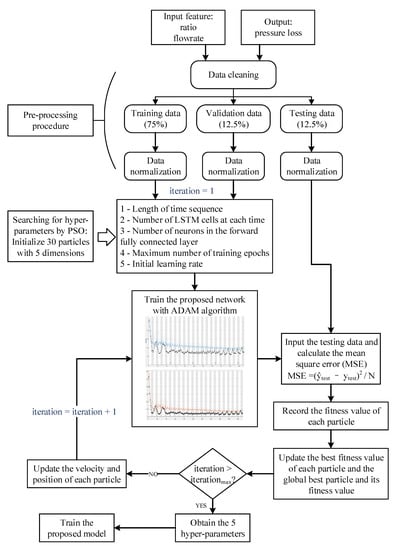
Figure 7.
Flow chart for training the proposed model using PSO.
3. Results and Discussion
3.1. Data Analysis before the Case Studies
The raw data of this paper are extracted directly from the SCADA system, which include the inlet and outlet pressure of the stations connected by the pipelines that determine the pressure loss, the flowrate of the pipelines, and the density of the oil flowing through the stations. This reflects the oil type distribution in the pipeline and helps calculate the length of each type of oil to get the input feature “”. In this paper, we investigate the pressure loss of seven real-world refined oil pipelines in Guangdong Province, China, which are a part of the Guangdong refined oil pipeline system providing refined oil for the whole province. To show the credibility that the data in this paper are acquired from the real-world multi-product refined oil pipeline system, batch migration charts of the pipeline schedule from the company are presented in Figure A4 and Figure A5 in Appendix D. Pipeline No. 1 has no drag reducer and pipeline Nos. 2 to 7 contain the drag reducer. The pipeline basic data are shown in Table 2. An example of the data pre-processing procedure of Pipeline No. 4 is shown in Section 2.2.3 as well as Appendix A. Moreover, the same procedure is implemented in the cases of the other pipelines.

Table 2.
The pipeline basic data.
The inspiration of considering the time effect of the drag reducer on the pressure loss using the LSTM network, is based on the exploration of the drag reduction rate of the refined oil pipelines on the production scene, when calculating the pressure loss for implementing the pump scheduling problems. We investigate the relationship between the pressure loss and flowrate of the pipelines as well as the changes in the drag reduction rate over time. This paper presents a typical case to specifically illustrate the idea. When analyzing the relationship between the pressure loss and flowrate, it can be seen from Figure 8 that under the same flowrate, the pressure loss has different values no matter what type of refined oil is in the pipeline. Additionally, Figure 9 shows the change of the drag reduction rate when diesel is injected into the pipeline filled with gasoline. Moreover, time stamp “0” in Figure 9 is the time when the drag reducer is added, and the initial stage of the curve is flat, which corresponds to the dispersing time effect of the drag reducer. Significantly in Figure A3, when the time lag changes from 0 to 140, the autocorrelation and partial autocorrelation of the calculated and measured sequences show a similar strong sequential relationship of pressure loss, which means that the proposed model has validity on capturing the sequential information of the pressure loss sequence data. Synthesizing what we found from the data, we came to a deduction that calculating the pressure loss has something to do with the time sequence. Here, we call the previous methods for calculating the pressure loss of only one time point at a time the “point-to-point” regression methods. As there is a corresponding relationship between the concentration of the drag reducer and the flowrate on the production scene, in the proposed model, the concentration is not used as the input, which is one of the advantages over the previous ones. On the basis of “point-to-point” regression methods, the proposed model is a “sequence-to-sequence” calculating method that can consider the information transfer between the time series and capture the sequential law of the fluctuant concentration of drag reducer (although the concentration is regulated to be added stably, there is still some fluctuation). Additionally, the model can achieve a more accurate calculation. At the same time, the information flow between the LSTM cells is equivalent to increasing the amount of input information. Therefore, we think that the proposed model is at least as good as the “point-to-point” regression methods.
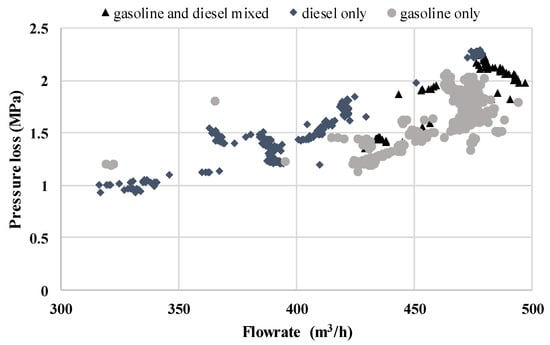
Figure 8.
Scatter plot between the pressure loss and flowrate of Pipeline No. 2. “Diesel/gasoline only” means that there is only diesel/gasoline in the pipeline; “gasoline and diesel mixed” means that the pipeline involves sequential batches of gasoline and diesel.
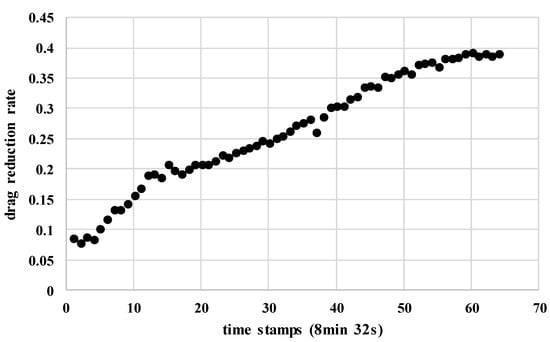
Figure 9.
The changes of the drag reduction rate over time in Pipeline No. 2.
3.2. Case Studies
3.2.1. Case 1
Case 1 aims to validate the proposed model and illustrates that the data-driven method has the advantage of not relying on the accurate refined oil property parameter. The pressure loss calculated by the proposed model includes the pressure loss caused by the terminal elevation, and thus, the effect of the terminal elevation has no more duplicate records. Here, we utilize the proposed model and Darcy-Weisbach Formula to calculate the pressure loss in Pipeline No. 1. As mentioned in Section 1, for the pipelines with no drag reducer, the Prandtl-Karman Law is used to calculate the Fanning friction factor. The physical properties of refined oil products as the parameters are listed in Table 3. As the inputs of Prandtl-Karman Law include the viscosity of the refined oil, which is changeable in each transportation schedule on the production scene and is inconvenient to be measured experimentally each time [37], the deviation will inevitably exist when calculating the pressure loss. We change the viscosity of diesel in steps of 0.02 in the range of 3.0 to 8.0 (×10−6 m2/s) and the viscosity of gasoline in steps of 0.005 in the range of 0.4 to 1.0 (×10−6 m2/s) to analyze the effect of viscosity. Moreover, we finally plot the results of the proposed model and Darcy-Weisbach Formula in comparison to the measured pressure loss on the production scene in Figure 10. The result of the Darcy-Weisbach Formula in Figure 10 is composed of 30,371 curves representing the change of viscosity of both diesel and gasoline. The results show that the proposed model has good accuracy for calculating the pressure loss and is valid for use, which proves our deduction (when analyzing the drag reduction rate of the refined oil pipelines on the production scene) that our proposed model is at least as good as the “point-to-point” regression methods. As the data are acquired from the real-world multi-product refined oil pipeline system and the proposed model can fit the data well, it can be concluded that the proposed model is capable of considering the multi-batch sequential transportation process as well as the differences in the physical properties between different kinds of refined oil. Although the Darcy-Weisbach Formula can provide accurate results at some time stamps, at time stamp 200–400 in Figure 10, it performs disappointing results with a large deviation. The reason is that the Darcy-Weisbach Formula strongly depends on the parameters and once the parameters are not accurately measured, the result will be frustrating. With the change of viscosity of diesel and gasoline, the result by the Darcy-Weisbach Formula has big changes, which means that the viscosity has much influence on the usage of Darcy-Weisbach Formula, while the proposed model is free from the influence. Additionally, we examine the statistics accuracy indicators listed in Table 4 on the full data set. Here, we specifically investigate the Darcy-Weisbach Formula under the condition of the listed kinematic viscosity in Table 3, which is given by the pipeline operators on the scene. The proposed model outperforms the Darcy-Weisbach Formula evidently, which again proved our deduction. Up to here, we validate the proposed model using comparisons and reveal that one of the advantages of the proposed model is its ability to handle the inaccuracy of the measurement of physical properties of the refined oil.

Table 3.
The physical properties of refined oil products in Case 1.
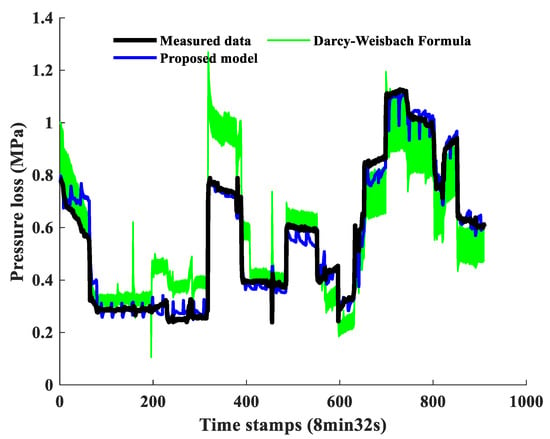
Figure 10.
Results for the models used in Case 1 (time interval 8 min 32 s).

Table 4.
Comparison of statistics accuracy indicators in Case 1.
3.2.2. Case 2
Case 2 is implemented to show the advantage of the proposed model on accuracy compared to the previous ones. The previous models depend on the Darcy-Weisbach Formula and MLP, shown in detail in Equations (2) and (4)–(6). We investigate six real-world pipelines from Pipeline Nos. 2 to 7 and take Pipeline No. 4 as an example to illustrate our opinion. The physical properties of refined oil products in Case 2 are listed in Table 5.

Table 5.
The physical properties of refined oil products in Case 2.
As all the studied pipelines in Case 2 have a drag reducer mixed in the transported refined oil, the method in Case 1 does not work. The proposed model is an effective tool to conquer the problem. We make detailed experiments on the proposed model and utilize four statistics accuracy indicators (shown in Table 6) to evaluate the performance of the models. The detailed definitions of the four indicators are given in Appendix C. In Table 6, the MAPEs of the proposed model are all less than 4.7% and the best performance on the testing data is 1.3627%, which can provide the calculation results of pressure loss in high accuracy. Combined with the results in Figure 11 and Figure A6, the tendency of the measured value from the production scene is captured by the proposed model, though an inevitable deviation exists at some time stamps. The MAE and RMSE of the proposed model are in accordance with the accuracy requirements of calculating the pressure loss for the pump and pipeline scheduling problems, leaving minimal impact on the scheduling result. The results of the R square value of the proposed model are close to 1, which means that the calculation result has a good performance on fitting the measured value. In the meantime, we also notice the problem that in some cases, the testing data set shows better performance than that of the training data set. Honestly, the effect on the training and testing data sets should be balanced according to the requirement. As far as we are concerned, the problem is caused by the division proportion of the full data set and remain in further experiments.

Table 6.
Results of statistics accuracy indicators in Case 2.
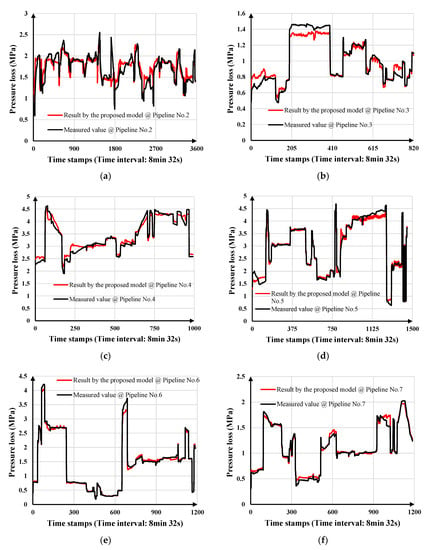
Figure 11.
Calculation results of the proposed model (on the full data set) for (a) Pipeline No. 2; (b) Pipeline No. 3; (c) Pipeline No. 4; (d) Pipeline No. 5; (e) Pipeline No. 6; (f) Pipeline No. 7.
In this paper, we specifically investigate Pipeline No. 4 to show the progressiveness of the proposed model. Additionally, we utilize Equations (2), (4) and (5), respectively to calculate the Fanning friction factor of Equation (11) and the MLP models in Equation (6) to obtain the pressure loss. According to what Karami et al. in [15] did, we also fit the curved surface of the Fanning friction factor versus the Reynolds number and concentration of the drag reducer. As we are studying the multi-batch refined oil pipelines, the surface of gasoline and diesel should be fitted, respectively. The curves are fitted using the MATLAB Curve Fitting Toolbox with the same data set of training the proposed model. The fitted curves of gasoline and diesel are shown in Figure 12 and the relationship is as follows:
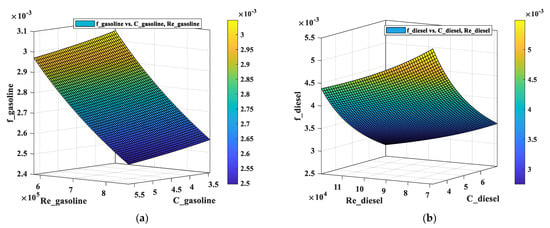
Figure 12.
Fitting result of the Fanning friction factor of Pipeline No. 4 using the formula from Karami et al. (2016) for (a) gasoline; (b) diesel.
The comparison of different models for calculating the pressure loss of Pipeline No. 4 on the full data set is shown in Figure 13. Without the drag reducer, the Prandtl-Karman Law can be an easy and convenient way to calculate the pressure loss with a relatively good performance, as can be seen in Figure 10. Nonetheless, due to the drag reducer in the pipeline, the commonly used method based on the Prandtl-Karman Law to calculate the Fanning friction factor of the Darcy-Weisbach Formula loses its effectiveness, leaving too large an error for practical use. Although Virk’s maximum drag reduction method considers the effect of drag reducer, it only reflects the extreme scenario. The curves of the pressure loss calculated by the methods of Karami, Zabihi, and Moayedi, as well as the proposed model in Figure 13 are between the ones calculated by the Prandtl-Karman Law and Virk’s method, which accord with the theory and validate the work. Additionally, it can be seen that the result of the proposed model is most close to the real-world measured data. The results of Karami’s method and the proposed model do equally well in most time stamps. However, from time stamps 850 to 1000, we can find that the result of the proposed model has better performance than that of Karami’s method. Comparing the methods based on the Darcy-Weisbach Formula, the artificial based methods present a better performance. Although Zabihi’s and Moayedi’s methods can have a good performance on the training data set, the MAPEs of the testing data set of the MLP models are 1.4% poorer than the proposed model, which means that the proposed model has a better generalization ability. From the comparison that the statistics accuracy indicators of the previous methods are poorer than the proposed model on MAE, RMSE, MAPE or R2 in Table 6, the model’s capturing time effect of drag reducer can really contribute to improving the performance.
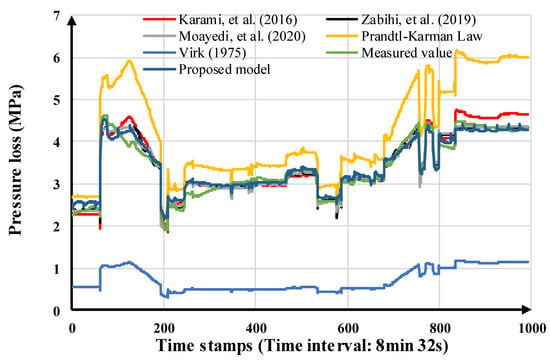
Figure 13.
Comparison of different models for calculating the pressure loss of Pipeline No. 4 (full data set).
In summary, the case studies presented in this paper validate the proposed model, show a better performance on dealing with historic data, as well as prove that the proposed model can consider the multi-batch sequential transportation process and the differences in the physical properties between different kinds of refined oil, thus enabling a better performance in calculating accuracy. The data-driven models including proposed model and comparing models in [15,21,22] show a better performance compared to the analytical models including comparing models in [6,11]. Furthermore, the artificial intelligence models involving proposed model and comparing models in [21,22] work better than the correlation model derived from the empirical formula given in [15]. Comparing the models based on artificial intelligence, the proposed model based on LSTM capturing the sequential information enhances the calculation accuracy and generalization ability. A shortcoming of the proposed model is that it costs more time to train than the compared models, but within tolerance.
The limitations should be pointed out in the end to notice the readers who intend to use our proposed model as a trial. First of all, the range of the flowrate of the studied pipelines is under 500 m3/h and the range of the concentration of the drag reducer is around 5 ppm (part per million cubic meters). The pipelines that are beyond that range still need to be verified. With the development of the pipeline transportation of refined oil, the maximum flowrate and some other factors may change. Therefore, the proposed model should be updated frequently to accord with the production scene. To follow the development of the pipelines, our future work includes building an offline database for retraining the proposed model from time to time. Secondly, though deep learning models can provide high accuracy, the hyperparameters are dependent on the researcher’s experience. Some of the hyperparameters are searched by the PSO algorithm in this paper, but there are still some remaining to be artificially chosen, such as the number of LSTM layers. According to the experiment when training the proposed model in this paper, properly increasing the number of LSTM layers and using more raw data to train the model will possibly produce a better result.
4. Conclusions
In this paper, the data-driven modeling of pressure loss in multi-batch refined oil pipelines with drag reducer, using the long short-term memory (LSTM) network with high accuracy, is proposed. Firstly, by analyzing the data, a deduction is made from the sequential data that the pressure loss has something to do with the time sequence and that the proposed model is at least as good as the calculation methods based on the Darcy-Weisbach Formula and MLP. Then, two case studies are implemented, which not only validate the proposed model but also show its superiority. For the pipelines without the drag reducer, the proposed model does not need strong volatility parameters such as the viscosity of the refined oil compared to the Prandtl-Karman Law. This implies that the proposed model is more practical on the production scene. Whether the pipeline has the drag reducer or not, the proposed model has a better performance on accuracy than the previous models. The MAPEs of the proposed model of pipelines with the drag reducer are all less than 4.7% and the best performance on the testing data is 1.3627%. The results of the R square value of the proposed model are close to 1. The high adaptability to data indicated that the proposed model can be utilized in refined oil pipelines with the drag reducer considering the multi-batch sequential transportation process and sequential effect of the drag reducer. Moreover, the results indicate that the model’s capturing time effect of the drag reducer from the input data set contributes to improving the calculation accuracy and generalization ability. In future work, the pressure loss given by the proposed model will be used as the input parameter of pump scheduling model or batch scheduling model of refined oil pipelines, which can ensure the safe operation of the pipeline system, achieve the goal of energy-saving and cost reduction, and eventually promote the process of carbon neutrality.
Author Contributions
Conceptualization, S.W.; methodology, S.W.; software, S.W., L.Z. and Q.L.; validation, S.W. and L.Z.; formal analysis, S.W. and Q.W.; investigation, S.W.; resources, Q.W. and M.L.; data curation, S.W.; writing—original draft preparation, S.W.; writing—review and editing, S.W., L.Z. and X.X.; visualization, S.W.; supervision, S.W. and X.X.; project administration, S.W., Q.W. and S.J.; funding acquisition, M.L., J.W. and X.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported in part by the South China Branch, PipeChina Co., Ltd., grant number GWHT20200001399 and in part by the State Grid HBEPC Economic and Technology Research Institute, grant number 521538210003.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data is not publicly available due to the funder’s restriction.
Acknowledgments
The authors are also thankful for the support by Zhongshan Tian, Xingwan Liao, Xiaoyin Huang, Mingyue Xiao, and Bin Li from the South China Branch, PipeChina Co., Ltd., Chao Li from Hanjing University, and the help of CET Electric Technology Inc.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Appendix A
The data cleaning procedure in this paper includes the outlier detection as well as the refill technique and is described concretely as follows. Once we get the raw data which include the sequential pressure loss, pipeline flowrate, and the density from the SCADA system on the production scene, the input parameters can be calculated through the multi-batch sequential transportation characteristics [7]. Firstly, the outliers are detected as elements more than three local standard deviations from the local mean over a window length specified by a variable “”. The raw data are firstly checked over a window length specified by 100, and the detected outliers are filled with the nearest non-outlier value. Then, the cleaned data are checked again over a window length specified by 20 and the detected outliers are filled using the piecewise cubic spline interpolation. The first check aims to detect the outliers over a larger data observation horizon, while the second one aims to detect the outliers in a local range. An example of the cross plot of raw and cleaned data is presented. By implementing data cleaning, some burr in the data is smoothed which helps get a better performance of the neural network model.
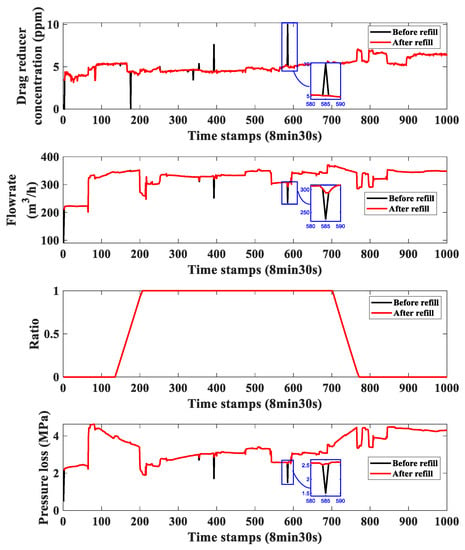
Figure A1.
The cross plot of raw data and cleaned data of Pipeline No. 4.
To show whether data cleaning really works and contributes to the performance of training the proposed neural network, the relative importance of input parameters with the output parameters before and after the refill of outliers is evaluated. The holdback input randomization (HIPR) method [41] is utilized to analyze the performance, whose main idea is that if a parameter contributes strongly to the predictive ability of the proposed neural network, the mean squared error (MSE) of the data set in which this parameter is randomized will be greater than the MSE of the original dataset. The network is trained using the training data after the refill of the outliers and examined by the testing data before and after the refill. Comparing the results before and after the refill in Figure A2, it is obvious that implementing the data cleaning technique does help in getting a better performance on the model’s accuracy. Additionally, we can draw a conclusion that the input parameter “flowrate” has more influence on the accuracy than the input parameter “ratio”, since the MSE of pressure loss when the “flowrate” is randomized changes greater than that when the “ratio” is randomized, no matter whether the outliers are refilled or not.
After cleaning the raw data, the sequential autocorrelation function and partial autocorrelation function [42] are implemented to reveal the time effect of the drag reducer on the pressure loss, as shown in Figure A3.
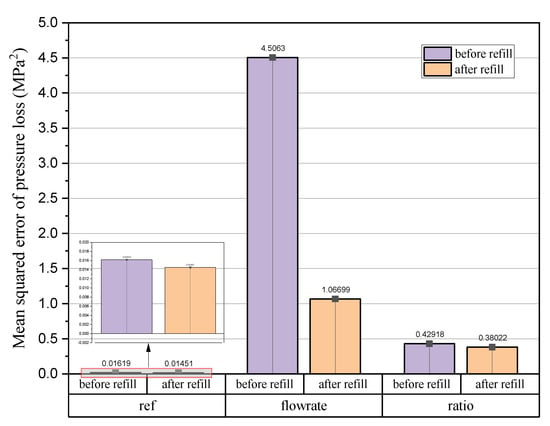
Figure A2.
The relative importance of input parameters with the output parameters before and after the refill of outliers of Pipeline No. 4. “Ref” means the result of the original testing dataset; “flowrate” means the input parameter flowrate is randomized in the testing data set and is evaluated; “ratio” means the input parameter ratio is randomized in the testing data set and is evaluated.
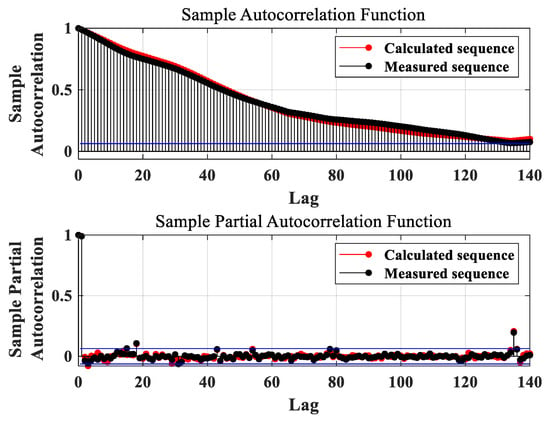
Figure A3.
The sequential autocorrelation and partial autocorrelation of the pressure loss sequential data (shown in Figure A1) of Pipeline No. 4.
Appendix B
The normalization or standardization technology is a common method for pre-processing the raw data to make the trained model more effective.
The formula for standardization is as follows. For a variable , it is standardized as:
The variable will be standardized in the range of 0 and 1.
The formula for normalization is as follows. For a variable , it is normalized as:
where and are the mean and standard deviation of the variable. The normalized variable will have a zero mean and unit standard deviation.
Appendix C
Suppose that is the measured sequential data set which contains data points and is the result calculated by the established regression model to fit . The definitions of MAE, MAPE, RMSE, and R2 are as follows:
- MAE is the acronym of mean absolute error, which is defined as:
- RMSE is the acronym of root mean squared error, which is defined as:
- MAPE is the acronym of mean absolute percentage error, which is defined as:
- R2 is the R squared value, which is the coefficient of determination in statistics and is defined as:
where is the mean value of the measured sequential data set.
Appendix D
Some other figures to prove the credibility of the results in this paper are as follows:
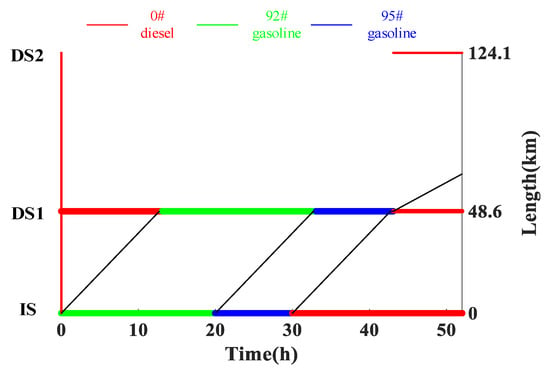
Figure A4.
Batch migration chart 1 for a local part of the studied pipeline system.
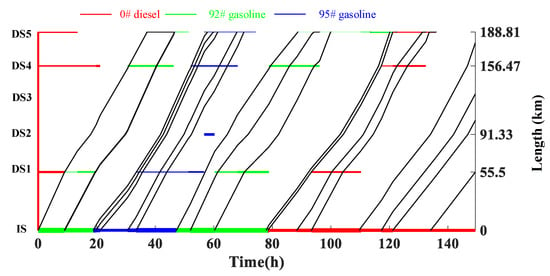
Figure A5.
Batch migration chart 2 for a local part of the studied pipeline system.
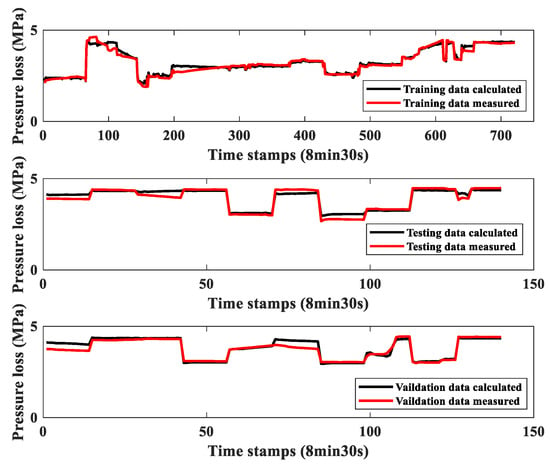
Figure A6.
Cross plot of the measured versus calculated pressure loss for three cases, training, testing, and validation of Pipeline No. 4.
References
- Ayegba, P.O.; Edomwonyi-Otu, L.C.; Abubakar, A.; Yusuf, N. Drag Reduction for Single-Phase Water Flow in and around 180o Bends. J. Non-Newton Fluid 2021, 295, 104596. [Google Scholar] [CrossRef]
- Abdel-Gawad, N.M.; El Dein, A.Z.; Magdy, M. Mitigation of induced voltages and AC corrosion effects on buried gas pipeline near to OHTL under normal and fault conditions. Electr. Pow. Syst. Res. 2015, 127, 297–306. [Google Scholar] [CrossRef]
- Liu, D.; Wang, Q.; Wei, J. Experimental study on drag reduction performance of mixed polymer and surfactant solutions. Chem. Eng. Res. Des. 2018, 132, 460–469. [Google Scholar] [CrossRef]
- Quan, Q.; Wang, S.; Wang, L.; Shi, Y.; Xie, J.; Wang, X.; Wang, S. Experimental study on the effect of high-molecular polymer as drag reducer on drag reduction rate of pipe flow. J. Pet. Sci. Eng. 2019, 178, 852–856. [Google Scholar] [CrossRef]
- Karami, H.R.; Mowla, D. Investigation of the effects of various parameters on pressure drop reduction in crude oil pipelines by drag reducing agents. J. Non-Newton Fluid 2012, 177–178, 37–45. [Google Scholar] [CrossRef]
- Virk, P.S. Drag reduction fundamentals. AICHE J. 1975, 21, 625–656. [Google Scholar] [CrossRef]
- Zhou, X.; Zhang, H.; Qiu, R.; Liang, Y.; Wu, G.; Xiang, C.; Yan, X. A hybrid time MILP model for the pump scheduling of multi-product pipelines based on the rigorous description of the pipeline hydraulic loss changes. Comput. Chem. Eng. 2019, 121, 174–199. [Google Scholar] [CrossRef]
- Huang, L.; Liao, Q.; Yan, J.; Liang, Y.; Zhang, H. Carbon footprint of oil products pipeline transportation. Sci. Total Environ. 2021, 783, 146906. [Google Scholar] [CrossRef]
- Zhou, B.; Fang, J.; Ai, X.; Yang, C.; Yao, W.; Wen, J. Dynamic Var Reserve-Constrained Coordinated Scheduling of LCC-HVDC Receiving-End System Considering Contingencies and Wind Uncertainties. IEEE Trans. Sustain. Energy 2021, 12, 469–481. [Google Scholar] [CrossRef]
- Gómez Cuenca, F.; Gómez Marín, M.; Folgueras Díaz, M.B. Energy-Savings Modeling of Oil Pipelines That Use Drag-Reducing Additives. Energy Fuels 2008, 22, 3293–3298. [Google Scholar] [CrossRef]
- Virk, P. Drag reduction by collapsed and extended polyelectrolytes. Nature 1975, 253, 109–110. [Google Scholar] [CrossRef]
- Zhao, J.; Chen, P.; Liu, Y.; Zhao, W.; Mao, J. Prediction of Field Drag Reduction by a Modified Practical Pipe Diameter Model. Chem. Eng. Technol. 2018, 41, 1417–1424. [Google Scholar] [CrossRef]
- Karami, H.R.; Mowla, D. A general model for predicting drag reduction in crude oil pipelines. J. Pet. Sci. Eng. 2013, 111, 78–86. [Google Scholar] [CrossRef]
- Dodge, D.; Metzner, A. Turbulent flow of non-Newtonian systems. AICHE J. 1959, 5, 189–204. [Google Scholar] [CrossRef]
- Karami, H.R.; Keyhani, M.; Mowla, D. Experimental analysis of drag reduction in the pipelines with response surface methodology. J. Pet. Sci. Eng. 2016, 138, 104–112. [Google Scholar] [CrossRef]
- Zhou, B.; Ai, X.; Fang, J.; Yao, W.; Zuo, W.; Chen, Z.; Wen, J. Data-adaptive robust unit commitment in the hybrid AC/DC power system. Appl. Energy 2019, 254, 113784. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Schmidhuber, J. Deep learning in neural networks: An overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [CrossRef] [Green Version]
- Elsisi, M.; Mahmoud, K.; Lehtonen, M.; Darwish, M.M. Effective Nonlinear Model Predictive Control Scheme Tuned by Improved NN for Robotic Manipulators. IEEE Access 2021, 9, 64278–64290. [Google Scholar] [CrossRef]
- Ali, M.N.; Mahmoud, K.; Lehtonen, M.; Darwish, M.M. Promising MPPT Methods Combining Metaheuristic, Fuzzy-Logic and ANN Techniques for Grid-Connected Photovoltaic. Sensors 2021, 21, 1244. [Google Scholar] [CrossRef]
- Zabihi, R.; Mowla, D.; Karami, H.R. Artificial intelligence approach to predict drag reduction in crude oil pipelines. J. Pet. Sci. Eng. 2019, 178, 586–593. [Google Scholar] [CrossRef]
- Moayedi, H.; Aghel, B.; Vaferi, B.; Foong, L.K.; Bui, D.T. The feasibility of Levenberg–Marquardt algorithm combined with imperialist competitive computational method predicting drag reduction in crude oil pipelines. J. Pet. Sci. Eng. 2020, 185, 106634. [Google Scholar] [CrossRef]
- Cao, D.; Li, C.; Li, H.; Yang, F. Effect of dispersing time on the prediction equation of drag reduction rate and its application in the short distance oil pipeline. Pet. Sci. Technol. 2018, 36, 1312–1318. [Google Scholar] [CrossRef]
- Lipton, Z.C.; Berkowitz, J.; Elkan, C. A critical review of recurrent neural networks for sequence learning. arXiv 2015, arXiv:1506.00019. [Google Scholar]
- Greff, K.; Srivastava, R.K.; Koutník, J.; Steunebrink, B.R.; Schmidhuber, J. LSTM: A search space odyssey. IEEE Trans. Neural Netw. Learn. Syst. 2016, 28, 2222–2232. [Google Scholar] [CrossRef] [Green Version]
- Song, E.; Soong, F.K.; Kang, H. Effective Spectral and Excitation Modeling Techniques for LSTM-RNN-Based Speech Synthesis Systems. IEEE/ACM Trans. Audio Speech Lang. Process. 2017, 25, 2152–2161. [Google Scholar] [CrossRef]
- Bengio, Y.; Simard, P.; Frasconi, P. Learning long-term dependencies with gradient descent is difficult. IEEE Trans. Neural Netw. 1994, 5, 157–166. [Google Scholar] [CrossRef]
- Yu, Y.; Si, X.; Hu, C.; Zhang, J. A Review of Recurrent Neural Networks: LSTM Cells and Network Architectures. Neural Comput. 2019, 31, 1235–1270. [Google Scholar] [CrossRef]
- Salehinejad, H.; Sankar, S.; Barfett, J.; Colak, E.; Valaee, S. Recent Advances in Recurrent Neural Networks. arXiv 2018, arXiv:1801.01078. [Google Scholar]
- Graves, A.; Schmidhuber, J. Framewise phoneme classification with bidirectional LSTM and other neural network architectures. Neural Netw. 2005, 18, 602–610. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Bengio, Y.; Goodfellow, I.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2017. [Google Scholar]
- Chu, X.; Ilyas, I.F.; Krishnan, S.; Wang, J. Data cleaning: Overview and emerging challenges. In Proceedings of the 2016 International Conference on Management of Data, San Francisco, CA, USA, 26 June–1 July 2016; pp. 2201–2206. [Google Scholar]
- Kotsiantis, S.B.; Kanellopoulos, D.; Pintelas, P.E. Data preprocessing for supervised leaning. Int. J. Comput. Sci. 2006, 1, 111–117. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. preprint. [Google Scholar]
- Del Valle, Y.; Venayagamoorthy, G.K.; Mohagheghi, S.; Hernandez, J.C.; Harley, R.G. Particle Swarm Optimization: Basic Concepts, Variants and Applications in Power Systems. IEEE Trans. Evol. Comput. 2008, 12, 171–195. [Google Scholar] [CrossRef]
- Fang, S.; He, C. A new one parameter viscosity model for binary mixtures. AICHE J. 2011, 57, 517–524. [Google Scholar] [CrossRef]
- Chai, T.; Draxler, R.R. Root mean square error (RMSE) or mean absolute error (MAE)?—Arguments against avoiding RMSE in the literature. Geosci. Model Dev. 2014, 7, 1247–1250. [Google Scholar] [CrossRef] [Green Version]
- Tayman, J.; Swanson, D.A. On the validity of MAPE as a measure of population forecast accuracy. Popul. Res. Policy Rev. 1999, 18, 299–322. [Google Scholar] [CrossRef]
- Blomquist, N.S. A note on the use of the coefficient of determination. Scand. J. Econ. 1980, 82, 409–412. [Google Scholar] [CrossRef]
- Kemp, S.J.; Zaradic, P.; Hansen, F. An approach for determining relative input parameter importance and significance in artificial neural networks. Ecol. Model 2007, 204, 326–334. [Google Scholar] [CrossRef]
- Tinungki, G.M. The analysis of partial autocorrelation function in predicting maximum wind speed. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2019; Volume 235, p. 012097. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).