Abstract
Cybersecurity is a critical issue for Real-Time IoT applications since high performance and low latencies are required, along with security requirements to protect the large number of attack surfaces to which IoT devices are exposed. Elliptic Curve Cryptography (ECC) is largely adopted in an IoT context to provide security services such as key-exchange and digital signature. For Real-Time IoT applications, hardware acceleration for ECC-based algorithms can be mandatory to meet low-latency and low-power/energy requirements. In this paper, we propose a fast and configurable hardware accelerator for NIST P-256/-521 elliptic curves, developed in the context of the European Processor Initiative. The proposed architecture supports the most used cryptography schemes based on ECC such as Elliptic Curve Digital Signature Algorithm (ECDSA), Elliptic Curve Integrated Encryption Scheme (ECIES), Elliptic Curve Diffie-Hellman (ECDH) and Elliptic Curve Menezes-Qu-Vanstone (ECMQV). A modified version of Double-And-Add-Always algorithm for Point Multiplication has been proposed, which allows the execution of Point Addition and Doubling operations concurrently and implements countermeasures against power and timing attacks. A simulated approach to extract power traces has been used to assess the effectiveness of the proposed algorithm compared to classical algorithms for Point Multiplication. A constant-time version of the Shamir’s Trick has been adopted to speed-up the Double-Point Multiplication and modular inversion is executed using Fermat’s Little Theorem, reusing the internal modular multipliers. The accelerator has been verified on a Xilinx ZCU106 development board and synthesized on both 45 nm and 7 nm Standard-Cell technologies.
1. Introduction
Nowadays the request for secure communication over a network is growing dramatically. Different areas such as automotive, Internet of Things (IoT), health-care, storage and financial services require the exchange of sensitive information on insecure channels. Symmetric and asymmetric cryptography can provide several security services as authentication, key exchange, digital signature and data encryption, ensuring the protection of data exchanged. Elliptic Curve Cryptography (ECC) is a kind of asymmetric cryptography, which provides the advantage of obtaining an equivalent security level key size that is smaller in respect to other public key algorithms, such as Rivest-Shamir-Adleman (RSA) [1] or schemes based on the Discrete Logarithm Problem (DLP) [2,3]. ECC was introduced by Victor Miller [4] and Neil Koblitz [5] in 1985 and has been adopted by many standardization institutes such as IEEE [6], NIST [7], ANSI [8] and SECG [9].
The main operation involved in every cryptography scheme based on ECC is the Point Multiplication (PM), also named Scalar Multiplication (SM). Given two points Q and G belonging to an elliptic curve and a scalar k, PM is denoted as and represents the sum of G to itself times to obtain the point Q. In ECC the point Q assumes the meaning of public key while k is the private key. The mathematical security of ECC relies on the hardness of the Elliptic Curve Discrete Logarithm Problem (ECDLP), that is, the problem of finding the value of k given the values of Q and G. In addition, the shape of the elliptic curve and its parameters must be properly selected in order to ensure the security and robustness of the whole system based on ECC. In 1999 NIST standardized five elliptic curves over a prime finite field [10], named NIST P-224, P-256, P-384 and P-521, that are widely used in many internet protocols and applications such as SSL (Secure Sockets Layer), TLS (Transport Layer Security) [11] and IPSec (IP Security) [12] and in some standards for automotive communication such as WAVE [13] and ETSI [14].
ECC algorithms can be implemented in software providing higher level of configurability respect to hardware solutions; however, hardware implementations can be suitable for particular scenarios such as power/energy and resource constrained devices or real time IoT applications. Work in [15] proposes a token-based security protocol for IoT devices that makes use of on-chip physically unclonable functions and ECC to authenticate devices in large-sized networks. The paper focuses on trading-off energy/quality of the protocol, and it shows that the required energy for executing the protocol is largely dominated by the ECC computation. The scheme proposed in [16] for Edge Computing and IoT is based also on ECC. In contexts like these, dedicated hardware for ECC could improve the performance in terms of speed/energy of the entire protocol. As stated in [17,18], for some markets (e.g., high-performance computing, automotive and Real-Time applications in general) hardware accelerators solutions could be mandatory in cases of ECC-based algorithms (e.g., ECDSA) due to their long execution times on low-power processors [18], or high energy consumption on general-purpose processors [17]. These remarks lead to the conclusion that hardware acceleration for ECC-based cryptographic algorithms seems to be mandatory for Real-Time IoT applications which simultaneously require high performance, low latency and limited power and energy consumption. This problem has been addressed by different researchers. The work in [19] is a review paper that shows some guidelines to aid hardware designers in choosing the combination of methods and algorithms for different application classes. Works like [20,21,22,23,24] focus on the acceleration of ECC.
In this paper, we propose a hardware architecture, configurable at synthesis level, to support NIST P-256 only, NIST P-521 only, or both the elliptic curves, which provides a security level from 128 to 256 bits. Such design is exploitable for accelerating the most used cryptographic schemes based on ECC. It makes use of a constant-time and Simple Power Analysis (SPA) resistant modified version of Double-and-Add algorithm to compute PM and of a constant-time version of Shamir’s trick (algorithm 3.48 in [25]) to speed-up the Double Point Multiplication (DPM) required in ECDSA verification, using projective coordinates in order to avoid modular division. In addition, Fermat’s Little Theorem has been adopted to reuse the internal modular multipliers avoiding to employ dedicated hardware for converting the coordinates in the standard domain. This work is part of the early development phase for the architecture of the ECC hardware accelerator within the Hardware Secure Module (HSM) of the European Processor Initiative [26] chip. NIST is running a standardization process for new public-key algorithmss, and currently ECC is adopted by several standards and the EPI project cryptographic functions based on ECC are required to provide the Root of Trust (RoT) of an EPI chip. The main contributions of this works are as follows:
- Architectural design of a configurable (at synthesis level) ECC crypto-processor for NIST P-256 and/or NIST P-521 elliptic curves, developed in the framework of the European Processor Initiative together with other cryptographic hardware accelerators (AES, RNG [27,28], SHA [29]). The proposed architecture supports the most used cryptographic schemes based on ECC such as ECDSA, ECDH, ECIES and ECMQV. The design is resistant to timing and SPA attacks and uses a constant-version of Shamir’s trick for Double Point Multiplication, and Fermat’s Little Theorem to execute modular inversion.
- A simulated environment to extract and evaluate the power consumption of the circuit, which allowed the evaluation of the proposed countermeasure against SPA. The proposed simulated approach does not require any dedicated equipment to acquire power samples and can be adopted in the early design phase to help designers find effective architectural and algorithmic solutions against Power attacks.
- Synthesis on the open source 45 nm NANDGATE45 [30] library and 7 nm TSMC silicon technology (the first contribution available to the best of authors’ knowledge) with a complete analysis of the performance in terms of complexity, throughput and power consumption.
- Verification and characterization in terms of resources utilization and throughput on a Xilinx ZCU106 development board equipped with Zynq UltraScale+ xczu7ev-ffvc1156-2-e MPSoC.
The remainder of this paper is organized as it follows: Section 3 discusses the preliminaries of ECC, PM and coordinates representation. Section 2 lists and analyzes the related works on hardware implementations of ECC accelerators. Section 4 presents the proposed hardware architecture and shows the FPGA verification approach. In addition, this section describes the power simulation environment we used to assess countermeasures against SPA and the power traces we extracted during PM operation; Section 5 shows the results of our design and a comparison with the state of the art. Finally, Section 6 concludes this paper.
2. Related Works
Several ECC hardware systems can be found in literature targeting high-performance, low-resources consumption or low-power. Research on hardware accelerators for ECC mainly focuses on improving the performance of PM operation, but sometimes no verification on side-channel attacks resistance is provided. The work in [31] is a Dual-Field ECC processor that exploits a hardware–software design to support an arbitrary elliptic curve. It adopts the radix-4 interleaved multiplication algorithm for modular multiplication and the Euclidean algorithm for modular inversion. To assess the resistance against power attacks, the authors implemented their design on a FPGA and recorded power traces by measuring the power consumption of the device. This work has been implemented in both XMC 55 nm CMOS technology and on Xilinx Virtex-4 FPGA platform. On CMOS technology it requires 1450 μs for a PM that is a relatively low speed. The design in [24] is the fastest we found in the literature; it adopts a full-word Montgomery multiplier and implements PA and PD operations concurrently. The authors synthesized their work in a 65 nm CMOS technology that requires only 12.5 μs for a PM, but the area consumption is extremely high. No consideration about side-channel resistance has been done. Their implementation is not suitable for resource-constrained devices and for IoT applications. The authors in [20] present a processor for NIST P-224 and P-256 elliptic curves. They used the Montgomery algorithm for modular multiplication, the binary inversion algorithm for modular inversion and Jacobian coordinates to represent the elliptic curve points. PM takes between 560 and 730 μs for 224-bit and 256-bit elliptic curves on a 65 nm CMOS technology. The area consumption is quite high and no side-channel countermeasures have been evaluated. The work in [32] is an elliptic curve processor over synthesized in TSMC 90 nm technology. The authors adopted a 3-pipelined-stage Montgomery multiplier and Standard projective coordinates, performing a PM in 120 μs with 540 K gate counts. The authors propose a Montgomery ladder algorithm with a swap operation for PM and claim their solution is resistant to SPA attacks, but no experimental results have been provided to confirm this assumption. In [33] a cryptographic processor for general curves over is presented. The authors in this work employed a systolic arithmetic unit to implement the operations of addition, subtraction, multiplication and inversion, sharing the hardware resources and obtaining good performance in terms of area occupation but low speed. No considerations about side-channel resistance are proposed. They synthesized the design on a 65 nm CMOS technology. The work in [21] is a ECC Processor for Weierstrass Curves over implemented on 7-series FPGA. It adopts a Montgomery multiplication which is constructed employing a large number of Digital Signal Processor (DSP) primitives. The PM is executed in constant time but no experimental verification about side-channel attacks resistance is provided. The performance in terms of speed is good but the resource consumption is very high. The work in [22] is a low hardware consumption design for elliptic curves from 160 to 256 bits over . Interleaved Modular Multiplication and Binary Modular Inversion algorithms have been used, and the PM algorithm is claimed to be resistant to SPA attacks, but no experimental results have been provided. The design in [23] presents a novel modular squaring scheme that has been synthesized on a 130 nm CMOS technology. It reaches good performance in terms of area and speed, but no side-channel attacks resistance is guaranteed.
3. Preliminaries on ECC
3.1. Elliptic Curve Cryptography
An elliptic curve over prime field is defined by the Weierstrass equation:
where the parameters a and b are integers included in the prime field which satisfies . A Weierstrass elliptic curve E over consists of a set of points , with together with an extra point O called “point at infinity”. The NIST P elliptic curves are Weierstrass curves over and their parameters can be found in [9]. The set of elliptic curve points plus the point at infinity forms a group where the following group law can be defined:
- Point Addition (PA): where
- Point Doubling (PD): wherewhere and are two points on the elliptic curve. It should be noted that all the arithmetic operations (additions, subtractions, multiplications and divisions) described above are on the prime field . PA and PD operations over such group are used to construct many elliptic curve crypto-systems, and a typical hierarchical structure of an ECC crypto-system is reported in Figure 1. At the top level there are protocols such as ECDSA, ECIES, ECDH and ECMQV. In the lower layer there are PM and DPM that will be discussed in Section 3.2; the next layer comprises the basic operations on the ECC points: PA and PD. They require the underlying level that consists of finite field arithmetic operations on such as modular addition, subtraction and multiplication. In our hierarchical structure we placed modular inversion at the same level of PA and PD because we implemented it using Fermat’s Little theorem that exploits the operations at the lowest layer.
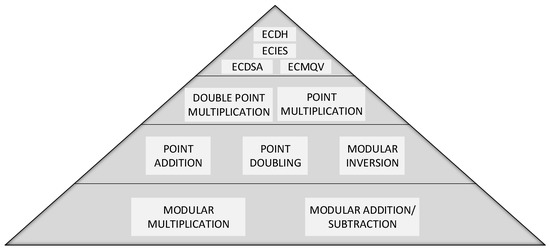 Figure 1. Implementation Hierarchy of the ECC Operations.
Figure 1. Implementation Hierarchy of the ECC Operations.
3.2. Point Multiplication and SPA
PM between an integer k and an elliptic curve point P is the main operation involved in every cryptographic scheme based on ECC. PM is indicated with , and represents the sum of the point P to itself times:
Many algorithms can be used to perform PM and the most know are based on Double-and-Add method. Algorithm 1 shows the Double-and-Add method for PM in Right-to-Left version.
| Algorithm 1 Double-and-Add Right-to-Left. |
Input: Output: 1: 2: 3: for to do 4: if then 5: 6: end if 7: 8: end for 9: return Q |
In Algorithm 1 the number of PA depends on the Hamming weight of k and its execution time is not fixed, making this kind of algorithm weak against timing attacks. In addition, the dissimilarity between PA and PD can be exploited by SPA [34] attacks. SPA involves the interpretation of power traces over time during the execution of PM in order to determine the integer k which in ECC must be secret. An attacker could easily extract the value of k by observing the power trace and understanding which operation the crypto-processor is performing. Timing attacks can be executed by an attacker at distance, by measuring the time needed to respond to a request, in contrast to SPA attacks that require physical access to the device equipped with the crypto-processor. In our work, we focused on protecting our ECC-system against both timing and SPA attacks. As reported in [35], the Double-and-Add-Always method can be used to hide the dependency of the key on the operations flow. As can be seen in Algorithm 2, in Double-and-Add-Always algorithm PA is executed even if the scalar bit is null and the result of this operation is discarded. This countermeasure theoretically does not allow to distinguish between real and dummy PA operations. Nevertheless, in Algorithm 2 the presence of operations between real points and the point-at-infinity allows to guess part of the key k. At line 1 of the Algorithm 2 it can be seen that both the variables Q and T are initialized to the point-at-infinity, and in lines 4 and 5 they are summed to the variable R. As long as Q and T are equal to the point-at-infinity (this happens in the case of Q as long as no 1 is encountered in the key, and in the case of T as long as no 0 is encountered), the first PA operation between either Q and T and a real point can be identified, and an attacker may be able to assume some part of the key k. These considerations will be explained in more detail in Section 4.6, where the power traces extracted during the execution of Algorithm 2 will also be shown. To overcome this issue, our design implements a modified version of Algorithm 2, reported in Algorithm 3. The variable is used to indicate whether a 1 has been encountered in the key k. As long as is 0, dummy PA is executed between the input point P and R. When becomes 1, PA is performed between Q and R, and the resulting point is sampled only when a 1 is encountered. This method allows avoiding PA at point-at-infinity. We selected Right-to-left version Double-and-Add algorithms since they allow performing PA and PD operations simultaneously. Furthermore, our PM implementation does not use precomputations on the base point, and allows using different points P as input. ECDH, ECMQV and ECIES algorithms require the performance of PM between private and public keys where the public key could be different from the base point. In addition, we support the DPM operation required in ECDSA verification. DPM is composed of two separated PMs and one PA, as reported in the equation below:
where Q, P and R are three different elliptic curve points while k and l are two scalars. A constant-time version of Shamir’s trick is used in our implementation, reported in Algorithm 4.
| Algorithm 2 Double-and-Add-Always Right-to-Left. |
Input: Output: 1: 2: 3: for to do 4: if then 5: 6: else 7: 8: end if 9: 10: end for 11: return Q |
| Algorithm 3 Modified Double-and-Add-Always Right-to-Left. |
Input: Output: 1: one_flag , 2: if then 3: , one_flag 4: end if 5: for to do 6: if then 7: if one_flag then 8: 9: else 10: , 11: end if 12: else 13: if one_flag then 14: 15: else 16: 17: end if 18: end if 19: 20: end for 21: return Q |
| Algorithm 4 Constant Time Version of Shamir’s Trick. |
Input: Output: 1: 2: 3: for to do 4: 5: if and then 6: 7: else if and then 8: 9: else if and then 10: 11: else 12: 13: end if 14: end for 15: return Q |
3.3. Coordinates Representation
PA and PD formulas reported in Section 3.1 can be used when the elliptic curve points are represented in the classical form (affine form). In this case both PA and PD require modular inversion on the prime field GF(p). However, since modular inversion is the most expensive finite field operation, a redundant projective representation can be used in order to avoid the modular inversion. Actually, only one modular inversion is needed to reconvert in affine coordinates. In projective representation, every point can be mapped to where may be chosen arbitrarily. Selecting a projective representation, the form of Weierstrass equation, the points over the elliptic curve and the addition and doubling formulas change. The most common coordinate systems are reported in Table 1, together with the number of modular multiplications and modular inversions required by each of them to compute PA and PD operations.

Table 1.
Computational Cost of PA and PD.
In this paper Standard projective coordinates are used. PA and PD in standard projective coordinates are reported respectively in Equations (1) and (2). The addition between two points and is the point such that:
where:
The double of a point is the point such that:
where:
4. Proposed Hardware Architecture
4.1. Modular Addition and Subtraction
Modular addition/subtraction algorithm is reported in Algorithm 5 where the steps 2–7 represent modular addition and the steps 10–15 represent modular subtraction. The hardware architecture is shown in Figure 2. In the case of modular addition , the signal shall be set to 0; the first adder executes addition between the two inputs providing sum and carry , and the second one performs subtraction between and p with outputs and . At the end, and are multiplexed according to line 4 of Algorithm 5. In the case of modular subtraction , the signal shall be set to 1, and the first adder performs subtraction between the inputs and the second one adds the result to the modulo p. Similarly to the first case, and are multiplexed according to to line 12 of Algorithm 5. This implementation requires one clock cycle.
| Algorithm 5 Modular Addition/Subtraction. |
Input: , p and Output: 1: if then 2: 3: 4: if then 5: 6: else 7: 8: end if 9: else 10: 11: 12: if then 13: 14: else 15: 16: end if 17: end if 18: return S |
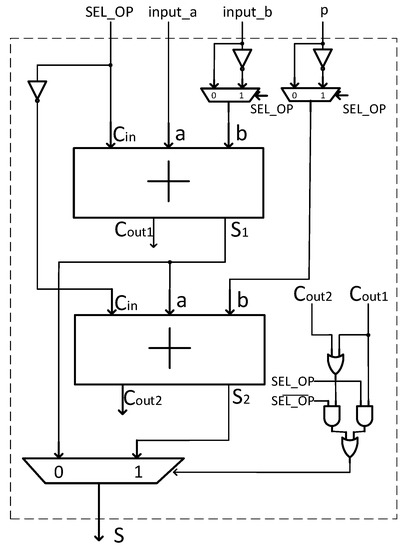
Figure 2.
Modular Addition and Subtraction Architecture.
4.2. Modular Multiplication
As reported in Section 3.3 a projective representation of the elliptic curve can be used to avoid modular inversion in PA and PD formulas, at the cost of increasing the number of modular multiplications. For this reason, in the design of hardware architectures for ECC that adopt projective coordinates, the modular multiplier is the most important block. In this work we focused on NIST P-256/521 curves that support a fast modular reduction algorithm, reported in Algorithms 6 and 7.
| Algorithm 6 Fast Modular Reduction for NIST P-256. |
Input: Output: 1: 2: 3: 4: 5: 6: 7: 8: 9: 10: return |
| Algorithm 7 Fast Modular Reduction for NIST P-521. |
Input: Output: 1: return |
Thanks to these reduction algorithms, the multiply-then-reduce approach can be efficiently used for modular multiplication. In this work we used a two-stage Schoolbook-based multiplier; the multiplication algorithm and the hardware architecture are reported respectively in Algorithm 8 and Figure 3. In this case our crypto-processor is configured to support the NIST P-256 curve only. The 256-bit inputs are split in four parts of 64 bits each and multiplied iteratively. The first stage of the multiplier is composed of two bits multipliers and a multiplexer network used to select the proper 64-bit words to be multiplied. Sixteen 64-bit multiplications are required to perform a 256-bit full-word multiplication, so each 64-bit multiplier has to execute eight multiplications. The results are registered into two pipeline registers and processed by the second stage. It is composed of a multiplexer-shifter module that shifts and selects properly the partial products stored into the pipeline registers and one 512-bit adder that sums the content of an accumulation register and the partial products. A finite state machine is used to control the multiplexer networks and to enable the accumulation register. As can be seen in Algorithm 6, modular reduction for NIST P-256 requires six modular additions and four modular subtractions. In our work we implemented it using modular addition/subtraction blocks, computing modular reduction iteratively in three clock-cycles. The latency of the modular multiplier is thirteen clock cycles for a single multiplication but the pipeline reduces the latency to eight cycles on average. Figure 4 shows the data timeline for a modular multiplication for NIST P-256. and indicate two different modular multiplications. When the pipeline is empty, the first clock cycle is needed to store the operands and both stages of the multiplier are unused; in the second clock cycle only the first stage works, executing two 64-bit multiplications simultaneously. From the third clock cycle to the ninth, both stages are occupied and at the ninth clock cycle the multiplier can store new data and starts a new modular multiplication. In the case where the crypto-processor is configured to support NIST P-521, the architecture of the modular multiplier is similar to the one discussed above. The two 64-bit multipliers are replaced by two 66-bit multipliers and the 512-bit adder by a 1042-bit adder. The 521-bit operands are split in eight parts, requiring thirty-four clock cycles for a 521-bit single multiplication. The reduction algorithm, reported in Algorithm 7, requires only one modular addition executed in one clock cycle. Thirty-five clock cycles are required for a single modular multiplication for the NIST P-521 curve, reduced to thirty-two in pipeline.
| Algorithm 8 Schoolbook-Based Multiplication Algorithm. |
Input: 256-bit integers such that: , . Output: × B 1: × ; × ; 2: × ; × ; 3: × ; × ; 4: × ; × ; 5: × ; × ; 6: × ; × ; 7: × ; × ; 8: × ; × ; 9: 10: return C |
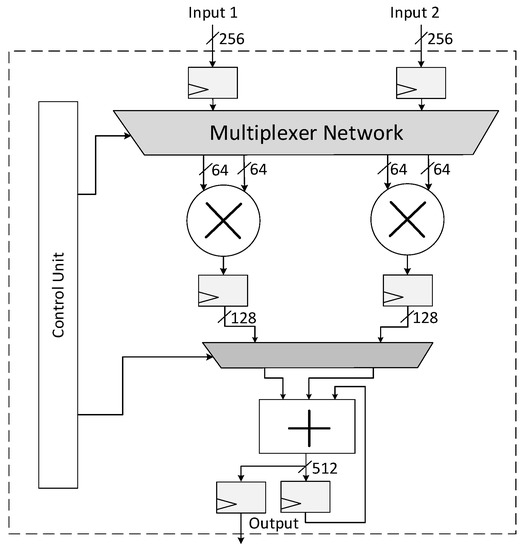
Figure 3.
Proposed Hardware Architecture for the 256-bit Multiplier.
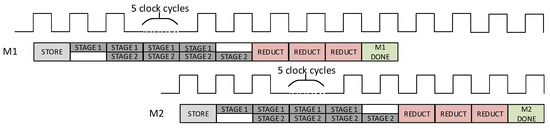
Figure 4.
Modular Multiplier Data Timeline for NIST P-256 Curve.
4.3. PA, PD and Modular Inversion
PA and PD operations in Standard projective coordinates have been shown in Equations (1) and (2) of Section 3.3. In this work we implemented two separate hardware modules for PA and PD, as showed in Figure 5. Each of them is composed of one modular multiplier, one modular adder/subtractor module, a multiplexer network and registers bank to store the intermediate results. The scheduling strategy is to parallelize PA and PD operations and to maximize the parallelism of the field operations that compose them. Considering that the time for computing modular addition/subtraction is negligible with respect to the one to compute modular multiplication, we scheduled the fields operations in order to perform modular addition/subtraction and modular multiplication simultaneously, avoiding stopping the multiplier. Table 2 and Table 3 show the scheduling for PA and PD respectively. For PA, 127 and 457 clock cycles (c.c. in Table 2 and Table 3) are required in cases of P-256 and P-521 curves, respectively, in contrast to PD, which requires 95 and 329 clock cycles for P-256 and P-521 curves, respectively. Modular inversion has been implemented using Fermat’s Little theorem because the presence of two separated modular multipliers allows to easily integrate this technique into the proposed design and to avoid use of a dedicated block, saving area. This theorem allows calculating the modular inverse of an integer a performing , where p is the modulus. A constant time right-to-left version of square-and-multiply has been used to calculate the modular exponentiation , reported in Algorithm 9. The modular multiplications given in lines 4 or 6 and 8 of the Algorithm 9 are executed concurrently by the two modular multipliers.
| Algorithm 9 Right-to-left Square-and-Multiply for Modular Exponentation. |
Input: Output: 1: 2: for i from 0 to do 3: if then 4: 5: else 6: 7: end if 8: 9: end for 10: return r1 |
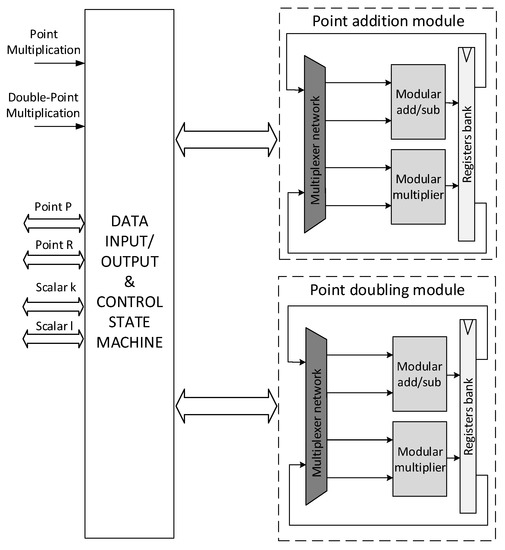
Figure 5.
Overall Architecture of the proposed ECC Crypto-Processor.

Table 2.
PA Operations Scheduling (c.c. stands for clock cycles).

Table 3.
PD Operations Scheduling (c.c. stands for clock cycles).
4.4. Overall Architecture
PM and DPM are realized based on PA and PD operations. In the case of PM, no precomputed values are used, and the crypto-processor allows selecting which point P has to be used as input between the base point recommended by NIST or another one provided by externally.
In the case of DPM, we used a constant time version of Shamir’s Trick reported in Algorithm 3. The scalar k and l together with the point R have to be provided externally while the point P, as in the case of PM, can be selected internally or externally. The overall architecture is reported in Figure 5; a main state machine is used to achieve PM and DPM based on PA and PD in standard projective coordinates. The state machine controls also the operations flow to convert the computed point in the affine domain.
4.5. FPGA Verification
The crypto-processor has been verified on a Xilinx ZCU106 board. We used the test vectors distributed by NIST for ECDSA in the Elliptic Curve Digital Signature Algorithm Validation System (ECDSA2VS) [36]. Our crypto-processor has been used to perform the PM operation required for the generation of a digital signature and the DPM operation required to verify the signature. In addition, our crypto-core has been verified by integration with the NIOS II and other crypto engines (AES and SHA) on Stratix IV FPGA to implement the Hardware Security Module of a WAVE (Wireless Access in the Vehicular Environment) IEEE 802.11p modem for V2X connectivity.
4.6. SPA Assessment through Simulated Approach
To evaluate the proposed SPA countermeasure we used a simulated approach to extract power traces from gate-level netlist without requiring any additional physical circuit or dedicated equipment for power samples acquisition. We implemented three different designs for the algorithms reported in Algorithms 1–3, which are based on the same overall architecture reported in Section 4.4 where the main difference among the three designs is related to the main state and control machine. The steps of our SPA assessment method are reported in Figure 6. The first step requires the logic synthesis of the RTL design, executed using Synopsys Design Compiler [37] with the Standard-cell library Artisan TSMC 7 nm (Typical corner case: 0.75 V, 85 °C). The output of the logic synthesis process is a gate-level netlist which represents an approximation of the physical circuit, and it is used together with the Standard-cell library as input for the gate-level simulations, performed with QuestaSim [38]. The switching activity of the circuit running testbenches is stored in a Value Change Dump (VCD) file during the gate-level simulations and the tool PrimeTime [39] is used to extract the power. Finally, the power trace is parsed and plotted by a Python script. The three different designs have been synthesized at 100 MHz (10 ns of period) and the sampling period has been set to 0.01 ns, in order to generate a fairly dense power trace. Figure 7, Figure 8 and Figure 9 show the plots of acquired power traces which have been restricted to 7810 ns for reasons of readability and space within the paper.
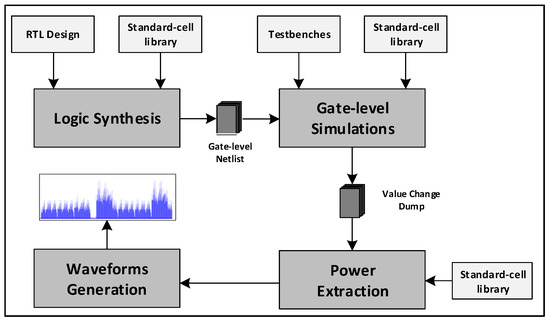
Figure 6.
Power Simulation Flow for SPA Assessment.
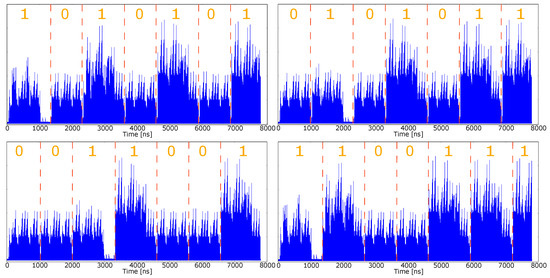
Figure 7.
Acquired Power Traces for the Double-and-Add (Algorithm 1) where the least significant part of the key k is (LSB first): -1010101 (top left), -0101011 (top right), -0011001 (bottom left), -1100111 (bottom right).
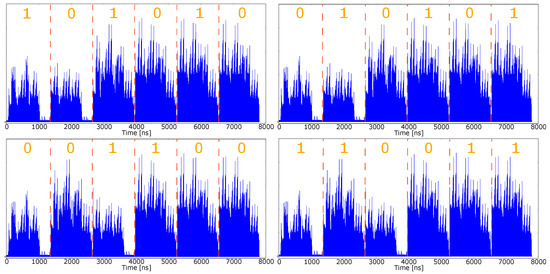
Figure 8.
Acquired Power Traces for the Double-and-Add-Always (Algorithm 2) where the least significant part of the key k is (LSB first): -101010 (top left), -010101 (top right), -001100 (bottom left), -110011 (bottom right).
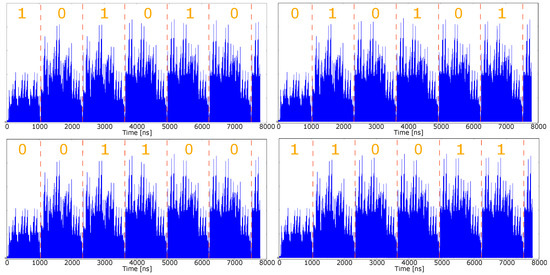
Figure 9.
Acquired Power Traces for the Modified Double-and-Add-Always (Algorithm 3) where the least significant part of the key k is (LSB first): -101010 (top left), -010101 (top right), -001100 (bottom left), -110011 (bottom right).
The traces in Figure 7 are the ones acquired during the execution of Algorithm 1. In this case, the value of the i-th bit of the key k can be easily guessed due to the dissimilarity of the power consumption during the execution of the algorithm. A higher power peak can be easily seen when 1 is encountered (PA and PD operations are executed concurrently), and a lower power peak can be seen when 0 (only PD is executed).
The traces in Figure 8 have been acquired during the execution of Algorithm 2. In this case, the power trace during PA with the point-at-infinity is quite different with respect to PA with real points. Referring to the top left and top right plots in Figure 8, two consecutive PAs with point-at-infinity can be seen. This information can be exploited by an adversary who may be able to understand the fact that the first two least significant digits of the key are different, and may assume the values 01 or 10. Referring to the bottom left and bottom right plots instead, the first and the third PAs are with the point-at-infinity as input. This means that the first two least significant bits of the key are equal, and the third one is different. In this case, an adversary can hypothesize that the value of the first three least significant bits of the key are 001 or 110. Therefore, in the Double-And-Add-Always algorithm in the Right-to-left version the information leakage of the private key is related to the number of equal bits starting from the least significant part of the key.
The traces in Figure 9 have been acquired during the execution of Algorithm 3. In this case there are no substantial differences among the acquired power traces. It should also be noted that in our simulation environment there are no additional circuits (e.g., processors, communication buses, etc.) that would be present in a real system and would contribute to power consumption, masking any small differences present in the power traces acquired during the execution of Algorithm 3 and depicted in Figure 9. In any case, the extraction and analysis of real power traces will be carried out to test the effectiveness of the proposed algorithm and the validity of the implemented simulation environment.
5. Results and Comparison
The design described in Section 4 has been synthesized with Design Compiler L-2016.03 both on 45 nm Silvaco and 7 nm Artisan TSMC (Typical corner case: 0.75 V, 85 °C) ASIC standard-cell libraries. Table 4 reports the post-synthesis results; Kcycles column indicates the number of clock cycles required to execute a PM operation; T [μs] column depicts the latency needed for PM at the maximum frequency reported in the column Freq; Column Configuration reports the three possible configurations at the synthesis level for the proposed crypto-processor. In our design, PM requires, respectively, 36.390 K and 254.456 K clock cycles for NIST P-256 and P-521 elliptic curves in all the configurations. DPM operation requires 61.344 K and 430.360 K clock cycles for NIST P-256 and P-521, respectively, reducing the computation latency of the 16% respect to executing two separated PM and one PA. On the 45 nm Standard-Cell, the maximum frequency is 400 MHz for the P-256 only configuration which decreases to 375 MHz for the other configurations. On the 7 nm Artisan TSMC Standard-Cell, the maximum clock frequency is 1820 MHz for the P-256 only configuration, and 1650 MHz for the other configurations. Table 5 reports the synthesis results on Xilinx ZCU106 board equipped with Zynq UltraScale+ xczu7ev-ffvc1156-2-e MPSoC; columns CLBs and DSPs indicate, respectively, the number of Configurable Logic Block (CLB) and DSP occupied, while T [μs] column depicts the latency for PM at the maximum frequency reported in the column Freq. In 7-series FPGAs, each CLB contains two slices which consist in four 6-input LUTs. No device-dependent optimizations were adopted on the FPGA platform because the goal was only to verify the functionality of the design.

Table 4.
Synthesis Results on ASIC Technologies.

Table 5.
ECC Crypto-Core Resources Utilization on Zynq UltraScale+ xczu7ev-vc1156-2-e MPSoC.
Discussion and Comparison
Several ECC processors proposed in the literature are implemented in different FPGA platforms or ASIC technologies, making the process of comparison and benchmarking extremely complicated. For this reason, in order to make a fair comparison with previous works, in this paper we present a comparison among our synthesis results on 45 nm and other ECC systems synthesized on ASIC technologies from 55 nm to 130 nm. The results are reported in Table 6. The column denoted with T [μs] indicates the time needed to execute a PM, and the column AT indicates the area-time product that is normalized into 45 nm to compare all the reported designs implemented in different processes.

Table 6.
Comparison among previous works for 256-bit PM.
The work in [31] is a Dual-Field ECC processor that supports an arbitrary elliptic curve. The result of this work is more flexible with respect to our design but achieves lower performance in terms of speed and AT. The design in [24] is faster in respect to ours, but it has higher AT and no SPA resistance has been guaranteed. The processor in [20] supports both NIST P-224 and P-256 elliptic curves. Their design requires more area with respect to our implementation and achieves a higher AT without any protection against power attacks. The work in [32] performs a PM in 120 μs with 540 K gate counts. Their design requires less c.c. with respect to our work, but the area consumption is higher together with the AT product. In this case, no experimental results have been provided to test the SPA resistance, but the authors claim their solution works well. Works in [23,33] do not implement any countermeasure against side-channel attacks. The design in [33] reaches good performance in terms of area occupation but lower speed with respect to our work. The modular square method proposed in [23] allows good performance and an AT similar to the one achieved by our crypto-processor. The work in [22] is a low hardware consumption design for ECC. The area consumption in fact is lower with respect to our work, but both speed and AT are higher. The adopted SPA countermeasure has not been tested and is only theoretical. In addition, our crypto-processor can be configured at a synthesis level to also support the NIST P-521 elliptic curve, providing a security level of 256 bits. Using the proposed crypto-processor on 7 nm Artisan technology for running ECDSA algorithms, up to 50 k and 29 k digital signatures per second can be generated and verified on the NIST P-256 curve. These results are up to four orders of magnitude better with respect to the ones achieved on Cortex-M processors reported in [18], where the power consumption comprises between 118.5 mW and 281.8 mW. In our work we estimated the power consumption of our crypto-processor (configured to support only NIST P-256 curve), which is around 49 mW @ 400 MHz and 102 mW @ 1.82 GHz, respectively, in 45 nm Silvaco at 1.1 V and 7 nm Artisan at 0.75 V. These results have been extracted by means of the PrimeTime tool.
6. Conclusions
In this paper, we proposed a fast and configurable ECC crypto-processor for NIST P-256/-521 elliptic curves. It has been synthesized both on 45 nm Silvaco and 7 nm Artisan TSMC technologies, and verified on a Xilinx ZCU106 board with official NIST test vectors for ECDSA. The presented processor can be used to accelerate ECDH, ECMQV, ECIES and ECDSA algorithms based on ECC. A simulation environment to extract and evaluate the power traces during the execution of PM has been implemented, allowing the design of a modified version of a Double-And-Add-Always algorithm as a countermeasure against SPA and timing attacks. This work is part of the early development phase for the architecture of the ECC crypto-accelerator that, together with other crypto-engines that we are also designing (i.e., AES, SHA, RNG), will be integrated into the HSM of the European Processor Initiative chip. Synthesis results on a 45 nm Standard-Cell show that performance in terms of speed and area consumption are aligned with the state-of-the-art with an optimal AT. On 7 nm technology the speed performance in absolute value outperforms most of the previous works. Our work is the first contribution in literature with synthesis results on 7 nm technology. Although NIST and other standardization institutes are running a standardization process for post-quantum public-key algorithms, currently ECC is one of the public-key system most often adopted for key agreement, encryption/decryption and digital signatures services.
Author Contributions
Conceptualization and methodology, S.D.M., L.B., L.C. and P.N.; validation, S.D.M. and L.C.; project administration and founding acquisition, S.S. and L.F. All authors have read and agreed to the published version of the manuscript.
Funding
This work has been partially funded by the European Processor Initiative (EPI) project, under grant agreement No. 826646.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Rivest, R.L.; Shamir, A.; Adleman, L. A method for obtaining digital signatures and public-key cryptosystems. Commun. ACM 1978, 21, 120–126. [Google Scholar] [CrossRef]
- Stallings, W. Symmetric Ciphers. In Cryptography and Network Security: Principles and Practice, 5th ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2010. [Google Scholar]
- Lenstra, A.K.; Verheul, E.R. Selecting cryptographic key sizes. J. Cryptol. 2001, 14, 255–293. [Google Scholar] [CrossRef] [Green Version]
- Miller, V.S. Use of elliptic curves in cryptography. In Proceedings of the Conference on the Theory and Application of Cryptographic Techniques, Linz, Austria, 9–11 April 1985; Springer: Berlin/Heidelberg, Germany, 1985; pp. 417–426. [Google Scholar]
- Koblitz, N. Elliptic curve cryptosystems. Math. Comput. 1987, 48, 203–209. [Google Scholar] [CrossRef]
- Group, I.W. IEEE 1363-2000: Standard Specifications for Public Key Cryptography; IEEE Standard: New York, NY, USA, 2000; Volume 10017. [Google Scholar]
- NIST. FIPS 186-4—Digital Signature Standard (DSS); Information Technology Laboratory, National Institute of Standards and Technology: Gaithersburg, MD, USA, 2013. [Google Scholar]
- ANSI. X9.62: Public key cryptography for the financial services industry. In The Elliptic Curve Digital Signature Algorithm (ECDSA); American National Standards Institute: Washington, DC, USA, 2005. [Google Scholar]
- Standards for Efficient Cryptography SEC 1, SEC 2: Elliptic Curve Cryptography; Certicom Research: Mississauga, ON, Canada, 2009; Available online: https://www.secg.org (accessed on 10 May 2021).
- Fips, P. 186-2. Digital Signature Standard (dss); National Institute of Standards and Technology (NIST): Gaithersburg, MD, USA, 2000; Volume 20, p. 13.
- Rescorla, E. The Transport Layer Security (TLS) Protocol Version 1.3, RFC, Volume 8446. 2018. Available online: https://www.rfc-editor.org/info/rfc8446 (accessed on 10 May 2021).
- Burgin, K.; Peck, M. Suite B Profile for Internet Protocol Security (IPsec); Technical Report, RFC 6380. 2011. Available online: https://www.rfc-editor.org/rfc/rfc6380.html (accessed on 7 June 2021).
- Group, I.W. IEEE Standard for Wireless Access in Vehicular Environments-Security Services for Applications and Management Messages; IEEE Std 1609.2-2016; IEEE: New York, NY, USA, 2016; pp. 1–240. [Google Scholar]
- ETSI Technical Specification. ETSI TS 103 097 v1. Intelligent Transport Systems (ITS); Security; Security Header and Certificate Formats, Standard, TC ITS. 2013. Available online: https://www.etsi.org/deliver/etsi_ts/103000_103099/103097/01.04.01_60/ts_103097v010401p.pdf (accessed on 17 April 2021).
- Naveed Aman, M.; Taneja, S.; Sikdar, B.; Chua, K.C.; Alioto, M. Token-Based Security for the Internet of Things With Dynamic Energy-Quality Tradeoff. IEEE Internet Things J. 2019, 6, 2843–2859. [Google Scholar] [CrossRef]
- AlMajed, H.; AlMogren, A. A Secure and Efficient ECC-Based Scheme for Edge Computing and Internet of Things. Sensors 2020, 20, 6158. [Google Scholar] [CrossRef] [PubMed]
- Baldanzi, L.; Crocetti, L.; Di Matteo, S.; Fanucci, L.; Saponara, S.; Patrice, H. Crypto accelerators for power-efficient and realtime on-chip implementation of secure algorithms. In Proceedings of the 2019 26th IEEE International Conference on Electronics, Circuits and Systems (ICECS), Genoa, Italy, 27–29 November 2019. [Google Scholar]
- Ledwaba, L.P.; Hancke, G.P.; Venter, H.S.; Isaac, S.J. Performance costs of software cryptography in securing new-generation Internet of energy endpoint devices. IEEE Access 2018, 6, 9303–9323. [Google Scholar] [CrossRef]
- Verri Lucca, A.; Mariano Sborz, G.A.; Leithardt, V.R.Q.; Beko, M.; Albenes Zeferino, C.; Parreira, W.D. A Review of Techniques for Implementing Elliptic Curve Point Multiplication on Hardware. J. Sens. Actuator Netw. 2021, 10, 3. [Google Scholar] [CrossRef]
- Hossain, M.S.; Kong, Y.; Saeedi, E.; Vayalil, N.C. High-performance elliptic curve cryptography processor over NIST prime fields. IET Comput. Digit. Tech. 2016, 11, 33–42. [Google Scholar] [CrossRef]
- Awaludin, A.M.; Larasati, H.T.; Kim, H. High-Speed and Unified ECC Processor for Generic Weierstrass Curves over GF(p) on FPGA. Sensors 2021, 21, 1451. [Google Scholar] [CrossRef] [PubMed]
- Hu, X.; Zheng, X.; Zhang, S.; Cai, S.; Xiong, X. A Low Hardware Consumption Elliptic Curve Cryptographic Architecture over GF(p) in Embedded Application. Electronics 2018, 7, 104. [Google Scholar] [CrossRef] [Green Version]
- Li, B.; Lei, B.; Zhang, Y.; Lei, S. A Novel and High-Performance Modular Square Scheme for Elliptic Curve Cryptography Over GF (p). IEEE Trans. Circuits Syst. II Express Briefs 2018, 66, 647–651. [Google Scholar] [CrossRef]
- Liu, J.; Cheng, D.; Guan, Z.; Wang, Z. A High Speed VLSI Implementation of 256-bit Scalar Point Multiplier for ECC over GF (p). In Proceedings of the 2018 IEEE International Conference on Intelligence and Safety for Robotics (ISR), Shenyang, China, 24–27 August 2018; pp. 184–191. [Google Scholar]
- Hankerson, D.; Menezes, A.J.; Vanstone, S. Guide to Elliptic Curve Cryptography; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- European Processor Initiative (EPI). Available online: https://www.european-processor-initiative.eu (accessed on 10 May 2021).
- Nannipieri, P.; Di Matteo, S.; Baldanzi, L.; Crocetti, L.; Belli, J.; Fanucci, L.; Saponara, S. True Random Number Generator Based on Fibonacci-Galois Ring Oscillators for FPGA. Appl. Sci. 2021, 11, 3330. [Google Scholar] [CrossRef]
- Baldanzi, L.; Crocetti, L.; Falaschi, F.; Bertolucci, M.; Belli, J.; Fanucci, L.; Saponara, S. Cryptographically Secure Pseudo-Random Number Generator IP-Core Based on SHA2 Algorithm. Sensors 2020, 20, 1869. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nannipieri, P.; Bertolucci, M.; Baldanzi, L.; Crocetti, L.; Di Matteo, S.; Falaschi, F.; Fanucci, L.; Saponara, S. SHA2 and SHA-3 Accelerator Design in a 7 nm Technology Within the European Processor Initiative. Microprocess. Microsyst. 2021. [Google Scholar] [CrossRef]
- Silvaco PDK 45 nm Open Cell Library. Available online: https://si2.org/open-cell-library (accessed on 30 July 2021).
- Liu, Z.; Liu, D.; Zou, X. An efficient and flexible hardware implementation of the dual-field elliptic curve cryptographic processor. IEEE Trans. Ind. Electron. 2016, 64, 2353–2362. [Google Scholar] [CrossRef]
- Chung, S.C.; Lee, J.W.; Chang, H.C.; Lee, C.Y. A high-performance elliptic curve cryptographic processor over GF (p) with SPA resistance. In Proceedings of the 2012 IEEE International Symposium on Circuits and Systems, Seoul, Korea, 20–23 May 2012; pp. 1456–1459. [Google Scholar]
- Chen, G.; Bai, G.; Chen, H. A High-Performance Elliptic Curve Cryptographic Processor for General Curves Over GF (p) Based on a Systolic Arithmetic Unit. IEEE Trans. Circuits Syst. II Express Briefs 2007, 54, 412–416. [Google Scholar] [CrossRef]
- Brier, E.; Joye, M. Weierstraß elliptic curves and side-channel attacks. In Proceedings of the International Workshop on Public Key Cryptography, Paris, France, 12–14 February 2002; pp. 335–345. [Google Scholar]
- Pontie, S.; Maistri, P.; Leveugle, R. Dummy operations in scalar multiplication over elliptic curves: A tradeoff between security and performance. Microprocess. Microsyst. 2016, 47, 23–36. [Google Scholar] [CrossRef]
- Hall, T.A.; Keller, S.S. Elliptic Curve Digital Signature Algorithm (ECDSA) Validation System (ECDSA2VS); NIST Information Technology Laboratory: Gaithersburg, MD, USA, 2014.
- Synopsys Design Compiler. Available online: https://www.synopsys.com/support/training/rtl-synthesis/design-compiler-rtl-synthesis.html (accessed on 22 June 2021).
- QuestaSim. Available online: https://eda.sw.siemens.com/en-US/ic/questa/simulation/advanced-simulator/ (accessed on 22 June 2021).
- PrimeTime. Available online: https://www.synopsys.com/implementation-and-signoff/signoff/primetime.html (accessed on 22 June 2021).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).