Abstract
Inducing spanwise motions in the vicinity of solid boundaries alters the energy, mass and/or momentum transfer. Under some conditions, these motions are such that drag is reduced and/or transition to turbulence is delayed. There are several possibilities to induce those spanwise motions, be it through active imposition a predefined velocity distribution at the walls or by careful design of the wall shape, which corresponds to passive control.In this contribution, we investigate the effect that wavy walls might have on delaying transition to turbulence. Direct Numerical Simulation of both planar and wavy-walled channel flows at laminar and turbulent regimes are conducted. A pseudo laminar regime that remains stable until a Reynolds number higher that the critical is found for the wavy-walled simulations. Dynamic Mode Decomposition applied to the simulation data reveals that in these configurations, modes with wavelength and frequency compatible with the surface undulation pattern appear. We explain and visualize the appearance of these modes. At higher Reynolds numbers we show that these modes remain present but are not dominant anymore. This work is an initial demonstration that flow control strategies that trigger underlying stable modes can keep or conduct the flow to new configurations more stable than the original one.
1. Introduction
Flows over wavy boundaries are of great relevance in both geophysics and engineering [1,2], e.g., the dynamics of sand dunes in deserts and sediment dunes in rivers or the interaction of the oceanic wind and surface waves and their impact on energy-generating devices. Flows over an undulated boundary are more involved than those past flat surfaces, but at the same time offer richer phenomena: for a specified Reynolds number, an adequate choice of the amplitude and wavelength of the undulation may lead to either an enhancement or an inhibition of heat, mass and/or momentum transfer [3].
Several authors have already addressed flows over wavy configurations; in the incompressible [1,4] and in the compressible [5,6,7] regimes. In either case, the induced pressure gradient created by the wall waviness modifies the flow behavior. Larger amplitude undulations lead to scenarios with multiple separations and reattachments. The intermittent nature of the locally separated area beyond a surface peak affects the turbulent production; under certain conditions the coherent structures can be inhibited, and streaks might even disappear then.
The relative angle between the wavy pattern and the bulk velocity also plays a role on the flow behavior. Chernyshenko [8] hinted that a fluid moving obliquely over a sinusoidal undulated surface might experience a reduction in drag, which would derive from the spanwise motions in the wall vicinity induced by the traverse pressure gradient. Indeed, the drag reducing effect of spanwise/streamwise periodic velocity enforced at the wall had been already investigated using Direct Numerical Simulation (DNS): [9,10,11] showed how the spatial Stokes layer disrupts the turbulent production cycle, resulting into a positive shift of the logarithm layer (much as riblets do, [12]). They went further as to identify combinations of forcing amplitudes, wavelengths and frequencies for the wall velocity leading to net-energy savings of up to . However, this impressive figure is obtained for velocity perturbations of the order of the bulk velocity, hence difficulty in the practical implementation of this active control approach. This motivated the interest in wavy walls, a fully passive means to achieve drag reduction. Departing from DNS data [10], Chernyshenko derived a first estimate of the angle and the wavelengths involved. The study was completed later using DNS [3] considering different Reynolds numbers, wave lengths and amplitudes (a sketch of the configuration is shown in Figure 1). The spanwise shear-strain profiles obtained were shown to resemble closely those associated with in-plane wall motions. Unfortunately, since the spanwise velocities were moderate, only a limited drag reduction efficiency was attained: a maximum net drag reduction of about was reported at for a wavy wall with amplitude , wavelength and flow angle , where the represents wall units. However, the authors mention that: “although net drag reduction levels of 1–2% were observed for the three Reynolds number tested (180, 360 and 1000), the value is not quantifiable with any greater degree of precision”.
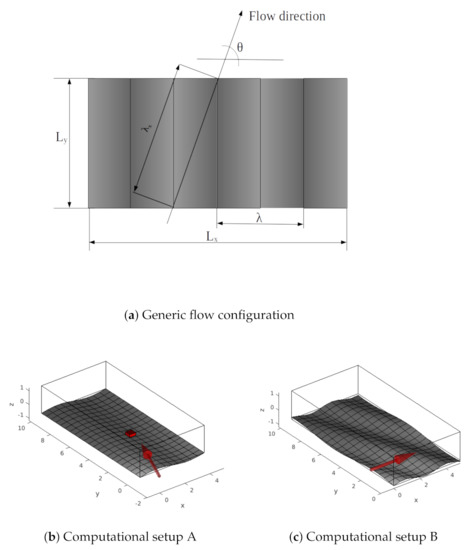
Figure 1.
Computational domains considered for DNS simulation (upper walls not shown). (a) shows a generic flow configuration used in this work and in reference [3]. Most computations conducted considering a slanted inlet velocity profile (b) with ; one verification computation has been conducted on a slanted domain (c). Additionally, in (b), one of the spectral domains used for discretization is shown.
Despite the mild drag reduction attained, the facts that no power supply is required, and the easier manufacturing and posterior maintenance make of wavy walls an interesting technique. However, the majority of the studies here referenced are in turbulent conditions and to the author knowledge, the effect of the waviness in transition to turbulence has not been reported yet in detail. As noted in [13], well-designed perturbations introduced in a boundary layer can potentially inhibit the growth of the most unstable disturbances. This has been recently confirmed by [14], who experimentally described how spanwise perturbation introduced by a wavy-walled roughness is more effective in delaying transition than its counterpart (transition 120,000 vs. 50,000). This experiment is performed in boundary layer flow and a not detailed explanation of the reason of this delay is concluded.
To shed some light about the physical reasons, in this contribution, we investigate the effect of wavy walls in delaying the transition to turbulence. To do that, we conduct DNS of planar and wavy-walled channels, and compare the results. Dynamic Mode Decomposition (DMD, [15]) is applied then to the DNS channel data [16,17], in an attempt to discern the effect of the wall undulation on the flow field. The document is structured as follows: next section describes the methodology employed. Section 3 describes the different computations conducted and offers a first analysis. Section 4 investigates the impact that wavy wall has on transition delay. The conclusions are stated then in the last section.
2. Methodology
2.1. Description of the Flow Solver
All the flow computations conducted in this work used our in-house High Order Discontinuous Galerkin Spectral Element solver, extensively described and validated in [18,19,20,21]. Direct Numerical Simulation of transitional and turbulent flows requires tracking accurately a wide range of spatio-temporal scales: high order spectral element methods, given its low diffusion and dispersion errors, are excellent candidates for this task.
Our solver employs a multidomain approach to discretize the compressible Navier–Stokes equations:
with denoting the vector of conserved variables (density, momentum and energy).
The flow domain (Figure 1) is partitioned into non-overlapping hexahedral elements (one of them shown in Figure 1). Inside every element, the unknown is expanded on a spectral basis constructed as the tensor product of Gauss-Legendre polynomials of degree . The different subdomains are connected in a weak sense by a Roe Riemann solver.
For the channel flow configurations considered in this work, periodic boundary conditions are considered along the streamwise and spanwise homogeneous directions x-y. A constant unitary mass flow rate is enforced through a homogeneous, time-dependent volumetric force/source term that is imposed at the Navier–Stokes equations:
where and penalize the instantaneous imbalance between the computed space average flow rate () and the desired . The constant is taken as in all the simulations considered in this work. This source term is a mathematical artefact (although equivalent to a physical force or external pressure gradient) that forces the “average” streamwise and spanwise momentum components to be, respectively, . It is important to highlight that although the integration of the Navier–Stokes in time and space is accurate with our methods, at the initial stages of the computation, the average momentum is far from the prescribed, and that difference can be positive or negative. This explains why the source terms (Equation (1)) could oscillate until the flow achieves its statistically steady state and the momentum converges (see e.g., Figure 2, more details in Section 2.1).
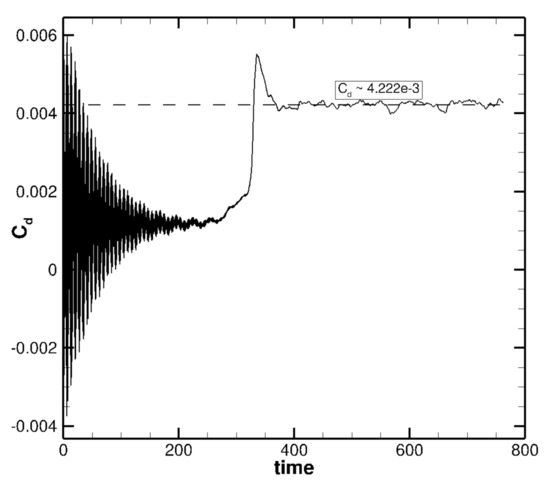
Figure 2.
Wavy wall channel flow at : evolution of (Equation (2)). Observe that during the initial steps of the simulation the average momentum is far from the prescribed , and taking into account that the source term is divided by , (Equation (1)), this produces unphysical strong oscillations of the drag.
The source term Equation (1) driving the flow is intimately related to the friction. In that sense, it will be used has a direct sensor to detect transition to turbulence, since drag undergoes a large increase when the flow turns turbulent. For the planar channel, this relation is direct, whereas for the wavy wall the total drag force splits into friction and pressure contributions. Friction and pressure may be further segregated through integration over the wavy surface and projection along the flow-direction, yielding the drag coefficients and , respectively. In this work, however, we are interested only in global drag, regardless the origin. Accordingly, we resort to the temporal average of the source term to compare the different configurations here studied:
with the average bulk velocity.
To conclude, for the wavy-walled channel simulations, adiabatic wall boundary conditions are enforced at surfaces given by the expressions (Figure 1). An amplitude of has been considered in this work, equivalent to in wall units at . The computational setup has the mesh aligned with the direction (wall crests/troughs along x, see Figure 1b). which makes the computation statistically more homogeneous. The spectral accuracy of the scheme is maintained through mapping from elements to a reference hexahedron using transfinite interpolation.
2.2. Dynamic Mode Decomposition
To uncover the physical feature causing the stabilization effect induced by the wavy wall, we make use of the Dynamic Mode Decomposition (DMD, [15]) technique, which we summarize here.
DMD works with a sequence of instantaneous flow fields numbered from 1 to (e.g., taking one or all recorded variables, denoted here generically by at different time steps of the simulation). The following data matrix is then constructed:
where the subindex and superindex identify, respectively, the first- and last-time instances of the sequence. The data are ordered in time, and separated by a constant sampling time interval such that: for all . In the case of linear stability analysis and within the exponential growth region, it is possible to define a linear operator (i.e., a numerical approximation of the linearized Navier–Stokes operator) such that . For non-linear systems, represents the Koopman operator. Equation (3) can be rewritten as a Krylov sequence:
For an ordered sequence, Equation (4) can be equated to Equation (3):
which can alternatively written in matrix form:
Next, the Singular Value Decomposition (SVD) of the snapshot matrix is used into Equation (6), leading to . Further manipulation leads to the reduced matrix:
The reduced matrix , which is the projection of the matrix onto the space spanned by the left singular vectors matrix , conveys most of the information codified into operator . Solving the eigenvalue problem provides the reduced DMD modes and the associated eigenvalues . The approximated eigenmodes of the matrix can then be recovered via a projection onto the original space, using relation . Relation allows recovery of the growth rate and the frequency .
Finally, note that the DMD decomposition allows reconstruction of the original data sequence as:
In this contribution, the amplitudes are computed following the formulation in [22]. That is, the ’s stem from the minimization problem in the Frobenius norm:
where the columns in matrix are the dynamic modes , diagonal matrix contains the unknown amplitudes and is a Vandermonde matrix whose columns are generated by the successive powers of the column vector , with . Since matrix is unitary, it does not affect the norm in Equation (9), and the optimization problem actually solved is:
with the columns in matrix the eigenvectors of matrix .
3. Numerical Validation: Direct Numerical Simulation of Planar and Wavy-Walled Channel Flows
3.1. DNS of Planar Walled (Canonical) Turbulent Channel Flow
To validate the current solver and our numerical methodology a Direct Numerical Simulation (DNS) of a turbulent Poiseuille flow between two parallel planes is performed. Similar to other authors, here we address a configuration at a Reynolds number based on the centerline mean velocity and channel half-height . For this flows the associated Reynolds number based on the friction velocity corresponds approximately to [23,24].
The domain extent and the discretization details are summarized in Table 1, where the indicate wall viscous scales. Please note that two different meshes are employed: a external (h) mesh consisting of elements and an internal spectral (p) mesh of order . For values of and are proposed. To achieve this resolution, the multidomain mesh is stretched in the normal direction following a cosine law between and 1. This leads to a wall normal distribution of points where for polynomial order 8, the first and second points are located at and respectively. Finally, since our Discontinuous Galerkin solver discretizes the compressible Navier–Stokes equations, compressibility effects are minimized by setting a Mach number of for all the computations described. In this regard, no distinction is made between velocities and momentums along the paper.

Table 1.
DNS computations: channel flow configurations and discretization details. Lengths have been made dimensionless with the friction velocity and kinematic viscosity and . , is the wall shear stress and the density.
For the planar wall case, the simulation is initialized from a laminar Poiseuille profile superposed with a random perturbation with amplitude of of the central velocity. Statistics are obtained averaging over 300,000 time steps taken at . The simulation takes approximately 12 h running in 80 Intel Xeon Gold 6230 cores at 2.1 GHz in the CESVIMA-UPM supercomputer center. Figure 3 shows the average and r.m.s. velocities, obtained by projecting along the edge aligned with the input streamline (). The profiles obtained practically overlap those reported in [23] () and [24] (.
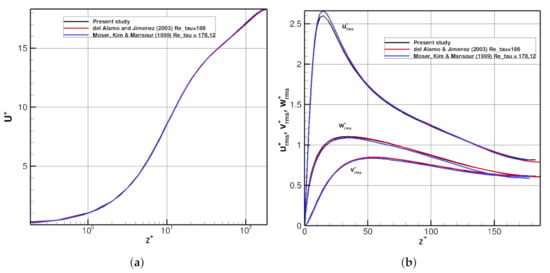
Figure 3.
Canonical (planar walled) channel flow at (): (a) velocity average and (b) r.m.s. in wall units compared against results in the bibliography. is the dimensionless velocity: the velocity u parallel to the wall as a function of z (distance from the wall), divided by the friction velocity.
3.2. DNS of Wavy Wall Turbulent Channel Flow
The validation of the wavy wall configuration is performed by comparing our results with those obtained by [3], details also in Table 1. The same external mesh with 2000 elements has been reused, but the polynomial degree has been progressively increased as the simulation proceeds. A degree of 8 has been finally set as a good compromise between accuracy and computational costs (see Table Figure 2).
The simulation is initialized from a laminar Poiseuille profile adjusted to the passage section. No perturbation has been necessary to trigger transition: as observed in Figure 2, the flow tends towards a laminar solution with , which is slightly above the laminar drag for a planar configuration, . This increase is due to the pressure drag introduced by the undulated surface. The transition to turbulence is clearly visible around time , where the drag increases suddenly to finally stabilize around . The drag reduction from the planar wall channel is about (Table 2), which is comparable to the reported by [3] for the incompressible case.

Table 2.
DNS computations: drag prediction for canonical and wavy-walled turbulent channel flows.
Table 2 summarizes the sensitivity of drag reduction figures to polynomial order : the specific values remain consistently around , even when considering the computational setup B, Figure 1c. As a final comparison, an additional computation has been conducted on a domain longer along x, i.e., , with external mesh density and polynomial order (thus doubling the number of degrees of freedom). The results obtained do not differ significantly from those in Table 2 and are not included here for conciseness. The consistency of the results obtained confirms then that at , the wavy wall considered brings a drag reduction which exceeds the pressure drag penalty and agrees with those obtained by [3].
4. Delay of the Transition to Turbulence
After the validation of our methodology, we address now the main part of this work; the impact that the wavy wall has on transition to turbulence. All the computations reported in this section reuse the element meshes with considered in Section 3: since the Reynolds numbers are lower, a higher accuracy is expected. In order to make a fair comparison between both configurations, planar and wavy, the simulation is initialized from a laminar Poiseuille profile superposed with a random perturbation with amplitude of 50% of the central velocity.
Transition to turbulence in channel flows has been reported to occur for , with some turbulent spots appearing even for [25]. In the simulations conducted in this work, a value between has been found for the planar case, where the friction drag experiences a large increase from for the laminar regime to for the turbulent regime. However, for the wavy-walled channel and , this increase is observed at a higher Reynolds number , with and in the laminar and turbulent cases, respectively. Specifically, the transition to turbulent is delayed around a 20% in terms of the Reynolds number.
The effect of the wall undulation is shown in Figure 4, where it is clearly shown the differences between the average vertical velocities. The magnitude of the vertical velocity is an order of magnitude higher for the turbulent case, which is consistent with a higher forcing (drag) term and penetrates much deeper into the channel core compared with the laminar case. Indeed, inspection of the instantaneous vertical velocity, Figure 5, discovers a persistent, organized structure connected to the wavelength of the wavy wall.
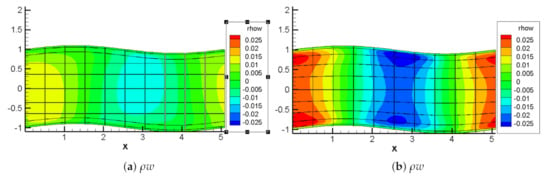
Figure 4.
Wavy wall channel flow: comparison of the average vertical velocity/momentum for the laminar (, a) and turbulent (, b) cases.
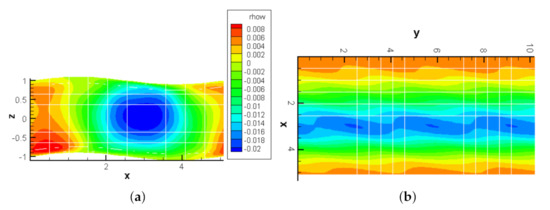
Figure 5.
Wavy wall channel flow at . Illustrative spanwise (a) and normal (b) sections of the instantaneous vertical velocity field.
The connection of the increased level of organization with the delay of the transition is investigated next using DMD. Two data sequences, laminar at and turbulent at respectively, are considered. Each sequence consists of velocity vector fields acquired at a uniform time step of over the non-dimensional time intervals —for —and for . For illustration, Figure 6 shows the vertical velocity at a tracer point located at . As expected, the laminar case shows a periodic and well-organized behavior with Strouhal , as opposed to the irregular, chaotic, of the turbulent regime. Please note that time step related to this Strouhal () is twice the time taken by the flow to traverse the wavelength , so that the wavy wall introduces passive excitation of a frequency given by the average velocity and the wavelength of the wavy wall. The critical issue here is that this excitation promotes a stable mode able that maintain the laminarity further.
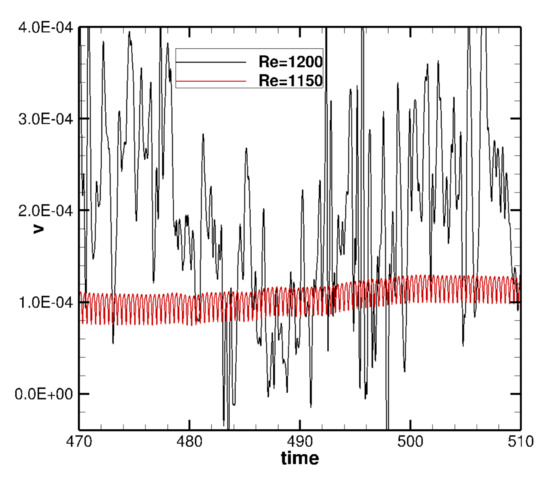
Figure 6.
Wavy wall channel flow: vertical velocity at a tracer point at at and 1200.
The application of the DMD algorithm returns modes , eigenvalues and amplitudes per data sequence. As usual [16,17], the major difficulty is to discern among all the modes obtained those most relevant for the process investigated. According to Equation (), the temporal evolution of is controlled by the product . Here, we introduce a new parameter , defined as:
and exploit it to categorize the modes according both to its amplitude and growth rate.
Figure 7 summarizes the DMD analysis for the data sequence. The - spectrum is shown in Figure 7a: apart from the average value, a dominant mode (highlighted in red) at and its harmonics are clearly visible. The streamwise and spanwise components of this dominant mode are visualized in Figure 7b,c. The streamwise perturbation velocity presents a z-uniform, streaky structure, with maximum (minimum) acceleration at the inflection points before (after) the crest. The spanwise component, which is an order of magnitude smaller is clearly modulated and attain more extreme values in the regions close to the wall and the crest of the wave. This spatial structure is better visible in Figure 7d: the positive (crest are, close to the wall) and negative (in the troughs but far from the boundary layer) forces the fluid to move from the troughs to the crest in the spanwise direction.
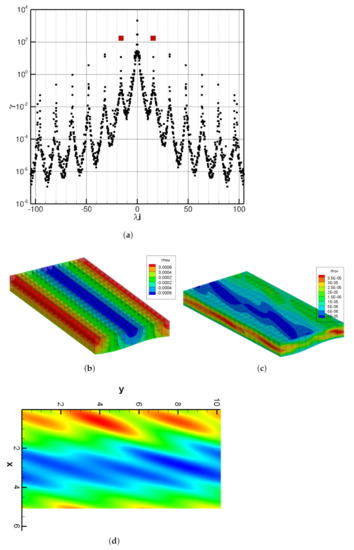
Figure 7.
DMD analysis of the laminar wavy wall channel flow. Relevance of the different modes, measured by Equation (11), in (a). Streamwise (b) and spanwise (c) fields of the dominant mode (in red in a); (d) shows (c) cut at .
The flow is more involved, as different structures begin to interact creating complex non-linear patterns. Inspecting the drag evolution (Figure 8a) in -just before transition- three different phases can be distinguished. In region (in blue) the solution is still “quasi-laminar” and the mode with dominates the evolution (and the drag) of the fluid. However, inspection of the DMD spectra (Figure 8b) reveal other incipient modes with a non-negligible relevance (note especially the mode with ) which may start interacting with other modes. The region (in red), with a sharp rise in drag, shows that the transition to turbulence is taking place. The original mode at remains present, but DMD picks up also new relevant features, and harmonics. As the time progresses, non-linear interactions gain more and more relevance. This effect becomes clearer in region , where many new dominant nodes appear as a result of non-linear combinations, showing the path to turbulence.
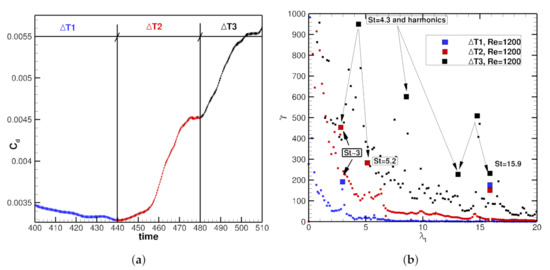
Figure 8.
Wavy wall flow at . (a): drag evolution (Equation (1)) before reaching statistical convergence, considering three successive temporal ranges. (b): associated DMD spectra.
As a final analysis, all the computations so far used [3]. We have been able to show that a fluid moving obliquely to an undulated wall is subject -provided the parameters are well adjusted- to a Stokes layer that delays transition and brings drag reduction. The following question arises then naturally: how important is the sweep angle? To answer this question, three more computations at and have been conducted. As Figure 9 shows, at the solution is turbulent whereas it is laminar at , confirming the fact that a threshold in the skew angle is necessary to create enough spanwise velocity to trigger the stable mode.
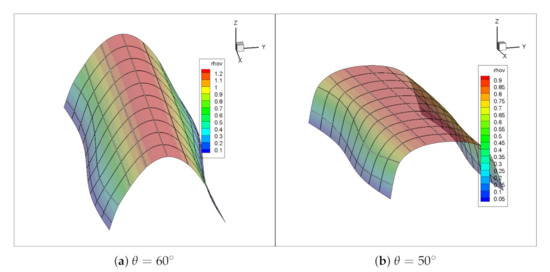
Figure 9.
Wavy-walled channel flow at : 3D view of the average spanwise velocity/momentum at two different sweep angles. At , velocity shows a laminar-shaped profile, resembling a typical parabolic Poiseuille flow. At , it is a typical flattened turbulent profile.
5. Conclusions
In this contribution, we have investigated the effect that wavy walls have on delaying transition to turbulence. Direct Numerical Simulation of both planar and wavy-walled channel flows at laminar and turbulent regimes has been conducted, using our in-house solver based on Discontinuous Galerkin Spectral Element Method.
The validation of the numerical methodology has been performed on the simulation of a turbulent channel at , where we have observed a good agreement between our results and those reported on the bibliography, confirming the moderate drag reduction of about .
In the wavy wall configuration, we have observed a pseudo laminar regime that remains stable until a Reynolds number higher that the critical one of the planar walled channel. Dynamic Mode Decomposition applied to the simulation data revealed that in the wavy-walled configuration, modes with wavelength and frequency compatible with the surface undulation pattern are triggered. The relative inclination of the flow over the wavy surface enhances a stable mode that is not shown for the plane wall case. We explained and visualized the appearance of these modes that are also present at higher Reynolds numbers, though they are not dominant anymore.
Certainly, this investigation is still preliminary (e.g. no optimal analysis of the wavelength has been conducted yet). However, the fact that the combination of a wavy surface and a slanted flow, allows the triggering of a stabilizing mode in a completely passive manner encourages to pursue further research into the application of wavy surfaces as passive flow control device.
Author Contributions
Conceptualization, E.V.; methodology, E.V., J.G.-M., A.M.-G., M.C.; software, E.V., J.G.-M., M.C.; validation, J.G.-M., E.V., A.M.-G., M.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Ministry of Science of Spain under project SIMOPAIR (REF: RTI2018-097075-B-I00) and by the European Union’s Horizon 2020 research and innovation programme under project DRAGY (GA-690623).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author, upon reasonable request.
Acknowledgments
The authors acknowledge the computer resources, technical expertise and assistance provided by the Supercomputing and Visualization Center of Madrid (CeSViMa).
Conflicts of Interest
The authors declare no conflict of interest. The funders have no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the result.
References
- Hsu, S.; Kennedy, J. Turbulent flow in wavy pipes. J. Fluid Mech. 1971, 47, 481–502. [Google Scholar] [CrossRef]
- Franklin, E.M.; Charru, F. Subaqueous barchan dunes in turbulent shear flow. Part 1. Dune motion. J. Fluid Mech. 2011, 675. [Google Scholar] [CrossRef] [Green Version]
- Ghebali, S.; Chernyshenko, S.; Leschziner, M.A. Can large-scale oblique undulations on a solid wall reduce the turbulent drag? Phys. Fluids 2017, 29, 105102. [Google Scholar] [CrossRef] [Green Version]
- Ohta, T.; Miyake, Y.; Kajishima, T. Direct Numerical Simulation of Turbulent Flow in a Wavy Channel. JSME Int. J. 1998, 41, 447–453. [Google Scholar] [CrossRef] [Green Version]
- Sun, Z.S.; Ren, Y.X.; Zhang, S.Y.; Yang, Y.C. High-resolution finite difference schemes using curvilinear coordinate grids for DNS of compressible turbulent flow over wavy walls. Comput. Fluids 2011, 45, 84–91. [Google Scholar] [CrossRef]
- Tyson, C.; Sandham, N. Numerical simulation of fully-developed compressible flows over wavy surfaces. Int. J. Heat Fluid Flow 2013, 41, 2–15. [Google Scholar] [CrossRef]
- Sun, Z.; Zhu, Y.; Hu, Y.; Zhang, Y. Direct numerical simulation of a fully developed compressible wall turbulence over a wavy wall. J. Turbul. 2018, 19. [Google Scholar] [CrossRef]
- Chernyshenko, S. Drag reduction by a solid wall emulating spanwise oscillations. Part 1. arXiv 2013, arXiv:1304.4638. [Google Scholar]
- Quadrio, M.; Ricco, P.; Viotti, C. Streamwise-travelling waves of spanwise wall velocity for turbulent drag reduction. J. Fluid Mech. 2009, 627, 161–178. [Google Scholar] [CrossRef] [Green Version]
- Viotti, C.; Quadrio, M.; Luchini, P. Streamwise oscillation of spanwise velocity at the wall of a channel for turbulent drag reduction. Phys. Fluids 2009, 21. [Google Scholar] [CrossRef]
- Skote, M. Comparison between spatial and temporal wall oscillations in turbulent boundary layer flows. J. Fluid Mech 2013, 730, 273. [Google Scholar] [CrossRef]
- García-Mayoral, R.; Jiménez, J. Hydrodynamic stability and breakdown of the viscous regime over riblets. J. Fluid Mech. 2011, 678. [Google Scholar] [CrossRef]
- Saric, W.; Reed, H.; White, E. Stability and Transition of Three-Dimensional Boundary Layers. Annu. Rev. Fluid Mech. 2003, 35, 413–440. [Google Scholar] [CrossRef] [Green Version]
- Hamed, A.M.; Sadowski, M.; Zhang, Z.; Chamorro, L.P. Transition to turbulence over 2D and 3D periodic large-scale roughnesses. J. Fluid Mech. 2016, 804, R6. [Google Scholar] [CrossRef]
- Schmid, P. Dynamic mode decomposition of numerical and experimental data. J. Fluid Mech. 2010, 656. [Google Scholar] [CrossRef] [Green Version]
- Garicano-Mena, J.; Li, B.; Ferrer, E.; Valero, E. A composite dynamic mode decomposition analysis of turbulent channel flows. Phys. Fluids 2019, 31, 115102. [Google Scholar] [CrossRef]
- Li, B.; Garicano-Mena, J.; Zheng, Y.; Valero, E. Dynamic Mode Decomposition Analysis of Spatially Agglomerated Flow Databases. Energies 2020, 13, 2134. [Google Scholar] [CrossRef]
- Manzanero, J.; Ferrer, E.; Rubio, G.; Valero, E. Design of a Smagorinsky Spectral Vanishing Viscosity turbulence model for discontinuous Galerkin methods. Comput. Fluids 2020, 200, 104440. [Google Scholar] [CrossRef]
- Manzanero, J.; Rubio, G.; Kopriva, D.A.; Ferrer, E.; Valero, E. A free energy stable nodal discontinuous Galerkin approximation with summation by parts property for the Cahn-Hilliard equation. J. Comput. Phys. 2020, 403, 109072. [Google Scholar] [CrossRef] [Green Version]
- Manzanero, J.; Rubio, G.; Kopriva, D.A.; Ferrer, E.; Valero, E. Entropy–stable discontinuous Galerkin approximation with summation–by–parts property for the incompressible Navier–Stokes/Cahn–Hilliard system. J. Comput. Phys. 2020, 408, 109363. [Google Scholar] [CrossRef] [Green Version]
- Garicano-Mena, J.; Ferrer, E.; Sanvido, S.; Valero, E. A stability analysis of the compressible boundary layer flow over indented surfaces. Comput. Fluids 2018, 160, 14–25. [Google Scholar] [CrossRef] [Green Version]
- Jovanović, M.R.; Schmid, P.J.; Nichols, J.W. Sparsity-promoting Dynamic Mode Decomposition. Phys. Fluids 2014, 26. [Google Scholar] [CrossRef]
- Moser, R.; Kim, J.; Mansour, N. Direct numerical simulation of turbulent channel flow up to Reτ = 590. Phys. Fluids 1999, 11, 943–945. [Google Scholar] [CrossRef]
- Del Álamo, J.; Jiménez, J. Spectra of the very large anisotropic scales in turbulent channels. Phys. Fluids 2003, 15. [Google Scholar] [CrossRef]
- Sano, M.; Tamai, K. A universal transition to turbulence in channel flow. Nat. Phys. 2016, 12, 249–253. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).