Abstract
In this paper, we propose a method for the identification of the differential inductance of saturable ferrite inductors adopted in DC–DC converters, considering the influence of the operating temperature. The inductor temperature rise is caused mainly by its losses, neglecting the heating contribution by the other components forming the converter layout. When the ohmic losses caused by the average current represent the principal portion of the inductor power losses, the steady-state temperature of the component can be related to the average current value. Under this assumption, usual for saturable inductors in DC–DC converters, the presented experimental setup and characterization method allow identifying a DC thermal steady-state differential inductance profile of a ferrite inductor. The curve is obtained from experimental measurements of the inductor voltage and current waveforms, at different average current values, that lead the component to operate from the linear region of the magnetization curve up to the saturation. The obtained inductance profile can be adopted to simulate the current waveform of a saturable inductor in a DC–DC converter, providing accurate results under a wide range of switching frequency, input voltage, duty cycle, and output current values.
1. Introduction
Inductors are key components in the design of high-power density DC–DC converters in high demand for automotive, aerospace, and telecommunications industries [1,2,3]. In these fields, the magnetic components need to have a small physical size, low power loss, and a high saturation magnetic flux density [4]. A further requirement is an ever-higher switching frequency in power converters, which reduces the inductor volume and increases the magnetic losses. Ferrite inductors represent a good trade-off between the required performance and cost of the component. However, their sharp inductance drop, even in gapped core components, often induce the designer to a conservative approach, ensuring that the inductor operates in the linear region of the core magnetization curve, where the inductance is nearly constant. The adoption of inductors operating in the weak saturation region allows optimizing the magnetic core to be used, reducing the volume and weight of the component [5,6,7]. However, the current ripple should be accurately computed to verify compliance with the application constraints. This task becomes even more challenging since the differential inductance profile of the component depends not only on the average current but also on the operating temperature of the core. In the literature, several methods for the characterization and modelling of the differential inductance of a saturable inductor for power electronics applications are described [8,9,10,11,12], some of which also consider the inductor operating temperature variation [13,14]. However, the temperature of a ferrite inductor is not easily measurable under normal operating conditions. Given the temperature dependence of the power dissipated by the component, some authors introduced a power-loss-dependent inductance model [15]. This approach allows describing the inductance of a saturable inductor as a function of operating current and power losses. This method requires a set of experimental measurements under different inductor current and power losses working conditions.
In many applications of saturable ferrite inductors in DC–DC converters, a significant amount of the losses depends only on the average operating current. In this case, the steady-state temperature of the inductor can be associated with the average current value. In this paper, we propose a method for the characterization of inductors for DC–DC converters, which considers the effect of temperature on the differential inductance variation of the device, relating it to the average operating current. This approach requires a smaller set of experimental measurements and allows identifying a DC thermal steady-state differential inductance profile of a ferrite inductor, suitable for evaluating the current ripple of a saturable inductor in a DC–DC converter under a wide range of operating conditions.
The paper is structured as follows: In Section 2, the experimental setup and the identification method of the differential inductance characteristic as a function of the DC thermal steady-state temperature are presented. The obtained characterization of two different commercial inductors is then described. In Section 3, the results of inductive current waveform simulations within a DC–DC buck converter are shown. The simulations adopt the differential inductance characteristic obtained through the described method, and the results are compared with experimental measurements performed under different converter operating conditions. Finally, in Section 4, the obtained results are discussed, and the conclusions of are provided.
2. Methodology
In the design stage of a DC–DC converter, it is crucial to evaluate the current ripple of the inductor correctly. It is especially true in the case of saturable ferrite inductors. A wide current variation can induce a non-negligible variation in the differential inductance, resulting in an unpredictable variation of the current ripple [8]. The inductance value, under a specific operating condition, permits correctly estimating the current ripple. However, the inductance of a ferrite component is influenced by the applied average current that determines the operative magnetic field of the core and by its working temperature [15]. It is recognized that temperature has a considerable influence on the permeability of a ferrite core. A temperature increase tends to increase the initial permeability of a ferrite core. Still, it implies reducing the saturation induction of the material, determining a further rapid decrease in the differential permeability as the imposed magnetomotive force increases. Thus, for a saturable inductor, the differential inductance characteristic reflects the actual properties of the component in a specific thermal condition.
2.1. Impact of Losses in an Inductor for DC–DC Converter
Inductor temperature rise is caused by its losses, assuming the part temperature is not affected by other components forming the DC–DC converter layout. Two loss contributions occur in an inductor adopted in a DC–DC converter: winding losses and core losses. In the winding losses, a term related to the average current value (DC winding losses) and a term related to the RMS value of the current ripple (AC winding losses) are separated. For an inductor operating in the region of weak saturation, meaning at the upper bound of its current operating range, the DC winding losses are supposed to be prevailing over the core and AC winding losses, independent of the average output current.
The applicability of this assumption can be verified by analyzing the power losses data of some commercial inductors, reported in Table 1. If DC winding losses are the prevalent heating contributor of the inductor, its steady-state temperature is determined by the average current value, which is an easily measurable quantity. Consequently, we propose defining a differential inductance characteristic obtained under the thermal steady-state caused solely by DC winding losses for each average current value up to the saturation of the inductor.

Table 1.
Declared losses for two Coilcraft inductor (MSS1260T-273 and SER1390-333) under different operating conditions [16,17].
2.2. Experimental Method for the Differential Inductance Measurement
The setup for measuring the differential inductance of the inductor under test comprised a synchronous DC–DC buck converter, based on the evaluation board circuit EPC90122 [18,19]. In Figure 1, the experimental measurement setup arrangement is described.
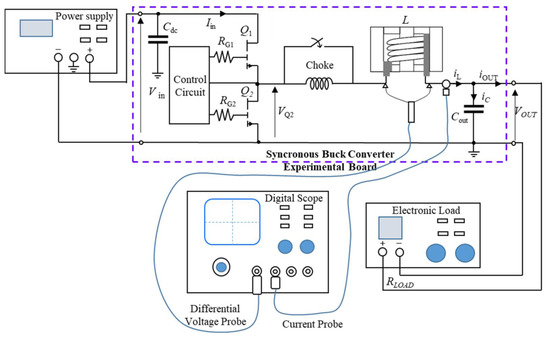
Figure 1.
Circuit diagram of the experimental setup for DC thermal steady-state differential inductance identification. A high inductance choke allows imposing negligible current ripple on the inductor under test. After reaching the DC thermal steady-state for a given average output current, the choke is short-circuited, and the inductor voltage and current waveforms are measured with a digital oscilloscope.
GaN devices (EPC2206) allowed increasing the maximum switching frequency up to 1 MHz in hard switching operating conditions. The input voltage was imposed through a regulated power supply, while the switching frequency and the duty cycle were controlled by an arbitrary waveform generator that controls the rectangular pulse wave. An electronic load regulated the output current. To reach the condition of negligible current ripple on the inductor under test, and the consequent zero AC losses, a choke with high values of inductance and saturation current (L = 600 µH and ISAT = 150 A) was added in series. For each load current condition, after a reasonable amount of time passed to reach thermal equilibrium, the choke was short-circuited, and the inductor voltage and current were quickly measured, assuming the temperature was unchanged. Measurements were performed with a digital oscilloscope, using a differential probe to measure inductor voltage and a current probe to measure the relative current (Figure 1). The measured voltage was corrected from the winding resistive voltage drop, as described in [9]
From vL(t), Φ(t) is obtained as
The obtained magnetic flux waveform is defined minus a constant term, that is, the value at t = 0. By relating the magnetic flux and the experimental current, the Φ(iL) characteristic is obtained. Due to the magnetic dissipative effects, it is a loop with a non-zero area [20]. The measurements were performed at duty cycle δ = 0.5, allowing us to assume the loss in the two half-periods was equal. Thus, the loop was symmetrical. Therefore, the average characteristic was adopted as the experimental Φ(iL) one. Assuming that in an appropriately defined range of current sweep around the average current, the Φ(iL) characteristic is linear, as shown in Figure 2; the differential inductance at each tested load current value is determined as
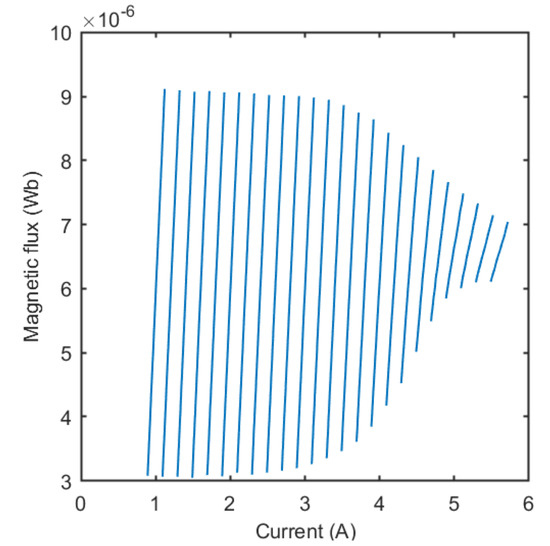
Figure 2.
Average Φ(iL) characteristics obtained for each measured output current value. The magnetic flux of each section is defined minus a constant term.
The differential inductance curve obtained for the Coilcraft MSS1260T-273 inductor [16] is presented in Figure 3. The comparison of the DC thermal steady-state measurements and the ambient temperature measurements highlights the effect of temperature on the inductor’s properties. The differential inductance characteristic obtained at ambient temperature from a spot measurement, not reaching the operating steady-state temperature, would be insufficient to effectively describe the behavior of a saturable inductor under the real operating conditions in a DC/DC buck converter, overestimating the differential inductance value. This is increasingly evident as the average current rises.
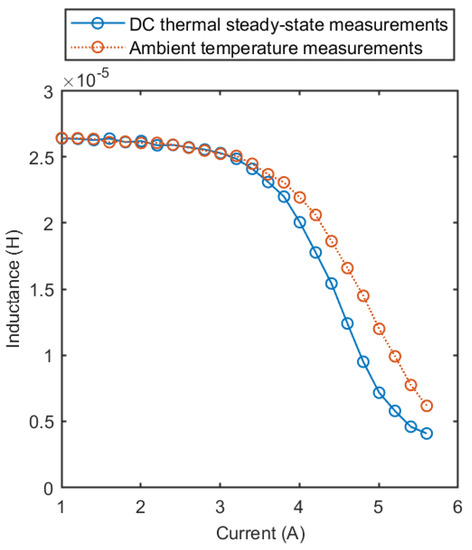
Figure 3.
Experimental DC thermal steady-state differential inductance curve for the Coilcraft MSS1260T-273 inductor compared to the curve obtained from ambient temperature measurements (25 °C).
The test conditions for the identification were:
- input voltage: 24 V;
- duty cycle: 0.5;
- switching frequency: 500 kHz;
- output current: 1–5.6 A.
The manufacturer’s datasheet specifies that the nominal inductance of the component is 27 µH and the current that causes a 30% inductance drop is 4.7 A. The measurements were performed up to the current values that cause a differential inductance drop exceeding the acceptable limits of a DC–DC converter application, as shown in Figure 3. At a current of 5.6 A, the differential inductance drop is 84.56% of the initial value.
The experimental L(iL) curve is now parametrized according to [4]
where the four parameters [LH, LL, σ, I*] that better describe the experimental curve were obtained with a deterministic pattern search optimization algorithm [21], minimizing an objective function (fmin) defined as the difference between the experimental and the parametrized differential inductance profile [9]:
The fitting process quickly converged to a satisfactory result. The parametrized curve obtained for MSS1260T-273 inductor is presented in Figure 4, and compared to the previously presented experimental DC thermal steady-state curve. The described methodology was also applied to identify the differential inductance curve for the inductor SER1390-333 [17], under the following test specifications:
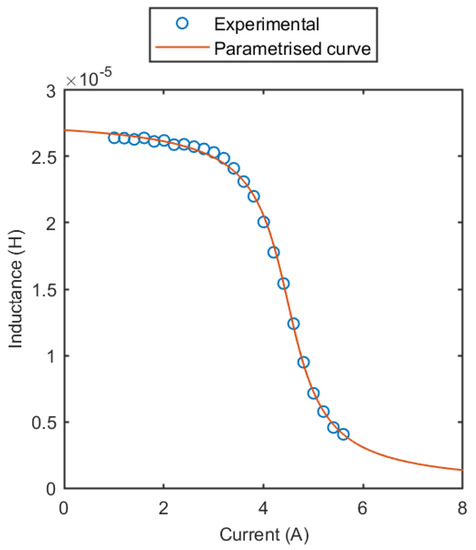
Figure 4.
Fitting of the parametrized characteristic on the experimental differential inductance curve for the Coilcraft MSS1260T-273 inductor.
- input voltage: 24 V;
- duty cycle: 0.5;
- switching frequency: 500 kHz;
- output current: 1–6.2 A.
In Figure 5, the experimental DC thermal steady-state differential inductance curve and the parametrized characteristics of SER1390-333 inductor are presented. The nominal inductance of the component is 33 µH and the current that causes a 30% inductance drop is 4.8 A. Therefore, the two analyzed inductors were found to have comparable nominal inductance and saturation current values, resulting in comparable testing operating conditions. As reported by the manufacturer, the temperature variation as a function of applied average current is less significant in the SER1390-333 inductor than in the MSS1260T-273 inductor due to different construction characteristics, as presented in Figure 6.
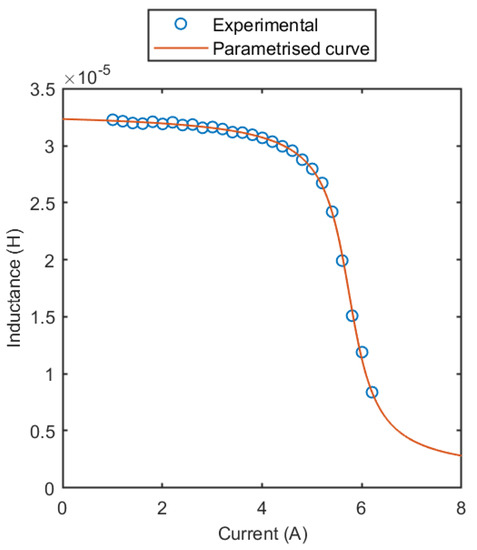
Figure 5.
Fitting of the parametrized characteristic on the experimental differential inductance curve for the Coilcraft SER1390-333 inductor.
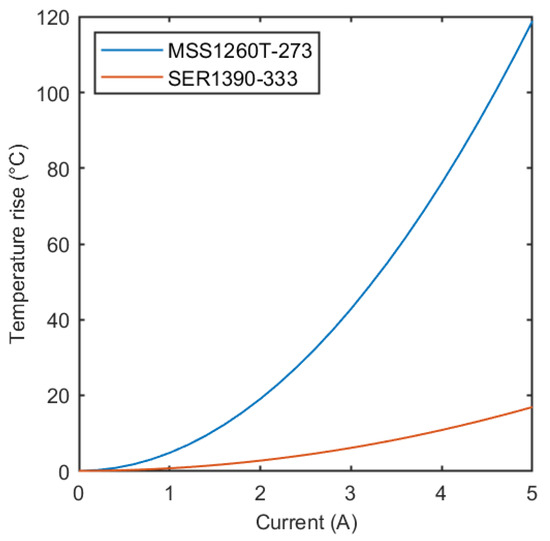
Figure 6.
Temperature rise vs. output current for the two tested inductors [16,17].
The temperature rise in the MSS1260T-273 inductor is significant. This determined, as observed in Figure 3, a considerable difference between the obtained incremental inductance curves under DC thermal steady-state conditions and ambient temperature conditions. However, as discussed in the following, the described methodology provides a differential inductance curve that effectively allows estimating the inductive current behavior. The lower temperature rise sustained by the SER1390-333 inductor will further increase the accuracy of the current waveform simulations.
3. Current Waveform Simulation Results
The previously discussed L(iL) characteristics, referring to the thermal behavior of the inductor caused by DC losses only, could be used to simulate current waveforms under different operating conditions tested experimentally. The nonlinear differential equations of a saturable inductor in a DC–DC buck converter circuit were solved through the polarization fixed point method [22,23].
3.1. MSS1260T-273 Inductor
The DC thermal steady-state characteristic obtained at 500 kHz was used to simulate the inductor operation under different input voltage and switching frequency values. For each operating condition tested, a reasonable amount of time passed to reach the thermal steady-state temperature. The measurements were therefore performed under the real operating condition of the inductor in a DC–DC converter. Figure 7, Figure 8 and Figure 9 show, for three switching frequency values (500 kHz, 750 kHz, and 1 MHz), the comparison between experimental and simulated current waveforms, and the relative error on the estimated RMS and peak value of the inductive current.
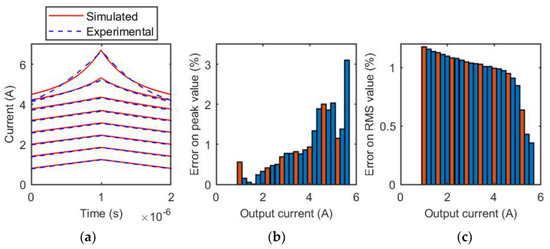
Figure 7.
Coilcraft MSS1260T-273 inductor, 500 kHz. (a) Comparison of experimental and simulated current waveforms for different output current values; (b) relative error of the estimation of the peak value of the inductive current for each tested output current value. The orange bars represent the test cases reported in (a), the blue bars are related to the other measurements of the evaluated current range; (c) relative error of the estimation of the RMS value of the inductive current for each tested output current value. The orange bars represent the test cases reported in (a), the blue bars are related to the other measurements of the evaluated current range.
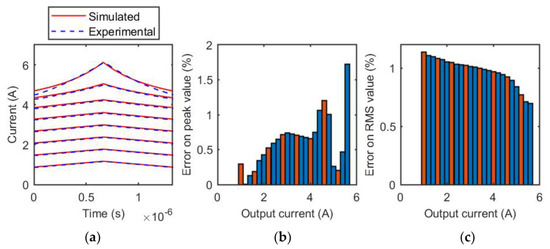
Figure 8.
Coilcraft MSS1260T-273 inductor, 750 kHz. (a) Comparison of experimental and simulated current waveforms for different output current values; (b) relative error of the estimation of the peak value of the inductive current for each tested output current values. The orange bars represent the test cases reported in (a), the blue bars are related to the other measurements of the evaluated current range; (c) relative error of the estimation of the RMS value of the inductive current for each tested output current value. The orange bars represent the test cases reported in (a), the blue bars are related to the other measurements of the evaluated current range.
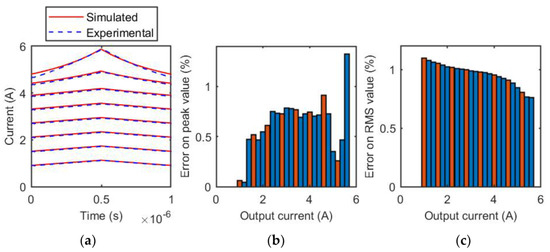
Figure 9.
Coilcraft MSS1260T-273 inductor, 1 MHz. (a) Comparison of experimental and simulated current waveforms for different output current values; (b) relative error of the estimation of the peak value of the inductive current for each tested output current value. The orange bars represent the test cases reported in (a), the blue bars are related to the other measurements of the evaluated current range; (c) relative error of the estimation of the RMS value of the inductive current, for each tested output current value. The orange bars represent the test cases reported in (a), the blue bars are related to the other measurements of the evaluated current range.
As the DC thermal steady-state characteristic is effective at different switching frequencies, a further verification was obtained by simulating currents measured under different input voltages (12 and 32 V). The duty cycle was fixed at δ = 0.5 as it represented the maximum AC losses condition given the other specifications. The switching frequency was fixed at 500 kHz. Figure 10 and Figure 11 show the comparison between measured and simulated current waveforms, followed by the relative errors of the RMS and peak value estimation.
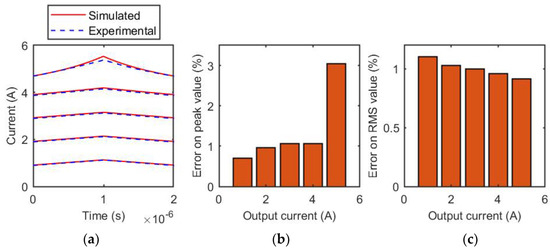
Figure 10.
Coilcraft MSS1260T-273 inductor, 12 V. (a) Comparison of experimental and simulated current waveforms for different output current values; (b) relative error of the estimation of the peak value of the inductive current; (c) relative error of the estimation of the RMS value of the inductive current.
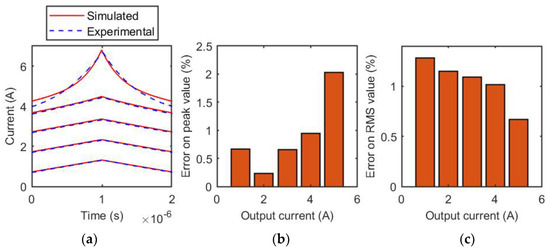
Figure 11.
Coilcraft MSS1260T-273 inductor, 32 V. (a) Comparison of experimental and simulated current waveforms for different output current values; (b) relative error of the estimation of the peak value of the inductive current; (c) relative error of the estimation of the RMS value of the inductive current.
3.2. SER1390-333 Inductor
The results obtained under the same operating conditions described in the previous section are reported for the other tested inductor. Figure 12, Figure 13 and Figure 14 show, for three switching frequency values (500 kHz, 750 kHz, and 1 MHz), the comparison between experimental and simulated current waveforms, and the relative error of the estimated RMS and peak value of the inductive current, while Figure 15 and Figure 16 represent the same results under different input voltages (12 and 32 V).
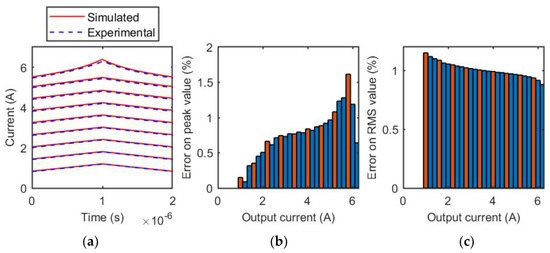
Figure 12.
Coilcraft SER1390-333 inductor, 500 kHz. (a) Comparison of experimental and simulated current waveforms for different output current values; (b) relative error of the estimation of the peak value of the inductive current for each tested output current value. The orange bars represent the test cases reported in (a), the blue bars are related to the other measurements of the evaluated current range; (c) relative error of the estimation of the RMS value of the inductive current for each tested output current value. The orange bars represent the test cases reported in (a), the blue bars are related to the other measurements of the evaluated current range.
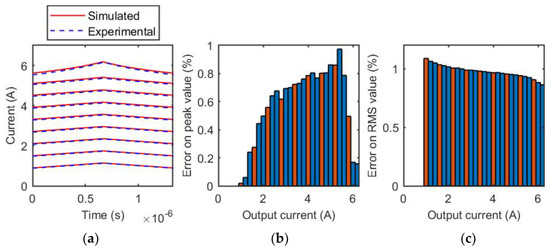
Figure 13.
Coilcraft SER1390-333 inductor, 750 kHz. (a) Comparison of experimental and simulated current waveforms for different output current values; (b) relative error of the estimation of the peak value of the inductive current for each tested output current value. The orange bars represent the test cases reported in (a), the blue bars are related to the other measurements of the evaluated current range; (c) relative error of the estimation of the RMS value of the inductive current for each tested output current value. The orange bars represent the test cases reported in (a), the blue bars are related to the other measurements of the evaluated current range.
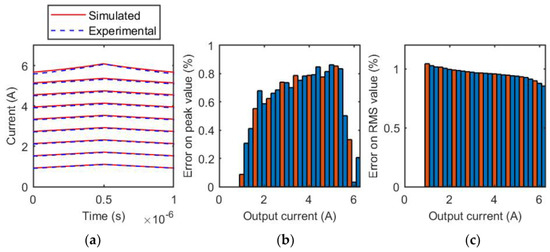
Figure 14.
Coilcraft SER1390-333 inductor, 1 MHz. (a) Comparison of experimental and simulated current waveforms for different output current values; (b) relative error of the estimation of the peak value of the inductive current for each tested output current value. The orange bars represent the test cases reported in (a), the blue bars are related to the other measurements of the evaluated current range; (c) relative error of the estimation of the RMS value of the inductive current for each tested output current value. The orange bars represent the test cases reported in (a), the blue bars are related to the other measurements of the evaluated current range.
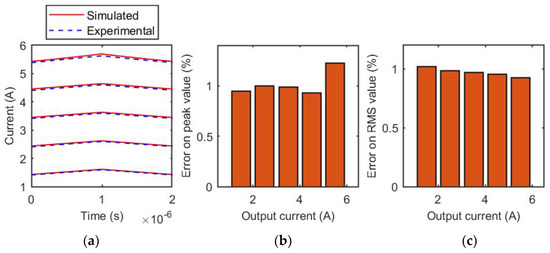
Figure 15.
Coilcraft SER1390-333 inductor, 12 V. (a) Comparison of experimental and simulated current waveforms for different output current values; (b) relative error of the estimation of the peak value of the inductive current for each tested output current value; (c) relative error of the estimation of the RMS value of the inductive current for each tested output current value.
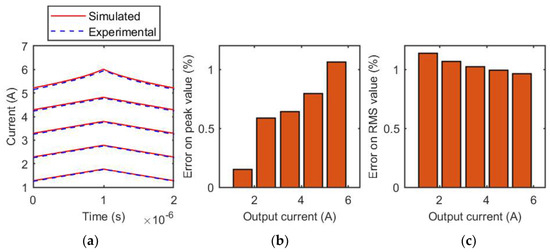
Figure 16.
Coilcraft SER1390-333 inductor, 32 V. (a) Comparison of experimental and simulated current waveforms for different output current values; (b) relative error of the estimation of the peak value of the inductive current for each tested output current value; (c) relative error of the estimation of the RMS value of the inductive current for each tested output current value.
4. Discussion
The following considerations apply to the adopted methodological approach. Several studies on the modeling of thermal effects in magnetic components were based on the development of mathematical models describing the equivalent thermal circuit of the inductor in order to evaluate losses and inductance variation as a function of temperature [24,25]. However, to obtain suitable modeling, detailed information is required on the geometry of the inductor, the characteristics of the realized winding, and the physical properties of the materials used. This information is not often available for commercial inductors. The proposed method, conversely, does not require any knowledge of the thermal model of the component, as it correlates the variation in the physical properties of the inductor only to the average operating current. The inductor identification was performed on experimental measurements of the inductor voltage and current waveforms, at different average current values, which led the component to operate at the steady-state temperature determined by the DC losses contributor. The obtained differential inductance profile is suitable for evaluating the current ripple of a saturable inductor in a DC–DC converter under a wide range of switching frequency, input voltage, and output current values.
The comparison of simulated and experimental current waveforms highlighted the effectiveness of the proposed differential inductance identification procedure under DC thermal steady-state conditions. The simulated waveforms well-matched the experimental measurements, and the error in the estimation of the peak and RMS value of the inductive current was always limited in the tested cases, never exceeding 3% under saturation conditions. Furthermore, for the Coilcraft SER1390-333 inductor, which is affected by a lower temperature variation as the average current increases, the error in the peak and RMS value estimation of the inductive current never exceeded 2% in the tested cases. The measurements were performed under different operating conditions to verify the procedure under several winding and core losses values. Different values of the main parameters affecting inductive losses, such as input voltage, average current, and switching frequency, were considered to extend the procedure’s effectiveness.
As further evidence of the accuracy of the performed characterization, in Figure 17, the measured and simulated waveforms for the Coilcraft MSS1260T-273 inductor are shown, highlighting the comparison for the three tested switching frequencies under two operating conditions: for average current values that led the component to operate in the linear region of the magnetic characteristic, and for values that instead led the inductor to operate in the saturation region. Even for high current ripple values, determined at the minimum switching frequency tested, the computation of the inductive current waveform does not significantly differ from the experimental measurements.
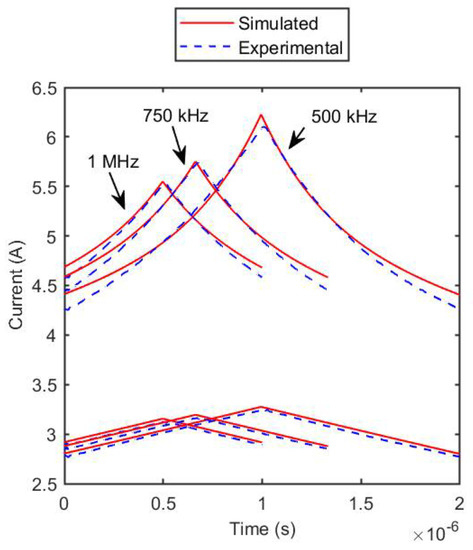
Figure 17.
Coilcraft MSS1260T-273 inductor. Comparison of experimental and simulated current waveforms for different output current values and different switching frequencies.
5. Conclusions
The presented characterization results highlight the critical role of DC winding losses in determining the temperature of an inductor for DC–DC converters operating in the weak saturation region. Temperature has a considerable influence on the magnetic properties of the core, affecting the permeability and therefore the differential inductance of the component. A differential inductance characteristic obtained at ambient temperature from a spot measurement would be insufficient to effectively describe the behavior of a saturable inductor under its real operating conditions. To overcome this gap, we presented a characterization approach for the differential inductance curve under the DC thermal steady-state conditions. The fundamental hypothesis of the described method is that the inductor under test operates in conditions where DC winding losses are the prevalent term of the inductive losses. Under this assumption, the obtained differential inductance curve proved to be suitable to evaluate the current ripple of a saturable inductor in a DC–DC converter under a wide range of switching frequency, input voltage, and output current values. The obtained current simulation results compared with the experimental waveforms showed the effectiveness of the proposed differential inductance identification under DC thermal steady-state conditions.
Author Contributions
Conceptualization, C.S.R.; investigation, L.S.; methodology, S.M., L.S., and C.S.R.; Software, L.S.; supervision, C.S.R.; writing—original draft, S.M., L.S., and C.S.R.; writing—review & editing, S.M., L.S., and C.S.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| ISAT | DC current at 25 °C that causes a 30% inductance drop from its value without current. Declared by the manufacturer. |
| vL,exp | Measured voltage across the inductor. |
| vL | Inductive component of the voltage across the inductor. |
| Rs | Winding resistance. |
| iL | Inductive current. |
| Φ | Magnetic flux. |
| L(iL) | Differential inductance. |
| LH | Upper horizontal asymptote of the differential inductance curve. |
| LL | Lower horizontal asymptote of the differential inductance curve. |
| I* | Abscissa of the inflection point of the differential inductance curve. |
| σ | Coefficient proportional to the slope of the curve in I*. |
| IL,max | Maximum value of the tested average current. |
| IL,min | Minimum value of the tested average current. |
| Lexp | Experimental differential inductance curve. |
| Lpar | Parametrised differential inductance curve. |
| fmin | Objective function of the optimization problem. |
References
- Trovão, J.P.; Pereirinha, P.G.; Ferreira, F.J.T.E.; Jorge, H.M. Study of inductor effects in a bidirectional DC-DC converter for electrical vehicle. In Proceedings of the XIX International Conference on Electrical Machines-ICEM 2010, Rome, Italy, 6–8 September 2010; pp. 1–6. [Google Scholar] [CrossRef]
- Safaee, A.; Bakhshai, A.; Jain, P. A resonant bidirectional dc-dc converter for aerospace applications. In Proceedings of the 2011 IEEE Energy Conversion Congress and Exposition, Phoenix, AZ, USA, 17–22 September 2011; pp. 3075–3079. [Google Scholar] [CrossRef]
- Bojoi, R.; Fusillo, F.; Raciti, A.; Musumeci, S.; Scrimizzi, F.; Rizzo, S. Full-Bridge DC-DC Power Converter for Telecom applications with Advanced Trench Gate MOSFETs. In Proceedings of the 2018 IEEE International Telecommunications Energy Conference (INTELEC), Turin, Italy, 7–11 October 2018; pp. 1–7. [Google Scholar] [CrossRef]
- IEC TC 51 Strategic Business Plan. Available online: https://assets.iec.ch/public/miscfiles/sbp/51.pdf (accessed on 25 March 2021).
- Kaiser, J.; Dürbaum, T. An Overview of Saturable Inductors: Applications to Power Supplies. IEEE Trans. Power Electron. 2021, 36, 10766–10775. [Google Scholar] [CrossRef]
- Milner, L.; Rincón-Mora, G.A. Small saturating inductors for more compact switching power supplies. IEEJ Trans. Electr. Electron. Eng. 2012, 7, 69–73. [Google Scholar] [CrossRef] [Green Version]
- Di Capua, G.; Femia, N.; Stoyka, K. Validation of inductors sustainable-saturation-operation in switching power supplies design. In Proceedings of the 2017 IEEE International Conference on Industrial Technology (ICIT), Toronto, ON, Canada, 22–25 March 2017; pp. 242–247. [Google Scholar] [CrossRef]
- Lodi, M.; Oliveri, A.; Storace, M. A low-cost online estimator for switch-mode power supplies with saturating ferrite-core inductors. In Proceedings of the 2019 26th IEEE International Conference on Electronics, Circuits and Systems (ICECS), Genoa, Italy, 27–29 November 2019; pp. 851–854. [Google Scholar] [CrossRef]
- Solimene, L.; Musumeci, S.; Ragusa, C. Saturable Ferrite Inductor Parameters Obtained Through a Double Step Optimization. In Proceedings of the 2020 55th International Universities Power Engineering Conference (UPEC), Turin, Italy, 1–4 September 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Di Capua, G.; Femia, N. A Novel Method to Predict the Real Operation of Ferrite Inductors With Moderate Saturation in Switching Power Supply Applications. IEEE Trans. Power Electron. 2016, 31, 2456–2464. [Google Scholar] [CrossRef]
- Stoyka, K.; Femia, N.; di Capua, G. Power Inductors Behavioral Modeling Revisited. IEEE Trans. Circuits Syst. I Regul. Pap. 2020, 67, 5636–5649. [Google Scholar] [CrossRef]
- Salas, R.A.; Pleite, J. Equivalent Electrical Model of a Ferrite Core Inductor Excited by a Square Waveform Including Saturation and Power Losses for Circuit Simulation. IEEE Trans. Magn. 2013, 49, 4257–4260. [Google Scholar] [CrossRef]
- Gurleyen, H.; Mese, E.; Kim, J.H.; Sarlioglu, B. Nonlinear analytical model of an inductance considering saturation and temperature variation. In Proceedings of the 2017 IEEE Energy Conversion Congress and Exposition (ECCE), Cincinnati, OH, USA, 1–5 October 2017; pp. 3150–3154. [Google Scholar] [CrossRef]
- Scirè, D.; Rosato, S.; Lullo, G.; Vitale, G. A Temperature Dependent Non-Linear Inductor Model for a DC/DC Boost Converter. In Proceedings of the 2018 15th International Conference on Synthesis, Modeling, Analysis and Simulation Methods and Applications to Circuit Design (SMACD), Prague, Czech Republic, 2–5 July 2018; pp. 237–239. [Google Scholar] [CrossRef]
- Oliveri, A.; di Capua, G.; Stoyka, K.; Lodi, M.; Storace, M.; Femia, N. A Power-Loss-Dependent Inductance Model for Ferrite-Core Power Inductors in Switch-Mode Power Supplies. IEEE Trans. Circuits Syst. I Regul. Pap. 2019, 66, 2394–2402. [Google Scholar] [CrossRef]
- MSS1260T Series High Temperature Power Inductors|Coilcraft’. Available online: https://www.coilcraft.com/ (accessed on 25 March 2021).
- ‘SER1390-333|Coilcraft’. Available online: https://www.coilcraft.com/ (accessed on 25 March 2021).
- Musumeci, S.; Solimene, L.; Ragusa, C.; Palma, M.; de la Barriere, O. Saturable Inductor Modelling in GaN FETs Based Synchronous Buck Converter. In Proceedings of the 2020 International Symposium on Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM), Sorrento, Italy, 24–26 June 2020; pp. 396–401. [Google Scholar] [CrossRef]
- ‘EPC90122–80 V, 40 A Development Board’. Available online: https://epc-co.com/epc/Products/DemoBoards/EPC90122.aspx (accessed on 25 March 2021).
- Solimene, L.; Ragusa, C.; Musumeci, S.; de la Barrière, O.; Fiorillo, F. Modeling of Saturable Inductors for Application in DC-DC Converters. In Proceedings of the 2019 26th IEEE International Conference on Electronics, Circuits and Systems (ICECS), Genoa, Italy, 27–29 November 2019; pp. 839–842. [Google Scholar] [CrossRef]
- Rosenbrock, H.H. An Automatic Method for Finding the Greatest or Least Value of a Function. Comput. J. 1960, 3, 175–184. [Google Scholar] [CrossRef] [Green Version]
- Ragusa, C.; Solimene, L.; Musumeci, S.; de la Barrière, O.; Fiorillo, F.; di Capua, G.; Femia, N. Computation of current waveform in ferrite power inductors for application in buck-type converters. J. Magn. Magn. Mater. 2020, 502, 166458. [Google Scholar] [CrossRef]
- Dlala, E.; Arkkio, A. Analysis of the Convergence of the Fixed-Point Method Used for Solving Nonlinear Rotational Magnetic Field Problems. IEEE Trans. Magn. 2008, 44, 473–478. [Google Scholar] [CrossRef]
- Hilal, A.; Raulet, M.A.; Martin, C. Magnetic Components Dynamic Modeling With Thermal Coupling for Circuit Simulators. IEEE Trans. Magn. 2014, 50, 1–4. [Google Scholar] [CrossRef] [Green Version]
- Wilson, P.R.; Ross, J.N.; Brown, A.D. Simulation of magnetic component models in electric circuits including dynamic thermal effects. IEEE Trans. Power Electron. 2002, 17, 55–65. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).