Abstract
The use of parallel applications in High-Performance Computing (HPC) demands high computing times and energy resources. Inadequate scheduling produces longer computing times which, in turn, increases energy consumption and monetary cost. Task scheduling is an NP-Hard problem; thus, several heuristics methods appear in the literature. The main approaches can be grouped into the following categories: fast heuristics, metaheuristics, and local search. Fast heuristics and metaheuristics are used when pre-scheduling times are short and long, respectively. The third is commonly used when pre-scheduling time is limited by CPU seconds or by objective function evaluations. This paper focuses on optimizing the scheduling of parallel applications, considering the energy consumption during the idle time while no tasks are executing. Additionally, we detail a comparative literature study of the performance of lexicographic variants with local searches adapted to be stochastic and aware of idle energy consumption.
1. Introduction
According to the website www.top500.org, accessed on 10 June 2021, in November 2018, the top rank of High-Performance Computing (HPC) system Summit from the Oak Ridge National Laboratory is composed of 2,397,824 CPU. This HPC consumes 9783 kW and achieves a performance of 14.668 GFlops/watt under testing conditions. The final energy consumption is directly related to the quality of the scheduling of the tasks in the HPC system. It is hard to imagine a single scheduling algorithm that solves every kind of task load, which relates to the no-free-lunch theorem [1,2]. Therefore, several scheduling methods have been developed in the literature; in our particular case, we review the approaches when HPC administrators have a restricted time to optimize the final scheduling. To this end, we use the local search approach, which fits for the above statement as in [3,4,5], where the stopping criterion is set to a small amount of fixed objective function evaluations or a small amount of time. Unlike constructive heuristics, which construct the solution, adding one decision variable at a time, or metaheuristics, which require thousands of objective function evaluations (a long-run) [6].
An HPC system is composed of a network of processing units as CPU cores or machines to provide high parallel computing power. These systems are, in most cases, heterogeneous in their processing capabilities and power consumption. To build HPC with significant computing capabilities is common to combine numerous processing units to the final system. However, adding more processing units or machines to the system increases energy consumption in every aspect of the HPC (network devices, ram, hard drives, etc.) [7,8,9]. From the general reader’s perspective, the HPC systems estimate that data centers (a particular case of HPC system focused on data storage) will consume 1/5 of earth’s energy consumption by 2025.
This work tackles the precedence-constraint task scheduling of parallel programs over HPC systems formed by heterogeneous machines, minimizing the energy consumption and makespan, both being NP-Hard [10,11]. We pay special attention to the case when machines are not computing any task, but still are powered on (idle time); in our study model of energy for dynamic voltage frequency scaling (DVFS) CPUs [12], we assume that machines consume a minimum fixed amount of energy while idle. Though the nature of this optimization problem is bi-objective, according to [13] the energy consumption during idle times has a strong effect on the energy consumption. Therefore, we present the first study on different stochastic lexicographic local searches for precedence-constraint task scheduling of parallel programs to our knowledge, giving priority to the makespan (tasks computing time) to reduce idle times in machines.
The paper organization is: Section 2 details our studied problem in heterogeneous systems. Section 3 describes the list scheduling principle. A review of the literature on scheduling using local searches appears in Section 4. The experimental settings and our stochastic lexicographic local search variants are presented in Section 5 and Section 6, respectively. Section 7 analyzes the experimental results according to the makespan and energy objectives. Finally, Section 9 contains the conclusions and future work in local search and scheduling precedence-constraint tasks on heterogeneous systems.
2. Problem Description
The HPC system studied in this work, consist of a set of heterogeneous processing units M completely interconnected. Each processing unit is DVFS capable. Thus, every machine operates on a set of multiple voltages. When the voltage is lower than the maximum, machines operate at a fraction of their top speed , the cardinality of the set S of relative speeds is equal to the cardinality of the set V of possible voltages inside the machine. The next table shows the set of voltage configurations with their respective relative speed used in our experimentation.
Every machine has assigned a DVFS configuration from Table 1. For instances with more than three machines, the remaining use of these configurations are assigned in order, first the number zero, followed by the number one, and so on, in a circular structure. Without loss of generality, we consider the assumptions presented in [14,15,16,17,18,19], and the following:

Table 1.
Machine settings.
- When a machine is not executing any task (idle time), it uses the lowest voltage possible.
2.1. Instances
An instance of the scheduling problem is composed of: (i) directed acyclic graph (DAG), and (ii) the computation time of the tasks in every . The set of tasks of the parallel program with their precedencies is a DAG. Thus, the program is represented as , where T is the set of tasks and C is the set of communication costs (see Figure 1). A complete instance is formed by G and the computational times of each task in every processing unit at maximum capacity, when (see Table 2).
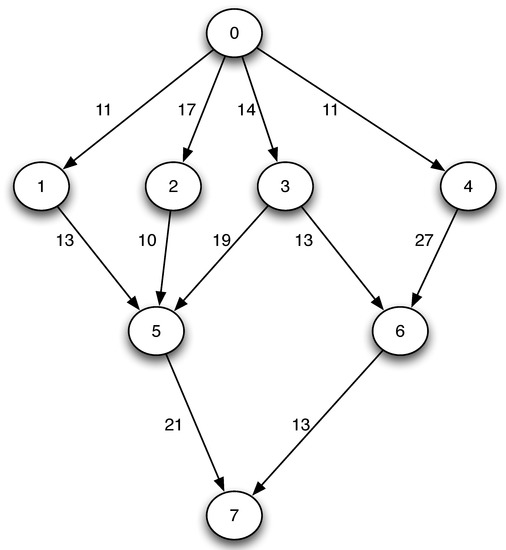
Figure 1.
Precedence tasks graph .

Table 2.
Computational times of the tasks at maximum capacity .
Each task cannot be initiated until all their precedence tasks and communication have been finalized. For any pair of tasks executed in the same , their communication cost is equal to zero.
2.2. Solution Representation
Our solution representation consists of two data structures. The first data structure is a matrix of size 2xn (see Table 3). n is the cardinality of T, the first row of the matrix stores the assigned processing unit, while the second stores the value of the k selected energy configuration. The machine configuration map to their respective voltage and relative speed from Table 1.

Table 3.
Configuration machine/voltage.
The second data structure is an array of size n with the priority execution order of the tasks (see Table 4). The execution order is a topological order from the task graph without violated precedence constraints.

Table 4.
Tasks order of execution.
The second data structure is not indispensable for scheduling but simplifies the problem’s search space because it does not necessarily verify the earliest start and finish tasks’ times to compute the makespan. However, this representation has the deficiency that the optimal value of execution time, also known as optimal makespan, may not be in the particular given execution order.
With the representation mentioned above, we detail the objective function to compute the makespan in Algorithm 1 to compute the makespan of complexity , similar as in [18,20,21]. The computation times of the tasks are calculated as the original computation time at maximum voltage divided by their relative speed in Table 1. We show the consider computation times on the following Table.
Using the computation times from Table 5 and a counter time in each machine for the last executed task in the machine when it finishes its execution . Algorithm 1 defines the objective function called makespan.

Table 5.
Computation times of the tasks with relative speed .
The function uses the variables: (the starting time of task i), (the finish time of task j), the communication cost between and , which is equal to zero in the case the tasks are executed in the same machine. The function is computed in sequence from the first task of the feasible execution order to the last one in the list. Finally, the parallel program makespan is the maximum completion time between the set of tasks.
| Algorithm 1 Makespan objective function |
|
For the energy consumption objective is not necessary the DAG representation, only to know the final makespan. The energy consumption of the tasks is the square power of the selected voltage multiplied by the task completion time in the machine , to add the machines respective idle energy consumption, it is necessary to compute the machine time during idle, which is equal to the makespan subtracting the tasks computation times. Algorithm 2 shows the pseudocode to compute the energy objective. The energy model derives from the complementary metal-oxide-semiconductor (CMOS) circuits in Equation (1). Where capacitive power is computed with the number switches per clock cycle A, the total capacitance load , the supply voltage V, and the frequency f.
The Equation (2) is our energy model consumption . Which is simplified version grouping the constants A, and f in a single constant K. For practical purposes, the constant K is equal to one in the computed results. Finally, represents the computing task time.
| Algorithm 2 Energy objective function |
|
3. List Scheduling Algorithms
Algorithm 3 shows the pseudocode of the general framework for list scheduling algorithms.
| Algorithm 3 List scheduling framework |
|
In the list scheduling principle, tasks are assigned according to priorities and placed in an ordered decreasing list. First, the tasks are sequenced to be scheduled in accordance with the DAG, respecting their precedences regarding a topological order. Then, each task of the list is assigned successively to a machine. Usually, the machine yields the minimum makespan.
Local Searches Related to the List Scheduling Framework
In [22,23] Arabnejad surveyed the most relevant algorithms using the framework for list scheduling in the literature. Among the most popular is the heterogeneous earliest finish time (HEFT) [24], a deterministic reference algorithm in many studies. It assigns to every task the machine, which allows its most immediate finish time. However, HEFT can modify the task’s priority order when detecting available idle time on a machine without precedence-constraint violation. It is out of the scope of the present study to modify the priority order of the tasks. In this paper, we assume the given priority of the tasks is fix. The above makes our objective function in Algorithm 1 feasible in all our studied cases. Recently, several papers regarding energy optimization have used the DVFS technique in several contexts, mathematical programming [25], metaheuristics [26,27,28], heuristics [29,30,31,32,33,34,35,36,37], parallel algorithms [38], among others. However, mainly constructive heuristic methods appear in the literature to schedule tasks in heterogeneous machines. Our perspective is that it could be because of the heavy computational cost of the objective function when no fixed task order execution is given (priority modification as in HEFT). Using the objective function described in Algorithm 1 the complexity is reduced to in the worst-case when every task has an equal number of precedences. However, the real complexity is considerably lower because DAGs do not have cycles.
Local searches are heuristic approximation methods that move a current solution to its nearest local optima solution. However, local searches cannot escape local optima as other more advanced approximation methods as metaheuristics.
Inside the machine tasks scheduling literature, local search is generally a part of a metaheuristic method; for example, we found: iterated local search [39,40,41,42,43], particle swarm optimization [44,45], ant colony optimization [46,47,48], memetic algorithm [49,50,51,52,53], GRASP [18], and variable neighborhood search [54], among others. In the previous examples, local search plays a crucial role in their performances, so we can infer a straightforward improvement is through new local search designs and studies to enlighten ways of improving the final performance of these methods.
Some studies investigate the use of isolating local search improvements; we found examples in [6,13,55,56]. To produce a complete experimental study, we choose to compare and adapt the more relevant ones from the above-mentioned local search works. To be lexicographic and stochastic.
4. Literature Review
In this section, we describe three relevant local search works in the state-of-the-art. A deterministic local search using an aggregation objective function to minimize the makespan and energy [19]. Two stochastic local searches using the best improvement pivot method with lexicographic importance of the objectives [13]. A stochastic local search using two neighborhood operators [6]. The selected works represent the broad ideas on the state-of-the-art scheduling precedence-tasks using local searches.
4.1. Energy Conscious Scheduling (ECS)
The energy conscious scheduling () is a heuristic using a special objective function formulation called relative superiority (RS) [19]; it consists of two phases. The first phase optimizes RS’s value in a given topological order ( used in the original paper) the possible machines with their respective voltages. The second phase uses the makespan-conservative energy reduction (MCER) technique [19], which visits the tasks in the same topological order. Which is considering the energy consumption in idle times, the variant is called , the one used for the experimental comparison. The RS computation for is shown in Equation (3).
In the original paper, the RS computation for is a little bit different. The negative sign of the case when its outside the entire equation, this has been corrected in Equation (3) to compute the correct results.
The Algorithm 4 shows the pseudocode for the heuristic. At the constructive first phase the objective functions are partially evaluated until the current evaluated task , for makespan, and for energy. At the MCER second phase, the objective functions evaluate the complete scheduling and visit neighbor solutions with different machine and voltage configurations. Neighbor solutions that do not increase the makespan and improve energy consumption become the current schedule.
4.2. Random Problem Aware Local Search (rPALS)
rPALS [6] is a stochastic local search for makespan minimization on heterogeneous machines. It is a stochastic version of the deterministic local search PALS [57] for DNA fragment assembly. rPALS achieves the best performance against other list-based heuristics, namely: sufferage, min–min, and p-CHC. rPALS uses two neighborhood operators and , similar to the principle of the variable neighborhood search (VNS) [58], without the stop criterion of finding a local optimal.
The Algorithm 5 shows the pseudocode for the rPALS local search. It starts with an initial constructed by the minimum completion time (MCT) heuristic [59]. Considering the tasks in any order, MCT assigns each task to the processing unit, which minimizes the finish time of the task.
Main loop iterates until it reach a maximum number of steps ; at each iteration, a machine and a neighborhood between and are select randomly.
In the case where the operator is selected, it starts a loop selecting a random task from the ones assigned to , and a random machine until is reached. Then a second inner loop iterates selecting random tasks assigned to for swapping with and , if the neighbor solution improves the overall makespan, it is assigned at the current best solution .
In the case the operator is selected it starts a loop, selecting a random machine until the stop condition is reached. This loop iterates selecting a random task assigned to , producing a neighbor solution by assigning the task to the machine . If the neighbor solution improves the makespan, the solution is assigned as the current best solution .
| Algorithm 4 |
|
| Algorithm 5 rPALS |
|
4.3. BEST_RT_MVk and BEST_RMVk_T
Our last consideration is of work from the literature is [13], where the authors propose two best improvement stochastic local searches: BEST_RT_MVk and BEST_RMVk_T. Both local search methods start with a solution constructed by the fast heuristic HEFT [24]. The main difference between the proposed local search methods is in their stochastic selections.
BEST_RT_MVk randomly selects a task to be evaluated within all the possible machines and voltages configurations. Although BEST_RMVk_T randomly selects a machine and voltage configurations to be considered within all the possible tasks. The Algorithms 6 and 7 shows the pseudocode for BEST_RT_MVk and BEST_RMVk_T, respectively.
The original methods in [13] are stochastic local searches (SLS) for makespan and energy optimization. However, every time the methods found a local improvement, the algorithm restarts the stop condition. The above could produce significant computation times when the algorithm does not search a local optimum, an issue presented in our preliminary experimentations.
| Algorithm 6 BEST_RT_MVk |
|
| Algorithm 7 BEST_RMVk_T |
|
5. Algorithms in Comparison
In the experimental comparison, two mandatory restrictions must be satisfied:
- The use of a fixed maximum number of neighbor solutions visited;
- Providing only one random initial solution.
The algorithms in Section 4 are adjusting in the following manner.
5.1. Stochastic Local Search
The original proposed is a deterministic heuristic. To investigate its effects as a stochastic lexicographic local improvement method, we proposed two new stochastic local search (SLS) using the RS objective function in Equation (3). We follow the best improvement pivot rule in [13], and the two SLS variants in the paper: random selection of task (ECS_RT_MVk) and random selection of machine and voltage (ECS_RMVk_T).
Algorithm 8 shows the procedure for the SLS ECS_RT_MVk. The function’s input is a feasible , the search select a random task to be evaluated in all the possible machines in M with their respective voltage configurations if the stopping condition has not been reached. The task is assigned to the best machine and voltage according to the RS objective function. The main loop iterates over random tasks until the counter reaches the maximum number of visited neighbors .
| Algorithm 8 random |
|
Algorithm 9 shows the procedure for the SLS ECS_RMVk_T. The function’s input is a feasible , the search select a random machine with a feasible random voltage inside the range of the machine to be evaluated in all the possible tasks in T if the stopping condition has not been reaching. The task is assigned to the best machine and voltage according to the RS objective function. The main loop iterates over random tasks until the counter reaches the maximum number of visited neighbor solutions .
5.2. rPALS Lexicographic Local Search
The original rPALS was proposed only for the improvement of the final makespan. To improve both objectives (energy and makespan), we follow the same lexicographic criteria to accept variable changes in the solutions as in [13]. If the makespan is not worsening and there is an energy improvement, the neighbor solution becomes the current best . The inner loops from rPALS are removing to control the visit neighbors. The following pseudocode shows the procedure for our proposed LS rPALS Lexicographic Algorithm 10 (rPALS_Lex).
| Algorithm 9 random |
|
| Algorithm 10 rPALS Lexicographic |
|
5.3. Fixed iterations BEST_RT_MVk and BEST_RMVk_T
For a fair experimental comparison, the commented lines in Algorithms 6 and 7 with the legend Line removed for the experimental comparison are not considered. Therefore the LSs are not initialized with the HEFT heuristic and visits the same number of neighbor solutions, fixed by their main loops stop criterion ().
5.4. Table of Notations Used in the Described Literature
The Table 6 shows the common mathematical notations in the mentioned literature.

Table 6.
Notation used in the described literature.
6. Experimental Setup
The reviewed works from Section 4 differ in their stop criteria. In the original publication of BEST_RMVk_T and BEST_RT_MVk, the maximum number of neighbor solutions visited is variable, a maximum of 100 continuous neighbor visited without improvements. In the work of rPALS, the maximum number of visited neighbors is 4,000,000. Although, in the deterministic search, the number is .
On the one hand, few visited neighbors could increase the variance at the final computed results. On the other hand, a high number of visited neighbors increase computational times. We suggest a reasonable fixed number of visited neighbors; we use the ratio between the maximum number of visited neighbors in [6] and the maximum number of visited neighbors without improvement in [13]. Giving a total number of maximum visited neighbors of = 40,000.
The set of machine and voltage configurations used for the experimentation has a cardinality of six, the ones in [13]. When a particular scheduling problem considers more than six machines, the first configuration is assigned to the next machine, later the second, and so on (round-robin rule) until every considered machine has a valid configuration. Finally, we perform 60 independent executions for every considered scheduling problem.
6.1. Parallel Instance Set
The applications in the experimental set are:
- Fpppp [60];
- LIGO [61];
- Robot [62];
- Sparse [62].
We used the set of instances from [18], consisting of 400 different scheduling problems.
6.2. Friedman Statistical Test
In order to assess the performance of this algorithms it is necessary to validate their outcomes through a statistical test. There are specific statistical tests for comparing two samples and others for more than two samples. A widely accepted statistical test to find significant differences between more than two samples is the analysis of variance (ANOVA) test. However, to use ANOVA it is mandatory that the data follow a normal distribution. There are other statistical tests that do not need to follow such an assumption, they are non-parametric tests. Among those tests, Friedman [63] is a non-parametric test used to compare the performance of several algorithms’ performance. The Friedman statistical test is computed using the following equation when no ties:
Where the number of independent executions is n, the number of algorithms is k, and the rank of each i algorithm is . Once the statistical is computed, a reference table is consulted for the achieved p-value [63]. A direct performance evaluation metric in many algorithms’ studies is the Friedman rankings [64] (). The original data of the independent executions is transformed into a table of places (ranks) according to the performance of each algorithm (see Table 7).

Table 7.
Example of ranks for three algorithms.
With Table 7, the Friedman ranking for the Algorithm 1 is compute as the sum of their ranks: , . The presented ranks in this work are in terms of the average of makespan and energy consumption. For our computational example, . This technique is a straightforward way to compare the performance of several algorithms over benchmarks. Using the tool in [65] the process is as simple as input the original data in CSV format, using the command line java Friedman data.csv > output.tex, the output.tex file has to be compiled with a compiler for  .
.
 .
.6.3. Task Priority Methods
We evaluate two widely used methods to generate a priority task list in our experimentation: the bottom level (b-level), and the top-level (t-level).
The b-level computes the critical path in the DAG from a current task node to the final task in the parallel program , taking into consideration the mean of the computing times in the machines (See Table 8) and the communication costs (edges of the DAG in Figure 1).

Table 8.
Mean values of the tasks computing times.
For the DAG in Figure 1 the b-level values of the tasks are shown in Table 9. The tasks’ priority is according to their b-level values in descending order. In a very similar manner, the algorithm calculates the t-level, finding a path from an actual task node to the initial task in the parallel program (See Table 10). The assigned priorities are according to their t-level values in ascending order.

Table 9.
b-level values for the DAG in Figure 1.

Table 10.
t-level values for the DAG in Figure 1.
The computation of the b-level and t-level needs to verify every possible path in the DAG; a straightforward way to do it is to use recursive functions as shown in the Algorithms 11 and 12.
| Algorithm 11 b-level recursive function |
|
| Algorithm 12 t-level recursive function |
|
7. Results
This section analyzes the computed results with the experimental settings in Section 6. Due to the considerable number of tables needed to present results, we decide not to include them in the final paper.
A more acceptable and brief way to examine the results is to produce Friedman’s average rankings [64] from the non-parametric Friedman statistical test (see Section 6.2). The ranking gives an insight into the algorithm’s performance (the lower the ranking, the better). We compute the Friedman ranking using a free tool presented in [65]; the website has extensive information on the Friedman test and rankings.
We found at every presented comparison in this work that there is a statistical difference after analyzing all the computed p-values by the Friedman statistical test, which satisfies the condition p-value , giving a statistical significance of 95% [63]. In the following subsections, we present the results by goal objective.
7.1. Makespan Results
First, we start by analyzing the computed results according to the makespan objective. Table 11 shows the Friedman ranking when considering the whole scheduling cases and the b-level priority execution.

Table 11.
Makespan Friedman ranking on the 400 scheduling problems (b-level).
Table 11 shows that ECS_RMVk_T gets the best performance when using the b-level priority execution while rPALS_Lex is the second best. Notice that both Local Searches, when selecting a random task to verify their machine and voltage possible configurations (ECS_RT_MVk, BEST_RT_MVk), perform the worst. The same algorithms produce low performance when using the t-level priority, as shown in the ranking from Table 12. However, in this case, rPALS_Lex obtains the best performance, followed by BEST_RMVk_T.

Table 12.
Makespan Friedman ranking on the 400 scheduling problems (t-level).
We infer from the results from Table 11 and Table 12 that the worst strategy for makespan optimization is when local searches evaluate from a random task their best neighbor among all their possible machine and voltage configurations. To give more insight into the results, we compute the Friedman average ranking on the individual subsets of instances: Fpppp, LIGO, Robot, and Sparse. The bests rankings in the table are highlighting in gray.
The Friedman rankings in Table 13 confirms the reports from Table 11, regarding the use of b-level, the worst performance is for the ECS_RT_MVk and BEST_RT_MVk local searches. ECS-RMVk-T achieves the best performance with three best average rankings (Fpppp, LIGO, Sparse) and one second-best (Robot). A highly competitive local search when using b-level priority is rPALS-Lex with three second-best average rankings (Fpppp, LIGO, Sparse) and one best (Robot). Considering only the Robot subset of instances, the local search BEST-RMVk-T achieves the best makespan average ranking.

Table 13.
Makespan Friedman rankings (b-level).
The results in Table 14 also confirms the results from Table 12, according to the use of t-level, rPALS-Lex achieves the best performance with three best average rankings (Fpppp, LIGO, Sparse) and one second-best (Robot) followed by BEST-RMVk-T with one best average ranking (Robot) and three second-best (Fpppp, LIGO, Sparse). In contrast, the worst performance is the b-level case with ECS_RT_MVk and BEST_RT_MVk.

Table 14.
Makespan Friedman rankings (t-level).
7.2. Energy Results
In the case of the energy objective, the order of the rankings of the algorithms when using b-level (See Table 15) and t-level (See Table 16) is the same.

Table 15.
Energy Friedman ranking on the 400 scheduling problems (b-level).

Table 16.
Energy Friedman ranking on the 400 scheduling problems (t-level).
As in the makespan results section, the worst achieved performance was obtained by ECS_RT_MVk and BEST_RT_MVk. For energy optimization, the best achievable performance is by rPALS_Lex followed by BEST_RMVk_T with an equal number of best and second-best rankings in Table 17 and Table 18.

Table 17.
Energy Friedman rankings (b-level).

Table 18.
Energy Friedman rankings (t-level).
8. Research Findings
A relevant result emerges from our empirical experimentation, the priority order technique in list scheduling may significantly change the performance of some algorithms, according to the makespan objective. The above is the particular case of the ECS function, which changes from first place (ECS_RMVk_T) in the b-level priority results to third place in the t-level results. A deeper examination of the ECS function in Equation (3) shows that if the energy consumption magnitude is significantly greater than the makespan magnitude, it will emphasize the energy objective over the makespan. According to the energy objective, different priorities for the tasks do not change the comparative performance of the algorithms, for the Friedman ranking remaining the same for the algorithms. Therefore, we infer that energy optimization is more sensitive to the DVFS configurations than the tasks’ order of execution.
9. Conclusions and Future Work
As far as we know, we present the first study of stochastic lexicographic local searches for precedence-constraint task scheduling on heterogeneous machines. We adapt three local searches from the literature to be stochastic, iterative, and lexicographic bi-objective (makespan and energy). The above produces three new variants: ECS_RMVk_T, ECS_RT_MVk, and rPALS_Lex. The experimental results show rPALS_Lex as the most competitive algorithm for makespan and energy optimization compared with the other local searches in the experimentation.
The relative superiority objective function from the ECS heuristic works slightly better when using the b-level priority of execution in the tasks, denoted by ECS_RMKV_T best performance achieved in makespan.
The worst strategy for the studied local searches is when an individual random task is selected to verify their possible machine and voltage configurations. Therefore, we recommend the approach when a random machine and voltage configuration is selected and verifies for improvements over the whole set of tasks.
Finally, as the experimental comparison shows, the task’s execution order is essential for the final performance of the algorithms, with radical place changes in the Friedman rankings when using the b-level and t-level priority.
As future work, we would like to study the design of new priority task heuristics, which could improve the performance of the proposed local searches for scheduling.
Author Contributions
Conceptualization, formal analysis, investigation, methodology, resources, software, supervision, validation, writing—original draft, writing—review and editing, A.S. and J.D.T.-V.; data curation, project administration, software, validation, writing–original draft, and writing–review and editing, M.P.-F. and F.B.; funding acquisition, project administration, visualization, S.I.M.; writing—review and editing, J.A.C.R., J.L.M., and M.G.T.B. All authors have read and agreed to the published version of the manuscript.
Funding
Alejandro Santiago would like to thank the CONACyT Mexico SNI for the salary award under the record 83525. The APC was funded by the Universidad Autónoma de Tamaulipas.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The benchmark instances for this study are available at https://github.com/AASantiago/SchedulingInstances, accessed on 10 June 2021.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Wolpert, D.H.; Macready, W.G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef]
- Igel, C.; Toussaint, M. A No-Free-Lunch theorem for non-uniform distributions of target functions. J. Math. Model. Algorithms 2005, 3, 313–322. [Google Scholar] [CrossRef]
- Muñoz, A.D.; Fernandez, J.J.P.; Carrillo, M.G. Metaheurísticas; Editorial Dykinson, S.L., Ed.; Ciencias Experimentales y Tecnología: Madrid, Spain, 2007. [Google Scholar]
- Hoos, H.H.; Stützle, T. Stochastic Local Search: Foundations and Applications; Elsevier: Amsterdam, The Netherlands, 2004. [Google Scholar]
- Aarts, E.; Aarts, E.H.; Lenstra, J.K. Local Search in Combinatorial Optimization; Princeton University Press: Princeton, NJ, USA, 2003. [Google Scholar]
- Nesmachnow, S.; Luna, F.; Alba, E. An Efficient Stochastic Local Search for Heterogeneous Computing Scheduling. In Proceedings of the 2012 IEEE 26th International Parallel and Distributed Processing Symposium Workshops PhD Forum, Shanghai, China, 21–25 May 2012; pp. 593–600. [Google Scholar] [CrossRef]
- Soto-Monterrubio, J.C.; Fraire-Huacuja, H.J.; Frausto-Solís, J.; Cruz-Reyes, L.; Pazos, R.R.; Javier González-Barbosa, J. TwoPILP: An Integer Programming Method for HCSP in Parallel Computing Centers. In Advances in Artificial Intelligence and Its Applications; Pichardo Lagunas, O., Herrera Alcántara, O., Arroyo Figueroa, G., Eds.; Springer International Publishing: Cham, Swizerland, 2015; pp. 463–474. [Google Scholar]
- Soto-Monterrubio, J.C.; Santiago, A.; Fraire-Huacuja, H.; Frausto-Solís, J.; Terán-Villanueva, D. Branch and Bound Algorithm for the Heterogeneous Computing Scheduling Multi-Objective Problem. Int. J. Comb. Optim. Probl. Inform. 2016, 7, 7–19. [Google Scholar]
- Monterrubio, J.C.S.; Huacuja, H.J.F.; Alejandro, A.; Pineda, S. Comparativa de tres cruzas y cuatro mutaciones para el problema de asignación de tareas en sistemas de cómputo heterogéneo. In Proceedings of the VIII Encuentro de investigadores en el Instituto Tecnológico de Ciudad Madero, Ciudad Madero, Mexico, November 2012; pp. 1–6. [Google Scholar]
- Sinnen, O. Task Scheduling for Parallel Systems (Wiley Series on Parallel and Distributed Computing); Wiley-Interscience: New York, NY, USA, 2007. [Google Scholar]
- Andrei, A.; Eles, P.; Peng, Z.; Schmitz, M.; Al-Hashimi, B.M. Voltage Selection for Time-Constrained Multiprocessor Systems. In Designing Embedded Processors: A Low Power Perspective; Springer: Dordrecht, The Netherlands, 2007; Chapter 12; pp. 259–284. [Google Scholar] [CrossRef]
- Wang, L.; von Laszewski, G.; Dayal, J.; Wang, F. Towards Energy Aware Scheduling for Precedence Constrained Parallel Tasks in a Cluster with DVFS. In Proceedings of the 2010 10th IEEE/ACM International Conference on Cluster, Cloud and Grid Computing, Melbourne, Australia, 17–20 May 2010; pp. 368–377. [Google Scholar] [CrossRef]
- Pecero, J.E.; Huacuja, H.J.F.; Bouvry, P.; Pineda, A.A.S.; Locés, M.C.L.; Barbosa, J.J.G. On the energy optimization for precedence constrained applications using local search algorithms. In Proceedings of the 2012 International Conference on High Performance Computing Simulation (HPCS), Madrid, Spain, 2–6 July 2012; pp. 133–139. [Google Scholar] [CrossRef]
- Pineda, A.A.S. Estrategias de Búsqueda Local para el Problema de Programación de Tareas en Sistemas de Procesamiento Paralelo. Master’s Thesis, Instituto Tecnológico de Ciudad Madero, Cd Madero, Mexico, 2013. [Google Scholar]
- Guzek, M.; Pecero, J.E.; Dorronsoro, B.; Bouvry, P. Multi-objective evolutionary algorithms for energy-aware scheduling on distributed computing systems. Appl. Soft Comput. 2014, 24, 432–446. [Google Scholar] [CrossRef]
- Lee, Y.C.; Zomaya, A.Y. On Effective Slack Reclamation in Task Scheduling for Energy Reduction. JIPS 2009, 5, 175–186. [Google Scholar] [CrossRef]
- Che, J.-J.; Yang, C.-Y.; Kuo, T.-W. Slack reclamation for real-time task scheduling over dynamic voltage scaling multiprocessors. In Proceedings of the IEEE International Conference on Sensor Networks, Ubiquitous, and Trustworthy Computing (SUTC’06), Taichung, Taiwan, 5–7 June 2006; Volume 1, p. 8. [Google Scholar] [CrossRef]
- Santiago, A.; Terán-Villanueva, J.D.; Martínez, S.I.; Rocha, J.A.C.; Menchaca, J.L.; Berrones, M.G.T.; Ponce-Flores, M. GRASP and Iterated Local Search-Based Cellular Processing algorithm for Precedence-Constraint Task List Scheduling on Heterogeneous Systems. Appl. Sci. 2020, 10, 7500. [Google Scholar] [CrossRef]
- Lee, Y.C.; Zomaya, A.Y. Energy Conscious Scheduling for Distributed Computing Systems under Different Operating Conditions. IEEE Trans. Parallel Distrib. Syst. 2011, 22, 1374–1381. [Google Scholar] [CrossRef]
- Soto, C.; Santiago, A.; Fraire, H.; Dorronsoro, B. Optimal Scheduling for Precedence-Constrained Applications on Heterogeneous Machines. In Proceedings of the MOL2NET 2018, International Conference on Multidisciplinary Sciences, 4th ed.; p. 5. Available online: https://mol2net-04.sciforum.net/ (accessed on 10 June 2021).
- Pineda, A.A.S.; Ángel Ramiro Zúñiga, M. Algoritmos exactos de calendarización de tareas para programas paralelos en sistemas de procesamiento heterogéneos. In VI Encuentro de Investigadores en el Instituto Tecnológico de Ciudad Madero; Ciudad Madero, Mexico, 2012; p. 8. Available online: https://www.researchgate.net/publication/327979984_Algoritmos_exactos_de_calendarizacion_de_tareas_para_programas_paralelos_en_sistemas_de_procesamiento_heterogeneos (accessed on 1 June 2021).
- Arabnejad, H. List based task scheduling algorithms on heterogeneous systems—An overview. In Doctoral Symposium in Informatics Engineering; 2013; p. 93. Available online: https://paginas.fe.up.pt/~prodei/dsie13/ (accessed on 10 June 2021).
- Arabnejad, H.; Barbosa, J.G. List Scheduling Algorithm for Heterogeneous Systems by an Optimistic Cost Table. IEEE Trans. Parallel Distrib. Syst. 2014, 25, 682–694. [Google Scholar] [CrossRef]
- Topcuoglu, H.; Hariri, S.; Wu, M.Y. Performance-effective and low-complexity task scheduling for heterogeneous computing. IEEE Trans. Parallel Distrib. Syst. 2002, 13, 260–274. [Google Scholar] [CrossRef]
- Hu, B.; Cao, Z.; Zhou, M. Energy-Minimized Scheduling of Real-Time Parallel Workflows on Heterogeneous Distributed Computing Systems. IEEE Trans. Serv. Comput. 2021, 1. [Google Scholar] [CrossRef]
- Deng, Z.; Cao, D.; Shen, H.; Yan, Z.; Huang, H. Reliability-aware task scheduling for energy efficiency on heterogeneous multiprocessor systems. J. Supercomput. 2021. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Mohamed, R.; Abouhawwash, M.; Chakrabortty, R.K.; Ryan, M.J. EA-MSCA: An effective energy-aware multi-objective modified sine-cosine algorithm for real-time task scheduling in multiprocessor systems: Methods and analysis. Expert Syst. Appl. 2021, 173, 114699. [Google Scholar] [CrossRef]
- Hosseinioun, P.; Kheirabadi, M.; Kamel Tabbakh, S.R.; Ghaemi, R. A new energy-aware tasks scheduling approach in fog computing using hybrid meta-heuristic algorithm. J. Parallel Distrib. Comput. 2020, 143, 88–96. [Google Scholar] [CrossRef]
- Huang, J.; Li, R.; An, J.; Zeng, H.; Chang, W. A DVFS-Weakly-Dependent Energy-Efficient Scheduling Approach for Deadline-Constrained Parallel Applications on Heterogeneous Systems. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 2021. [Google Scholar] [CrossRef]
- Hussain, M.; Wei, L.F.; Lakhan, A.; Wali, S.; Ali, S.; Hussain, A. Energy and performance-efficient task scheduling in heterogeneous virtualized cloud computing. Sustain. Comput. Inform. Syst. 2021, 30, 100517. [Google Scholar] [CrossRef]
- Kumar, N.; Vidyarthi, D.P. A novel energy-efficient scheduling model for multi-core systems. Clust. Comput. 2021, 24, 643–666. [Google Scholar] [CrossRef]
- Ahmad, W.; Alam, B.; Atman, A. An energy-efficient big data workflow scheduling algorithm under budget constraints for heterogeneous cloud environment. J. Supercomput. 2021. [Google Scholar] [CrossRef]
- Moulik, S.; Das, Z.; Devaraj, R.; Chakraborty, S. SEAMERS: A Semi-partitioned Energy-Aware scheduler for heterogeneous MulticorE Real-time Systems. J. Syst. Archit. 2021, 114, 101953. [Google Scholar] [CrossRef]
- Maurya, A.K.; Modi, K.; Kumar, V.; Naik, N.S.; Tripathi, A.K. Energy-aware scheduling using slack reclamation for cluster systems. Clust. Comput. 2020, 23, 911–923. [Google Scholar] [CrossRef]
- Hassan, H.A.; Salem, S.A.; Saad, E.M. A smart energy and reliability aware scheduling algorithm for workflow execution in DVFS-enabled cloud environment. Future Gener. Comput. Syst. 2020, 112, 431–448. [Google Scholar] [CrossRef]
- Kumar, M.; Kaur, L.; Singh, J. Dynamic and Static Energy Efficient Scheduling of Task Graphs on Multiprocessors: A Heuristic. IEEE Access 2020, 8, 176351–176362. [Google Scholar] [CrossRef]
- Hu, Y.; Li, J.; He, L. A reformed task scheduling algorithm for heterogeneous distributed systems with energy consumption constraints. Neural Comput. Appl. 2020, 32, 5681–5693. [Google Scholar] [CrossRef]
- Xie, G.; Xiao, X.; Peng, H.; Li, R.; Li, K. A Survey of Low-Energy Parallel Scheduling Algorithms. IEEE Trans. Sustain. Comput. 2021, 1. [Google Scholar] [CrossRef]
- Pineda, A.A.S.; Pecero, J.; Huacuja, H.; Barbosa, J.; Bouvry, P. An iterative local search algorithm for scheduling precedence-constrained applications on heterogeneous machines. In Proceedings of the 6th Multidisciplinary International Conference on Scheduling: Theory and Applications (MISTA 2013), Ghent, Belgium, 27–30 August 2013; pp. 472–485. [Google Scholar]
- Fanjul-Peyro, L.; Ruiz, R. Iterated greedy local search methods for unrelated parallel machine scheduling. Eur. J. Oper. Res. 2010, 207, 55–69. [Google Scholar] [CrossRef]
- Iturriaga, S.; Nesmachnow, S.; Luna, F.; Alba, E. A parallel local search in CPU/GPU for scheduling independent tasks on large heterogeneous computing systems. J. Supercomput. 2015, 71, 648–672. [Google Scholar] [CrossRef]
- Gaspero, D. Local Search Techniques for Scheduling Problems: Algorithms and Software Tool. Ph.D. Thesis, Universita‘ degli Studi di Udine, Údine, Italy, 2003. [Google Scholar]
- Kang, Q.; He, H.; Song, H. Task Assignment in Heterogeneous Computing Systems Using an Effective Iterated Greedy Algorithm. J. Syst. Softw. 2011, 84, 985–992. [Google Scholar] [CrossRef]
- Zhang, L.; Chen, Y.; Sun, R.; Jing, S.; Yang, B. A task scheduling algorithm based on PSO for grid computing. Int. J. Comput. Intell. Res. 2008, 4, 37–43. [Google Scholar] [CrossRef]
- Zhan, S.; Huo, H. Improved PSO-based task scheduling algorithm in cloud computing. J. Inf. Comput. Sci. 2012, 9, 3821–3829. [Google Scholar]
- Ritchie, G. Static Multi-Processor Scheduling with Ant Colony Optimisation & Local Search. Ph.D. Thesis, University of Edinburgh, Edinburgh, UK, 2003. [Google Scholar]
- Ying, K.C.; Lin, S.W. Multiprocessor task scheduling in multistage hybrid flow-shops: An ant colony system approach. Int. J. Prod. Res. 2006, 44, 3161–3177. [Google Scholar] [CrossRef]
- Tawfeek, M.A.; El-Sisi, A.; Keshk, A.E.; Torkey, F.A. Cloud task scheduling based on ant colony optimization. In Proceedings of the 2013 8th International Conference on Computer Engineering & Systems (ICCES), IEEE. Cairo, Egypt, 26–28 November 2013; pp. 64–69. [Google Scholar]
- Moscato, P.; Schaerf, A. Local search techniques for scheduling problems. In Proceedings of the Notes of the Tutorial Given at the 13th European Conference on Artificial Intelligence, ECAI. Údine, Italy, 1 January 1998; pp. 1–50. [Google Scholar]
- Keshanchi, B.; Navimipour, N.J. Priority-based task scheduling in the cloud systems using a memetic algorithm. J. Circuits Syst. Comput. 2016, 25, 1650119. [Google Scholar] [CrossRef]
- Padmavathi, S.; Shalinie, S.M.; Someshwar, B.C.; Sasikumar, T. Enhanced Memetic Algorithm for Task Scheduling. In Swarm, Evolutionary, and Memetic Computing; Panigrahi, B.K., Das, S., Suganthan, P.N., Dash, S.S., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 448–459. [Google Scholar]
- Sutar, S.; Sawant, J.; Jadhav, J. Task scheduling for multiprocessor systems using memetic algorithms. In Proceedings of the 4th International Working Conference Performance Modeling and Evaluation of Heterogeneous Networks (HET-NETs ‘06); 2006; p. 27. Available online: https://www.researchgate.net/profile/Jyoti-More/publication/337155023_Task_Scheduling_For_Multiprocessor_Systems_Using_Memetic_Algorithms/links/5dc8438592851c8180435093/Task-Scheduling-For-Multiprocessor-Systems-Using-Memetic-Algorithms.pdf (accessed on 10 June 2021).
- Huacuja, H.J.F.; Santiago, A.; Pecero, J.E.; Dorronsoro, B.; Bouvry, P.; Monterrubio, J.C.S.; Barbosa, J.J.G.; Santillan, C.G. A Comparison Between Memetic Algorithm and Seeded Genetic Algorithm for Multi-objective Independent Task Scheduling on Heterogeneous Machines. In Design of Intelligent Systems Based on Fuzzy Logic, Neural Networks and Nature-Inspired Optimization; Melin, P., Castillo, O., Kacprzyk, J., Eds.; Springer International Publishing: Cham, Swizerland, 2015; pp. 377–389. [Google Scholar] [CrossRef]
- Wen, Y.; Xu, H.; Yang, J. A heuristic-based hybrid genetic-variable neighborhood search algorithm for task scheduling in heterogeneous multiprocessor system. Inf. Sci. 2011, 181, 567–581. [Google Scholar] [CrossRef]
- Wu, M.-Y.; Shu, W.; Gu, J. Efficient local search far DAG scheduling. IEEE Trans. Parallel Distrib. Syst. 2001, 12, 617–627. [Google Scholar] [CrossRef]
- Pecero, J.; Bouvry, P.; Barrios, C.J. Low energy and high performance scheduling on scalable computing systems. In Proceedings of the Latin-American Conference on High Performance Computing (CLCAR 2010), Gramado, Brazil, 25–28 August 2010; p. 8. [Google Scholar]
- Alba, E.; Luque, G. Alba, E.; Luque, G. A New Local Search Algorithm for the DNA Fragment Assembly Problem. In Evolutionary Computation in Combinatorial Optimization; Cotta, C., van Hemert, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; pp. 1–12. [Google Scholar]
- Hansen, P.; Mladenović, N. Variable neighborhood search: Principles and applications. Eur. J. Oper. Res. 2001, 130, 449–467. [Google Scholar] [CrossRef]
- Nesmachnow, S. Parallel Evolutionary Algorithms for Scheduling on Heterogeneous Computing and Grid Environments. Ph.D. Thesis, Universidad de la República (Uruguay), Montevideo, Uruguay, 2010. [Google Scholar]
- Saavedra, R.H.; Smith, A.J. Analysis of benchmark characteristics and benchmark performance prediction. ACM Trans. Comput. Syst. 1996, 14, 344–384. [Google Scholar] [CrossRef]
- Brown, D.A.; Brady, P.R.; Dietz, A.; Cao, J.; Johnson, B.; McNabb, J. A Case Study on the Use of Workflow Technologies for Scientific Analysis: Gravitational Wave Data Analysis. In Workflows for e-Science: Scientific Workflows for Grids; Springer: London, UK, 2007; Chapter 4; pp. 39–59. [Google Scholar] [CrossRef]
- Tobita, T.; Kasahara, H. A standard task graph set for fair evaluation of multiprocessor scheduling algorithms. J. Sched. 2002, 5, 379–394. [Google Scholar] [CrossRef]
- Corder, G.W.; Foreman, D.I. Nonparametric Statistics for Non-Statisticians; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2009. [Google Scholar]
- García, S.; Molina, D.; Lozano, M.; Herrera, F. A study on the use of non-parametric tests for analyzing the evolutionary algorithms’ behaviour: A case study on the CEC’2005 Special Session on Real Parameter Optimization. J. Heuristics 2008, 15, 617–644. [Google Scholar] [CrossRef]
- García, S.; Fernández, A.; Luengo, J.; Herrera, F. The Software for Computing the Advanced Multiple Comparison Procedures Described in (S. García, A. Fernández, J. Luengo, F. Herrera, Advanced Nonparametric Tests for Multiple Comparisons in the Design of Experiments in Computational Intelligence and Data Mining: Experimental Analysis of Power. Inf. Sci. 2010, 180, 2044–2064. Available online: https://sci2s.ugr.es/sicidm (accessed on 25 May 2021). [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).