Investigation of Compact Hollow-Anode Discharge Source for Copper Thin Films by Sputtering Processes
Abstract
1. Introduction
2. Model
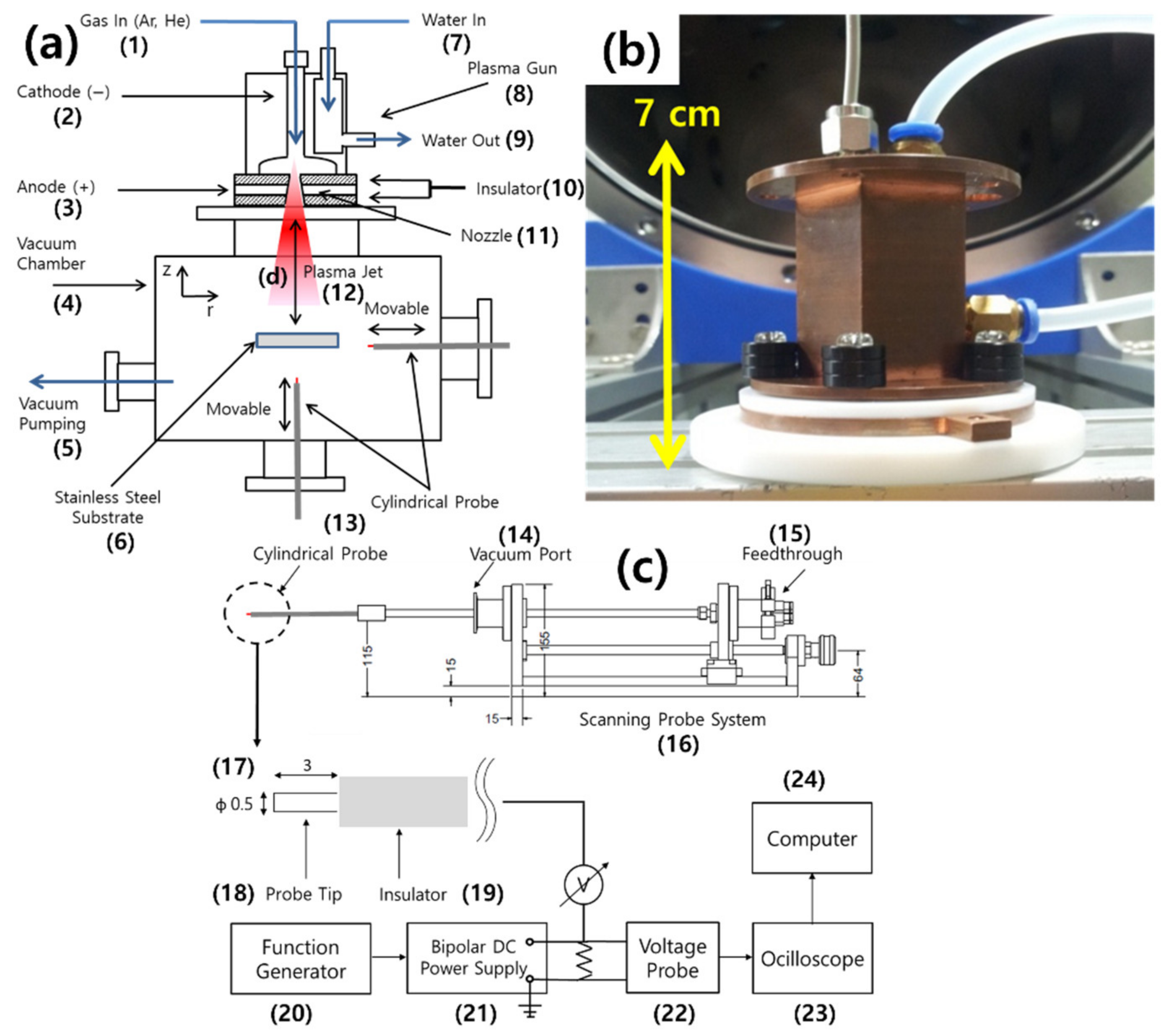
3. Experiment
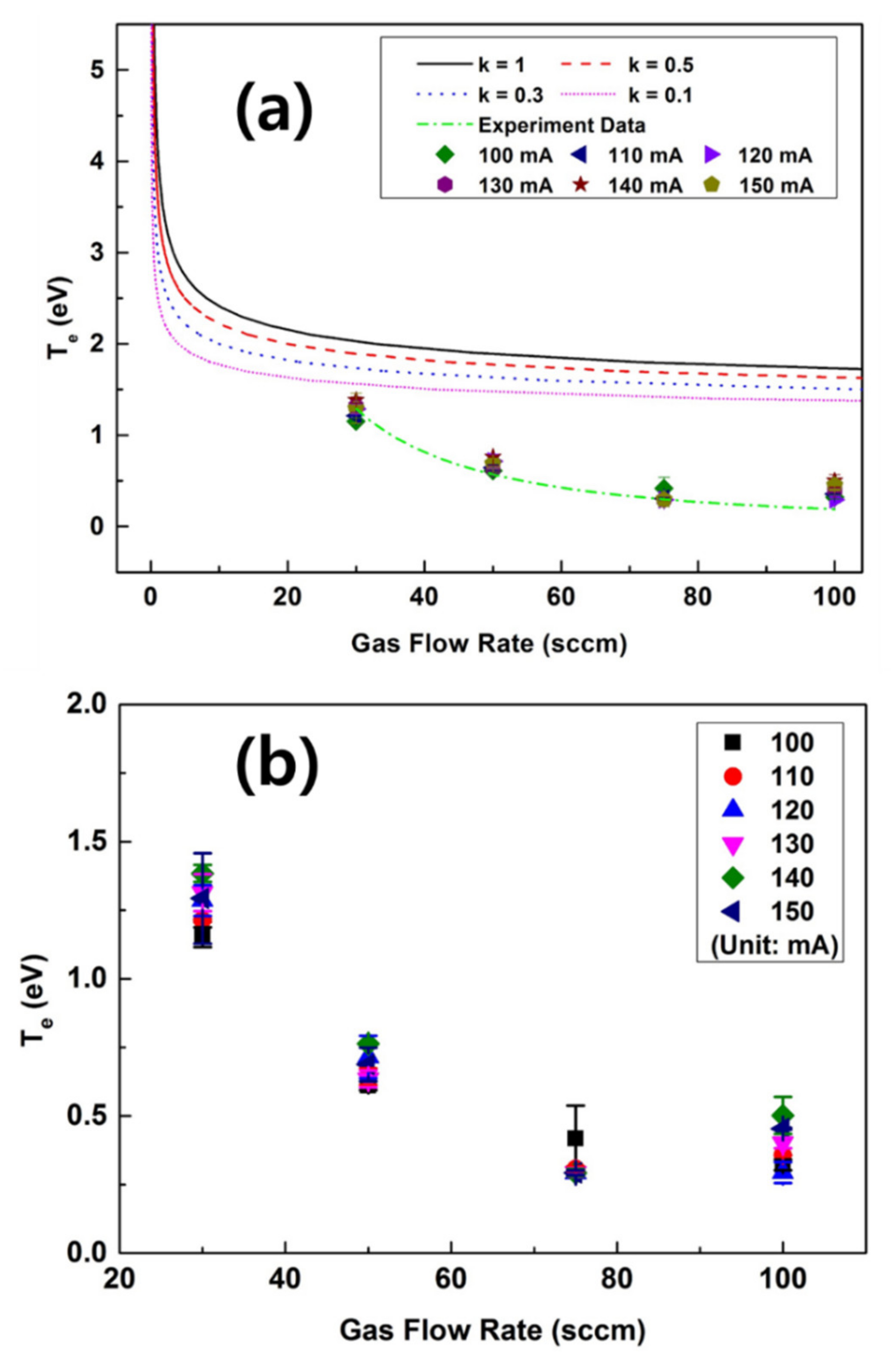
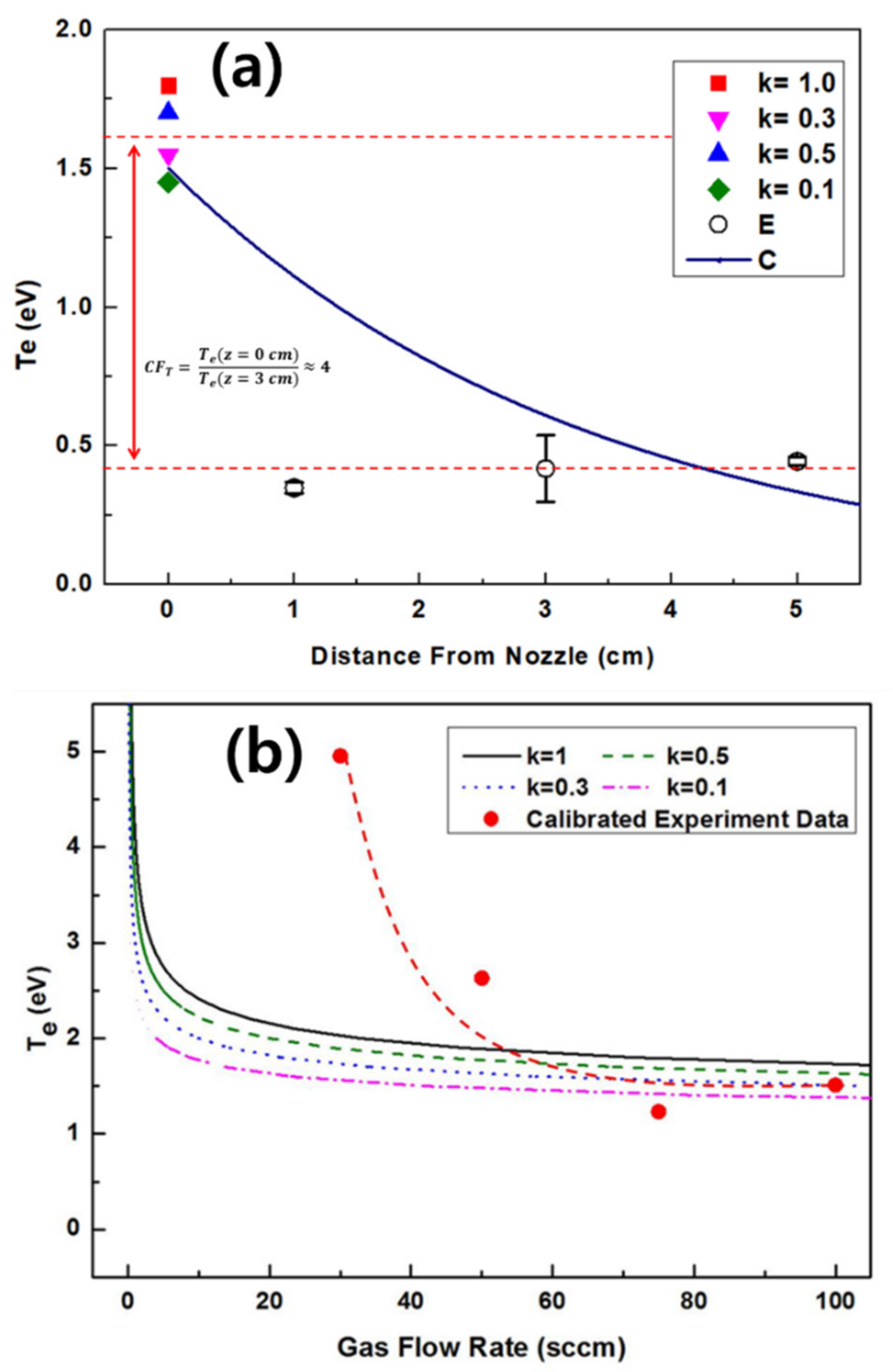
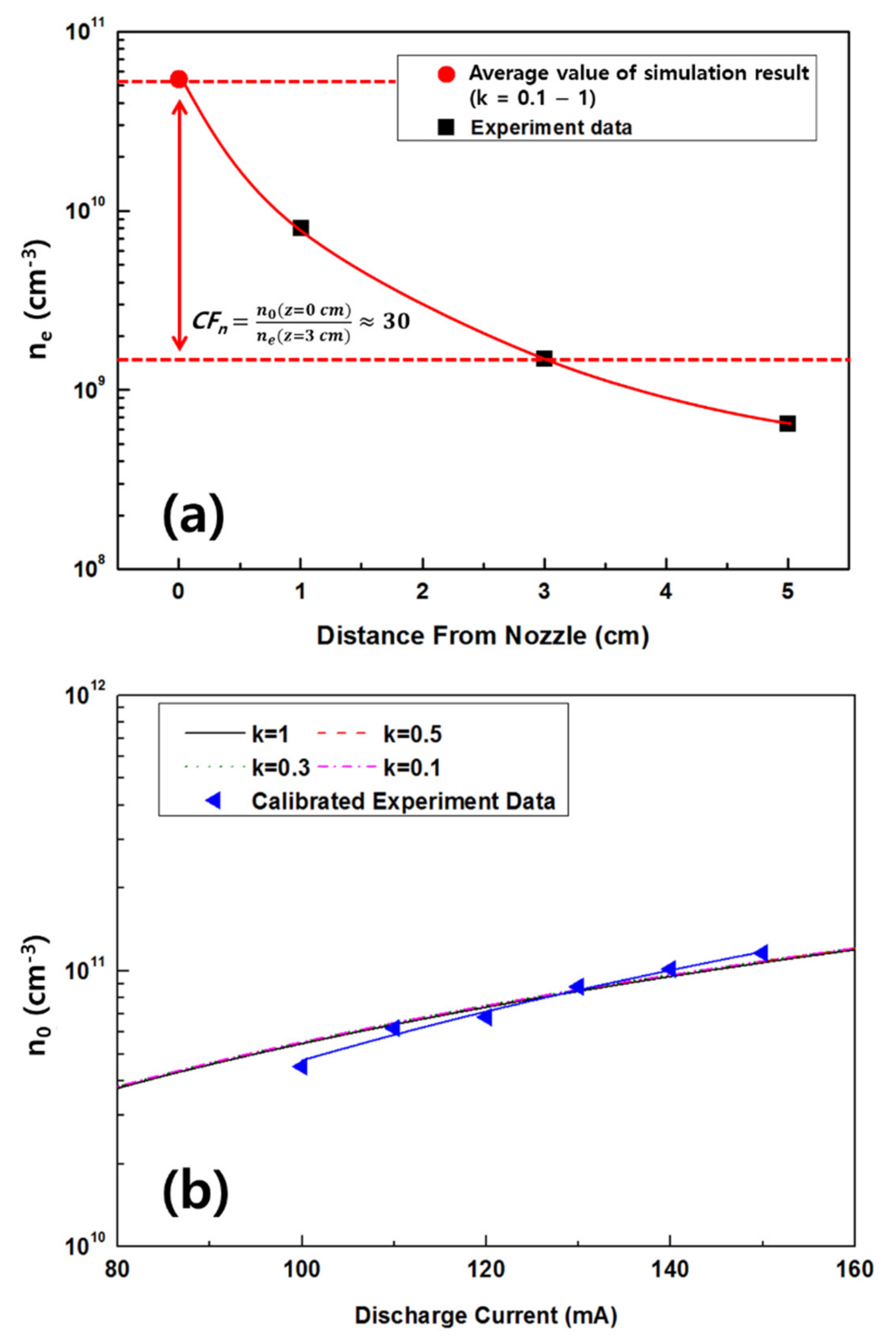
4. Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kang, I.J.; Joa, S.B.; Lee, H.J. Study on effect of plasma surface treatments for diamond deposition by DC arc plasmatron. J. Nanosci. Nanotechnol. 2013, 13, 7370–7375. [Google Scholar] [CrossRef] [PubMed]
- Kang, I.J.; Ko, M.G.; Yang, J.K.; Lee, H.J. Plasma surface treatments by using a dielectric barrier discharge for the deposition of diamond films. J. Korean Phys. Soc. 2013, 63, 199–205. [Google Scholar] [CrossRef]
- Terasawa, T.; Saiki, K. Growth of Graphene on Cu by Plasma Enhanced Chemical Vapor Deposition. Carbon 2012, 50, 869–874. [Google Scholar] [CrossRef]
- Jeong, J.Y.; Babayan, S.E.; Tu, V.J.; Park, J.; Henins, I.; Hicks, R.F.; Selwyn, G.S. Etching materials with an atmospheric-pressure plasma jet. Plasma Source Sci. Technol. 1998, 7, 282–285. [Google Scholar] [CrossRef]
- Miljevic, V.I. Hollow anode ion–electron source. Rev. Sci. Instrum. 1984, 55, 931–933. [Google Scholar] [CrossRef]
- Anders, A.; Anders, S. The working principle of the hollow-anode plasma source. Plasma Source Sci. Technol. 1995, 4, 571–575. [Google Scholar] [CrossRef]
- Granda-Gutiérrez, E.E.; López-Callejas, R.; Peña-Eguiluz, R.; Valencia, A.R.; Mercado-Cabrera, A.; Barocio, S.R.; de la Piedad-Beneitez, A.; Benítez-Read, J.S.; Pacheco-Sotelo, J.O. V-I curves and plasma parameters in a high density DC glow discharge generated by a current-source. J. Phys. Conf. Ser. 2008, 100, 062019. [Google Scholar] [CrossRef]
- Abdelsalam, F.W.; Helal, A.G.; Saddeek, Y.B.; Abdelrahman, M.M.; Soliman, B.A. Investigation and application of hollow anode glow discharge ion source. Nucl. Instrum. Methods Phys. Res. Sect. B 2010, 268, 3464–3467. [Google Scholar] [CrossRef]
- Park, Y.-S.; Hwang, Y.S. Enhancement in ion beam current with layered-glows in a constricted dc plasma ion source. Rev. Sci. Instrum. 2010, 81, 02B309. [Google Scholar] [CrossRef] [PubMed]
- Lieberman, M.A.; Lichtenberg, A.J. Principles of Plasma Discharges and Materials Processing, 2nd ed.; Wiley: Hoboken, NJ, USA, 2005. [Google Scholar]
- Godyak, V.A. Soviet Radio Frequency Discharge Research; Delphic: Falls Church, VA, USA, 1986. [Google Scholar]
- Kimura, T.; Ohe, K. Global model of inductively coupled Ar plasmas using two-temperature approximation. J. Appl. Phys. 2001, 89, 4240–4246. [Google Scholar] [CrossRef]
- Chen, F.F. Introduction to Plasma Physics and Controlled Fusion, 3rd ed.; Springer: Los Angeles, CA, USA, 2016. [Google Scholar]
- Hutchinson, I.H. Principles of Plasma Diagnostics, 2nd ed.; Cambridge University Press: New York, NY, USA, 2002. [Google Scholar]
- Green, T.S. Beam Formation and Space Charge Neutralisation. IEEE Trans. Nucl. Sci. 1976, NS-23, 918–928. [Google Scholar] [CrossRef]
- Abdelsalam, F.W.; Helal, A.G.; Abdelrahman, M.M.; Soliman, B.A. Operating characteristics of the hollow anode glow discharge ion source. Vacuum 2010, 84, 405–409. [Google Scholar] [CrossRef]
- Chung, K.-S.; Hong, S.-H.; Chung, K.-H. Measurements of Plasma Flow Velocity in DC Plasma Jets Using Perpendicular and Parallel Mach Probes. Jpn. J. Appl. Phys. 1995, 34, 4217–4222. [Google Scholar] [CrossRef]
- Kim, J.-W.; Cho, S.-G.; Bae, M.-K.; Kim, H.-J.; Chung, T.H.; Chung, K.-S. Analysis of Electron Temperature in DC Ar/SF6 Plasma Using Cylindrical and Planar Probes. Jpn. J. Appl. Phys. 2013, 52, 11NC03. [Google Scholar] [CrossRef]
- Kang, I.J.; Bae, M.-K.; Lho, T.; Chung, K.-S. Experimental investigation of free and bounded presheaths in weakly magnetized plasmas. Curr. Appl. Phys. 2017, 17, 358–365. [Google Scholar] [CrossRef]
- Chen, F.F. Langmuir probe analysis for high density plasmas. Phys. Plasmas 2001, 8, 3029–3041. [Google Scholar] [CrossRef]
- Callen, J.D. Model of Plasma Confinement and Heating in Tokamaks; University of Wisconsin: Madison, WI, USA, 1989. [Google Scholar]
- Choi, Y.-S.; Woo, H.-J.; Chung, K.-S.; Lee, M.-J. Determination of Plasma Flow Velocity by Mach Probe and Triple Probe with Correction by Laser-Induced Fluorescence in Unmagnetized Plasmas. Jpn. J. Appl. Phys. 2006, 45, 5945–5950. [Google Scholar] [CrossRef]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kang, I.-J.; Kim, J.-H.; Park, I.-S.; Chung, K.-S. Investigation of Compact Hollow-Anode Discharge Source for Copper Thin Films by Sputtering Processes. Energies 2021, 14, 3138. https://doi.org/10.3390/en14113138
Kang I-J, Kim J-H, Park I-S, Chung K-S. Investigation of Compact Hollow-Anode Discharge Source for Copper Thin Films by Sputtering Processes. Energies. 2021; 14(11):3138. https://doi.org/10.3390/en14113138
Chicago/Turabian StyleKang, In-Je, Ji-Hun Kim, In-Sun Park, and Kyu-Sun Chung. 2021. "Investigation of Compact Hollow-Anode Discharge Source for Copper Thin Films by Sputtering Processes" Energies 14, no. 11: 3138. https://doi.org/10.3390/en14113138
APA StyleKang, I.-J., Kim, J.-H., Park, I.-S., & Chung, K.-S. (2021). Investigation of Compact Hollow-Anode Discharge Source for Copper Thin Films by Sputtering Processes. Energies, 14(11), 3138. https://doi.org/10.3390/en14113138





