Maximum Power Point Tracking and Voltage Regulation of Two-Stage Grid-Tied PV System Based on Model Predictive Control

Abstract

This paper proposes a maximum power point tracking (MPPT) and voltage regulation method based on model predictive control (MPC) for the two-stage grid-tied photovoltaic (PV) system, which can achieve MPPT and output voltage regulation of a PV system simultaneously. The MPPT algorithm based on MPC is implemented in a DC-DC boost converter. The reference voltage at maximum power point is obtained by dual step Incremental Conductance (I&C) algorithm under the rapidly varying illumination intensity, and the MPPT controller only needs to minimize one cost function of PV current, without pulse width modulation (PWM) module. To inject the generated PV power into the grid with high quality, this paper designs voltage regulation controller based on MPC to maintain the output voltage of the PV system at the desired value. The MPC controller outputs the optimal duty signal with the input and state constraints in the inner loop, and the PI controller in the outer loop is designed to improve the dynamic performance. The proposed method based on MPC was demonstrated using the SimPower systems tool in MATLAB/Simulink. Analysis and simulation results for the PV system show possible improvements on the closed-loop performance such as fast response and low overshoot.

1. Introduction

With the development of renewable energy sources, solar energy, as a widespread and clean energy, has attracted the scientific and industrial interest in recent years. The applications of the distributed photovoltaic system and DC microgrid increase the utilization of solar energy. Meanwhile, the rise of the power electronic technology (e.g., DC-DC conversion) further extends the research boundaries of the photovoltaic system and improves the efficiency of energy conversion [1,2]. However, the rapid change of environmental conditions still has a harmful effect on efficiency and stabilization of PV system. In addition, to inject the generated PV power into the grid with high quality, the output voltage of the PV system also needs to be regulated. Hence, for the PV system, it is necessary to solve the maximum power point tracking and output voltage regulation issues. Many studies have researched the MPPT control issue of the PV system in recent years [3,4,5,6,7,8,9,10,11,12]. The MPPT methods for the PV system are summarized and compared in [13]. As the traditional MPPT technology, Perturbation and Observation (P&O) and Incremental Conductance (I&C) are the most extensively used in PV MPPT system [14], which can combine Grey Wolf Optimization (GWO) [15] or Particle Swarm Optimization (PSO) [16], but an obvious oscillation can appear at maximum power point (MPP). The fuzzy logic control (FLC) method without precise model is presented in [17] and genetic algorithm (GA) based FLC is used in [18] to achieve the optimum control. However, the drawback of fuzzy-based MPPT algorithms is that the tracking point is located away from the MPP when the weather conditions change [19]. Recently, the model predictive control has been used for MPPT of the PV system. The MPC-MPPT algorithm is considered in one-step horizon to enhance tracking performance [20,21,22,23]. Furthermore, the number of the required sensors for the MPC controller is minimized. In [24], the MPC-based MPPT is designed for PV system with pulse width modulation (PWM) module, which increases the complexity of DC-DC converter. By estimating the equivalent voltage and resistance of the PV module, the predicted PV power is calculated for ON or OFF state. However, the above MPC-based MPPT need to predict the instantaneous value in ON or OFF state, rather than the average value in the whole switch cycle via one cost function, which can cause prediction errors if sampling time is not short enough.

For the voltage regulation technology, the related control method is often studied, such as the Proportional-Integral-Differentive (PID) control [25], fuzzy logic control [26], feedback linearization control [27], and sliding mode control [28,29,30]. The MPC method is an attractive alternative to control the output voltage of DC-DC converter in power systems. Wei et al. [31] presented the DC-MPC scheme for cascaded modular DC–DC converter. The PI controller is employed for load voltage regulation and the MPC controller is used for duty cycles prediction. However, it does not consider the current and duty cycle constraints of each module. The Generalized Proportional Integral (GPI) observer-based discrete MPC is designed in [32] to predict a lumped time-varying disturbances, and the MPC controller therein regulates the output voltage even the control input gain is not known precisely. The pre-compensated MPC scheme is proposed in [33,34], which can steer a reference voltage value to the primal controller dynamically, without modifying the primal control structure. However, it has to run at slower frequency than the primal controller to meet computational constraints, which limits the ability of the MPC controller.

To inject the generated PV power into the grid with high quality and improve the efficiency of the PV system, it is crucial to achieve MPPT of the PV system together with voltage regulation. Unfortunately, as mentioned above, most studies focus on only one aspect, either MPPT or voltage regulation, instead of dealing with both simultaneously [35]. Besides, no matter what kind of single control structure is adopted, the PV cell cannot achieve the voltage regulation when the PV system operates in MPPT mode [36]. Therefore, the two-stage converter topology structure is considered for the PV system control in this paper. The first converter matches the output and load impedance and tracks the maximum power point, and the second converter regulates the output voltage to the desired value. This paper proposes the MPPT and cascade voltage regulation control strategy based on MPC for the two-stage type PV system, which can achieve MPPT and output voltage regulation of PV system simultaneously. The main contribution can be summarized as follows:

•

The MPPT method based on MPC is proposed to track the maximum power point of PV cell module via DC-DC boost converter. The reference voltage at maximum power point is obtained by dual step I&C algorithm under the rapidly varying illumination intensity, and the MPPT controller only needs to minimize one cost function of PV current, without PWM module.

•

The voltage control method based on MPC is applied to the DC-DC buck converter to improve the response speed and reduce the overshoot for output voltage regulation. The MPC controller outputs the optimal duty signal with the input and state constraints in inner loop, and the PI controller in outer loop is designed to improve the dynamic performance of DC-DC buck converter.

The rest of this paper is organized as follows. Section 2 describes the PV system model including the PV cell and the DC-DC converter. The MPPT control method and the voltage regulation method based on MPC are presented in Section 3 and Section 4, respectively. Then, simulation results are given using SimPower systems tool in Section 5, and the conclusions are drawn in Section 6.

2. Modeling of Photovoltaic System

The PV system is divided into two essential parts: the PV cell module and the conversion circuit. The proposed PV system in this paper uses a two-stage topology structure, as shown in Figure 1. The first DC-DC boost converter matches the output impedance of PV cell module with the load impedance and tracks the maximum power point. Then, the stable output voltage can be obtained by the second DC-DC buck converter to supply electricity for the load.

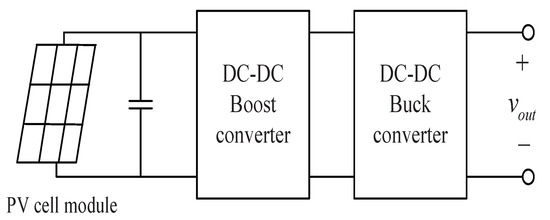
Figure 1. Two-stage grid-tied PV system topology.

2.1. Photovoltaic Cell

PV cell is the smallest unit of the photo-electricity conversion process. The equivalent circuit of PV cell can be seen as an ideal current source and a diode in parallel. The series and parallel resistance of PV cell internal losses are denoted as $R_s$ and $R_{sh}$ and the output current $I_{PV}$ of PV cell is described as

$$I_{PV}=I_{ph}-I_r(e^{\frac{q(V_{PV}+I_{PV}{R}_s)}{p\ast K\ast T_j}}-1)-\frac{V_{PV}+I_{PV}{R}_s}{R_{sh}},$$

(1)

where $V_{PV}$ is the output voltage of PV cell; $I_{ph}$ and $I_r$ are the light-generated current and the reverse saturation current of diode; and p, q, K, and $T_j$ are constants and represent the diode characteristic factor, electronic charge, Boltzmann’s constant and junction temperature of PV cell, respectively.

Ignoring the impact of series and parallel resistance for PV cell, the short-circuit current $I_{sc}$ of PV cell approximately equals to the light-generated current $I_{ph}$, and Equation (1) can be rewritten as [37]

$$I_{PV}=I_{sc}(1-C_1(e^{\frac{V_{PV}}{C_2{V}_{oc}}}-1)),$$

(2)

where $V_{oc}$ is the open-circuit voltage of the PV cell. Considering the following two conditions: $I_{PV}=I_m$, $V_{PV}=V_m$ at the maximum power point and $I_{PV}=0$, $V_{PV}=V_{oc}$ at open-circuit state, the coefficients $C_1$ and $C_2$ can be obtained as

$$\begin{array}{cc}\hfill & C_1=(1-\frac{I_m}{I_{sc}})exp(-\frac{V_m}{C_2{V}_{oc}}),\hfill \\ \hfill & C_2=(\frac{V_m}{V_{oc}}-1){(ln(-\frac{V_m}{C_2{V}_{oc}}))}^{-1}.\hfill \end{array}$$

Under the different illumination intensity and temperature, $I_{sc}$, $I_m$, $V_{oc}$, and $V_m$ will change in a certain range. By introducing the compensation factors a, b, and c, corresponding parameters can be obtained by [38]

$$\begin{array}{cc}\hfill & I_{sc}=I_{sc-ref}\ast \frac{S}{S_{ref}}\ast (1+a\Delta T),\hfill \\ \hfill & I_m=I_{m-ref}\ast \frac{S}{S_{ref}}\ast (1+a\Delta T),\hfill \\ \hfill & V_{oc}=V_{oc-ref}\ast ln(e+b\Delta S)\ast (1-c\Delta T),\hfill \\ \hfill & V_m=V_{m-ref}\ast ln(e+b\Delta S)\ast (1-c\Delta T),\hfill \end{array}$$

where e is natural constant; $\Delta S=S-S_{ref}$ represents the deviation between the current illumination intensity S and the reference illumination intensity $S_{ref}$; $\Delta T=T-T_{ref}$ represents the deviation between the current temperature T and temperature reference $T_{ref}$; and $I_{sc-ref}$, $V_{oc-ref}$, $I_{m-ref}$, and $V_{m-ref}$ are the short-circuit current, open-circuit voltage, maximum current, and maximum voltage at reference environmental conditions ($S_{ref}=1000$ W/m${}^2$ and $T_{ref}$ = 25 ${}^{°}$C), respectively. According to many data fittings of PV cell, the compensation factor a, b, and c are obtained as follows [38]

$$\begin{array}{cc}\hfill & a=0.0025{/}^{°}\mathrm{C},\hfill \\ \hfill & b=0.0005{\left({\mathrm{W}/\mathrm{m}}^2\right)}^{-1},\hfill \\ \hfill & c=0.00288{/}^{°}\mathrm{C}.\hfill \end{array}$$

2.2. DC-DC Converter

The DC-DC converter is used to achieve the MPPT and output voltage regulation of the PV cells. The boost converter is chosen as an example in this section, which can switch the two operation states (ON and OFF) under high frequency. The circuit topology of the DC-DC boost converter is shown in Figure 2.

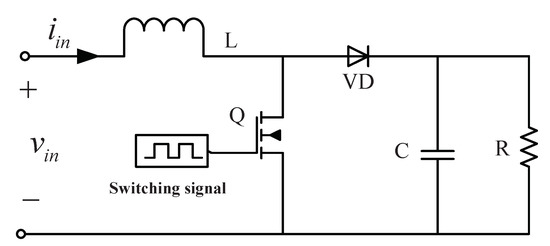
Figure 2. The topology of DC-DC boost converter.

Assuming the inductor current is continuous, the parasitic parameters of components are ignored. The inductor current $i_L$ and capacitor voltage $v_C$ are chosen as state vector $x={\left[i_L{v}_C\right]}^T$. When the switch is ON and the switch is OFF, the state equations are, respectively, described as

$$\begin{array}{c}\hfill \dot{x}\left(t\right)=A_{1}x\left(t\right)+B_{1}w\left(t\right),\end{array}$$

(3a)

$$\begin{array}{c}\hfill \dot{x}\left(t\right)=A_{2}x\left(t\right)+B_{2}w\left(t\right),\end{array}$$

(3b)

in which

$$\begin{array}{cc}\hfill A_1& =\left(\begin{array}{cc}-\frac{R_o}{L}& 0\\ 0& -\frac{1}{RC}\end{array}\right),B_1=\left(\begin{array}{cc}\frac{1}{L}& 0\\ 0& 0\end{array}\right),\hfill \\ \hfill A_2& =\left(\begin{array}{cc}0& -\frac{1}{L}\\ \frac{1}{C}& -\frac{1}{RC}\end{array}\right),B_2=\left(\begin{array}{cc}\frac{1}{L}& -\frac{1}{L}\\ 0& 0\end{array}\right),\hfill \\ \hfill w& ={\left(\begin{array}{cc}{v}_{in}& V_D\end{array}\right)}^T,\hfill \end{array}$$

where $R_0$ is the on-resistance of the switch, R is the load resistance, $v_{in}$ is the input voltage of boost converter, and $V_D$ is the forward voltage of the diode.

In terms of the average state-space method, the DC-DC boost converter could be modeled by the following state function [39]

$$\dot{x}\left(t\right)=(d{A}_1+(1-d)A_2)x\left(t\right)+(d{B}_1+(1-d)B_2)w\left(t\right),$$

(4)

where d represents the duty ratio and $d\in \left[0,1\right]$. Denoting the input signal $u=d$, Equation (4) can be rewritten as

$$\dot{x}\left(t\right)=\overline{A}x\left(t\right)+(\overline{F}\left(t\right)+\overline{G}x\left(t\right))u\left(t\right)+\overline{B}w\left(t\right),$$

(5)

in which

$$\begin{array}{cc}\overline{A}=A_2,\hfill & \overline{B}=B_2,\hfill \\ \overline{F}\left(t\right)=(B_1-B_2)w\left(t\right),\hfill & \overline{G}=A_1-A_2.\hfill \end{array}$$

Using the forward discrete transformation, Equation (5) can be described as

$$x(k+1)=Ax\left(k\right)+\left(F\right(k)+Gx(k\left)\right)u\left(k\right)+Bw\left(k\right),$$

(6)

where

$$A=T_s\overline{A}+I,F\left(k\right)=T_s\overline{F}\left(k\right),G=T_s\overline{G},B=T_s\overline{B},$$

and $T_s$ is a sampling time. Similarly, the DC-DC buck converter model can be obtained by the above procedure.

3. MPPT Control Based on MPC Method

In this section, the MPPT controller based on MPC is designed to control the electronic switch without the PWM module. The MPPT principle is that controller switches the operation states (ON or OFF) of DC-DC boost converter by different switching signals u (1 or 0). Hence, the output power will be matched with the load power of the boost converter, and the MPPT will be achieved.

For the PV cell, it is clear that the derivative of output power to the output voltage is equal to zero at the maximum power point

$$\frac{\mathrm{d}P}{\mathrm{d}V}=\frac{\mathrm{d}\left(VI\right)}{\mathrm{d}V}=I+V\frac{\mathrm{d}I}{\mathrm{d}V}=I+V\frac{\Delta I}{\Delta V}=0,$$

in which

$$\begin{array}{cc}\hfill & \Delta I=I_{PV}\left(k\right)-I_{PV}(k-1),\hfill \\ \hfill & \Delta V=V_{PV}\left(k\right)-V_{PV}(k-1).\hfill \end{array}$$

Therefore, by the classical Incremental Conductance (I&C) algorithm [14], one has

$$\left\{\begin{array}{cc}\frac{I_{PV}}{V_{PV}}+\frac{\Delta I}{\Delta V}=0\hfill & \mathrm{at}\mathrm{MPP}\hfill \\ \frac{I_{PV}}{V_{PV}}+\frac{\Delta I}{\Delta V}>0\hfill & \mathrm{at}\mathrm{left}\mathrm{of}\mathrm{MPP}\hfill \\ \frac{I_{PV}}{V_{PV}}+\frac{\Delta I}{\Delta V}<0\hfill & \mathrm{at}\mathrm{right}\mathrm{of}\mathrm{MPP}\hfill \end{array}\right.$$

Then, by taking the appropriate step size at current time k, the output current reference $I_{PV}^{\ast }$ of the PV cell at next time $k+1$ can be obtained. The proposed dual step I&C method to determine reference current is shown by the flowchart in Figure 3, in which ${\lambda }_1$ and ${\lambda }_2$ represent the different step sizes, and they are set to be ${\lambda }_1=0.001$ and ${\lambda }_2=0.002$ to reduce oscillation.

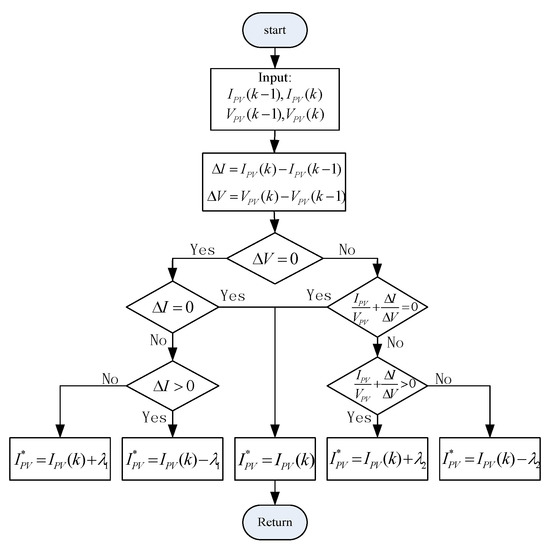
Figure 3. Flowchart to determine reference current by dual step I&C algorithm.

To satisfy the high-frequency switching action, one-step horizon for MPC is chosen. Define the output current of PV cell $I_{PV}=i_L$, the prediction model can be derived by Equation (6) as follow

$$\begin{array}{c}\hfill I_{PV}(k+1)=(1-\frac{u{T}_s{R}_o}{L})I_{PV}\left(k\right)+\frac{T_s}{L}{V}_{PV}\left(k\right)-\frac{(1-u)T_s}{L}(V_C\left(k\right)+V_D).\end{array}$$

(7)

The control objective of MPPT is that the output current of the PV cell tracks the reference value. Hence, the cost function $J_1$ can be written as

$$J_1=\left|I_{PV}(k+1)-I_{PV}^{\ast }\right|.$$

(8)

For the MPPT of PV system, the MPC optimization problem can be written as

$\underset{u}{min}{J}_1(u=1\mathrm{or}0)$

subject to (7).

Then, the switch state will be determined by solving the above optimization problem, and the control system structure of DC-DC boost converter is illustrated in Figure 4.

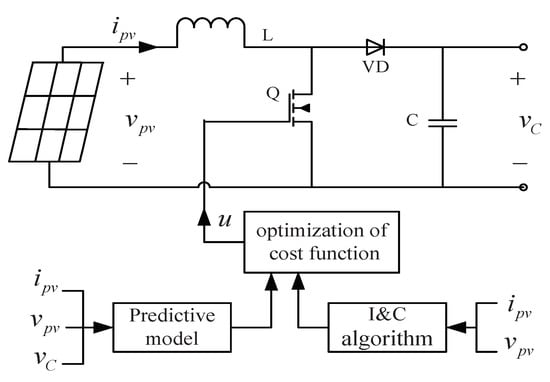
Figure 4. Control system structure of DC-DC boost converter.

4. Voltage Regulation Based on MPC Method

In this section, the control scheme for the output voltage regulation of the PV system based on MPC is proposed. First, the MPC controller in the inner loop is designed to satisfy the high-frequency switching action. Meanwhile, we select the short sampling time and control horizon by trial and error such that the closed system can achieve better performance while online computational burden is not too heavy. Then, the PI controller in the outer loop is designed to improve the dynamic response performance of the DC-DC buck converter.

4.1. Inner Loop MPC Design

According to the average current control method, the MPC objective is that the inductor current $i_L$ can always be maintained at reference current $I_{ref}$, while the input constraints are satisfied. The total block diagram for voltage regulation with buck converter is shown in Figure 5.

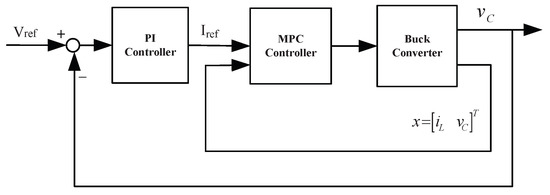
Figure 5. The block diagram of voltage regulation.

The MPC controller consists of two parts: predictive model and optimization of cost function. The predictive model can be obtained from Equation (6)

$$\begin{array}{cc}\hfill & x(k+1|k)=Ax(k)+(F+Gx\left(k\right)\left)u\right(k)+Bw(k)\hfill \end{array}$$

(9a)

$$\begin{array}{cc}\hfill & x(k+2|k)=Ax(k+1\left|k\right)+(F+Gx(k+1\left|k\right))\ast u(k+1\left|k\right)+Bw(k+1|k)\hfill \end{array}$$

(9b)

$$\begin{array}{cc}\hfill & x(k+3|k)=Ax(k+2\left|k\right)+(F+Gx(k+2\left|k\right))\ast u(k+2\left|k\right)+Bw(k+2|k)\hfill \\ \hfill & ⋮\hfill \end{array}$$

(9c)

where $(k+i|k)$ represents the prediction for time $k+i$ at current time k.

Define $x_{ss}={\left[I_{ss}{V}_{ss}\right]}^T$ as the state variable at steady-state and $u_{ss}$ as the steady-state input. The numerical equation is expressed as follow:

$$x_{ss}(k+1)=A{x}_{ss}\left(k\right)+(F+G{x}_{ss}\left(k\right))u_{ss}\left(k\right)+Bw\left(k\right),$$

(10)

where $x_{ss}(k+1)=x_{ss}\left(k\right)$. By replacing $I_{ss}$ with $I_{ref}$, the $u_{ss}$ and $V_{ss}$ at time k can be obtained from Equation (10)

$$\begin{array}{cc}\hfill u_{ss}& =\frac{-A(1,2)V_{ss}-B(1,1)w\left(1\right)-B(1,2)w\left(2\right)}{F\left(1\right)+G(1,2)V_{ss}},\hfill \end{array}$$

(11a)

$$\begin{array}{cc}\hfill V_{ss}& =\frac{\sqrt{{\alpha }_1^2-4{\alpha }_2{\alpha }_0}-{\alpha }_1}{2{\alpha }_2},\hfill \end{array}$$

(11b)

in which

$$\begin{array}{cc}\hfill {\alpha }_2=& (1-A(2,2\left)\right)G(1,2),\hfill \\ \hfill {\alpha }_1=& (1-A(2,2))F\left(1\right)-A(2,1)G(1,2)I_{ref}+A(1,2)G(2,1)I_{ref},\hfill \\ \hfill {\alpha }_0=& -A(2,1)F\left(1\right)I_{ref}+G(2,1)B2(1,1)W\left(1\right)I_{ref}+G(2,1)B2(1,2)W\left(2\right)I_{ref},\hfill \end{array}$$

where $A(m,n)$ represents the element of the mth row and nth column in matrix A, $F\left(m\right)$ represents the mth element of column vector F, and so on.

Considering the closed-loop characteristic, the following cost function $J_2$ with quadratic performance index is designed, which includes the state $x(k+i|k)$ and input $u(k+i-1)$.

$$J_2=\sum _{i=1}^{T_P}({∥x(k+i|k)-x_{ss}∥}_P^2+{∥u(k+i-1)-u_{ss}∥}_Q^2),$$

(12)

where P and Q are positive definite symmetric weighting matrices and $T_P$ is the predictive and control horizon.

Considering input and state constraints, the duty ratio of the buck converter will be chosen in $\left[d_{min}{d}_{max}\right]\subseteq \left[01\right]$, and the inductor current $i_L$ should not be too large. Hence, the variables will also be bounded as follows

$$s.t:\left\{\begin{array}{c}{i}_{Lmin}<i_L<i_{Lmax},\hfill \\ d_{min}<u<d_{max}.\hfill \end{array}\right.$$

(13)

Therefore, the MPC optimization problem can be formulated as

$\underset{U}{min}{J}_2$

subject to Equations (9) and (13).

Obviously, the optimization problem is a simple programming problem about $U\left(u\right(k),u(k+1),u(k+2),\cdots )$. Hence, the optimal solution of cost function in Equation (12) can be obtained using Matlab Optimization Toolbox, and the solving process will be omitted because of limited space.

According to MPC theory, the first element of the optimal solution is applied to the boost converter, the control input $U\left(k\right)$ of current time can be expressed as

$$U\left(k\right)=[100\cdots ]{[u\left(k\right)u(k+1)u(k+2)\cdots ]}^T=u\left(k\right).$$

4.2. Outer Loop PI Design

This subsection introduces an outer loop PI voltage controller, which can compensate for the offset of MPC and quicken the dynamic response of the buck converter. The control output $I_{ref}$ of the outer loop is the MPC reference current for the inner loop. The control objective is to track the reference voltage signal $V_{ref}$

$$\underset{k\to \infty }{lim}{v}_c\left(k\right)=V_{ref}.$$

Therefore, the PI control law can be written as follow:

$$I_{ref}=k_P(V_{ref}-v_C\left(k\right))+k_I\sum _{j=0}^k(V_{ref}-v_C\left(j\right)).$$

(14)

Then, when the system is in steady state, by Equation (6), $v_C(k+1)$ and $v_C(k+2)$ are written as

$$\begin{array}{cc}\hfill & v_C(k+1)=\frac{T_s}{C}{i}_L\left(k\right)+(1-\frac{T_s}{RC})v_C\left(k\right),\hfill \end{array}$$

(15a)

$$\begin{array}{cc}\hfill & v_C(k+2)=\frac{T_s}{C}{i}_L(k+1)+(1-\frac{T_s}{RC})v_C(k+1).\hfill \end{array}$$

(15b)

Meanwhile, we have

$$\begin{array}{cc}\hfill & i_L\left(k\right)=I_{ref}\left(k\right),\hfill \end{array}$$

(16a)

$$\begin{array}{cc}\hfill & i_L(k+1)=I_{ref}(k+1).\hfill \end{array}$$

(16b)

By defining the capacitor voltage error as $e_{v_C}\left(k\right)=V_{ref}-v_C\left(k\right)$ and combining Equations (14)–(16), the steady-state error equation can be obtained as follows:

$$e_{v_C}(k+2)+{\beta }_1{e}_{v_C}(k+1)+{\beta }_0{e}_{v_C}\left(k\right)=0,$$

(17)

where

$$\begin{array}{cc}\hfill & {\beta }_1=\frac{T_s}{C}(k_P+k_I)+\frac{T_s}{RC}-2,\hfill \\ \hfill & {\beta }_0=1-\frac{T_s}{C}(k_P+\frac{1}{R}).\hfill \end{array}$$

All the poles of the characteristic in Equation (17) are within the unit circle after z-transformation in order to ensure the stability of the system. According to Routh’s stability criterion, the value range of $k_P$ and $k_I$ can be given as

$$\left\{\begin{array}{c}{k}_I>0,\hfill \\ k_P>-\frac{1}{R},\hfill \\ 2k_P+k_I<\frac{4C}{T_s}-\frac{2}{R}.\hfill \end{array}\right.$$

(18)

5. Simulation Results

The proposed MPPT and voltage regulation control methods based on MPC for the PV system were applied using SimPower systems tool in MATLAB/Simulink, which provides component libraries and analysis tools to investigate system-level performance for the electrical power system. The parameters of DC-DC boost and buck converter were designed by Ang and Oliva [39] and the quantitative comparison was to evaluate the control performance of different control methods.

Remark 1.

The sampling time $T_s$ was chosen as 10 μs, which corresponds to a sampling frequency of 100 kHz. To get good performance controller, the sampling frequency should be much higher than the switching frequency, such as 10–20 times higher according to the guidelines for accurate modeling of power electronics [40]. In this simulation, the switching frequency was 10 kHz, which results in the sampling frequency of 100∼200 kHz, i.e., the sampling time of 5∼10 μs. In addition, this sampling time was also chosen based on the capability of the dSPACE DS1007 platform processor, which we plan to use for expedited prototyping in the future. The control algorithm was implemented in MATLAB/Simulink. If we employed the real-time algorithm called C/GMRES (continuation method combined with Generalized Minimum Residual) to solve the optimal control problem in MATLAB [41], the execution time within the sample time would be about 0.1 ms. It is clear that the on-line optimization is a computationally expensive task and may preclude real-time implementations of the proposed algorithm with a sampling period of 10 μs. However, based on dSPACE implementation, the execution time within the sample time for the proposed MPPT and voltage regulation schemes based on MPC would be greatly reduced [40]. In addition, readily available and low-priced microprocessors, such as the Altera DEO-Nano FPGA, are capable of handling the controller’s execution time for the real application [42].

5.1. MPPT Simulation

As an example, the PV module composed of three cell in series on the basis of STP0950S-36 PV array was considered. The parameters of each PV cell and the DC-DC converter are shown in Table A1 in Appendix A. According to the PV model in Equation (2) in Section 2.1, each PV cell power and current characteristics under different illumination intensity at 25 ${}^{°}$C are shown in Figure 6.

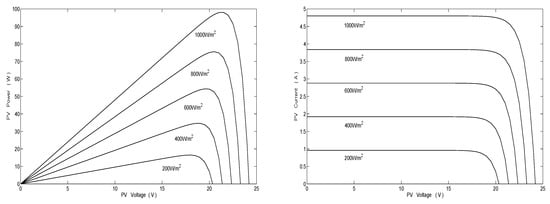
Figure 6. Characteristics of PV power and PV current with PV voltage for each PV cell under different illumination intensity.

Figure 7 shows the output response of power, voltage and current of the PV cell module under the sudden variation of illumination intensity. For comparison, the traditional P&O algorithm was also applied to MPPT control of the PV system and the simulation results are depicted in Figure 7 as dashed lines. At time $t=0.1$ s, the illumination intensity changes from 1000 W/m${}^2$ to 800 W/m${}^2$, and at time $t=0.2$ s, the illumination intensity changes from 800 W/m${}^2$ to 900 W/m${}^2$. In Figure 7b, we can see that the power of PV module settles at their expected values at the steady state quickly for proposed MPPT scheme, and the overshoot of PV power for proposed MPPT scheme is smaller than the traditional P&O algorithm with variation of the illumination intensity. Meanwhile, the ripples of PV voltage and PV current are smaller than the traditional P&O algorithm. Detailed simulation data results of proposed MPC method and traditional P&O algorithm are given in Table 1. In Table 1, it is obvious that the proposed MPPT method has a shorter settling time and a lower power ripple than the traditional P&O algorithm, which reduces the oscillation of output voltage at the maximum power point.

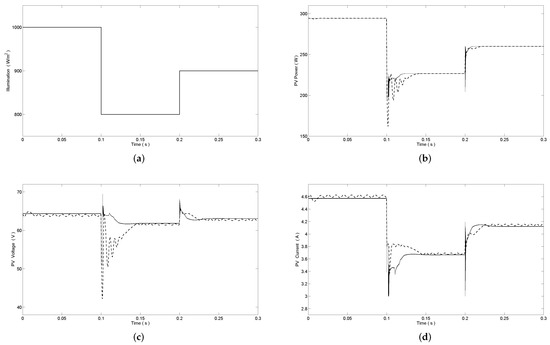
Figure 7. (a) The illumination variation; (b) corresponding output power; (c) output voltage; and (d) output current of PV module (proposed MPPT method (―), traditional P&O algorithm ($--$)).

Table 1. The simulation data of PV module.

Illumination		Settling Time	Power Ripple
1000 $\left({\mathrm{W}/\mathrm{m}}^2\right)$	MPC	―	0.0776 W
	P&O	―	0.1136 W
800 $\left({\mathrm{W}/\mathrm{m}}^2\right)$	MPC	0.024 s	0.0325 W
	P&O	0.043 s	0.0625 W
900 $\left({\mathrm{W}/\mathrm{m}}^2\right)$	MPC	0.012 s	0.0354 W
	P&O	0.025 s	0.0726 W

5.2. Voltage Regulation Simulation

The proposed voltage regulation scheme was next applied to a 24 V∼36 V buck converter. The parameters of DC-DC buck converter are shown in Table A1 in Appendix A, and the controller parameters were chosen as

$$\begin{array}{cc}\hfill & P=\left(\begin{array}{cc}0.001& 0\\ 0& 0.001\end{array}\right),Q=0.02,\hfill \\ \hfill & k_P=0.06,k_I=0.011,\hfill \\ \hfill & T_P=3.\hfill \end{array}$$

With the step change of the illumination intensity, the output voltage of the PV module changes by the proposed MPPT method via boost converter. Considering the impact of different illumination, the wide range of step change would be chosen to simulate the output voltage of the boost converter, i.e., at time $t=0.1$ s, the input voltage of the buck converter changes from 100 V to 60 V and the step-down change of input voltage is from 60 V to 80 V at $t=0.2$ s. Assume the reference output voltage $V_{ref}=32$ V and the voltage response of DC-DC buck converter is illustrated in Figure 8b. The output voltage of proposed voltage regulation method is maintained at 32 V without overshoot. As comparisons, the simulation results of the traditional PI cascade control method are also given in Figure 8 as dashed lines. In Figure 8b,c, we can see that the response time of duty cycle is longer and the voltage overshoot is 14.4 V and 10.7 V by PI cascade control method respectively, while the control input (duty cycle) obtained by the proposed control scheme varies very quickly to ensure that output voltage of DC-DC buck converter remains practically unaffected while satisfying the input constraints.

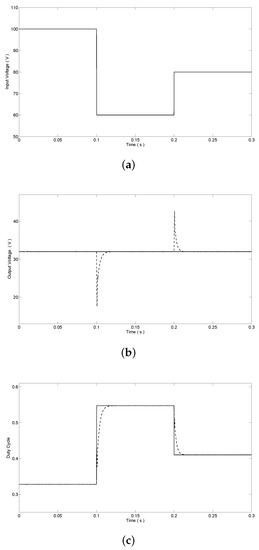
Figure 8. (a) The input voltage; (b) corresponding output voltage regulation; and (c) duty cycle input of DC-DC buck converter (proposed voltage regulation method (―), PI cascade control ($--$)).

The next simulation was performed with step changes in the reference voltage to show the regulation performance. Firstly, a step-up change of reference voltage from 28 V to 34 V at $t=0.1$ s and a step-down change from 34 V to 28 V at $t=0.2$ s were given, and the corresponding response results are illustrated in Figure 9. The output voltage of the proposed voltage regulation method is maintained at the reference voltage quickly. The response time of voltage regulation is 0.007 s in both step changes. However, the simulation results of the traditional PI cascade control method show the response time of voltage regulation is 0.017 s and 0.024 s, respectively. Consequently, the response time of the proposed MPC voltage regulation method is much shorter than the traditional PI cascade control.

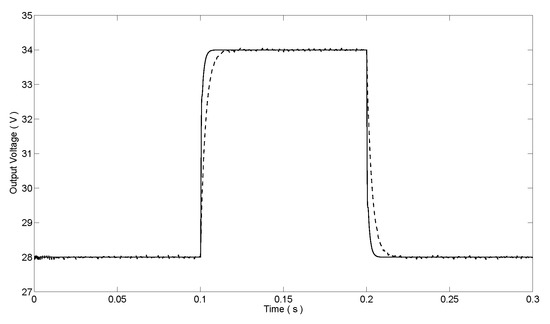
Figure 9. Output voltage of DC-DC buck converter with reference voltage change (proposed voltage regulation method (―), PI cascade control ($--$)).

5.3. MPPT and Voltage Regulation Simulation

The simulation of the MPPT and voltage regulation of the PV system was studied next. The reference output voltage $V_{ref}=32$ V was chosen and the simulation results are shown in Figure 10. The illumination intensity changes from 900 W/m${}^2$ to 1000 W/m${}^2$ at time $t=0.1$ s and changes from 1000 W/m${}^2$ to 800 W/m${}^2$ at time $t=0.2$ s, as illustrated in Figure 10a. For comparison, we combined the traditional P&O algorithm for MPPT and the PI cascade control method for voltage regulation to design the combined controller. The simulation results of the traditional P&O and PI cascade control for two-stage PV system are also illustrated in Figure 10 as dashed lines. In Figure 10b, we can see that the proposed MPPT method tracks the maximum power point of the PV module at 0.107 s and 0.222 s under the variation of illumination intensity, respectively. The overshoot of PV power for the proposed MPPT scheme is smaller than the traditional P&O algorithm. In Figure 10c, the ripple of PV voltage is smaller comparing with the traditional PI cascade control method. Meanwhile, as shown in Figure 10d, the output voltage of proposed PV system is always maintained at 32 V without overshoot, while the overshoot of output voltage for traditional P&O and PI cascade control is 1.17 V and 5.05 V, respectively, which verifies the effectiveness of the proposed MPPT and voltage regulation methods.

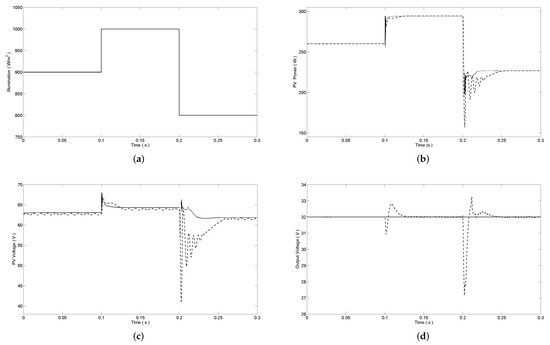
Figure 10. (a) The illumination variation; (b) corresponding output power; (c) output voltage of PV module; and (d) output voltage of DC-DC buck converter (proposed method (―), traditional P&O and PI cascade control ($--$)).

6. Conclusions

This paper proposes the cascaded MPPT and cascade voltage regulation control strategy based on MPC for the two-stage grid-tied PV system, which can achieve MPPT and output voltage regulation of PV system, simultaneously. The proposed MPPT method based on MPC tracks the maximum power point of PV cell module via DC-DC boost converter. The dual step I&C algorithm is used to obtain the reference voltage at maximum power point, and the different step sizes are set under a rapidly changing illumination condition, which can reduce the oscillation deviation of PV output power. Moreover, the proposed MPPT controller based on MPC predicts the future average current of PV cell and only needs to minimize a cost function without PWM module. Consequently, the design of both hardware and software are simplified. In addition, the voltage control method based on MPC is applied to the DC-DC buck converter. The MPC controller outputs the optimal duty signal with the input and state constraints in inner loop, and the PI controller in outer loop is designed to enhance the dynamic performance of DC-DC buck converter, which improves the response speed and reduces the overshoot for output voltage regulation of PV system. Further, the proposed MPC-based method was demonstrated using SimPower systems tool in MATLAB/Simulink. The simulation results show that the proposed MPPT method could achieve the fast response and low output ripple of the PV system, and the fast dynamic performance of the voltage regulation method was also verified.