Abstract
Modelling for very fast transients (VFTs) requires good knowledge of the behaviour of gas insulated substation (GIS) components when subjected to high frequencies. Modelling usually takes the form of circuit-based insulation coordination type studies, in an effort to determine the maximum overvoltages and waveshapes present around the system. At very high frequencies, standard transmission line modelling assumptions may not be valid. Therefore, the approach to modelling of these transients must be re-evaluated. In this work, the high frequency finite element analysis (FEA) was used to enhance circuit-based models, allowing direct computation of parameters from geometric and material characteristics. Equivalent models that replicate a finite element model’s frequency response for bus-spacer and 90° elbow components were incorporated in alternative transients program-electromagnetic transients program (ATP-EMTP) using a pole-residue equivalent circuit derived following rational fitting using the well-established and robust method of vector fitting (VF). A large model order is often required to represent this frequency dependent behaviour through admittance matrices, leading to increased computational burden. Moreover, while highly accurate models can be derived, the data extracted from finite element solutions can be non-passive, leading to instability when included in time domain simulations. A simple method of improved stability for FEA derived responses along with a method for identification of a minimum required model order for stability of transient simulations is proposed.
1. Introduction
With the exception of certain types of electromagnetic pulse (EMP) phenomena, very fast transients (VFTs) are the highest frequency class of transients that pose a direct threat to the insulation of high voltage equipment. They are damped oscillatory transients most commonly associated with disconnector switching in gas insulated substations (GIS). During disconnector operation, due to its relatively slow movement, multiple breakdowns of the gas gap will occur between the contacts. During each breakdown event, following the subsequent collapse of the electric field sustained between the contacts, an EMP is initiated with a rise time of several nanoseconds and propagates throughout the system, reflecting, refracting and attenuating at discontinuities. The superposition of electromagnetic waves at any point within the system can lead to overvoltages, termed very fast transient overvoltages (VFTOs), which have magnitudes up to 2.5 pu, with frequencies extending up to 100 MHz [1]. VFTs have been identified as a potential threat to insulation through ageing and surface breakdown and are also a significant source of interference to control systems through both conducted, near field and far field coupling [2].
Accurate modelling and simulation of a GIS is essential for equipment design, insulation coordination and even for post-failure investigations following surface flashover of insulating spacers. One of the principal outcomes for VFT studies is the correct estimation of reflected and transmitted electromagnetic wave behaviour at impedance discontinuities. Determination of a component’s transient behaviour is essential for the accurate calculation of the maximum overvoltage, waveshape and frequency content; all important factors when trying to determine the probability of a breakdown under VFTO. Following a modelling task, it should be possible to identify the potential system vulnerabilities, allowing informed, preventative action to be taken to avoid further risk. A circuit-based modelling approach for VFTs consists of an electromagnetic transient (EMT) study, which involves the representation of each component within the range of interest by its lumped or distributed parameters. Models are constructed to incorporate each anticipated change in characteristic impedance.
While models for VFT analysis are very detailed, interaction with the wider system is not usually a concern, owing to the perceived increase in attenuation of high frequency electromagnetic waves when propagating externally over a lossy ground. Distributed line models should account for frequency-dependent behaviour, which is evident across the VFT frequency range. However, existing frequency-dependent line models available in alternative transients program-electromagnetic transients program (ATP-EMTP) [3] have proven to be numerically unstable at very high frequencies [4]. New methods reported in [5], adopt a modified transmission line approximation, due to the possible mode conversion for waves propagating over a lossy ground from transverse electromagnetic (TEM) mode to surface wave propagation in the VFT frequency range, which are subject to lower attenuation. This finding could impact the extent of the region under study and also allow numerically stable, frequency-dependent line or cable parameters to be produced directly in ATP-EMTP.
In this paper, an alternative method to the parameter-based calculation approach, commonly used by various EMTPs is proposed. The method is adapted from those used in simulations for high frequency printed circuit board (PCB) development, utilising elements of circuit-based modelling, along with enhancements, introduced through finite element analysis (FEA), which is the application of the finite element method (FEM). Through the combined use of circuit-based and FEA methods, a more accurate estimation of component behaviour can be realised. The proposed method focusses on the extraction of frequency dependent behaviour from finite element models, initially in the form of scattering parameters (S-parameters) which describe a component’s reflection and transmission coefficients. Following the conversion of S-parameters to admittance matrices, the frequency-dependent behaviour is captured as a rational function approximation using vector fitting (VF). This rational approximation is then used to derive multiple order, pole-residue equivalent circuits, capable of replicating a component’s frequency response. With any VF derived model, a major concern is the stability of the model in the time domain. To achieve stability, the model must be passive, i.e., it must not generate energy. Passivity enforced, high order models produce good results in most cases, although the incorporation of many high order models in a large circuit can exceed program limits. As a result, a systematic approach was developed to identify the lowest possible order approximation for a stable transient simulation, prior to its inclusion in ATP-EMTP, giving significant savings in both user and computation times.
The proposed techniques can be applied to most passive GIS components. However, for the purpose of this study, the techniques were compared with a circuit-based modelling approach for two complex and important GIS components, the bus-spacer and the 90° elbow. The bus-spacer and 90° elbow equivalent models were included in ATP-EMTP, replacing their traditional lumped and distributed component representations. Simulations were then carried out for several circuit termination scenarios in order to determine any limitations of the proposed method. As with any modelling technique, model validation is of the highest importance and is usually achieved by performing controlled on-site or laboratory-based measurements. In the absence of measurement data, validation was achieved by comparison with results produced using the proven software package, advanced design system (ADS) [6]. ADS permits the inclusion of multiple components via their S-parameters directly in transient simulations, using a convolution-based technique. This allows single or multiple pole-residue equivalents to be validated.
2. Finite Element Method for Very Fast Transients
While computationally intensive, FEA can provide a more intuitive understanding of the complex behaviour of various components and materials when subjected to a set of physical conditions. Finite element modelling for electromagnetic applications can be divided into static, low and high frequencies. Static and low frequency simulations can be useful for obtaining a good initial estimate for conditions at the lower end of the VFT spectrum. However, the accuracy of solutions deteriorates as the wavelength approaches the geometric dimensions of the system under study. As a rule of thumb, for frequencies above which the dimensions of a component exceed one tenth of the corresponding wavelength, a full-wave solution is required [7]. In the VFT frequency range, the coaxial bus can behave as a coaxial waveguide, with many changes in characteristic impedance (discontinuities) and numerous unshielded apertures from which fields can couple externally or radiate. It is, therefore, more appropriate to analyse the problem in terms of electromagnetic waves.
At very high frequencies, when observing distributed components, voltages and currents are not easily determined, as their distribution within a system varies spatially and temporally. At a specific location, these quantities are considered as the line integrals of electric and magnetic fields respectively [8], as given by Equations (1) and (2).
where and are the electric and magnetic field vectors, respectively.
Instead, at very high frequencies, it is more appropriate to represent components by their S-parameters, which are multi-port representations of complex reflection and transmission coefficients [8], as shown in Equation (3).
where and are related to reflected voltage waves, and are related to transmitted voltage waves of their respective ports.
S-parameters are commonly used to characterise the frequency-dependent behaviour of devices in many high frequency engineering disciplines, as they simply and effectively describe the relationship between incident and reflected waves at the device ports when terminated with a chosen reference impedance. While they are also useful for the characterisation of components at low frequencies, they are particularly useful for identifying the behaviour of components when subjected to high-frequency conditions, where parasitic capacitances and inductances become more relevant but are sometimes difficult to predict or incorporate in circuit-based models. Some circuit simulators allow S-parameters to be included directly in transient and frequency domain simulations. For simulators without this functionality, the information contained can be converted to alternative forms including impedance and admittance parameters [9].
While the physics of a finite element simulation are dependent on the type of study being performed, for a general frequency domain VFT study using FEA [10], a weak form of a boundary value problem representing a time harmonic wave equation of the form given in Equation (4) is solved.
where εr is the relative permittivity, μr is the relative permeability, k0 is the wavenumber of free space, σ is the electrical conductivity, and is the electric field vector.
For completely enclosed sections of bus, the skin effect confines the transients internally for the VFT frequency range and above. Meshing of the entire metallic domain can thus be avoided and metal losses can be accounted for by applying an impedance boundary condition, represented by Equation (5).
where is the magnetic field vector, is the unit vector, i.e., a vector perpendicular to the boundary surface with a magnitude of 1, and is the source electric field vector used to specify a source surface current on the boundary [10].
For a completely sealed system, only the gaseous domain within the bus and dielectric barriers require meshing for computations. Where apertures are present, such as the gas-air bushing or unshielded spacer, an external air domain may be required. A Scattering boundary condition, given in Equation (6) can be applied to the outer walls of the external air domain to absorb outgoing waves, reducing unrealistic reflections from the discontinuity created by an artificially truncated domain. For any other conductive boundary, where losses are of no concern, the perfect electric conductor (PEC) boundary condition of Equation (7) is applied.
A port boundary condition can provide both excitation of the structure and absorption of outgoing waves. Complex port shapes require numerical analysis to determine the propagation modes at a specific frequency. Simple port shapes, such as the coaxial port, allow specification of the port impedance, calculated analytically for a coaxial structure, as shown in Equation (8). Lumped ports provide a convenient method of excitation and absorption at the frequencies of interest, while also allowing the extraction of S-parameters and hence, provide sufficient detail to enable the extraction of frequency dependent behaviour for the enhancement of circuit models.
where εr is the dielectric constant, Rout is the radius of the enclosure, and Rin is the radius of the main conductor.
To demonstrate the use of FEA for GIS components, the bus-spacer intersection and 90° elbow models, shown in Figure 1, were created using the RF module of COMSOL Multiphysics® (Burlington, MA, USA) [10]. Insulating spacers provide mechanical support to the HV conductor and can provide a gas tight partition between gas zones.
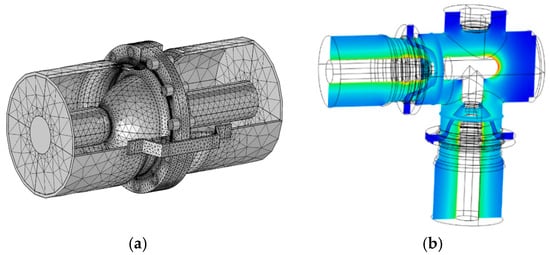
Figure 1.
Three dimensional finite element models: (a) section of bus-spacer intersection; and (b) 90° elbow.
Electric and magnetic field distributions become extremely complex at the bus–spacer junction, particularly at high frequencies. They are a common location for surface discharges under VFTs; hence, the importance of accurate circuit representations is crucial. The 90° elbow is another complex GIS component. At very high frequencies, the 90° angle can encourage resonances and even the conversion to higher order transverse electric (TE) or transverse magnetic (TM) modes of propagation [11]. For many GIS components, even in the VFT frequency range, standard transmission line assumptions may no longer be valid [12].
The spacers are represented by a conical geometry with the material defined by some basic electrical properties for epoxy resin; permittivity, permeability and conductivity. Dielectric and resistive losses are included using a complex permittivity and a finite conductivity. To simplify the models for the purpose of this study, the external surfaces of the spacers (radiating apertures) were assigned PEC boundaries, providing a significant saving in computation time (up to 62% for the entire frequency sweep). A summary of the simulation parameters is provided in Table 1. The results in S-parameter format (reflectance and transmittance) are given in Figure 2.

Table 1.
Summary of finite element method (FEM) simulation parameters.
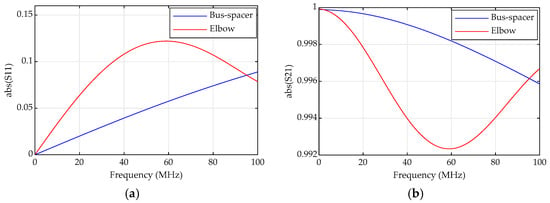
Figure 2.
Bus-spacer and elbow scattering parameters (S-parameters): (a) S11 (reflectance); and (b) S21 (transmittance).
3. Vector Fitting and Equivalent Circuit Extraction
As discussed in the previous section, many elements of the GIS are represented as distributed parameter lines. Where multiple frequencies are anticipated, it is common practice to initialise line models at a dominant frequency. With the wide spectrum present in VFTs, this can result in the inaccurate treatment of other frequencies. While frequency-dependent distributed parameter line models exist in ATP-EMTP, the Carson/Pollaczek earth return approaches, on which many line models are based, do not accurately account for displacement currents in regions with εr > 1 at very high frequencies [13]. These earth return admittances are, however, inherently considered when using field solvers that implement full Maxwell’s equations, when appropriate modelling domains are included. Several commercial software packages allow full frequency-dependent models through the use of black box macromodels, created with rational approximations of a frequency response through VF [14]. VF is a robust method of fitting measured or simulated frequency responses, with a rational function approximation. The resulting fit can be expressed as the pole residue form in Equation (9) and the state space form in Equation (10) as given in [15]:
where an and cn are the poles and residues either in real or complex conjugate pairs, d and e are the constant and proportional terms, A, B, C, D and E are the state space matrices.
The VF toolbox created by Gustavsen et al. [14,15,16] for MATLAB was used to derive a rational approximation for a set of frequency-dependent matrices. The toolbox requires specification of an initial pole type; for both the bus-spacer and elbow models, linearly spaced, complex poles were chosen. After specifying the initial pole type, the poles are iteratively relocated to achieve a better fit. Once the poles are obtained, the residues of Equation (9) are computed as a linear least-squares problem. In the frequency domain, the accuracy of the fitted response for both components is high. However, a good time domain solution is more difficult to attain, as stability, passivity and causality must be preserved. The stability of the solution is partially enforced during iterations, by flipping unstable (positive) poles to the left half of the complex plane [16]. While stable poles are assured, this does not guarantee a stable time domain response, as instability can result due to passivity violations. A passive system is one that does not generate energy. Small numerical errors produced by field solvers, noise, non-physical models or even artificially modified results can result in non-passive data [17]. Passivity is traditionally assessed using a Hamiltonian matrix [18], whereby the identification of purely imaginary eigenvalues constitutes a non-passive model. An issue with the Hamiltonian matrix is its size, resulting in excessive computation times for large models. The VF toolbox algorithms utilise one of two slightly different passivity assessment methods. For the assessment of S-parameter models, a half size passivity matrix is constructed, whereby the square root of the matrix eigenvalues are equal to the eigenvalues of the Hamiltonian matrix [19]. For admittance-based models, a half size singularity test matrix is constructed, which identifies the frequencies at which the conductance matrix becomes singular, thereby identifying bands of non-passivity [20]. Passivity is then enforced using fast residue perturbation (FRP) [21], which perturbs elements of the residue and constant matrices until eigenvalues are greater than zero, while minimising the change to the elements of the admittance matrix. Another stability determining criterion is causality. A non-causal system is one in which a response precedes an input. Causality is a requirement for passivity. Therefore, passivity enforcement should also ensure a causal model [22].
3.1. ATP-EMTP Circuit Inclusion
The VF approach is applicable to a wide range of components and transmission line types, represented by scattering, admittance and impedance parameters or transfer functions. An approximation of a component can be included in EMT type software packages in a number of ways. While not available in ATP-EMTP at present, other line types that utilise VF include the universal line model (ULM) [23], which is based on fitted characteristic admittance and propagation matrices and inclusion through Norton equivalent conductances using recursive convolution. Another suitable alternative to the ULM is the folded line equivalent (FLE) proposed by Gustavsen and Semlyen [24], which utilises a transformed nodal admittance matrix, based on open and short circuit admittances.
The proposed method, after conversion from S-parameters, applies VF to elements of the admittance matrix, e.g., for a two-port component representation, VF is applied to the input, transfer and output admittances. While the spread of eigenvalues in a direct admittance-based representation can lead to error magnification under some terminal conditions, it is postulated that short circuit (electric wall) and open circuit (magnetic wall) conditions are rarely encountered in appropriately terminated VFT circuit simulations. It is, therefore, considered appropriate to fit a multiport admittance matrix directly, provided the careful consideration of component terminations is maintained when incorporated in a larger circuit. Inclusion of the rational approximation could take a convolution-based form, as previously mentioned. The alternative and relatively straightforward option used in this work is inclusion of components via pole-residue equivalent circuits. The VF Toolbox’s Netgen routine [15] uses the fitted pole residue approximation to create an ATP-EMTP ready, equivalent multi-port network, which replicates the input, transfer and output behaviour of the component, as shown in Figure 3, using Equations (11)–(19). Provided an appropriate model order is selected, this equivalent circuit can be used to capture frequency dependent behaviour of most GIS components. Multiple equivalent networks are incorporated into the circuit using ATP-EMTP ‘branch include’ cards, with each port included via a small resistance or a measuring switch. The complete method for generation of pole-residue equivalent branch cards from a Finite Element model is further explained in Section 4.
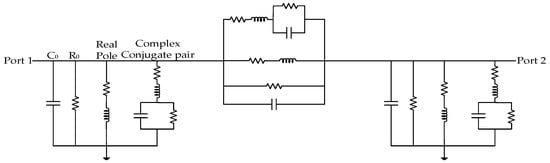
Figure 3.
General representation of a 1st order, two port pole-residue equivalent circuit.
For constant and proportional branches, we have:
for real poles RL branches, we have:
the complex conjugate pairs are:
and the resulting branch terms are:
Aside from the input and output port termination considerations while using this approach, it is important to ensure that the input, output and transfer admittance phase responses remain accurate after fitting. Furthermore, an awareness of the impact of finite precision branch cards is required [25]. ATP uses 14.6e precision (floating point number in scientific notation with a field of 14 characters, with 6 digits after the decimal point) as standard, with the option of 16.8e precision. Where concerns over branch precision exist, it may be more suitable to include the model using a convolution-based technique in order to avoid this limitation, although if using a convolution-based approach, it should be ensured that frequency dependent propagation delays and hence distortion characteristics are not lost. For the purpose of computing the voltage distribution during VFT events, propagation is assumed to be confined inside the gas insulated bus (GIB) and thus, for the purposes of this study, alternative modal propagation terms are disregarded. A more advanced method which considers these modal propagation terms is certainly required for the study of external transient enclosure voltages (TEVs). In addition, whilst it is possible that higher order modes are excited at very high frequencies, only the TEM mode is considered at the ports to simplify the equivalent model generation process. As it is only necessary to compute the input and output voltages and currents of small sections of single-phase bus under strictly controlled termination conditions, fitting an admittance matrix representation directly seems appropriate. The admittance matrix can be obtained from the S-parameters produced by the field solver when port terminations with equal reference impedances are assigned [8]. After subsequently fitting the admittance matrices, it was observed that many poles were identified at the lower frequency end of the spectrum, i.e., below a few MHz, leading to a noisy response. This was likely a result of numerical errors, as it is well known that full-wave solutions are known to break down at lower frequencies [26]. The extracted equivalent circuits showed various signs of instability ranging from an underdamped response when subjected to a step input to complete instability over a wide range of order approximations. Fitting and enforcing passivity on the S-parameters prior to conversion to admittance matrices significantly improved this, despite introducing a small degree of error, which can be expected following passivity enforcement.
3.2. Model Order Approximation
It is possible to estimate a suitable order of approximation from the number of resonance peaks present in the response. While this approach can result in a satisfactory fit, it was found for some fitting orders, various degrees of instability occurred for the time domain responses, even after pre-fitting the S-parameters and enforcing passivity. While limited by the number of frequencies present in the input data [27], a high order approximation, in most cases, provides reasonable results. However, intermittent higher order bands of instability were observed. In addition, including multiple high order circuit equivalents in EMTP becomes computationally demanding, with program limits being exceeded for a standard solver configuration. A trial and error approach for stability assessment, identifying an equivalent circuit for each order of approximation over a wide range and each time assessing the stability by transient simulation, would eventually identify stable solutions. This approach would require an excessive amount of effort as each order of approximation would need to be compared for each fitting option, i.e., every combination of order, weighting and treatment of the constant and proportional terms. Another simple but seemingly effective option was identified by observing the apparently converging behaviour of the root mean square (RMS) error between pre-fit and post-fit admittance matrices. Figure 4 demonstrates that as the model order is increased, the RMS error deviation converges to a more stable value. Comparison of individual error terms with the error at the asymptote allows identification of the minimum order of approximation for a stable transient solution and unstable order selections, as given by Equation (20):
where is lowest model order, is the RMS error of the admittance matrix, n is the model order, and s is the number of frequencies present in the input data.
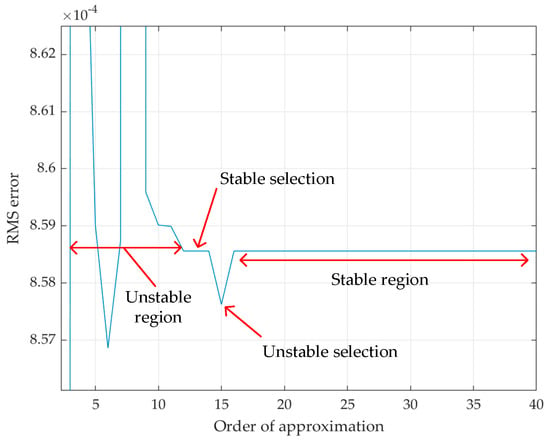
Figure 4.
Identification of stable model order.
The method is effective for the previously fitted admittance parameters and is untested for admittance parameters obtained via other methods, including those with noise. A simple algorithm presented in Appendix A, highlights the steps used to find the minimum order of approximation to achieve a stable transient simulation and generate equivalent circuits.
4. Simulations and Results
A comparison of modelling techniques is required in order to determine the scope of use of the VF approach. Simulations were carried out for various terminations. Initially, a comparison of the frequency response of each pole-residue model (computed in ATP-EMTP) with the frequency response of the finite element model (extracted from COMSOL Multiphysics®) was carried out to assess the accuracy of the fit. The frequency responses were further compared with the response of a circuit-based modelling approach based on a mixture of lumped components and distributed lines to identify any significant differences. For the comparison, a 13th order bus-spacer equivalent and a 15th order elbow equivalent circuit were used. For the circuit-based modelling approach, the 1 m bus section was represented by two 0.5 m distributed transmission lines (Bergeron lines intialised at 5 MHz) and the spacer at the center was represented as a 10 pF capacitance to ground. The elbow was represented by a 0.5 m section of distributed line at each end, two spacers, each having a 10 pF capacitance to ground, representing the capacitance between the conductor and the inner surface of the enclosure, along with two parallel sections of distributed line of differing lengths. To achieve a comparison, the input impedance was evaluated in EMTP using a frequency scan with a 1 A current source, with the equivalent circuit terminated by its characteristic impedance. The results are shown in Figure 5.
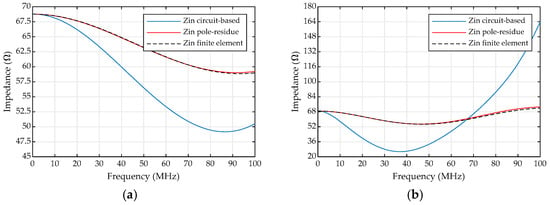
Figure 5.
Impedance-frequency comparison of modelling techniques: (a) bus-spacer; and (b) 90° elbow.
A close match between the pole-residue models and the finite element models implies a good fit in the frequency domain. The behaviour of the circuit-based elbow model differs significantly from both the pole-residue and finite element models. In order to validate the model in the time domain, the equivalent circuit was variously terminated by open/short circuit, a 68.7 Ω resistance (bus ZC), a 434 Ω resistor (maximum OHL ZC) and a capacitive-resistive termination (open disconnector 5 pF capacitor and bus ZC resistor). The validity of the pole-residue model results was assessed by comparison with the results of a transient simulation computed directly with the S-parameters in ADS for the same terminations. An overview of the VF/pole-residue modelling process and ADS comparison is given in Figure 6.
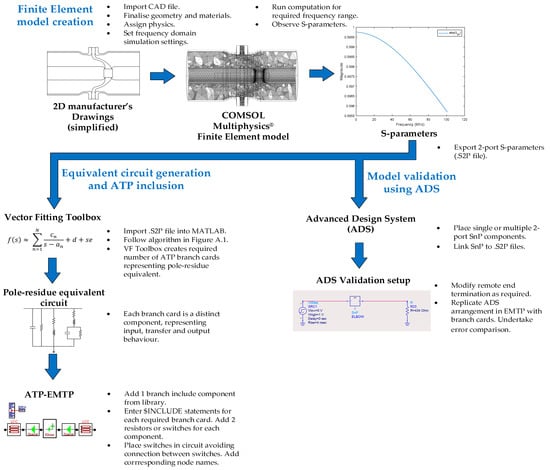
Figure 6.
Vector fitting (VF) modelling workflow and method validation using advanced design system (ADS).
The deviation of the pole-residue model response compared with the response computed in ADS was assessed over a 5 μs period using a 100 ps timestep, when excited by a 4 ns step impulse. The RMS error terms given in Table 2 provide a comparison of the difference when compared with the ADS transient response, which is also subjected to an error tolerance and is not the error to an exact solution. The responses for matched and OHL terminations for the elbow are given in Figure 7. The results given in Table 2 show a good match with the ADS representation for the matched, 1 Ω, OHL and capacitive-resistive terminations. The error for open and short circuit terminations is comparatively high as expected. Therefore, the method of directly fitting admittance matrices is limited. The error for the applied voltage is not shown in the table, as an ideal voltage source is applied directly to the input port of the model. Applying an ideal current source instead also maintains good accuracy for loaded circuit conditions.

Table 2.
Root mean square (RMS) error comparison of pole-residue model with ADS representation.
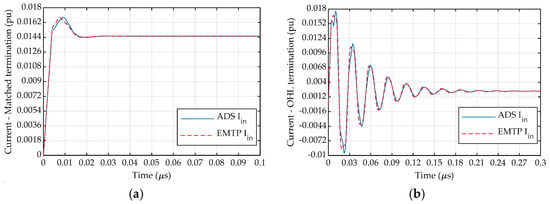
Figure 7.
EMTP vs. ADS elbow transient responses showing good agreement for: (a) matched termination; and (b) OHL termination.
The overall system response when multiple pole-residue equivalent circuits were integrated into a larger circuit was compared against the circuit-based representations in the 400 kV GIS model, for the system shown in Figure 8. Figure 9 provides the overall system diagram for clarification of the switching arrangement. The circuit-based GIS model was created following guidance from [2], using the elements shown in Table 3. Parasitic elements were added where required, however, most of the system is modelled by distributed components. Both models are identical, with the exception of the representation of the elbows and bus-spacer elements. For the pole-residue model, a total of nineteen bus-spacer sections and five elbow sections were replaced and reductions were made to the individual lengths of the bus to maintain the correct lengths.
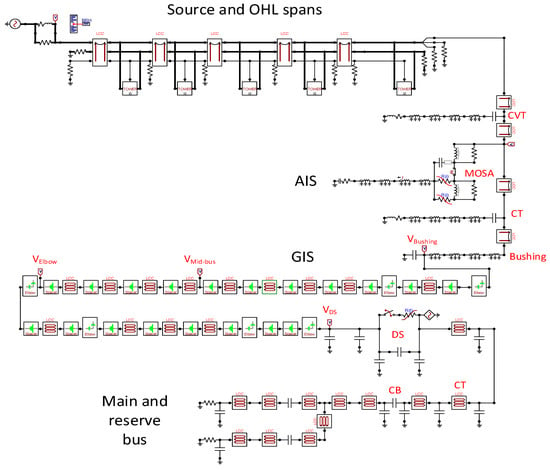
Figure 8.
Detailed circuit model.
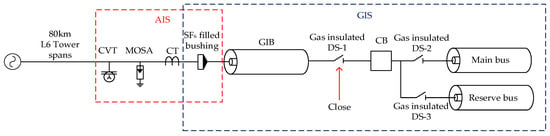
Figure 9.
400 kV system diagram.

Table 3.
Circuit model components.
A single VFT was simulated by closing DS-1, shown in Figure 9, represented by a simple exponentially decaying resistance, calculated using Toepler’s spark law [28]. A 1.1 pu 50 Hz source was used at one side of the disconnector and a −1.1 pu (peak) trapped charge was used at the disconnected side of the bus [29] to determine the highest possible magnitude of VFT for the specified circuit representation. The waveforms generated close to the gas to air bushing are shown for both the circuit-based model and pole-residue equivalent circuit in Figure 10 and Figure 11 respectively. A comparison of peak magnitudes at various locations was also made, as given in Table 4.
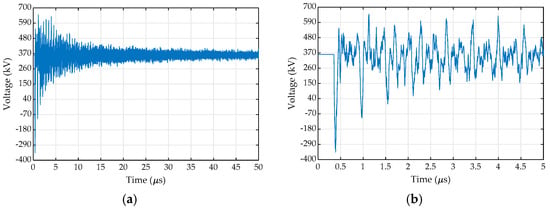
Figure 10.
Voltage at gas-air bushing for circuit-based model: (a) 50 μs duration; and (b) magnified 5 μs.
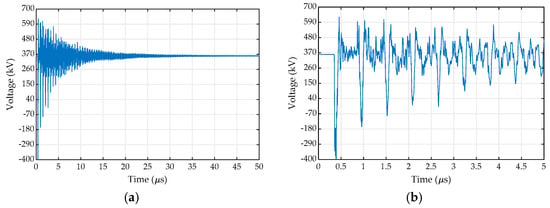
Figure 11.
Voltage at gas-air bushing for pole-residue model: (a) 50-μs duration; and (b) magnified 5-μs.

Table 4.
Comparison of maximum peak voltage around system.
Based on the results shown in Table 4, it is clear that the circuit-based modelling approach predicts slightly higher magnitude overvoltages than the pole-residue model, with the exception of voltage measured at the mid-bus location, as shown in Figure 8. Furthermore, the time of peak occurrence is also earlier for the pole-residue model. The differences in magnitudes and time of peak magnitude are due to the differences in impedance of the models from each modelling approach over the frequency range, however, it is difficult to quantify each difference due to the number of frequency-dependent components included in the model. For example, the pole-residue model has a much earlier peak at the bushing than the circuit-based model. The impedance at the top of the bushing is calculated as 302 Ω. Based on the impedance-frequency plot of the elbow in Figure 5b, at the higher frequency range it can be observed that the difference in impedance of the elbow adjacent to the bushing for the pole-residue representation, is higher than that of the circuit-based representation; hence, a more significant positive reflection is possible. Subsequently, an in-phase superposition occurs to achieve the later peak for the circuit-based model, whilst around the same time, a 180° out-of-phase wavefront limits the peak for the pole-residue model.
5. Conclusions
In the VFT frequency range, standard transmission line approximations can result in error or numerical instability. The need for an alternative representation of GIS components in transient studies is apparent. The proposed technique based on the fitting of a frequency response derived from finite element models has no such frequency limitations. The procedure developed to identify the lowest possible stable model order approximation, allows considerable savings in time and computational resources.
While there is not a significant difference in magnitudes for the presented case, for systems in which the computed magnitudes are close to the insulation levels of system components, a standard circuit-based modelling approach could provide justification for unnecessary mitigation. For a general VFT coordination study, the minor difference in magnitudes in the presented case may not justify the additional effort required. However, for post-failure investigations, where more detailed analysis of magnitudes and waveshapes are required, when accompanied by measurements, this modelling approach can assist with the identification of the conditions that led to failure. As implied, the proposed modelling approach is limited by a circuit’s termination impedance and has only been tested for single phase sections of GIS. Strict observation of the overall circuit behaviour is required as inaccuracies can be significant under some termination conditions. Further investigation of the method and validation of models will ultimately determine the full scope of its use.
Author Contributions
Conceptualization, J.J., M.A., D.C., and A.H.; methodology, J.J.; software, J.J.; validation, J.J., M.A., D.C. and A.H.; formal analysis, J.J.; investigation, J.J.; data curation, J.J.; writing—original draft preparation, J.J.; writing—review and editing, J.J., M.A., D.C., D.G. and A.H.; visualization, J.J.; supervision, M.A., D.G. and A.H. All authors have read and agreed to the published version of the manuscript.
Funding
This ICASE research project is co-funded by the Engineering and Physical Sciences Research Council (EPSRC) and National Grid, Grant Number 1809397.
Acknowledgments
The authors would like to thank the other members of the Advanced High Voltage Engineering Research Centre (AHIVE) for their assistance throughout this project, with special mention to Chris Stone and Meirion Hills, whose technical support has been invaluable throughout.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
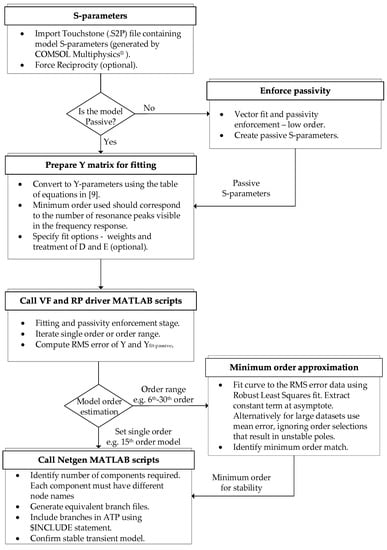
Figure A1.
Algorithm for pole-residue model generation and determination of the minimum order of approximation.
References
- Working Group 33/13-09. Very fast transient phenomena associated with Gas Insulated Substations. In Proceedings of the International Conference on Large High Voltage Electric Systems, Cigre, Paris, 28 August–3 September 1988; Available online: https://e-cigre.org/publication/33-13_1988-very-fast-transient-phenomena-associated-with-gis (accessed on 5 February 2020).
- IEEE Working Group 15.08.09. Modeling and Analysis of System Transients Using Digital Programs—Part 2; IEEE PES Technical Report PES-TR7; IEEE: Piscataway, NJ, USA, 1998; Available online: https://resourcecenter.ieee-pes.org/technical-publications/technical-reports/PESTR7.html (accessed on 5 February 2020).
- Meyer, W.S.; Liu, T. Alternative Transients Program (ATP) Rule Book 1992. Available online: https://www.eeug.org/index.php/downloads/new-downloads (accessed on 5 February 2020).
- Xue, H.; Ametani, A.; Mahseredjian, J.; Baba, Y.; Rachidi, F.; Kocar, I. Transient Responses of Overhead Cables Due to Mode Transition in High Frequencies. IEEE Trans. Electromagn. Compat. 2018, 60, 785–794. [Google Scholar] [CrossRef]
- Xue, H.; Ametani, A.; Mahseredjian, J. Very Fast Transients in a 500 kV Gas-Insulated Substation. IEEE Trans. Power Deliv. 2019, 34, 627–637. [Google Scholar] [CrossRef]
- Keysight. Advanced Design System 2017. Available online: http://edadownload.software.keysight.com/eedl/ads/2017/updates/update_0.5/pdf/Advanced_Design_System_2017_Update_Release_Notes.pdf (accessed on 3 February 2020).
- Swanson, D.G.; Hoefer, W.J.R. Microwave Circuit Modeling Using Electromagnetic Field Simulation; Artech House: Boston, MA, USA, 2003. [Google Scholar]
- Pozar, D.M. Microwave Engineering; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2012. [Google Scholar]
- Frickey, D.A. Conversions Between S, Z, Y, H, ABCD, and T Parameters which are Valid for Complex Source and Load Impedances. IEEE Trans. Microw. Theory Tech. 1994, 42, 205–211. [Google Scholar] [CrossRef]
- COMSOL Multiphysics® v. 5.4. Available online: https://www.comsol.com/release/5.4 (accessed on 5 February 2020).
- Behrmann, G.; Smajic, J. RF PD signal propagation in GIS: Comparing S-parameter measurements with an RF transmission model for a short section of GIS. IEEE Trans. Dielectr. Electr. Insul. 2016, 23, 1331–1337. [Google Scholar] [CrossRef]
- James, J.; Albano, M.; Guo, D.; Haddad, A.M. Application of Multiple Modelling Techniques for Analysis of Very Fast Transient Overvoltages in GIS. In Proceedings of the 2018 IEEE International Conference on High Voltage Engineering and Application (ICHVE), Athens, Greece, 10–13 September 2018. [Google Scholar] [CrossRef]
- Ametani, A.; Miyamoto, Y.; Baba, Y.; Nagaoka, N. Wave Propagation on an Overhead Multiconductor in a High-Frequency Region. IEEE Trans. Electromagn. Compat. 2014, 56, 1638–1648. [Google Scholar] [CrossRef]
- Gustavsen, B.; Semlyen, A. Rational approximation of frequency domain responses by vector fitting. IEEE Trans. Power Deliv. 1999, 14, 1052–1061. [Google Scholar] [CrossRef]
- Gustavsen, B. Computer code for rational approximation of frequency dependent admittance matrices. IEEE Trans. Power Deliv. 2002, 17, 1093–1098. [Google Scholar] [CrossRef]
- Gustavsen, B. Improving the Pole Relocating Properties of Vector Fitting. IEEE Trans. Power Deliv. 2006, 21, 1587–1592. [Google Scholar] [CrossRef]
- Grivet-Talocia, S.; Gustavsen, B. Passive Macromodeling; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2016; ISBN 9781118094914. [Google Scholar]
- Boyd, S.; Balakrishnan, V.; Kabamba, P. A bisection method for computing the H∞ norm of a transfer matrix and related problems. Math. Control Signals Syst. 1989, 2, 207–219. [Google Scholar] [CrossRef]
- Gustavsen, B.; Semlyen, A. Fast Passivity Assessment for S-Parameter Rational Models Via a Half-Size Test Matrix. IEEE Trans. Microw. Theory Tech. 2008, 56, 2701–2708. [Google Scholar] [CrossRef]
- Semlyen, A.; Gustavsen, B. A Half-Size Singularity Test Matrix for Fast and Reliable Passivity Assessment of Rational Models. IEEE Trans. Power Deliv. 2009, 24, 345–351. [Google Scholar] [CrossRef]
- Gustavsen, B. Fast Passivity Enforcement for Pole-Residue Models by Perturbation of Residue Matrix Eigenvalues. IEEE Trans. Power Deliv. 2008, 23, 2278–2285. [Google Scholar] [CrossRef]
- Triverio, P.; Member, S.; Grivet-Talocia, S.; Member, S.; Nakhla, M.S.; Canavero, F.G.; Achar, R. Stability, Causality, and Passivity in Electrical Interconnect Models. IEEE Trans. Adv. Packag. 2007, 30, 795–808. [Google Scholar] [CrossRef]
- Morched, A.; Gustavsen, B.; Tartibi, M. A universal model for accurate calculation of electromagnetic transients on overhead lines and underground cables. IEEE Trans. Power Deliv. 1999, 14, 1032–1038. [Google Scholar] [CrossRef]
- Gustavsen, B.; Semlyen, A. Admittance-Based Modeling of Transmission Lines by a Folded Line Equivalent. IEEE Trans. Power Deliv. 2009, 24, 231–239. [Google Scholar] [CrossRef]
- Lima, A.C.S.; Gustavsen, B.A.; Fernandes, A.B. Inaccuracies in Network Realization of Rational Models Due to Finite Precision of RLC Branches. 2007. Available online: https://www.semanticscholar.org/paper/Inaccuracies-in-Network-Realization-of-Rational-Due-Lima-Gustavsen/1b2c63cbeb645f93274227420a01bd0ac0322ff5 (accessed on 3 February 2020).
- Zhu, J.; Jiao, D. Fast Full-Wave Solution That Eliminates the Low-Frequency Breakdown Problem in a Reduced System of Order One. IEEE Trans. Compon. Packag. Manuf. Technol. 2012, 2, 1871–1881. [Google Scholar] [CrossRef]
- Gustavsen, B. Matrix Fitting Toolbox 2009. Available online: https://www.sintef.no/projectweb/vectfit/downloads/matrix-fitting-toolbox/ (accessed on 15 December 2019).
- Toepler, M. Zur Bestimmung der Funkenkonstante. Arch. für Elektrotechnik 1927, 18, 549–562. (In German) [Google Scholar] [CrossRef]
- British Standards Institute. High-Voltage Switchgear and Controlgear. Alternating Current Disconnectors and Earthing Switches; BS EN IEC 62271-102:2018; BSI Standards Limited: London, UK, 2018. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).