A Decentralized Optimization Strategy for Distributed Generators Power Allocation in Microgrids Based on Load Demand–Power Generation Equivalent Forecasting
Abstract
1. Introduction
- All processes and parameters of the proposed decentralized optimization strategy are designed in a fully distributed way, which do not need any center or leader to assign global variables or parameters. Each DG only needs to communicate with its neighbors under sparse communication to reach the optimal results.
- A load demand–power generation equivalent forecasting method is proposed to improve the decentralized optimization strategy, which replaces the load prediction center and the load sensor devices. The balance constraint only needs information of predicted power output instead of load demand. The historical power generation data, which is used for prediction, has already satisfied the balance constraint of power supply and load demand. When the sum of real power output equals to the sum of predicted output, the balance between power supply and load demand is achieved.
- The uncertainty of renewable generation is considered in the cost modeling process to optimize the expense comprehensively. A penalty term is introduced into the cost model for adjustment of the expense cost by the fluctuation of renewable energy sources and the forecasting error.
2. Load Demand–Power Generation Equivalent Forecasting Based Distributed Generators (DGs) Power Allocation Strategy Formulation
- As mentioned in Section 1, the centralized optimization algorithms deeply depend on the control center, which requires collecting global information from the whole network. With the rapid increasing number of DG units, those approaches are not suitable for a large-scale network, due to significance communications and massive computational overhead. On the contrary, decentralized optimization algorithms mainly rely on consensus or multi-agent systems, which merely need sparse communication with neighbor DGs to achieve information interaction and cooperation [18]. Therefore, the decentralized mode is more suitable to implement the optimization.
- The optimization problem is aiming at the minimum cost of the outputs of DGs. When the total outputs of DGs is determined, a ‘Power Allocation Strategy’ need to be studied to obtain the output of each DG unit. Thereby, we can get the accurate dispatching plan of each DG unit. The Power Allocation Strategy consists of the optimization objective and the optimization algorithm.
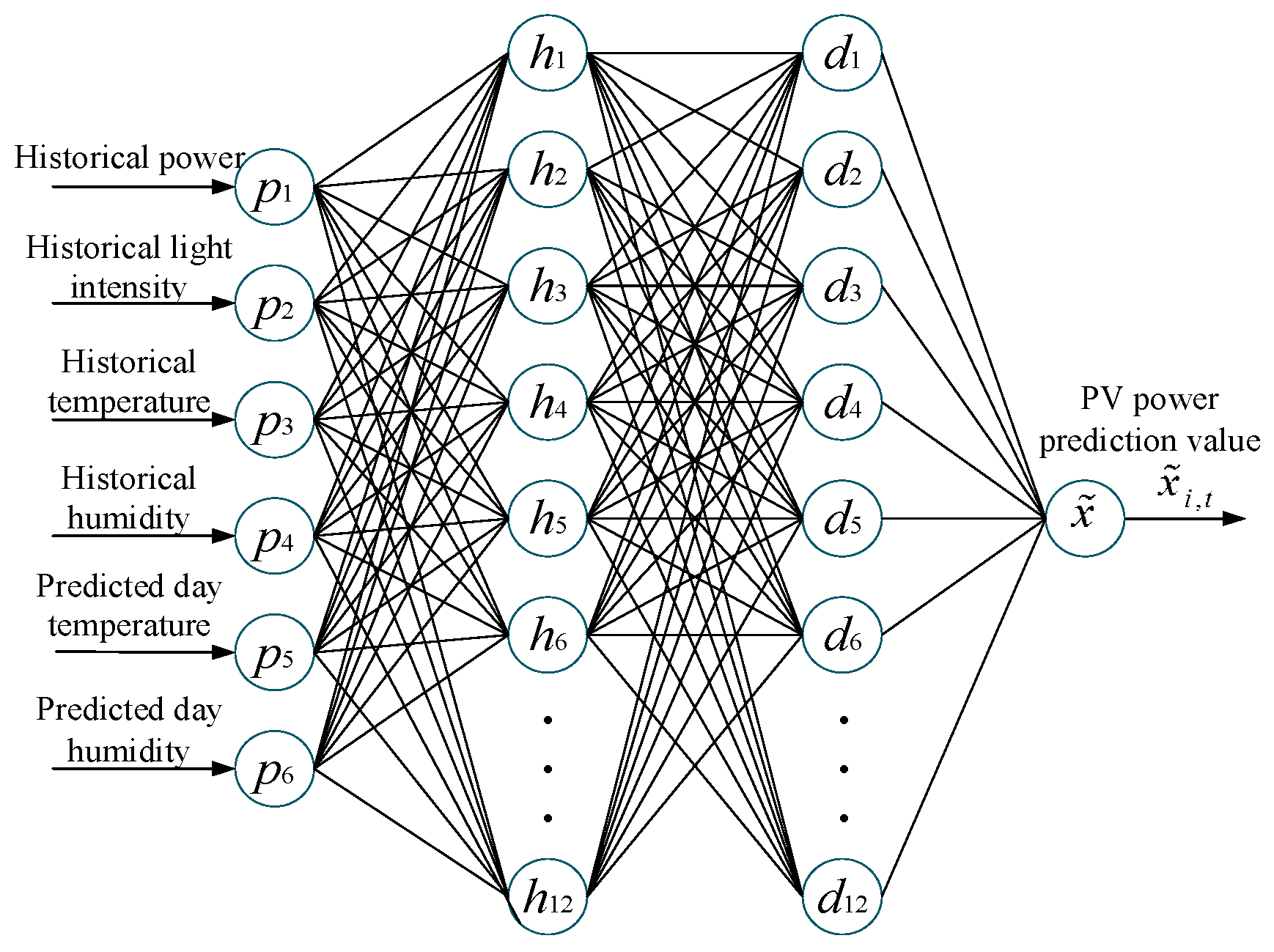
- A load demand–power generation equivalent forecasting method is proposed in the optimization algorithm, which only needs the information of predicted power output instead of load demand. The historical power generation data, which is used for prediction, has already satisfied the balance constraint of power supply and load demand. Therefore, when the balance between the real power output and the predicted output is gained, the equation constraint of power supply and load demand is satisfied. Thereby, the load demand information could be substituted by the predicted power generation in a local way.
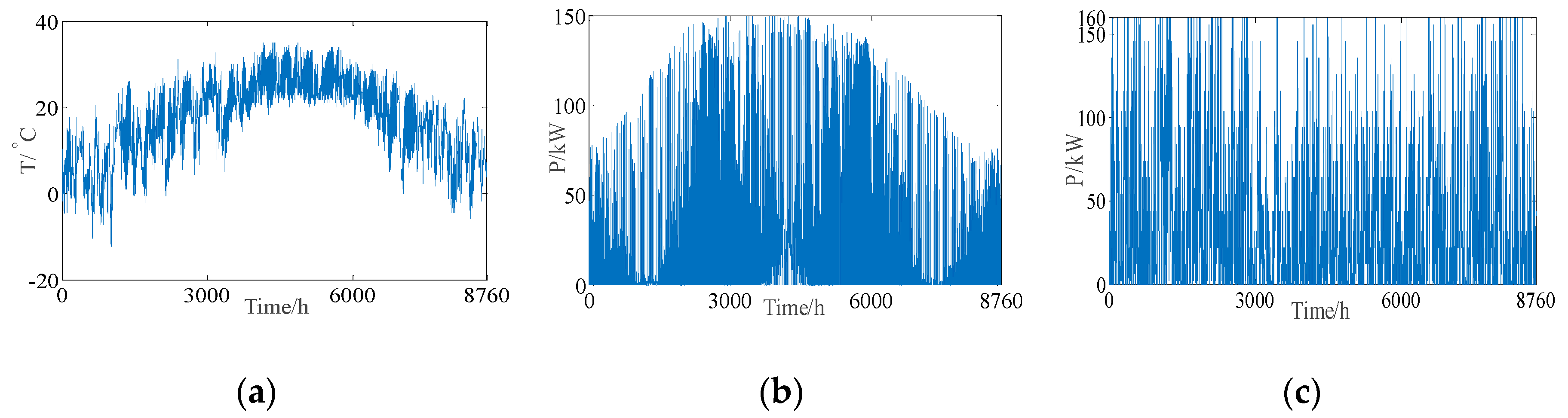
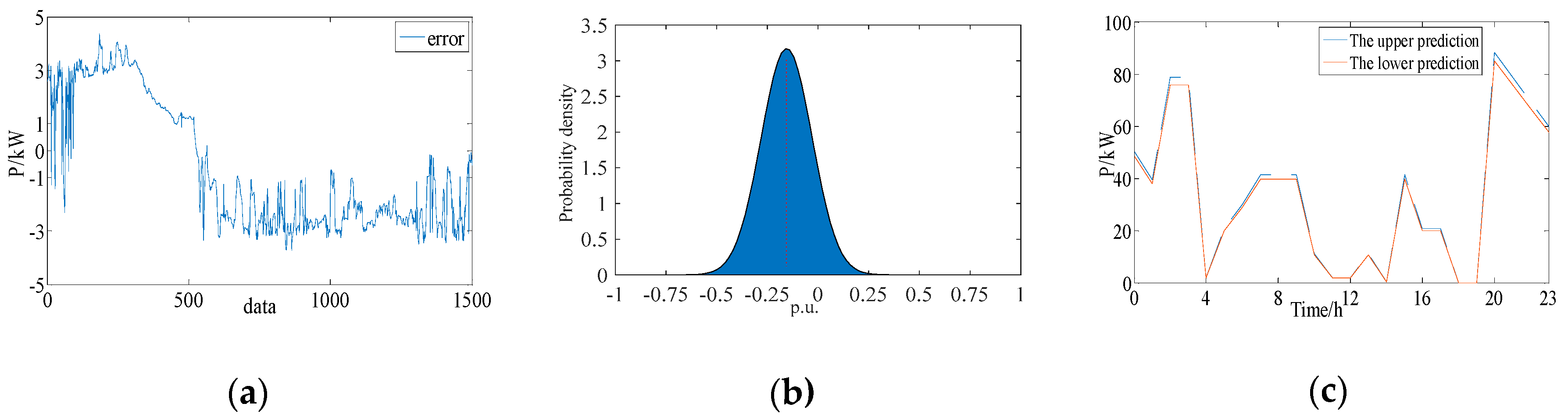
- Due to the uncertainty and fluctuation of the renewable energy sources, the prediction error is considered when gaining the predicted value for fitting a feasibility interval, and the real values of the predicted day are added to the training data to update the training process for a rolling optimization. Before establishing the model of optimization, the prediction method needs to be analyzed to support the optimization strategy.
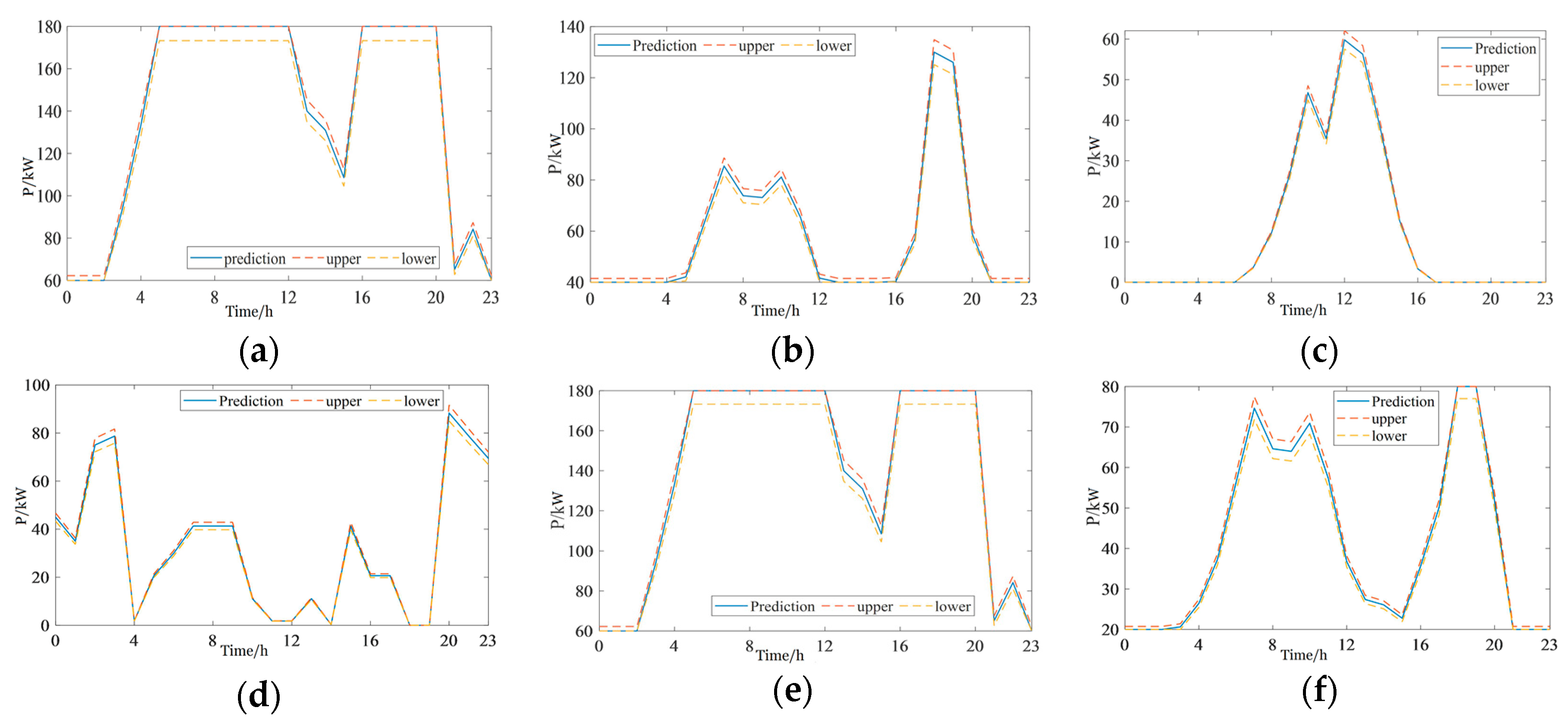
2.1. Generation Output Prediction Interval Model
2.2. Optimization Model and Formulation
2.2.1. Optimization Objective
2.2.2. Cost Functions and Constraints of DGs
2.3. Optimization Solution
3. The Decentralized Optimization Method Analysis
3.1. Preliminary Knowledge
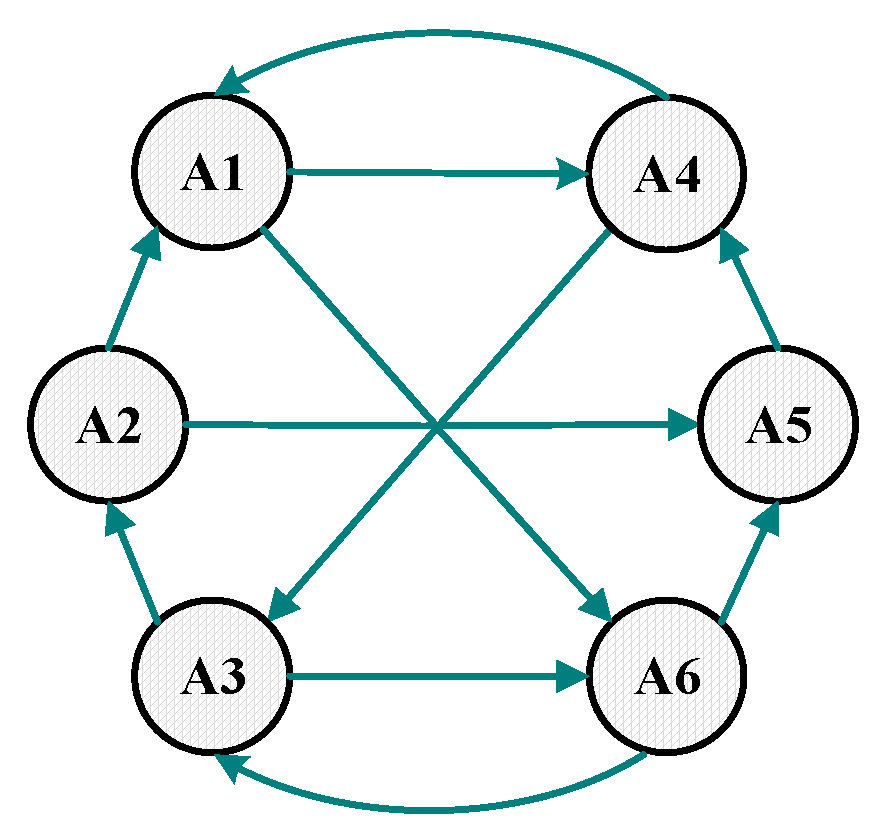
3.1.1. Graph Theory
3.1.2. The Design of Communication Weight
3.1.3. Assumptions and Lemmas
- 1.
- 1is a right eigenvector of all,and
- 2.
- 1 is a left eigenvector of all , and
3.2. Consensus-Based Optimization Algorithm
3.3. Proof of Convergence
3.4. Generalization to Constrained Condition
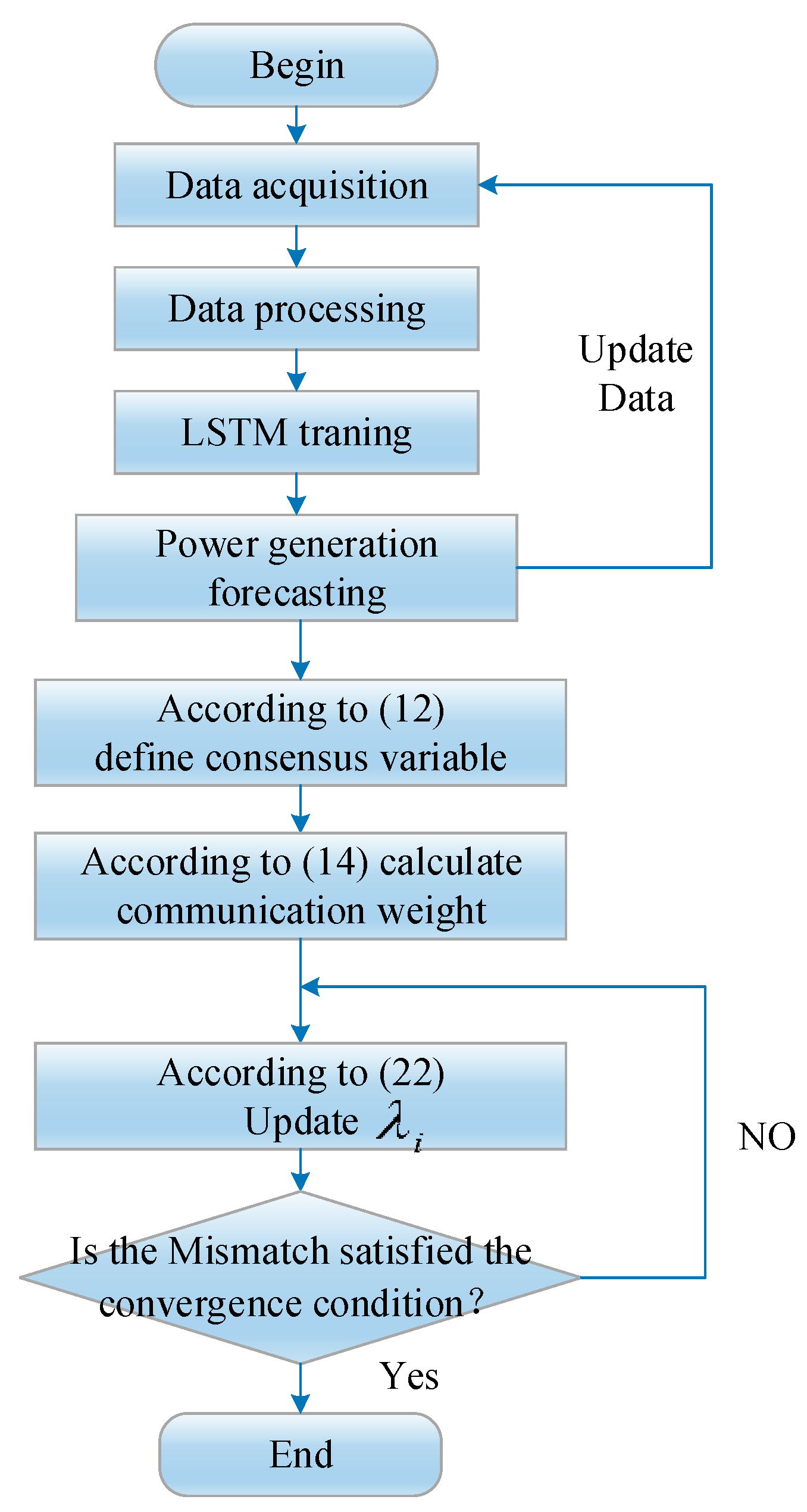
3.5. Solution Algorithm Flow
4. Simulation and Case Study
4.1. Verification of the Proposed Method
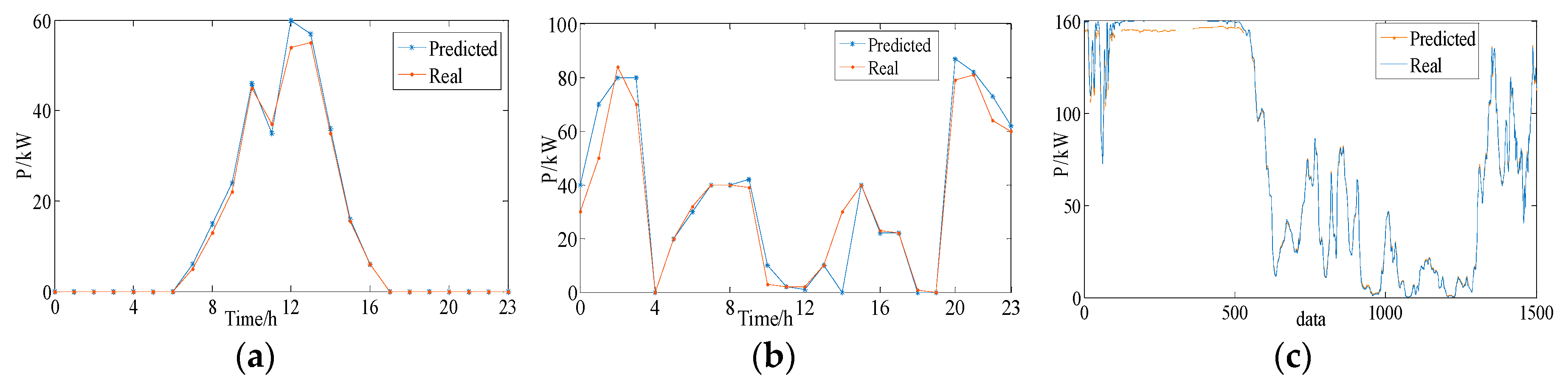
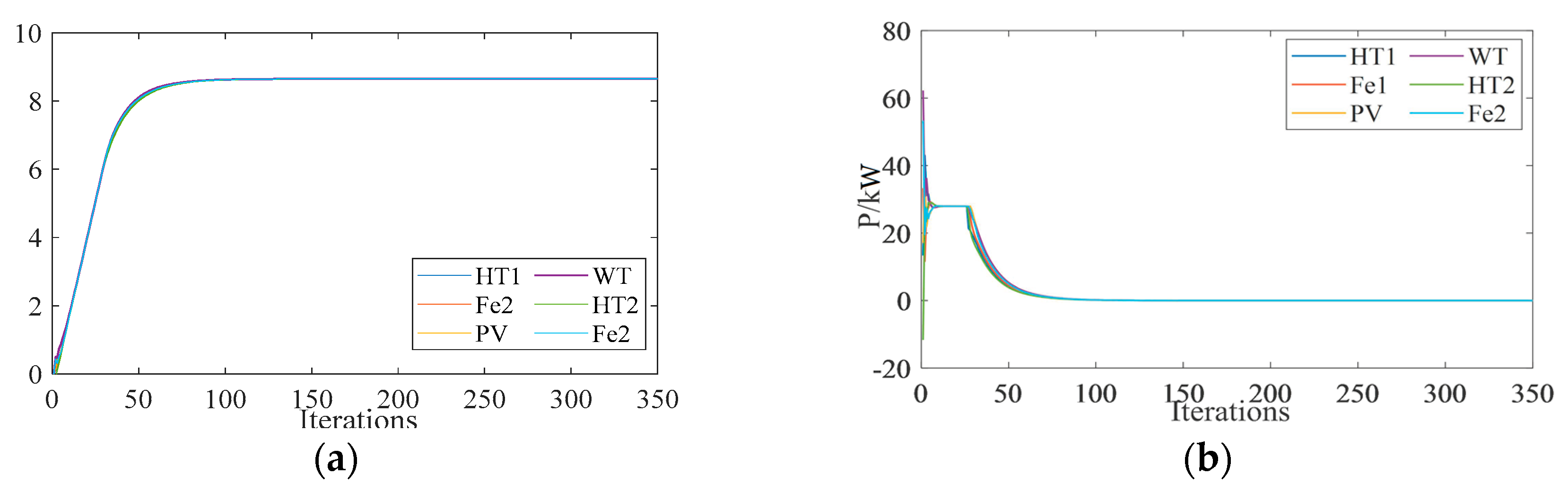
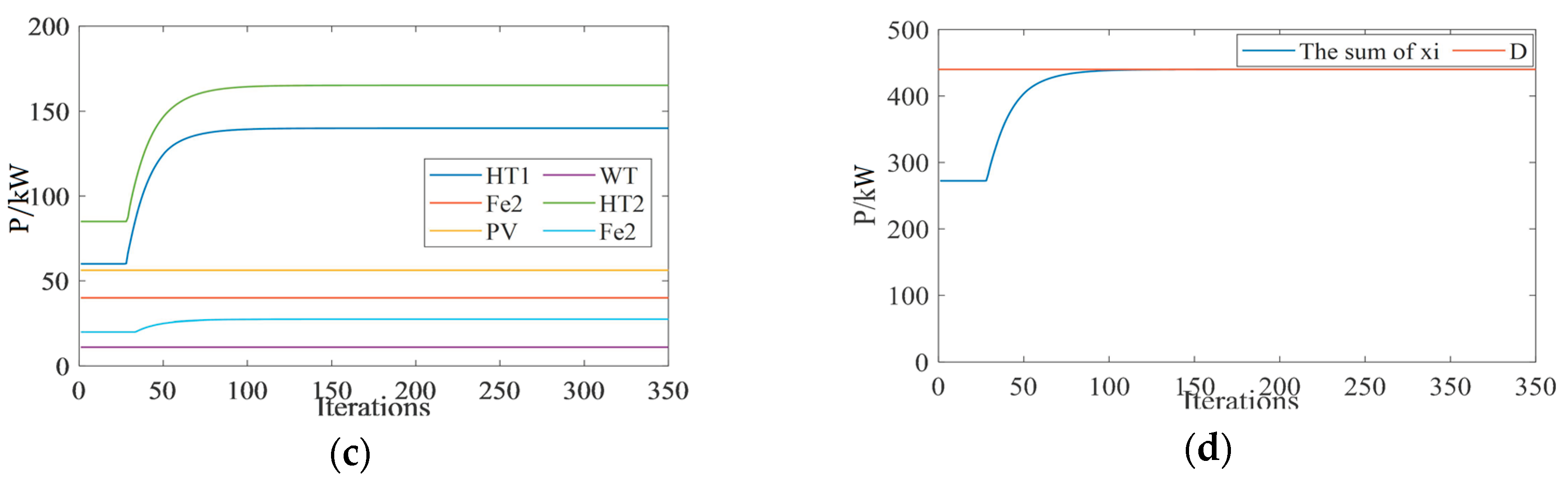
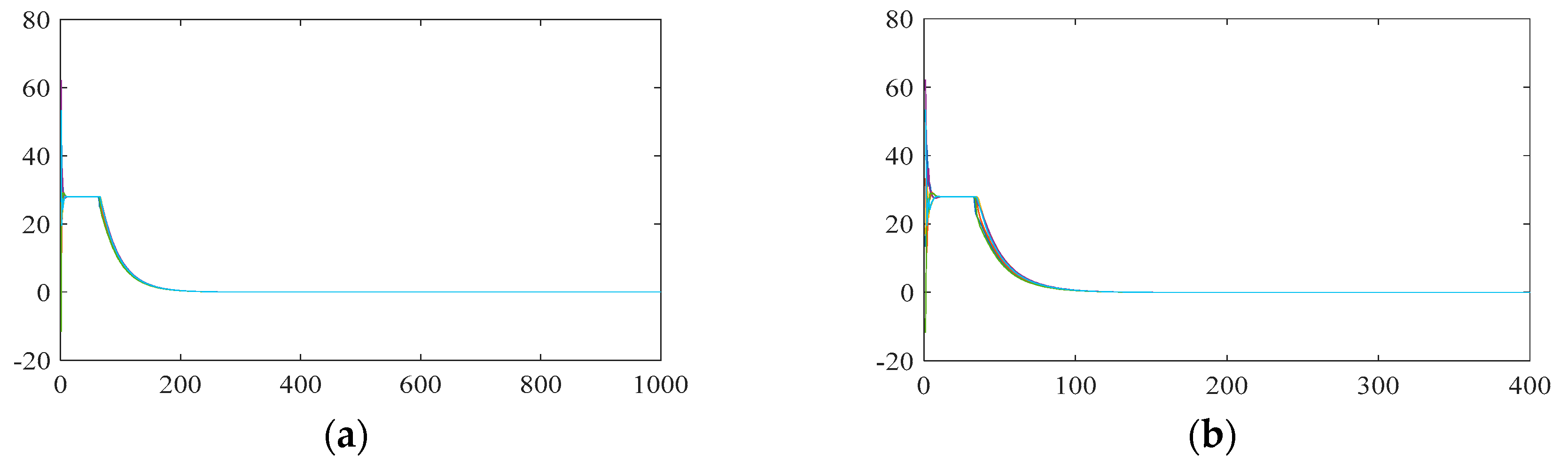
4.1.1. Verification of the Convergence
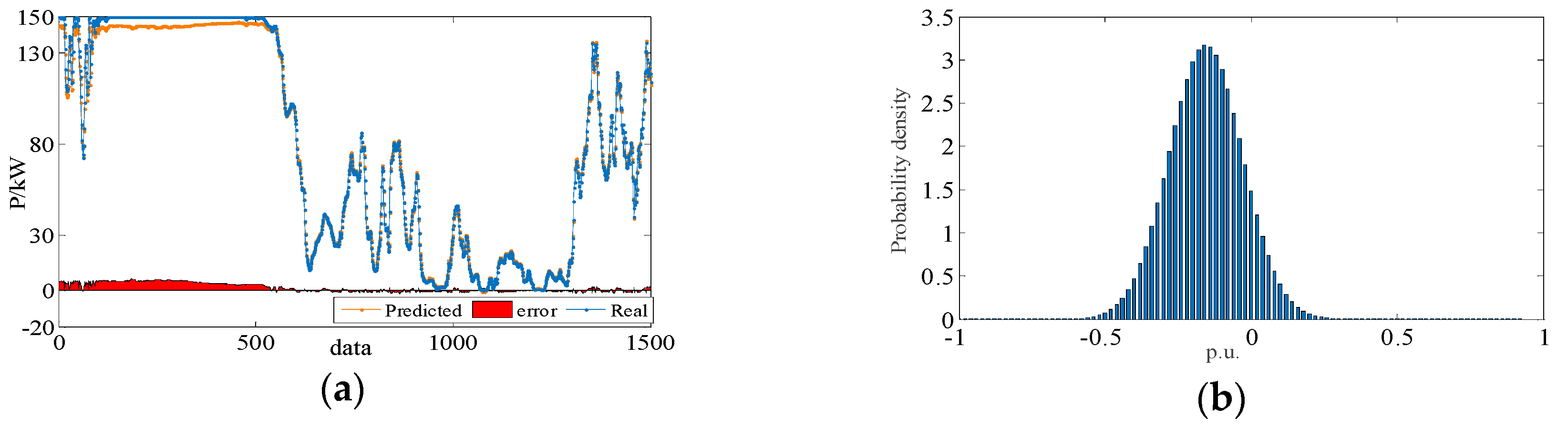
4.1.2. Verification of the Accuracy
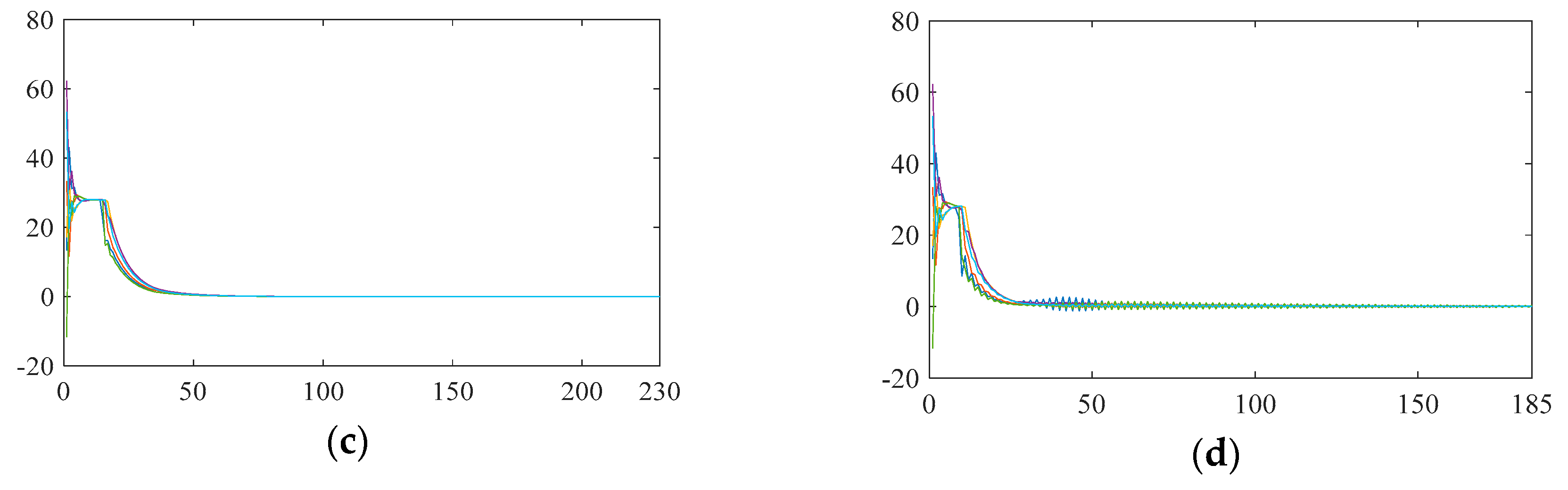
4.2. The Effect of Feedback Gain
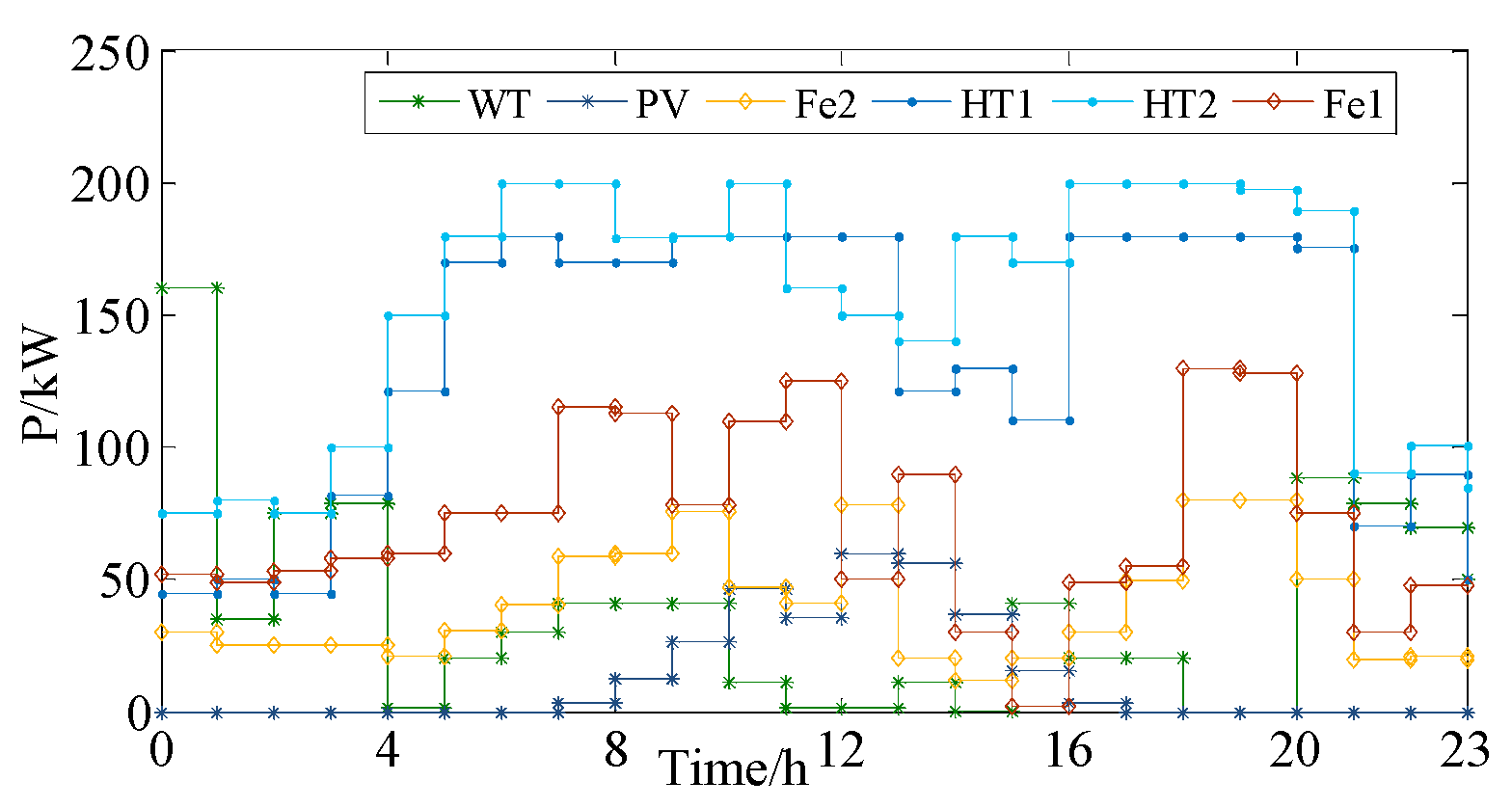
4.3. Analysis of Daily Optimization Result on Hourly Time-scale
5. Conclusions
- More types of equipment, such as energy storage devices and electric vehicles, are supposed to be considered during the operation optimization of a microgrid.
- Multi-energy utilizations, including cold, heat, power, and gas, should be introduced into the optimization model to fully maximize the benefit.
- The cost function in practice is more complex instead of a simple polynomial function form. It is usually non-convex, which is difficult to solve numerically. Therefore, a more widely applicable distributed solution algorithm needs to be studied in the future.
Author Contributions
Funding
Conflicts of Interest
References
- Strasser, T.; Andrén, F.; Kathan, J.; Cecati, C.; Buccella, C.; Siano, P.; Mařík, V. A Review of Architectures and Concepts for Intelligence in Future Electric Energy Systems. IEEE Trans. Ind. Electron. 2015, 62, 2424–2438. [Google Scholar] [CrossRef]
- Cheng, Z.; Duan, J.; Chow, M. To Centralize or to Distribute: That Is the Question: A Comparison of Advanced Microgrid Management Systems. IEEE Ind. Electron. Mag. 2018, 12, 6–24. [Google Scholar] [CrossRef]
- Huang, A.; Crow, M.L.; Heydt, G.T.; Zheng, J.P.; Dale, S.J. The Future Renewable Electric Energy Delivery and Management (FREEDM) System: The Energy Internet. Proc. IEEE 2011, 99, 133–148. [Google Scholar] [CrossRef]
- Han, Y.; Zhang, K.; Li, H.; Coelho, E.A.A.; Guerrero, J.M. MAS-Based Distributed Coordinated Control and Optimization in Microgrid and Microgrid Clusters: A Comprehensive Overview. IEEE Trans. Power Electron. 2018, 33, 6488–6508. [Google Scholar] [CrossRef]
- Liu, W.; Gu, W.; Sheng, W. Decentralized multi-agent system-based cooperative frequency control for autonomous microgrids with communication constraints. IEEE Trans. Sustain. Energy 2014, 5, 446–456. [Google Scholar] [CrossRef]
- Divényi, D.; Dán, A.M. Agent-Based Modeling of Distributed Generation in Power System Control. IEEE Trans. Sustain. Energy 2013, 4, 886–893. [Google Scholar] [CrossRef]
- Yang, S.; Tan, S.; Xu, J.X. Consensus based approach for economic dispatch problem in a smart grid. IEEE Trans. Power Syst. 2013, 28, 4416–4426. [Google Scholar] [CrossRef]
- Xu, Y.; Han, T.; Cai, K.; Lin, Z.; Yan, G.; Fu, M. A distributed algorithm for resource allocation over dynamic digraphs. IEEE Trans. Signal Process. 2017, 65, 2600–2612. [Google Scholar] [CrossRef]
- Ullah, M.H.; Alseyat, A.; Multi-Agent, J.P. System-based Distributed Energy Management in Smart Grid under Uncertainty. In Proceedings of the 2019 IEEE Energy Conversion Congress and Exposition (ECCE), Baltimore, MD, USA, 29 September–3 October 2019; pp. 3462–3468. [Google Scholar]
- Yang, Z.; Wu, R.; Yang, J.; Long, K.; You, P. Economical operation of microgrid with various devices via distributed optimization. IEEE Trans. Smart Grid 2016, 7, 857–867. [Google Scholar] [CrossRef]
- Zhang, H.; Li, Y.; Gao, D.W.; Zhou, J. Distributed optimal energy management for energy internet. IEEE Trans. Ind. Inform. 2017, 13, 3081–3097. [Google Scholar] [CrossRef]
- Costa DA, C.; Otto, R.B.; Piardi, A.B.; Ramos, R.A. A Survey of State-of-the-Art on Microgrids: Application in Real Time Simulation Environment. In Proceedings of the 2019 IEEE PES Innovative Smart Grid Technologies Conference—Latin America (ISGT Latin America), Gramado, Brazil, 15–18 September 2019; pp. 1–6. [Google Scholar]
- Kar, S.; Hug, G. Distributed robust economic dispatch in power systems: A consensus + innovations approach. In Proceedings of the IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 22–26 July 2012. [Google Scholar]
- Olama, N.; Bastianello, P.; Mendes, R.C.; Camponogara, E. Relaxed hybrid consensus ADMM for distributed convex optimisation with coupling constraints. IET Control Theory Appl. 2019, 13, 2828–2837. [Google Scholar] [CrossRef]
- Wan, X.; Xu, Z.; Pinson, P.; Dong, Z.Y.; Wong, K.P. Probabilistic forecasting of wind power generation using extreme learning machine. IEEE Trans. Powers Syst. 2014, 29, 1033–1044. [Google Scholar] [CrossRef]
- Ospina, J.; Newaz, A.; Faruque, M.O. Forecasting of PV plant output using hybrid wavelet-based LSTM-DNN structure model. IET Renew. Power Gener 2019, 13, 1087–1095. [Google Scholar] [CrossRef]
- Chen, B.; Li, J. Combined probabilistic forecasting method for photovoltaic power using an improved Markov chain. IET Gener. Transm. Distrib. 2019, 13, 4364–4373. [Google Scholar] [CrossRef]
- Olfati-Saber, R.; Fax, J.A.; Murray, R.M. Consensus and Cooperation in Networked Multi-Agent Systems. Proc. IEEE 2007, 95, 215–233. [Google Scholar] [CrossRef]
- Zhang, J.; Cui, M.; He, Y. Robustness and Adaptability Analysis for Equivalent Model of Doubly Fed Induction Generator Wind Farm Using Measured Data. Appl. Energy 2020, 261, 114362. [Google Scholar] [CrossRef]
- Ghamkhari, M.; Mohsenian-Rad, H. A Convex Optimization Framework for Service Rate Allocation in Finite Communications Buffers. IEEE Commun. Lett. 2016, 20, 69–72. [Google Scholar] [CrossRef]
- Xiao, L.; Boyd, S. Fast linear iterations for distributed averaging. In IEEE Conference on Decision and Control; Elsevier: Amsterdam, The Netherlands, 2004. [Google Scholar]
- Pagnier, L.; Jacquod, P. Optimal Placement of Inertia and Primary Control: A Matrix Perturbation Theory Approach. IEEE Access 2019, 7, 145889–145900. [Google Scholar] [CrossRef]



| DG Number | (kW) | (kW) | |||
|---|---|---|---|---|---|
| A1 HT1 | 0.0184 | 3.5 | 15 | 180 | 60 |
| A2 Fe1 | 0.1080 | 2.0 | 10 | 130 | 40 |
| A3 PV | 0.0087 | 1 | / | 150 | 0 |
| A4 WT | 0.0040 | 0.1 | / | 160 | 0 |
| A5 HT2 | 0.0174 | 2.9 | 20 | 200 | 85 |
| A6 Fe2 | 0.1250 | 1.8 | 25 | 80 | 20 |
| DGs Serial Number | Time 1 | Time 2 | ||||
|---|---|---|---|---|---|---|
| M1 | M2 | P1 | M1 | M2 | P1 | |
| A1 HT1 | 139.99 | 139.98 | 121.26 | 180 | 180 | 175.43 |
| A2 Fe1 | 40 | 40 | 91.04 | 58.79 | 58.95 | 75.8 |
| A3 PV | 56.26 | 56.26 | 56.26 | 0 | 0 | 0 |
| A4 WT | 11.08 | 11.08 | 11.07 | 88.32 | 88.32 | 88.32 |
| A5 HT2 | 165.27 | 165.27 | 140.14 | 200 | 200 | 189.44 |
| A6 Fe2 | 27.40 | 27.41 | 20.21 | 51.60 | 51.73 | 50 |
| Total | 440 | 440 | 439.98 | 578.71 | 579 | 578.99 |
| DG | HT1 | Fe1 | PV | WT | HT2 | Fe2 |
|---|---|---|---|---|---|---|
| 4 h | [78.69, 84.83] | [62.08, 66.92] | [0, 1.12] | [75.79, 81.69] | [96.16, 103.66] | [24.06, 25.94] |
| 5 h | [116.71, 125.84] | [63.32, 68.25] | [0, 1.12] | [1.73, 1.86] | [144.37, 155.63] | [20.34, 21.93] |
| 6 h | [163.63, 176.37] | [75.92, 81.84] | [0, 1.12] | [19.88, 21.43] | [173.35, 186.86] | [29.31, 31.59] |
| 7 h | [173.25, 180] | [76.90, 82.89] | [0, 1.12] | [28.81, 31.06] | [192.5, 200] | [38.64, 41.65] |
| 8 h | [163.62, 176.37] | [107.41, 115.77] | [3.40, 3.67] | [39.76, 42.86] | [192.5, 200] | [56.34, 60.73] |
| 9 h | [163.63, 176.38] | [105.24, 113.44] | [11.73, 12.65] | [39.76, 42.86] | [172.28, 185.71] | [57.88,62.39] |
| 10 h | [173.25, 180] | [78.56, 84.68] | [25.55, 27.54] | [39.77, 42.85] | [173.25, 186.75] | [72.68, 78.34] |
| 11 h | [173.25, 180] | [100.91, 108.77] | [45.05, 48.56]] | [10.66, 11.49] | [192.5, 200] | [45.48, 49.03] |
| 12 h | [173.25, 180] | [117.02, 126.14] | [34.08, 36.74]] | [1.73, 1.86] | [154, 166] | [39.66, 42.75] |
| DG | Optimal Output (kW) | ||||||||
| 4 h | 5 h | 6 h | 7 h | 8 h | 9 h | 10 h | 11 h | 12 h | |
| HT1 | 93.99 | 133.43 | 180 | 180 | 180 | 180 | 180 | 180 | 180 |
| Fe1 | 40 | 40 | 42.14 | 63.98 | 85.48 | 73.87 | 73.14 | 81.17 | 65.45 |
| PV | 0 | 0 | 0 | 0 | 3.54 | 12.19 | 26.54 | 46.81 | 35.41 |
| WT | 78.74 | 1.79 | 20.65 | 29.94 | 41.32 | 41.31 | 41.31 | 11.07 | 1.8 |
| HT2 | 116.63 | 158.33 | 200 | 200 | 200 | 200 | 200 | 200 | 200 |
| Fe2 | 20.63 | 26.44 | 37.21 | 56.08 | 74.66 | 64.62 | 63.99 | 70.93 | 57.35 |
| Total | 349.99 | 359.99 | 480 | 530 | 585 | 571.99 | 584.98 | 589.98 | 540.01 |
| DG | Predicted Output (kW) | ||||||||
| 4 h | 5 h | 6 h | 7 h | 8 h | 9 h | 10 h | 11 h | 12 h | |
| HT1 | 81.76 | 121.26 | 170 | 180 | 170 | 170 | 180 | 180 | 180 |
| Fe1 | 64.5 | 65.79 | 78.88 | 79.9 | 111.59 | 109.34 | 81.62 | 104.84 | 121.58 |
| PV | 0 | 0 | 0 | 0 | 3.54 | 12.19 | 26.55 | 46.82 | 35.41 |
| WT | 78.74 | 1.79 | 20.66 | 29.94 | 41.32 | 41.32 | 41.31 | 11.08 | 1.79 |
| HT2 | 99.91 | 150 | 180.11 | 200 | 200 | 179 | 180 | 200 | 160 |
| Fe2 | 25 | 21.14 | 30.45 | 40.15 | 58.54 | 60.14 | 75.51 | 47.26 | 41.21 |
| D | 349.91 | 359.98 | 480.10 | 529.99 | 584.99 | 571.99 | 584.99 | 590 | 539.99 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, S.; Yu, Z.; Zhou, B.; Yang, Z.; Yang, D. A Decentralized Optimization Strategy for Distributed Generators Power Allocation in Microgrids Based on Load Demand–Power Generation Equivalent Forecasting. Energies 2020, 13, 648. https://doi.org/10.3390/en13030648
Zhang S, Yu Z, Zhou B, Yang Z, Yang D. A Decentralized Optimization Strategy for Distributed Generators Power Allocation in Microgrids Based on Load Demand–Power Generation Equivalent Forecasting. Energies. 2020; 13(3):648. https://doi.org/10.3390/en13030648
Chicago/Turabian StyleZhang, Shicong, Zilong Yu, Bowen Zhou, Zhile Yang, and Dongsheng Yang. 2020. "A Decentralized Optimization Strategy for Distributed Generators Power Allocation in Microgrids Based on Load Demand–Power Generation Equivalent Forecasting" Energies 13, no. 3: 648. https://doi.org/10.3390/en13030648
APA StyleZhang, S., Yu, Z., Zhou, B., Yang, Z., & Yang, D. (2020). A Decentralized Optimization Strategy for Distributed Generators Power Allocation in Microgrids Based on Load Demand–Power Generation Equivalent Forecasting. Energies, 13(3), 648. https://doi.org/10.3390/en13030648







