Functional Energy Accumulation, Photo- and Magnetosensitive Hybridity in the GaSe-Based Hierarchical Structures

Abstract

We report on the complex GaSe-based hierarchical structures GaSe(CS(NH₂)₂), GaSe(SmCl₃) and GaSe(CS(NH₂)₂(SmCl₃)) synthesized by an intercalation method. The conductive properties of synthesized clathrates and their relation to hierarchical structural complexity were explored by an impedance spectroscopy technique. The impedance response, thermostimulated discharge spectra, and photo- and magnetoresistive effects are reported. Based on the obtained results, the impurity energy spectra were calculated. A strong low-frequency inductive response, observable in the GaSe(SmCl₃) clathrate, makes this material promising for the development of gyrator-free nanodelay lines potentially applicable in nanoelectronics. Hierarchical GaSe(CS(NH₂)₂(SmCl₃)) clathrate, on the other hand, reveals hysteresis of the current–voltage characteristics, apparently confirming an accumulation of electric energy at interphase boundaries. A relevant spin battery effect, observable experimentally in stationary magnetic fields, demonstrates a principal possibility of the electric energy accumulation at a quantum level.

1. Introduction

The tremendous interest in supramolecular structures is caused by the considerable progress and advances in relevant fields of science, engineering, and technology, observed over the past decades [1,2,3]. Supramolecular physics and chemistry deal with entities of greater complexity, rather than individual molecules representing assemblies that are organized through intermolecular interactions of noncovalent origin, such as electrostatic and van der Waals forces, hydrogen, coordination, or interfacial bonding. Corresponding studies aim to explore the underlying properties and mechanisms of supramolecular systems and the potential applications of relevant materials.

Semiconducting clathrates, known also as phonon glasses [4,5,6], appear on the list of most promising thermoelectric materials. Slack’s hypothesis [7,8] assumes the possibility of the formation of structures with weakly bonded guest atoms or molecules that may oscillate in a discrete volume, usually in the frequency range of resonance phonon scattering. It thereby enables the combination of low thermal conductivity and high electrical conductance along the bonds of a host matrix [9]. Accordingly, physical aspects of supramolecular ensembles, such as the electronic structure [10,11,12] and excitation energy transfer mechanisms [13,14,15], appear to be of great interest both in fundamental and practical aspects. The clathrates of a hierarchical supramolecular subhost (host(guest)) structure may form inorganic/organic systems with the required functional hybridity. The hierarchical clathrates synthesized in several earlier works [16,17] may be considered prominent examples. They exhibited colossal magnetoresistive effects, negative capacitance and energy accumulation at a quantum level at room temperature, and a weak magnetic field. Undoubtedly, the hierarchical clathrates appear to be of great importance, especially in understanding a correlation between the underlying physical mechanisms or processes, the type of subhost crystal lattice structures, and the intercalated guest components.

In the present work, we report on complex the GaSe-based hierarchical structures GaSe(CS(NH₂)₂), GaSe(SmCl₃), and GaSe(CS(NH₂)₂(SmCl₃)), synthesised by an intercalation method. Conductive properties of the synthesised clathrates are characterized by impedance spectroscopy, aiming to explore the complexity of their hierarchical structure. The hierarchical structures exhibit the spin battery effect, demonstrating a principal possibility of the electric energy accumulation on a quantum level.

2. Materials and Methods

The supramolecular hierarchical structures GaSe(CS(NH₂)₂), GaSe(SmCl₃) and GaSe(CS(NH₂)₂(SmCl₃)) were synthesized by the intercalation method. The photosensible quasi two-dimensional semiconducting crystals of gallium selenide (GaSe), grown by the Bridgman–Stockbarger method, were used as the subhost crystal material. GaSe belongs to the n-type semiconductors, with the band gap of 2.02 eV [18]. It is characterized by a well-developed layered structure [17] and the affordability of guest positions within Van der Waals regions oriented perpendicularly to the crystallographic c-axis (Figure 1). Due to a weak interlayer bonding, the interlayer space can be enlarged multiple times by applying the intercalation method. Such an expanded GaSe lattice appears to be appropriate for the intercalation of guest atoms or molecules [19,20].

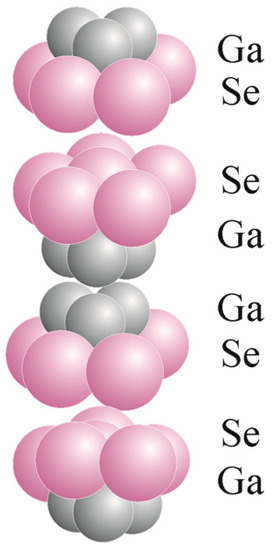
Figure 1. Schematic representation of the GaSe structure.

Thiourea CS(NH₂)₂ is one of the simplest thioamides (Figure 2) that was used as a host substance for the hierarchical clathrate formation. Because of its nonlinear optical properties, thiourea is widely applied in the fabrication of optoelectronic components and devices, such as polarizing filters, electronic optical switches, electrooptical and electroacoustic modulators and deflectors. Thiourea, on the other hand, is also widely used in different electrochemical processes [21]. The molecules of thiourea can form a matrix with unilateral disjointed channels of rhombohedral structure (see Figure 3) that are available for guest components, which are oriented in an unordered way.

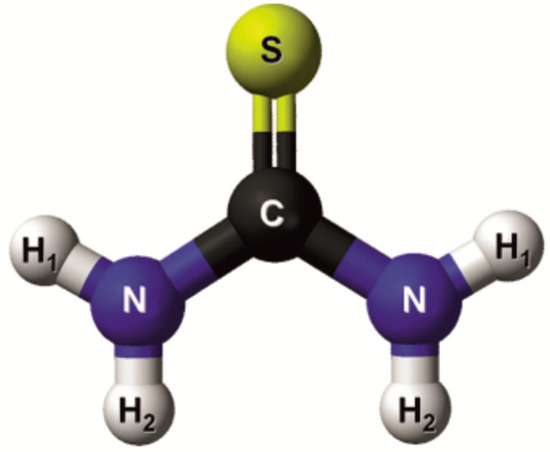
Figure 2. Schematic representation of the thiourea molecule.

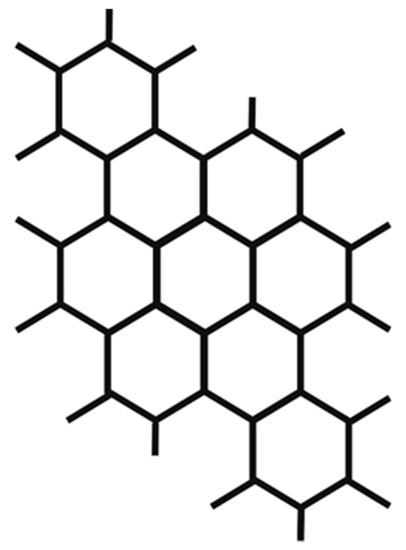
Figure 3. Plane schematic representation of rhombohedral thiourea structure. Nine complete tunnels with a distance of 9.2 Å between their centres are shown.

In many cases, this rhombohedral structure transforms into a monoclinic structure at low temperatures. The intrinsic surface of the thiourea tunnel is not uniform, and there are narrowing (down to 5.8 Å in diameter) and thickening (up to 7.1 Å in diameter) regions there. Typically, guest components are intercalated into thiourea with a guest/thiourea ratio of 1:3 [22]. The dipole moment of thiourea equals 18.9 × 10⁻³⁰ C⋅m and the dielectric constant is 2.224 [23].

Samarium (III) chloride (Figure 4) was used as guest component [24]. This material, applied in the synthesis of Sm-organic compounds, demonstrates paramagnetic properties on a nanoscale level. Thus, it is sensitive to external fields with the desired magnetic properties.

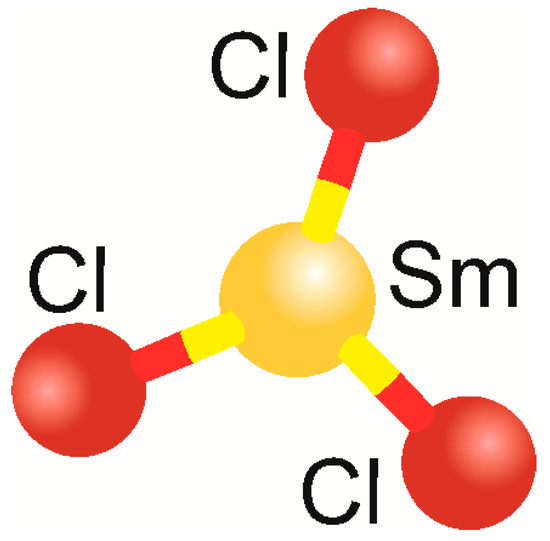
Figure 4. Structural formula of the SmCl₃ molecule.

The three-stage intercalation–deintercalation technique, described in detail in [25,26], was applied to synthesise the GaSe-based hierarchical structures. At the first stage, the semiconductor GaSe samples were submerged into a NaNO₂ melt at 300 °C for 5 min, resulting in a 4-fold lattice expansion. At the second stage, the NaNO₂ was deintercalated from the GaSe by washing the samples in deionised water (DW) until the pH value of the DW was reached. The samples were then dried in a vacuum at 110 °C, until their constant mass was achieved. Finally, at the third stage, the guest components were intercalated into the expanded GaSe matrix by a direct exposure of GaSe in relevant saturated solutions of CS(NH₂)₂, SmCl₃ or CS(NH₂)₂ + SmCl₃, respectively, for 48 h at room temperature. The samples were then washed with DW and dried in a vacuum until the constant mass was reached. The intercalated GaSe-structures obtained in this way were subjected to X-ray diffraction (XRD) analysis carried out with a DRON-3 diffractometer, employing Cu-Kα radiation and an LiF single crystal as a monochromator.

Impedance analysis along the crystallographic c-axis of the GaSe-based hierarchical structures was performed by the measuring device Autolab (Metrohm Autolab B.V., Utrecht, The Netherlands) integrated with FRA-2 module and GPES software. Spectra were measured in the frequency range 10⁻³ ÷ 10⁶ Hz. A Dirichlet filter [27,28] was applied to eliminate questionable datapoints. The frequency-dependant complex impedance Z was analysed with a graph–analytic method by means of a ZView 2.3 software (Scribner Associates, Inc., Southern Pines, NC, USA) package, and errors in approximations did not exceed 4%. The measurements were executed under normal conditions (NC) in an external magnetic field (MF) (strength value H = 2.75 kOe) applied perpendicularly to the sample, which was illuminated (L) by visible light (radiant flux 65 W).

3. Results and Discussion

The XRD powder patterns of the initial GaSe matrix and intercalated hierarchical structures are given in Figure 5. XRD analysis reveals that the initial GaSe sample is of hexagonal structure [29], and the synthesized intercalates do not change it substantially. Some variations were observed in the XRD peak positions with the content of the hierarchical substances. The values of the corresponding interplanar distances were calculated based on the analysis of the angular positions of the relevant XRD peaks. The (004) peaks for intercalated samples are slightly shifted to the small-angle region compared to the expanded non-intercalated matrix (Figure 5). The profile of the XRD reflex of the GaSe(CS(NH₂)₂(SmCl₃)) structure is characterized by two evident maxima, suggesting a coexistence of regions with slightly different interlayer distances.

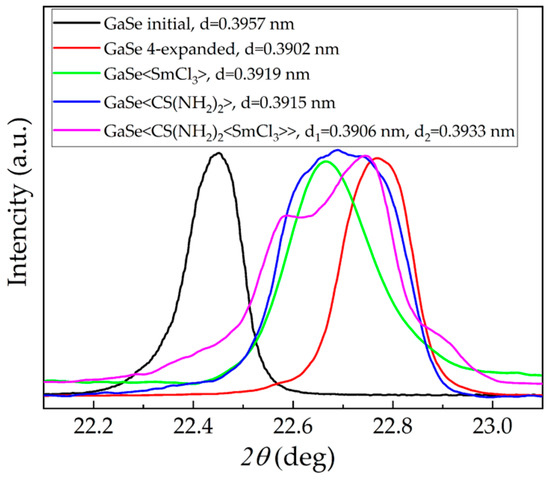
Figure 5. The XRD powder patterns of the initial GaSe and the synthesised hierarchical structures.

The intercalation of CS(NH₂)₂ into 4-fold expanded GaSe lattice leads to about 4-fold decrease in the real part of complex impedance ReZ of GaSe⟨CS(NH₂)₂⟩ supramolecular ensemble and it is evident from relevant frequency dependences ReZ(ω), which are demonstrated in Figure 6. The frequency independent part of ReZ(ω) is observable for the non-intercalated GaSe lattice in the 10⁻³−200 Hz frequency range. The GaSe(CS(NH₂)₂) supramolecular structure, however, reveals a stable ReZ magnitude in the entire frequency range.

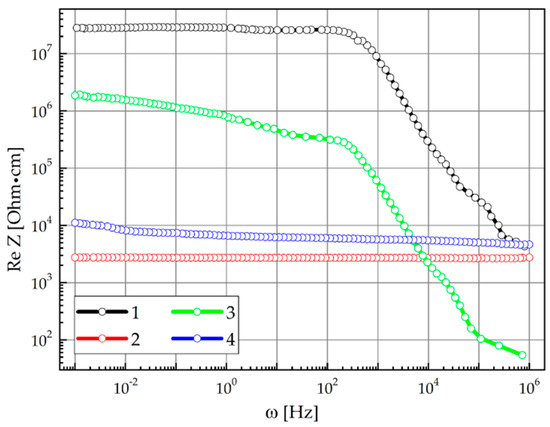
Figure 6. Frequency dependences of the real part of the complex impedance of non-intercalated 4-fold expanded GaSe matrix (1 black) and synthesized GaSe(CS(NH₂)₂) (2 red), GaSe(SmCl₃) (3 green) and GaSe(CS(NH₂)₂(SmCl₃)) (4 blue) structures measured along the crystallographic C axis.

The intercalation of Sm³⁺ into a 4-fold expanded GaSe lattice results in a decrease in the ReZ value in the low-frequency region, by about one order of magnitude. The character of the ReZ(ω)-dependence for the GaSe(SmCl₃) changes significantly at higher frequencies, where it falls substantially.

The intercalation of CS(NH₂)₂(SmCl₃) into the GaSe lattice leads just to a slight increase in the ReZ value compared to the GaSe(CS(NH₂)₂) clathrate. Comparing, on the other hand, ReZ(ω)-dependences of the GaSe(CS(NH₂)₂(SmCl₃)) and GaSe(SmCl₃) clathrates, one may recognize their similarity only in the low-frequency region, roughly below 200 Hz. Hence, there is a non-additive influence of the subhost GaSe lattice, and the guest molecules in the frequency region related with a band carrier’s conductivity. It follows that there is a substantial influence of hierarchical modulating potential on the impurity electron spectrum, which provides current flow at room temperature. The density of states at the Fermi level N(E_F), calculated with Pollak–Geballe theory [30] (see Figure 7), confirms the dominance of the impurity electron spectrum over the possible charge mobility growing perpendicularly to layers of the semiconductor. It is obvious that the actual density of deep trapping centres in the GaSe(CS(NH₂)₂(SmCl₃)) is considerably higher compared to the associated influence of the guest CS(NH₂)₂ and SmCl₃ molecules. At the same time, histograms explicitly indicate a decrease in the hopping radius of charge carriers caused by the influence of the hierarchy of complex clathrate barrier potential.

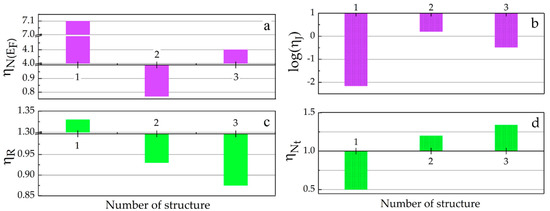
Figure 7. Histograms of changes in the density of states at Fermi level N(E_F) (a), trapping centres scattering J (b), hopping radius R (c) and density of deep trapping centres N_t (d) relative to initial fourfold expanded GaSe matrix for GaSe(SC(NH₂)₂) (1), GaSe(SmCl₃) (2) and GaSe(SC(NH₂)₂(SmCl₃)) (3).

The frequency dependences of the real part of the complex impedance for the GaSe with an expanded lattice (curve 1) and the GaSe(SmCl₃) clathrate (curve 3) in Figure 6 are well described by Jonscher‘s formula [31,32] for resistivity ρ

$$\rho \left(\omega \right)=\frac{1}{{\rho }_0+A{\omega }^s}$$

(1)

where σ₀ is the limiting zero frequency conductivity, A is the pre-exponential constant, ω is the angular frequency, and s is the power law exponent, where 0 < s < 1. The second term in the denominator represents the hopping conduction. The first term represents the simple drift motion of electrons in a material, and is defined by the distribution function of the waiting period φ(t) describing the probability for an electron jump expected in the period of time t after the previous jump

$$\phi \left(t\right)=\frac{1}{\tau }{e}^{-t/\tau }$$

(2)

where τ is the average waiting period. The second frequency-dependent term is a reflection of the following distribution function

$$\phi \left(t\right)=\frac{Cs{t}^{-1-s}}{\mathsf{\Gamma }\left(1-s\right)},0<s<1$$

(3)

where Γ(1 − s) is the gamma function, and C is the constant [27].The physical reason for this distribution function is an exponential distribution of the activation energy

$$K\left(E\right){~\mathrm{e}}^{-\frac{E}{kT}}$$

(4)

The characteristics, ReZ(ω), of the hierarchiral structures of GaSe(CS(NH₂)₂) (curve 2, Figure 6) and GaSe(CS(NH₂)₂(SmCl₃)) (curve 4, Figure 6), on the other hand, are practically frequency-independent apparently, indicated by the hopping conduction mechanism realized with a sequence of identical potential wells without long-range interactions. Such an approach results in a unique value of activation energy, thus, the distribution function of the waiting period gets an exponential character. De facto, it is an implication of the hierarchical potential explaining the increase in a number of deep trapping centres. Therefore, these trapping centres can be modelled by a sequence of δ-wells. Considering this case, and when the Fermi level is far from the maximum density of states ($E_F>>kT$), the conductivity σ reads as

$$\sigma =\frac{16{\epsilon }^2{r}^{2}N}{\pi h{a}_0}{e}^{-2r/a_0}{e}^{-E_a/kT}$$

(5)

where ε is the material dielectric constant, N is the number of trapping centres, r is the distance between them, a₀ is the radius of wave-function localization, E_a is the activating energy, T is the temperature, k is the Boltzmann constant, and ħ is the Plank constant. Ignoring long-range interactions, the wave-function for the system of two δ-wells separated by distance r takes the form

$${\psi }_0\left(x\right){~\mathrm{e}}^{{-\mathrm{k}}_0\left|x-\frac{r}{2}\right|}+e^{-k_0\left|x+\frac{r}{2}\right|}$$

(6)

where k₀ is a solution of the equation

$$\frac{h^2}{m\alpha }{k}_0=1+e^{-k_{0}r}$$

(7)

where α is the factor before the δ-well potential, m is the electron mass, and $k_0=\sqrt{2mE/ħ}$ is the wave-number. If the $k_{0}r<<1$ Equation (7) can be expanded into series and represented by its first two terms

$$k_0=2{\left(\frac{{ħ}^2}{m\alpha }+r\right)}^{-1}$$

(8)

the localisation length and activation energy are then given as

$$a_0=\frac{1}{k_0}=\frac{{ħ}^2}{2m\alpha }+\frac{r}{2}$$

(9)

$$E_a=\frac{{ħ}^2{k}_0^2}{2m}=\frac{{ħ}^2}{2m}{\left(\frac{{ħ}^2}{2m\alpha }+\frac{r}{2}\right)}^{-2}$$

(10)

Considering Equations (9) and (10), the values α and $a_0$ can be evaluated. Analysing the data scattering of trapping centres, jump distances and their dependence on the temperature, one obtains: $\alpha =2\cdot {10}^{-30}$ J, $a_0=1.3\cdot {10}^{-8}$ m.

The resistivity can be presented in the form

$$\rho =\frac{\pi ħ}{16{\epsilon }^2{r}^3{N}^d}\left(\frac{{ħ}^2}{2m\alpha }+\frac{r}{2}\right)\exp \left[\frac{2r}{\frac{{ħ}^2}{2m\alpha }+\frac{r}{2}}\right]\exp \left[\frac{{ħ}^2}{2mkT{\left(\frac{{ħ}^2}{2m\alpha }+\frac{r}{2}\right)}^2}\right]$$

(11)

where d is the coefficient of inhomogeneous volume distribution of trapping centres caused by intercalation of components into an interlayered space of lattice. Its value is assumed to be equal 4/5. One should notice that, in the ideal case when trapping centres are distributed uniformly, d equals 1.

From Equation (11), it follows that the resistivity is minimal at the α-value, satisfying the equation

$$a_0^2+\frac{2rmkT{ħ}^2}{3r^2{m}^{2}kT+4{ħ}^{2}m}{a}_0-\frac{kT{ħ}^4}{3r^2{m}^{2}kT+4{ħ}^{2}m}=0$$

(12)

therefore, one obtains:

$$a_0=-\frac{rmkT{ħ}^2}{3r^2{m}^{2}kT+4{ħ}^{2}m}+\sqrt{\frac{r^2{m}^2{k}^2{T}^2{ħ}^4}{{\left(3r^2{m}^{2}kT+4{ħ}^{2}m\right)}^2}+\frac{kT{ħ}^4}{3r^2{m}^{2}kT+4{ħ}^{2}m}}$$

(13)

For the present system, $\alpha =2\cdot {10}^{-31}$ J, whereas the electron localization length and the conductivity may undergo an increase of three and two times, respectively.

Photo- and magnetoresistive effects measured in the low-frequency region for the hierarchical GaSe(SC(NH₂)₂), GaSe(SmCl₃) and GaSe(SC(NH₂)₂(SmCl₃)) structures are presented in Figure 8. The photoresistance value of the synthesised structures depends on the clathrates’ structural complexity. This fact correlates well with theoretical calculations of the impurity energy spectrum: the highest increase in the density of deep trapping centres is exhibited by the clathrate with the most complex hierarchical architecture (Figure 7). At the same time, the magnetoresistivity is remarkably less for GaSe(CS(NH₂)₂(SmCl₃)) compared to SmCl₃ in the potential field of the subhost lattice only (Figure 8), in accordance with a decrease in the density of deep trapping centres in the magnetic field caused by a Zeeman modification of the impurity energy spectrum (Figure 9).

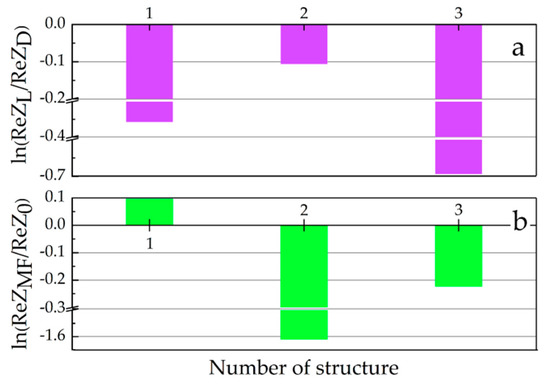
Figure 8. Photo-(a) and magnetoresistive (b) effects measured in the low-frequency region for GaSe(SC(NH₂)₂) (1), GaSe(SmCl₃) (2) and GaSe(SC(NH₂)₂(SmCl₃)) (3).

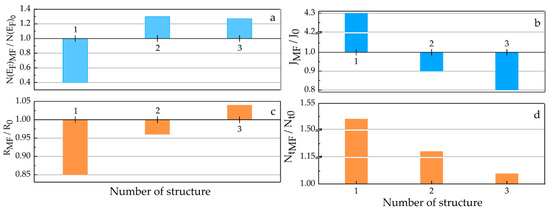
Figure 9. Histograms of change in the density of the states at the Fermi level N(E_F) (a), trapping centres scattering J (b), and hopping radius R (c) and density of deep trapping centres N_t (d) in applied magnetic field for GaSe(SC(NH₂)₂) (1), GaSe(SmCl₃) (2) and GaSe(SC(NH₂)₂(SmCl₃)) (3).

The Nyquist plot for complex impedance for the 4-fold expanded non-intercalated GaSe matrix (see Figure 10) demonstrates a classic two-arch shape. High-frequency and low-frequency arches represent current flow, in packages of unexpanded crystal lattice layers, and between them, respectively. The lowest frequency dispersion is also worth mentioning, because it reflects the quantum capacity [33] caused by the discretization of the energy spectrum perpendicularly to the layers.

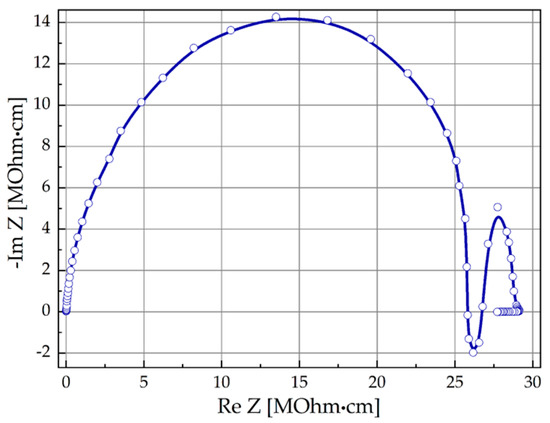
Figure 10. Nyquist plot for non-intercalated 4-fold expanded GaSe matrix.

Intercalation of the subhost GaSe lattice by the guest CS(NH₂)₂, SmCl₃ or CS(NH₂)₂(SmCl₃) components changes the character of the complex impedance substantially (Figure 11). In the case of GaSe(SmCl₃), the strong inductive response was observed in the low-frequency region. Such inductive response, however, disappeared in an applied external magnetic field. This phenomenon, known as negative capacitance [34,35], was studied intensively in a number of works [17,25,36], basically due to the potential related nanoelectronic applications—particularly, with the development of gyrator-free nanodelay lines. The equivalent electric circuit for the relevant low-frequency region of the Nyquist plot is presented in Figure 12. Using the complex amplitude method, such a circuit can be represented by analytical expression

$$Z=\frac{1}{\frac{1}{R_1}+j\omega C_1}+\frac{1}{\frac{1}{R_2}+\frac{1}{j\omega L_2+\frac{1}{j\omega C_2}}}$$

(14)

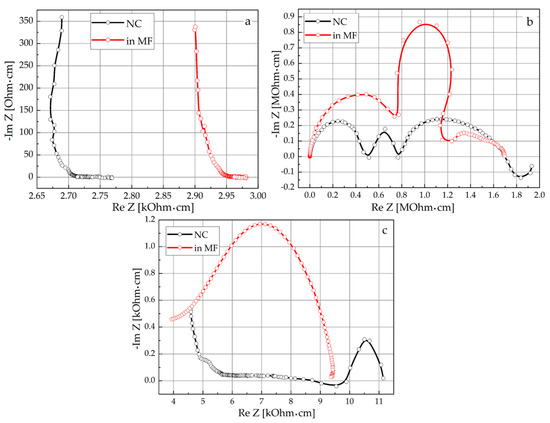
Figure 11. Nyquist plots for the synthesised hybrid structures GaSe(SC(NH₂)₂) (a), GaSe(SmCl₃) (b) and GaSe(SC(NH₂)₂(SmCl₃)) (c) measured under normal conditions (black) and under applied magnetic field (red).

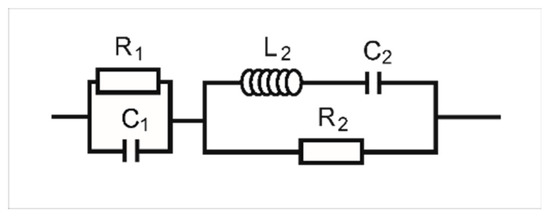
Figure 12. Equivalent electric circuit for the impedance response of GaSe(SmCl₃) (Figure 10b, black curve) measured in low-frequency region.

Let us introduce here the notations for the impedance components, Z_I and Z_II, of Equation (14), as follows:

$$Z_I=\frac{1}{\frac{1}{R_1}+j\omega C_1}$$

(15)

$$Z_{II}=\frac{1}{\frac{1}{R_2}+\frac{1}{j\omega L_2+\frac{1}{j\omega C_2}}}$$

(16)

After their simplification

$$Z_I=\frac{R_1-j\omega C_1{R}_1^2}{1+{\omega }^2{C}_1^2{R}_1^2}$$

(17)

$$Z_{II}=\frac{R_2\left(1-j{\omega }^2{C}_2{L}_2\right)}{1-{\omega }^2{C}_2{L}_2+j\omega C_2{R}_2}$$

(18)

we get

$$\begin{array}{l}Z=Z_I+Z_{II}\\ =\frac{{\left(1-{\omega }^2{C}_2{L}_2\right)}^2\left[R_1+R_2\left(1+{\omega }^2{C}_1^2{R}_1^2\right)\right]+{\omega }^2{C}_2^2{R}_2^2{R}_1}{\left(1+{\omega }^2{C}_1^2{R}_1^2\right)\left[{\left(1-{\omega }^2{C}_2{L}_2\right)}^2+{\omega }^2{C}_2^2{R}_2^2\right]}\\ -j\omega \frac{\left(1-{\omega }^2{C}_2{L}_2\right)\left[C_1{R}_1^2\left(1-{\omega }^2{C}_2{L}_2\right)+C_2{R}_2^2\left(1+{\omega }^2{C}_1^2{R}_1^2\right)\right]+{\omega }^2{C}_2^2{R}_2^2{C}_1{R}_1^2}{\left(1+{\omega }^2{C}_1^2{R}_1^2\right)\left[{\left(1-{\omega }^2{C}_2{L}_2\right)}^2+{\omega }^2{C}_2^2{R}_2^2\right]}\end{array}$$

(19)

therefore,

$$\mathrm{Re}Z=\frac{{\left(1-{\omega }^2{C}_2{L}_2\right)}^2\left[R_1+R_2\left(1+{\omega }^2{C}_1^2{R}_1^2\right)\right]+{\omega }^2{C}_2^2{R}_2^2{R}_1}{\left(1+{\omega }^2{C}_1^2{R}_1^2\right)\left[{\left(1-{\omega }^2{C}_2{L}_2\right)}^2+{\omega }^2{C}_2^2{R}_2^2\right]}$$

(20)

$$\mathrm{Im}Z=-\omega \frac{\left(1-{\omega }^2{C}_2{L}_2\right)\left[C_1{R}_1^2\left(1-{\omega }^2{C}_2{L}_2\right)+C_2{R}_2^2\left(1+{\omega }^2{C}_1^2{R}_1^2\right)\right]+{\omega }^2{C}_2^2{R}_2^2{C}_1{R}_1^2}{\left(1+{\omega }^2{C}_1^2{R}_1^2\right)\left[{\left(1-{\omega }^2{C}_2{L}_2\right)}^2+{\omega }^2{C}_2^2{R}_2^2\right]}$$

(21)

The presented analytical expressions for real (20) and imaginary (21) components of complex impedance enable the further detailed analysis of the inductive mechanism. Particularly, it lets us determine optimal conditions, providing an efficient accumulation of the electric energy at quantum level.

The significant increase in the impedance response observed in the middle-frequency region under the applied magnetic field (Figure 11) is related with the additional energy barriers caused by the SmCl₃ intercalation. At the same time, a strong charge carriers’ delocalization (ReZ >> ImZ) at Zeeman levels appears in the same frequency region.

The Nyquist plot of the complex hierarchical structure GaSe(CS(NH₂)₂(SmCl₃)) demonstrates the combination of impedance contributions originating from the guest CS(NH₂)₂(SmCl₃) component and non-intercalated GaSe lattice (Figure 11). In addition, the impedance response measured in the magnetic field demonstrates an increase in the low-frequency range and is almost constant in its value in the high-frequency range, thus confirming the charge accumulation at the phase-interface region. Apparently, it is caused by Zeeman changes in the asymmetry of the density states above and below the Fermi level, which blocks resonant tunnelling.

The photo-impedance response for the synthesized hierarchical structures is demonstrated in Figure 13. Two aspects induced by light should be mentioned here:

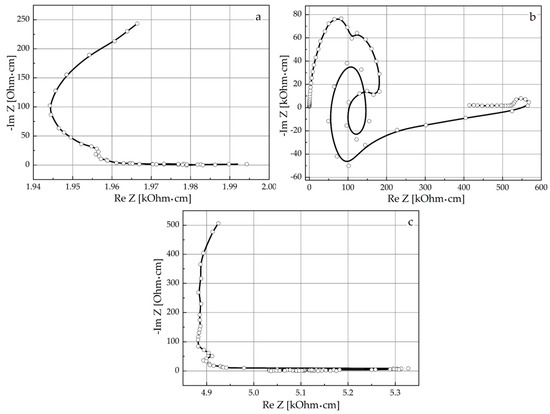
Figure 13. Nyquist plots for the synthesised hybrid structures GaSe(SC(NH₂)₂) (a), GaSe(SmCl₃) (b) and GaSe(SC(NH₂)₂(SmCl₃)) (c) measured perpendicularly to layers under illumination.

• The characteristic inductive response shifts into the middle-frequency region for GaSe(SmCl₃) (see Figure 13a and Figure 11b, black online color);
• The light illumination of the GaSe(CS(NH₂)₂(SmCl₃)) structure causes tunnel current flow, levelling the contribution caused by charge accumulation in the infra-low-frequency region (Figure 13c).

Figure 14 presents the current spectra of thermostimulated depolarisation measured perpendicularly to the layers of the non-intercalated 4-fold expanded GaSe matrix and hierarchal GaSe(SC(NH₂)₂), GaSe(SmCl₃) and GaSe(SC(NH₂)₂(SmCl₃)) structures. The hierarchy of relevant clathrate structures evidently influences the origin of the current spectra. Particularly, going from clathrate structures of low hierarchy, such as GaSe(SmCl₃), to the clathrate structures of higher hierarchy, such as GaSe(SC(NH₂)₂(SmCl₃)), it transforms from the band-type spectrum to the continuous one with homo- and heterocharge relaxations. The clathrate of complex hierarchical architecture, GaSe(CS(NH₂)₂(SmCl₃)), appears to be promising material for a quantum accumulation of the electric energy. It particularly results from cycling voltammetry experiments. The hysteresis character of the current-voltage (CV) characteristics measured perpendicularly to the layers of the hierarchical GaSe(CS(NH₂)₂(SmCl₃)) structure (Figure 15), confirm the assumption regarding the charge accumulation at the interphase boundaries. One should emphasize that the hysteresis behaviour remains practically the same in the case of a constant magnetic field and light illumination. Amazingly, in a zero magnetic field (H = 0), the light illumination alone does not result in a current flow. In combination with an applied magnetic field (H ≠ 0), however, the current is generated, as evidenced by the CV-characteristics presented in Figure 15b. Particularly, at the magnetic field of H = 2.75 kOe, the CV-curve intersects the voltage axis at 21 and −23 mV in forward and reverse directions, respectively. This fact confirms the appearance of a spin electromotive force (EMF), which may be considered a basic effect, lying in the fundamentals of quantum energy accumulation and the prospective spin capacitor devices and relevant applications [37]. The distinctive feature of this finding is demonstration of the spin EMF at room temperature and relatively weak magnetic fields.

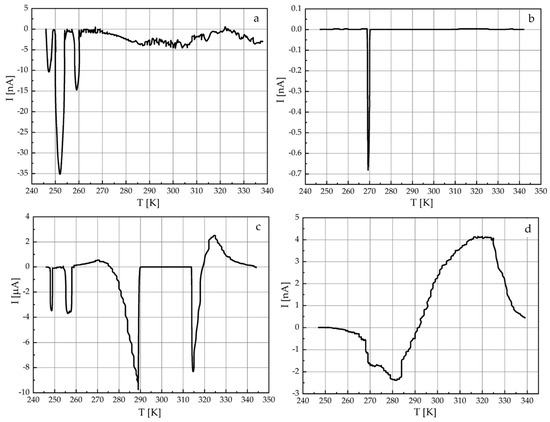
Figure 14. Current spectra of thermostimulated depolarisation measured perpendicularly to layers of the non-intercalated 4-fold expanded GaSe matrix (a), synthesized hierarchal GaSe(SC(NH₂)₂) (b) GaSe(SmCl₃) (c) and GaSe(SC(NH₂)₂(SmCl₃)) (d) structures.

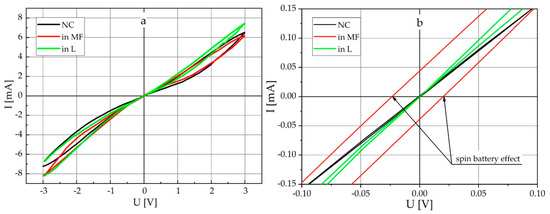
Figure 15. Current-voltage (CV) characteristics of GaSe(SC(NH₂)₂(SmCl₃)) measured perpendicularly to the layers under normal conditions (black), in the applied magnetic field (red) and under light illumination (green) (a). Spin battery effect: experiment under normal conditions (black), in the magnetic field H = 2.75 kOe (red) and under light illumination (green) (b).

Figure 16 shows the temperature dependence of the real component of the complex impedance measured perpendicularly to layers for the hierarchical GaSe(SC(NH₂)₂(SmCl₃)) structure. The anomalous increase of ReZ with temperature is observed in the temperature range 0–20 °C. To clarify the nature of such an effect, the temperature dependence of the density of states at the Fermi level N(E_F), hopping radius R, trapping centres scattering J, and the density of the deep trapping centres are presented in Figure 17. The critical temperature point T = 20 °C represents the minimal distribution in trapping centres at a relatively low value of the density of states at the Fermi level. One must mention that a considerable impact on the carriers’ mobility perpendicularly to the nanolayers has scattering mechanisms being temperature-dependent.

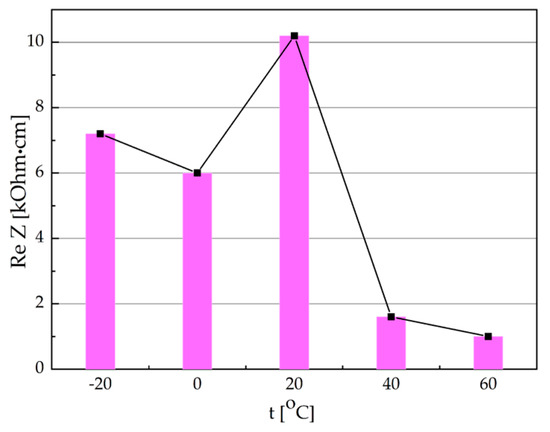
Figure 16. Temperature dependence of the real part of the complex impedance for GaSe(SC(NH₂)₂(SmCl₃)), measured perpendicularly to the layers.

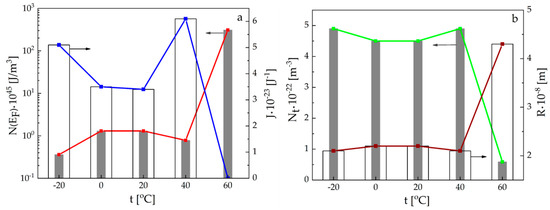
Figure 17. Temperature dependences of the density of states at the Fermi level N(E_F) and trapping centres scattering J (a), density of deep trapping centres N_t and hopping radius R (b) for GaSe(SC(NH₂)₂(SmCl₃)).

The peculiar energy structure of GaSe(SC(NH₂)₂(SmCl₃))—and the unique character of its thermostimulated depolarisation current spectra (see Figure 14d) and relevant quantum effects—suggest more detailed investigations of their electrical conduction properties that could shed light on the origin of the physical effects observed there. The magnetoresistive and photoresistive characteristics of the GaSe-based hierarchical structures, as well as prospective fields of their applications, are summarized in Table 1. The GaSe(SmCl₃) structure evidently demonstrates quite a large magnetoresistive efficiency, opening prospects for magnetic sensing applications. The hierarchical GaSe(SC(NH₂)₂(SmCl₃)) structure, on the other hand, exhibits abilities for the energy accumulation at quantum level. The spin battery effect revealed in this system opens prospects for magnetovoltaic applications.

Table 1. The magnetoresistive and photoresistive characteristics of the GaSe-based hierarchical structures and the prospective fields of their applications.

Structures	Magnetoresistive Effect ln(ReZMF/ReZ0)	Photoresistive Effect ln(ReZL/ReZD)	Inductive Response	Energy Accumulation at Quantum Level	Spin Battery Effect
GaSe(CS(NH2)2)	0.09531	−0.35667	−	−	−
GaSe(SmCl3)	−1.60944	−0.10536	+	−	−
GaSe(CS(NH2)2(SmCl3))	−0.22314	−0.69315	−	+	+

4. Conclusions

• The complex hierarchical structures of GaSe(CS(NH₂)₂), GaSe(SmCl₃), and GaSe(CS(NH₂)₂(SmCl₃)) were synthesized by intercalation technique. The non-additive influence of both the subhost and the guest components on the real part of the complex impedance for the GaSe(CS(NH₂)₂(SmCl₃)) clathrate is observable in the frequency region characteristic for band carriers. This proves that hierarchical modulating potential has a considerable impact on the electron impurity spectrum, which provides current flow under normal conditions;
• The GaSe(CS(NH₂)₂(SmCl₃)) clathrate is characterised by an unproportionally higher density of deep trap centres compared to the associative influence of the guest CS(NH₂)₂ and SmCl₃ components. The hierarchy of barrier potential, on the other hand, results in a decrease in the hopping radius of charge carriers;
• The increase in the photoresistive effect is provided by the complexity of the hierarchical structure. The magnetoresistive effect in GaSe(CS(NH₂)₂(SmCl₃)), on the other hand, is considerably smaller compared to SmCl₃ in the subhost potential field. The Zeeman effect influences the impurity energy spectrum, thus decreasing the density of deep trapping centres in the magnetic field;
• The strong inductive response, observable in the low-frequency region for the hierarchical GaSe(SmCl₃) clathrate, makes this material promising for the development of gyrator-free nanodelay lines, with prospects for nanoelectronics applications;
• The hysteresis in the volt-ampere characteristics of the hierarchical GaSe(CS(NH₂)₂(SmCl₃)) clathrate confirms the electric energy accumulation at the interphase boundaries. The EMF observed in the experiment is generated due to the spin battery effect in the stationary magnetic field.