Effects of Intercooling and Inter-Stage Heat Recovery on the Performance of Two-Stage Transcritical CO₂ Cycles for Residential Heating Applications

Abstract

Due to the harmful effects of synthetic refrigerants, such as chlorofluorocarbons (CFCs) and hydrochlorofluorocarbons (HCFCs)n the environment, natural refrigerants like carbon dioxide (CO₂) have been attracting great interest. The higher inter-stage superheating of CO₂ makes it difficult to predict the effects of the intercooling on heating performance of a two-stage transcritical CO₂ cycle. In addition, very little is known about the potential of inter-stage heat rejection recovery in the heating performance enhancement of this cycle. In order to explore the effects of intercooling and inter-stage heat rejection recovery potential, three “sub-cycles”—(1) a sub-cycle with heat recovery, (2) a sub-cycle without heat recovery, and (3) a sub-cycle without intercooling—were modeled in Engineering Equation Solver (EES) software for three commonly-used two-stage transcritical cycles: (1) an intercooler cycle, (2) a flash cycle, and (3) a split cycle. Then, the discharge pressure and intermediate pressure were simultaneously optimized. Based on the optimization results, the heating performance of the sub-cycles for each cycle were compared. The results demonstrate that the incorporation of intercooling without heat recovery was detrimental to the heating performance in comparison to the absence of intercooling. It is also clear that there is a great potential for heating performance improvement through inter-stage heat recovery.

1. Introduction

Increased concern for the world energy crisis and environmental problems has led to greater interest in eco-friendly refrigerants that are suitable for high-efficiency heat pump applications. Due to the abolition of chlorofluorocarbons (CFCs) and hydrochlorofluorocarbons (HCFCs) in the Montreal Protocol and the regulation of Hydrofluorocarbon (HFCs) in the Kyoto Protocol, the “natural” refrigerants have attracted considerable attention. Among the existing natural refrigerants, carbon dioxide (CO₂) is considered especially attractive because it is nonflammable, nontoxic, free from mutagens and carcinogens, and very low in cost [1]. However, the major disadvantage of the CO₂ cycle that influences its acceptance in the market is its lower performance [2,3,4].

Multi-stage heat pump/refrigeration cycles are typically used for large temperature differences between the source and sink, which cannot be overcome with single-stage systems [5]. Also, multi-stage cycles are an effective solution to provide power savings and improve the system performance. Two-stage cycles are usually used in food refrigeration and air conditioning for cooling applications and space or domestic water heating for heating applications, especially in cold climates.

Due to the low critical temperature of CO₂, in most areas of application, cycles are operated in transcritical conditions, and the existence of an “optimum” discharge pressure has received significant attention in the research community. In terms of the two-stage transcritical CO₂ cycle, both the intermediate pressure and discharge pressure influence system performance, with each having an optimum value. Due to this unusual nature, many researchers have conducted studies on the optimization of the discharge pressure and intermediate pressure for two-stage transcritical CO₂ cycles.

In cooling applications, Groll and Kim [6] conducted a literature review of the available research on transcritical CO₂ cooling cycles. They reported that the ideal intermediate pressure has frequently been found to differ from the classical estimation of the geometric mean of the evaporator and discharge pressure. The formula for the classical estimation is $\sqrt{Pev\times Pd}$, where $Pev$ is the pressure in the evaporator and $Pd$ is the discharge pressure of the second-stage compressor. Additionally, an optimum discharge pressure has generally been found to exist, with a higher gas cooler temperature leading to a higher optimum discharge pressure. Hwang et al. [7] measured the experimental performance of intercooler and split cycles, and found that every cycle displayed an optimum discharge pressure. Cavallini et al. [8] performed a theoretical analysis on a split cycle and an experimental analysis on an intercooler cycle. They investigated the effect of the second-stage pressure ratio on performance. Manole [9] found that the optimum intermediate pressure differed from the classical estimate also. Agrawal et al. [10] simultaneously optimized the discharge pressure and inter-stage pressure for flash and intercooler cycles, and found an optimum intermediate pressure and optimum discharge pressure for each cycle. Ozgur [11] performed a theoretical simulation of an intercooler cycle and determined the optimum discharge pressure for various gas cooler outlet temperatures. Ozgur and Bayrakci [12] studied the effect of the intermediate pressure on performance and concluded that there was an optimum intermediate pressure that maximized both first-law and second-law efficiencies. Cecchinato et al. [13] studied the split, flash, and intercooler systems experimentally, and confirmed that the optimum intermediate pressure deviated from the classical estimate by examining different intermediate pressures at specific discharge pressures. Srinivasan [14] studied an intercooler system and also found that the optimal intermediate pressure differed from the classical estimate. Almeida and Barbosa [15] simulated transcritical CO₂ cycles with and without intercooling. They found that intercooling provided a significant increase in the coefficient of performance (COP). Ozgur and Tosun [16] simulated flash and intercooler cycles and noted that the intermediate pressure had a greater effect on flash cycles. Zhang et al. [17] examined the effect of the discharge pressure, intermediate pressure, and mass flow rate on various flash and intercooler systems, and found an optimum value for all parameters investigated. Bush et al. [3] tested a lab-scale two-stage system to explore the effects of the mechanical subcooling on the system performance. A steady-state model for the system was developed and presented. To improve the performance of the transcritical CO₂ system, different combinations of a liquid suction heat exchanger after-cooler and two-stage compression were embedded into the system configuration by Mohammadi [4]. The modified configurations were modeled in detail using Engineering Equation Solver (EES) software, and energy and exergy analyses were performed for each configuration.

Due to the large throttle loss in the expansion valve, the two-stage cycles with advanced expansion devices, such as ejector, expander, and vortex tubes, have been of interest in the research community in recent years. Manjili and Yavari [18] proposed a new two-stage multi-intercooling refrigeration cycle employing an ejector, where the performance of this cycle was compared with two one-stage ejector refrigeration cycles. Sun et al. [19] compared the performance of six transcritical CO₂ cycles with and without an expander-compressor, which used an expander as an expansion device and served as an assistant compressor or the main compressor. Several different expander-compressor arrangements, including the two-stage cycle, were investigated. Bayrakci et al. [20] also analyzed the expander usage in a two-stage transcritical CO₂ cooling system. Variable parameters in this study were the gas cooler pressure, inter-stage pressure, and evaporation temperature of the refrigerant. Xing et al. [21] proposed a cycle with two ejectors as expansion devices. The performance of the improved two-stage cycles were evaluated and then compared with those of the basic two-stage cycle with a flash tank. Nemati et al. [22] compared the performance of a two-stage ejector-expansion transcritical refrigeration cycle using ethane and CO₂ as refrigerants. The theoretical analysis of the cycle performance characteristics was carried out for both refrigerants according to the first and second laws of thermodynamics. Zhang et al. [23] conducted a sensitivity study for three typical expander-based transcritical CO₂ cycles, including a two-stage cycle. The sensitivities of the maximum COP to the key operating parameters, including the inlet pressure of the gas cooler, the temperatures at evaporator inlet and gas cooler outlet, the inter-stage pressure, and the isentropic efficiency of expander, were obtained.

In heating applications, Wang et al. [24] tested the heating COP variation with discharge pressure and intermediate pressure. The result confirmed both of the pressures’ influence on the overall system heating performance, which is similar to that in cooling performance. Pitarch et al. [25] analyzed and optimized a two-stage split CO₂ cycle for heating applications regarding COP in terms of the discharge pressure. The classical estimate of the intermediate pressure was employed in this analysis. This finding differs from cooling cycle in that the heating COP decreases as the refrigerant is cooled down at the intercooler.

Many researchers have dealt with the two-stage transcritical CO₂ system for cooling applications while few paid attention to cycles for heating applications. In fact, the inter-stage superheating of compressed CO₂ vapor is far higher than that of traditional refrigerants [13]. For example, when R134a, R410a, and CO₂ are compressed between an evaporating temperature of 270 K and a condensing temperature of 290 K, R134a is superheated by only 2.88 K and R410a is superheated by 8.89 K, while CO₂ is superheated by 16.57 K. This feature leads to the difficulty in predicting whether the intercooling has a beneficial effect on the heating performance of the two-stage cycle. This is because the removal of heat decreases the second-stage work but it also reduces the amount of heat that can be released from the gas cooler. As a result, it is not apparent which of these opposing effects has a greater influence on heating COP. In addition, it would be a waste of energy if the inter-stage heat is rejected to the ambient environment. However, very little is known about the potential of inter-stage heat rejection recovery in the heating performance enhancement of two-stage transcritical CO₂ cycles.

In order to understand the effects of intercooling and inter-stage heat rejection recovery on the performance of two-stage transcritical CO₂ cycles for heating applications, three “sub-cycles” have been optimized and compared based on the models developed in EES 10.0 software (University of Wisconsin, WI, USA) for two-stage transcritical CO₂ cycles. Because both the two pressures could affect the performance, unlike using classical estimate of intermediate pressure in Pitarch et al. [25], the two optimal pressures for each sub-cycle were identified simultaneously in this study. The three sub-cycles were: (1) a sub-cycle with heat recovery (with HR), (2) a sub-cycle without heat recovery (without HR), and (3) a sub-cycle without intercooling (without IC). In terms of two-stage cycle selection for investigation, due to the unavailability of advanced expansion technology in the market and the findings that the throttling valve heating cycles are able to be applied to the advanced expansion cycles, in this study, the three commonly-used cycles with a throttling valve were investigated: (1) a basic two-stage compression intercooler cycle, (2) a flash cycle, and (3) a split cycle.

This paper is organized as follows. First, the optimum discharge pressure from the second-stage compressor ($P_D$) and intermediate pressure ($P_M$) for each sub-cycle were identified simultaneously. Second, the heating coefficients of performance (COPs) of the sub-cycles over a range of evaporating temperatures were compared. Finally, the cause of the observed trends in the COP for each sub-cycle was explained based on heating capacity ($\dot{Q}$) and compression work ($W$).

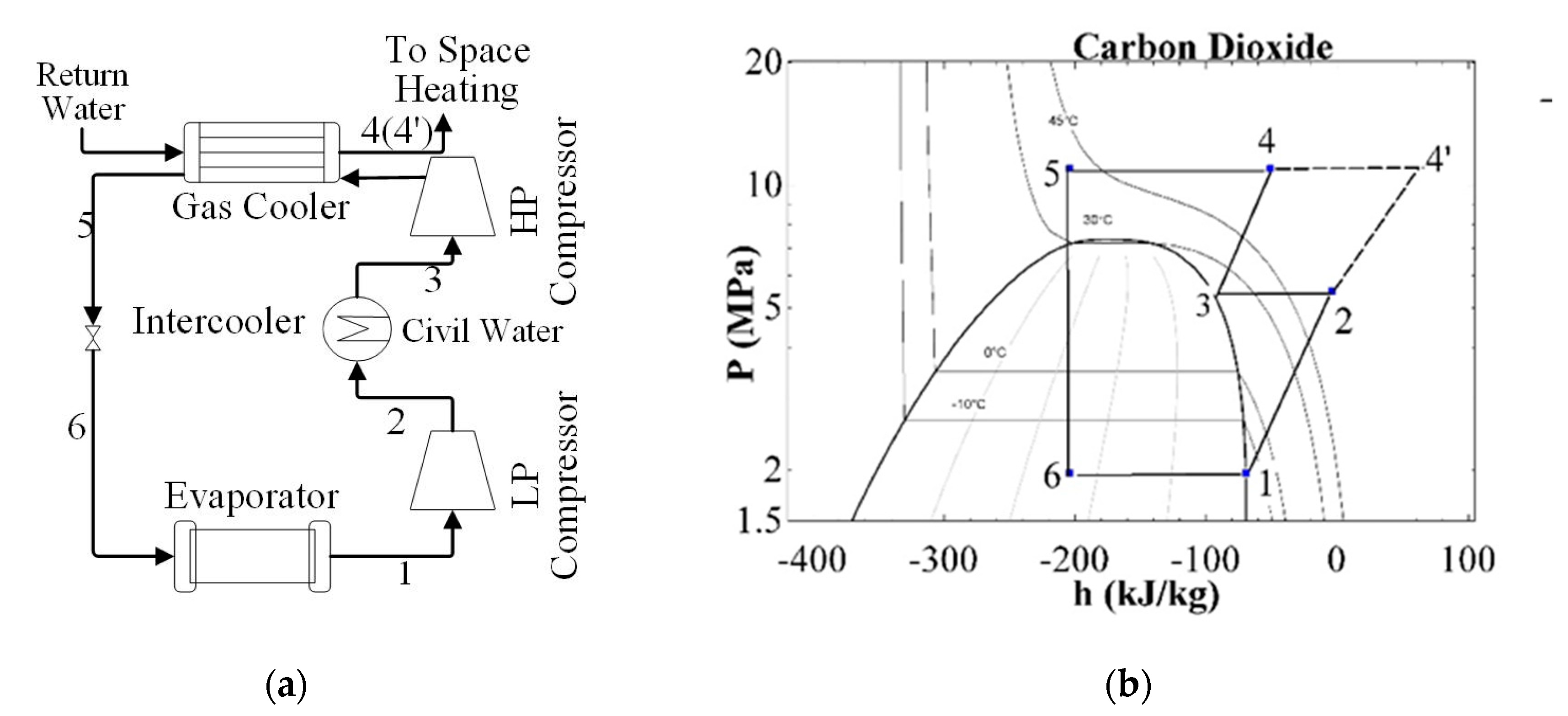
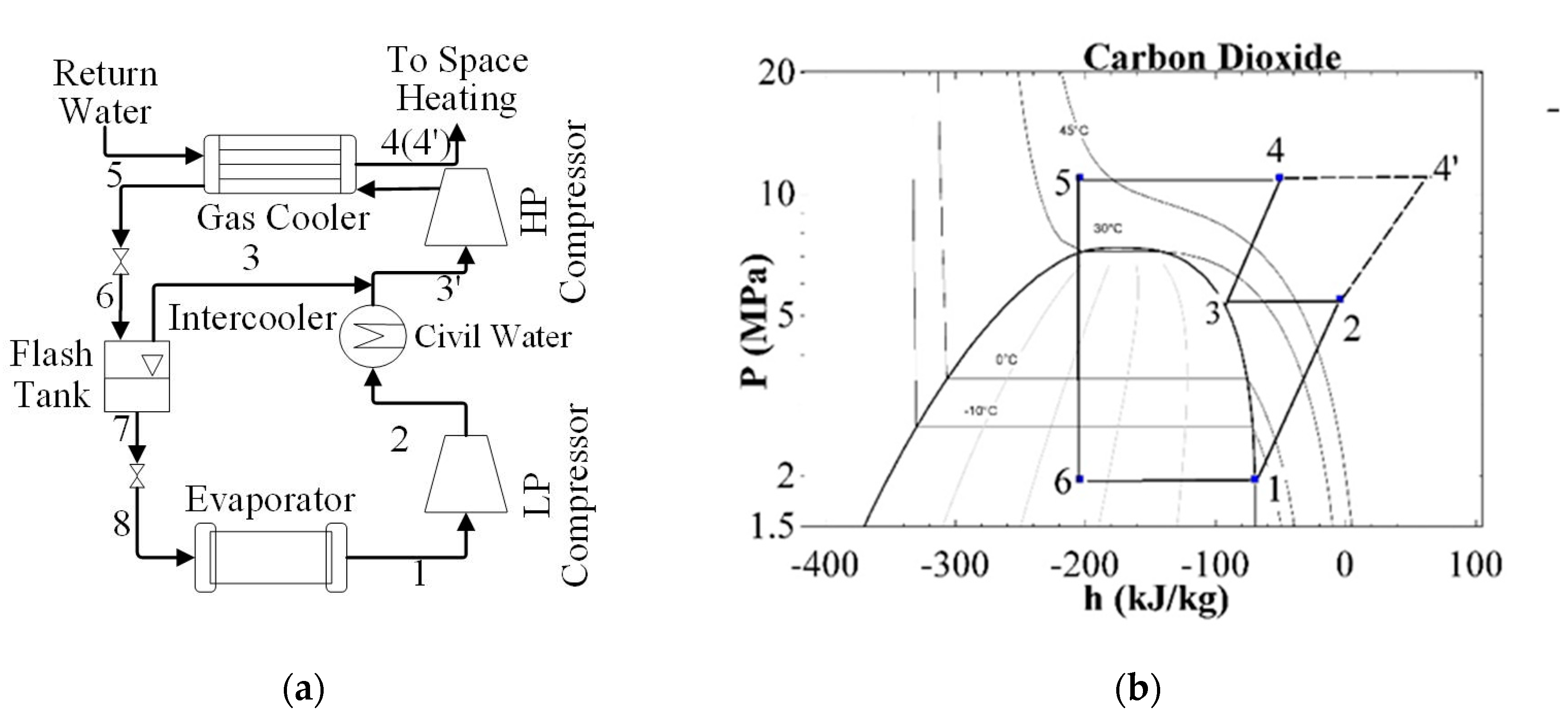
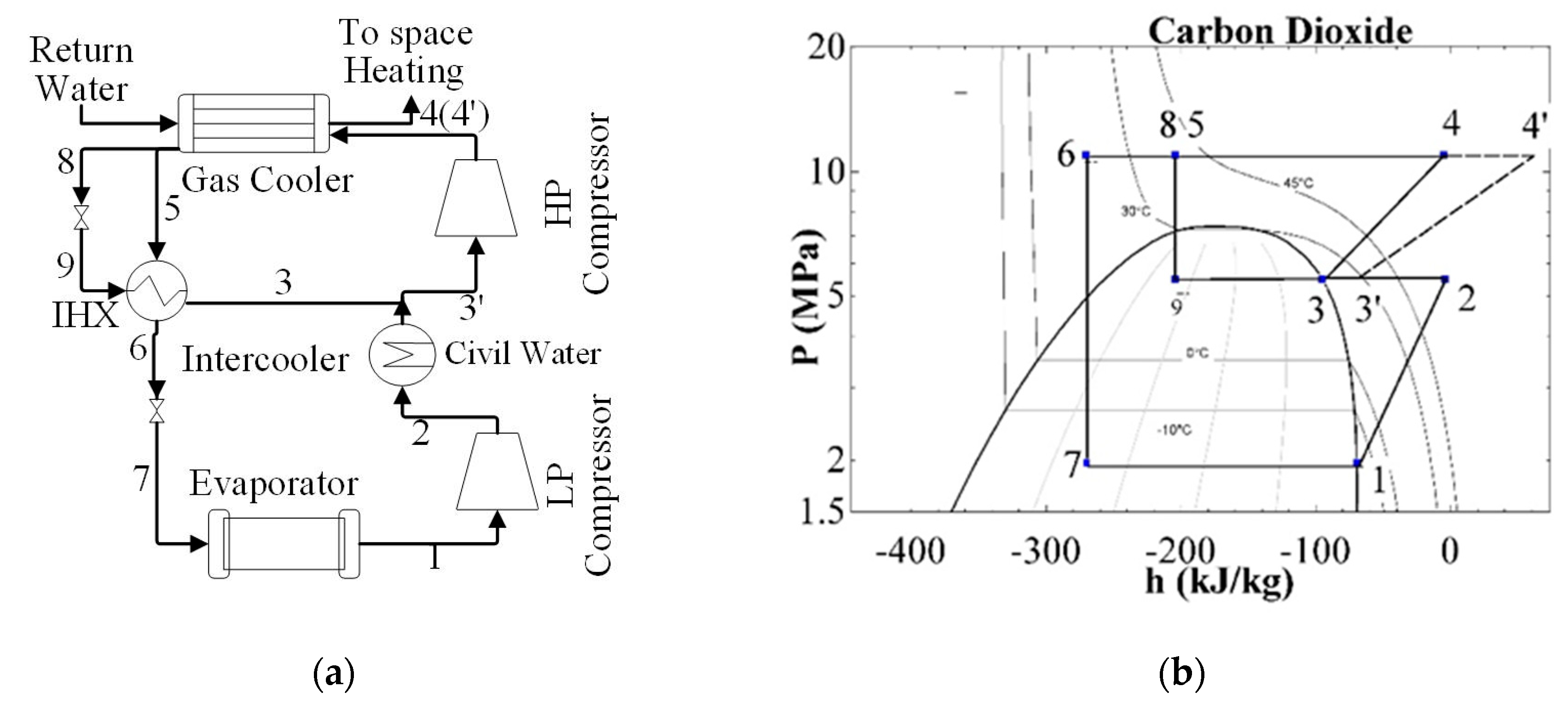
2. Cycles and Sub-Cycles under Analysis

Figure 1, Figure 2 and Figure 3 present the schematics and P–h diagrams of the intercooler cycle, the flash cycle, and the split cycle. Here are the descriptions of the three commonly-used cycles investigated: (1) Intercooling cycle: The intercooler cycle incorporates a low-pressure (LP) and high-pressure (HP) compressor and a single expansion valve. The two compressors work in series and interact with the mass flow leaving the evaporator. (2) Flash Cycle: The cycle operates similarly to the basic intercooling cycle, but with the addition of a flash tank and an expansion valve. The CO₂ expanding after the gas cooler enters a flash tank at the inter-stage pressure, where the vapor will be drawn by the HP compressor and the liquid will be throttled to the evaporator pressure. (3) Split Cycle: The cycle incorporates an LP and HP compressor in series, and two expansion valves. The mass flow splits after the gas cooler, where one part expands through the valve and enters the evaporator, and the other part expands and is injected with the outgoing stream of the low-pressure compressor.

To investigate the effects of intercooling and inter-stage heat rejection recovery on the heating performance of the above cycles, three sub-cycles were evaluated for each of the selected cycles. In this analysis, the heat rejected from the gas cooler was used for space heating and the civil water was used as coolant for the intercooler. The heat recovered through civil water can be used for domestic hot water (e.g., preheating or direct utilization), which makes this sub-cycle more practical.

The layout of the sub-cycles are as follows: (1) Sub-cycle with heat recovery: In the sub-cycle with heat recovery, an intercooler was installed after the first-stage compressor. Both the heat rejected from the gas cooler and the heat rejected from the intercooler were included for heating capacity calculations. (2) Sub-cycle without intercooling: In the sub-cycle without intercooling, no intercooler was installed after the first-stage compressor. (3) Sub-cycle without heat recovery: In the sub-cycle without heat recovery, an intercooler was installed after the first-stage compressor. However, only the heat rejected from the gas cooler was included for heating capacity calculations.

Table 1. The features of the three sub-cycles.

Name of the Sub-Cycle	Feature	Abbreviation
Sub-cycle with heat recovery	With both intercooling and heat recovery	with HR
Sub-cycle without intercooling	With neither intercooling or heat recovery	without IC
Sub-cycle without heat recovery	With only intercooling	without HR

shows the features of the three sub-cycles.

The heating COP of each sub-cycle for the intercooler cycle was defined as follows:

$$CO{P}_{\mathit{with}HR}=\frac{{\dot{Q}}_{\mathit{with} HR}}{{\dot{W}}_{\mathit{with} HR}}=\frac{{\dot{m}}_2\left(h_2-h_3\right)+{\dot{m}}_4(\left(h_4-h_5\right)}{{\dot{m}}_1\left(h_2-h_1\right)+{\dot{m}}_3(\left(h_4-h_3\right)},$$

(1)

$$CO{P}_{\mathit{without}IC}=\frac{{\dot{Q}}_{\mathit{without}IC}}{{\dot{W}}_{\mathit{without}IC}}=\frac{{\dot{m}}_{4^{\prime }}(\left(h_{4^{\prime }}-h_5\right)}{{\dot{m}}_1\left(h_2-h_1\right)+{\dot{m}}_2(\left(h_{4^{\prime }}-h_2\right)},$$

(2)

$$CO{P}_{\mathit{without}HR}=\frac{{\dot{Q}}_{\mathit{without}HR}}{{\dot{W}}_{\mathit{without}HR}}=\frac{{\dot{m}}_4(\left(h_4-h_5\right)}{{\dot{m}}_1\left(h_2-h_1\right)+{\dot{m}}_3(\left(h_4-h_3\right)}.$$

(3)

The heating COP of each sub-cycle for the flash cycle was defined as follows:

$$CO{P}_{\mathit{with}HR}=\frac{{\dot{Q}}_{\mathit{with} HR}}{{\dot{W}}_{\mathit{with} HR}}=\frac{{\dot{m}}_2\left(h_2-h_3\right)+{\dot{m}}_4\left(h_4-h_5\right)}{{\dot{m}}_1\left(h_2-h_1\right)+m_3(\left(h_4-h_3\right)},$$

(4)

$$CO{P}_{\mathit{without}IC}=\frac{{\dot{Q}}_{\mathit{without}IC}}{W_{\mathit{without}IC}}=\frac{{\dot{m}}_{4^{\prime }}(\left(h_{4^{\prime }}-h_5\right)}{{\dot{m}}_1\left(h_2-h_1\right)+{\dot{m}}_{3^{\prime }}(\left(h_{4^{\prime }}-h_{3^{\prime }}\right)},$$

(5)

$$CO{P}_{\mathit{without}HR}=\frac{{\dot{Q}}_{\mathit{without}HR}}{{\dot{W}}_{\mathit{without}HR}}=\frac{{\dot{m}}_4(\left(h_4-h_5\right)}{{\dot{m}}_1\left(h_2-h_1\right)+{\dot{m}}_3(\left(h_4-h_3\right)}.$$

(6)

The heating COP of each sub-cycle for the split cycle was defined as follows:

$$CO{P}_{\mathit{with}HR}=\frac{{\dot{Q}}_{\mathit{with} HR}}{{\dot{W}}_{\mathit{with} HR}}=\frac{{\dot{m}}_2\left(h_2-h_3\right)+{\dot{m}}_4(\left(h_4-h_5\right)}{{\dot{m}}_1\left(h_2-h_1\right)+{\dot{m}}_3(\left(h_4-h_3\right)},$$

(7)

$$CO{P}_{\mathit{without}IC}=\frac{{\dot{Q}}_{\mathit{without}IC}}{{\dot{W}}_{\mathit{without}IC}}=\frac{{\dot{m}}_{4^{\prime }}(\left(h_{4^{\prime }}-h_5\right)}{{\dot{m}}_1\left(h_2-h_1\right)+{\dot{m}}_{3^{\prime }}(\left(h_{4^{\prime }}-h_{3^{\prime }}\right)},$$

(8)

$$CO{P}_{\mathit{without}HR}=\frac{{\dot{Q}}_{\mathit{without}HR}}{{\dot{W}}_{\mathit{without}HR}}=\frac{{\dot{m}}_4(\left(h_4-h_5\right)}{{\dot{m}}_1\left(h_2-h_1\right)+m_3(\left(h_4-h_3\right)},$$

(9)

where $\dot{Q}$ is the heating capacity (kJ/s); $\dot{W}$ is the compression work (kJ/s); ${\dot{m}}_1$ is the mass flowrate of CO₂ (kg/s);$h$ is the specific enthalpy of CO₂ (kJ/kg).

3. Mathematical Modelling

3.1. Thermodynamic Analysis

An Engineering Equation Solver (EES) [26] is a numerical equation-solving program with many built-in mathematical and thermophysical property functions useful for engineering calculations. The high accuracy thermodynamic and transport property database means that EES is widely used in thermodynamic and heat transfer fields. The reliability and the accuracy of the numerical models in this study depend on the compressor efficiency correlation, the temperature calculation of the internal heat exchanger (IHX), and the temperature difference between CO₂ and water, which are presented as follows from the former research results.

The efficiency of the compressor is estimated by employing the following correlation for the semi-hermetic compressor [27]:

$$\eta =-0.26+0.7952\left(\frac{P_{c,o}}{P_{c,i}}\right)-0.2803{\left(\frac{P_{c,o}}{P_{c,i}}\right)}^2+0.0414{\left(\frac{P_{C,O}}{P_{c,i}}\right)}^3-0.0022{\left(\frac{P_{c,o}}{P_{C,i}}\right)}^4,$$

(10)

where $\eta$ is the compressor efficiency, $P_{c,o}$ is the CO₂ pressure at the outlet of the compressor (MPa), and $P_{c,i}$ is the CO₂ pressure at the inlet of the compressor (MPa). For the split cycle, the temperatures for the high-pressure IHX could be given by [25]:

$$T_6=T_9+3.$$

(11)

The outlet enthalpy of the expansion valve could be calculated using:

$$h_{\mathrm{outlet}}=h_{\mathrm{inlet}},$$

(12)

where $h_{\mathrm{outlet}}$ is the CO₂ enthalpy at the outlet of the expansion valve (kJ/kg) and $h_{\mathrm{inlet}}$ is the CO₂ enthalpy at the inlet of the expansion valve (kJ/kg).

Llopis et al. [28] tested a CO₂ transcritical refrigeration plant, where the difference between the gas cooler outlet CO₂ temperature and inlet water temperature was reported to be less than 5 °C. Hence, the temperature difference between the inlet water and outlet CO₂ was taken as 5 °C in this study.

In practical applications, the superheat is controlled at a constant to adjust the refrigerant mass flow rate to meet the various demands. In simulated analyses, the constant is usually selected to be a small value, like 0 °C, 5 °C, or 10 °C. The superheat assumption will affect the optimization results, but a similar trend will be found for different superheat assumptions. In this study, the superheat at the inlet of the first stage compressor was assumed to be 0 °C. Compared to the high operating pressure of the CO₂ cycle, the pressure drop in the pipes and heat exchanger is very small. Hence, the pressure drop in the pipes and heat exchangers were considered to be negligible. This assumption has little influence on the thermodynamic state parameters and thus the optimization results.

3.2. Optimization Conditions

In this paper, each cycle was optimized regarding the maximum heating COP using the conjugate directions method in EES. The discharge pressure and the intermediate pressure were simultaneously optimized. Because the critical temperature and critical pressure of CO₂ are 31.1 °C and 7.39 MPa, this means the heat is rejected in a supercritical process in residential heating applications. Hence, the lower bound of the P_D for the second stage compressor was taken to be 7.4 MPa and the upper bound of the P_M, namely the discharge pressure of the first stage compressor, was taken to be 6.8 MPa. The manufacturer could provide a CO₂ compressor capable of operating at the maximum of 14 MPa; therefore, the upper bound of the P_D was taken to be 14 MPa.

For the two sub-cycles with heat recovery and the sub-cycle without heat recovery, civil water was used as a coolant for the intercooler. If the temperature in the intercooler is lower than that of civil water, the civil water neither has an effect on cooling down the intercooler nor has the capability of recovering the heat rejected from the intercooler. With the assumption of the 5 °C temperature difference between the civil water temperature and the CO₂ temperature (discussed in Section 3.1), the lower bound of P_M for these two sub-cycles was set to be 5.1 MPa, where 5.1 MPa is the corresponding saturated pressure of CO₂ at 15 °C.

Table 2. The optimization conditions of the three sub-cycles.

Name of the Sub-Cycles	PD		PM
	Lower bound	Upper bound	Lower bound	Upper bound
Sub-cycle with heat recovery	7.4 MPa	14 MPa	5.1 MPa	6.8 MPa
Sub-cycle without intercooling	7.4 MPa	14 MPa	2.5 MPa	6.8 MPa
Sub-cycle without heat recovery	7.4 MPa	14 MPa	5.1 MPa	6.8 MPa

presents the optimization conditions.

4. Results and Discussion

The cycle performance was evaluated on the basis of a maximum heating COP to obtain optimum values for P_D and P_M. The performance was evaluated over an evaporator temperature range of −20 °C to 0 °C. The heat rejected from gas cooler was used for space heating, so the gas cooler outlet temperature of CO₂ was fixed at 40 °C to meet the requirements of space heating. This temperature could be achieved by adjusting the inlet water flow rate according to the heat demand. The performance parameters and their optimum values are displayed graphically and elucidated below.

4.1. Optimization Results

4.1.1. Intercooler Cycle

Figure 4 shows the variation of the optimum P_D and P_M for each sub-cycle with the change of T_ev from −20 °C to 0 °C for the intercooler cycle. It was found that for the sub-cycle without heat recovery, the optimum P_M was calculated to have an optimum value of 5.1 MPa for all operating conditions. This means the that sub-cycle without heat recovery had a maximum COP when P_M was operating at its minimum limit. The sub-cycle without intercooling had an optimum P_M of 5.1 MPa when the T_ev was less than −15 °C. It was also observed that the optimum P_D of each sub-cycle decreased linearly with T_ev. For the sub-cycle with heat recovery, the optimal P_D decreased linearly with T_ev, while P_M increased with T_ev.

4.1.2. Flash Cycle

Figure 5 shows the variation of the optimum P_D and P_M for each sub-cycle with the change of T_ev from −20 °C to 0 °C for the flash cycle. With the similarity of the intercooler cycle, the sub-cycle without heat recovery had an optimum P_M of 5.1 MPa. The sub-cycle without intercooling had an optimum P_M of 5.1 MPa at T_ev equals −20 °C. It was also observed that the optimum P_D decreased almost linearly with T_ev for all the sub-cycles while P_M increased with T_ev for the sub-cycle with heat recovery. The optimum P_D of the sub-cycle without HR showed a significant decrease, while the optimum P_D had a slight decrease for the other two sub-cycles.

4.1.3. Split Cycle

Figure 6 shows the variation of the optimum P_D and P_M for each sub-cycle with the change of T_ev from −20 °C to 0 °C for the split cycle. It can be observed that, regarding the optimal P_M of the sub-cycle without heat recovery, the split cycle resembled the other two cycles investigated above. The sub-cycle without heat recovery had an optimum P_M of 5.1 MPa until T_ev was around −5 °C. Like the flash cycle, the optimum P_D decreased almost linearly with the increase of the T_ev for all the sub-cycles and the P_M increased with the increase of the T_ev for the sub-cycle with heat recovery and the sub-cycle without intercooling. This might be because the sub-cycle without heat recovery had the maximum COP at the lower bound of the P_M when the T_ev was less than −5 °C. Therefore, the P_D without HR was larger than the P_D with HR when the T_ev was less than −5 °C and lower than the P_D with HR when T_ev was 0 °C and −5 °C.

From the optimal P_D and P_M values of the three cycle types, it can be concluded that the optimal P_D decreased with T_ev and the optimal P_M increased with T_ev for two-stage heating operations. These findings agree with the results of Agrawal et al. [10] for cooling operations.

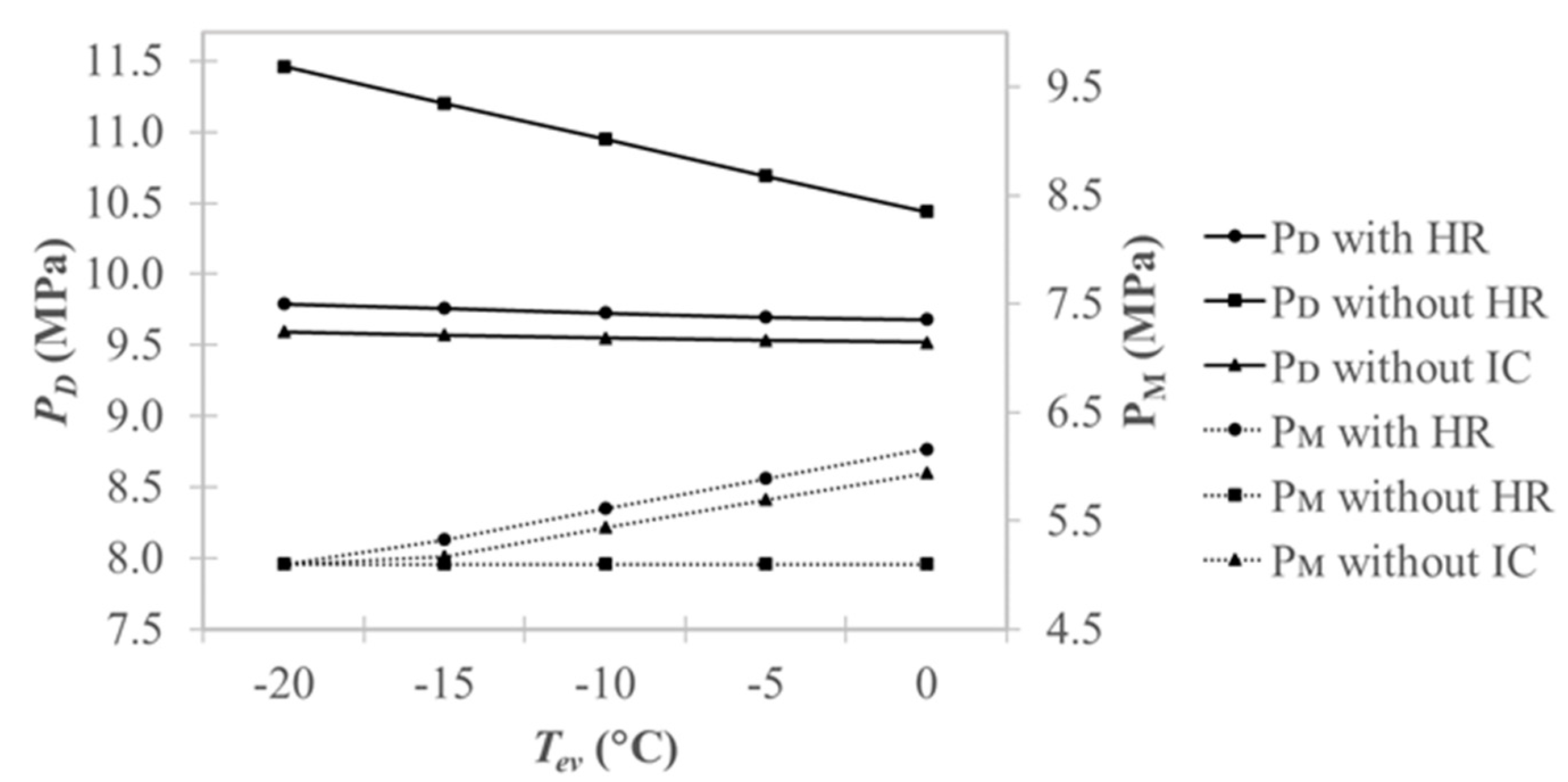
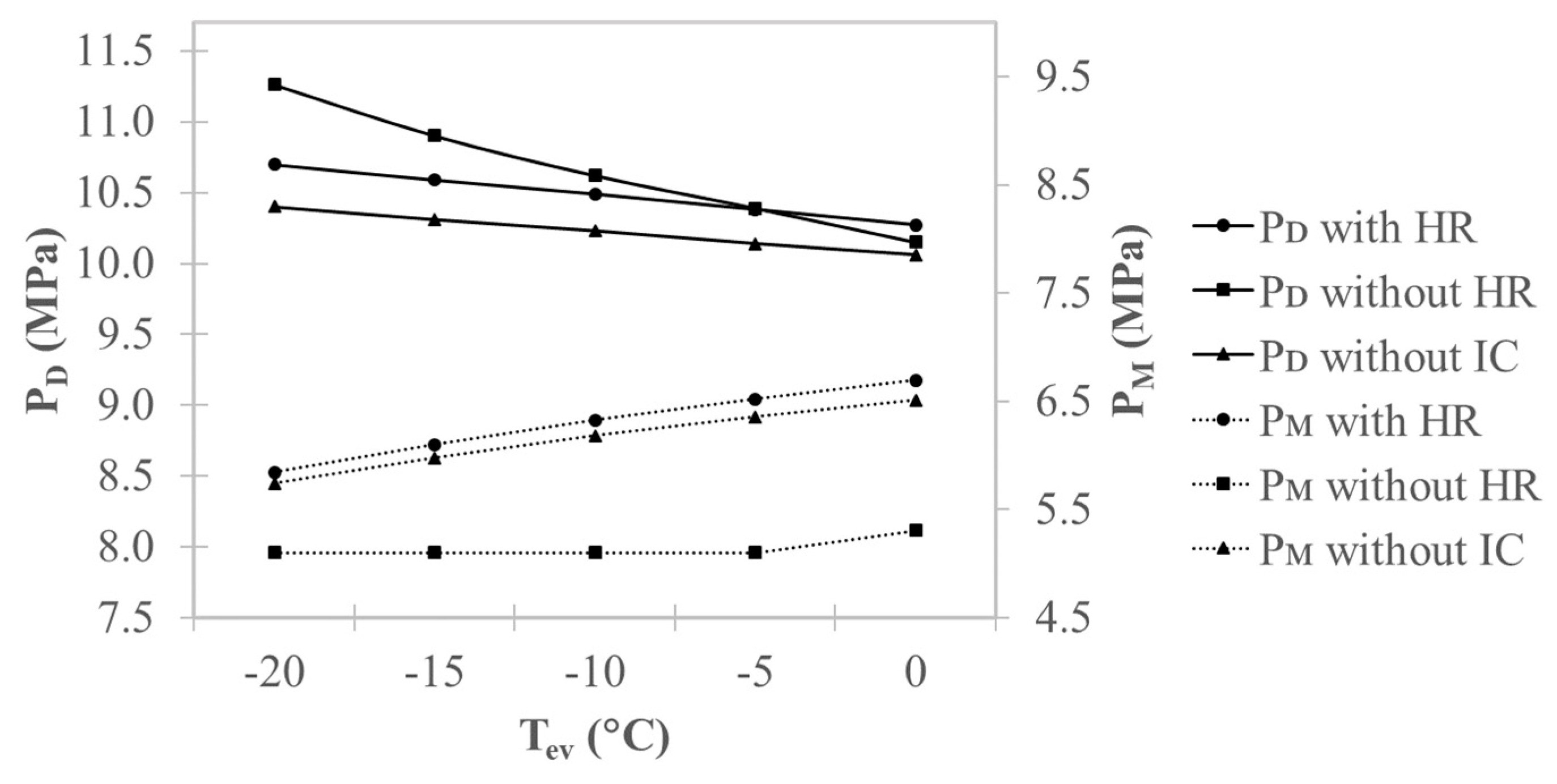
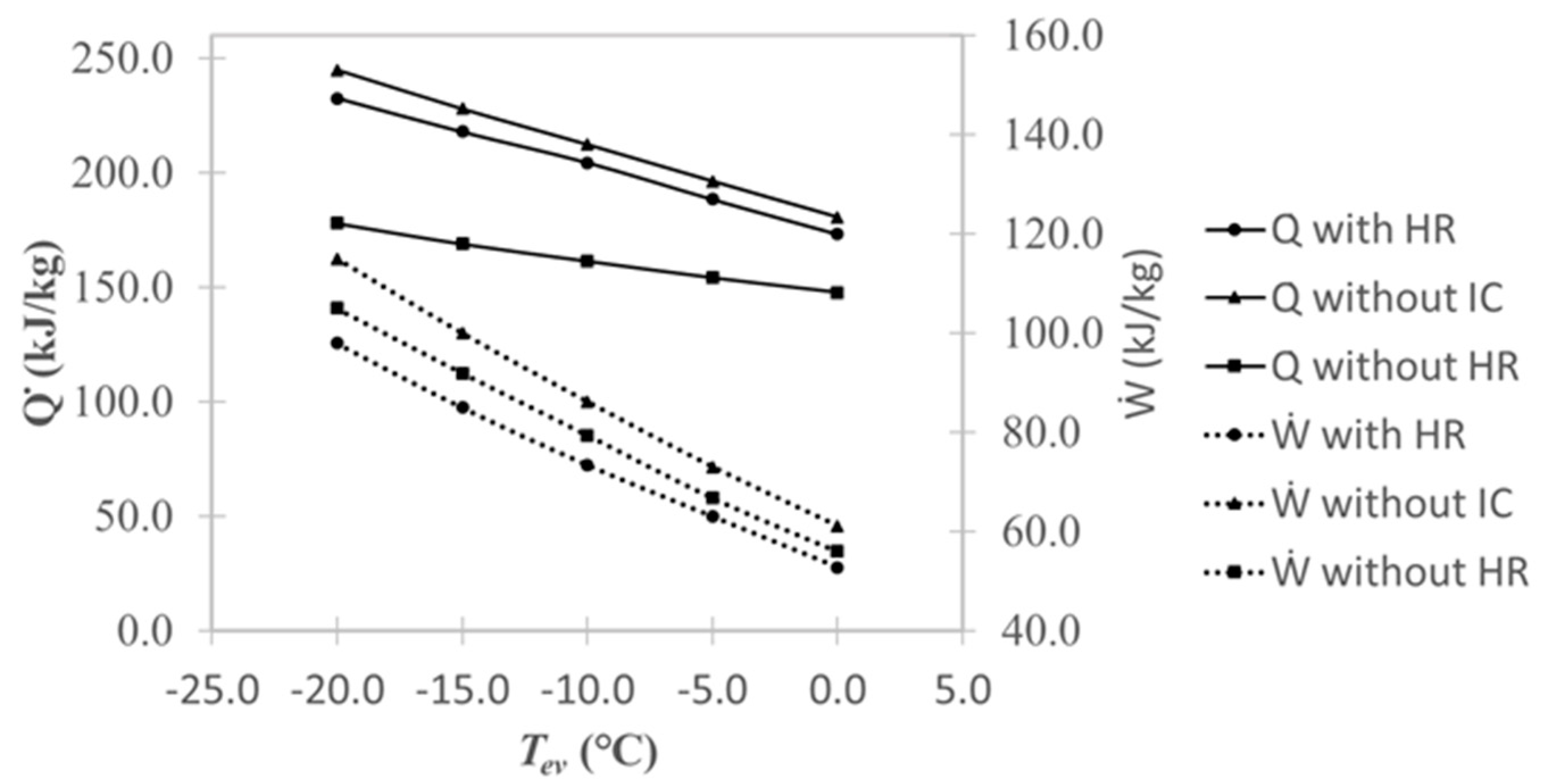
4.2. Effects on Performance

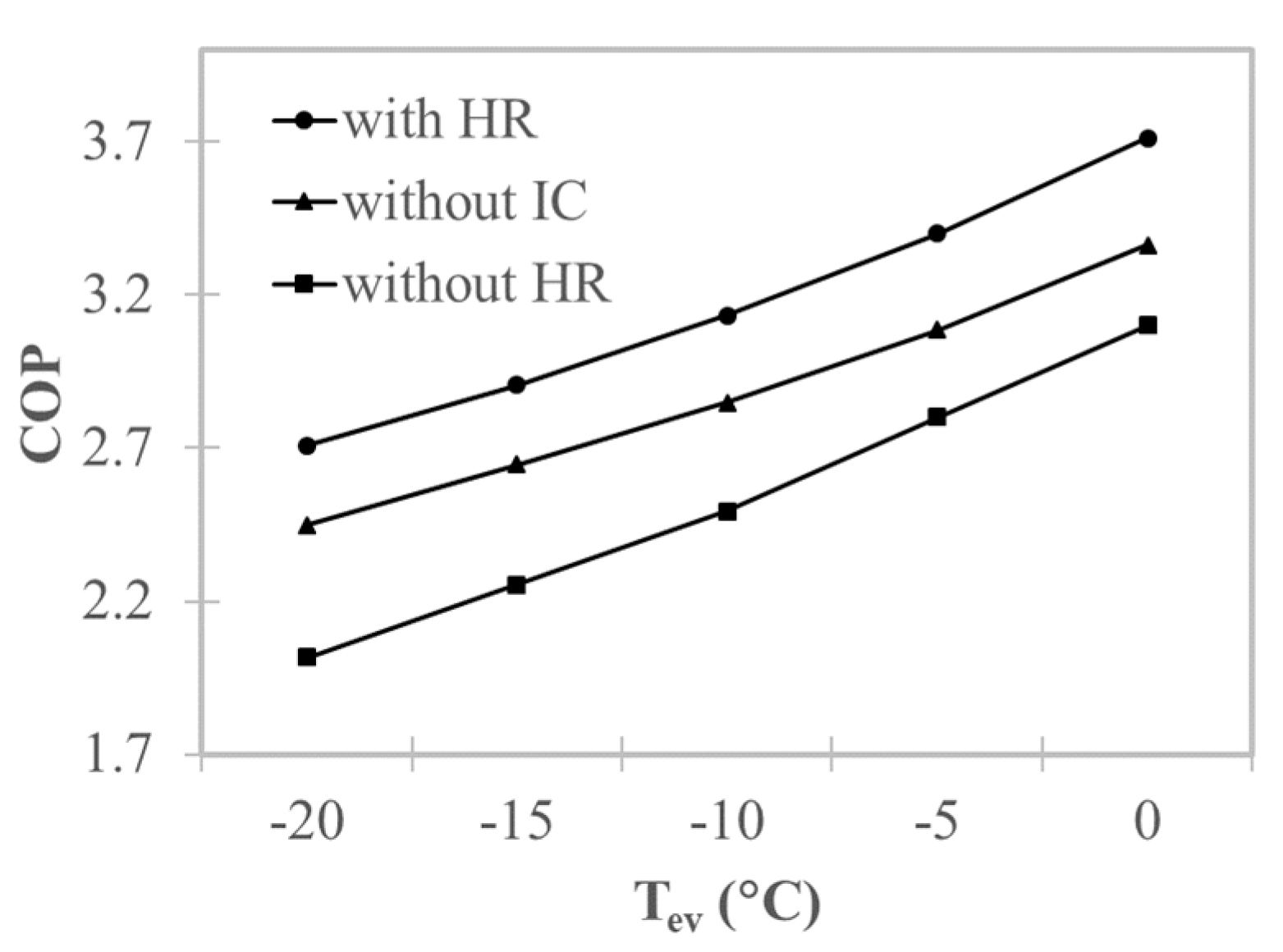
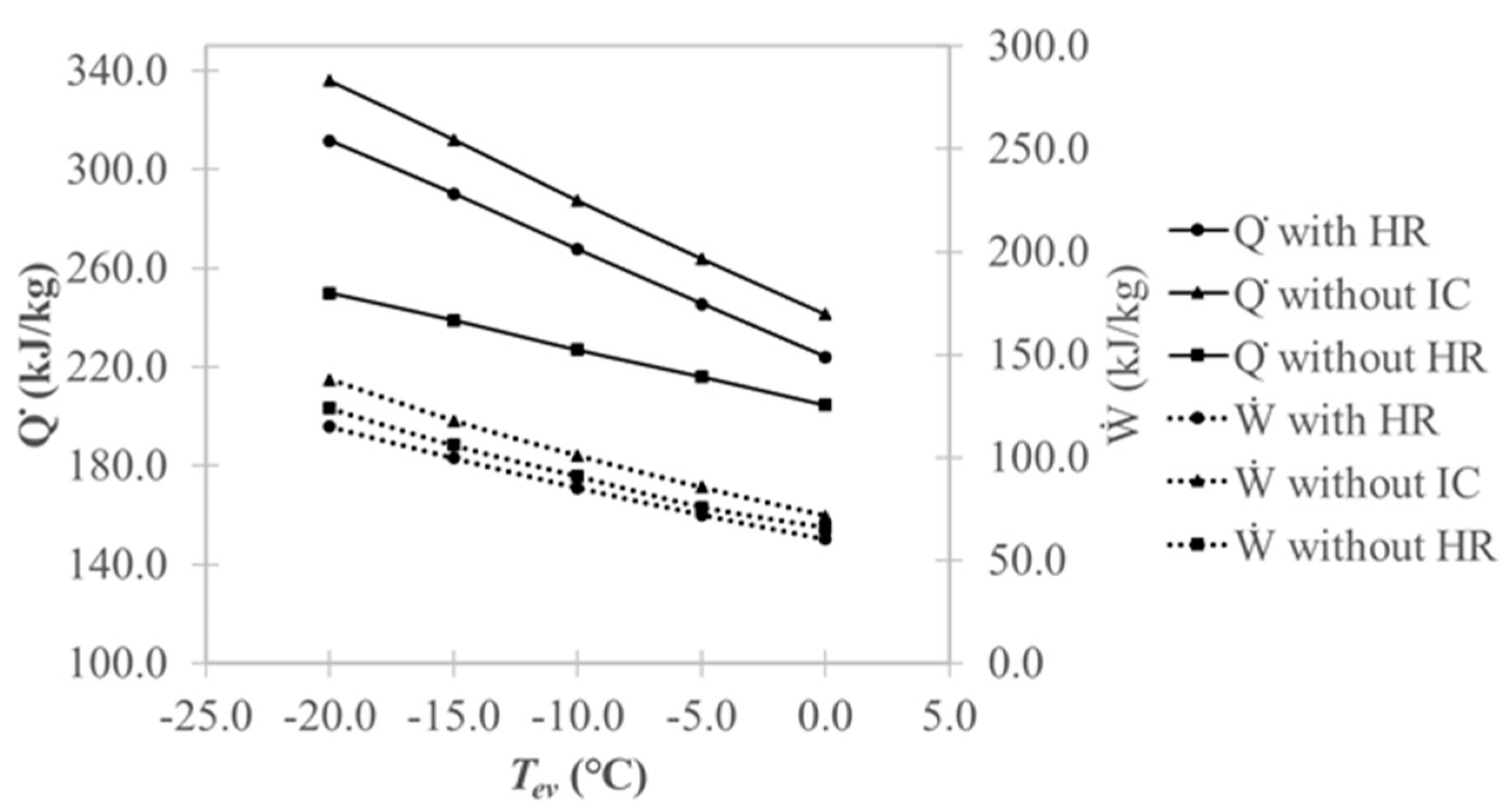
4.2.1. Intercooler Cycle

Figure 7 illustrates the comparison of the COP for all sub-cycles operating at optimum conditions for the intercooler cycle. It can be seen that the sub-cycle with heat recovery had the highest COP and the sub-cycle without heat recovery had the lowest COP. As T_ev varied from −20 °C to 0 °C, the sub-cycle with heat recovery experienced an increase in COP from 2.4 to 3.3. The COP of the sub-cycle with heat recovery was greater than that of the sub-cycle without intercooling by 11.2% to 14.1%, and greater than that of the sub-cycle without heat recovery by 24.2% to 50.3%.

The results show that the recovery of heat from the intercooler yielded the highest COP among the sub-cycles. The COP of the sub-cycle with heat recovery was even greater than the COP of the sub-cycle without intercooling, with an advantage of about 13.1%. It had a 37.5% advantage over the sub-cycle without heat recovery. However, installing an intercooler without heat recovery after the first-stage compression led to a COP about 17.4% lower than that of the sub-cycle with no intercooler at all.

The COP trends for the intercooler cycle is explained via the differing compression work and heating capacity of the sub-cycles. Figure 8 illustrates the heating capacity and compression work per unit of CO₂ mass for the sub-cycles operating at optimum conditions in the intercooler cycle.

It can be observed that both the heating capacity and compression work of the sub-cycle without intercooling were greater than those of the sub-cycle with heat recovery. Although both the heating capacity and work values of the sub-cycle without intercooler were greater than those of the sub-cycle with heat recovery, the higher COP of the sub-cycle with heat recovery was attributed to the compression work having a more significant influence on COP than heating capacity. For example, when T_ev = −20 °C, the heating capacity of the sub-cycle without intercooling was greater than that of the sub-cycle with heat recovery by 5.3%. Meanwhile, the compression work of the sub-cycle without intercooling was greater than that of the sub-cycle with heat recovery by 17.3%. As a result, the sub-cycle with heat recovery outperformed the sub-cycle without intercooling.

Regarding the COP comparison of the sub-cycle without intercooling and the sub-cycle without heat recovery, both the heating capacity and compression work of the sub-cycle without intercooling were greater than those of the sub-cycle without heat recovery. The difference in heating capacity ranged between 37.6% and 22.2%, and the difference in work ranged between 9.5% and 8.5% as the evaporator temperature rose. It can be concluded that the decrease in the heating capacity was proportionally greater. Therefore, the sub-cycle without heat recovery had a lower COP compared to the sub-cycle without intercooling.

Regarding the COP comparison of the sub-cycle with heat recovery and the sub-cycle without heat recovery, the situation was different. The sub-cycle with heat recovery had a higher heat capacity and a lower compression work, leading to a better COP.

4.2.2. Flash Cycle

Figure 9 illustrates the comparison of the COP for all sub-cycles at optimum conditions for the flash cycle. The COP of the sub-cycle with heat recovery increased with T_ev from 2.7 to 3.7, and was greater than that of the sub-cycle without intercooling by 9.8% to 10.4%. It was also greater than that of the sub-cycle without heat recovery by 34.3% to 19.7% as the evaporator temperature increased. In addition, the COP of the sub-cycle without heat recovery was less than that of the sub-cycle without intercooling by 17.7% to 7.8% as T_ev increased.

The results show that for the flash cycle, the recovery of heat from the intercooler was also beneficial to the performance. The COP of the sub-cycle with heat recovery was greater than the COP of the sub-cycle without intercooling by about 10.2%, and greater than the COP of the sub-cycle without heat recovery by about 26.0%. Additionally, installing an intercooler after the first-stage compression without heat recovery led to a lower COP than having no intercooler; the COP of the sub-cycle without heat recovery was less than that of the sub-cycle without intercooling by around 12.4%.

Figure 10 illustrates the heating capacity and compression work values of all sub-cycles at optimum conditions for the flash cycle. Regarding the COP comparison of the sub-cycle with heat recovery and the sub-cycle without intercooling, similar to the intercooler cycle, both the heating capacity and compression work of the sub-cycle without intercooling were greater. The difference in heating capacity ranged between 7.9% and 7.7%, and the difference in work ranged between 19.9% and 18.9% with increasing evaporator temperature. Since the higher compression work was a more significant factor than the higher heating capacity, the sub-cycle with heat recovery outperformed the sub-cycle without intercooling.

In terms of the COP comparison of the sub-cycle without intercooling and the sub-cycle without heat recovery, the heating capacity of the sub-cycle without intercooling was greater than that of the sub-cycle without heat recovery by 34.4% to 17.9% when T_ev increased. The compression work of the sub-cycle without intercooling was more than that of the sub-cycle without heat recovery by 11.3% to 8.7% as T_ev increased. Obviously, the greater heating capacity of the sub-cycle without intercooling was a more significant factor that its better performance. Hence, the sub-cycle without intercooling yielded a higher COP than the sub-cycle without heat recovery.

Regarding the COP comparison of the sub-cycle with heat recovery and the sub-cycle without heat recovery, the compression work of the sub-cycle with heat recovery was lower and its heating capacity was higher compared to the sub-cycle without heat recovery. Hence, the sub-cycle with heat recovery yielded a higher COP than the sub-cycle without heat recovery.

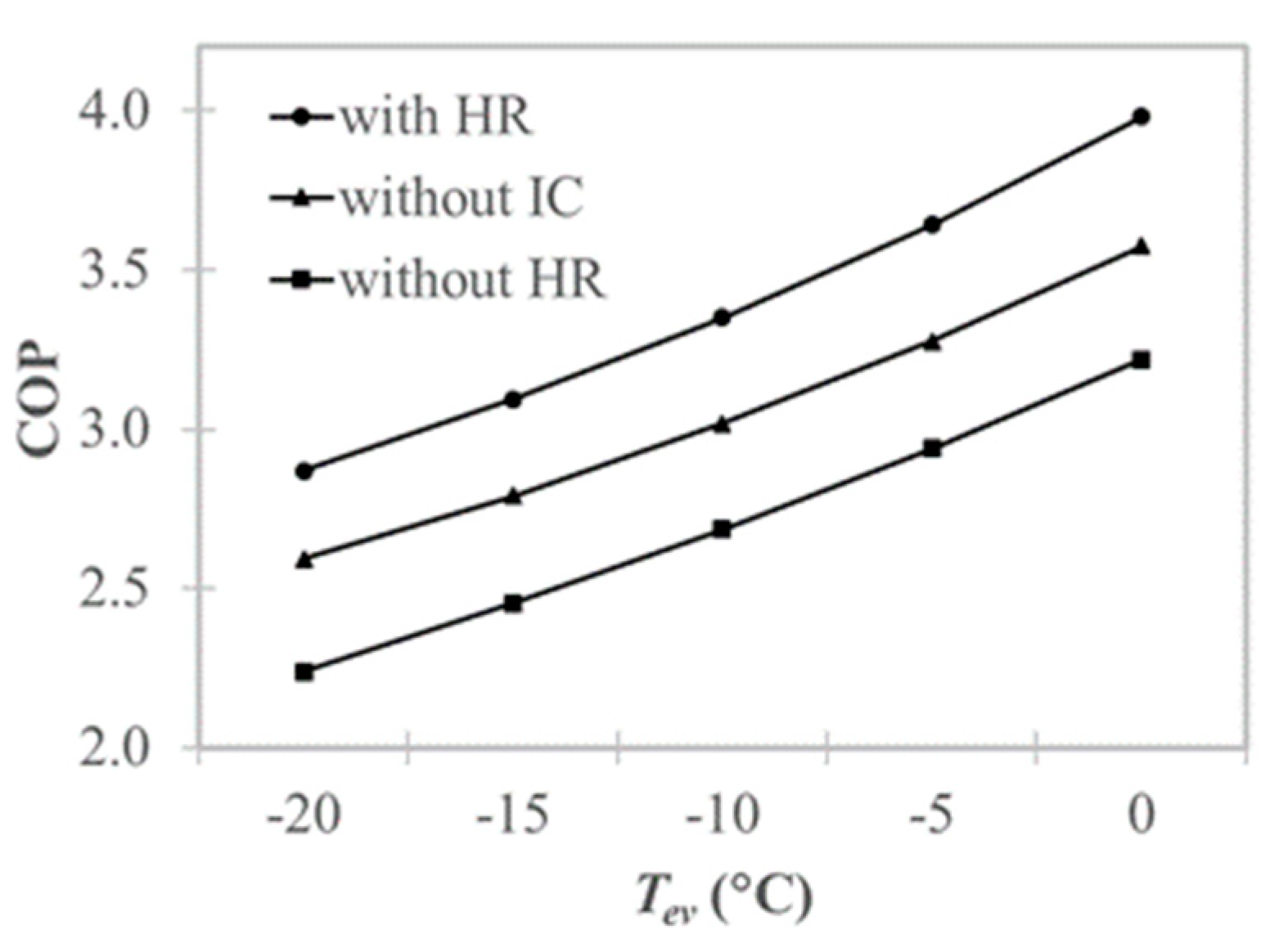
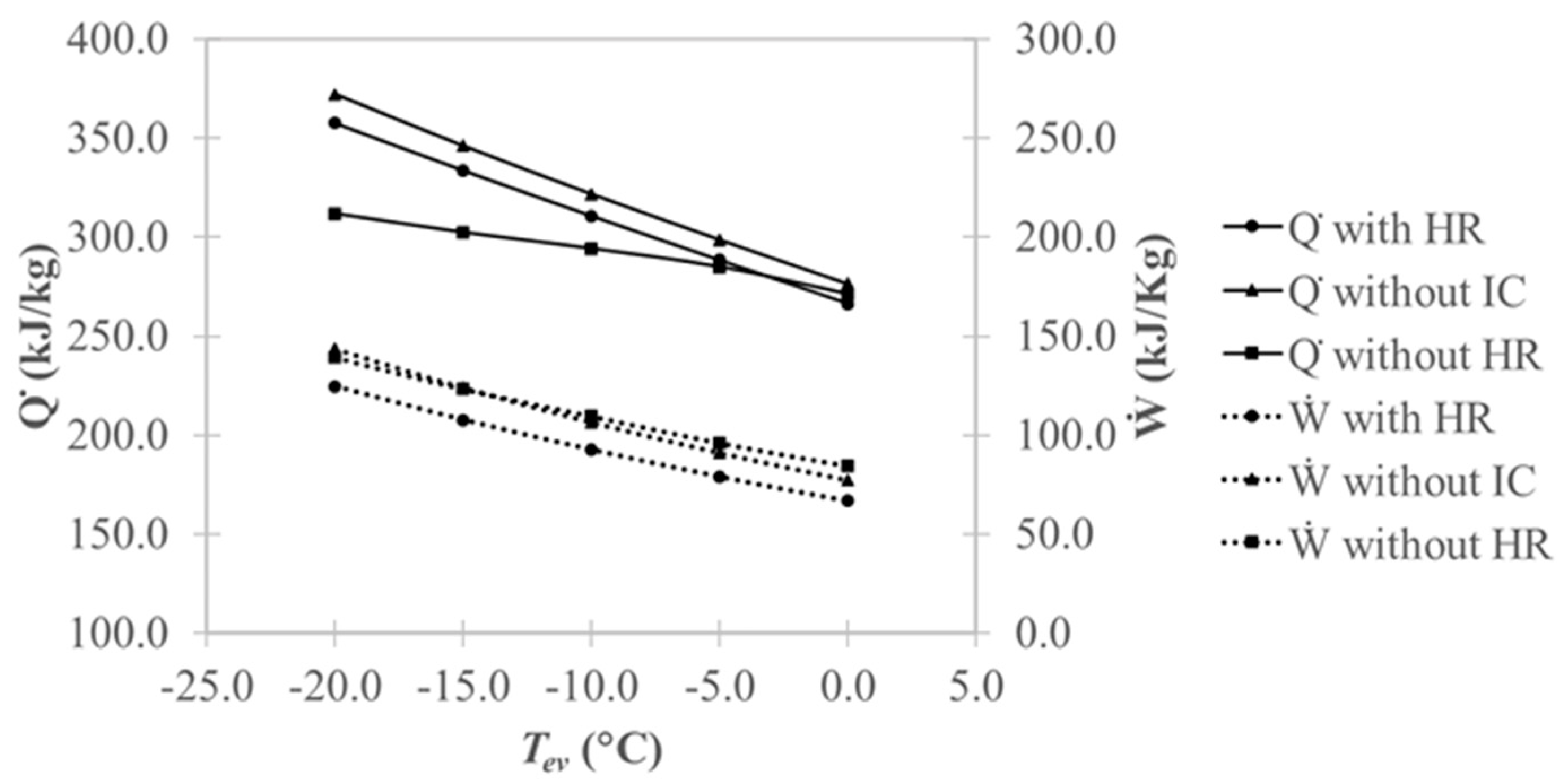
From the above discussion, it can be concluded that the reasons for the differing COPs among the flash sub-cycles was the same as for the intercooler cycle.

4.2.3. Split Cycle

Figure 11 illustrates the COP of all sub-cycles at optimum conditions for the split cycle. It can be seen that the COPs of this cycle had the same behavior as in the intercooler and flash cycles. The COP of the sub-cycle with heat recovery increased from 2.9 to 4.0 in the range investigated. The COP of the sub-cycle with heat recovery was greater than that of the sub-cycle without intercooling by between 10.8% and 11.4%. The COP of the sub-cycle with heat recovery was greater than that of the sub-cycle without heat recovery by 28.2% to 23.7%. The COP of the sub-cycle without heat recovery was less than that of the sub-cycle without intercooling by a value ranging from 13.6% to 9.9% with rising T_ev.

The results show that for the split cycle, the recovery of heat from the intercooler still resulted in the highest COP, while the installation of an intercooler without heat recovery after the first-stage compression still resulted in the lowest COP. The COP of the sub-cycle with heat recovery was greater than the COP of the sub-cycle without intercooling by about 10.9%, and greater than the COP of the sub-cycle without heat recovery by about 25.4%. Installation of an intercooler after the first-stage compression reduced the COP compared to the sub-cycle without intercooling by around 11.4%.

Figure 12 illustrates the heating capacity and compression work comparison at optimal conditions for the split cycle. The results may be due to the sub-cycle without heat recovery having an optimum P_M at the lower bound until T_ev was around −5 °C. Consequently, the heating capacity slope of the sub-cycle without HR changed at around −5 °C. This led to the heating capacity of the sub-cycle without HR being greater than the sub-cycle with HR when T_ev was more than −5 °C.

The heating capacity and compression work of the sub-cycle without intercooling were greater than those of the sub-cycle with heat recovery. The difference in heating capacity ranged from 4.1% to 3.7% and the difference in work ranged from 16.5% to 15.2% with rising evaporator temperature. This was due to the fact that the higher compression work appeared to be more significant than the difference in heating capacity. The sub-cycle with heat recovery had a higher COP than the sub-cycle without intercooling.

Regarding the COP comparison of the sub-cycle with heat recovery and the sub-cycle without heat recovery, the higher heating capacity and lower compression work of the sub-cycle with heat recovery yielded a relatively higher COP. The sub-cycle without intercooling yielded a higher COP than the sub-cycle without heat recovery for the same reason: lower compression work and higher heating capacity.

The reasons for the differing COPs among the sub-cycles of the split cycle was different from the above two cycles. Regarding the effect of intercooling on performance, the sub-cycle without intercooling yielded a higher COP than the sub-cycle without heat recovery because of its lower compression work and higher heating capacity.

5. Conclusions

In this study, the effects of intercooling on the heating performance of the two stage transcritical CO₂ cycle and inter-stage heat rejection recovery potential were explored for three commonly used two-stage cycles—intercooler, flash, and split cycles—through a performance comparison of three sub-cycles. When the sub-cycles operated at optimal conditions, the main findings were as follows:

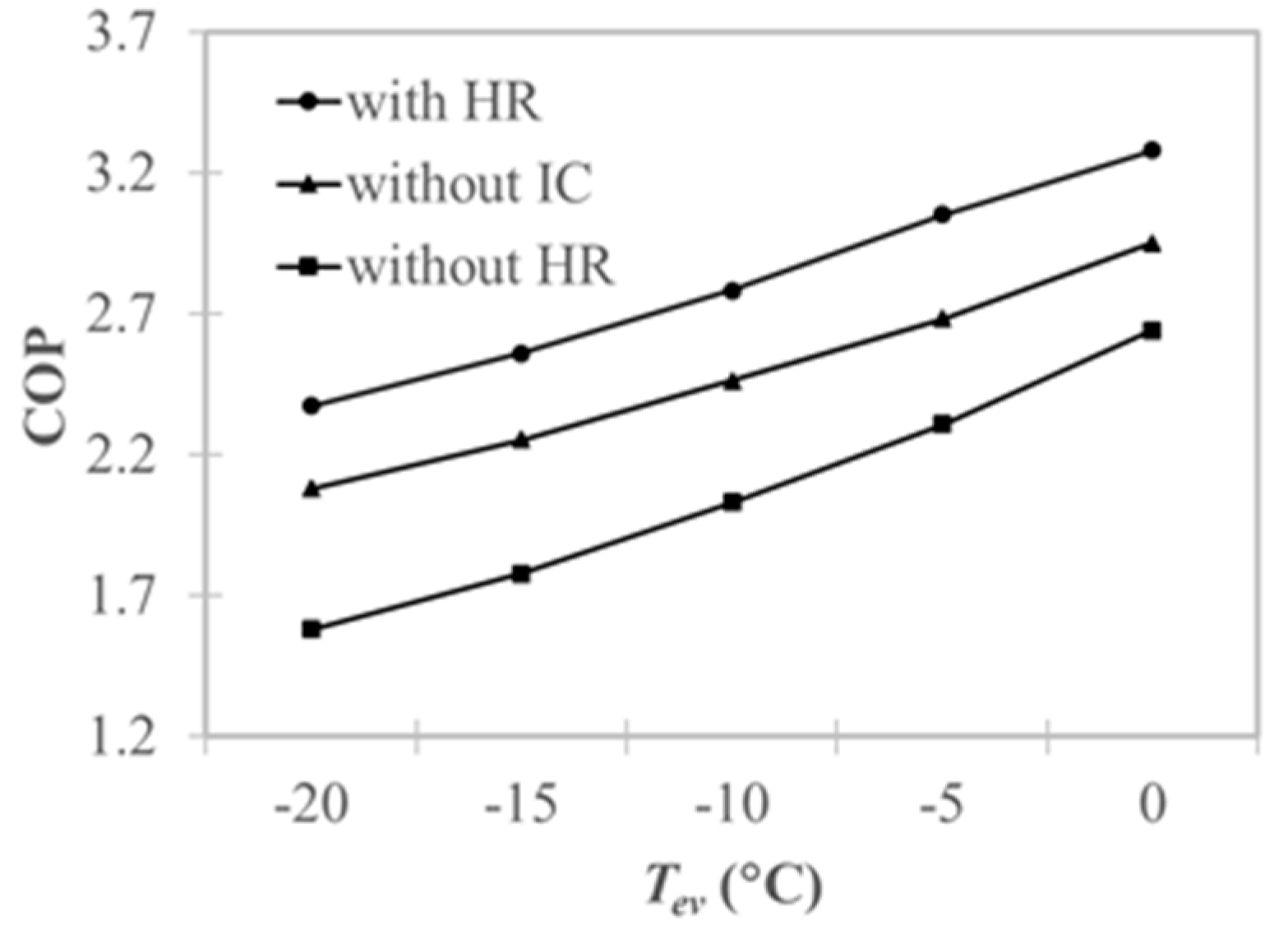
• There was a great potential for performance improvement via the recovery of heat from the intercooler. The COP of the sub-cycle with heat recovery was greater than that of the sub-cycle without intercooling by around 13.1% for the basic intercooler cycle, 10.2% for the flash cycle, and 10.9% for the split cycle; furthermore, it was greater than that of the sub-cycle without heat recovery by around 37.5% for the basic intercooler cycle, 26.0% for the flash cycle, and 25.4% for the split cycle.
• Incorporating an intercooler without heat recovery reduced the COP compared to the sub-cycle without intercooling for all cycle types. The COP of the sub-cycle without heat recovery was less than that of the sub-cycle without intercooling by around 17.4% for the basic intercooler cycle, 12.4% for the flash cycle, and 11.4% for the split cycle.
• The sub-cycle with heat recovery had a better COP than the sub-cycle without intercooling for all three cycle types examined; this was because the sub-cycle with heat recovery had lower compression work and lower heating capacity. However, the lowered compression work was a more significant factor, which led to a better performance. Similarly, the lower COP of the sub-cycle without heat recovery compared to the sub-cycle without intercooling was attributed to the fact that the decrease in heating capacity was more significant than the difference in compression work.
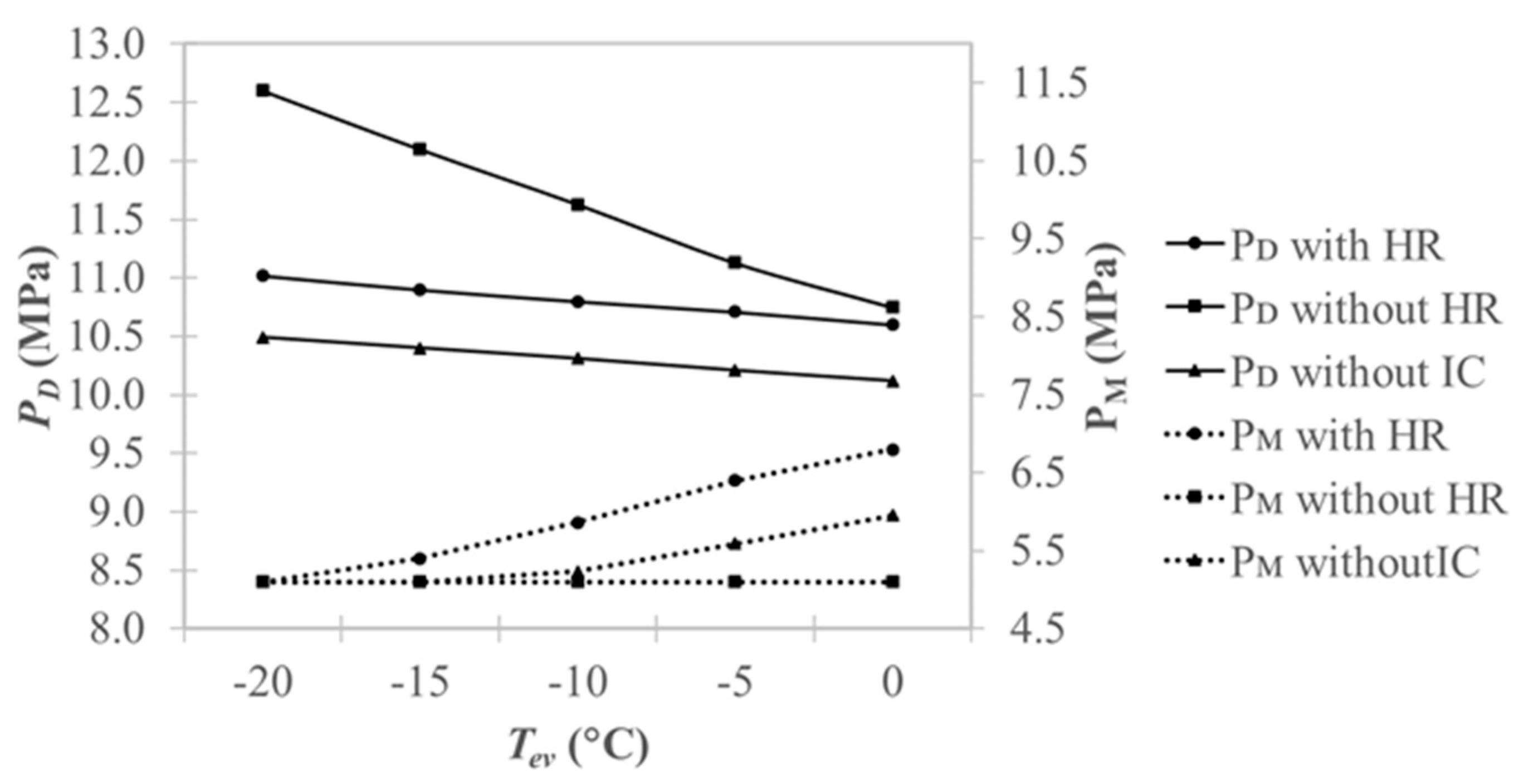
• It was found that the optimum discharge pressure, P_D, decreased with the evaporating temperature, T_ev, and the optimum intermediate pressure, P_M, increased with T_ev. This result was consistent with the results for cooling operations in the literature.