Abstract
In order to reduce the calculation effort during the simulation of the emission of polychlorinated dibenzo-p-dioxins and furans (PCDD/F) during municipal solid waste incineration, minimizing the number of simulated components is mandatory. For this purpose, two new multilinear regression models capable of determining the dioxins total amount and toxicity of an atmospheric emission have been adjusted based on previously published ones. The new source of data used (almost 200 PCDD/F analyses) provides a wider range of application to the models, increasing also the diversity of the emission sources, from industrial and laboratory scale thermal processes. Only three of the 17 toxic congeners (1,2,3,6,7,8-HxCDD, 2,3,7,8-TCDF and OCDF), whose formation was found to be linearly independent, were necessary as inputs for the models. All model parameters have been statistically validated and their confidence intervals have been calculated using the Bootstrap method. The resulting coefficients of determination (R2) for the models are 0.9711 ± 0.0056 and 0.9583 ± 0.0085; its root mean square errors (RMSE) are 0.2115 and 0.2424, and its mean absolute errors (MAE) are 0.1541 and 0.1733 respectively.
1. Introduction
In several countries of the eurozone, municipal solid waste (MSW) generation has constantly increased since the 90s, so its management is a critical environmental issue that society must solve at a future time. The European Commission collects data about the techniques used to it, such as recycling, landfilling, composting, and incineration [1]. Despite the fact that European institutions and many authors consider landfilling as more demanding than MSW incineration [2], other environmental questions, like polychlorinated dibenzo-p-dioxins and dibenzofurans (PCDD/F) atmospheric emissions during combustion processes should be considered [3,4]. Each PCDD/F molecule can contain up to eight chlorine atoms in eight different places on the molecule. This combination of number of chlorines and places results in an extensive family of molecules, where each molecule is called a congener.
Combustion processes emit PCDD/Fs as a mixture of up to 210 congeners, of which only 10 dioxins and 7 furans are considered to be toxic and thus most frequently analysed. In order to evaluate the impact of atmospheric emissions, the most common approach is to calculate the amount of toxic equivalents (TEQs) according to NATO/CCMS (North Atlantic Treaty Organization/Committee on the Challenges of Modern Society) [5]. This criterion uses toxic equivalency factors (TEFs) that proportionally modify the amount of each congener considering the most toxic one (2,3,7,8-TCDD) as the reference (unity factor). Despite the fact that TEFs have been questioned [6,7] and updated [8], the International Toxicity Equivalency Factors (I-TEFs) [9] prevail internationally, since most regulations for atmospheric emissions refer to them [10].
Despite the fact that the emission of PCDD/F has been related to industrial processes and human activity, some authors highlight the contribution of forest fires to the total emission of PCDD/Fs [11]. Several studies have been published on the formation of PCDD/F during the combustion of biomass and e-waste [12], demolition and construction wood [13], viscoelastic memory foam [14], furniture [15] and many other different residues. A publication addressing the emissions of a cement production plant [16] determined that, focusing on the distribution of the congeners of their samples, no big differences were observed among their emissions despite the fuel used in the kiln. The formation of PCDD/Fs from MSW incineration showed a strong interdependence with phenols, chlorinated benzenes and other precursors [17]. This interaction was used to suggest a model for the formation of dioxins’ precursors during thermal processes of degradation with the purpose of establishing an on-line measurement instrument [18].
Extensive investigations and reviews related to the formation of PCDD/F during combustion processes have been published [3,19]. However, despite the gigantic attempts, the governing mechanism and the parameters involved such as activity rates still remain uncertain [18]. Once the equilibrium constants of the PCDD/F formation reactions were calculated, it was found that those thermodynamic parameters strongly promote its generation [20,21,22,23]. Besides, the distribution of congeners calculated using the equilibrium constants is not consistent with the experimental one [24]. This evidence indicates that other formation mechanisms, along with gas phase reactions, should contribute to PCDD/F formation. Besides, the experimental PCDD/Fs emission values are considerably below the calculated emission values using the thermodynamic equilibrium constants; thus, the thermodynamic equilibrium is never reached. This fact suggests that kinetic mechanisms control the formation of PCDD/F, rather than thermodynamic ones.
The relevance of the kinetic mechanisms reinforces the suggestion that the formation of the PCDD/Fs congeners is interdependent [25], which should lead to a correlation between the amounts of the different congeners produced. This interdependence between the less-chlorinated PCDD/Fs congeners and the TEQ has been modelled [26]; as well as the correlation between TEQ and PCDD/Fs precursors like tri/tetra-chlorobenzene [27], or naphthalene, fluorene, and phenanthrene [28].
The main goal of the present research is to develop a simulation model of a MSW incineration facility and estimate the PCDD/Fs atmospheric emissions on it. A critical consideration during the optimization of the model is reducing the number of simulated chemical species. Specifically, the objective of this study is to update and refine two previously published models [29] in order to increase the scale and the sources of data: From only industrial processes, to both industrial and laboratory thermal decomposition processes. These models are capable of determining the dioxins total amount and toxicity of an atmospheric emission using only the amount of three congeners as regressors. Data on PCDD/Fs atmospheric emission of similar combustion processes are available, containing both concentration and TEQ for all the 17 toxic studied congeners.
As in every statistical analysis, it is also necessary to limit the interval of confidence of the parameters of the models. In this study, in order to evaluate the statistical inference, we used the Bootstrap method, which applies computing power to a fundamental reasoning based on asking “What would happen if we applied this method many times?” Statistical inference is based on the sampling distributions of sample statistics. The Bootstrap method allows to find the sample distribution, at least approximately, from just one sample [30]. The main steps of this procedure are the following: (a) Resampling: The sampling population is determined using multiple random samples from the population, which are the same size as the original random sample. In order to ensure that, sampling with replacement is performed. This means that, after choosing an observation from the population, it is returned to the population before drawing the next observation, so all observations can be repeated in each sample [31]. (b) Distribution: Depending on the distribution of all the sampling populations, the method of determining values for the estimations will differ [32,33].
In this case, we expect to achieve a normal distribution to associate the values of the parameters of the models to the average of all the observations, its standard error to the standard deviation, and the limits of the interval of confidence to the percentiles 2.5 and 97.5.
2. Experimental
2.1. Data Sources
In our previous work, a set of 130 PCDD/F analyses from IQS-URL Environmental Laboratory were used. The whole analytical method, including sampling, extraction and purification operations for determining the total amount of each PCDD/F congener, was carried out in line with UNE EN 1948:2007 [34]. The data were used to identify the linear dependence between the 17 toxic congeners of PCDD/Fs during their formation. As a result, two models able to determine the total PCDD/F amount and the TEQ of a sample using only the amount of three congeners were adjusted. This dataset, using the decimal logarithm of the values, was named as 𝕏OLD matrix (130 × 17) since it was used in a previous publication [29].
A new set of 64 analyses was obtained from the “Waste, Energy, Environment and Nanotechnology research group (WEEN)” from the University of Alicante, which also contained information about the amounts of all the toxic PCDD/F congeners from their experimental research related to thermal decomposition processes of several kinds of wastes. Within this set, all the PCDD/F concentrations were higher than the limit of quantification (LOQ), trying to reduce all possible interferences due to its uncertainty. The set of values used consists of the decimal logarithm of the amounts of each congener. The interaction between the dataset and the regression line was not excessive in any case. This interaction is studied following the Hat Matrix criterion, considering that its influence should be lower than 3p/n, where p is the number of regressors and n is the number of samples [35]. This set was named as 𝕏NEW matrix (64 × 17). From this set, a subset was defined discarding the analyses whose values of total PCDD/F amount or TEQ were outside the range of the 𝕏OLD set. This subset, comprising all new data within the range of 𝕏OLD set, was named as 𝕏NEW,INT (28 × 17).
2.2. Methodology
The data set called 𝕏NEW has been used to evaluate the linear dependence between all congeners using the variance inflation factors (VIFs). This methodology has been explained in a previous publication [29]. It is expected that the more independent congeners are similar for both datasets, 𝕏NEW and 𝕏OLD. If so, this process is repeated considering all datasets as a unique one.
The data subset called 𝕏NEW,INT has been used to check two linear models that determine the total PCDD/F amount and the TEQ of an atmospheric emission using only the amount of three PCDD/Fs congeners. For this purpose, a graph was constructed whose ordinates were the total amount or TEQ from the analysis and whose abscissae were the amount or TEQ determined by the model. In the best-case scenario, it was supposed to obtain a correlation with a strong linear trend, with its slope equal to one and its intercept equal to zero.
Once the multicollinearity was studied and the previous models were checked using 𝕏NEW,INT, a new linear regression was performed using 𝕏NEW and 𝕏OLD together. The methodology used to adjust a model to data, where the total dioxins’ amount was a linear combination of the independent congeners, was Ordinary Least Squares [36].
Since the total concentration of PCDD/F cannot be used to determine the toxicity, another linear regression was conducted directly between the amount of each linearly independent congener and the TEQ.
where Cj was the amount of each congener j, CTOT was the total PCDD/F amount in the sample, TTOT was the total TEQ of the sample, b′0 or b0 were the intercepts of the linear adjustment, and b′j or bj were the parameters of the models related to each regressor (where k is the number linearly independent regressors).
Evaluation of the accuracy of the models is checked by making a graph where the ordinate is the total amount or TEQ from the dataset, and the abscissa is the calculated amount or TEQ using model 1 and model 2, respectively.
Model 1 and model 2 are directly conditioned by the datasets used in their adjustment. In order to quantify how the ability of the models to predict the total amount or the toxicity will vary depending on the dataset used, the resampling Bootstrapping method was used.
This method randomly determines which particular analyses from the sets 𝕏NEW and 𝕏OLD are used to adjust the models. Since the total amount of analyses will remain constant, some analyses may be used more than once in each adjustment. This process is iterated a large number of times (3000 iterations in this case) and all the parameters of each fit are collected in order to determine the confidence interval of the regression parameters. The value of the parameter of the model is equalled to the average of that parameter through all the iterations, and the standard error of that parameter is associated to its standard deviation. The confidence intervals are determined using the percentiles related to the selected statistical significance (95% in this case).
2.3. Software
All calculations and plots have been performed using Microsoft Excel 2013, Version 15.0.5093.1001 by Microsoft Corporation, Redmondm Washington, EUA; R Version 3.3.2 (2016-10-31) by The R Foundation for Statistical Computing, and R Package Rcmdr Version: 2.3.2 (2017-01-02) by Fox (2016).
3. Results
3.1. Multicollinearity and VIFs
Table 1 shows the results of the multicollinearity study. The left half side of the table reflects the VIFs and the associated value of R2 of the 17 congeners from both datasets 𝕏OLD and 𝕏NEW. The right half side of the table, which is used for comparison purposes only, reflects the same parameters but only using 𝕏OLD [29].

Table 1.
Results for VIFs of each congener calculated sequentially, discarding the most linearly dependent congener after each iteration. The left half shows the results for both datasets mixed together (𝕏OLD + 𝕏NEW) and the right half shows the results from 𝕏OLD as a comparison [29].
Considering the 𝕏OLD dataset, the formation of the congeners 2,3,7,8-TCDF, OCDF and 1,2,3,6,7,8-HxCDD was determined as linearly independent since its R2 value, which is related to its VIF value following VIFi = 1/(1 − Ri2), is significantly below 0.90. R2 value related to OCDD is 0.89 but it is not significantly below 0.90 and is to be treated as linearly independent.
Considering the 𝕏OLD + 𝕏NEW dataset, it can be observed that all VIFs are lower. This may be caused by the fact that the 𝕏OLD dataset comes from industrial processes and 𝕏NEW dataset comes from laboratory scale and experimental research. Despite these lower values, it is noticeable that the seven more independent congeners are the same in both datasets, although in a different order, as shown in Table 1. This fact reflects that the correlation between the formation of all 17 congeners is similar enough in both datasets, even considering the differences that may occur between industrial processes and laboratory scale processes.
Since this similar behaviour has been demonstrated, combining both datasets cannot be considered as arbitrary. Thus, congeners 2,3,7,8-TCDF, OCDF and 1,2,3,6,7,8-HxCDD are still considered as the ones linearly independent.
3.2. Testing Previous Models Using 𝕏NEW,INT
Two previous models capable of determining the dioxins total amount and toxicity (TEQ) of an atmospheric emission based on the concentration of 1,2,3,6,7,8-HxCDD, OCDF and 2,3,7,8-TCDF which have been tested with the dataset 𝕏NEW,INT. As explained above, this dataset comprises a number of 28 new PCDD/F analyses from laboratory experiments whose total amount and TEQ fall within the range of the 𝕏OLD set. Figure 1 shows the interrelationship between the calculated dioxins total amount and TEQ using previous models 1 and 2 and the values from dataset 𝕏NEW,INT. In these graphs, it is worth mentioning that the linear trend is still strong, even acknowledging that the slope is not close to 1 and the intercept is not close to zero. This fact suggests that a new adjustment of the model may be needed.
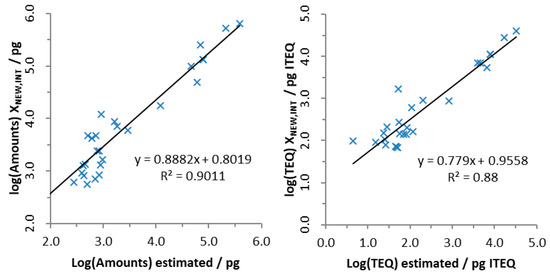
Figure 1.
Total amounts estimated from previous model 1 (left) and total toxicity estimated from previous model 2 (right) using 𝕏NEW,INT dataset.
3.3. Readjusting Previous Models Using 𝕏OLD and 𝕏NEW
A new model 1′ was adjusted based on Equation (1), where the total dioxins amount was a linear combination of the amount of 2,3,7,8-TCDF, OCDF and 1,2,3,6,7,8-HxCDD. The datasets used were 𝕏OLD and 𝕏NEW. The R2 of model 1′ was 0.9705, and the Adjusted R2 was 0.9702. The Adjusted R2 takes into consideration the amount of regressors used in the model in order to avoid overfitting. Since both R2 and Adjusted R2 are almost equal, the possibility of overfitting is discarded. The parameters of the model are shown in Table 2. The same table includes the p-value assigned to each parameter when the null hypothesis (H0) supposes that the tested congener and the total PCDD/F amount are not interdependent at all (H0 : Parameter b′j = 0). Since the evaluation of p-values gave extremely low quantities, all of the parameters of model 1′ can be considered as significantly different to zero. This fact and the high value of R2 are enough to validate model 1′ for Equation (1).

Table 2.
Parameters and statistic data for the readjusted models: model 1′ for predicting PCDD/F amounts (pg) and model 2′ for TEQ values (pg I-TEQ).
The same method was replicated to adjust model 2′ based on Equation (2), where the TEQ was a linear combination of the amount of 2,3,7,8-TCDF, OCDF and 1,2,3,6,7,8-HxCDD. The results for this model 2′, using datasets 𝕏OLD and 𝕏NEW, are shown in Table 2. The value of R2 for model 2′ was 0.9575, and the Adjusted R2 was 0.9570. Following the same criteria as for model 1′, the possibility of overfitting is discarded since both R2 and Adjusted R2 are almost equal.
Figure 2 shows the relationship between the dioxins amount or TEQ, determined with models 1′ and 2′, respectively, and the results from the chemical analysis provided by the laboratory.

Figure 2.
Total amount determined by model 1′ (left) and total toxicity determined by model 2′ (right), both calculated considering congeners 1, 10 and 14 as linearly independent.
The correlation parameters and main statistical information of the testing of the linear regressions for models 1′ and 2′ are shown in Table 3. The same table includes the p-value assigned to the slope when the null hypothesis (H0) supposes that the calculated total PCDD/F amount or TEQ and the results from the chemical analysis are equal (H0 : slope = 1). The p-value assigned to the intercept when the null hypothesis supposes this parameter equal to zero is also included. These values confirm that model 1′ and model 2′ are highly efficient correlations since their slope is significantly equal to one and their intercept is significantly equal to zero.

Table 3.
Parameters for the testing of the readjusted model linear regressions.
3.4. Validating Model 1′ and Model 2′ Using Bootstrapping
Once models 1′ and 2′ are adjusted, the confidence intervals of their parameters are determined by an iterative resampling method with replacement. The resulting values obtained using the bootstrap method follow a normal (Gaussian) distribution. Hence, the value of each parameter used to define model 1′ and model 2′ will be equalled to the average of the values collected through 3000 iterations. The values of the percentile 2.5 and 97.5 represent the limits of the interval of confidence of 95%. The results of the bootstrapping are shown in Table 4.

Table 4.
Bootstrapping method results.
Comparing the values of the parameters determined in Table 2 with the interval of confidence determined in Table 4, it is noticeable that all of them are in the interval of confidence and also close to the average value.
Regarding the values of R2 and its low standard error it can be concluded that the percent of variability expressed through model 1′ and model 2′ is very stable to changes in the used dataset.
The accuracy of the models has also been evaluated calculating the mean absolute error and the root mean squared error. Mean absolute error (MAE) values were 0.1541 and 0.1733 for model 1′ and model 2′, respectively. Root mean square error (RMSE) values were 0.2115 and 0.2424.
3.5. Comparison with Previous Models
As shown in the previous sections, models 1′ and 2′ proposed in the present work can satisfactorily determine the total PCCD/F amount and TEQ from thermal processes based on the amount of only three congeners as an input. Compared to our previously published models [29], the current ones have a wider range of application, with increased number and sources of data. The dataset used to adjust the new models comprised 194 analyses (𝕏OLD + 𝕏NEW), as opposed to the 130 used in our previous work (𝕏OLD), which represents an increase of almost 50% in the number of considered sources. In addition, the new dataset included data not only from industrial processes, but also from laboratory thermal decomposition experiments, broadening the scope of application of the models.
Considering that all 194 analyses come from thermal decompositions from plenty of different industrial and laboratory-scale processes, our models 1′ and 2′ can be considered suitable for combustion processes overall. This assumption increases the range of application of our first models considerably.
In the same way as in the previously published models, their main limitation to calculate the total PCDD/F amount or TEQ is that the values of the amounts of the three congeners must be above the LOQ.
Many other models have been proposed, based on the interdependence between the concentration of mono- to tri-chlorinated dibenzo-p-dioxins and TEQ or the total concentration [26], with lower values for the coefficient of determination. The P-values of many of these models that use low chlorinated PCDD/Fs as regressors also reflect that the correlations may be determined by chance. Furthermore, the use of mono- to tri-chlorinated dibenzo-p-dioxins as a regressor is not as favourable as the use of some of the 17 toxic congeners, since the low-chlorinated PCDD/F congeners frequently are not analysed nor controlled by the legislation. The coefficient of determination of another model that determines the correlation between PAHs and PCDD/Fs was 0.62, while the value of the same parameter considering the multiple regression analysis with naphthalene, fluorene and phenanthrene as regressors was 0.85 [28]. This correlation between PAHs and PCDD/Fs has also been considered as obvious in emissions produced by the co-incineration of MSW and coal, modifying the S/Cl ratio [37]. Our new models 1′ and 2′ are still more accurate than other correlations used to estimate the PCDD/Fs concentration on-line, based on the concentration of precursors like trichlorobenzene and tetrachlorobenzene, whose coefficients of determination were around 0.89 [27].
Despite a multilinear model has been able to estimate the total amount and toxicity properly, these models could be improved in the future fitting a neural network model. The next step in our investigation is to use these new models to determine a kinetic model able to estimate the emission of PCDD/Fs from process parameters such as temperature, oxygen ratio, pressure, etc. The main advantage of using these new models is that only the formation of three congeners has to be determined to be able to estimate the total emission. Once this kinetic model is determined it can be used to optimize the process of municipal solid waste incineration and reduce the emission of PCDD/Fs.
4. Conclusions
Two previous models that estimate the total PCDD/F amount and toxicity (TEQ) based on the amounts of 1,2,3,6,7,8-HxCDD, OCDF and 2,3,7,8-TCDF have been tested using new analyses from laboratory runs.
The use of these models verifies the existence of a strong linear trend, despite the value of the slope being significantly different to 1 and the value of the intercept being significantly different to 0 when applied to the new data.
The multicollinearity of the 130 analyses used to determine those previous models has been compared to the multicollinearity of 64 new analyses, producing very similar results. It has been assumed that for the dataset of all the 194 analyses, the same congeners can be considered as linearly independent.
Those two models have been readjusted with the 194 analyses using multiple linear regression. The new models have been validated examining the residual analysis of the regression and also checking the validity of the slope and the intercept with its associated p-value.
The intervals of confidence of the parameters of the models have been calculated using Bootstrapping method. It has been demonstrated that the percent of variability expressed through model 1′ and model 2′ is very stable to changes in the used dataset.
The accuracy of the models has also been evaluated calculating the mean absolute error and the root mean squared error. MAE values were 0.1541 and 0.1733 and RMSE values were 0.2115 and 0.2424 for model 1′ and model 2′.
Thanks to the readjustment of the models with more analyses, the current ones present a wider scope of application, with an increase in the scale and the sources of data, modelling combustion processes overall.
These new models are now ready to be used to simplify a kinetic model that estimates the formation of PCDD/Fs during municipal solid waste incineration. This kinetic model will only need to estimate the formation of three congeners instead of 17, which will decrease the calculation effort when using it.
Author Contributions
Conceptualization, D.P. and L.G.-S.; Data curation, D.P.; Formal analysis, D.P.; Funding acquisition, J.A.C. and J.D.-F.; M.L.G.-S.; Supervision, J.A.C. and N.O.; Validation, J.O.P., J.D.-F.; J.A.C. and N.O.; Writing—original draft, D.P.; Writing—review & editing, J.O.P., J.D.-F., J.A.C. and N.O.
Funding
Juan A. Conesa and Nuria Ortuño acknowledge the support for this work by the CTQ2016-76608-R project from the Ministry of Economy, Industry and Competitiveness (Spain). Damià Palmer thanks IQS—Universitat Ramon Llull for its financial support.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Eurostat. Municipal Waste Generation and Treatment, by Treatment Method. Available online: http://ec.europa.eu/eurostat/tgm/refreshTableAction.do?tab=table&plugin=1&pcode=tsdpc240&language=en (accessed on 6 March 2017).
- Hogg, D.; Favoino, E.; Nielsen, N.; Thompson, J.; Wood, K.; Penschke, A.; Papageorgiou, D.; Economides, S. Economic Analysis of Options for Managing Biodegradable Municipal Waste: Final Report to the European Commission; Publications Office of the European Union: Luxembourg, 2002. [Google Scholar]
- McKay, G. Dioxin characterisation, formation and minimisation during municipal solid waste (MSW) incineration: Review. Chem. Eng. J. 2002, 86, 343–368. [Google Scholar] [CrossRef]
- Shaub, W.M.; Tsang, W. Dioxin formation in incinerators. Environ. Sci. Technol. 1983, 17, 721–730. [Google Scholar] [CrossRef] [PubMed]
- NATO/CCMS. Scientific Basis for the Development of The International Toxicity Equivalency Factor (I-Tef) Method of Risk Assessment for Complex Mixtures of Dioxins and Related Compounds; North Atlantic Treaty Organization committee on the Challenges of Modern Society: Washington, WA, USA, 1988. [Google Scholar]
- Gallo, M.A.; Scheuplein, R.J. Banbury Report 35: Biological Basis for Risk Assessment of Dioxins and Related Compounds; Cold Spring Harbor Laboratory Press: New York, NY, USA, 1991; ISBN10: 0879692359. [Google Scholar]
- Nagao, T.; Golor, G.; Hagenmaier, H.; Neubert, D. Teratogenic potency of 2,3,4,7,8-pentachlorodibenzofuran and of three mixtures of polychlorinated dibenzo-p-dioxins and dibenzofurans in mice. Problems with risk assessment using TCDD toxic-equivalency factors. Arch. Toxicol. 1993, 67, 591–597. [Google Scholar] [CrossRef] [PubMed]
- Van Den Berg, M.; Birnbaum, L.S.; Denison, M.; De Vito, M.; Farland, W.; Feeley, M.; Fiedler, H.; Hakansson, H.; Hanberg, A.; Haws, L.; et al. The 2005 World Health Organization reevaluation of human and mammalian toxic equivalency factors for dioxins and dioxin-like compounds. Toxicol. Sci. 2006, 93, 223–241. [Google Scholar] [CrossRef] [PubMed]
- Kutz, F.W.; Barnes, D.G.; Bottimore, D.P.; Greim, H.; Bretthauer, E.W. The international toxicity equivalency factor (I-TEF) method of risk assessment for complex mixtures of dioxins and related compounds. Chemosphere 1990, 20, 751–757. [Google Scholar] [CrossRef]
- European Parliament and of the Council. Directive 2010/75/EU on Industrial Emissions. Available online: https://eur-lex.europa.eu/LexUriServ/LexUriServ.do?uri=OJ:L:2010:334:0017:0119:en:PDF (accessed on 5 March 2017).
- Relvas, H.; Lopes, M.; Coutinho, M. Portuguese inventory of dioxins and furans atmospheric emissions. Chemosphere 2013, 93, 1569–1577. [Google Scholar] [CrossRef]
- Soler, A.; Conesa, J.A.; Iñiguez, M.E.; Ortuño, N. Pollutant formation in the pyrolysis and combustion of materials combining biomass and e-waste. Sci. Total Environ. 2018, 622–623, 1258–1264. [Google Scholar] [CrossRef]
- Edo, M.; Ortuño, N.; Persson, P.; Conesa, J.A.; Jansson, S. Emissions of toxic pollutants from co-combustion of demolition and construction wood and household waste fuel blends. Chemosphere 2018, 203, 506–513. [Google Scholar] [CrossRef]
- Garrido, M.A.; Font, R.; Conesa, J.A. Pollutant emissions from the pyrolysis and combustion of viscoelastic memory foam. Sci. Total Environ 2017, 7, 183–194. [Google Scholar] [CrossRef]
- Moreno, A.I.; Font, R.; Conesa, J.A. Characterization of gaseous emissions and ashes from the combustion of furniture waste. Waste Manag. 2016, 58, 299–308. [Google Scholar] [CrossRef]
- Conesa, J.A.; Ortuño, N.; Abad, E.; Rivera-Austrui, J. Emissions of PCDD/Fs, PBDD/Fs, dioxin like-PCBs and PAHs from a cement plant using a long-term monitoring system. Sci. Total Environ. 2016, 571, 435–443. [Google Scholar] [CrossRef]
- Lacatus, E.; Konnov, A.; De Ruyck, J. Measuring dioxins’ precursors—A way to ensure a cleaner environment. Organohalogen Compd. 2002, 59, 45–48. [Google Scholar]
- Lavric, E.D.; Konnov, A.A.; De Ruyck, J. Modeling the formation of precursors of dioxins during combustion of woody fuel volatiles. Fuel 2005, 84, 323–334. [Google Scholar] [CrossRef]
- Zhang, M.; Buekens, A.; Li, X. Dioxins from biomass combustion: An overview. Waste Biomass Valor. 2017, 8, 1–20. [Google Scholar] [CrossRef]
- Ritter, E.R.; Bozzelli, J.W. Pathways to chlorinated dibenzodioxins and dibenzofurans from partial oxidation of chlorinated aromatics by oh radical: Thermodynamic and kinetic insights. Combust. Sci. Technol. 1994, 101, 153–169. [Google Scholar] [CrossRef]
- Dorofeeva, O.V.; Iorish, V.S.; Moiseeva, N.F. Thermodynamic properties of dibenzo-p-dioxin, dibenzofuran, and their polychlorinated derivatives in the gaseous and condensed phases. 1. thermodynamic properties of gaseous compounds. J. Chem. Eng. Data. 1999, 44, 516–523. [Google Scholar] [CrossRef]
- Dorofeeva, O.V.; Iorish, V.S.; Moiseeva, N.F. Thermodynamic properties of dibenzo-p-dioxin, dibenzofuran, and their polychlorinated derivatives in the gaseous and condensed phases. 2. thermodynamic properties of condensed compounds. J. Chem. Eng. Data 2001, 46, 286–298. [Google Scholar] [CrossRef]
- Dorofeeva, O.V.; Yungman, V.S. Enthalpies of formation of dibenzo-p-dioxin and polychlorinated dibenzo-p-dioxins calculated by density functional theory. J. Phys. Chem. A 2003, 107, 2848–2854. [Google Scholar] [CrossRef]
- Addink, R.; Govers, H.A.J.; Olie, K. Isomer distributions of polychlorinated dibenzo-p-dioxins/dibenzofurans formed during de novo synthesis on incinerator fly ash. Environ. Sci. Technol. 1998, 32, 1888–1893. [Google Scholar] [CrossRef]
- Shao, K.; Li, X.; Wei, Y.; Liu, J. Correlation between PCDD/F, PCB and PCtivBz formed by de novo synthesis. Adv. Mater. Res. 2012, 356–360, 998–1005. [Google Scholar] [CrossRef]
- Gullett, B.K.; Wikström, E. Mono- to tri-chlorinated dibenzodioxin (CDD) and dibenzofuran (CDF) congeners/homologues as indicators of CDD and CDF emissions from municipal waste and waste/coal combustion. Chemosphere 2000, 40, 1015–1019. [Google Scholar] [CrossRef]
- Guo, Y.; Chen, T.; Yang, J.; Cao, X.; Lu, S.; Li, X. Study on on-line detection of dioxins based on correlation model. Chin. J. Environ. Eng. 2014, 8, 3524–3529. [Google Scholar]
- Yan, M.; Li, X.; Zhang, X.; Liu, K.; Yan, J.; Cen, K. Correlation between PAHs and PCDD/Fs in municipal solid waste incinerators. J. Zhejiang Univ. 2010, 44, 1118–1121. [Google Scholar]
- Palmer, D.; Pou, J.O.; Gonzalez-Sabaté, L.; Díaz-Ferrero, J. Multiple linear regression based congener profile correlation to estimate the toxicity (TEQ) and dioxin concentration in atmospheric emissions. Sci. Total Environ. 2018, 622–623, 510–516. [Google Scholar] [CrossRef]
- Vergura, S.; Vacca, F. Bootstrap technique for analyzing energy data from PV plant. In Proceedings of the 2009 International Conference on Clean Electrical Power, Capri, Italy, 9–11 June 2009. [Google Scholar]
- Alborzi, S.; Aminian, A.; Mojtahedi, S.M.H.; Mousavi, S.M. An analysis of project risks using the non-parametric bootstrap technique. In Proceedings of the 2008 IEEE International Conference on Industrial Engineering and Engineering Management, Singapore, 8–11 December 2008. [Google Scholar]
- Hesterberg, T.; Moore, D.S.; Monaghan, S.; Clipson, A.; Epstein, R. Bootstrap Methods and Permutations Test; W.H.Freeman and Company: New York, NY, USA, 2004. [Google Scholar]
- Efron, B. Nonparametric estimates of standard error: The jackknife, the bootstrap, and other methods. Dep. Stat. Stanford Univ. 1980, 68, 589–599. [Google Scholar] [CrossRef]
- AENOR. Stationary Source Emissions—Determination of the Mass Concentration of PCDDs/PCDFs 424 and Dioxin-like PCBs—Part 3: Identification and Quantification of PCDDs/PCDFs; British Standards Institution: London, UK, 2007. [Google Scholar]
- Hoaglin, D.C.; Welsch, R.O.Y.E. The hat matrix in regression and ANOVA. Am. Stat. 1978, 32, 17–22. [Google Scholar]
- Kutner, M.H.; Nachtsheim, C.J.; Neter, J.; Li, W. Applied Linear Statistical Models, 5th ed.; McGraw-Hill Irwin: New York, NY, USA, 2005; ISBN 9780071122214. [Google Scholar]
- Li, X.-D.; Yin, X.-F.; Lu, S.-Y.; Gu, Y.-L.; Yan, J.-H.; Ni, M.-J.; Cen, K.-F. Correlation between PAHs and dioxins formation during coal and municipal solid waste co-incineration process. K. Cheng Je Wu Li Hsueh Pao/J. Eng. Thermophys. 2006, 27, 691–694. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).