Fractional-Order Model Predictive Frequency Control of an Islanded Microgrid

Abstract

Optimal frequency control of an islanded microgrid has been a challenging issue in the research field of microgrids. Recently, fractional-order calculus theory and some related control methods have attempted to handle this issue. In this paper, a novel fractional-order model predictive control (FOMPC) method is proposed to achieve the optimal frequency control of an islanded microgrid by introducing a fractional-order integral cost function into model predictive control (MPC) algorithm. Firstly, a discrete state-space model is derived for the optimal frequency control problem of an islanded microgrid. Afterward, a fractional-order integral cost function is designed to guide the FOMPC algorithm to obtain optimal control law by borrowing the Grünwald-Letnikov (GL) definition of fractional order calculus. Six simulation studies have been carried out to illustrate the superiority of FOMPC to conventional MPC under dynamical load disturbances, perturbed system parameters and random dynamical power fluctuation of wind turbines.

1. Introduction

In the past decade, microgrids have been widely studied because of their potential environmental and economic benefits in regard to the integration distributed energy resources, especially renewable energy systems [1,2,3]. Due to the different types of distributed energy resources, dynamical load characteristics, power quality constraints, and perturbed system parameters, how to optimize control of a microgrid, for it to operate well under grid-connected and islanded modes, has been a challenging issue [4,5,6]. When a microgrid is islanded, an optimal controller should be designed to minimize the frequency deviations. In recent years, some research works have been reported related to the optimal frequency control issue of an islanded microgrid [7,8,9,10], but most works have focused on proportional-integral-derivative (PID) control method and its different kinds of improved versions based on intelligent optimization algorithms.

As one of the most widely-applied control methods in industry, model predictive control (MPC) ranks second only after PID control algorithm [11]. Recently, MPC has been extended to solve the optimal load frequency control (LFC) problems of power systems [12,13,14,15,16] and operation optimization issues of microgrids [17,18,19,20]. Especially, it should be noted that there are some existing works regarding MPC-based frequency control of microgrids [12,19,20,21,22,23]. Reference [12] developed a MPC-based coordinated load frequency control method for a microgrid under the condition regarding varied number of electric vehicles. By introducing a rule-based fuzzy controller to dynamically tune the weighting parameter used in cost function, a fuzzy MPC is proposed for the optimal LFC issue of an isolated microgrid [21]. In Reference [22], a MPC method is developed to implement the torque compensation of each wind turbine generator for the optimal frequency control of an isolated grid. Recently-reported work [23] focuses on a conventional MPC-based optimal frequency control method in terms of a traditional integer-order cost function for a standalone microgrid. The simulation results have illustrated the superiority of MPC to traditional proportional-integral (PI) controller.

On the other hand, fractional-order control theories and applications of traditional integer-order and fractional-order systems have attracted increasing attention over the past two decades [24]. The fractional-order PI/PID control algorithm has been considered as one of the most widely and successfully used methods in complex systems, such as servo systems [25,26], a nonlinear vertical tank system [27], electric balance vehicle system [28], an induction motor drive system [29], permanent magnetic synchronous generator [30], automatic voltage regulator systems [31], single-area delayed power systems [32], and multi-area interconnected power systems [33]. One particular concern is the fractional-order frequency control of an isolated microgrid. Multi-objective extremal optimization algorithm has been adopted to optimize the fractional-order PID frequency controller for islanded microgrids [34]. Additionally, some MPC or fractional-order MPC methods have been developed for traditional integer-order or fractional-order systems [35,36,37,38,39,40,41,42]. However, to the best knowledge of the authors, few works regarding the fractional-order model predictive frequency control of islanded microgrids have been reported so far.

As one of the most important applications concerning fractional-order calculus theory in single processing and optimal control areas, a novel fractional-order integral performance index has been introduced as an improved cost function to improve the system performance. As a seminal research work, Romero et al. [43] proposed a new type of arbitrary real-order integral cost function for infinite impulse response filter design. The work in Reference [44] used a real-coded genetic algorithm to optimize the weighting matrices used in Linear Quadratic Regulator (LQR) systems by designing a fractional-order integral cost function. Furthermore, Romero et al. [36] also introduced a fractional-order definite integration operator into the cost function and then presented a fractional-order generalized predictive control method to deal with the optimal speed control issue for gasoline-propelled cars. Moreover, Bigdeli [37] designed a genetic algorithm-based fractional-order predictive functional controller (FOPFC) for fractional-order systems by adopting a fractional-order integral cost function. In Reference [45], Grünwald-Letnikov (GL) definition of fractional-order calculus theory has also been introduced in the cost function of a FOPFC to enhance the performance of fractional-order industrial processes. In addition, Zhang el al. [40] proposed a fractional-order MPC method for the optimal temperature control issue of industrial heating furnaces by using a fractional-order cost function based on the GL definition. These above research works have illustrated the superiority of fractional-order integral cost functions to conventional integer-order ones in the applications of signal processing, optimal LQR design and optimal predictive functional control.

Inspired by the aforementioned descriptions, this work proposes a fractional-order MPC, termed the FOMPC method, to achieve optimal frequency control performance for an islanded microgrid by introducing a fractional-order integral cost function into a model predictive control (MPC) algorithm. Firstly, an extended discrete state-space model is derived for the optimal frequency control problem of an islanded microgrid by considering some disturbance variables. Then, a fractional-order integral cost function is designed to guide the model predictive control algorithm to obtain optimal control law by borrowing the GL definition of fractional-order calculus theory. Six simulation studies on a typical microgrid have been carried out to illustrate the superiority of FOMPC over a conventional MPC under dynamical load disturbances, perturbed system parameters and the dynamic fluctuation of wind.

The major contribution of this paper can be summarized by the following three points:

(1)

A fractional-order model predictive control (FOMPC) method is proposed for the optimal frequency control problem of an islanded microgrid for the first time.

(2)

The proposed FOMPC method extends the traditional quadratic cost function and introduces a fractional-order integral cost function based on the GL fractional-order integral definition.

(3)

In comparison with the conventional integer-order MPC algorithm, the proposed FOMPC can improve the performance of an islanded microgrid especially under several conditions of load disturbance, parameter uncertainty and random dynamical fluctuations of wind turbines.

The rest of this work is structured as follows. The discrete-time space model of an islanded microgrid is derived in Section 2. Section 3 proposes the FOMPC-based frequency control method. In Section 4, the simulation results for six cases and the effects of two fractional-order parameters on frequency control performance will be provided. Finally, the conclusions and some open issues are presented in Section 5.

2. Discrete-Time Space Model

The block diagram of the frequency control issue for an islanded microgrid with a FOMPC controller is shown in Figure 1. For convenient, fair comparison with the traditional integer-order MPC method [23], the system model of the microgrid tested in this paper is the same as that in Reference [23]. The transfer functions and related system parameters of the distributed generations in an islanded microgrid under study are described in Table 1. The distributed subsystems in this microgrid under study include a wind turbine generator (WTG), diesel-engine generator (DEG), and energy storage system (ESS). As mentioned in Chapter 11 of Reference [46], EES can be considered as a fuel cell (FC)/battery, flywheel energy storage system (FESS), superconducting magnetic energy storage (MESS) or a combination of these. Here, we adopt FESS as the ESS in the microgrid under study.

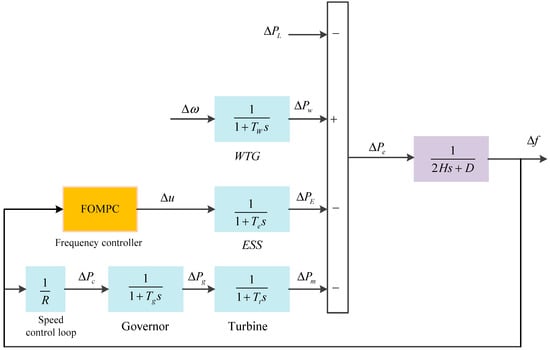
Figure 1. The block diagram of an islanded microgrid under study with a FOMPC-based frequency controller.

Table 1. The transfer functions and the related parameters used in each subsystem.

Subsystem	Transfer Function	Parameters
WTG	$\frac{1}{1+T_{W}s}$	TW = 1.5 s
Speed control loop	$\frac{1}{R}$	R = 3 Hz/pu
Governor	$\frac{1}{(1+T_{g}s)}$	Tg = 0.08 s
Turbine	$\frac{1}{(1+T_{t}s)}$	Tt = 4 s
Microgrid system	$\frac{1}{2Hs+D}$	D = 0.015 pu/Hz, H = 1/12 pu·s
ESS	$\frac{1}{1+T_{e}s}$	Te = 0.1 s

Define x(t) = [∆P_E(t), ∆P_w(t), ∆P_g(t), ∆P_m(t), ∆f(t)]^T, u(t) = ∆u(t), w(t) = [∆w(t), ∆P_L(t)]^T, and y(t) = ∆f(t) in the microgrid under study. Here, ∆P_E(t), ∆P_w(t), ∆P_g(t), and ∆P_m(t) represent the power deviations of ESS, WTG, governor, and turbine, respectively. ∆u(t) represents the incremental form of control signal, ∆w(t) represents the input power fluctuation of WTG, ∆P_L(t) is the load fluctuation, and ∆P_e(t) represents the power deviation of the whole microgrid system, i.e., ∆P_e(t) = ∆P_w(t) − ∆P_E(t) − ∆P_m(t) − ∆P_L(t). The continuous-time state space model for the frequency control of an islanded microgrid is defined by Equations (1) and (2).

$$\dot{x}(t)=A_{c}x(t)+B_{c1}u(t)+B_{c2}w(t)$$

(1)

$$y(t)=Cx(t)$$

(2)

where A_c, B_c1, B_c2, and C are defined as follows:

$$A_c=\left[\begin{array}{ccccc}-\frac{1}{T_e}& 0& 0& 0& 0\\ 0& -\frac{1}{T_W}& 0& 0& 0\\ 0& 0& -\frac{1}{T_g}& 0& \frac{1}{R{T}_g}\\ 0& 0& \frac{1}{T_t}& -\frac{1}{T_t}& 0\\ -\frac{1}{2H}& \frac{1}{2H}& 0& -\frac{1}{2H}& -\frac{D}{2H}\end{array}\right]$$

(3)

$$B_{c1}={\left[\begin{array}{ccccc}\frac{1}{T_e}& 0& 0& 0& 0\end{array}\right]}^T$$

(4)

$$B_{c2}={\left[\begin{array}{ccccc}0& \frac{1}{T_W}& 0& 0& 0\\ 0& 0& 0& 0& -\frac{1}{2H}\end{array}\right]}^T$$

(5)

$$C={\left[\begin{array}{ccccc}0& 0& 0& 0& 1\end{array}\right]}^T$$

(6)

The discrete-time state space model of an islanded microgrid is obtained by the following equations:

$$x(k+1)=A_{d}x(k)+B_{d1}u(k)+B_{d2}w(k)$$

(7)

$$y(k)=C_{d}x(k)$$

(8)

where $A_d=e^{A_c{T}_s}$, $B_{d1}={\displaystyle {\int }_0^{T_s}{e}^{A_{c}t}{B}_{c1}dt}$, $B_{d2}={\displaystyle {\int }_0^{T_s}{e}^{A_{c}t}{B}_{c2}dt}$, and T_s is the sampling period.

It should be noted, the discrete-time space model can also be derived by a similar method for a more complex microgrid system, with more types of distributed generations, e.g., hydric, thermal, or photovoltaic generations. The only difference is that x(t), u(t), w(t), A_c, B_c1, B_c2, and C in Equations (1) and (2) should be redefined according to the topology structure and block diagram of a new microgrid system.

3. FOMPC-Based Optimal Frequency Control Method

In this section, we propose a novel FOMPC method for the optimal frequency control issue of an islanded microgrid.

Firstly, let us define the predictive output vector as $Y_P(k)={\left(\begin{array}{c}y\left(k|k\right)\\ ⋮\\ y\left(k+P-1|k\right)\end{array}\right)}_{P\times N_y}$, the predictive state vector as $X\left(k\right)={\left(\begin{array}{c}x\left(k\right)\\ ⋮\\ x\left(k+P-1\right)\end{array}\right)}_{P\times N_x}$, the predictive disturbance vector as $W\left(k\right)={\left(\begin{array}{c}w\left(k\right)\\ ⋮\\ w\left(k+P-1\right)\end{array}\right)}_{P\times N_w}$, the predictive control vector as $\Delta U\left(k\right)={\left(\begin{array}{c}\Delta u\left(k\right)\\ ⋮\\ \Delta u\left(k+M-1\right)\end{array}\right)}_{M\times N_u}$, where N_x, N_y, N_u and N_w are the dimensions of x(k), y(k), u(k) and w(k), respectively. Then, the predictive output vector Y_P(k) is computed according to Equations (9)–(13):

$$Y_P(k)=GX(k)+Hu(k-1)+EW(k)+F\Delta U(k)$$

(9)

$$G=\left[\begin{array}{c}{C}_d\\ C_d{A}_d\\ ⋮\\ C_d{A}_d^{P-1}\end{array}\right]$$

(10)

$$H=\left[\begin{array}{c}0\\ C_d{B}_{d1}\\ ⋮\\ C_d\left\{{\displaystyle \sum _{j=0}^{P-2}{A}_d^j}\right\}{B}_{d1}\end{array}\right]$$

(11)

$$E=\left[\begin{array}{c}0\\ C_d{B}_{d2}\\ ⋮\\ C_d\left\{{\displaystyle \sum _{j=0}^{P-2}{A}_d^j}\right\}{B}_{d2}\end{array}\right]$$

(12)

$$F=\left[\begin{array}{cccc}\mathbf{0}& \mathbf{0}& \cdots & \mathbf{0}\\ C_d{B}_{d1}& \mathbf{0}& \cdots & \mathbf{0}\\ ⋮& ⋮& \ddots & ⋮\\ C_d\left\{{\displaystyle \sum _{j=0}^{P-2}{A}_d^j}\right\}{B}_{d1}& C_d\left\{{\displaystyle \sum _{j=0}^{P-1}{A}_d^j}\right\}{B}_{d1}& \cdots & C_d\left\{{\displaystyle \sum _{j=0}^{P-M-1}{A}_d^j}\right\}{B}_{d1}\end{array}\right]{\left[\begin{array}{cccc}\mathbf{1}& \mathbf{0}& \cdots & \mathbf{0}\\ \mathbf{1}& \mathbf{1}& \cdots & \mathbf{0}\\ ⋮& ⋮& \ddots & ⋮\\ \mathbf{1}& \mathbf{1}& \cdots & \mathbf{1}\end{array}\right]}_{M\times M}$$

(13)

where P and M are the prediction horizon and the control horizon, respectively.

Reference trajectory y_r (k+p|k) used in this paper is defined as follows [11]:

$$y_r\left(k+p|k\right)={\eta }^{p}y\left(k\right)+\left(1-{\eta }^p\right)c\left(k\right),p=0,\dots (P-1)$$

(14)

where η represents a soften factor, and c(k) represents the set value of system output. In terms of vector-based form, Equation (14) can be also reformulated using the following equation:

$$Y_r(k)={\left(\begin{array}{c}{y}_r\left(k|k\right)\\ \dots \\ y_r\left(k+P-1|k\right)\end{array}\right)}_{P\times N_y}$$

(15)

From the perspective of traditional MPC, the optimal frequency control issue of an islanded microgrid is formulated as follows:

$$J(k)=\min \left\{{\left(Y_P(k)-Y_r(k)\right)}^{T}Q\left(Y_P(k)-Y_r(k)\right)+{\left(\Delta U\left(k\right)\right)}^{T}R\left(\Delta U\left(k\right)\right)\right\}$$

(16)

$$\begin{array}{cc}s.t.& u_{\min }\le u(k)\le u_{\max }\\ & \Delta u_{\min }\le \Delta u(k)\le \Delta u_{\max }\\ & y_{\min }\le y(k)\le y_{\max }\end{array}$$

(17)

where Q is a weight vector to adjust the performance of predicted errors, and R is another weight vector for the future control vector. u_min, ∆u_min, and y_min are defined as the lower limits of u(k), ∆u(k), and y(k), respectively, and u_max, ∆u_max, and y_max are the corresponding upper limits.

For an islanded microgrid, Figure 2 represents a schematic diagram of FOMPC-based optimal frequency control method. More specifically, by introducing the GL definition of fractional order calculus [43] into Equation (16), a fractional-order integral cost function J_FO(k) is approximated by Equations (18)–(21). The detailed derivation process from Formulation (16) to Formulation (18) can be found in Reference [43].

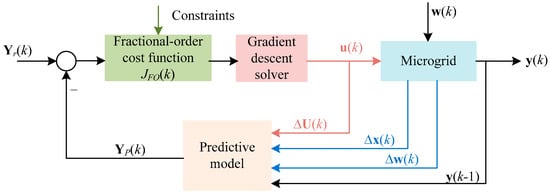
Figure 2. The schematic diagram of FOMPC-based optimal frequency control method.

$$J(k)\cong J_{FO}(k)={\left(Y_P(k)-Y_r(k)\right)}^{T}Q\left(\mathsf{\Lambda }(T_s,\gamma )\right)\left(Y_P(k)-Y_r(k)\right)+{\left(\Delta U(k)\right)}^{T}R\left(\mathsf{\Lambda }(T_s,\beta )\right)\left(\Delta U(k)\right)$$

(18)

$$\mathsf{\Lambda }(T_s,\gamma )=T_{s}diag(m_{P-1},m_{P-2},\dots ,m_1,m_0)$$

(19)

$$m_j={\lambda }_j^{(-\gamma )}-{\lambda }_{j-(P-1)}^{(-\gamma )}$$

(20)

$${\lambda }_j^{(-\gamma )}=\{\begin{array}{ll}\left(1-\left(1-\gamma \right)/j\right){\lambda }_{j-1}^{(-\gamma )},& j>0;\\ 1,& j=0;\\ 0,& j<0.\end{array}$$

(21)

By combining Equations (9)–(13), the fractional-order integral cost function described by Equation (18) is reformulated as follows:

$$\begin{array}{cc}\hfill J_{FO}(k)& ={\left(GX(k)+HU(k-1)+EW(k)-Y_r(k)\right)}^{T}Q\left(\mathsf{\Lambda }(T_s,\gamma )\right)\left(GX(k)+HU(k-1)+EW(k)-Y_r(k)\right)+\hfill \\ & {\left(\Delta U(k)\right)}^T{\rm K}\Delta U(k)-{\left(\Delta U(k)\right)}^{T}T\hfill \end{array}$$

(22)

$$K=F^{T}Q\left(\mathsf{\Lambda }(T_s,\gamma )\right)F+R\left(\mathsf{\Lambda }(T_s,\beta )\right)$$

(23)

$$T=2F^{T}Q\left(\mathsf{\Lambda }(T_s,\gamma )\right)\left(GX(k)+HU(k-1)+EW(k)-Y_r(k)\right)$$

(24)

where β and γ are the fractional-order parameters.

Based on the gradient descent method, we can obtain the following optimal control vector u(k):

$$u(k)=u(k-1)+\Delta u(k)$$

(25)

$$\Delta u(k)=\left(\begin{array}{cc}{I}_{N_u}& {\mathbf{0}}_{N_u\times (P-1)}\end{array}\right)\Delta U_{opt}(k)$$

(26)

$$\Delta U_{opt}(k)=\frac{1}{2}{K}^{-1}T$$

(27)

where $I_{N_u}$ represents an identity matrix with N_u rows and N_u columns.

The flowchart of the proposed FOMPC-based optimal frequency control method for an islanded microgrid is shown in Figure 3.

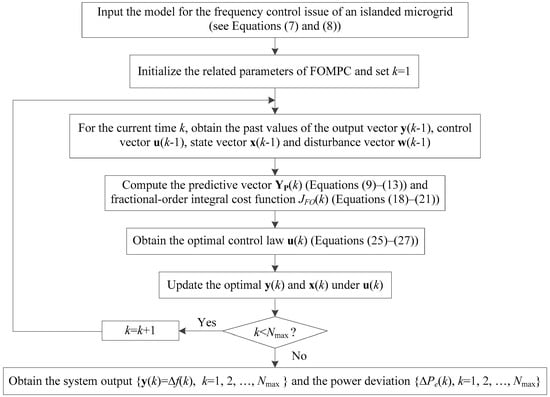
Figure 3. The flowchart of FOMPC-based optimal frequency control method for an islanded microgrid.

In conclusion, the detailed steps of the proposed FOMPC-based optimal frequency control method for an islanded microgrid are summarized as follows:

Step 1:

Input a discrete-time state space model with sampling period T_s for the frequency control issue of an islanded microgrid system described by Equations (7) and (8).

Step 2:

Initialize the algorithm parameters of FOMPC including maximum number of sampling times N_max, P, M, Q, R, β and γ, and set k = 1.

Step 3:

For the current time k, obtain y(k − 1) = ∆f(k − 1), u(k − 1) = ∆u(k − 1), x(k − 1) = [∆P_E(k − 1), ∆P_w(k − 1), ∆P_g(k − 1), ∆P_m(k − 1), ∆f(k − 1)]^T and w(k − 1) = [∆w(k − 1), ∆P_L(k − 1)]^T.

Step 4:

Obtain the predictive vector Y_P(k) according to Equations (9)–(13) and fractional-order integral cost function J_FO(k) by Equations (18)–(21).

Step 5:

Compute the optimal control vector u(k) by Equations (25)–(27) based on gradient descent method.

Step 6:

Update the optimal y(k) and x(k) under u(k).

Step 7:

Set k = k + 1, and repeat the loop from Step 4 to Step 7 until k = N_max.

Step 8:

Output {y(k) = ∆f(k), k=1, 2, …, N_max } and {∆P_e(k), k = 1, 2, …, N_max}.

4. Simulation Results

The simulation results in Reference [23] have illustrated the superiority of MPC to traditional PI controller for the optimal frequency control issue of an islanded microgrid. To make a fair comparison between the proposed FOMPC and traditional MPC method [23], simulation studies are carried out for the same microgrid system model, as shown in Figure 1 [23]. The parameters of system model are set as in Table 1. Six experiments are designed as Table 2 to demonstrate the superiority of FOMPC to the traditional integer-order MPC method under dynamical load disturbances, perturbed system parameters and random dynamical power fluctuation of wind turbines. The parameter settings for FOMPC and MPC are shown in Table 3. All the following simulation experiments have been performed by the aid of MATLAB 2014b software on a 2.50 GHz PC with i7-6500U processor and 8GB RAM.

Table 2. The conditions of six experiments for an islanded microgrid.

Experiment	Condition
Case 1	Normal system parameters, ∆PL = 0.02 p.u. after 1 s.
Case 2	Normal system parameters, dynamical fluctuations of ∆PL.
Case 3	Normal system parameters, random dynamical fluctuations of Δw.
Case 4	Perturbed system parameters, i.e., Tt = 0.6 (increase 50%), R = 1.5 (decrease 50%), H = 0.0833 (decrease 50%), dynamical fluctuations of ∆PL.
Case 5	Perturbed system parameters, i.e., Tt = 0.6 (increase 50%), R = 1.5 (decrease 50%), H = 0.0833 (decrease 50%), random dynamical fluctuations of Δw.
Case 6	Perturbed system parameters, i.e., Tt = 0.6 (increase 50%), R=1.5 (decrease 50%), H = 0.0833 (decrease 50%), dynamical fluctuations of ∆PL, random dynamical fluctuations of Δw.

Table 3. The parameters settings for FOMPC and MPC.

Algorithm	Parameters Setting
MPC	P = 10, M = 2, Q = IP×P, and R = 0.1IM×M.
FOMPC	P = 7, M = 2, Q = IP×P, R = IM×M, γ = β = 6.2.

4.1. Case 1: Normal System Parameters and Step Load Fluctuations

In case 1, we consider the condition of normal system parameters of an islanded microgrid and ∆P_L = 0.02 p.u. after 1 s. Figure 4 presents the comparative results of frequency deviation ∆f, and power deviation ∆P_e obtained by FOMPC and MPC for an islanded microgrid under case 1. Obviously, the transient-state and steady-state responses of ∆f and ∆P_e obtained by FOMPC are better than those by MPC [23]. The performance of FOMPC and MPC methods is evaluated by the indices including the integral of absolute value of the error (IAE) for ∆f and ∆P_e denoted as IAE₁ and IAE₂, respectively, the overshoot of ∆f and ∆P_e denoted as M_p1 and M_p2, respectively, the rising time of ∆f and ∆P_e denoted as t_u1 and t_u2, respectively, the settling time of ∆f and ∆P_e denoted as t_s1 and t_s2, respectively, and the steady-state error of ∆f and ∆P_e denoted as E_ss1 and E_ss2, respectively. The IAE₁ and IAE₂ are defined as follows:

$$IA{E}_1={\displaystyle \sum _{k=1}^{N_{\max }}|\Delta f(k)|}$$

(28)

$$IA{E}_2={\displaystyle \sum _{k=1}^{N_{\max }}|\Delta P_e(k)|}$$

(29)

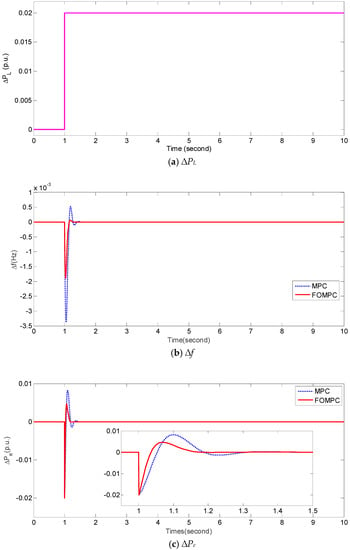
Figure 4. Responses of ∆f and ∆P_e obtained by FOMPC and MPC under case 1.

Table 4 shows the performance comparison of FOEMPC and MPC for an islanded microgrid under case 1. Clearly, all the indices except Ess₁ obtained by FOMPC are better than those by MPC [23].

Table 4. Control performance indices obtained by FOMPC and MPC for an islanded microgrid under case 1. The best values are marked in bold.

Algorithm	IAE1	Mp1	tu1	ts1	Ess1	IAE2	Mp2	tu2	ts2	Ess2
MPC	0.0335	5.27 × 104	1.12	1.19	4.73 × 1017	0.1793	0.0082	1.18	1.27	2.62 × 1017
FOEMPC	0.0141	5.96 × 105	1.08	1.18	5.19 × 1017	0.0909	0.0047	1.05	1.14	2.36 × 1017

4.2. Case 2: Normal System Parameters and Dynamical Load Fluctuations

For case 2, the dynamical fluctuations of ∆P_L (e.g., Figure 5a) and normal system parameters are considered. Figure 5b,c compare ∆f and ∆P_e obtained by FOMPC and MPC for an islanded microgrid, respectively. From the perspective of quantitative comparison, the control performance of ∆f and ∆P_e obtained by FOMPC and MPC is evaluated by the indices including IAE₁, IAE₂, ITAE₁, ITAE₂, ISE₁, ISE₂, ITSE₁, and ITSE₂. To be more specific, the ITAE₁, ITAE₂, ISE₁, ISE₂, ITSE₁, and ITSE₂ are defined as follows:

$$ITA{E}_1={\displaystyle \sum _{k=1}^{N_{\max }}k{T}_s|\Delta f(k)|}$$

(30)

$$ITA{E}_2={\displaystyle \sum _{k=1}^{N_{\max }}k{T}_s|\Delta P_e(k)|}$$

(31)

$$IS{E}_1={\displaystyle \sum _{k=1}^{N_{\max }}{\left(\Delta f(k)\right)}^2}$$

(32)

$$IS{E}_2={\displaystyle \sum _{k=1}^{N_{\max }}{\left(\Delta P_e(k)\right)}^2}$$

(33)

$$ITS{E}_1={\displaystyle \sum _{k=1}^{N_{\max }}k{T}_s{\left(\Delta f(k)\right)}^2}$$

(34)

$$ITS{E}_2={\displaystyle \sum _{k=1}^{N_{\max }}k{T}_s{\left(\Delta P_e(k)\right)}^2}$$

(35)

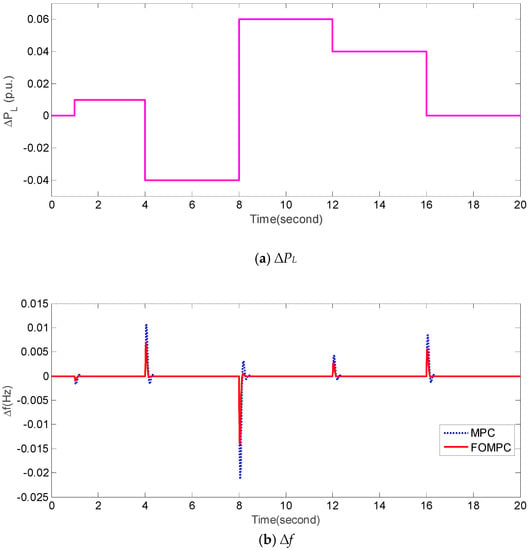
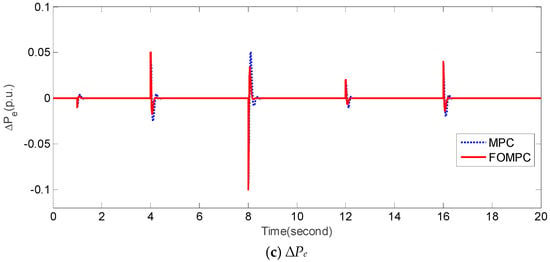
Figure 5. Responses of ∆f and ∆P_e by FOEMPC and MPC under case 2.

Table 5 also shows the control performance indices obtained by FOMPC and MPC for an islanded microgrid under case 2. Obviously, all the indices obtained by FOMPC are better than those by MPC 23.

Table 5. Performance comparison of FOMPC and MPC for an islanded microgrid under case 2. The best values are marked in bold.

Algorithm	IAE1	ITAE1	ISE1	ITSE1	IAE2	ITAE2	ISE2	ITSE2
MPC	0.4704	4.1198	0.0045	0.0378	2.6375	23.1068	0.0920	0.7645
FOEMPC	0.2276	1.9946	0.0015	0.0127	1.6009	14.0405	0.0605	0.5020

4.3. Case 3: Normal System Parameters and Random Dynamical Fluctuations of Δw

In case 3, we designed an experiment under normal system parameters and random dynamical fluctuations of Δw shown in Figure 6a. It should be noted that the random dynamical fluctuations of Δw are modeled based on Reference [34]. Figure 6b,c compares ∆f and ∆P_e of FOMPC and MPC, respectively. Intuitively, the fluctuations of ∆f and ∆P_e obtained by FOMPC are also less than those by MPC [23]. From a quantitative perspective, Table 6 compares the performance indices, such as IAE₁, IAE₂, ITAE₁, ITAE₂, ISE₁, ISE₂, ITSE₁ and ITSE₂ obtained by FOMPC and MPC. It is evident that FOMPC outperforms MPC under case 3.

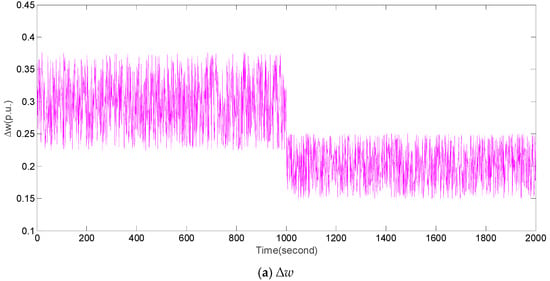
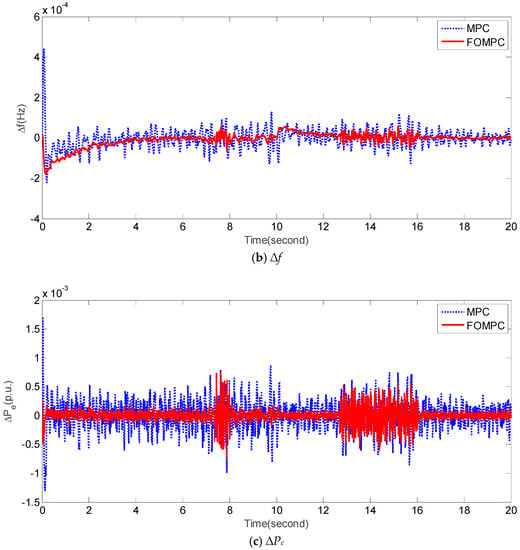
Figure 6. Responses of ∆f and ∆P_e by FOEMPC and MPC under case 3.

Table 6. Performance indices obtained by FOMPC and MPC for an islanded microgrid under case 3. The best values are marked in bold.

Algorithm	IAE1	ITAE1	ISE1	ITSE1	IAE2	ITAE2	ISE2	ITSE2
MPC	0.3044	3.7000	1.84 × 105	2.04 × 104	2.2401	27.3855	7.50 × 104	0.0090
FOEMPC	0.1454	1.5672	5.36 × 106	4.12 × 105	1.5521	19.4406	4.35 × 104	0.0054

4.4. Case 4: Perturbed System Parameters and Dynamical ΔP_L

In order to test the robustness of FOMPC and MPC against perturbed system parameters and dynamical ∆P_L, we design an experiment under the following condition: T_t = 0.6 (increase 50%), R = 1.5 (decrease 50%), H = 0.0833 (decrease 50%), and dynamical fluctuations of ∆P_L (e.g., Figure 7a). Figure 7b,c present the responses of ∆f and ∆P_e by FOMPC and MPC, respectively. It is apparent that the responses of ∆f and ∆P_e obtained by FOMPC are better than those by MPC because of its more smooth flucutations and faster stabilization. Furthermore, the corresponding comparison of IAE₁, IAE₂, ITAE₁, ITAE₂, ISE₁, ISE₂, ITSE₁, and ITSE₂ is shown in Table 7. It is obvious that the proposed FOMPC method is superior to the traditional MPC [23] under case 4.

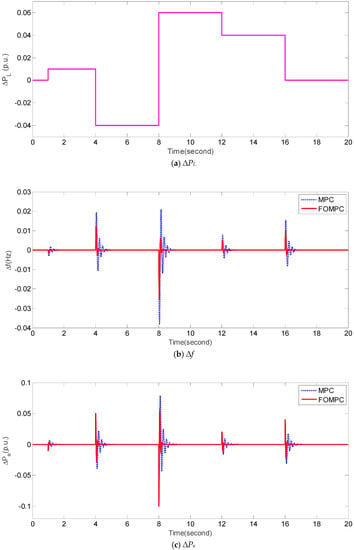
Figure 7. Reponses of ∆f and ∆P_e by FOMPC and MPC under case 4.

Table 7. Performance indices obtained by FOMPC and MPC for an islanded microgrid under case 4. The best values are marked in bold.

Algorithm	IAE1	ITAE1	ISE1	ITSE1	IAE2	ITAE2	ISE2	ITSE2
MPC	1.2148	10.7375	0.0157	0.1312	4.7186	41.6843	0.1417	1.1831
FOEMPC	0.3481	3.0523	0.0037	0.0307	1.8927	16.6041	0.0699	0.5801

4.5. Case 5: Perturbed System Parameters and Random Dynamical Fluctuations of Δw

For case 5, we consider the condition of perturbed system parameters, e.g., T_t = 0.6 (increase 50%), R = 1.5 (decrease 50%), H = 0.0833 (decrease 50%), and random dynamical fluctuations of ∆w shown in Figure 8a. Figure 8b,c compare ∆f and ∆P_e obtained by FOMPC and MPC under case 5, respectively. It is obvious that these fluctuations of ∆f and ∆P_e obtained by FOMPC are less than MPC. Additionally, Table 8 also shows the comparison of the aforementioned eight indices. Clearly, the eight peformance indices of FOMPC are all better than those by MPC [23]. In other words, FOMPC is more robust than MPC under case 5.

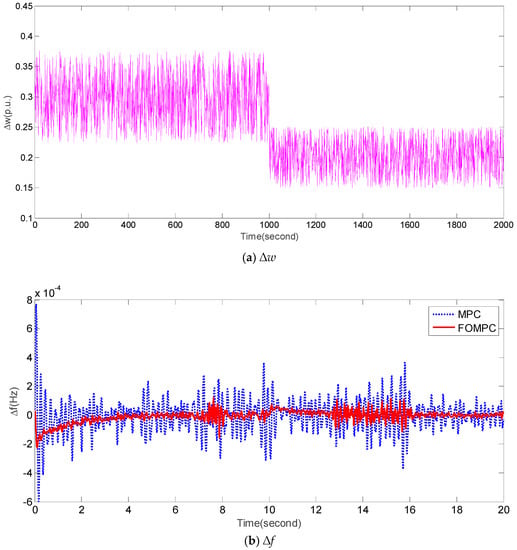
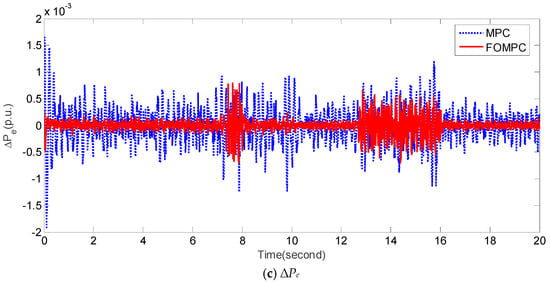
Figure 8. Responses of ∆f and ∆P_e by FOMPC and MPC under case 5.

Table 8. Performance indices obtained by FOMPC and MPC for an islanded microgrid under case 5. The best values are marked in bold.

Algorithm	IAE1	ITAE1	ISE1	ITSE1	IAE2	ITAE2	ISE2	ITSE2
MPC	0.8047	10.1467	1.28 × 104	0.0016	3.4273	42.6849	0.0015	0.0182
FOEMPC	0.2674	3.1144	1.54 × 105	0.0002	1.7745	22.2558	0.0005	0.0064

4.6. Case 6: The Worst Case

In case 6, we consider the worst case, i.e., under the following combined condition: T_t = 0.6 (increase 50%), R = 1.5 (decrease 50%), H = 0.0833 (decrease 50%), dynamical fluctuations of ∆P_L shown in Figure 9a, and random dynamical fluctuations of Δw shown in Figure 9b. For case 6, Figure 9c,d show the reponses of ∆f and ∆P_e by FOMPC and MPC, respectively. Obviously, It is apparent that the fluctuations of ∆f and ∆P_e by FOMPC are also more smooth than those by MPC even under the worst case. Moreover, Table 9 compares the corresponding performance indices obtained by FOMPC and MPC. Clearly, FOMPC performs better than MPC in terms of all the indices, which indicates that FOMPC has better robustness than the traditional MPC [23] under the worst case.

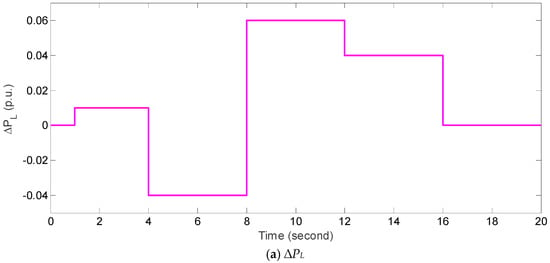
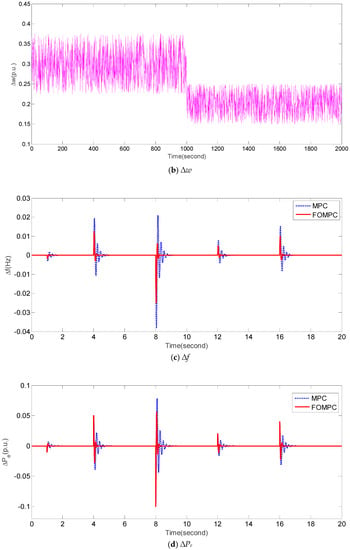
Figure 9. Dynamical responses of ∆f and ∆P_e obtained by FOMPC and MPC under case 6.

Table 9. Performance indices obtained by FOMPC and MPC for an islanded microgrid under case 6. The best values are marked in bold.

Algorithm	IAE1	ITAE1	ISE1	ITSE1	IAE2	ITAE2	ISE2	ITSE2
MPC	2.0268	20.8613	0.0163	0.1366	13.2341	135.7164	0.5758	5.0990
FOEMPC	0.6563	6.5357	0.0042	0.0351	8.8832	91.6722	0.5056	4.5115

4.7. The Effects of Fractional-Order Parameters on Frequency Control Performance

As the aforementioned description of the FOMPC method in Section 3, fractional-order parameters β and γ play important roles in adjusting the frequency control performance. To illustrate the effects of β and γ on the frequency control performance, Figure 10 presents the frequency deviation ∆f under a set of different values for β and γ. Intuitively, the dynamical responses become faster, and the steady-state performance becomes better as the values of β and γ increase.

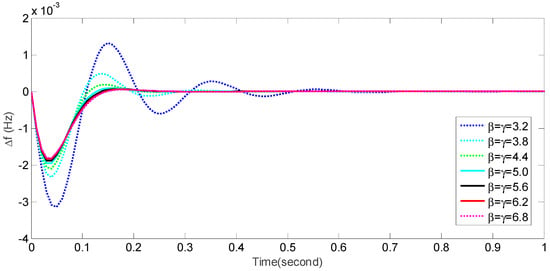
Figure 10. Effects of fractional-order parameters on the frequency control performance of an islanded microgrid.

5. Conclusions and Open Issues

In this work, a novel FOMPC-based optimal frequency control method is designed for an islanded microgrid. The proposed FOMPC method has extended the traditional quadratic cost function and introduced a fractional-order integral cost function based on the GL fractional-order integral definition. Simulation results have demonstrated the superiority of FOMPC to conventional MPC [23] with integer-order cost function under dynamical load disturbances, perturbed system parameters and random dynamical power fluctuation of wind turbines. Moreover, this paper discussed the effects of two important fractional-order parameters used in the FOMPC method on frequency control performance. In conclusion, the FOMPC method can be considered as a promising solution for the optimal frequency control issue of an islanded microgrid. Nevertheless, some of the following open issues are still rather remarkable for future research. Firstly, the fractional-order calculus theory can also be introduced into the gradient descent method used in FOMPC. Secondly, it is still challenging to tune a set of optimal algorithm parameters used in FOMPC from the multi-objective optimization perspective. Furthermore, the extension of the proposed FOMPC to more complex power systems is another interesting research issue.