Abstract
Efficient energy management is strongly dependent on determining the adequate power contracts among the ones offered by different electricity suppliers. This topic takes special relevance in healthcare buildings, where noticeable amounts of energy are required to generate an adequate health environment for patients and staff. In this paper, a convex optimization method is scrutinized to give a straightforward analysis of the optimal power levels to be contracted while minimizing the electricity bill cost in a time-of-use pricing scheme. In addition, a sensitivity analysis is carried out on the constraints in the optimization problems, which are analyzed in terms of both their empirical distribution and their bootstrap-estimated statistical distributions to create a simple-to-use tool for this purpose, the so-called mosaic-distribution. The evaluation of the proposed method was carried out with five-year consumption data on two different kinds of healthcare buildings, a large one given by Hospital Universitario de Fuenlabrada, and a primary care center, Centro de Especialidades el Arroyo, both located at Fuenlabrada (Madrid, Spain). The analysis of the resulting optimization shows that the annual savings achieved vary moderately, ranging from −0.22 % to +27.39%, depending on the analyzed year profile and the healthcare building type. The analysis introducing mosaic-distribution to represent the sensitivity score also provides operative information to evaluate the convenience of implementing energy saving measures. All this information is useful for managers to determine the appropriate power levels for next year contract renewal and to consider whether to implement demand response mechanisms in healthcare buildings.
1. Introduction
Conventionally, demand side management (DSM) is defined as the planning, implementation, and monitoring of distribution network utility activities designed to influence the customer use of electricity in a way that will produce some desired changes in the time pattern and load magnitude [1,2]. Even tough DSM is still an active research topic with significant practical implications in the electrical industry, DSM scope has evolved rapidly in the last decade, mainly due to the improved communication and control capabilities offered by modern information and communications technologies (ICTs). In particular, the load management concept has evolved into the so-called Demand Response (DR) [3]. DR schemes depend on the entities involved (i.e., electricity market, utility, and customers) and the objective of the DR request (i.e., Price-Based DRs and Physical DRs). Pricing schemes can range from simple (e.g., single, flat, or block rates) to complex rates, such as seasonal, time-of-use (TOU), or real-time pricing (RTP) rates. Nevertheless, TOU pricing is the most worldwide employed scheme for electrical energy billing [4,5,6]. On the other hand, physical-DR request may include load shifting, turning-off non-essential loads, peak shaving, or turning-on allowable on-site generators [7], and more recently the so-called battery energy storage systems (BESS) [8]. In this context, a very special kind of industrial consumers which need to adopt DR programs are healthcare buildings, as they usually are large and complex buildings that are continuously operating, consuming energy on large scale, and playing a vital role in health services [9,10,11]. Energy needs of large hospitals can be comparable to a small city and they manage expensive electricity bills. This considerable energy consumption and its subsequent billing require an effective load management to obtain savings without affecting the quality of service in the patient healthcare [12].
Before adopting a DR program, facility managers need to analyze the energy performance to quantify the cost associated with energy consumption and to quantify the impact of implementing those DRs actions that require investment, finance viability and payback time [13,14]. In this regard, the aim of this paper is to support healthcare building managers in adopting a Price-Based DR program, specifically in a TOU pricing scheme. For this purpose, we formulate the DR problem subject to TOU pricing constraints based on convex optimization that finds the contracted power level that minimizes the cost of electricity bill and satisfies the TOU pricing. Convex optimization is a widely used tool for this purpose, and it refers to the minimization of a convex objective function subject to convex constraints [15]. Not only can convex optimization provide with a direct solution of the most convenient power level by block rate to be contracted by a healthcare building in terms of the its power demand, but it can also provide the sensitivity of the problem to the involved constraints, although it could be highly informative from a managerial point of view.
To our best knowledge, the literature review provides limited information about the optimization of the electricity bill with data from this special type of customer. Most of the existing research related to TOU rates is concerned about utilities and industrial customers, and these approaches exhibit different mathematical methods. Among others, several complex methods were considered in [16,17,18] as optimization approaches. In [16], the authors studied mathematical models for the consumer and the utility companies to optimize the cost to the parties individually and in combination. In [17], an approach was proposed for TOU design based in quadratically constrained quadratic programming and stochastic optimization techniques from the utility point of view. Furthermore, in [18] a game-theoretic approach is considered for optimal TOU electricity pricing. Other works (e.g., [19,20]) have focused on evaluating electricity rates though characterization and forecasting of energy consumption to advise companies for the contract renewal. All these studies have different approaches from ours and they have paid little attention to the sensitivity analysis.
We evaluated our approach on two different kinds of healthcare buildings: (1) a recently created hospital with modern facilities and general design, which virtually represents a small city itself, i.e., Hospital Universitario de Fuenlabrada (HUF); and (2) a primary healthcare center referred to it, namely Centro de Especialidades el Arroyo (CEA), with lower power consumption. Both are located in the city of Fuenlabrada (Spain) and can provide us with a contrasted and differential analysis on their energy consumption on the basis of a shared geographical and demographical context.
The main contributions of this paper can be summarized as follows. First, we propose a novel yet simple methodology based on convex programming that allows us to determine the optimal power levels to be contracted with the electricity company into a TOU-rate scheme. Second, we model the sensitivity of the annual cost of energy by block and period, and use non-parametric resampling techniques (specifically, bootstrap resampling [21]) to generate an easy-to-handle tool for analyzing the sensitivity of the cost in terms of months and consumption blocks, in a unified statistical form. This proposal allowed us to identify at a glance where the demanded power exceeded the contracted power and its impact from a statistical point of view. This sensitivity analysis using mosaic distributions can straightforwardly drive managers towards the specific TOU block where DR programs need to be prioritized and implemented, hence supporting an improved energy management in healthcare buildings; however, the entire approach could also be useful in other scenarios.
The rest of this paper is organized as follows. In Section 2, we formulate the DR problem subject to TOU pricing scheme, and we detail the methodology used for sensitivity analysis. In Section 3, we describe the datasets, corresponding to the two aforementioned healthcare buildings, as well as the blocks of the TOU rates considered in this work. In Section 4, we present the experimental results in pricing optimization and sensitivity analysis for both scenarios (large and small scale healthcare buildings). Finally, Section 5 summarizes the discussion and main conclusions of this work.
2. Demand Response Optimization: Sensitivity Analysis and Mosaic Distribution
In this section, we formulate the DR problem subject to TOU pricing constraints. More specifically, we formulate a constrained optimization problem that, using as inputs the power demand and the pricing schemes, finds the contracted power level that minimizes the cost and satisfies the TOU pricing constraints imposed by the operator. This optimization will be the key not only to finding the optimal contracted powers, but also to analyzing the sensitivity of the solutions with respect to changes in the power demand. To that end, the first part of the section focuses on the problem formulation and discusses how this problem could be solved using convex programming tools [22]. The second part addresses the sensitivity analysis by discussing the empirical distribution of the Lagrange multipliers (LM) associated with the optimization, and the usefulness of the bootstrap re-sampling techniques [21] to yield a unified view of the relevance of the constraints through different blocks and month periods.
Regarding the problem formulation, we start by introducing the main notational conventions and, then, identify the state variables (which serve as inputs to our problem), the optimization variables (which serve as outputs), the constraints relating the different variables, and the cost to minimize.
- Power consumption. We focus on optimizing the power consumption during one year (12 months) and consider that the time is divided into regularly sampled 15-min periods. Variable N is used to denote the total number of periods in a year (i.e., ) and variable n is used to index those periods of 15 min each). Similarly, we use to denote the total number of months in a year and the variable m to index the corresponding month. With this notation in place, we can define the column vector as the one-year load consumption (in kWh). Moreover, suppose that at period n the contracted power is not enough to meet the current demand, thus additional power from the supplier are needed. Then, we use to denote the excess power at period n (in kW) and collect all those values in vector . Defining as the number of 15-min periods in month m, we also define the monthly counterparts of the previous vectors as and and write and .
- Pricing mechanisms. The operator considers different tariff periods, which are indexed by variable t. The unitary cost of the power during the tariff period t is denoted as , and all those prices are collected in vector . At the beginning of each year, the customer must decide the amount of power that is contracted for each of the tariff periods. To that end, we use to denote the contracted power at tariff period t and collect all those variables in the column vector . Moreover, to penalize the amount of excess power that the customer needs to buy every month, the supplying company establishes a cost coefficient for each tariff t, which are collected in the column vector. Finally, to account for the TOU pricing mechanism, we consider the binary variable , which is one if the time period n of the month m is charged with the tariff t and zero otherwise. Moreover, for each month m and tariff t, we can collect the corresponding binary variables in the vector . Those vectors are used to define the diagonal matrices for all as well as the matrices for all m.
Using the state variables , and as inputs, and viewing the optimization variables and as outputs, our DR optimization problem subject to TOU constraints can be formulated as
In the above optimization, the constraints in Equation (2) account for the fact that the power variables are non-negative; Equation (3) are balance constraints that guarantee that the power demand is always satisfied; and the constraints in Equations (4) and (5) are imposed by the power supplier as part of its TOU pricing mechanisms. Regarding the cost, we note that two terms are considered. The first one simply accounts for the cost of the power contracted at the beginning of the year for each of the T tariffs. The second one, which is a bit more involved, accounts for the excess of power that the customer must buy when the demand exceeds the contracted power. More specifically, this second term considers all month–tariff pairs and, for a given pair, finds the cost as the multiplication of the coefficient with the norm of the vector collecting the excesses during the pair, which can be conveniently obtain as .
All the constraints in Equations (1)–(5) are linear; the cost to minimize is the sum of a linear term and norms; and the domains of the optimization variables are . As a result, the formulated problem is convex and can be efficiently solved, either upon developing tailored first/second order algorithms (recommended when computational complexity is an issue), or using a generic off-the-shelf solver such as CVX (if the dimensionality of the problem is not large) [22].
Note that, if , and are given, the formulated optimization yields the value of that minimizes the cost paid by the customer. Unfortunately, while the prices and are known at the beginning of the year, the demand is not. Different approaches arise to handle this issue. If the joint probability distribution of is known, the optimization can be reformulated as a stochastic problem whose objective is to minimize, for example, an average or a worst-case cost. Alternatively, one can use as input the demand of the previous year and, then, analyze the sensitivity of the problem to variations of such a demand, which is is one of the goals of the ensuing section.
2.1. Sensitivity Analysis
Whereas it is easy to identify the time instants when the consumption has overpassed the power limits, it is not so immediate to provide with an operative view on which are the periods for each month when the consumption is statistically closer or over the limits. An intuitive and heuristic solution should be to represent the histograms of the consumption excesses per block and month period. Two improvements can be done to this simple approach. On the one hand, the use of the sensitivities provided by the convex optimization solver for the excess constrains is statistically more representative than that of the empirical values of the overshoots itself, because, for instance, the LM associated with the constraints are less affected by outliers or atypical samples. On the other hand, the statistical distribution of the sensitivities are often complex, probably a mix of a Bernoulli distribution with another continuous distribution (e.g., Bernoulli–Gaussian) due to the time instants per block and month when the consumption remains below the limit are associated with a null Lagrange multiplier. This can be arranged by the estimation of the average value, and improved by yielding the statistical distribution of that average value per period and month, which can be tackled efficiently using bootstrap resampling the available on the yearly consumption samples and on the optimization problem statement.
The sensitivity analysis in convex optimization [22,23] aims to quantify the impact on the solution of the constrains, either all of them, or some subset of special interest. If we denote by the LM associated with the constraints in Equation (3), those LM represent the sensitivity of the optimization cost with respect to the variation on the demand (and, hence, on power consumption excess), taking into account their distribution in periods and months, as required by the optimization primal functional. The empirical distribution functions for these Lagrange multipliers can be expressed as
where is the number of consumption samples in cost period t and month m, and denotes the Dirac’s delta function. This empirical probability density function (PDF) is often indirectly visualized by using a histogram and choosing an appropriate number of bins, which is denoted here as . The histogram representation is more useful for visualization, but we should keep in mind that the empirical PDF is the basis for the plug-in principle in bootstrap resampling techniques [21,24]. Estimated means can be obtained as an operator (the sample average), denoted by , on the set of Lagrange multipliers, as follows
where represents the set of Lagrange multipliers grouped according to elements in that TOU block and that month.
The Bernoulli-mixed character of the sensitivity distribution can be hard to handle for management purposes, and, given that the sample mean represents a partial information on its actual and statistical relevance, bootstrap resampling techniques can be used to provide us with the distribution of the mean sensitivities, as follows. The PDF of an estimator is not always easy to estimate analytically; hence, we can use instead bootstrap resampling, which is a non-parametric technique turning especially useful when the statistical distribution of the problem is unknown, as it is our case of analysis [25,26]. We denote by the operator that yields the set of sensitivities grouped into cost periods and months from a set of consumption measurements on a year, this is,
for and , and where denotes on a compact form all the constrains that have to be fulfilled and considered when building the convex optimization problem.
A bootstrap resample of the population sample is given by , which corresponds the bth repetition of the process of sampling with replacement the load consumption samples, while restricted to hold the conditions in the given problem (e.g., constraints on the periods, distribution per cost periods and months, and all others). If we repeat this process B times (i.e., from ), we obtain B replications of the sensitivities, as follows,
and then we can obtain the replications of the average values for each, given by
This way, we can represent the histogram distribution for each estimator of the average as .
Finally, as a way to show the results of the sensitivity estimations, we introduce the concept of mosaic-distribution, which for a given set of distributions is defined as follows:
- The mosaic distribution will be a three-dimensional set of representation cells, where horizontal plane performs a grid of indexed squares that corresponds to their respective TOU block and month. In the vertical axis, we are representing the normalized histogram of the sensitivity distributions.
- In our plots, the squares that are disjoint in the TOU blocks conditions are represented using grey color; those PDF in whose 95% confidence interval (CI) overlaps zero are represented with a blank cell; and those PDF whose CI are significant, and their average sensitivity are low, moderate, and high, are shown in green, orange, and red color line, respectively.
In this work, we use the mosaic distribution for the histogram-estimated PDF of the sensitivities, hence denoted by , and for the average bootstrap sensitivities, denoted by , as shown in Section 4. Note that the calculation of the mosaic representations has to be seen as a post-processing, and that bootstrap resampling is not part of the optimization process, but rather the optimization is replicated with the set of resampled consumption measurements. Algorithm 1 summarizes the process steps for clarity.
| Algorithm 1 Mosaic Representation |
| Input: one-year consumption d in kWh, and periods with the corresponding costs . Output: Contracted power and mosaic representation of sensitivities .
|
3. Databases
We analyzed historical load data of high voltage (e.g., ≥ 1 kV) consumers as case study from two different sized healthcare buildings. They both followed a six-block TOU rate, and their supplier constraints required that at least one of the six contracted power levels were greater than 450 kW. The first dataset has been provided by the HUF, located at the Comunidad de Madrid, Spain. The HUF serves a population of about 220,000 people, and it has a total surface of 64,000 m, capacity for 406 beds, and 9 surgery theaters. The second dataset corresponded to the power consumption of the CEA, which is also located in the Comunidad de Madrid, a few kilometers away from the HUF. This is a primary attention center that carries out specialty outpatient activities, with a surface of 10,050 m.
These datasets can be represented by their corresponding boxplots (Figure 1) and both contain quarter-hourly demand from 1 January 2013 to 1 December 2017. We notice, for the HUF case, that the demand exceeds the current power contracted level, in such a way that values above this limit are considered as overshoots of the demanding power and they causes penalties in the final price. For this case, the optimal set of power levels should be higher than the current ones. On the other hand, for CEA case, the load profile mainly remains below the limits indicated by the dashed lines, which suggests that the current contracted power levels were higher than the optimal.
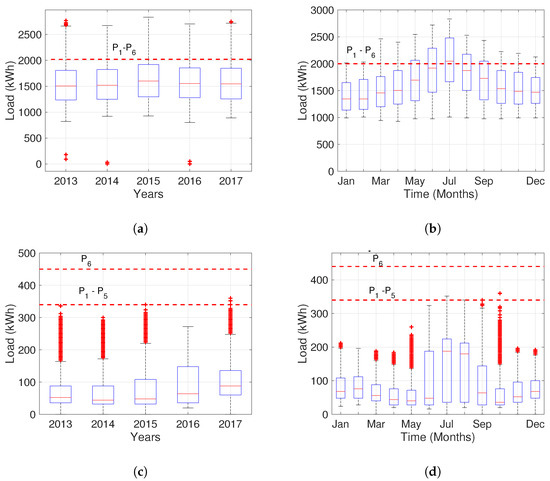
Figure 1.
Load demand representations with the data available from 2013 to 2017 period: at Hospital Universitario de Fuenlabrada (HUF) (a) yearly boxplot and (b) monthly boxplot; and at Centro de Especialidades el Arroyo (CEA) (c,d) yearly and monthly boxplot, respectively. Red dashed lines represent the current contracted power levels, in the HUF case the same level for all t blocks, while for CEA case we have two power levels, one for , and another one for .
The historical database contains 35,040 consumption registers by year with a sampling period of 15 minutes (i.e., 4 × 24 × 365 = 35,040 samples). These registers must be allocated by block (1–6) and by month, day, and hours (i.e., time block division for TOU pricing), as detailed in Table 1.

Table 1.
Six-block time division for the used time-of-use (TOU) rates in our data.
4. Experimental Results
In this section, we analyze the results obtained when applying the proposed methodology to the available databases from the HUF and CEA buildings. The optimization problems were solved using Matlab-based CVX software (version 2.1, CVX Research, Inc., Austin, TX, USA) for convex optimization [27]. First, we present the results of evaluating the function cost when the optimal set of power levels is applied. Then, we present the results of data processing followed to determine the sensitivity description, which basically consisted of performing bootstrap resampling from the LM for every pair of months and TOU block. Finally, we analyze the sets of sensitivities in terms of the introduced mosaic representations, showing that they allow us to readily identify where the optimization constraints and demand need to be focused to adopt DR mechanisms in a TOU scenario.
4.1. Cost Analysis in Terms of the Optimal Power Level
The upper part of Table 2 presents the optimal power set found by the proposed optimization method for the HUF and CEA cases in every analyzed year. With this approach, the optimal set of power levels calculated in the current year are the recommended ones to be contracted with the power supplier during the next year. According to the HUF demand profile, depicted in Figure 1a,b, these results confirm that the optimal set of powers should be higher than the current one, and they tend to stabilize in 2016 with the values in 2014. The table also shows how the optimized levels in the HUF, presented for the current year, affect the annual cost if they are applied to the next year (e.g., optimal power calculated with 2013 demand is applied to calculate the cost with 2014 demand). We obtained a saving metric for this evaluation when compared with their corresponding current cost by year. Moderate savings (max 2.86%) indicate that the current contracted power levels are close to the optimal. In this case, the DR strategy suggest that it is possible and recommendable to increase the power to be contracted during the next year.

Table 2.
Power levels and results of cost evaluation.
For the CEA healthcare building, a different behavior was observed compared with the HUF, as in this case, the optimal set of powers are located below the current ones (see Table 2, lower part). Whereas the relative savings are apparently higher (max 27.39%), the amounts are noticeably much smaller. It can be seen that the optimum remains in general stabilized, except for the increment observed in 2015. There is a trend on the forward prediction to yield a slight overcost in the last three years, which was due to the fact that a change in the management was followed in which the building required to be increasingly cooled in the summer, which caused a change in the dynamics and a non-stationary modification on the conditions. However, the method is capable of providing a closer-to-the-optimum estimation.
In both cases, we see that several quantitative advantages can be obtained. Rather than the impact on the savings, this shows evidence that the consumption dynamics are being adequately captured by the optimization procedure. Accordingly, and rather than just giving a recommendation for the next-year tariff to contract, it seems desirable to provide information on these changes in the dynamics from one year to another, so that this information can be handled by healthcare building managers, as described next.
4.2. Overshoot, Lagrange Multipliers and Bootstrap
When formulating the optimization problem, one of our decisions was to consider the power excess (overshoot) as an explicit variable and to relate this variable to the power demand and the contracted power using a constraint. Such a decision brings two benefits: (i) the LMs associated with the constraint capture the sensibility of the cost in the objective to variations (uncertainties) on the demand; and (ii) we can rely on dual theory and sensitivity analysis to characterize those LMs. In this section, we evaluate the value of those LMs and use the results to asses the sensitivity to overshoots for every block and period.
For the HUF case, Figure 2 shows an example of post-optimization data treatment allowing us to obtain the mean bootstrap sensitivity value and its distribution from the LM analysis. In Figure 2a, we can observe the load profile and the time instants when it overpasses the power limit. Note that the green dashed line depicts the current power level and the red line shows the overshoot with respect the optimal level. Figure 2b depicts the corresponding LM provided by the optimization algorithm output as a function of the same time instants, where it is clear that these LM track the overshoot with their instantaneous values, whereas these values remain at zero level with no overshoot. Figure 2c shows every overshoot as discrete variable that is active only for the specific constraint (i.e., block, month) defined in Equation (3). In the histogram in Figure 2d, the empirical PDF is represented for this price evolution, and the presence of complex shapes can be appreciated, as given in this case by bi-modalities. Figure 2e shows the average-values for every bootstrap replication, together with Figure 2f depicting its empirical PDF. Whereas the statistical distribution of the bootstrap-estimated values still includes the information of the overshoots that take place at every resample, its statistical distribution is not so affected by specific peaks happening in a specific realization. This provides a robust set of estimators, which are less affected by atypical samples, while respecting the impact of the overshoots on the statistical distribution description.
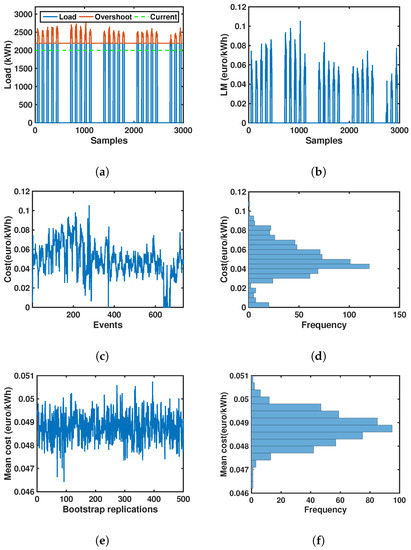
Figure 2.
Example of implementation of the sensitivity analysis for HUF: (a) Load profile plot corresponding to Month 7 and Block 1; (b) Lagrange multipliers (LM) plot associated with the constraint (1,7); (c) LM discrete event representation; (d) LM empirical distribution function; (e) Bootstrap replications mean plot; and (f) Mean bootstrap distribution.
For the CEA case, the counterpart to Figure 2 is shown in Figure 3. Load consumption and the time instants when it overshoots the optimal power limit (red line) are shown in Figure 3a. Note that, for the currently contracted level (green dashed line), we can see that the optimal level is well below the contracted one, which in this case implies that in the equilibrium point it is preferable to allow some overshoots. LMs and their discrete representation are shown in Figure 3b,c, respectively. In the PDF distribution shown in Figure 3d, we observe a different distribution profile compared with the HUF case for these same conditions, where it is noticeable a trend to zero value. Finally, in Figure 3e,f, the average values by bootstrap replication and its bootstrap distribution are shown, respectively. These statistical profiles are much alike the ones in the HUF case example, and again, they are including the information about the overshoots for the optimized problems, hence it represents a robust statistical measurement and characterization of the dynamics, which in turn can be readily compared with other situations. Hence, the use of sensitivity analysis in combination with bootstrap resampling yields a unified and robust representation of the underlying dynamics, which is subsequently analyzed in the next subsection.
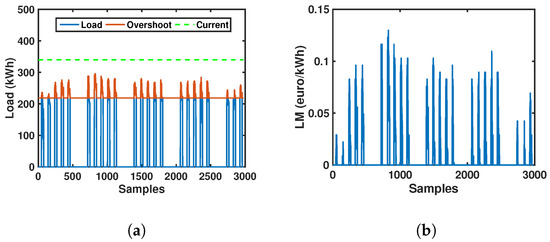
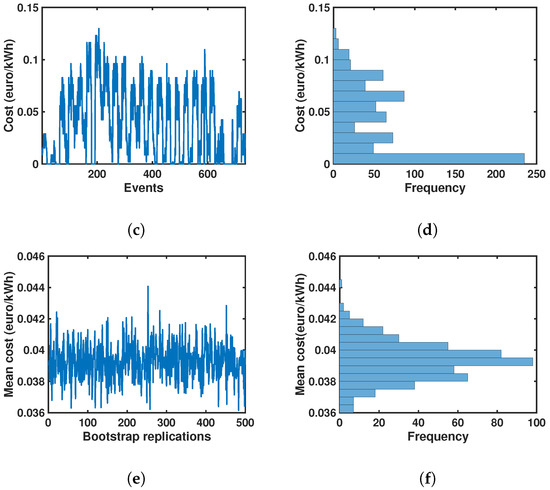
Figure 3.
Implementation of the sensitivity analysis for CEA: (a) Load profile plot corresponding to Block 1, Month 7; (b) LM plot associated with the constraint (1,7); (c) LM discrete event representation; (d) LM empirical distribution function; (e) bootstrap replications mean plot; and (f) bootstrap mean distribution.
4.3. Mosaic-Distribution and Sensitivity Results
We addressed the representation of mosaic distributions for the data from the available years (i.e., 2013–2017) according to Algorithm 1. Recall that, in the mosaic distributions for the LM empirical distributions, in horizontal plane, blank cells represent a distribution which demand do not overshoot optimal power level, and grey cells indicate that the corresponding month does not match with any TOU block. In addition, in the mosaic distributions for the bootstrap sensitivity analysis, blank cells represent a distribution whose CI overlaps zero and then it is not statistically significant, and hence, that distribution is not represented in the mosaic. Recall also that the estimated PDFs of the LM are depicted with green, orange, and red color when their corresponding average is low, moderate, and high, respectively.
Figure 4 shows the mosaic distribution for the LM empirical distributions in the HUF case. The peak load is represented for each year in Figure 4a, so that we can have a view of the consumption profile. We can observe that the load overshoots the and even optimal power levels, which are identified by the dotted lines therein.
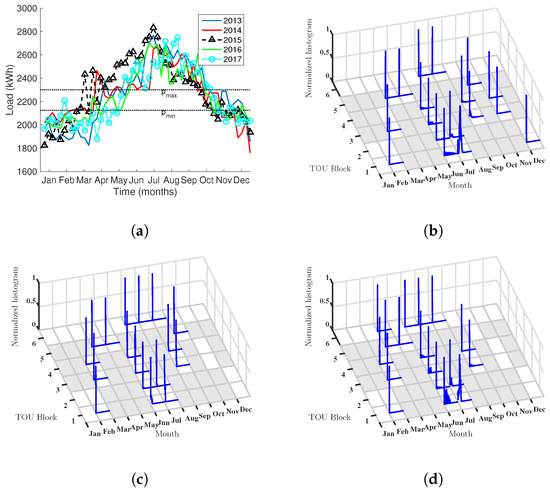
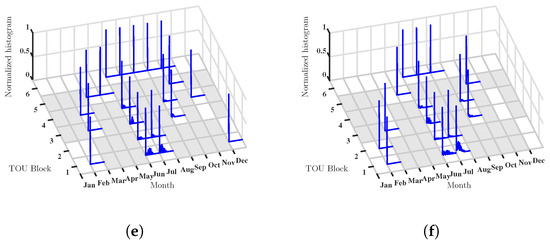
Figure 4.
Mosaic distribution for LM in HUF: (a) peak load representation for the available data; and (b–f) mosaic representation for the LM empirical distributions by month and TOU, in Years 2013, 2014, 2015, 2016, and 2017, respectively.
In Figure 4, those tiles whose 95% CI overlaps zero have been removed from the representation; nevertheless, most of the distributions are significantly present with this criterion. It can be also seen in Figure 4b–f that there is a noticeable bimodality and heavy tails in the distributions of the LM, which is just due to the threshold effect on the LM. This representation makes hard to identify which are the more crucial periods and months, and not much difference can be observed from one year to another.
Conversely, Figure 5 shows the mosaic distributions for the bootstrap estimated averages. It can be clearly seen that distributions in red have clearly higher values, and more, there are temporal trends that can be observed through years. For instance, the red distributions are mostly grouped on the months of June, July, and September, for periods 1 to 4, and mostly repeated with minor changes. However, there is a trend in the red distributions following an inverted-U shape, which are more present in 2013 for the ending months, then they trend to reduce in those months but to increase in March and April during 2014 and 2015, and finally to be less evident in 2017. Hence, two sets of policies need to be separately considered, one for the summer, and another for the winter, which will be obviously different, but can be scrutinized in terms of what happened in those specific months in the observed years.
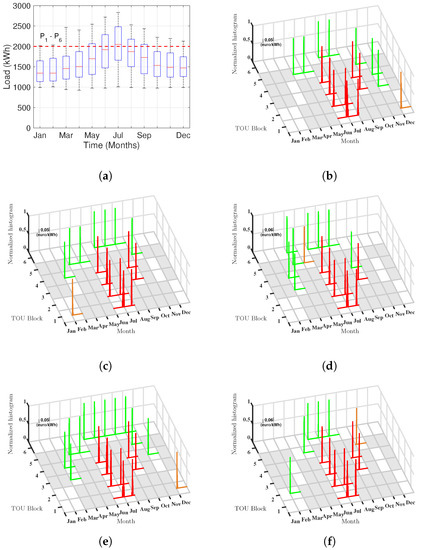
Figure 5.
Bootstrap sensitivity analysis in HUF: (a) monthly load profile representation for the available data; and (b–f) mosaic representation of mean distributions by month and TOU blocks, for Years 2013, 2014, 2015, 2016 and 2017, respectively.
Different dynamics are observed in CEA. Figure 6 shows the peak load with a very different profile from the triangular trend in HUF, and, in this case, there is a flat trend in the summer months, probably related with the cooling air connection, and then a peak-trend with maximum in January but linearly decreasing, corresponding to the Winter months. In this case, the mosaic distribution for the LM empirical distributions has a different profile from the HUF distribution, and more, it remains stable and repeated through years. However, as seen in Figure 7, the mosaic representations for the bootstrap sensitivity analysis is very different from stationary. The U-shape set of significant green distributions is not present here, whereas the significant sensitivity is now condensed in the months of June, July, and September, being non-significant the other tiles. Nevertheless, the relevance of the significant tiles changes from one year to another, with a trend to increase the sensibility during years 2015 and 2017. These were the years where the policies on the air-conditioned management changes, and this trend is detected within this analysis to change the impact on the mosaic distribution. In Table 3, we summarize the maximum sensitivity values obtained for CEA and HUF. In both cases, the maximum corresponds to 2015 and 2017 years.
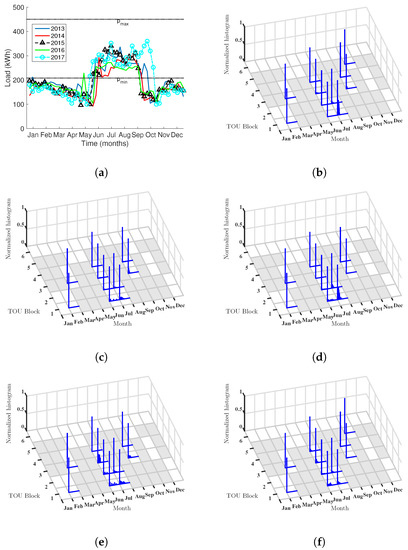
Figure 6.
Mosaic distribution for LM in CEA: (a) peak load representation for the available data (from 2013 to 2017); and (b–f) mosaic representation for the LM empirical distributions by month and TOU, in years 2013, 2014, 2015, 2016, and 2017, respectively.
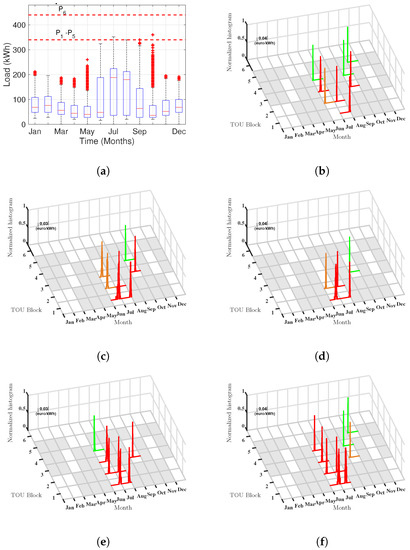
Figure 7.
Bootstrap sensitivity analysis in CEA: (a) monthly load profile representation for the available data (from 2013 to 2017); and (b–f) mosaic representation of mean distributions by moth and TOU blocks, for Years 2013, 2014, 2015, 2016, and 2017, respectively.

Table 3.
Summary of maximum sensitivity by year.
5. Discussion and Conclusions
In this paper, we have proposed a twofold application of convex optimization to support managers of healthcare buildings in adopting a time-of-use based demand response program (DR-TOU). First, a simple yet novel method has been proposed which has been solved using convex programming tools. The analyzed scenario corresponds to the five years of data consumption available from two different sized healthcare buildings and the rate scheme to a six-block TOU pricing. Second, we provided the managers with additional information about the most relevant constraints to be paid attention, and, for this purpose, the statistical distribution of the constraint sensitivity of the time periods and pricing levels was scrutinized, giving a good view of which are the most critical of them on a new, systematic, and easy-to-handle representation with the so-called mosaic distributions.
Sensitivity analysis has been shown to identify at a glance where and when the interventions will be more urgent and more necessary to reduce the cost. The use of statistical tests based on nonparametric bootstrap resampling makes this instrument more than a visualization tool, and is solidly based on the statistical distribution analysis. The application of this method in two very different cases of study (different healthcare buildings) highlights the effective convenience and usability of this approach.
In our results, the analysis of the resulting optimization showed a cost reduction in the electricity bill of up to 27.81% per year, obtained in the smaller building with conventional energy management strategy. Clearly, it should not be used as an autonomous and isolated prediction tool, but rather as a support to the deep knowledge of the managers in their field. The statistical profiles in the distributions of the raw LM was shown to have limited information, whereas the profiles given by bootstrap resampling provided with useful and operative information about the dynamics and the most convenient tiles to scrutinize in order to manage the cost. Thus, the mean sensitivity of 0.06 €/kWh (for the larger building) and 0.04 €/kWh (for the the smaller building) could be a useful evaluation metric for those energy saving measures that require investment, finance viability and payback time (e.g., to invest in battery energy storage systems (BESS)). It can be concluded that the proposed novel system can be useful to determine the suitable power levels for the next year contract renewals, while giving a robust and operative overview of the optimized solution for DR-TOU management purposes. Finally, although our formulation is suitable for healthcare buildings, it could also be useful in other scenarios.
Author Contributions
R.G.-O., L.M.L.-R., S.M.-R., and J.L.R.-Á. conceived, designed, and performed the experiments. R.G.-O. and J.L.R.-Á. organized and wrote the paper, and performed the analysis of the experimental results. L.M.L.-R., S.M.-R., D.A.-A. and A.G.M. contributed to writing and reviewing several sections of the manuscript. R.C. elaborated on the hospital data structure. A.G.M., and R.C. collaborated with a multidisciplinary review.
Acknowledgments
Special thanks are given to Paz Iglesias and the staff of the HUF for their kind support in the data assembling. This work was partly supported by FINALE project (TEC2016-75161-C2-1-R and TEC2016-75161-C2-2-R), and project TEC2015-64835-C3-1-R with FEDER funds, and by PRICAM (S2013/ICE-2933), from the Comunidad de Madrid, Spain.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Qureshi, W.A.; Nair, N.K.C.; Farid, M.M. Impact of energy storage in buildings on electricity demand side management. Energy Convers. Manag. 2011, 52, 2110–2120. [Google Scholar] [CrossRef]
- Olatomiwa, L.; Mekhilef, S.; Ismail, M.; Moghavvemi, M. Energy management strategies in hybrid renewable energy systems: A review. Renew. Sustain. Energy Rev. 2016, 62, 821–835. [Google Scholar] [CrossRef]
- Pasetti, M.; Rinaldi, S.; Manerba, D. A Virtual Power Plant Architecture for the Demand-Side Management of Smart Prosumers. Appl. Sci. 2018, 8, 432. [Google Scholar] [CrossRef]
- Tang, Y.; Song, H.; Hu, F.; Zou, Y. Investigation on TOU pricing principles. In Proceedings of the Transmission and Distribution Conference and Exhibition: Asia and Pacific, 2005 IEEE/PES, Dalian, China, 18 August 2005; pp. 1–9. [Google Scholar] [CrossRef]
- Ding, J.Y.; Song, S.; Zhang, R.; Chiong, R.; Wu, C. Parallel Machine Scheduling Under Time-of-Use Electricity Prices: New Models and Optimization Approaches. IEEE Trans. Autom. Sci. Eng. 2015, 13, 1138–1154. [Google Scholar] [CrossRef]
- Wang, Y.; Li, L. Time-of-use based electricity demand response for sustainable manufacturing systems. Energy 2013, 63, 233–244. [Google Scholar] [CrossRef]
- Patrick, T.; Moseley, J.G. Electrochemical Energy Storage for Renewable Sources and Grid Balancing; Elsevier: New York, NY, USA, 2014; pp. 26–28. [Google Scholar]
- Marchi, B.; Pasetti, M.; Zanoni, S. Life cycle cost analysis for BESS optimal sizing. Energy Procedia 2017, 113, 127–134. [Google Scholar] [CrossRef]
- Gordillo-Orquera, R.; Lopez-Ramos, L.M.; Muñoz-Romero, S.; Iglesias-Casarrubios, P.; Arcos-Avilés, D.; Marques, A.G.; Rojo-Álvarez, J.L. Analyzing and Forecasting Electrical Load Consumption in Healthcare Buildings. Energies 2018, 11, 493. [Google Scholar] [CrossRef]
- García-Sanz-Calcedo, J.; Al-Kassir, A.; Yusaf, T. Economic and Environmental Impact of Energy Saving in Healthcare Buildings. Appl. Sci. 2018, 8, 440. [Google Scholar] [CrossRef]
- Ashourian, K.T.; Young, S.T. Greening Healthcare: The Current State of Sustainability in Manhattan’s Hospitals. Sustain. J. Rec. 2016, 9, 73–79. [Google Scholar] [CrossRef]
- Gordo, E.; Campos, A.; Coelho, D. Energy efficiency in a hospital building case study: Hospitais da universidade de Coimbra. In Proceedings of the 3rd International Youth Conference on Energetics (IYCE), Leiria, Portugal, 7–9 July 2011; pp. 1–6. [Google Scholar]
- García-Sanz-Calcedo, J.; Gómez-Chaparro, M. Quantitative analysis of the impact of maintenance management on the energy consumption of a hospital in Extremadura (Spain). Sustain. Cities Soc. 2017, 30, 217–222. [Google Scholar] [CrossRef]
- Marchi, B.; Zanoni, S. Supply Chain Management for Improved Energy Efficiency: Review and Opportunities. Energies 2017, 10, 1618. [Google Scholar] [CrossRef]
- Luo, Z.Q.; Yu, W. An introduction to convex optimization for communications and signal processing. IEEE J. Sel. Areas Commun. 2006, 24, 1426–1438. [Google Scholar] [CrossRef]
- Cui, T.; Goudarzi, H.; Hatami, S.; Nazarian, S.; Pedram, M. Concurrent optimization of consumer’s electrical energy bill and producer’s power generation cost under a dynamic pricing model. In Proceedings of the IEEE PES Innovative Smart Grid Technologies (ISGT), Washington, DC, USA, 16–20 January 2012; pp. 1–6. [Google Scholar] [CrossRef]
- De Sá Ferreira, R.; Barroso, L.A.; Rochinha Lino, P.; Carvalho, M.M.; Valenzuela, P. Time-of-use tariff design under uncertainty in price-elasticities of electricity demand: A stochastic optimization approach. IEEE Trans. Smart Grid 2013, 4, 2285–2295. [Google Scholar] [CrossRef]
- Yang, P.; Tang, G.; Nehorai, A. A game-theoretic approach for optimal time-of-use electricity pricing. IEEE Trans. Power Syst. 2013, 28, 884–892. [Google Scholar] [CrossRef]
- Hatami, S.; Pedram, M. Minimizing the electricity bill of cooperative users under a quasi-dynamic pricing model. In Proceedings of the First IEEE International Conference on Smart Grid Communications (SmartGridComm), Gaithersburg, MD, USA, 4–6 October 2010; pp. 421–426. [Google Scholar] [CrossRef]
- Di Silvio, B.; Cesarotti, V.; Introna, V. Evaluation of electricity rates through characterization and forecasting of energy consumption: A case study of an Italian industrial eligible customer. Int. J. Energy Sect. Manag. 2007, 1, 390–412. [Google Scholar] [CrossRef]
- Efron, B.; Tibshinari, R.J. An Introduction to the Bootstrap; CRC Press: Boca Raton, FL, USA, 1994. [Google Scholar]
- Luenberger, D.G. Optimization by Vector Space Methods; John Wiley & Sons: New York, NY, USA, 1997. [Google Scholar]
- Vandenberghe, L.; Boyd, S. Semidefinite programming. SIAM Rev. 1996, 38, 49–95. [Google Scholar] [CrossRef]
- Rojo-Alvarez, J.L.; Arenal-Maiz, A.; Artes-Rodriguez, A. Discriminating between supraventricular and ventricular tachycardias from EGM onset analysis. IEEE Eng. Med. Biol. Mag. 2002, 21, 16–26. [Google Scholar] [CrossRef] [PubMed]
- Corral-De-Witt, D.; Carrera, E.V.; Muñoz-Romero, S.; Rojo-Álvarez, J.L. Statistical, Spatial and Temporal Mapping of 911 Emergencies in Ecuador. Appl. Sci. 2018, 8, 199. [Google Scholar] [CrossRef]
- Rocco, C.; Zio, E. Bootstrap-based techniques for computing confidence intervals in Monte Carlo system reliability evaluation. In Proceedings of the RAMS 2005: Annual Reliability and Maintainability Symposium, Alexandria, VA, USA, 24–27 January 2005; pp. 303–307. [Google Scholar] [CrossRef]
- Guimaraes, D.A.; Floriano, G.H.F.; Chaves, L.S. A Tutorial on the CVX System for Modeling and Solving Convex Optimization Problems. IEEE Latin Am. Trans. 2015, 13, 1228–1257. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).