Abstract
In micro grid (MG), active/reactive power sharing for all dis-patchable units is an important issue. To meet fluctuating loads’ active and reactive power demands, the units generally adopt primary P-f and Q-U droop control methods. However, at different state of charge (SOC) values, the capability of Lead Acid Battery Bank (LABB) based units to take loads varies in a large range; active power should not be shared according to the units P capacities in a constant ratio. Besides, influenced by the output and line impedance between units, reactive power is not able to be shared in proportion to the units Q capacities. Another problem, after MG power balance requirement is satisfied, frequency and voltage are deviating from their rated values thus power quality is reduced. This paper presents a new smart MG which is based on the multi agent system. To solve the problems mentioned above, P-f and Q-U droop curves are adjusted dynamically and autonomously in local agents. To improve the power quality, secondary restoration function is realized in a decentralized way, the computation tasks are assigned to local, the computation capability and communication reliability requirements for central PC are low, and operation reliability is high. Simulation results back the proposed methods.
1. Introduction
With the continuing large-scale consumption of fossil energy resources in thermal power stations of large power systems and the increasing efforts of government for energy saving and reducing emissions, a micro grid (MG) that has the ability to cleanly and effectively utilize renewable energy is the most promising technology to achieve this goal. MG generally contains distributed generations (DGs) with greater randomness and fluctuation output like photo-voltaic (PV) cells and wind turbine (WT) generators, and DGs with higher controllability output like micro gas turbine (MT) and LABB [1]. MG can work in interconnected or standalone mode.
In standalone mode, to realize the long-term coordinate operation stability of MG, frequency and voltage stabilization, active and reactive power sharing between LABB based energy storage system (ESS) and MTs are two important issues. Adopting primary P-f [2,3,4,5,6,7] and Q-U [3,4,5,6,7] droop control in outer control loops of inverter interfaces of LABB and MTs is an effective method to simultaneously handle the two issues. Under ideal conditions, adopting droop control, active and reactive power can be shared according to DG’s respective P and Q capacities [1,2,3,4,5]. However, for active power sharing and frequency stabilization, due to LABB SOC varies in a wide range during MG operation, at different SOC values the capabilities of ESS to supply loads varies accordingly. If the value of P-f droop rate of ESS is fixed, it is not only the capability of ESS to stabilize frequency that is not being fully exploited and utilized, but also ESS’s own stable operation cannot be guaranteed when SOC are in extreme conditions. This aspect has not yet been investigated in the vast majority of literatures [1,2,3,4,5,6,7]. To solve this problem, this paper proposes an auto-revised variable droop curve strategy. The strategy is based on SOC value and takes energy resource limitation into consideration [8,9] to dynamically change ESS’s P-f droop rate. As a result, ratios of power sharing between ESS and MTs are changed accordingly. For reactive power sharing and voltage stabilization, influenced by the output impedance of DGs and line impedance between DGs, DGs’ terminal voltage are not equal, so reactive power cannot be shared [10,11]. To handle this issue, this paper proposes a self-adjusted variable droop curve strategy. Local DG acquires other DGs’ output reactive power information to adjust its own Q-U droop curve autonomously, as a result, the reactive power sharing accuracy between DGs will be increased.
As load active and reactive power demands in MG and renewable power generation have high randomness, although adopting P-f and Q-U droop control methods can dynamically maintain power supply-consumption balance between DGs and loads. However, this balance is achieved at the expense of MG frequency and voltage deviation [1,2,3,4,5,6,7,8,9]. Secondary control to restore them and increase power quality is another important issue [9,10,11,12,13]. In power system, secondary frequency and voltage control generally adopt centralized methods [14], instructions are send by central SCADA/EMS to the actuators that are scattered around to implement. However, centralized secondary control has high computation capability, working, and communication reliability requirements for the central controller and communication system. Contrary to this, most of the measurement, computation, communication and control tasks in distributed control [10,11,12,13] are carried out in local; secondary function is realized in local DGs. Multi agent is an intelligent control system, its inherent distributed characteristics fit MG’s distributed and hierarchical control demands [15,16,17,18]. To implement distributed secondary frequency and voltage restoration control, this paper proposes multi agent based smart MG. Smart MG [19] adopts hierarchical control method [1,3,5,6]. The method contains three layers which are primary, secondary and tertiary. In smart MG, the distributed secondary restoration function is carried out in local DG agents. The agents communicate and cooperate with each other to obtain other DGs’ frequency, voltage and output power information and adopt PI controller to restore frequency and voltage. Frequency and voltage stabilization, active and reactive power sharing functions mentioned above are also implemented in local DG agents, in which the variable droop curve algorithms are realized dynamically and autonomously. The communication requirement is low and working reliability is high [16,17]. If noncritical faults happen, MG can keep supply loads and realize its secondary restoration function.
The main contributions are as follows.
- (1)
- A new smart MG which is closely integrated with the inner and outer control loops of inverter is presented.
- (2)
- Several new agent functions are defined and utilized in MG.
- (3)
- A novel SOC based auto-revised P-f droop curve and self-adjusted Q-U droop curve—variable droop curve strategies, taking ESS energy resource abundance into consideration and realizing reactive power sharing, are proposed.
- (4)
- The proposed variable droop curve adjustment algorithms are implemented autonomously in local. Secondary frequency and voltage restoration function are also carried out in local in decentralized ways. Secondary control working reliability for MG has been improved.
This paper is organized as follows. In Section 2, multi agent based smart MG and its functions are introduced. In Section 3, the SOC based distributed frequency control strategy is proposed. Section 4 introduces the distributed voltage control strategy. In Section 5, the proposed approaches are tested and results are given. Finally, Section 6 gives the conclusions.
2. Multi Agent Based Smart MG
From the perspective of structure, agent based smart MG [15,16,17,18,19] has three control levels. On the bottom level is the micro source, inverter interface and corresponding control system based local agents; on the middle level is the communication system based SCADA agent; on the top level is the agents based smart system, as shown in Figure 1. From the perspective of constitution, the smart MG contains dis-patchable and non-dispatchable DG agents, intelligent house agents, load agents and sub-MGs. Dis-patchable DG agents could adjust their output power according to command or autonomously, however, non-dispatchable DG agents’ output power are determined by their resource conditions. The agents are intelligent and capable of responding to external events, having clear control objectives. SCADA agent, DG agents, Load agents, Intelligent House agents [19] and Energy Management System (EMS) agent [20,21] communicate and interact with each other autonomously and form a small-scale smart MG system. The networked structure greatly improves the reliability of communication. The smart MG can operate in standalone or inter connected mode. In standalone mode, dis-patchable DG agents operate coordinately and autonomously to maintain MG active and reactive power supply-load demands balance and keep system frequency and voltage stable; in connected mode, the MG can accept utility grid SCADA/EMS or dispatcher’s schedule commands, then reply to it, and based on its own control objectives, make tie-line exchange power, following the schedule. There is no need for manager’s direct participation.
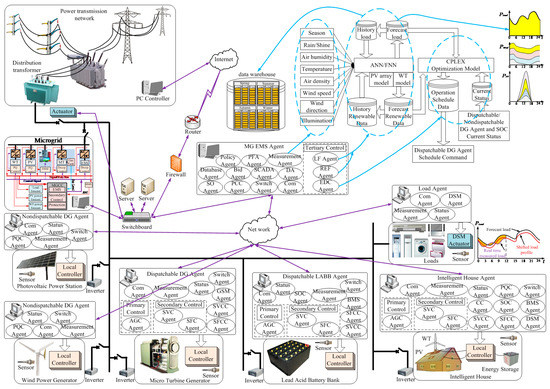
Figure 1.
Multi agent based distributed smart micro grid (MG).
2.1. Smart DG Agents
Dis-patchable DG agents generally contain four main parts, (1) MT or ESS based power source and corresponding control circuits; (2) voltage source inverter (VSI) power electronic interface and corresponding control circuits; (3) voltage and current measurement circuits; (4) communication systems. In ESS based dis-patchable agent, the cascaded DC/DC converter before the VSI is bidirectional, therefore this agent could release and store energy as needed. In the bottom level controller of VSI, the inner control loop adopts PQ decouple control method, the outer control loop employs P-f and Q-U droop control methods. Applying droop control, power set points of the droop curve are set by EMS agent, following the operation schedule. Using the droop curve, dis-patchable DG agents could operate in parallel and share active/reactive power according to their rated capacities. When net load power demands change, dis-patchable DG agents change their power accordingly rapidly to keep load demands-power supply balance and stabilize frequency and voltage autonomously. After the new balance is reached, DG agents’ terminal frequency and voltage would have changed. To improve power quality, secondary restoration function is realized in VSI outer control loop to restore them within normal range. For the sake of increasing information reliability and reducing total processing time, during the regulating process, locally measured terminal voltage/current amplitude and phase information are directly processed in the local DSP controller.
Non-dispatchable DG agents contain WT or PV arrays as their power source, and have VSI, measurement, controller and communication circuits as well. Due to WT and PV output power having high randomness and low controllability, their power output cannot follow dispatch commands and are determined by renewable energy resource conditions. In the agent, MPPT algorithm is adopted to track maximum possible power and maximize renewable energy utilization in DC/DC converter control loop. In VSI inner control loop, PQ decouple methods are applied to directly control output active and reactive power.
Intelligent House agent is a small-scale smart MG. It contains household electric appliance loads, WT, PV, LABB, sensors and smart controller etc. Based on sensors’ real time measured information and smart controller’s preset control logic, all parts of intelligent house could coordinate with each other and make the life of humans smarter and more comfortable.
Load agent has household electric appliances, agricultural and industrial use motors, etc., as its loads. It contains local Demand Side Management (DSM) [22] actuator to directly shift some controllable loads at peak load times to decrease total load demands. In addition, load agent switches on some loads that have energy storage functions at valley load times to decrease the peak-valley difference. In case of an urgent shortage of power supply, DSM actuator directly curtails some noncritical loads to increase critical loads power supply reliability.
2.2. Agent Functions
Agent functions in smart MG [15,16,17,18,19] are as follows.
Com agent and SCADA agent are responsible for gathering and transmitting DG agents’ terminal voltage, current and other information, and deliver control commands and data between EMS and DG agents, among DG agents, and to corresponding actuators.
Measurement agent measure and sample voltage, current and all necessary information.
PQC agent applies MPPT algorithm to control interface VSI, maximizing non-dispatchable DG agent’s output power and curtailing some renewable power according to command.
AGC agent is based on set points information released by EMS, in its inner VSI adopting P-f and Q-U droop control methods to instantaneous satisfy load active and reactive power demands, and stabilize MG frequency and voltage. The most important function of AGC agent is adjusting its P-f and Q-U droop curve dynamically and autonomously to realize active and reactive power sharing functions according to needed information, for instance, SOC, active and reactive power, etc.
Secondary frequency control (SFC) agent shifts P-f droop curve to restore MG frequency to rated value and improve power quality.
SFCC agent acquires dis-patchable DG agents’ terminal frequency values information and send calculated average value to SFC agent to control frequency.
Secondary voltage control (SVC) agent shifts Q-U droop curve to restore voltage within allowable range and improve power quality.
SVCC agent gathers dis-patchable DG agents’ terminal voltage and reactive power value information. Then it sends average value and expected reactive power value to SVC agent and AGC agent to revise droop curve.
LF agent and REF agent forecast day-ahead short/ultra-short load demands, and PV and WT power according to historical data and real time measured weather data.
EDC agent generates dis-patchable DG agents’ economic dispatch schedule according to forecast load and renewable data, optimizing MG operation and improve long term economy.
DSM agent could directly curtail some controllable loads to reduce peak valley difference and help maintain supply critical loads.
SOC agent real-time supervises LABB state of charge value. Control the charge/discharge process of LABB to prevent it from running out of normal range.
BMS agent prevents LABB from overcharge/discharge, and optimizes its charge/discharge procedure to maximize service life.
Switch agent executes the smooth transition process of MG between standalone and interconnected mode, and avoid short time power impact.
Status agent judges current and voltage etc. inside status, based on measured information.
PCC agent controls tie-line power between smart MG and utility grid.
CC agent is responsible for the coordination control of exchange power between intelligent house and MG.
PFA agent analyzes MG’s power flow and decides whether and when the schedule is islands or reconnects to utility grid.
Database agent stores weather, history/forecast load and renewable power data and other operation commands and voltage/current information. Call them out if necessary.
Data analysis (DA) agent analyzes all needed and useful operation information to help MG investor to decide whether to expand its scale or down scale.
Gas storage management (GSM) agent monitors MT natural gas tank pressure in case of leakage, and manage gas valve opening and closing process.
Policy agent acquires the operation, consumes large scale renewable energy and increases critical loads power supply reliability reward policies sent by utility grid EMS.
Bid agent sends electricity average price, peak and valley price, which are decided by MG facility total investment, depreciation and fuel consumption expense, to utility grid.
System operation (SO) agent, keeps the whole smart MG to operate stably and normally; accepts power system SCADA/EMS dispatching instruction and sends it to PCC agent; releases MG standalone/interconnected operation mode transition signal based on distribution network operation state; applies tertiary control and releases tie-line exchange power command. Smart MG integrated overall operation function is shown in Figure 2.
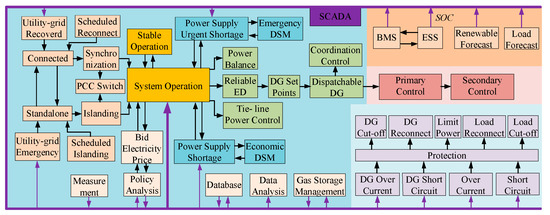
Figure 2.
Smart MG overall function.
3. SOC Based Distributed Frequency Control
In the operation of standalone MG, dis-patchable DG agents apply P-f and Q-U droop control methods to instantaneously balance power supply and load demands. Induced by load active and reactive power demands and renewable energy power generation volatile and fluctuation characteristic and forecast errors, MG system frequency and bus voltage fluctuate frequently. The actual active and reactive power operation points on the droop curve are deviating from the setting points released by EDC agent. The bottom level control structure of smart MG is shown in Figure 3.
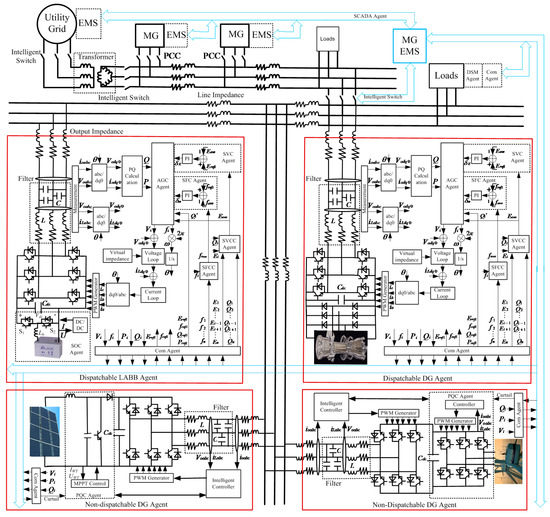
Figure 3.
Smart MG voltage source inverter (VSI) based bottom level control structure.
3.1. SOC Based Auto-Revised Variable Droop Curve Distributed Primary Control Algorithms
Adopting distributed droop control algorithm in AGC agent is shown in Figure 4 and Figure 5. At time period ΓP, operating point of ESS based DG agent is running at rated A0, disturbed by net load variation, actual operating point of this DG stably stays at A1, its active power output increased to Pi[ΓP] to meet increased load demands and consequently frequency decreased to fi[ΓP]. Thus, active power of ESS and MT based dis-patchable DG agents are shared according to their rated P capacities, or in other words P-f droop rates.
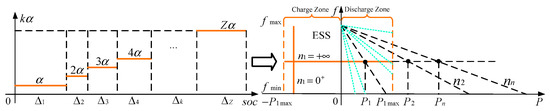
Figure 4.
State of charge (SOC) based variable droop curve change.
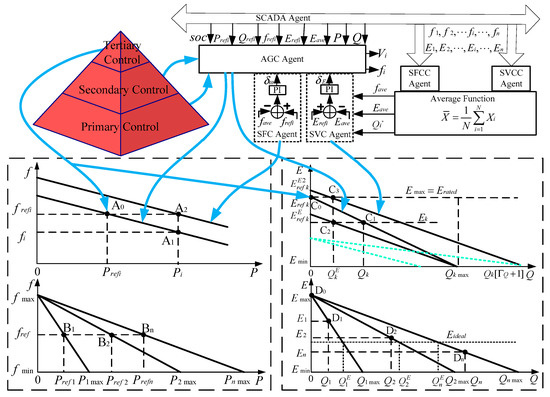
Figure 5.
Distributed primary and secondary control algorithms.
However, at different SOC values, loads supplying capabilities of the ESS based DG agent vary in a large range. For instance, if SOC value is high, the potential capability of this DG to share loads is high, it is reasonable to take more loads and increase droop curve rate. On the contrary, if SOC value is low, this DG should take few loads and decrease droop curve rate to prevent the SOC value from dropping too rapidly. Hence, ESS based DG P-f droop rate is revised dynamically in AGC agent according to SOC values. Ratio of power sharing between ESS based DG and MT based DGs is changed.
Divide the total length of SOC interval into Z parts, except for the 1th and the Zth intervals, the length of the rest Z − 2 intervals are divided into geometric series, but we should note that the total numbers should not be too many, as shown in Figure 4.
Revised droop rate is given by:
In the case that SOC is too high or too low, the slope of the droop curve correspondingly trends to infinity or zero. If SOC > SOChigh, then AGC agent adjust droop rate toward infinity to increase ni[ΓP + τP], larger ni means taking more loads. Bottom level VSI transforms droop control to master-slave control autonomously and assumes all the load and renewable energy generation fluctuation power to stabilize the frequency. Due to the frequency at this time being almost constant, output of MT based dis-patchable DG agents is almost constant as well; the power variance of net loads is compensated solely by ESS based dis-patchable DG agent. However, if SOC < SOClow, then AGC agent adjusts droop rate toward zero and VSI transforms droop control to PQ control to charge the ESS at a constant power. At this time, the agent is not taking part in frequency regulation.
After the process of the droop curve slope adjustment is finished, DG control its output power according to the new droop curve, revised droop curve is formulated by:
Applying droop control, load active power demands are satisfied instantaneously by dis-patchable DG agents in a distributed way. Voltage and current signals that are used for control are measured locally in measurement agent and sent to local VSI DSP controller directly, therefore time delay of control is very short.
3.2. Distributed Secondary Control Algorithms
Utilizing primary droop control method, after load demands are satisfied, although MG frequency is stabilized, frequency is deviated from the rated value. Frequency deviation would affect the normal work of frequency sensitive electric appliances, for instance, electronic devices and motors. Thus, applying secondary control to restore frequency is necessary.
After applying droop control dis-patchable DG agent is running at A1, a short period of time later SFC agent starts to realize secondary control. Local SFCC agent acquires other dis-patchable DG agents’ frequency information, then calculates and sends the average value to SFC agent. SFC agent uses PI controller to control the error between average and rated system frequency to implement secondary control. Finally, the control signals are sent to AGC agent to shift droop curve to reduce frequency error. Due to PI is an error-free control method, system frequency is restored back to rated value and DG’s operating point is changed from A1 to A2.
Note that the secondary frequency control function is carried out in dis-patchable DG agents that are dispersed throughout MG in distributed way. Owing to sampling errors of Measurement agent or malfunction of Com agent, control errors of secondary control are inevitable. Benefited from distributed algorithm and the average function in SFCC agent, the errors can be reduced and the frequency control accuracy can be improved.
3.3. Active Power Sharing Algorithms
Large-scale MG generally has several PV/WT based non-dispatchable DG agents and MT/ESS based dis-patchable DG agents. These DG agents’ total generating capacities must be greater than maximum load demands to ensure load power supply. At extreme conditions in which non-dispatchable DG agents’ power output is zero, dis-patchable DG agents must remain supply critical loads.
Value of β is important. The larger means MG can supply more critical loads, the smaller indicates Load agent can curtail more noncritical loads, and asset owner can pay less MG initial investment, but power supply reliability will decrease.
DG agents power supply—Load agent power consumption balance equation:
Active power sharing algorithm:
Despite net load fluctuating continually, due to DG Agents’ terminal frequencies being almost the same, all running dis-patchable DG agents’ active power output are shared according to their revised droop rates instead of their rated maximum power capacities. In the power sharing functions, frequency rated reference set point frefi[ΓP] is released by EDC agent and generally is 50 Hz, actual frequency fi is measured locally.
Note that, for the sake of sampling errors and other reasons, sampled frequency values of DGs’ are not strictly equal to their actual values, power cannot be accurately shared. Applying average algorithm in SFCC agent the power sharing accuracy can be increased.
4. Distributed Voltage Control
Q-U droop control method [6,15,16] is implemented in AGC agent to keep MG reactive power output-reactive load power demands balance and maintain voltage amplitude stability.
4.1. Distributed Primary Control Algorithms
At initial kth dis-patchable DG agent is running at C0, its reactive power output is zero and voltage amplitude is at maximum value, as is shown in Figure 5. A short period of time later load reactive power demands increase to Qk[ΓQ + υQ] and voltage decreases to Ek[ΓQ + υQ], DG’s operating point changed to C1. Through the effort of DG of stopping voltage amplitude from dropping, load reactive power demands are instantaneously satisfied. Voltage amplitude value is serving as a media for local DG to acquire load reactive power demands information in the decentralized method.
4.2. Self-Adjusted Variable Droop Curve Reactive Power Sharing Algorithms
Under ideal conditions dis-patchable DG agents’ self-adjusted Q-U droop curve reference voltage values and terminal output voltage values are respectively same, as a result these agents could share reactive power according to their capacities.
Expected reactive power sharing amount of dis-patchable DG agent k is given by:
Actual reactive power sharing amount of dis-patchable DG agent k is given by:
However, affected by three main factors, (1) line impedances between DG agents; (2) VSI output impedance and line impedance of DG agents; (3) different reactive power output of DG agents, voltage drops on impedances are different. Under steady state, DGs’ terminal voltage are different and generally are not equal to expected voltage values, therefore disable dis-patchable DG agents to share reactive power.
To make dis-patchable DG agents share reactive power Qk[ΓQ + υQ] = [ΓQ + υQ], adjust Q-U droop curve droop coefficients and voltage reference values dynamically in AGC agent, self-adjusted Q-U droop curve is formulated by:
The crossover point of Q-U droop curve and E coordinate axis are reactive power and voltage reference values pair. For ease of calculation,
Adopting the self-adjusted Q-U droop curve in Equation (32), reactive power is shared according to DG agents rated maximum reactive power capacities (or self-adjusted Q-U droop rate).
During the process of revising primary Q-U droop curve, kth dis-patchable DG agent acquires other n − 1 dis-patchable DG agents’ output reactive power information through SCADA agent and Com agent, and sends it to SVCC agent to calculate [ΓQ + υQ] and other data. Then AGC agent uses them to calculate [ΓQ + υQ + τQ] and [ΓQ + υQ + τQ] to revise Q-U droop curve and realize reactive power sharing function. The process is implemented in local AGC agent in a distributed way, if some communication lines are interfered or disconnected, power sharing accuracy is affected but load demands could still be satisfied, therefore power supply reliability is high.
4.3. Distributed Secondary Control Algorithms
After finishing primary control, secondary control is carried out to increase power quality. At initial kth dis-patchable DG agent is running at C1, after adjust Q-U droop curve DG agent is running at C2, DG’s actual terminal voltage is Ek[ΓQ + υQ + τQ] (Ek[ΓQ + υQ + τQ] ≠ Erated). A short period of time later SVC agent starts to use PI controller to implement secondary voltage restore function and shift the adjusted droop curve.
Adjusted droop curve after secondary control is formulated by:
After shifting revised Q-U droop curve, the crossover point of droop curve and Q coordinate axis namely virtual maximum reactive power capacity Qk[ΓQ + 1], may exceed dis-patchable DG agent’s actual rated capacity. Next period AGC agent applies primary droop control and revises droop curve, replaces Qk max[ΓQ] with Qk[ΓQ + 1] in droop function.
In the process of secondary control, both voltage and current measurement and communication are implemented in local, adjusting droop curve is also carried out in local AGC agent, therefore secondary voltage control function is also realized in distributed ways.
5. Simulation Results
To better demonstrate the effectiveness of the proposed strategies, the MG for simulation contains an ESS based dis-patchable DG agent 1 and MT based dis-patchable DG agent 2 and 3, and corresponding VSI interfaces. Parameters are shown in Table 1. Note that, in practice there is no need to contain three DGs for such a scale MG. MG single phase rated voltage RMS value/frequency is 220 V/50 Hz. Simulations are carried out using MATLAB/Simulink tool box and C++ language. Simulation methods are as follows.

Table 1.
Parameters of P-f and Q-U droop control.
- (1)
- SOC intervals are divided into four, and static droop rate ratios between DG agents are chosen accordingly, seen in Table 1. To better demonstrate the process of droop rate change according to SOC value, actually droop rate ratios are changed for each 5 min.
- (2)
- DGs’ reactive power output results with and without adopting the proposed power sharing strategy are compared to verify the effectiveness of the proposed strategies.
- (3)
- MG frequency and bus voltage with and without applying the proposed secondary control are compared to show the validity of the frequency and voltage restoration strategies.
- (4)
- Agent 1 and agent 3 secondary control failures are simulated respectively to prove that the distributed secondary control has higher operation reliability.
For SOC based static droop rate change, at the beginning of stage 1, SOC is extremely high, droop rate of ESS based DG 1 is set as infinity, and as a result it assumes all the fluctuating power of loads. The constant power of loads is supplied by MT based DG 2 and 3. Frequency supporting task is taken only by DG1. In fact, the control method of DG 1 is constant V/f control and DG 2 and 3 are constant PQ control, the frequency is kept at 50 Hz. In stage 2, static droop rate ratios between DG 1 and 2 and 3 decreases to 1:1:1, consequently power sharing ratios between them is 1:1:1. As SOC continues to decrease, in stage 3 static droop rate ratios between DG 1 and 2 and 3 continue to decreases to 1:2:2. In the final stage, SOC is extremely low and static droop rate of DG 1 is transformed to zero, therefore DG 1 is not involved in frequency control and charging at a constant power, the liabilities of frequency control is taken solely by DG 2 and 3. The overall trend of SOC is continuing to decline from stage 1 to stage 4, static droop rate ratios between DG 1 and 2 and 3 continuing decline from ∞:0:0 to 0:1:1 accordingly, as shown in Figure 6 and Figure 7. Additional results are shown in Figure 8 and Figure 9.
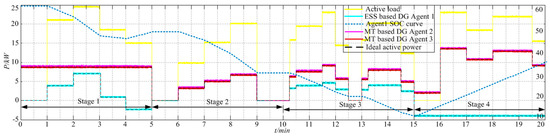
Figure 6.
Active power outputs of DGs applying the SOC based strategy.
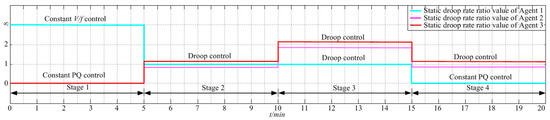
Figure 7.
Static droop rate ratio of DGs.

Figure 8.
MG frequency.
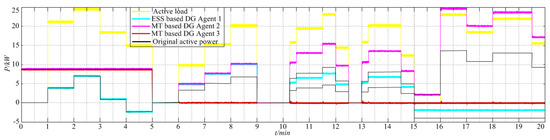
Figure 9.
Active power outputs of DGs when secondary control of DG 3 failure.
For reactive power sharing based dynamic droop rate change, reactive power outputs of DGs utilize only virtual impedance loop are given as comparison in Figure 10a. It is evident that the degree of reactive power sharing accuracy is not satisfactory. Seen in Figure 10b, after slightly and dynamically regulating the droop rates, reactive power sharing accuracies between DGs have been improved.
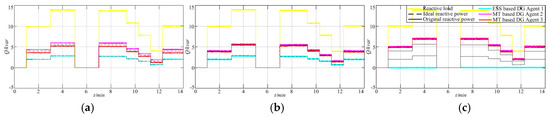
Figure 10.
Reactive power outputs of DGs. (a) Before applying Q sharing; (b) After applying Q sharing; (c) DG 1 secondary control failure.
For improving the power quality of MG, distributed secondary control is applied. MG frequency and bus voltage without secondary control are given in Figure 8 and Figure 11 as comparison. MG frequency and bus voltage after applying distributed secondary control are also given in these figures, which demonstrate that the proposed distributed secondary restoration function can effectively improve the power quality. Because of the frequency curves overlap, one curve moved backwards for nearly 3 seconds intentionally for better display in Figure 8.

Figure 11.
Bus voltage root mean square (RMS) value. (a) Before applying Q sharing; (b) After applying Q sharing; (c) DG 1 secondary control failure.
For working reliability improvement, the decentralized secondary control is used, compared to centralized control method. DG 3 and DG 1 secondary control failures are simulated in P-f and Q-U droop control, as shown in Figure 9 and Figure 10c, respectively. Corresponding frequency and bus voltage are also given in Figure 8 and Figure 11c, respectively. It is shown that by adopting the decentralized methods, frequency and bus voltage restoration functions can also be implemented, and power quality can be improved. However, applying the centralized methods, if central controller failure happens, frequency and bus voltage restoration functions cannot be implemented. Note that, utilizing P-f and Q-U droop control, DGs active and reactive power outputs are directly determined by their terminal frequency and voltage. Due to the secondary restoration functions being carried out only by other two DGs which have no secondary control failures, when frequency and bus voltage are kept near rated value, active and reactive power outputs of DG with secondary control failure is near zero. Static and dynamic droop rate ratio is shown in Figure 12.
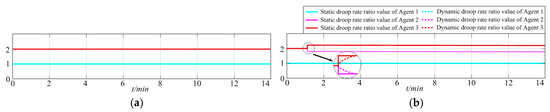
Figure 12.
Static and dynamic droop rates between DGs. (a) Static droop rate ratio; (b) Static and dynamic droop rate ratio.
6. Conclusions
This paper has presented a novel structure and several control strategies for smart MG. In the MG, the salient features of the power sharing control algorithms are taking SOC value and line impedance unbalance into consideration, by means of adjusting droop curve dynamically and autonomously in local agent. In addition, the secondary frequency and voltage restoration functions are realized in local in decentralized ways. Applying the proposed power sharing strategy, the power sharing accuracy has been effectively improved. The needed information is accessed by local agent automatically from other DGs in the decentralized approach. The working reliability of the MG is high. When noncritical faults happen, loads remain supplied and secondary restore function will still be implemented. The proposed power sharing and decentralized secondary control strategies have been successfully tested. Simulation results verified the feasibility of the proposed strategies.
Acknowledgments
This work was supported by National Key Research and Development Program of China (No. 2017YFB0903705, 2017YFB0903700). An earlier simplified and abridged version of this paper was presented at 2017 9th IEEE GCC Conference and Exhibition (GCCCE).
Author Contributions
Yahong Chen wrote the paper. Changhong Deng made suggestions on the whole idea and structure of the manuscript. Jin Tan, Pei Xia, Ning Liang, Weiwei Yao and Yuan-ao Zhang provided valuable materials on the contents of the main body of the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
Functions, variables, parameters, and constants:
| Κ | SOC interval length ratio. |
| Z | Total number of SOC intervals. |
| τP, τQ | Droop curve slope adjustment time τP « ΓP, τQ « ΓQ. |
| υP, υQ | Droop power adjustment time, υP < ΓP, υQ < ΓP. |
| ΓP, ΓQ | Operation period. |
| ε | Step function. |
| β | DSM effect coefficient (0 ≤ β ≤ 1). |
| Prefi[ΓP] | ith (I = 1,2, …, n) DG agent rated active power set point. |
| frefi[ΓP] | ith DG agent rated frequency setting point. |
| Pi[ΓP] | ith DG agent actual active power after primary control. |
| fi[ΓP] | ith DG agent actual frequency after primary control. |
| n0i[ΓP] | ith DG agent initial P-f droop curve rate. |
| ni[ΓP] | ith DG agent auto-revised droop curve rate. |
| Si[ΓP], Bi[ΓP] | ith DG agent on-off status binary variable. |
| x | Arbitrary time value within period ΓP. |
| x P, xQ | Secondary control time. |
| kfp/kfi, kEp/kEi | PI controller parameter. |
| δf, δE | Secondary control droop curve shift coefficient. |
| fave | Sampled frequencies average value. |
| ΔPi | Power induced by loads power-frequency characteristics. |
| Pi max | Rated capacity of ith dis-patchable DG agent. |
| PPVj max | Rated capacity of jth PV agent. |
| PWTk max | Rated capacity of kth WT agent. |
| PLoad max | Maximum load demands. |
| PnetLoad | Net load. |
| Ek[ΓQ + υQ] | kth DG agent actual terminal voltage after primary control. |
| Eref k[ΓQ] | kth DG agent Q-U droop curve reference voltage. |
| Emax[ΓQ] | kth DG agent maximum operating voltage. |
| Erated[ΓQ] | kth DG agent rated operating voltage. |
| Qk[ΓQ + υQ] | kth DG agent actual reactive power output after primary control. |
| Qref k[ΓQ] | kth DG agent Q-U droop curve reference reactive power. |
| mk[ΓQ] | kth DG agent initial Q-U droop curve rate. |
| Qk max[ΓQ] | kth DG agent rated reactive power capacity (crossover point of the initial Q-U droop curve and Q coordinate axis). |
| QLoad[ΓQ + υQ] | Load reactive power demands. |
| Eideal | Expected ideal voltage value. |
| QE k[ΓQ + υQ] | Expected ideal reactive power output of DG agent k. |
| QE ref k[ΓQ + υQ + τQ] | Expected reactive power reference value of self-adjusted droop curve. |
| EE ref k[ΓQ + υQ + τQ] | Expected voltage reference value of self-adjusted droop curve. |
| mE k[ΓQ + υQ + τQ] | Expected droop coefficient of self-adjusted droop curve. |
| Ek min[ΓQ] | Minimum allowable voltage. |
| EE2 ref k | Expected voltage reference value of self-adjusted droop curve after secondary control. |
| Qk[ΓQ + 1] | Next period crossover point of the droop curve and Q coordinate axis. |
References
- Hatziargyriou, N.; Asano, H.; Iravani, R.; Marnay, C. Microgrids. IEEE Power Energy Mag. 2007, 5, 78–94. [Google Scholar] [CrossRef]
- Yoo, H.-J.; Nguyen, T.-T.; Kim, H.-M. Multi-Frequency Control in a Stand-Alone Multi-Microgrid System Using a Back-To-Back Converter. Energies 2017, 10, 822. [Google Scholar] [CrossRef]
- Olivares, D.E.; Mehrizi-Sani, A.; Etemadi, A.H.; Canizares, C.A.; Iravani, R.; Kazerani, M.; Hajimiragha, A.H.; Gomis-Bellmunt, O.; Saeedifard, M.; Palma-Behnke, R.; et al. Trends in Microgrid Control. IEEE Trans. Smart Grid 2014, 5, 1905–1919. [Google Scholar] [CrossRef]
- Li, D.; Zhao, B.; Wu, Z.; Zhang, X.; Zhang, L. An Improved Droop Control Strategy for Low-Voltage Microgrids Based on Distributed Secondary Power Optimization Control. Energies 2017, 10, 1347. [Google Scholar] [CrossRef]
- Guerrero, J.M.; Výsquez, J.C.; Teodorescu, R. Hierarchical control of droop-controlled DC and AC microgrids—A general approach towards standardization. IEEE Trans. Ind. Electron. 2009, 58, 158–172. [Google Scholar] [CrossRef]
- Vandoorn, T.L.; Vasquez, J.C.; Kooning, J.D.; Guerrero, J.M.; Vandevelde, L. Microgrids: Hierarchical Control and an Overview of the Control and Reserve Management Strategies. IEEE Ind. Electron. Mag. 2013, 7, 42–55. [Google Scholar] [CrossRef]
- Rocabert, J.; Luna, A.; Blaabjerg, F.; Rodríguez, P. Control of Power Converters in AC Microgrids. IEEE Trans. Power Electron. 2012, 27, 4734–4749. [Google Scholar] [CrossRef]
- Wu, D.; Guerrero, J.M.; Vasquez, J.C.; Dragicevic, T.; Tang, F. Coordinated power control strategy based on primary-frequency-signaling for islanded microgrids. In Proceedings of the 2013 IEEE Energy Conversion Congress and Exposition, Denver, CO, USA, 15–19 September 2013; pp. 1033–1038. [Google Scholar]
- Wu, D.; Tang, F.; Dragicevic, T.; Vasquez, J.C.; Guerrero, J.M. Coordinated primary and secondary control with frequency-bus-signaling for distributed generation and storage in islanded microgrids. In Proceedings of the IECON 2013, 39th Annual Conference of the IEEE Industrial Electronics Society, Vienna, Austria, 10–13 November 2013; pp. 7140–7145. [Google Scholar]
- Shafiee, Q.; Stefanovic, C.; Dragicevic, T.; Popovski, P.; Vasquez, J.C.; Guerrero, J.M. Robust Networked Control Scheme for Distributed Secondary Control of Islanded Microgrids. IEEE Trans. Ind. Electron. 2014, 61, 5363–5374. [Google Scholar] [CrossRef]
- Micallef, A.; Apap, M.; Staines, C.S.; Zapata, J.M.G. Secondary control for reactive power sharing and voltage amplitude restoration in droop-controlled islanded microgrids. In Proceedings of the 2012 3rd IEEE International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Aalborg, Denmark, 25–28 June 2012; pp. 492–498. [Google Scholar]
- Shafiee, Q.; Vasquez, J.C.; Guerrero, J.M. Distributed secondary control for islanded MicroGrids—A networked control systems approach. In Proceedings of the IECON 2012, 38th Annual Conference on IEEE Industrial Electronics Society, Montreal, QC, Canada, 25–28 October 2012; pp. 5637–5642. [Google Scholar]
- Bidram, A.; Davoudi, A.; Lewis, F.L.; Qu, Z. Secondary control of microgrids based on distributed cooperative control of multi-agent systems. IET Gener. Transm. Distrib. 2013, 7, 822–831. [Google Scholar] [CrossRef]
- Kundur, P.; Balu, N.J.; Lauby, M.G. Power System Stability and Control; McGraw-Hill: New York, NY, USA, 1994. [Google Scholar]
- Oyarzabal, J.; Jimeno, J.; Ruela, J.; Engler, A.; Hardt, C. Agent based micro grid management system. In Proceedings of the 2005 International Conference on Future Power Systems, Amsterdam, The Netherlands, 16–18 November 2005; p. 6. [Google Scholar]
- Liu, W.; Gu, W.; Sheng, W.; Meng, X.; Wu, Z.; Chen, W. Decentralized Multi-Agent System-Based Cooperative Frequency Control for Autonomous Microgrids With Communication Constraints. IEEE Trans. Sustain. Energy 2014, 5, 446–456. [Google Scholar] [CrossRef]
- Mao, M.; Jin, P.; Hatziargyriou, N.D.; Chang, L. Multiagent-Based Hybrid Energy Management System for Microgrids. IEEE Trans. Sustain. Energy 2014, 5, 938–946. [Google Scholar] [CrossRef]
- Meiqin, M.; Wei, D.; Chang, L. Design of a novel simulation platform for the EMS-MG Based on MAS. In Proceedings of the 2011 IEEE Energy Conversion Congress and Exposition, Phoenix, AZ, USA, 17–22 September 2011; pp. 2670–2675. [Google Scholar]
- Byun, J.; Hong, I.; Park, S. Intelligent cloud home energy management system using household appliance priority based scheduling based on prediction of renewable energy capability. IEEE Trans. Consum. Electron. 2013, 58, 1194–1201. [Google Scholar] [CrossRef]
- Kanchev, H.; Lu, D.; Colas, F.; Lazarov, l.; Francois, B. Energy Management and Operational Planning of a Microgrid with a PV-Based Active Generator for Smart Grid Applications. IEEE Trans. Ind. Electron. 2011, 58, 4583–4592. [Google Scholar] [CrossRef]
- Palma-Behnke, R.; Benavides, C.; Lanas, F.; Severino, B.; Reyes, L.; Llanos, J.; Sáez, D. A Microgrid Energy Management System Based on the Rolling Horizon Strategy. IEEE Trans. Smart Grid 2013, 4, 996–1006. [Google Scholar] [CrossRef]
- Saad, W.; Han, Z.; Poor, H.V.; Basar, T. Game-Theoretic Methods for the Smart Grid: An Overview of Microgrid Systems, Demand-Side Management, and Smart Grid Communications. IEEE Signal Process. Mag. 2012, 29, 86–105. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).