Abstract
Thermal response test (TRT) is a common procedure for characterization of ground and borehole thermal properties needed for the design of a shallow geothermal heat pump system. In order to investigate and to develop more accurate and robust procedures for TRT control, modelling, and evaluation in semi-permeable soils with large water content, a pilot borehole heat exchanger was built in the main campus of the Universitat Politècnica de València. The present work shows the results of the experiments performed at the site, analysing the improvements that have been introduced both in the control of the heat injected during TRTs and in the methods to infer the ground thermal parameter. Three models are compared: two based on the infinite-line source theory and one based on the finite-line source scheme. The models were tested under two possible configurations of the equipment, i.e., with and without strict control of injected heat. Our results show the importance of heat injection control for a robust parameter assessment and the existence of additional heat transfer processes that the used models cannot completely characterize and that are related to the presence of significant groundwater flow at the site. In addition, our experience with the current installation and the knowledge about its strengths and weaknesses have allowed us to design a new and more complete test-site to help in the analysis and validation of new ground heat exchanger geometries.
1. Introduction
The characterization of ground thermal properties using in situ thermal response tests (TRTs) [1] is a common procedure for designing HVAC systems based on geothermal heat pumps. TRT is particularly necessary in large size installations, where an inappropriate design of the borehole heat exchanger will mean a poor performance of the system in the case of being undersized or an unjustified cost overrun in the case of being oversized.
TRT is based on the thermal response of a BHE to a steady, several days long, heat injection, or extraction pulse [2]. The most relevant variables measured in a TRT are the temperature of the heat carrier fluid at the input and output of the heat exchanger, taken throughout the execution of the test. Comparing these experimental data against a model that describes heat transfer between the fluid and the ground, thermal properties of the ground can be estimated. The Kelvin infinite line source (ILS) model of conductive heat transfer is the most widely used for evaluation of the data acquired in a TRT for reasons of simplicity and speed [3,4]. However, many concerns about its applicability, reliability, and robustness have been raised through the years and different approaches and corrections to specific issues have been proposed including the effects of heat transfer with the ambient [5], effects due to the finite length or the geometry of the BHE [6,7,8], statistical effects due to varying heat transfer rates, presence of groundwater [9], etc.
In literature, it is more usual to find studies of numerical models that simulate the thermal interaction between borehole and ground rather than experimental studies, partly due to the cost and complexity of such experiments [10].
Due to the lack of experimental data, at Universitat Politècnica de València (UPV) we decided to build a BHE test-site dedicated to research and teaching [11] that was constructed in 2010 with National Research Energy Plan (ENE2008-00599) funding [12]. Since then, we have been using this facility to carry out different experimental programs to systematically asses relevant aspects in TRT testing, ranging from a typical four-day test to much longer experiments.
In the first experiments, the same control techniques as in portable TRTs were used. This allows a check of the performance of accepted BHE models like the infinte line source (ILS) [13] and the finite line source (FLS) [6]. In a second phase, the system was improved by introducing a Proportional–Integral–Derivative (PID) controller to keep the injected heat rate constant, independent of the influence of ambient temperature. This has enabled validation of new or modified BHE models [5] and to verify the performance improvement of other models with minimum modification of the installation.
This paper presents the comparison of the data obtained in the first TRTs performed without controlling the injected power with those recorded in the tests carried out with a PID control that regulated the power injected in the borehole.
2. Method
2.1. Description of Borehole Heat Exchanger
The BHE is located inside the Valencia city UPV campus(392846.4 N and 02014.8 W and at 0 m above the sea level) at a distance of 1200 m from the Mediterranean Sea. It also includes a hydraulic system and a control and monitoring system. The following sections contain a summarized description, and a more detailed explanation about the construction and subsequent modifications of the test site can be found in [14].
Figure 1b shows the horizontal layout of the borehole heat exchanger. The borehole has diameter of 160 mm and metal casing. The diameter of each U-pipe is 40 mm, being its centre 50 mm distance from the centre of the metallic cylinder. To maintain this horizontal layout structure, spacers are located every meter along the whole length of the U-pipes.
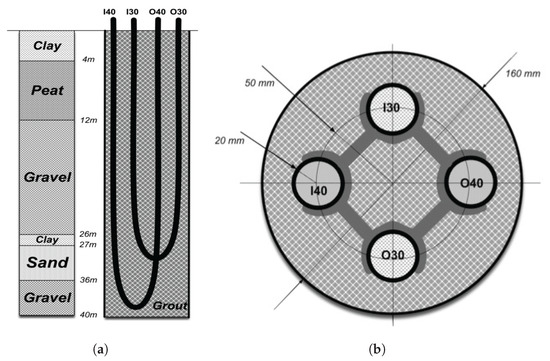
Figure 1.
Diagram showing: (a) the vertical layout of the borehole, indicating the underground stratigraphy and (b) the top layout with the position and diameter of installed pipes.
The BHE is 40 m deep and is composed of an inserted double-U pipe. Due to difficulties during its insertion, the first U-pipe depth is only 29.5 m, while the second U-pipe depth is 39.5 m (see Figure 1a). Although both two pipes are functional, only the longest one was used in the experiments described in this work.
The borehole was grouted with a mixture of one part of bentonite and twelve parts of cement (CEMEX 32.5 raff). This mixture was chosen because it is particularly appropriate for grounds with a significant presence of groundwater, as is the case of the coastal areas.
Samples were collected while drilling, providing a good insight into the ground layer structure (Figure 1a).
2.1.1. Hydraulic Components and Sensors
The basic scheme with the main components of the hydraulic system and the sensors location can be seen in Figure 2a. There is a water intake connected to the water supply network to fill the installation and a drain valve to empty it. As the installation is in a garden, the water can be drained directly into the ground (Figure 2b). In any case, filling and draining are manual actions that are performed only occasionally.
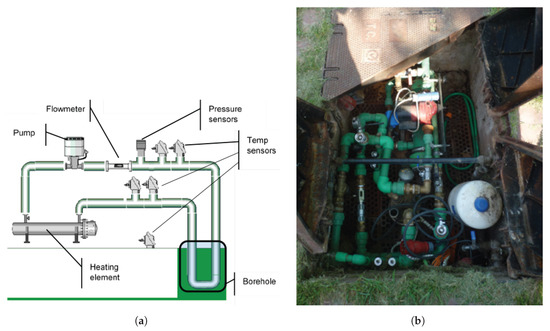
Figure 2.
Hydraulic system: (a) basic diagram and (b) actual installation.
To generate the heat rate required to inject during the test, there is an electric immersion heater with a maximum electric output power of 3 kW. Water circulation is ensured by a centrifugal impeller pump GRUNDFOS MAGNA 25-60-180 [15].
Table 1 lists the sensors installed in the hydraulic circuit where, like in any TRT installation, the most sensible measurement is the inlet and outlet temperatures into the borehole. To increase reliability, we installed redundant temperature sensors and performed a careful calibration program. Additionally, when reading sensor signals, a current loop is preferred over direct voltage measurements in order to minimize any electromagnetic noise due to the used cables lengths (several meters) and the environment.

Table 1.
List of the sensors and their main characteristics.
2.1.2. System Control and Data Acquisition
System control and data acquisition is based on a PLC Siemens Simatic S7-1200 [19] outfit with three analogue input/output modules to receive and interpret sensor signals. These modules include analogue and digital outputs, used to control the electric immersion heater and the circulation pump.
An Ethernet connection allows the programming and monitoring of the system remotely, allowing the change of the TRT parameter settings and the modification of the state of the different variables and signals that the PLC handles. An additional functionality is the incorporation of a web server with an internal website (only available through intranet) divided into two categories: management and user pages. The first one serves to modify the operation of the PLC and to check its status. The user page enables one to remotely write and read the main PLC variables. In our case, we have defined two sections: the first one provides an interface to the current status of the sensors and the second one allows one to set the operating parameters of each thermal test. The configurable parameters are:
- (i)
- the state of the pump (on or off)
- (ii)
- the type of control for the electric immersion heater: PID or a manual
- (iii)
- the reference for internal PID heating control (heat injection rate in kW) or manual setting (fixed rate of use of the electric immersion heater in percentage)
- (iv)
- the sample period for data acquisition in milliseconds
2.1.3. Setting of a TRT Experiment
When an experiment starts, the data from the sensors and the time are logged on the PLC. This log can be downloaded using any web browser or by a web downloading tool, e.g., curl or wget. PLC storage capacity limits the log size to 2048 entries, whereby a log download can be performed at any time without destroying data, which remain afterwards stored in the PLC.
Currently the pump drive control is an on/off type, allowing the user to decide whether the pump has to be running or not. The PLC signal that activates the pump is directed to a three-phase relay that switches the pump with a response time much faster than the rest of the system.
In contrast, to control the electric immersion heater a PID controller has been implemented in the PLC. The PID block generates a control signal between 0% and 100% that is sent to an electric current modulator that performs a pulse width modulation (PWM) in order to actuate the 3 kW three-phase electric immersion heater. According to the requirements of the experiment, the PID can be configured in two possible settings. For the first configuration, the PID input (control variable ) is the difference between the readings of the borehole inlet and outlet temperature sensors. For the second set-up, the reference is the power to be injected into the borehole, taking into account in this case, the temperature difference and the water flow.
The main role of the aforementioned control scheme is to keep the heat injection rate into the ground as stable as possible within the duration of the entire TRT test, as will be described in detail in the following sections.
2.2. Experiments Description
Table 2 summarizes the main characteristics of the TRT experiments presented in this work and performed since 2010. All experiments performed are heat injection tests, which in principle require the heat injection rate into the ground to be as constant as possible. In this regard we should distinguish early tests, where the electric immersion heater was operated at constant power without regard to the ambient temperature influence, from more recent tests, in which the effect of ambient temperature was minimized by using the PID control scheme to stabilize heat injection into the ground.

Table 2.
Brief description of included experiments. Column Control indicates what system has been used to control the injected heat rate as described in the above section. Column Reference indicates the power used to operate the electric immersion heater when no control is used or the set-point for PID controller.
The duration of the tests performed is variable but, in any case, longer than the usual 72 h requested for commercial-use TRTs done by means of mobile devices. The longest test performed so far lasted 31 days, but for the purpose of parameter identification in this work we have chosen to use exclusively the first 84 h of each test to make our analysis comparable between the different sets of data and also with the recommendations included in the current Standards such as the IEA-ECES Annex 21 Final Report, see [20].
2.2.1. Raw Data Description
From all the sensors in the system [14], we will use:
- : temperature at the inlet of the borehole
- : temperature at the outlet of the borehole
- G: water flow
- : ambient temperature
The heat flow (Q) is calculated from the above variables and the volumetric heat capacity of water (), using the following equation (for measuring units see Abbreviations table):
Table 2 summarizes the most representative heat transfer statistics for each of the experiments. Figure 3 shows a signal time plot where the variability of temperature signals obtained at various heat injection rates for both modes of control is depicted.
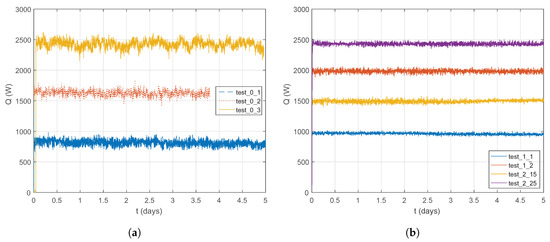
Figure 3.
Time plot of heat injection flow rates obtained in the different TRT experiments: (a) using a fixed amount of energy on the heating element and (b) using a PID to control the injected heat flow rate.
The observed variability can be attributed to the fluctuation in the environmental temperature, as clearly shown in Figure 4. temperature fluctuations correlate with changes in .
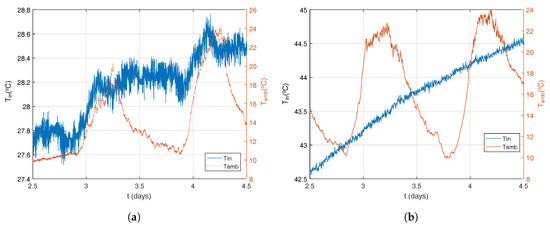
Figure 4.
Comparing ambient temperature effect: (a) when there are no automatic control on injected power and (b) using a PID to maintain stable the amount of injected heat rate.
The raw outcome of selected TRT experiments is shown in Figure 5, Figure 6, Figure 7 and Figure 8. In some of these sets there is information about the temperature evolution of the sensors prior to TRT start up (see e.g., Figure 6, where almost one day of previous information was collected).
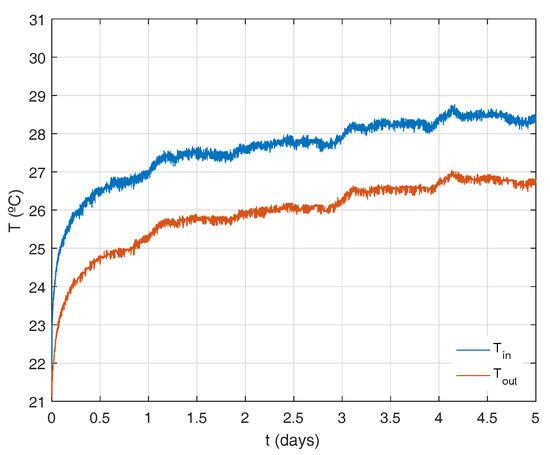
Figure 5.
Input and output temperatures for experiment test_0_1.
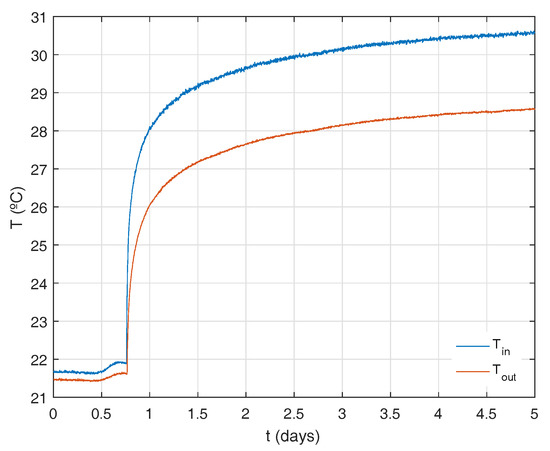
Figure 6.
Input and output temperatures for experiment test_1_1.
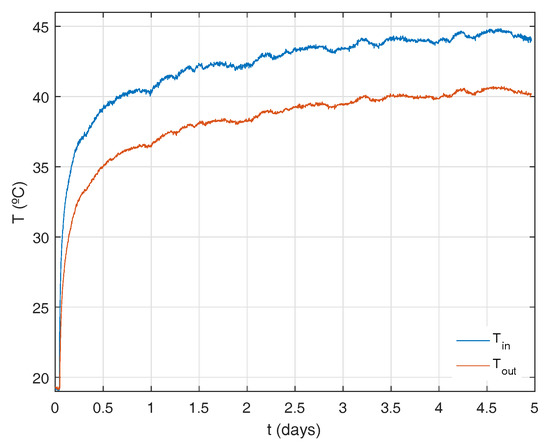
Figure 7.
Input and output temperatures for experiment test_0_3.
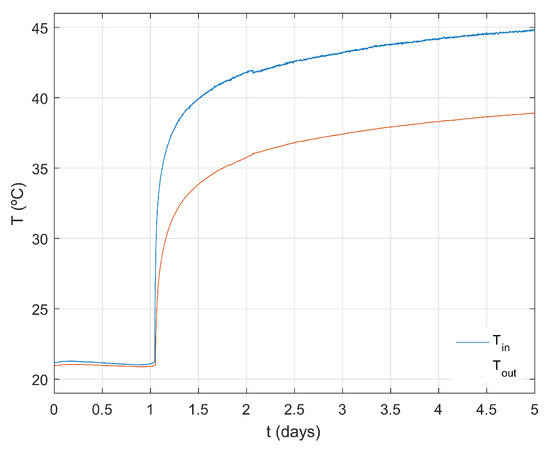
Figure 8.
Input and output temperatures for experiment test_2_25.
2.3. Data Processing
The dataset consist of two parts, before and after the start of heat injection. Data before injection can be useful to gather information about the undisturbed underground temperature. Data recorded during the heat injection form the basis for the parameter identification algorithms we will describe in the next sections.
A basic process variable is the mean temperature in the BHE, T, calculated as the average between and , considering the sensors closest to the inlet, and outlet of the BHE. The injected heat rate is calculated for each time bin using Equation (2), averaged over the complete time series to determine the value to be used within the models.
2.4. Application of Different Analytic Models to TRT Data
2.4.1. Infinite Line Source Theory
According to the well established Kelvin ILS theory [13,21], the time evolution of the mean temperature in the BHE could be represented by a semi-infinite linear heat source surrounded by a solid heat transfer medium of heat conductivity , at initial homogeneous temperature . The line source is supposed to inject heat at a constant heat rate per unit length of (assimilated to the experimentally obtained heat injection rate of the actual heat source, Equation (2)). The axisymmetric, exact, solution for the temperature at any point located at the distance from the line is given by an expression involving the error function, which is usually substituted by the following widely used approximation:
where represents the borehole resistance of the BHE when equals the borehole radius, (see [1] for details).
For infering values of and , one can linearise the above expression or use a LSQ approach (see Section 2.4.2). With respect to the first option, we can express Equation (3) in the linear form:
where
and b is the borehole heat resistance, , and a is connected to the equivalent ground conductivity by:
The linear form allows us to compare experiments made with different heat injection rates. Ideally, all possible TRT experimental data would fall on the same line in the y–x representation , if Equation (4) would hold strictly. We used, as undisturbed ground temperature, the value of C, derived from the extensive analysis of temperatures in the boreholes as described by [12]. This transformation result is shown in Figure 9.
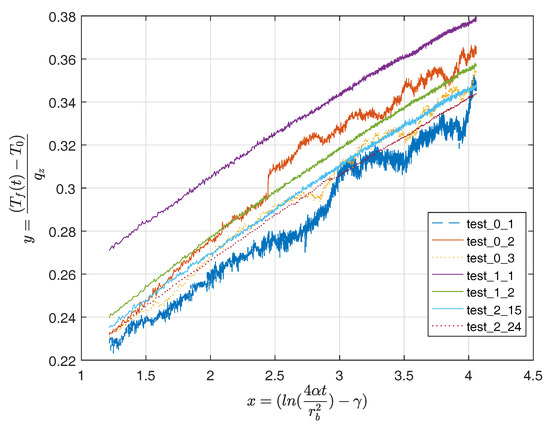
Figure 9.
Graphical representation of measured data once it is transformed using Equation (5).
The slopes are similar and it is easy to identify the tests performed with a PID control. There is however a clear shift, even in the cases where the controller is acting, between the vertical position of the curves in the diagram, pointing to a different value in each case. This is due to the fact that the hypothesis of a constant undisturbed soil temperature from one experiment to another is only an approximation. For instance, the curve corresponding to test_1_1 is the one that more clearly departs from the rest in terms of b, as measurements were carried out in October, when highest underground temperatures in the soil are recorded.
The results of the fitting procedure for a and b are shown in Table 3. The same table shows and from Equations (6) and (5), with their respective confidence intervals ( and ) calculated using equations:

Table 3.
Values of coefficients of Equation (4), thermal parameters and confidence intervals as inferred with the Infinite Line Source Model (ILS) method.
If we compare the confidence intervals obtained for the soil conductivity and , the advantage of using the PID control is clear (Table 3).
2.4.2. Least Square Approach with FLS and ILS
We attempted to determine whether finite length corrections, as included in the FLS model [6], can improve parameter estimation. The most suitable expression with the correction due to the finite-length of the line source adds an additional term to the basic ILS expression. Using this correction, adapted from [6], Equation (3) becomes:
where and is the so-called “long time scale” related to the length of the borehole. In the case of our test, and thus all the tests conform to the intermediate time scales, within which the above expression is valid.
LSQ methods, based on either Equation (3) or Equation (8) can give the values of and , directly minimising the error between experimental data and the ILS or FLS models. On the other hand, the method based on linearising the ILS model, hereinafter the ILS line method, is based on the identification of lines defined by Equations (4) and (5), and then uses Equation 6 for obtaining and . The results of all tests together with the confidence intervals of the inferred parameters are shown in Table 4. Values for thermal diffusivity, m s and undisturbed initial temperature C are assumed in all cases.

Table 4.
Thermal parameters inferred with ILS line method and the Lest squares fitting algorithm (LSQ) method for ILS and FLS models.
The values of underground thermal conductivity obtained with the LSQ method range between 1.80–2.08 Wm K. Excluding test_0_2, with the largest uncertainties (in terms of confidence intervals and MSE), the interval closes up to 1.88–2.08 Wm K, considering only ILS models, and 1.91–2.11 Wm K, considering FLS models. There is thus a small but systematic increase of the thermal conductivity values whether we consider FLS corrections or not.
Figure 10 presents another interesting view, comparing optimized model prediction with measured data for two of the experiments with similar heat injection, without (Figure 10a) and with automatic PID control (Figure 10b). Qualitatively, theoretical and experimental results show a similar agreement in the rest of the analysed cases. Although there is seemingly a good correlation between theory and experiment, specially in Figure 10b, it can be appreciated that a slight systematic deviation is present at the end of the 3.5 day period, where experimental data tend to fall somewhat below the theoretical predictions of either ILS and FLS models. In the next section this effect will be discussed more in depth.
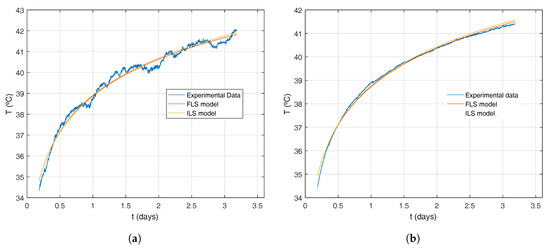
Figure 10.
Experimental data against ILS and FLS model prediction for experiments with (a) 3 kW fixed heat rate and (b) 2.5 kW controlled heat rate.
It is interesting to compare the squared errors for all the considered models (Figure 11), derived according to the following expression:
where y is the measured data vector and is the corresponding calculated value at each time point using any of the considered models. We can conclude that the best model adequacy is obtained for FLS model and LSQ approach improves the result compared to the linearised equation in the case of ILS models.
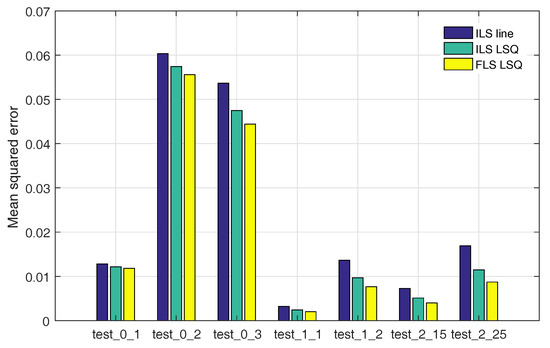
Figure 11.
Squared mean error for each method and test.
Furthermore, PID controlled experiments tend to behave much better in this respect. The only dataset without PID control that shows similar error values compared to tests with PID is the experiment in which the least power was injected. It is also the least noisy experiment in terms of influence of the ambient temperature fluctuations. Although connection pipes are not well insulated in the case of our test rig, their length is comparatively small (less than 1 m) because of its compactness. This shows the difficulty of isolating ambient effects in normal TRT settings and the importance of an adequate control scheme for parameter extraction.
2.5. Model Adequacy and Long Term Effects
In regards to the improvement of the traditional TRT methods, the inclusion of a PID to control heat injection achieves its objective by smoothing the effects of ambient temperatures (see Figure 3 and Figure 4). In this way, the constant injected heat rate requirement of ILS [4,13] and FLS [6] methods is satisfied and, hence, it is possible to avoid the need for further processing of data as proposed by [5].
For a deeper analysis of model adequacy, Figure 12 shows the evolution of residuals—the difference between predicted and actually measured data—with time for the FLS-LSQ models (the one that shows the best adequacy overall). If non-PID controlled tests are considered (Figure 12a), the residual timeline resembles the noisy pattern of the curves (as in Figure 4a). These ambient temperature influences may mask other effects, errors, or sources of information present in the residuals. Clearly, the use of a PID control reduces the residuals (Figure 12b) and isolates them from ambient effects. In Figure 4a a common pattern appears that only can be attributed to some systematic inability of the used models to capture some intrinsic system behaviour.
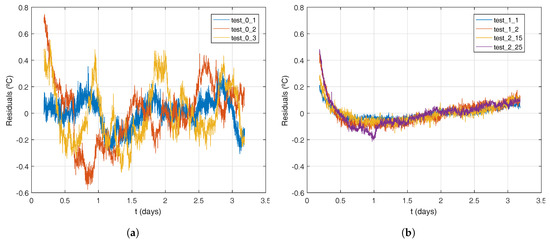
Figure 12.
Temperatute residuals (in C) versus time (in days) for: (a) tests with traditional setup and (b) tests with controlled heat injection rate.
If we consider longer tests, a legitimate question is how do these systematic effects behave? We can see for test_2_25 that the model obtained with 3.5 days experiment data fits very well to data (Figure 13a), but if we use that model against a longer run, the result is not so good (Figure 13b). Figure 13b shows a systematic overestimation of temperatures predicted by the models as compared to the data, a pattern that is clearer in longer test durations (data not shown).
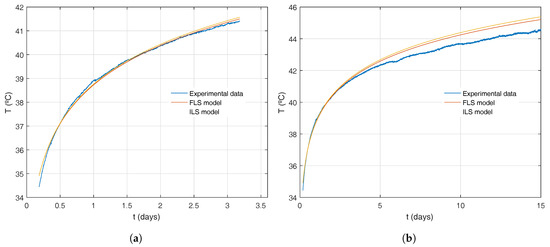
Figure 13.
Experimental data against ILS and FLS model prediction for experiment test_2_25. Using the same three days obtained model for (a) comparing only the first 3 days and (b) comparing 15 days.
It can be concluded that the ILS and FLS models are accurate and precise within the usual test duration but do not describe other heat transfer mechanisms present in longer term tests, at least in the case of our installation. At our test site, groundwater is present and, as discussed in several articles [9,22,23], groundwater flow effects can affect observed temperature patterns, although effects are usually visible in longer duration tests. To more precisely quantify these, we need to implement a more complex set of models for data interpretation and parameter extraction, such as the finite or infinite moving line source theory. This work is currently ongoing.
3. Conclusions
The comparative review of TRT experiments performed at a test site at Universitat Politècnica de València has been useful to identify the strengths and weaknesses and evaluate the processes and models currently used in the interpretation of TRTs.
First, it has been found that the use of a PID control system to keep the injected heat rate constant notably reduces the noise and errors associated to the measurements, allowing more accurate analysis and thermal parameter assessments.
Second, it has been proven that the use of LSQ-based identification algorithms leads to the inference of parameter values that better fit the data. The finite line source approach gave better results, although the difference with the infinite line source is small. In our case, this is reasonable due to the small value of parameter , i.e., the ratio between the depth ( m) and borehole radius ( m). In case of a much shallower heat exchanger, it would be certainly advisable to use the full FLS expression for parameter assessment.
Third, although the fact that samples recovered while drilling were not analysed, thermal conductivity of samples of a near installation yielded values around 2.3 Wm K [24], which are similar to the results of present paper. Further work is needed in this regard.
Finally, we could show that either ILS and FLS models are insufficiently accurate to simulate tests as long as 15 days. This may be attributed to groundwater flow effects. We are currently developing new approaches to incorporate such effect into BHE modelling.
In addition, our experience with the current installation has allowed us to design a new and more complete test-site to help in the analysis and validation of new ground heat exchanger geometries that will be carried out in the framework of Horizon 2020 projects Cheap-GSHPs (http://cheap-gshp.eu) and GEOCOND ( http://geocond-project.eu). In this new test site, we intend to implement several ideas arising from the limitations and observations made in the current test-site.
Acknowledgments
This work has received funding from the European Union’s Horizon 2020 Research and Innovation program under grant agreement Nos. (657982) and (727583).
Author Contributions
Borja Badenes, Miguel Ángel Mateo Pla and Javier F. Urchueguía took part in the conception, design, performance and analysis of experiments; Lenin G. Lemus-Zúñiga and Begoña Sáiz Mauleón took part in the analysis of experiments; Borja Badenes and Miguel A. Mateo Pla wrote the article under the supervision of Lenin G. Lemus-Zúñiga, Begoña Sáiz Mauleón and Javier F. Urchueguía.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations and nomenclature are used in this manuscript:
| Abbreviations | |
| UPV | Universitat Politècnica de València |
| HVAC | Heating, ventilation and air conditioning |
| TRT | Thermal Response Test |
| BHE | Borehole Heat Exchanger |
| PID | Proportional, Integral and Derivative |
| PWM | Pulse Width Modulation |
| ILS | Infinite Line Source Model |
| FLS | Finite Line Source Model |
| LSQ | Lest squares fitting algorithm |
| MSE | Mean Squared Error |
| Cheap-GSHPs | Cheap and Efficient Application of reliable Ground Source Heat Exchangers and Pumps |
| GEOCOND | Advanced materials and processes to improve performance and cost-efficiency of Shallow Geothermal systems and Underground Thermal Storage |
| Nomenclature | |
| H | BHE depth (m) |
| temperature observation point distance to the line source (m) | |
| BHE radius (m) | |
| Ambient temperature (C) | |
| Inlet temperature at te BHE (C) | |
| Outlet temperature at te BHE (C) | |
| Mean temperature at the BHE (C) calculated by means of the ILS model | |
| Mean temperature at the BHE (C) calculated by means of the FLS model | |
| Undisturbed ground temperature (C) | |
| G | Water flow (m s) |
| Injected heat flow per unit length (W m) | |
| Water volumetric heat capacity (J m k) | |
| Ground thermal diffusivity (m s) | |
| Ground thermal conductivity (W K m) | |
| Borehole thermal resistance (K m W) | |
| Euler’s constant | |
| ratio between and H | |
| mean of squared residuals |
References
- Gehlin, S. Thermal Response Test—Method Development and Evaluation. Ph.D. Thesis, Department of Environmental Engineering, Luleå University of Technology, Luleå, Sweden, 2002. [Google Scholar]
- Sanner, B.; Hellström, G.; Spitler, J.D.; Gehlin, S. More than 15 years of mobile Thermal Response Test—A summary of experiences and prospects. In Proceedings of the European Geothermal Congress (EGC 2013), Pisa, Italy, 3–7 June 2013. [Google Scholar]
- Witte, H.J.L.; Van Gelder, G.J.; Spitier, J.D. In situ measurement of ground thermal conductivity: A Dutch perspective. Ashrae Trans. 2002, 108, 263–272. [Google Scholar]
- Hellström, G. Ground Heat Storage: Thermal Analyses of Duct Storage Systems. Ph.D. Thesis, Lund University, Lund, Sweden, 1991. [Google Scholar]
- Bandos, T.; Montero, A.; Fernández de Córdoba, P.; Urchueguía, J. Improving parameter estimates obtained from thermal response tests: Effect of ambient air temperature variations. Geothermics 2011, 40, 136–143. [Google Scholar] [CrossRef]
- Bandos, T.V.; Montero, A.; Fernández, E.; Santander, J.L.G.; Isidro, J.M.; Pérez, J.; Córdoba, P.; Urchueguía, J.F. Finite line-source model for borehole heat exchangers: Effect of vertical temperature variations. Geothermics 2009, 38, 263–270. [Google Scholar] [CrossRef]
- De Carli, M.; Tonon, M.; Zarrella, A.; Zecchin, R. A computational capacity resistance model (CaRM) for vertical ground-coupled heat exchangers. Renew. Energy 2010, 35, 1537–1550. [Google Scholar] [CrossRef]
- Lamarche, L.; Beauchamp, B. New solutions for the short-time analysis of geothermal vertical boreholes. Int. J. Heat Mass Transf. 2007, 50, 1408–1419. [Google Scholar] [CrossRef]
- Molina-Giraldo, N.; Blum, P.; Zhu, K.; Bayer, P.; Fang, Z. A moving finite line source model to simulate borehole heat exchangers with groundwater advection. Int. J. Thermal Sci. 2011, 50, 2506–2513. [Google Scholar] [CrossRef]
- Spitler, J.D.; Gehlin, S.E. Thermal response testing for ground source heat pump systems—An historical review. Renew. Sustain. Energy Rev. 2015, 50, 1125–1137. [Google Scholar] [CrossRef]
- Sliwa, T.; Knez, D.; Gonet, A.; Sapinska-Sliwa, A.; Szlapa, B. Research and Teaching Capacities of the Geoenergetics Laboratory at Drilling , Oil and Gas Faculty AGH University of Science and Technology in Kraków (Poland). In Proceedings of the World Geothermal Congress, Melbourne, Australia, 19–25 April 2015. [Google Scholar]
- Montero, A.; Urchueguía, J.F.; Martos, J.; Badenes, B.; Picard, M.A. Ground temperature profile while thermal response testing. In Proceedings of the European Geothermal Congress (EGC 2013), Pisa, Italy, 3–7 June 2013; pp. 1–6. [Google Scholar]
- Eskilson, P. Thermal Analysis of Heat Extraction Boreholes. Ph.D. Thesis, Lund University, Lund, Sweden, 1987. [Google Scholar]
- Badenes, B.; Mateo Pla, M.A.; Magraner, T.; Lemus, L.; Urchueguía, J.F. Experimental facility to perform Thermal Response Tests and study the thermal behaviour of the ground. In Proceedings of the European Geothermal Congress (EGC 2016), Strasbourg, France, 19–14 September 2016; pp. 19–24. [Google Scholar]
- Grundfos Web Page. Available online: https://www.grundfos.com (accessed on 31 July 2017).
- IFM TA3130. Available online: https://www.ifm.com/gb/en/product/TA3130 (accessed on 31 July 2017).
- OSAKA web page. Available online: http://osakasolutions.com (accessed on 1 September 2017).
- IFM SM8000. Available online: https://www.ifm.com/gb/en/product/SM8000 (accessed on 31 July 2017).
- Siemens AG Simatic S7-1200. Available online: http://www.siemens.com/s7-1200 (accessed on 31 July 2017).
- Tinti, F.; Bruno, R.; Focaccia, S. Thermal response test for shallow geothermal applications: A probabilistic analysis approach. Geotherm. Energy 2015, 3, 6. [Google Scholar] [CrossRef]
- Luo, J.; Rohn, J.; Xiang, W.; Bertermann, D.; Blum, P. A review of ground investigations for ground source heat pump (GSHP) systems. Energy Build. 2016, 117, 160–175. [Google Scholar] [CrossRef]
- Austin, W. Development of an In-Situ System for Measuring Ground Thermal Properties. Master’s Thesis, Oklahoma State University, Stillwater, OK, USA, 1998. [Google Scholar]
- Verdoya, M.; Chiozzi, P. Influence of groundwater flow on the estimation of subsurface thermal parameters. Int. J. Earth Sci. 2016, 1–8. [Google Scholar] [CrossRef]
- Badenes, B.; de Santiago, C.; Nope, F.; Magraner, T.; Urchueguía, J.F.; de Groot, M.; de Santayana, F.P.; Arcos, J.L.; Martín, F. Thermal characterization of a geothermal precast pile in Valencia (Spain). In Proceedings of the European Geothermal Congress (EGC 2016), Strasbourg, France, 19–14 September 2016. [Google Scholar]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).