Abstract
This paper presents a single-degree-of-freedom energy optimization strategy to solve the energy management problem existing in power-split hybrid electric vehicles (HEVs). The proposed strategy is based on a quadratic performance index, which is innovatively designed to simultaneously restrict the fluctuation of battery state of charge (SOC) and reduce fuel consumption. An extended quadratic optimal control problem is formulated by approximating the fuel consumption rate as a quadratic polynomial of engine power. The approximated optimal control law is obtained by utilizing the solution properties of the Riccati equation and adjoint equation. It is easy to implement in real-time and the engineering significance is explained in details. In order to validate the effectiveness of the proposed strategy, the forward-facing vehicle simulation model is established based on the ADVISOR software (Version 2002, National Renewable Energy Laboratory, Golden, CO, USA). The simulation results show that there is only a little fuel consumption difference between the proposed strategy and the Pontryagin’s minimum principle (PMP)-based global optimal strategy, and the proposed strategy also exhibits good adaptability under different initial battery SOC, cargo mass and road slope conditions.
1. Introduction
Hybrid electric vehicles (HEVs) are regarded as an important domain of the future automobile industry due to their superiority in reducing fuel consumption and emissions. Generally, HEVs are equipped with an internal combustion engine (ICE) and an energy storage system (ESS). They can be classified into three types, including series hybrid system, parallel hybrid system and series-parallel hybrid system [1]. The series-parallel hybrid system often utilizes a power-split device to split and combine the power produced by electric motors and ICE [2]. The prominent examples are the one-mode power-split in the Toyota Prius or Ford electronic-continuously variable transmission (e-CVT) and two-mode power-split in the general motors (GM)-Allison electric variable transmission (EVT), Timken EVT or Renault Infinitely Variable Transmission (IVT) [3].
Due to their complex electromechanical structure, designing an efficient energy management strategy (EMS) for power-split HEVs is a challenging task. The strategy must ensure the vehicle’s performance with minimum fuel consumption under different operation conditions and driver characteristics. Previous investigations can be basically divided into rule-based strategies and optimization-based strategies and all other subcategories are classified into these two main categories [4].
The major benefit of rule-based strategies is the effectiveness in real-time supervisory control, such as the thermostat strategy [5] and the logic threshold control strategy [6,7]. Subsequently, many more efforts have been made to further improve the fuel economy, for example, by extracting optimization rules from global optimal control strategies [8,9], optimizing the rules combined with intelligent algorithms [10,11], or establishing driving pattern recognizers [12]. However, these strategies are mainly dependent on the results of extensive experiments or expert knowledge. The optimality can’t be theoretically guaranteed. Nowadays, many artificial intelligent methods have been successfully introduced to solve the energy management problem of HEVs. The fuzzy control strategies [1,13,14] have to make considerable effort to build the fuzzy logic table, and only an approximately optimal result can be obtained. The neutral network (NN) strategies [15,16] need sufficient experimental data to train all possible combinations of driving conditions. The genetic algorithm (GA) [17,18] is time-consuming due to the fact that it must complete a series of actions including crossover, mutation and elite selection. The particle swarm optimization strategy [19,20] provides a suboptimal solution and it will be not effective when the solution parameters are highly related.
The target of optimization-based strategies is to minimize the specific cost function, which may include the fuel consumption, emissions, battery state of charge (SOC) or engine on/off switching frequency. The energy management strategies, which based on Bellman’s dynamic programming (DP) [21,22,23] or Pontryagin’s minimum principle (PMP) [24,25,26], have been widely investigated in recent years. The DP-based strategy is a global optimization method to achieve the best fuel economy for a given driving cycle, such as Mansour and Clodic [27] proposed a DP-controller for the Toyota Hybrid System-II (THS-II) and Liu et al. [28] utilized the DP-based strategy to minimize a combination of fuel consumption and selected emission species over a given driving cycle. Generally, a DP-based strategy directly produces optimal trajectories rather than control laws [29], so it is always used as a benchmark to evaluate other strategies or to optimize the parameters.
The PMP-based strategy looks for the solution to satisfy necessary conditions for optimality, so it needs less computational time than that of the DP-based strategy [29,30]. Kim proposed that the PMP-based strategy could provide a near-optimal solution if the future driving conditions were known in advance [31]. Based on the theoretical background of PMP, the equivalent consumption minimization strategy (ECMS) was presented, which converted electricity into equivalent fuel consumption and minimized it at each control cycle [32,33]. The optimal co-state or the equivalence factor can be determined only when the driving conditions are known a priori. The mismatch between co-state and the driving cycle will result in over-charge or over-discharge of the battery. Considering about this problem, the adaptive equivalent consumption minimization strategy (A-ECMS) was presented to adjust equivalence factors based upon the SOC feedback or the prediction technique [34,35]. Except for the requirement of keeping the terminal SOC equal to the initial value, both the PMP-based strategy and the ECMS are difficult to handle the constraint of the SOC fluctuation during the operation process.
The quadratic optimal control theory has been comprehensively applied in power systems, aerospace systems, social economic systems, and so on. For the classical linear quadratic regulator (LQR) problem, the quadratic performance index represents a trade-off between the distance of the state variable from the equilibrium point and the cost of the control input variable. In previous studies [36,37], the pedal signal was interpreted as a vehicle’s speed command. When the square of vehicle’s speed v2 and the battery’s residual energy E·SOC were chosen as the state variables, a quadratic performance index was designed to ensure the vehicle’s driving performance, sustain the battery SOC and restrain frequent and large-scale fluctuation of engine power simultaneously. The fuel economy was improved indirectly and the energy management problem was transformed into the LQR problem or the quadratic optimal tracking problem. The quadratic optimal control theory was firstly introduced by authors to deal with this kind of problem. The strategy had two control variables: the engine power and the motor power, so it was called as double-degree-of-freedom energy management strategy.
In this paper, a further improvement is made based on the previous research. Generally, the pedal signal is interpreted as a torque command for power-split HEVs. When the battery’s residual energy E·SOC is chosen as the state variable, the quadratic performance index is designed only containing two items: the quadratic error of actual SOC from the desired value and the fuel consumption rate. The motor power has no longer been restricted to take full advantage of the battery-motor system dynamic behavior. Different from the conventional LQR problem, an extended quadratic optimal control problem is formulated by approximating the fuel consumption rate as a quadratic polynomial of engine power, where the state variable is adjusted around the desired value rather than zero, and the quadratic form of the control variable is not about the control variable, but about the difference between the control variable and an given function of time. The approximated optimal control law is derived by utilizing the solution properties of the Riccati equation and adjoint equation. It is only related with one control variable: the battery-motor system power, so it is called as single-degree-of-freedom quadratic performance index strategy (SQPIS). To verify effectiveness of the proposed strategy, the Toyota Prius is chosen as the research target due to the fact that it is the most typical power-split HEV. The vehicle simulation model is developed based on the ADVISOR software, and the control performance and oil-saving effect are tested repeatedly. The simulation results show that the fuel economy is improved directly without sacrificing driving performance. The fuel consumption of SQPIS is very close to that of the PMP-based global optimal strategy. Furthermore, the SQPIS exhibits good adaptability with unchanged parameters under different initial battery SOC, cargo mass and road slope.
The contributions of this paper can be summarized as follows: firstly, the quadratic performance index is designed to restrict the fluctuation of battery SOC and reduce fuel consumption simultaneously, which is still difficult to handle by the PMP-based global optimal strategy or ECMS. Secondly, an extended quadratic optimal control problem is formulated by approximating the fuel consumption rate as a quadratic polynomial of engine power. The concrete form of the optimal control law is derived theoretically, which is different from the conventional LQR problem. Thirdly, when the vehicle requested power is regarded as a random process and its average changes slowly, an approximate optimal control strategy is obtained, which is easy to be real-time implemented. Finally, the engineering significance of the proposed strategy SQPIS is discussed in details.
2. Drivetrain Architecture and Energy Management Problem Description
The configuration of the Toyota hybrid system (THS) is illustrated in Figure 1. It mainly includes the ICE, planetary gear, battery package, controller, motor/generator MG1 and MG2. The sun gear is connected with the MG1, the ring gear is connected with the MG2 and the planet carrier is connected with the ICE. The torque and speed between the wheel and engine are decoupled by the planetary gear. That is to say, the engine could operate on the optimal operating line (OOL) by jointly adjusting the MG1’s speed and engine’s torque, and the MG2’s torque is regulated simultaneously to guarantee the sum of MG1’s power and MG2’s power is equal to the battery-motor system power Pess. In the following discussion, only the static models of engine and motor are considered because their transient processes are relatively short and can be ignored. Firstly, a brief introduction of the battery-motor system model is given; the engine model and planetary gear model will be discussed in details in Section 4.
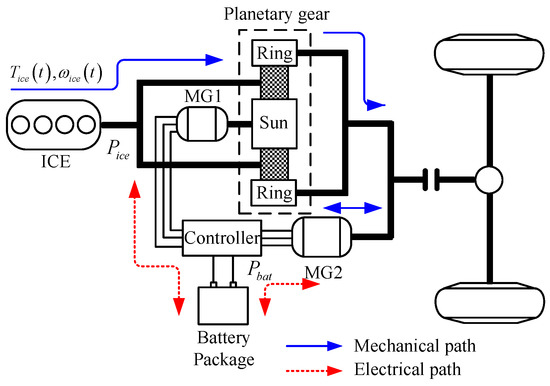
Figure 1.
Drivetrain configuration of the Toyota hybrid system.
2.1. Efficiency Model of Battery-Motor System and Its Simplification
The battery package used in Toyota Prius is a nickel metal hydride (NiMH) battery. The vehicle always operates in “charging sustaining mode” in which the SOC is kept within a predefined small range throughout a driving cycle. This is a high efficiency region for the battery and it could provide sufficient capacity to restrict large-scale fluctuation of engine power.
The battery charging and discharging are complex electrochemical reaction processes. Generally, the battery package is described by an equivalent circuit model that is composed by a voltage source in series with a resistance. As shown in Figure 2, both the open-circuit voltage VOC and the internal resistor Rint are associated with the battery SOC. The battery efficiency is defined as:
where , indicates the battery is discharging and indicates the battery is charging. As shown in Figure 3, the battery efficiency is related to its output power and SOC, so the battery efficiency model can be expressed as [37]:
where the battery capacity is 6 Ah, is the battery’s total energy and is the battery’s residual energy.
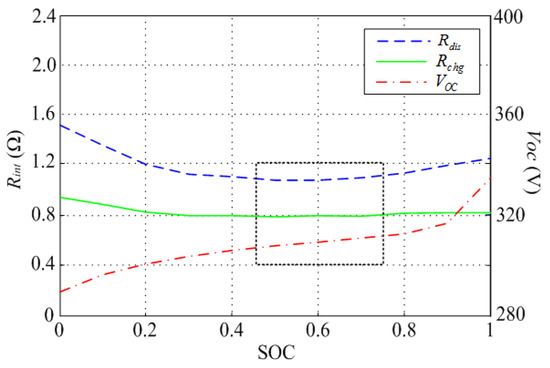
Figure 2.
Characteristics of and . ( is the charge resistance and is the discharge resistance).
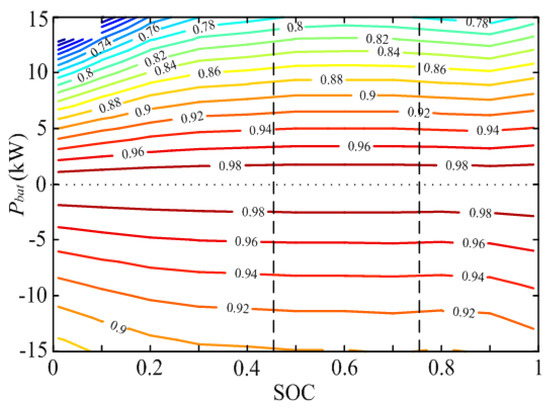
Figure 3.
Efficiency MAP of battery package.
The motor/generator MG1 and MG2 are both permanent magnet motors. They have sufficient capability of short-time overload, wide flux-weakening range and high efficiency region. For the permanent magnet motors and their controllers, a static efficiency model is adopted as:
where is the motor/generator MG1’s power, is the motor/generator MG2’s power, is the efficiency of MGs and its controller, and .
By substituting Equation (3) into Equation (2), the efficiency model of the battery-motor system can be obtained as:
The battery-motor system power satisfies:
If the efficiency of the two-motor system is defined as:
then the efficiency model of Equation (4) can be rewritten as:
where .
The efficiencies and are associated with the operating point of the battery and motor (see Figure 3 and Figure 4). Therefore, the efficiencies and are available online according to the operating points of the battery, the motor/generator MG1 and MG2.
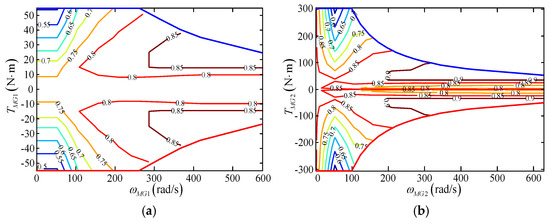
Figure 4.
Efficiency MAP of motor/generator MG1/MG2 and its controller. (a) MG1 and its controller; (b) MG2 and its controller.
2.2. Energy Management Problem
Generally, the pedal signal reflects the driver’s intention and it can be interpreted as a torque command. The requested power is determined by the vehicle control unit (VCU) based on the pedal signal and vehicle speed, and it satisfies:
where is the engine power.
The purpose of energy management is to reasonably assign the requested power between engine and battery-motor system. In order to sustain the battery SOC and improve the fuel economy simultaneously, the performance index can be established as:
where is the initial time, is the final time, is a desired value that the battery SOC should change around for efficiently using and protecting the battery and is the fuel consumption rate. The weight coefficient can be tuned to restrict the fluctuation of battery SOC and can be tuned to achieve a better fuel economy.
As mentioned above, the engine can be adjusted to work on the OOL (see Figure 5). Each working point of OOL has the minimum fuel consumption for a given engine power. Therefore, the fuel consumption rate can be regarded as a function only related to the engine power (see the point line in Figure 6) and the fuel consumption over a driving cycle is equal to the integral of . In order to apply the linear quadratic optimal control theory, the curve fitting method is used to approximate as a quadratic polynomial of engine power , that is:
where , and (see the solid line in Figure 6).
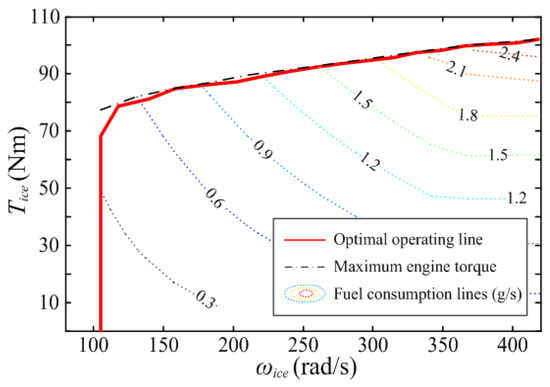
Figure 5.
Fuel consumption MAP of the engine.
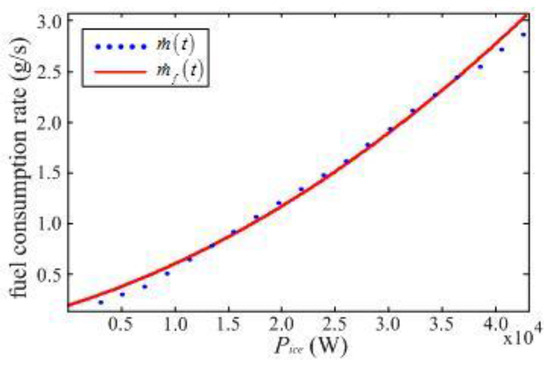
Figure 6.
Optimal fuel consumption rate line.
By substituting Equations (8) and (10) into Equation (9), the performance index becomes:
where and are constants and is determined by the driver. Hence, the optimization problem of Equation (9) or (11) is equivalent to that of Equation (12):
The requested power is determined by the VCU, that is to say, the energy management problem can be deemed as a single-degree-of-freedom energy optimization problem where only one control variable needs to be determined. If is selected as the state variable, is the control variable, from the Equation (7), a first order system is obtained as:
where , . And the quadratic performance index Equation (12) is rewritten as:
where is a constant and:
is a function of time only related to the requested power . The weight coefficients are:
Because is a constant, tuning the weight coefficients and are equivalent to tuning the weight coefficients and . Both and are positive value and the value range of is . The specific reason will be explained in the next section.
3. Single-Degree-of-Freedom Quadratic Performance Index Strategy
The linear quadratic optimal control theory is easy to achieve the close loop state feedback control and to be applied in actual engineering. In Section 2, the energy management problem has been transformed into the quadratic optimal control problem of Equation (12), which is different from the conventional LQR problem. In this section, the optimal control law is derived in theory for the problem that has the performance index as Equation (14), and the practical significance is discussed with engineering concepts.
3.1. Extended Quadratic Optimal Control Problem and Relevant Results
For the linear system as:
the optimal control law will be found to minimize the quadratic performance index:
where and are the actual and desired state variable, is the control variable, is a function of time which has been given. and are the weight coefficient matrices, and the terminal time is limited to ensure the performance index Equation (18) is finite. Note that the above optimal control problem is different from the conventional LQR problem. It is called as an extended quadratic optimal control problem, where the state variable is adjusted around the desired value rather than zero, and the quadratic form of the control variable is not about the control variable , but about the difference between the control variable and an given function of time , which comes from the optimization problem of Equation (12).
The target is to find the optimal control law to minimize the quadratic performance index Equation (18). According to the quadratic optimal control theory, the Hamiltonian function of extended quadratic optimal control problem is:
where is the co-state variable that satisfies:
and the minimum value of Hamiltonian function (Equation (19)) can be obtained by making its partial derivative of equal to zero, i.e.,
That is:
Further, assuming that:
where is the solution of differential Riccati equation and is the adjoint variable. Substituting Equation (23) into Equation (22) gives:
and the derivative of Equation (23) is:
Substituting Equations (17) and (24) into Equation (25) gives:
Substituting Equation (23) into Equation (20) yields:
Now, Equation (28) can be derived by comparing Equation (26) with Equation (27):
For any time , the Equation (28) holds for arbitrary , and . Therefore, the corresponding items are equal, and the Riccati equation and adjoint equation are received, i.e.,
Because there is no terminal item in performance index Equation (18), the terminal condition of Equations (29) and (30) are and respectively. In adjoint equation Equation (30), is a new added item and it makes the extended quadratic optimal control problem different from the previous ones. Note that, this difference is very important and how this added item works will be explained in the following section.
3.2. Derivation of Single-Degree-of-Freedom Quadratic Performance Index Strategy
For the energy management problem stated in Section 2, the related matrices and variables are scalars (see in Equations (13) and (14)). According to the results of the extended quadratic optimal control problem mentioned above, the optimal control law can be obtained as:
where is a given function of time defined by Equation (15), satisfies the Riccati equation:
and satisfies the adjoint equation:
3.3. Analysis from the Perspective of Engineering Application
The optimal control algorithm must look ahead and back, and the quadratic performance index-based control algorithm is also no exception. The Equations (29) and (30) are end boundary value problems. The solving process should be along the opposite direction of time, and of Equation (15) for time must be known in advance. Consequently, it will bring about a real-time implementation issue. In following discussion, we will mainly focus on the algorithm of Equations (31)–(33), and find out the specific solutions. The main results are described as follows:
(a) According to the characteristics of the solution of Riccati equation, if is large enough (for example, ), the solution of Equation (32) will keep as a constant except for the time near to . In other words, in most time of , is a constant and satisfies the algebraic Riccati equation:
Solving the Equation (34) for gives , so the solution is independent of the driving cycle and .
(b) For the constant , the adjoint Equation (33) is a linear differential equation that satisfies the superposition principle. The solution of Equation (33) can be divided into two responses of and , i.e., , and satisfies:
Obviously, along the opposite direction of time, Equations (35) and (36) are the stable first order filters with time constant , and the steady amplification coefficients of their solutions about and are and respectively. Because is a constant, in most time of , the solution of Equation (35) is a constant , except for the time near to , i.e., . And if the average value of requested power changes slowly, the following filtering result along the positive direction of time:
can be used to replace the filtering result along the opposite direction of time (note that, in general, if Equation (36) does not represent a filtering arithmetic, the above results can’t be obtained). Defining a new variable:
replacing with and letting in Equation (31), the approximated optimal control law can be obtained as:
In the approximated optimal control law of Equations (37) and (39), only the present and past information of and are used to achieve the present control variable , so the real-time implementation problem no longer exists.
(c) The control law of Equation (39) consists of two parts, is the feedback item to restrict the fluctuation of the battery SOC, and is the feedforward item that the battery-motor power plays a role of peak shaving and valley filling for engine power. It is obvious that, as increases or decreases, and or the efficiency of battery-motor system increases, the time constant increases, the alternating component of increases and approaches the average value of . The feedback action is weakened, and the feedforward action is enhanced. As a result, the fluctuation of battery SOC is enlarged and the degree of hybridization is deepened, which is helpful to improve the fuel economy. Conversely, as decreases or increases, and or the efficiency of battery-motor system decreases, the time constant decreases, and tend to counteract with each other. The feedback action will be enhanced, and the feedforward action will be weakened. As a result, the fluctuation of battery SOC is shrunken and the degree of hybridization is decreased, which is not helpful to reduce fuel consumption. In general, the recommended value of time constant is dozens of seconds. The specific selection process can be obtained by combining typical driving cycles. Except for achieving a better fuel economy, the battery-motor system power , the engine power and the battery SOC should also satisfy the following test conditions:
where and are the maximum and minimum power of battery-motor system, is the maximum engine power, and are the maximum and minimum battery SOC, respectively.
(d) For a given filter time constant , when the requested power changes violently, the battery-motor system is just trying to peak shaving and valley filling for engine power. When the requested power is relatively steady, the battery-motor system power will tend to be zero. It is implied that the proposed strategy has the ability to adapt various driving conditions, such as the urban or suburb driving condition.
(e) In this paper, three operation modes are added to further reduce the fuel consumption and they are switched according to the requested power . The basic logics are listed as follows: if the is less than , the battery-motor system provides the requested power or recycles the braking energy; otherwise, the engine and the battery-motor system provide the requested power together and the battery package acts as an energy buffer unit.
Thus, the final power-split algorithm is:
where and are decided by Equations (15) and (37), respectively.
4. Vehicle Simulation Model
The ADVISOR software can be used to make rapid analysis for HEVs, such as driving performance, fuel consumption, emissions and etc. All the component models in software are public and they can be easily modified under the Matlab/Simulink environment. In this paper, a forward-facing vehicle simulation model is developed and embedded in ADVISOR platform to verify the effectiveness of the proposed strategy SQPIS. As shown in Figure 7, each module represents an actual drivetrain component in a Toyota Prius.
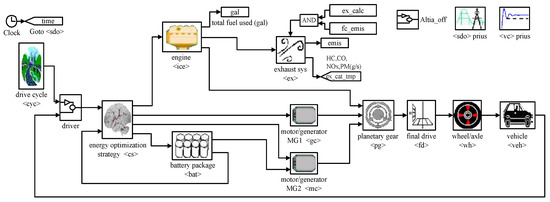
Figure 7.
Vehicle simulation model.
The simulation process can be simply described as follows: the speed versus time information for a given driving cycle is stored in the drive cycle module. At each control cycle, it provides the desired speed to the driver module. In order to trace the given driving cycle, the accelerator pedal or the brake pedal should be continuously regulated by the driver. In the driver module, this process is realized by a proportion-integral (PI) regulator. Through the PI regulator, the difference between desired speed and actual speed is converted into the requested power . The proposed strategy SQPIS is embedded in the energy optimization strategy module. The engine power and battery-motor system power are obtained by Equation (43), and then they are converted into corresponding torque or speed command for engine, motor/generator MG1 and MG2. If these commands don’t exceed the power limitation of these components, they will provide the actual torque signal to the planetary gear module. Taking the gear ratio into consideration, the actual torque signal is passed forward through the final drive module until it results in a driving force at the wheel/axle module interface. Generally, the vehicle should overcome the rolling resistance, aerodynamic resistance and grade resistance. The actual vehicle speed can be derived by Equation (44) in the vehicle module and it eventually feedbacks to the driver module as an input variable:
where is the rotating mass efficient and , is the vehicle total weight including the passengers mass and cargo mass, is the gravitational acceleration constant, is the rolling resistance coefficient, is the road slope, is the air density, is the aerodynamic drag coefficient and is the vehicle frontal area.
4.1. Engine Model
The Toyota Prius is powered by a 1.5-L 1NZ-FXE four-cylinder gasoline engine. As shown in Figure 8, the fuel consumption model is used to describe the input/output characteristics of engine, and the fuel consumption rate can be defined as:
where is the engine torque and is the engine speed.
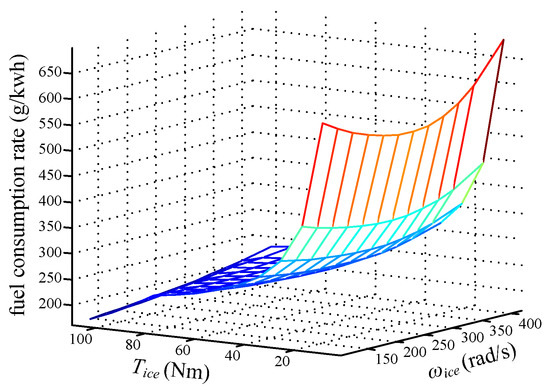
Figure 8.
Fuel consumption rate of 1NZ-FXE (Coolant Temperature is 95 °C).
This model has been verified by ADVISOR software, and the actual fuel consumption rate can be derived by using the linear interpolation method. Note that the engine temperature also has a significant impact on the fuel consumption rate, especially during the cold starting process. Therefore, the temperature correction factor is introduced to ensure the simulation precision:
4.2. Planetary Gear Model
The planetary gear consists of three basic components: sun gear, planet carrier and ring gear (see Figure 9). The motor/generator MG1 is connected with the sun gear and the engine is connected with the planet carrier. The motor/generator MG2 and the final drive are connected with the ring gear. Since the rotation direction of engine is unchangeable, the rotation direction of planet carrier can’t be reversed. Both the sun gear and the ring gear can rotate forward and reverse, so the rotation speed of any gear can be determined by the other two gears. Assuming that the radius of the sun gear is S and the radius of ring gear is R, the speed and torque of these components should satisfy the kinematic constraints as Equations (47) and (48):
where is the ratio of ring gear radius and sun gear radius, , , and are output torque of engine, MG1, MG2 and output axle respectively, , , and are output speed of engine, MG1, MG2 and output axle respectively. Because the MG2 is directly connected with the output axle, the speed can be determined by the vehicle speed :
where is the ratio of final drive, is the wheel radius.
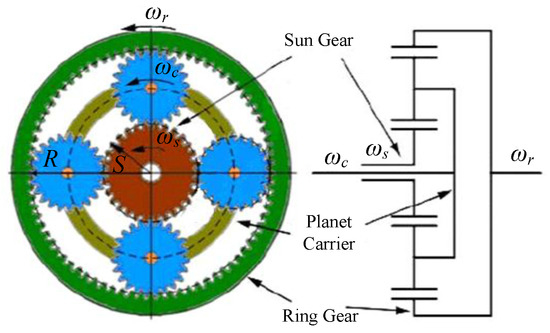
Figure 9.
Configuration of planetary gear system.
4.3. Energy Optimization Strategy Model
As shown in Figure 10, the energy optimization strategy module can be divided into three parts. In the first part, the operation mode switch block generates the operation mode signal . If the requested power , the system operates in regenerative braking mode and . When , the system operates in electric drive mode and . Otherwise, represents the system operates in hybrid mode. In order to avoid the frequent switch among these three modes, a hysteresis loop controller is added. The second part is the core algorithm of SQPIS. Taking the operation mode signal , requested power and battery’s residual energy as input variables, the engine power and the battery-motor system power can be obtained by the approximate optimal control law of Equation (43).
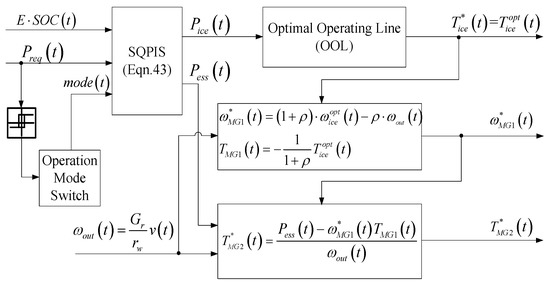
Figure 10.
Simulation diagram of energy optimization strategy model.
At last, the control command of engine, motor/generator MG1 and MG2 will be generated in the third part. The OOL has been converted and stored in a data table (see Figure 5). The corresponding engine optimal operating point can be derived by utilizing the interpolation and table lookup method. As shown in Figure 10, the MG1’s speed should be regulated together to make the engine operate at the given optimal working point, and the command is set equal to . On the other hand, the sum of output power from MG1 and MG2 should be adjusted equal to the battery-motor system power . Therefore, the MG2’s torque command is obtained by:
5. Simulation Results and Comparative Analysis
In order to quantitatively demonstrate the effectiveness of the proposed strategy SQPIS in this paper, the simulation tests are performed over different driving conditions. The results are compared with the rule-based energy management strategy (rule-based EMS) [38], which have been applied to Toyota Prius with impressive success, the A-ECMS [34] and the PMP-based global optimal control strategy [31].
5.1. Test Design and the Selection of Weight Coefficient
The rule-based EMS is summarized as follows: when the vehicle decelerates, the engine power is set to zero. If the requested braking power doesn’t exceed the maximum battery charging power, the MG2 will operate as a generator. When the vehicle accelerates, if the requested power is lower than and the battery SOC is high enough, the MG2 will be used as a motor and drive the vehicle individually. As the requested power increases or the battery SOC is lower than the minimum value , the engine will be started. It not only provides the requested power, but also tries to sustain the battery SOC around the desired value, that is:
where is the fitting coefficient. When the requested power exceeds the maximum engine power, the engine will operate at the maximum value and the MG2 will provide assistant power to keep the vehicle still owning better driving performance.
The PMP-based global optimal control strategy attempts to search for the optimal control variable to minimize fuel consumption under a given driving cycle. As shown in Figure 6, the fuel consumption rate is a function only related to engine power . Then, the total fuel consumption can be treated as the integral performance index:
For the given requested power , the engine power and battery-motor system power should satisfy Equation (8). Therefore, taking Equations (1), (7) and (8) into consideration, the optimal control variable can be obtained by searching the minimum value of the Hamiltonian function [31], that is:
where is the co-state variable, which converts the electric energy consumption into virtual fuel consumption, is the battery open-circuit voltage, is the battery internal resistor, and is the efficiency of the two-motor system.
As mentioned above, the physical meaning of Hamiltonian function Equation (53) is the equivalent fuel consumption and it has a similar formulation as ECMS. The co-state variable can be deemed as the equivalence factor in ECMS. The optimality of ECMS is especially sensitive to the value of equivalence factor, which should be tuned appropriately only when the driving cycle is known in prior. The A-ECMS, which is on the basis of SOC feedback, is a better method to improve the robustness and make it applicable in real-world conditions. Firstly, an initial guess value is given for the equivalent factor , and then it must be adjusted according to the adaptation law every T seconds [34]:
where is the new equivalence factor when , is the equivalence factor when , is the equivalence factor when and is the proportional gain of feedback controller.
The detailed vehicle model specifications of the Toyota Prius are shown in Table 1. For the proposed strategy SQPIS, the switching power in Equation (43) is 5 kW, which is the same as that of the rule-based EMS. In order to avoid frequent switching between different opearation modes, a 2 kW hysteresis loop is added. The weight coefficients could be determined by combining a certain driving cycle. Different coefficient value is chosen to carry out the simulation test until a better fuel economy is obtained. Meanwhile, the test conditions (see Equations (40)–(42)) also should be verified. In this paper, the urban dynamometer driving schedule (UDDS) cycle, which represents a typical city test schedule and is always used to evaluate the fuel economy of electric vehicles, is chosen to determine the weight coefficients. When the weight coefficients , , the filter time constant is calculated as , and solutions of the Riccati equation and adjoint equation are shown in Figure 11.

Table 1.
Toyota Prius model specifications.
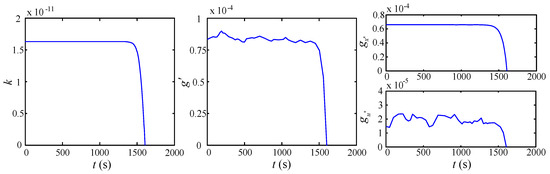
Figure 11.
Solution of the Riccati equation and the adjoint equation.
5.2. The simulation Test Results and Analysis
Abundant simulation tests are applied to validate the proposed strategy under some typical driving cycles. Figure 12, Figure 13, Figure 14 and Figure 15 are the simulation results of the rule-based EMS, A-ECMS, SQPIS and PMP-based global optimal strategy under the UDDS driving cycle respectively. The initial value and desired value are set to 0.6. In order to make comparison analysis among different strategies, when the final value is not equal to the initial value , the charge deviation will be converted into corresponding virtual fuel consumption by equivalent method. The equivalent fuel consumption (EFC) could be expressed as:
where is the fuel consumption rate (g/s), is the fuel density (749 g/L), is the total distance of given driving cycle (km) and is the equivalent factor, which is calculated by:
where is total battery energy (J), is fuel low heating value (42,600 J/g), is average efficiency of engine used to charge battery, is average efficiency of two-motor system and is average efficiency of battery.
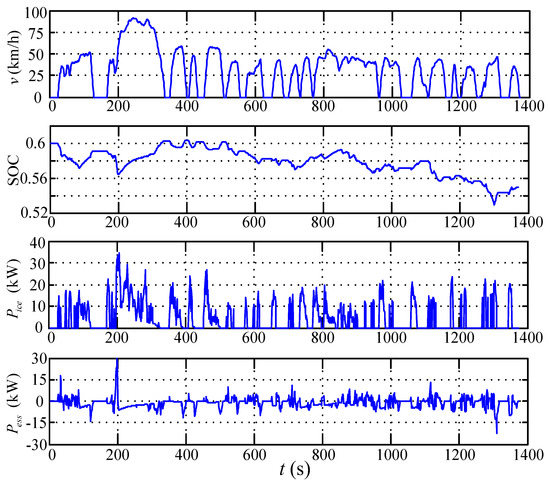
Figure 12.
The simulation result of rule-based energy management strategy (EMS).
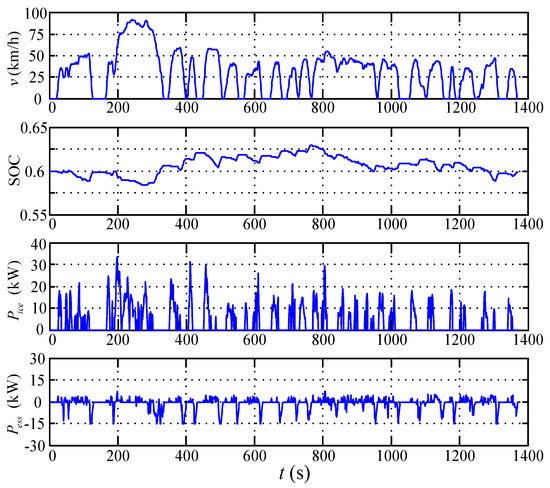
Figure 13.
The simulation result of adaptive equivalent consumption minimization strategy (A-ECMS).
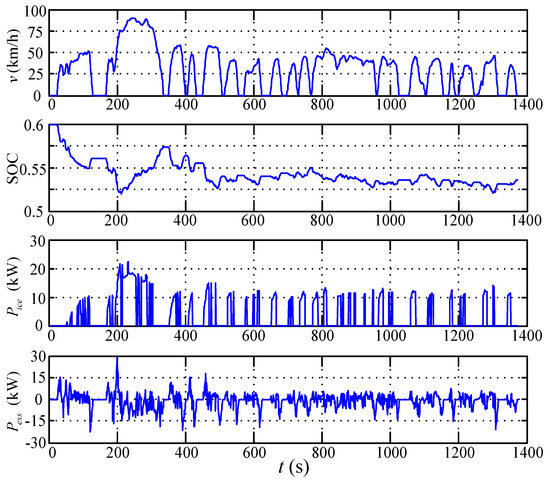
Figure 14.
The simulation result of single-degree-of-freedom quadratic performance index strategy (SQPIS).
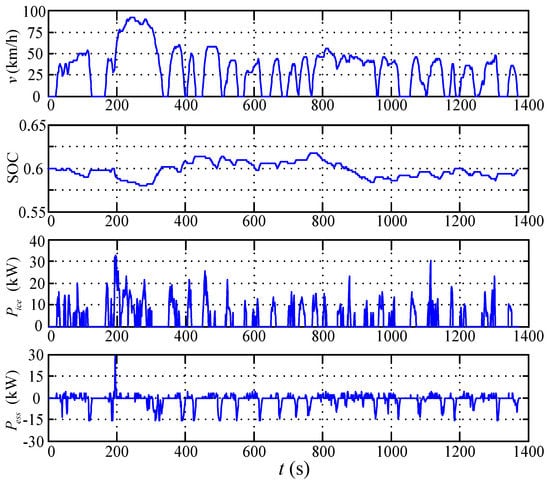
Figure 15.
The simulation result of Pontryagin’s minimum principle (PMP)-based global optimal strategy.
As shown in the first line of Table 2, the PMP-based strategy has the best fuel economy since it is a global optimal strategy. On the other hand, comparing with the rule-based EMS, both the A-ECMS and the SQPIS achieve a noticeable improvement in fuel economy, but the fuel economy of SQPIS is a little better than that of the A-ECMS.

Table 2.
Simulation results of different drive cycles.
For the SQPIS, the average tracing error between the required and achieved speed is only 0.1472 km/h, and it could adjust the output power of MG1 and MG2 actively in order to avoid large scale fluctuation of engine power. As shown in Figure 16, the engine efficiency distribution for the rule-based EMS is relatively dispersed, but it will be more concentrated for the SQPIS and PMP-based global optimal strategy. That is a powerful evidence to explain why the SQPIS is a more effective strategy for reducing the fuel consumption.
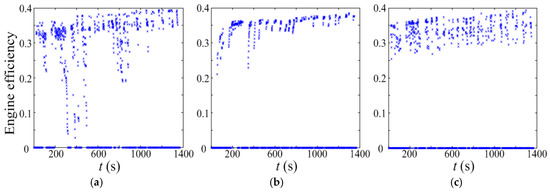
Figure 16.
Engine efficiency distribution under urban dynamometer driving schedule (UDDS) driving cycle. (a) rule-based EMS; (b) SQPIS; and (c) PMP-based strategy.
Just as the analysis of previous section indicated, the SQPIS has a good adaptability under various driving cycles. Other seven driving cycles, including the urban and suburb condition, are chosen to verify this point with unchanged weight coefficients. The EFC and final value of different strategies have been listed in Table 2. Obviously, the fuel consumption difference between the rule-based EMS and PMP-based global optimal strategy varies according to the driving cycle. The minimum difference is 16.17% under the HWFET cycle and the maximum difference is about 44.34% under the UDDS cycle.
The nature of PMP-based strategy is an open-loop optimization algorithm and it carries out one-dimension optimization at each control cycle by utilizing the Equation (53). In addition to the large amount of calculation, prior knowledge of the whole driving conditions is needed. Hence, as shown in Table 2, the value of co-state variable can only be derived by off-line calculation and it should be adjusted under different driving cycles to ensure the final value is equal to its initial value. Different from the PMP-based strategy, the SQPIS has the ability to restrict the SOC fluctuation and reduce fuel consumption simultaneously. The simulation results indicate that the SQPIS achieves a better compromise between the fuel economy and driving performance, i.e., the minimum fuel consumption difference between the SQPIS and PMP-based global optimal strategy is only 1.43% under the CSHVR cycle, and the maximum difference is 10.6% under the HWFET cycle. As mentioned above, the SQPIS generates only a state feedback solution. Comparing with the PMP-based global optimal strategy, the SQPIS can be real-time implemented in various driving cycles with the same weight coefficients. Therefore, the robustness of the proposed strategy SQPIS is better than that of the PMP-based global optimal strategy.
In order to solve the mismatch problem existing in the PMP-based strategy and ECMS, the A-ECMS is proposed to adjust equivalence factor based on the SOC feedback value. Although the A-ECMS is a better way to be implemented in real-world conditions, it still needs extensive calculation in one-dimension optimization at each control cycle. Furthermore, as listed in Table 2, simulation results indicate the fuel consumption of A-ECMS is also a little higher than that of the SQPIS. For example, the minimum fuel consumption difference is 0.67% under the HWFET cycle and the maximum fuel consumption difference is 3.75% under the INDIA_URBAN cycle.
The aforementioned results are obtained while the cargo mass and road slope stay the same. The simulation results with and road slope under the UDDS driving cycle are listed in Table 3. The vehicle dynamic performance could be ensured by the rule-based EMS, A-ECMS and SQPIS with unchanged parameters, but for the PMP-based global optimal strategy, the co-state variable should be adjusted according to the cargo mass or road slope. Comparing with the rule-based EMS and A-ECMS, the fuel consumption of SQPIS is closer to that of the PMP-based global optimal strategy.

Table 3.
Impacts of cargo mass and road slope on fuel consumption under urban dynamometer driving schedule (UDDS) driving cycle.
As mentioned above, when the initial value is set to 0.6, the final value obtained by SQPIS can be brought back near to the desired value . However, in the actual driving process, the initial value may be not 0.6. For the PMP-based global optimal strategy, the co-state variable has to be adjusted off-line according to the initial value . But for the SQPIS, it is easier to be implemented without changing any weight coefficient. When the initial value ranges from 0.5 to 0.7, the SOC trajectories under UDDS driving cycle are given in Figure 17. The simulation results indicate that the SOC trajectories tend to be convergent after 460s and the final values are same under different initial battery SOC. The adaptability of the proposed strategy SQPIS is exhibited.
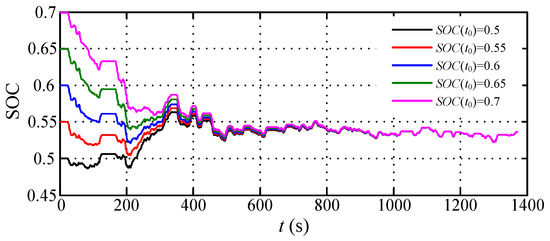
Figure 17.
State of charge (SOC) trajectories with various under UDDS driving cycle.
6. Conclusions
The quadratic performance index is innovatively applied to solve the energy management problem of power-split HEVs. It is designed to restrict the fluctuation of battery SOC and reduce fuel consumption simultaneously. By approximating the fuel consumption rate as a quadratic polynomial of engine power, an extended quadratic optimal control problem is formulated. When the average value of requested power changes relatively slow, the adjoint equation can be treated as a filtering process and an approximate optimal strategy SQPIS is obtained. The SQPIS generates only a state feedback solution and the amount of calculation is negligible.
The forward-facing vehicle simulation model of a Toyota Prius is established and embedded in ADVISOR platform to validate the effectiveness of SQPIS. Compared with the rule-based EMS, A-ECMS and PMP-based global optimal control strategy, our simulation results show that the SQPIS has better oil-saving effect than that of the rule-based EMS and A-ECMS without sacrificing driving performance and its fuel economy is nearly the same as that of the PMP-based global optimal control strategy. Furthermore, the SQPIS also exhibits good adaptability under different initial battery SOC, cargo mass and road slope. The proposed strategy SQPIS has good robustness with unchanged weight coefficients and it is easy to be real-time implemented, so this strategy is extremely valuable in engineering application.
Author Contributions
Chaoying Xia gave the concrete ideas of proposed strategy, the specific algorithm and its engineering explanation. Zhiming Du and Cong Zhang performed the simulations. All of the authors wrote and revised the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Syed, F.U.; Ying, H.; Kuang, M.; Okubo, S.; Smith, M. Rule-based fuzzy gain-scheduling PI controller to improve engine speed and power behavior in a power-split hybrid electric vehicle. In Proceedings of the Fuzzy Information Processing Society, NAFIPS’06 Annual Meeting of the North American, Montreal, QC, Canada, 3–6 June 2006; pp. 284–289. [Google Scholar]
- Borhan, H.; Vahidi, A.; Phillips, A.M.; Kuang, M.L.; Kolmanovsky, I.V.; Cairano, S.D. MPC-based energy management of a power-split hybrid electric vehicle. IEEE Trans. Control Syst. Technol. 2012, 20, 593–603. [Google Scholar] [CrossRef]
- Cipek, M.; Pavković, D.; Petrić, J. A control-oriented simulation model of a power-split hybrid electric vehicle. Appl. Energy 2013, 101, 121–133. [Google Scholar] [CrossRef]
- Panday, A.; Bansal, H.O. A review of optimal energy management strategies for hybrid electric vehicle. Int. J. Veh. Technol. 2014, 2014. [Google Scholar] [CrossRef]
- Mohammadian, M.; Bathaee, M.T. Motion control for hybrid electric vehicle. In Proceedings of the 4th International Power Electronics and Motion Control Conference, Xi’an, China, 14–16 August 2004; pp. 1490–1494. [Google Scholar]
- Chen, L.; Zhu, F.; Zhang, M.; Huo, Y.; Yin, C.; Peng, H. Design and analysis of an electrical variable transmission for a series–parallel hybrid electric vehicle. IEEE Trans. Veh. Technol. 2011, 60, 2354–2363. [Google Scholar] [CrossRef]
- Fu, Z.; Wang, B.; Song, X.; Liu, L.; Wang, X. Power-split hybrid electric vehicle energy management based on improved logic threshold approach. Math. Probl. Eng. 2013, 2013, 840648. [Google Scholar] [CrossRef]
- Shabbir, W.; Evangelou, S.A. Real-time control strategy to maximize hybrid electric vehicle powertrain efficiency. Appl. Energy 2014, 135, 512–522. [Google Scholar] [CrossRef]
- Peng, J.; He, H.; Xiong, R. Rule based energy management strategy for a series–parallel plug-in hybrid electric bus optimized by dynamic programming. Appl. Energy 2017, 185, 1633–1643. [Google Scholar] [CrossRef]
- Khayyam, H.; Bab-Hadiashar, A. Adaptive intelligent energy management system of plug-in hybrid electric vehicle. Energy 2014, 69, 319–335. [Google Scholar] [CrossRef]
- Tian, H.; Lu, Z.; Wang, X.; Zhang, X.; Huang, Y.; Tian, G. A length ratio based neural network energy management strategy for online control of plug-in hybrid electric city bus. Appl. Energy 2016, 177, 71–80. [Google Scholar] [CrossRef]
- Zhang, S.; Xiong, R. Adaptive energy management of a plug-in hybrid electric vehicle based on driving pattern recognition and dynamic programming. Appl. Energy. 2015, 155, 68–78. [Google Scholar] [CrossRef]
- Yin, H.; Zhou, W.; Li, M.; M, C.; Zhao, C. An adaptive fuzzy logic-based energy management strategy on battery/ultracapacitor hybrid electric vehicles. IEEE Trans. Transp. Electrification 2016, 2, 300–311. [Google Scholar] [CrossRef]
- Hu, Y.; Li, W.; Xu, H.; Xu, G. An online learning control strategy for hybrid electric vehicle based on fuzzy Q-Learning. Energies 2015, 8, 11167–11186. [Google Scholar] [CrossRef]
- Prokhorov, D.V. Toyota Prius HEV neurocontrol and diagnostics. Neural Netw. 2008, 21, 458–465. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Mi, C.C.; Xu, J.; Gong, X.; You, C. Energy management for a power-split plug-in hybrid electric vehicle based on dynamic programming and neural networks. IEEE Trans. Veh. Technol. 2014, 63, 1567–1580. [Google Scholar] [CrossRef]
- Zhang, X. Multi-objective optimization of hybrid electric vehicle control strategy with genetic algorithm. Chin. J. Mech. Eng. 2009, 45, 36–40. [Google Scholar] [CrossRef]
- Chen, Z.; Mi, C.C.; Xiong, R.; Xu, J.; You, C. Energy management of a power-split plug-in hybrid electric vehicle based on genetic algorithm and quadratic programming. J. Power Sources 2014, 248, 416–426. [Google Scholar] [CrossRef]
- Zhao, L.Y.; Zhang, N.N. Energy control of HEV based on fuzzy controller optimized by particle swarm optimization. Adv. Mater. Res. 2014, 936, 2155–2159. [Google Scholar] [CrossRef]
- Chen, S.Y.; Hung, Y.H.; Wu, C.H.; Huang, S.T. Optimal energy management of a hybrid electric powertrain system using improved particle swarm optimization. Appl. Energy 2015, 160, 132–145. [Google Scholar] [CrossRef]
- Li, Y.; Kar, N.C. Advanced design approach of power split device of plug-in hybrid electric vehicles using dynamic programming. In Proceedings of the 2011 IEEE Vehicle Power and Propulsion Conference, Chicago, IL, USA, 6–9 September 2011; pp. 1–6. [Google Scholar]
- Ansarey, M.; Panahi, M.S.; Ziarati, H.; Mahjoob, M. Optimal energy management in a dual-storage fuel-cell hybrid vehicle using multi-dimensional dynamic programming. J. Power Sources 2014, 250, 359–371. [Google Scholar] [CrossRef]
- Larsson, V.; Johannesson, L.; Egardt, B. Analytic solutions to the dynamic programming sub-problem in hybrid vehicle energy management. IEEE Trans. Veh. Technol. 2015, 64, 1458–1467. [Google Scholar] [CrossRef]
- Kim, N.; Cha, S.; Peng, H. Optimal control of hybrid electric vehicles based on Pontryagin's minimum principle. IEEE Trans. Control Syst. Technol. 2011, 19, 1279–1287. [Google Scholar]
- Chen, Z.; Mi, C.C.; Xia, B.; You, C. Energy management of power-split plug-in hybrid electric vehicles based on simulated annealing and Pontryagin’s minimum principle. J. Power Sources 2014, 272, 160–168. [Google Scholar] [CrossRef]
- Hou, C.; Ouyang, M.; Xu, L.; Wang, H. Approximate Pontryagin’s minimum principle applied to the energy management of plug-in hybrid electric vehicles. Appl. Energy 2014, 115, 174–189. [Google Scholar] [CrossRef]
- Mansour, C.; Clodic, D. Dynamic modeling of the electro-mechanical configuration of the Toyota hybrid system series/parallel power train. Int. J. Automot. Technol. 2012, 13, 143–166. [Google Scholar] [CrossRef]
- Liu, D.X.; Zou, Y.; Liu, T. Modeling and control for the Toyota Prius under consideration of emissions reduction. In Proceedings of the IEEE Transportation Electrification Conference and Expo 2014, Beijing, China, 31 August–3 September 2014; pp. 1–5. [Google Scholar]
- Kim, N.W.; Lee, D.H.; Zheng, C.; Cha, S.W. Realization of PMP-based control for hybrid electric vehicles in a backward-looking simulation. Int. J. Automot. Technol. 2014, 15, 625–635. [Google Scholar] [CrossRef]
- Kim, N.W.; Rousseau, A.; Lee, D.H. A jump condition of PMP-based control for PHEVs. J. Power Sources 2011, 196, 10380–10386. [Google Scholar] [CrossRef]
- Kim, N.W.; Cha, S.W.; Peng, H. Optimal equivalent fuel consumption for hybrid electric vehicles. IEEE Trans. Control Syst. Technol. 2012, 20, 817–825. [Google Scholar]
- Peng, H. Modeling and control of a power-split hybrid vehicle. IEEE Trans. Control Syst. Technol. 2008, 16, 1242–1251. [Google Scholar]
- Tulpule, P.; Marano, V.; Rizzoni, G. Energy management for plug-in hybrid electric vehicles using equivalent consumption minimization strategy. Int. J. Electr. Hybrid Veh. 2010, 2, 329–350. [Google Scholar] [CrossRef]
- Onori, S.; Serrao, L.; Rizzoni, G. Adaptive equivalent consumption minimization strategy for hybrid electric vehicles. In Proceedings of the ASME 2010 Dynamic Systems and Control Conference, Cambridge, MA, USA, 12–15 September 2010; pp. 499–505. [Google Scholar]
- Sun, C.; He, H.; Sun, F. The role of velocity forecasting in adaptive-ECMS for hybrid electric vehicles. Energy Procedia 2015, 75, 1907–1912. [Google Scholar] [CrossRef]
- Xia, C.Y.; Zhang, C. Real-time optimization control algorithm of energy management strategy for hybrid electric vehicles. Acta Autom. Sin. 2015, 41, 508–517. [Google Scholar]
- Xia, C.Y.; Zhang, C. Power management strategy of hybrid electric vehicles based on quadratic performance index. Energies 2015, 8, 12458–12473. [Google Scholar] [CrossRef]
- Liu, J.; Peng, H.; Filipi, Z. Modeling and analysis of the Toyota hybrid system. In Proceedings of the 2005 IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Monterey, QC, Canada, 24–28 July 2005; pp. 134–139. [Google Scholar]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).