Abstract
Empirically based modeling is an essential aspect of design for a wave energy converter. Empirically based models are used in structural, mechanical and control design processes, as well as for performance prediction. Both the design of experiments and methods used in system identification have a strong impact on the quality of the resulting model. This study considers the system identification and model validation process based on data collected from a wave tank test of a model-scale wave energy converter. Experimental design and data processing techniques based on general system identification procedures are discussed and compared with the practices often followed for wave tank testing. The general system identification processes are shown to have a number of advantages, including an increased signal-to-noise ratio, reduced experimental time and higher frequency resolution. The experimental wave tank data is used to produce multiple models using different formulations to represent the dynamics of the wave energy converter. These models are validated and their performance is compared against one another. While most models of wave energy converters use a formulation with surface elevation as an input, this study shows that a model using a hull pressure measurement to incorporate the wave excitation phenomenon has better accuracy.
1. Introduction
Wave energy converters (WECs) must be designed to perform well and provide energy, often through operating at resonance, over the wide range of frequencies at which energy is carried by ocean waves. A number of studies have shown that more advanced control design for WECs has the potential to improve device dynamics to optimize energy absorption [1,2]. While a wide variety of control strategies can be considered, the successful design and implementation of these strategies generally relies on access to an accurate dynamic model of the WEC system. The full WEC system includes hydrodynamic wave-body interactions, mooring systems, mechanical/power-take-off (PTO), and power-electronic dynamics. As a first step, the various components of such a model can be obtained from numerical predictions. For example, boundary element method (BEM) solvers such as WAMIT [3] and NEMOH [4] are often used to obtain a linear hydrodynamic model. However, experimental testing is generally needed to insure, and improve, the accuracy of such models.
Standard practices for wave tank testing and model development of WECs have grown out of practices in the naval architecture field for ships and offshore oil and gas structures. In this approach, experiments are built around the linear decomposition model formulation commonly used for wave-body interaction, separating the problem in radiation and excitation components. Distinct tests are conducted, often using primarily monochromatic waves although polychromatic waves have also been used, for both the excitation and radiation components to determine the system response. Excitation and radiation frequency response functions can then be constructed from the discrete frequency components.
This approach, while systematic and time-tested, fails to utilize a number of system identification (SID) approaches which have proven greatly beneficial in other fields (see, e.g., Ljung [5], Pintelon and Schoukens [6]). The differences between a more general SID approach and traditional tank testing can be grouped into two major categories: experimental design and data analysis. Experimental design, in the framework of SID, is mostly defined by the excitation signals employed in testing. Periodic multisine excitation signals offer a number of attractive benefits for SID [6]. Since a linear time-invariant (LTI) system can only respond at the frequencies at which it is excited, a multisine excitation signal with carefully chosen frequency components provides an opportunity to perform systematic nonlinear distortion characterization. Additionally, by considering the n independent cycles from a periodic excitation, one may characterize the noise disturbance in the input/output system. Some key considerations and methods for SID data analysis are considered later in this paper.
Recent work to apply these general SID methods to WECs has been completed using a computational fluid dynamics based experiments [7,8]. In th is paper, we consider the application of these methods in a model-scale wave tank test of a WEC, focusing on the wave-body interaction component of the larger system model. First, we discuss the SID considerations and the procedures used to obtain models. Next, the test WEC device, experimental system and relevant hardware are summarized. Experimental data is then used to derive three separate models. The uncertainty of these models is considered and a systematic validation study is performed to compare the accuracy of the different models.
2. System Identification: Overview
SID methods are used across a range of engineering fields to produce dynamic models of various systems. While a wide variety of methods and approaches have been developed for SID, they are all focused on developing models that describe how the input of a system relates to its output. These models form the basis for system design, control design, and performance assessment.
2.1. Model Categories
The intended application of a model can often determine the most appropriate model structure and therefore the SID process used to construct it. White-box models use a first-principles understanding of the system to influence the model formulation. Black-box models map input and output behavior of a system without any specific physics-based structure. While white-box models can supply useful insights into the various factors that influence the behavior of a system, black-box models can be more straightforward to produce and sometimes provide a more accurate model which is still fully applicable for the task at hand (e.g., control design). Grey-box models do not follow a first-principles approach, but are based on some physical understanding. Within wave energy, the common linearly-decomposed radiation/diffraction formulation (see, e.g., [9,10]) is a good example of a grey-box model. Another mode of categorization exists with parametric and non-parametric models. Parametric models are described by parametric curves whereas non-parametric models are defined by a series of discrete points. Non-parametric models are often more straightforward to produce, while parametric models require some fitting procedures, which introduces a potential source of error. Parametric models have the advantage of providing physical insights, such as the locations of zeros and poles within a system, which can be helpful for control design. Non-parametric models are commonly used in wave energy in both the frequency- and time-domain. For example, boundary element methods (BEM) tools like NEMOH and WAMIT produce frequency response functions (FRFs), which are non-parametric frequency-domain models, for the excitation force and radiation force. Examples of time-domain non-parametric models are the impulse response functions (IRFs) used for the computation of the excitation forces and radiation forces. Non-parametric models in both time- and frequency-domain can be approximated using parametric models by means of fitting procedures, as shown for example in [11,12] for the radiation problem. Time-domain parametric models in the form of systems of first-order ordinary differential equations are known as state space models; these models are well suited to describe the behavior of both linear and nonlinear systems, and when the system is linear, these models can be written in the well known matrix form:
where u is the input to the system, y is the output and x is the state. The dynamic of the system is described by the matrix A, whereas B and C are, respectively, the input and output matrices, and D is the feedthrough matrix. For time-domain discrete-time systems, the state space model takes the form of difference equations. Frequency-domain parametric models for linear systems are generally described in the form of rational transfer functions in the Laplace domain, for continuous time models, or in the z-domain for discrete-time models [7]. Although the majority of the literature for frequency-domain models is concerned with linear systems, a generalization of the concepts of frequency-domain description has been provided also for some classes of nonlinear systems by means of Volterra series [13].
2.2. Experiments for System Identification
A fundamental step in the identification of dynamic models is the design of the experiment. The first aspect to be considered is whether a feedback loop is present in the system to be modeled. It is known from the theory that identification of a systems with output feedback (i.e. closed loop) is more sensitive to noise and, if the feedback block is “too simple” it may completely prevent identification of the plant (see, e.g., Section 13.4 in [5]). In the case of wave energy converters, a “closed loop” situation can occur any time the device is being controlled. In particular, devices are commonly tested using a linear damper to simulate the effect of the PTO, or tests for the identification of the radiation coefficients are carried out by prescribing motion (position or velocity). In all of these cases, if the test objective is SID, it is preferable to carry out experiments in the wave tank in “open loop”, as depicted in Figure 1. When the tests are carried out in closed loop, the input signals (e.g., PTO force, ) are calculated based on the output measurements. For example, considering the diagram in Figure 1a, the input , which is the PTO force, depends on the velocity, v, as , where C describes the dynamic of the control system (in the case of linear damping, C is simply a negative constant). However, ideally the input signals should be “rich” enough to excite as many dynamics of the system as possible that can be then observed in the measurements [5].
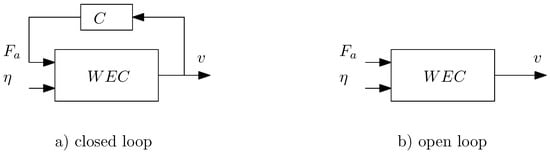
Figure 1.
Closed loop layout (a) compared to open loop layout (b).
A wave energy converter, at a very high level of abstraction, can be considered as a system with two inputs: the surface elevation, , and the force exerted by the PTO, , as depicted in Figure 1. It is general practice to assume the system to be linear for small motion and small waves, and thus apply superposition, which consists of modeling the effects of each input separately. In this case the system is considered to be composed of two single input single output (SISO) models, as depicted in Figure 2. The general procedure in wave tank testings is to apply only one input at a time: radiation is modeled by forcing the device without waves in the tank, and excitation is modeled by locking the device and measuring the force exerted by the waves. In practice, however, nonlinear effects are often present, and a better linear approximation can be obtained by applying both inputs at the same time. In this case, the system is considered as a multiple input single output (MISO). Performing experiments by forcing both inputs at the same time with independent inputs has two main advantages [6]:
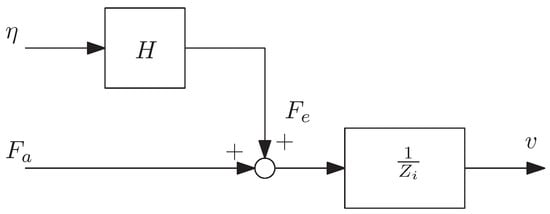
Figure 2.
Block diagram of the WEC base on radiation/diffraction model. The surface elevation is denoted by , the actuator force is and the velocity is v.
- Improved signal-to-noise ratio—For the same frequency resolution and RMS value, the signal-to-noise ratio is smaller; or for the same signal-to-noise ratio and RMS value, the measurement time is half as long.
- Increased range of physical regimes—Experiments where the system is tested using one input at the time (dual SISO) do not mimic the operational conditions, which may be a problem if the system behaves nonlinearly (i.e., single input tests may not reach the relevant physical regimes, therefore the test fails to observe important system dynamics).
Input signals are also particularly important for the identification process, as they affect the quality of the models, the data processing procedure and the time necessary to carry out the experiment, which translates directly into the cost of the experimental campaign (see, e.g., Section 13.3 in [5]). Among the most commonly used input signals are the filtered Gaussian white noise, random and pseudo random binary signal (PRBS), chirp signals (swept sinusoids) and multisines. The choice of these input signals is mostly dictated by the main goal of the experiment and the capabilities of the experimental system. These signals can be classified as periodic or non-periodic, each of which have their own advantages and disadvantages (see, e.g., [14]). Non-periodic signals have a higher frequency resolution for a given duration of the experiment; however, the spectrum is less smooth than a well designed periodic signal. In addition, dips in the power spectrum may results in higher noise sensitivity. Dips in the spectrum can be reduced by frequency smoothing, but only at the cost of decreased frequency resolution.
This concept is illustrated in Figure 3, which depicts the same Bretschneider spectrum, obtained by measurements in the wave tank using both periodic and non-periodic (“pseudo-random”) wave trains. The non-periodic wave train was generated for a 30 minute experiment using a very small frequency spacing so that the repeating period of the signal was 2 hours. The periodic wave train was generated with a lower frequency resolution, so as to have a repeat period of 5 minutes. For this experiment the input signal was repeated for two cycles, resulting in a total experiment duration of 10 minutes. For the periodic wave train, the spectral curve has been obtained by extracting exactly 10 minutes from the signal collected by a wave probe, and simply taking the discrete Fourier transform (via a fast Fourier transform: FFT). No other signal conditioning has been applied. Figure 3 also contains a curve of the smoothed spectrum of the non-periodic wave train. The smoothed spectrum is very close to the spectrum of the periodic wave train, but it has a lower frequency resolution. Figure 3 clearly shows that by using a periodic signal it is possible to generate smooth spectra with a high frequency resolution in a fraction of the time required when using non-periodic signals. One additional advantage of using periodic signals for SID is that it is possible to average over multiple periods to improve the signal-to-noise ratio, and to also estimate the noise level (see further discussion in Section 4.1.1 and Figure 16). Furthermore, when models are estimated in the frequency-domain, periodic inputs do not give rise to spectrum leakage, considerably simplifying the data processing, as will be illustrated in Section 4 andSection 5.
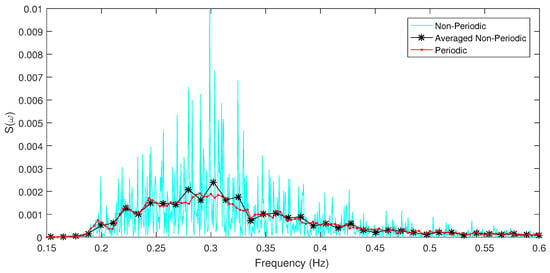
Figure 3.
Comparison of Bretschneider spectra from periodic and non-periodic experiments.
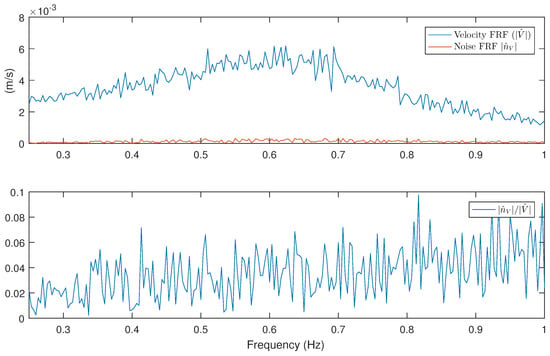
Figure 16.
FRFs of the velocity , of the estimated noise and of their ratio .
A final consideration regarding the design of the input signals should be given to the bandwidth. It would be ideal to generate spectra with a very large number of components over a broad frequency range so as to allow for the identification of the system’s FRF over a sufficiently wide band with a single experiment. However, keeping other factors such as amplitude and frequency spacing constant, broader bandwidths require higher power from the actuator (PTO or wavemaker). Therefore, when designing experiments for SID, a trade-off between amplitude and bandwidth may be required, such as, if the input signals require power larger than the power rating of the actuators. In these situations, one solution could be to perform multiple experiments over different frequency ranges and then combine the results.
3. Description of Experimental Setup
A 1/17th-scale WEC device was tested to provide data for SID and model validation [15]. This device, a diagram of which is shown in Figure 4, was designed to provide dynamics ranging from mostly-linear in a single degree-of-freedom to increasingly nonlinear in multiple degrees-of-freedom. For this study, the device was allowed to move in heave only. Table 1 lists the WEC’s relevant physical parameters.
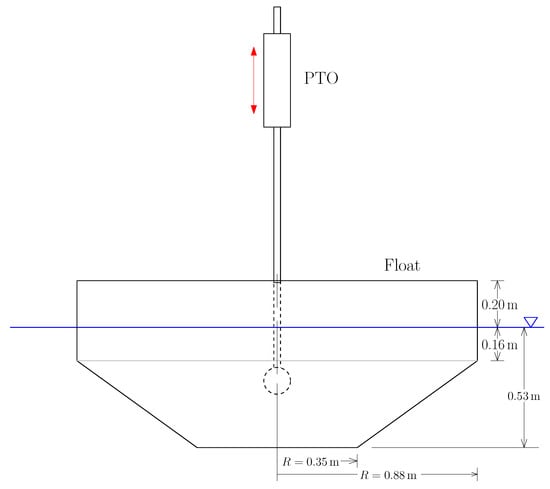
Figure 4.
Test device diagram.

Table 1.
Model-scale WEC physical parameters.
A LinMot P10-70x400U linear actuator driven by Tritium WaveSculptor 200 three-phase controller acted as the WEC’s PTO. A Transducer Techniques MLP-750 load cell, rated for 750 lbf (3340 N) was used to measure the force output by the actuator. For diffraction tests, in which vertical motion was restricted, a Transducer Techniques LPO-2K load cell, rated for 2000 lbf. (8900 N), was employed. A spherical rod-end joint was used to isolate this “lock-out” load cell from cross-loading.
Tests were conducted in the Naval Surface Warfare Center, Carderock Division Maneuvering and Sea Keeping (MASK) basin. As shown in Figure 5, the MASK basin has an overall length of 110m (360 ft), a width of 73m (240 ft) and a depth of 6.1m (20 ft) except for a 10.7m (35 ft) deep trench that is 15.2m (50 ft) wide and parallel to the long side of the basin (on the south side). The MASK basin is spanned by a 115m (376 ft) bridge, which is supported on a rail system that permits it to transverse to the center of the basin width as well as to rotate up to from the centerline as shown in Figure 5. Along the two edges of the basin opposite of the wavemakers, artificial beaches with a slope are used to reduce reflections. The beaches are composed of seven concrete layers and are effective in mitigating the mass flux of water back into the tank during wave generation. The hydrodynamic properties of the beaches are detailed in Brownell [16]. The MASK is equipped with a wavemaker system consisting of 216 individual paddle-style wavemakers. The wavemaker system uses a dry-back force feedback system, which is controlled via Edinburgh Designs Limited (EDL) runtime software.
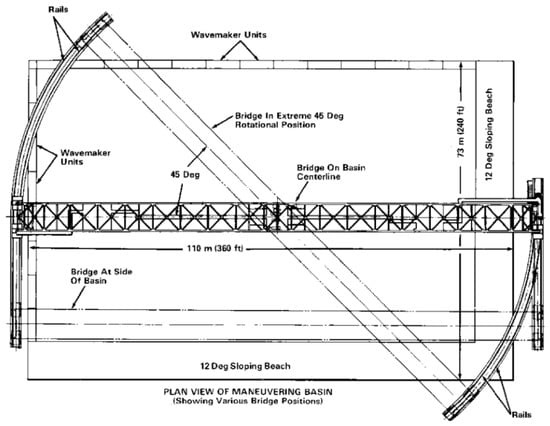
Figure 5.
Top view diagram of MASK basin with gantry bridge.
A number of sonic, capacitive and resistive sensors were used throughout the basin to measure incident, diffracted and radiated waves during testing. The locations of these sensors within the basin were recorded using a TotalStation survey tool. Figure 6 and Table 2 give the locations of the wave probes used for this study (“WP1”, “WP2”, and “WP3”) as well as the location of the test device (“Float”).
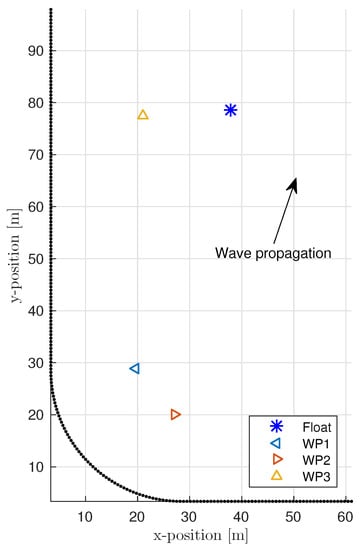
Figure 6.
Basin layout for testing with locations of wave probes (“WP1”, “WP2”, and “WP3”) and test device (“Float”). Wave propagation was at with respect to the x-axis.

Table 2.
Wave sensor locations in MASK basin.
The wavemaker paddles in Figure 6 are shown along the x and y axes. Figure 6 also shows the path of wave propagation within the basin, which was with respect to the x-axis.
Measurements from hull mounted pressure sensors were utilized in this study. Data was collected from over thirty pressure sensors located on the hull of WEC (see [15] for more details on pressure sensor locations). Pressure data for this study was measured with sensor “PT-01”, as depicted in Figure 7. This sensor is located near the max draft of the float, at incidence to incoming waves.
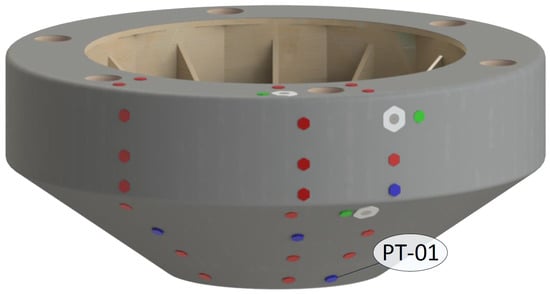
Figure 7.
Pressure sensor locations on the hull of WEC test device.
Data collected from this testing campaign is publicly available at https://mhkdr.openei.org/submissions/151 [17]. A test log, with three-digit dataset identifiers, is also available for download. Throughout this paper, specific references to datasets used for certain SID and validation steps are provided. Table 3 provides a listing of these experiments/datasets.

Table 3.
Experimental datasets utilized in this study. For experiment 105, both the wave train and actuator input are non-periodic: in particular, the actuator input is a band-limited white noise (BLWN) and the wave spectra is Bretschneider (BS) (* indicates reseeded phasing).
4. WEC Modeling in the Classical Framework: Radiation and Excitation
This section examines the radiation/diffraction formulation for WEC modeling. First the general formulation is considered, next separate radiation and excitation components are discussed and models for these systems are constructed. The composite model formed by combining the radiation and diffraction blocks is then validated. Finally, a slightly altered approach, viewing the WEC as a MISO system, is examined.
The traditional radiation/diffraction model often used for reduced-order modeling of WECs can be constructed from two components. A block diagram for this system is shown in Figure 2. Here, the excitation FRF is denoted by H and the intrinsic impedance, which combines the hydrodynamic radiation effects with inertia and hydrostatic stiffness, is denoted by . The frequency-domain equation of motion of the WEC as depicted in Figure 2 is
where is the velocity of the buoy, is the surface elevation and is the force exerted by the actuator/PTO; the hat symbol denotes that these variables are complex quantities defined in the frequency-domain. The mass of the buoy is denoted by M, the hydrostatic stiffness is denoted by K and is a friction coefficient describing losses in the system which are proportional to the buoy velocity (more details on considerations for friction will be provided in Section 4.1.1). The hydrodynamic interactions are described by the added mass , the radiation damping and the excitation force coefficients , which is used for the calculation of the excitation force as
According to the diagram in Figure 2, and by defining the intrinsic impedance as [10]
The model of the WEC in (2) can be decomposed by applying superposition as
Before proceeding with the data analysis, it is helpful to make an important observation regarding the dual SISO model in Figure 2. In general, the quantity is calculated by forcing the buoy with a known force and then measuring its response in terms of velocity (it has been discussed in Section 2.2 why internal feedback loops are undesirable for SID and how it is thus more desirable to prescribe the force exerted on the device, rather than prescribing its motion), when waves are not being generated by the wavemakers.The quantity H can be calculated by locking the device in place, and by measuring the force that waves exert on the locked device. It is common practice to calculate H by first calibrating the surface elevation, a procedure that consists of placing a wave probe in the location of the buoy when the buoy is not present, and then record the surface elevation time series. The buoy is then put in place and the same wave time series are run again, this time measuring the force on the buoy caused by the waves. This procedure seems to be the only option for the calculation of the excitation coefficients H based on the most straightforward conceptual definition. However, for control purposes this procedure is of little use, since it is clearly not possible to measure the surface elevation at the point where the device is located, once the device is in place.
It is more realistic then to use a wave probe at a certain distance from the device, and measure both the force on the WEC and the surface elevation at the same time. In this case, however, the diagram in Figure 2 does not apply anymore, as the signal measured by the wave probe will contain also a component due to the radiation and scattering effects generated by the buoy, as depicted in the diagram in Figure 8. The scattering effects are only due to the presence of the buoy itself, they do not depend on the motion or other states of the system, therefore for the sake of control purposes, these effects can be embedded into the excitation function H, and can be taken into account when designing the controller and estimator. The radiation component of the measured surface elevation, , can be taken into account by means of the block , which provides a model for the radiated wave as function of the velocity. For control and estimation design purposes, the system in Figure 8 can still be modeled as a two-input one-output system by considering the total surface elevation as input by some mathematical manipulation. In fact, the diagram in Figure 8 can be reshaped to obtain the equivalent diagram in Figure 9. The output, v, is
By rearranging and solving for the velocity, v, as
the result is the two-input linear system in Figure 9.
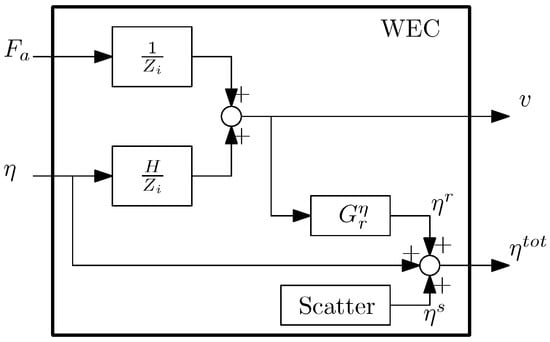
Figure 8.
Block diagram of the system when including effects of radiated and scattered waves on the surface elevation measurements. The measured surface elevation includes terms due to the scattered waves and radiated waves , in addition to the incoming wave train .
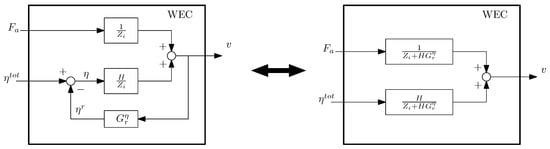
Figure 9.
The diagram in Figure 8 can be rearranged as a two input system where the total surface elevation is considered as an input.
It is possible to derive the blocks H and by using the formulation in (7), as will be shown in Section 5 in a case where the input is pressure rather than surface elevation. However, in this case we are exploiting the fact that the amplitudes of the radiated waves are inversely proportional to the distance from the buoy [10]. Therefore, if the distance between the buoy and the wave probe is large enough, the term describing the radiated waves becomes very small (, and (7) becomes equal to the original model of the WEC described by (5). In fact:
For this study, we have followed this approach and we have used data from wave probes located at a large distance in front of the device (WP1 and WP2 in Figure 6).
4.1. Intrinsic Impedance and Radiation Impedance
The results presented in this section have been obtained by applying a periodic PTO force signal to the buoy. Two types of periodic signals have been used: “white” type of multisine, where all the frequency components have the same amplitude, and a “pink” type multisine, where the amplitude of each component is inversely proportional to the frequency. In both cases, the phase has been obtained by minimizing the crest factor, that is the ratio between the peak value and the RMS value of the signal. The magnitude of the spectra for the white and pink multisines are shown in Figure 10 and Figure 11, respectively.
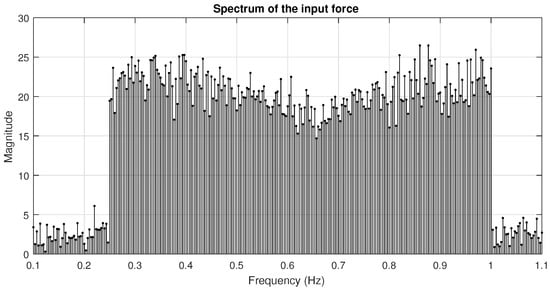
Figure 10.
Spectrum of the input force: “white” (flat) multisine.
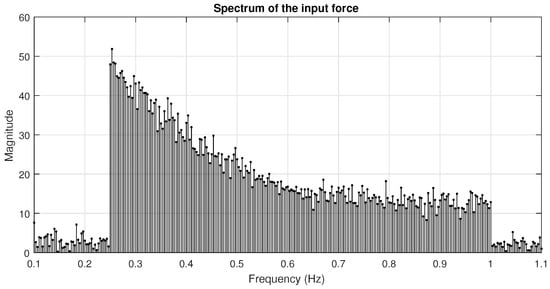
Figure 11.
Spectrum of the input force: “pink” multisine.
The FRF of the intrinsic impedance can be calculated from the experimental data by taking the ratio
where and are, respectively, the estimated force and velocity, described as complex quantities in the frequency-domain. The values of and can be calculated using the discrete Fourier transform via the FFT when the input signals are periodic, by trimming the time series so its total length is equal to an integer multiple of the period of the signal. If this condition is satisfied, the frequency transform of the signal is not affected by spectrum leakage (see, e.g., [6]). For example, the result presented in this section have been obtained by sampling the signals at 20 Hz, and the period of the multisines is 300 s; therefore each period contains 6000 samples. In order to avoid spectrum leakage, it is necessary to extract a number of samples equal to:
where is a positive integer number.
As discussed in Section 2.2, one of the advantages of using periodic signals is the possibility of averaging the signals over multiple periods in order to reduce the effects on noise and nonlinearities. Returning to the previous example, the procedure is to divide the time series in segments of 6000 samples, take the FFT of each of the segment and then average their transformed value. In particular, if is the discrete Fourier transform obtained by taking the FFT of the k-th segment of 6000 samples, the estimated velocity is obtained be taking the average:
The same procedure applies for the force .
4.1.1. Nonparametric Models
Nonparametric models for the intrinsic impedance in the FRFs can be calculated by applying (4) and (11). Figure 12 depicts the FRF of calculated using data from experiment 089, in which the buoy has been forced with a pink multisine. Here, the FRF is shown in terms of magnitude, , phase, , as well as real part, and imaginary part, . The experimental response is compared to the intrinsic impedance obtained using WAMIT to calculate the radiation and excitation terms. The plots show that the mismatch between the numerical and the experimental data is mostly due to the real part of the intrinsic impedance. In particular, it seems that the mismatch in the real part is due to an offset. Using the definition of the intrinsic impedance in (4), the probable cause of the mismatch can be attributed to friction in the system, described by the term .
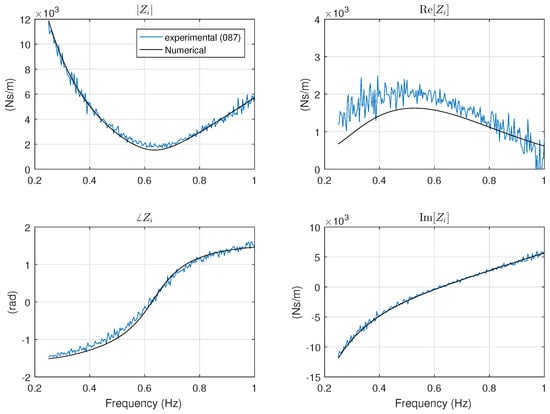
Figure 12.
FRF of the intrinsic impedance calculated from one experiment. The figure also shows the FRF of calculated numerically using WAMIT and the physical properties of the buoy.
A deeper investigation into this issue shows that the friction term is indeed dependent on the type of experiment, which means that it is behaving in a nonlinear fashion. This can be confirmed by looking at Figure 13. It is evident that the offsets in the real part of between the curve obtained by numerical simulation and the experimental curves depends on the type of experiment. In particular, the damping is larger for smaller amplitude of the forcing signal. In fact, the real part of can be considered as an equivalent linearized friction term , which is related to the RMS value of the buoy velocity. Figure 14 shows a scatter diagram of the equivalent linear damping as function of the inverse of the 2-norm of the buoy’s velocity. The plot also shows that the relation can be closely approximated by a linear function of the inverse of the 2-norm of velocity, that is
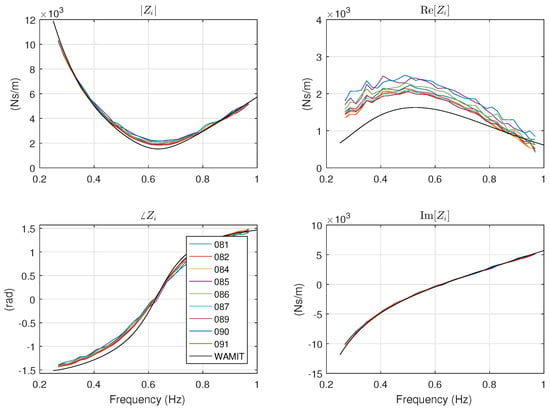
Figure 13.
Intrinsic impedance estimated from all the experiments. Frequency smoothing has been performed over a window of 12 frequencies.
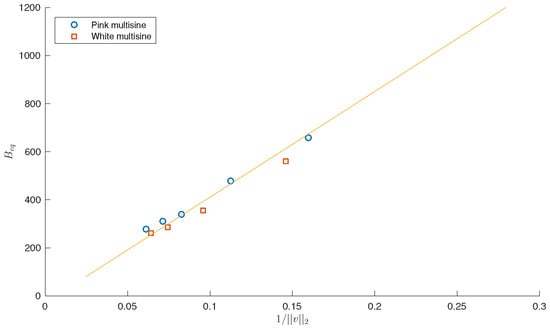
Figure 14.
Equivalent linear damping is linearly proportional to the inverse of the 2-norm of the buoy velocity ().
By using (12) to estimate the equivalent linear damping, the mismatch between experimental data and numerical simulation can be significantly reduced, as shown by Figure 15. However, two observations have to be made by looking at : first, of all the plots from the experimental data closely overlap, and second, there is still a smaller frequency dependent offset between the the experimental data and the numerical simulations. The overlap between the experimental curves confirms that the the approximation of the friction using a frequency independent coefficient is acceptable. The frequency dependent offset between the experimental and numerical results can be attributed to the inaccuracy of the numerical calculations. The practical implication of this linear approximation for the nonlinear friction is that it may be possible to use local linear models to obtain a good description of the system in specific working conditions. That is, for a given sea state, it may be possible to estimate the RMS value of the velocity, and then estimate the equivalent linear friction , which will then be used as in (4).
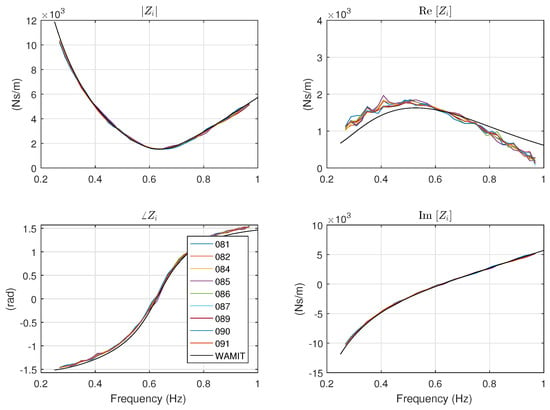
Figure 15.
By using the linearized equivalent damping in (12), the offset in the real part of the intrinsic impedance has been significantly reduced.
When working with experimental data, it is important to estimate the level of noise or distortion in the signals (see, e.g., [5,6]). By using periodic input signals, the separation of noise from the estimated signal can be carried out by subtracting the estimate value from the measured signal. As discussed previously, an estimate of the signal can be obtained by averaging over a number of periods from the measured time series. For example, let be the signal measured in the experiment, the duration of which is N periods. The signal is first divided into N segments , for , each of which with a duration of one period. An estimate of the signal in the time-domain can be obtained as
and the noise in the k-th interval can be obtained as
As an illustrative example, the top plot in Figure 16 shows the magnitudes of the Fourier transforms of the velocity and of the noise, calculated as described by (14). The bottom plot shows the ratio between the magnitude of the noise and the magnitude of the estimated velocity as function of the frequency. For this case, the ratio is generally on the order of 5%.
Radiation Force Modeling
It is sometimes desirable to estimate the values of the radiation damping, , and added mass, . From the expression of the intrinsic impedance in (4), the estimated values of the radiation components and can be calculated as
where is the estimated value of the intrinsic impedance obtained using (9). The quantities K and M were calculated based on geometric measurements of experimental model. The linear friction terms , has been calculated using the linear approximation previously described in (12). Figure 17 shows the estimated FRFs of the radiation damping and added mass calculated from all the forced oscillation experiments 081-091.
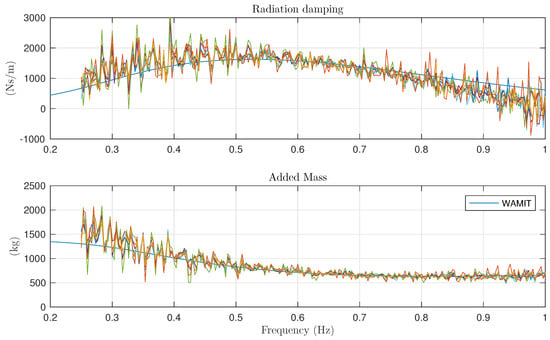
Figure 17.
Comparison of radiation damping and added mass provided by WAMIT and calculated from all the forced oscillation experiments 081-091.
4.1.2. Parametric Models
As discussed in Section 2, it is sometimes useful to produce a parametric model of a system. In this section, two approaches will be described: in the first part the modeling will be carried out in a Black box framework, where the intrinsic admittance , defined as the inverse of the intrinsic impedance (), will be identified directly from the input/output data. The reason for considering the admittance rather than the impedance is due to the definition of the inputs and the outputs. When using the admittance, the input of the system is force and the output is velocity, which is the same as in the real situation, where the motion of the buoy (output) is caused by the force exerted by the actuator (input), that is
In the second part, SID will be applied to produce a Grey box parametric model of the radiation part, which will be included in the WEC model using first principle derivations.
Black Box Modeling
Black box SID of the intrinsic admittance has been performed using the MATLAB function tfest (included in the System Identification toolbox), which computes an estimation of continuous-time transfer functions. The data used for the SID is the same that has been used for the derivation of the nonparametric models described in Section 4.1.1. Bode plots of the parametric models of are shown in Figure 18; the same figure also shows nonparametric FRFs of . Each curve corresponds to a different experiment, which makes it very clear that the system shows a nonlinear behavior. This can be further confirmed from the pole-zero map shown in Figure 19.
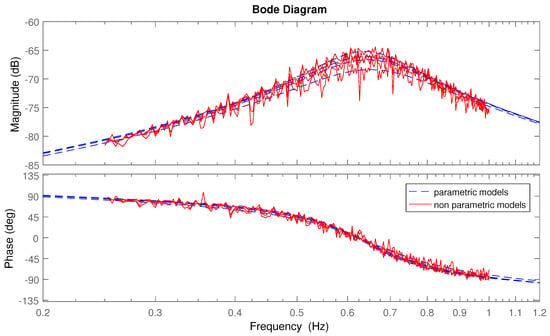
Figure 18.
FRFs and Bode plots of parametric models of the intrinsic admittance for different experiments, showing nonlinear behavior as the response depends on the experiment.
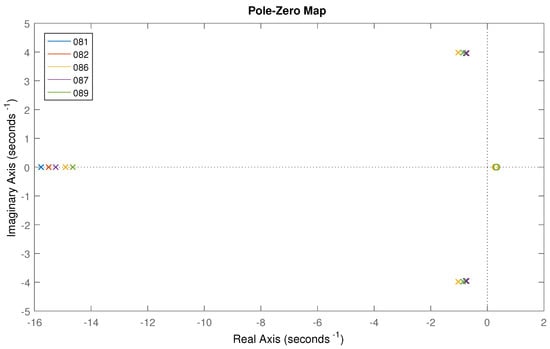
Figure 19.
Pole-zero maps of the intrinsic admittance from different experiments (experiments: 081, 082, 086, 087 and 089).
Based on the observation discussed in Section 4.1.1 regarding the relation between the 2-norm of the velocity and the equivalent linear friction (12), for practical purposes it may be convenient to identify one parametric model with zero friction, and then “tune” the model based on the 2-norm of the velocity by means of the equivalent friction term. This can be done by considering the intrinsic admittance with zero equivalent friction , where . The intrinsic admittance can then be written in terms of and as
In this case, only one model needs to be identified in order to have a whole family of parametric models, that can be tuned by choosing the equivalent friction terms using (12). Figure 20 shows the Bode plots and the FRFs of for a number of experiments. The resulting models overlay each other closely, confirming that the model is the same for all the tests. The corresponding pole-zero maps are shown in Figure 21, which also confirms the similarities between these models for . Comparing this mapping with the models shown in Figure 19 confirms that the parametric models for the admittance obtained from different experiments are very similar. In fact, the pair of complex conjugate poles and the (non-minimum phase) zero in Figure 21 are almost overlapped for , whereas in Figure 19 the position of the pair of complex conjugate poles depends on the experiment. However, in both cases the poles on the real axis are dependent on the experiment, although they are not the dominant poles and they do not have a big effect on the response of the system.
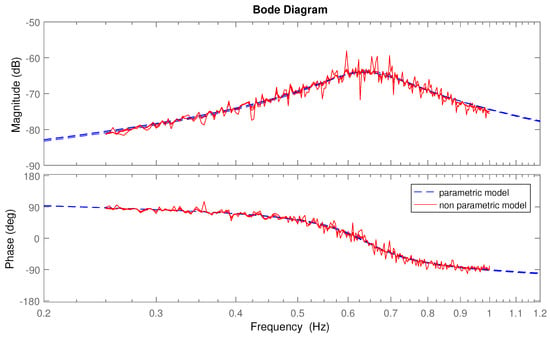
Figure 20.
Bode plots and FRFs of the intrinsic admittance with zero friction .
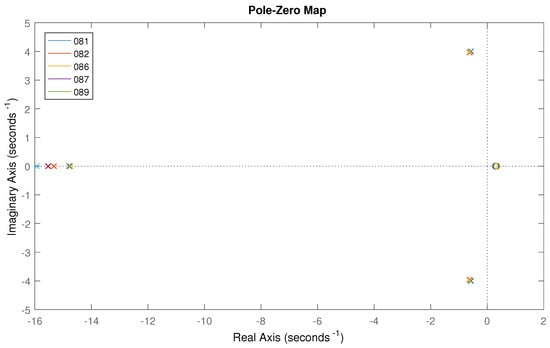
Figure 21.
Pole-Zero maps of the intrinsic admittance with zero friction .
Grey Box Modeling
In the Grey box model approach for the radiation of a floating body, the intrinsic impedance is decomposed as
where is the asymptotic value of the added mass for , is the radiation impedance defined as
Thus, is defined as
The reason for subtracting from is that the added mass does not converge to zero as , thus the inverse Fourier transform of the radiation impedance does not exist. However, converges to zero “fast enough” as , so the quantity can be inversely Fourier transformed (see, e.g., [10,12]). The asymptotic value used in this paper has been obtained from WAMIT, although it can also be estimated, e.g., with the FDI toolbox [18]. If the inverse Fourier transform of the quantity exists, then its inverse is the impulse response , that is
where denotes the Fourier transform operator. By using the impulse response , the radiation force can be written, in the time domain, as [9]
where denotes the velocity in the time domain. The last term on the right hand side is a convolution integral that can be interpreted as the solution of a system of linear ordinary differential equation, i.e., the input-output response of a linear dynamical system [19]. In the literature, several approaches have been proposed and used to described the radiation component in terms of parametric models, among which the most common are the approximation of the impulse response by means of Prony’s method [20], the approximation of the convolution integral with a state space model [11], and the approximation of with a transfer function [18]. In this paper we follow the last approach, where SID is carried out to obtain a transfer function approximating from frequency domain data. By rearranging (19), the term can be written as
where (9) has been used to write the intrinsic impedance in terms of the measurements and . All the terms on the right hand side of (24) are known, and the system identification can be carried out using the MATLAB function tfest. The algorithm used by the function tfest considers the system to be described by a parametric model in the “Output-Error” form, and it calculates the coefficients of the transfer function by minimizing the prediction error [5].
Figure 22 illustrates the Bode plots of the parametric models for obtained by processing data from different experiments. This comparison shows a good agreement among the models. Agreement amongst the models can also be confirmed from the pole-zero map in Figure 23, which shows that the poles are all clustered in a small region. All of the models, however, exhibit a zero in the right hand plane, meaning that all of the models are non-minimum phase (The model obtained from experiment 083 has the zero on the left had side of the complex plane; however, it is very close to the imaginary axis and, due to the large uncertainty, its 95% confidence interval crosses into the the right hand side of the complex plane.) [19]. Figure 22 also shows the 95% confidence interval around the frequency response curve of the models, indicating that, although the data seems noisy (i.e., FRFs are not smooth) all the parametric models have a low uncertainty, especially in the range around resonance ( Hz).
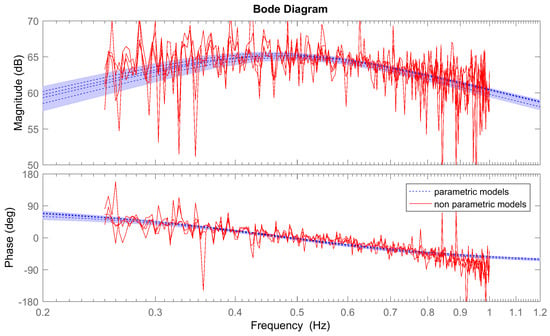
Figure 22.
Comparison of Bode plots and FRFs of obtained from different experiments (experiments: 081, 082, 086, 087 and 089). The 95% confidence interval is the shaded area around the magnitude and phase plots of the parametric models.
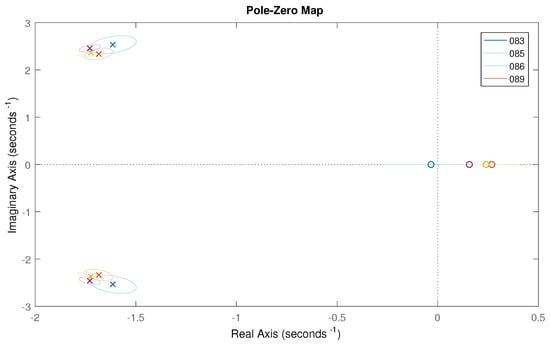
Figure 23.
Pole-zero maps of the parametric models for obtained from different experiments (experiments: 081, 082, 086, 087 and 089). The 95% confidence interval is shown as a circle around the poles and a line for the zeros.
Comparison of Grey Box and Black Box Models, and Cross-Validation
Before comparing the dynamic properties of the Grey box model with the Black box model, it is necessary to reconstruct the intrinsic admittance from the , as described in (19). The comparison can be made at first by looking at the Bode plots in Figure 24, showing that there is a slight disagreement mostly around the resonance peak ( Hz), in terms of both magnitude and phase. It is much more informative to look at the pole-zero map in Figure 25. Here, one can see clearly that both the Black box and the Grey box models have a pair of complex conjugate poles in the same location which dominate the response. In fact, their imaginary value (∼4 rad/s) corresponds to the resonance frequency of the device which is Hz rad/s (see peak in Figure 24). The Grey box model shows a pair of complex conjugate poles close to a pair of complex conjugate zeros, leading one to suspect that their effect is so small that they almost cancel each other (since the Black box model has not identified any pole or zero around that area). On the other hand, the Black box model has a pole on the real axis with a fast decay (far on the left hand side of the plot), and a zero on the right hand side of the complex plane (non-minimum phase). The Grey box model has a zero at the origin, which is quite close to the positive zero of the Black box model. This may be due to the fact that the frequency range of input signal used for the identification is limited to the interval Hz, and there is not enough power at low frequency to correctly detect the location of that zero.
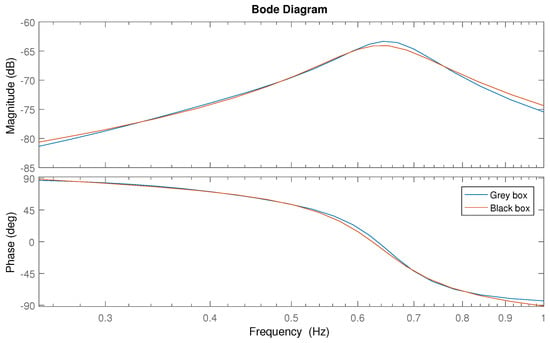
Figure 24.
Comparison between the Bode plots of the Black box and the Grey box models.
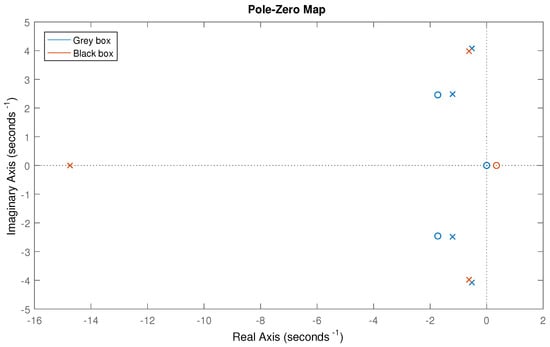
Figure 25.
Comparison between the Pole-Zero maps of the Back-box and the Grey-box models.
Comparison between the Black box model and the Grey box model has also been carried out through cross-validation. In this case, the models have been identified with a set of data from one experiment, then the models have been used to simulate a different experiment, using as inputs the recorded data. The fitting is calculated as the normalized RMS (NRMSE) value of the error between the simulated response and the measured response.
where the NRMSE is the normalized root means square error calculated as
and where is the validation (simulated) time series, is the experimental time series, and is the mean value of the experimental time series.
As an illustrative example, Figure 26 shows the time series of the output velocity calculated with both the Black box and Grey box models, compared to the measured velocity. Models have been identified using a pink spectra for the force (experiment 091), whereas the validation has been carried out using white multisine with a different amplitude (experiment 085). The friction term has been adjusted according to the approximation in (12). In this situation, the Black box model performed marginally better as it resulted in a 96% fitting compared to 94% of the Grey box model.
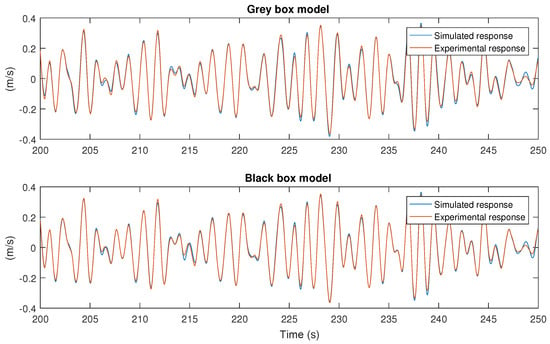
Figure 26.
Time-domain responses of the both the black box model and the grey box model, compared to the experimental response. The identification has been carried out using experiment 091 and validation has been carried using data from experiment 085, where the linear equivalent damping has been adjusted according to (12).
4.2. Excitation Force Modeling
Two methods have been used to obtain a model for the excitation of a WEC. First, the traditional approach was employed in which the device is locked; then, a second approach was used which does not require the device to be locked.
4.2.1. Estimation of the Excitation FRF from Diffraction Tests
Using the data from a diffraction test, in which the locked device is subjected to incoming waves, the excitation FRF can be determined from
where is the force measured on the lockout load cell (i.e., the force required to prevent the buoy from moving) and is the surface elevation measured with a wave probe. Using data from experiment 010, (27) produces the FRF shown in Figure 27. Results are shown using three different wave probes for (WP1, WP2, and WP3, see Table 2 for details). The excitation FRF magnitudes in Figure 27 show good agreement with numerical results provided by WAMIT, and are fairly consistent between the FRFs obtained via different wave probes. However, for frequencies between 0.3 Hz and 0.5 Hz, the experimental results and the numerical analysis show a small variation. Additionally, for frequencies below 0.3 Hz, there is a small difference also among the experimental curves, particularly the FRF obtained by WP3 when compared to WP1 and WP2. These effects are likely caused by reflections, because of the imperfect ability of the beaches to absorb waves at all frequencies. The phases of the excitation FRFs show larger variation. This is due to the fact that the wave probes are all located in different locations. Thus, the nonlinear dispersion of the waves as they propagate from each wave probe to the device creates a unique frequency-dependent phase shift. The FRF from WAMIT uses the wave phase at the location of the device, but as discussed previously in Section 4, measuring waves at the device location is rather impractical.
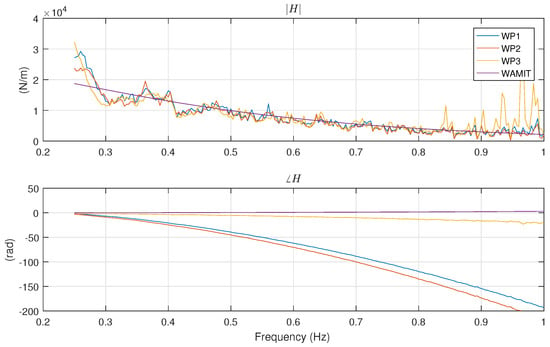
Figure 27.
Excitation FRFs for different wave probes and comparison with WAMIT.
4.2.2. Estimation of the Excitation FRF without Locking the Buoy
An alternative approach to producing an excitation model has been employed here to explore methods applicable for SID of full-scale WECs at sea. For this procedure, data from two experiments has been used. The first step is to determine the radiation FRF using forced oscillation tests (see Section 4.1.1). In the second experiment, the device is subject to both waves and force from the actuator (i.e., a dynamic response test). The process can be summarized as
- Execute forced oscillation experiments in calm water to obtain a model of the intrinsic impedance as described in Section 4.1.1 and obtain either a parametric or nonparametric model for .
- Execute the forced oscillation experiment in presence of waves. In this case, the available measurements are the actuator force (), the buoy velocity (v) and the surface elevation (). By using the frequency-domain equation of motionit is possible to write the excitation FRF as function of the known quantities as:
Following this procedure, a second empirical excitation model was produced. Steps 1 and 2 were conducted using data from experiments 087 and 112 respectively. The FRF for this model (“Lock OFF”), along with that from the traditional diffraction test (“Lock ON”) and WAMIT, is shown in Figure 28. Both the “Lock OFF” and “Lock ON” models here used the WP1 surface elevation. This alternative approach to obtain an excitation model shows very good agreement with both the numerical model and the model obtained using a diffraction test.
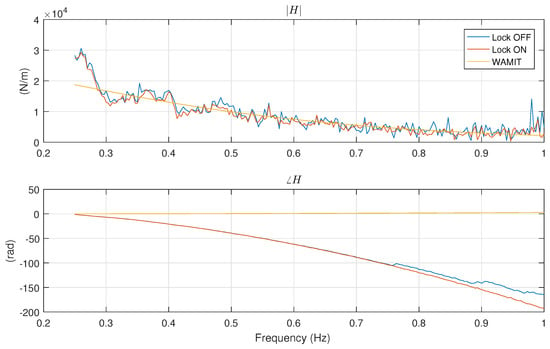
Figure 28.
Excitation FRFs obtained from experiment with locked and unlocked device. The surface elevation is measured using the capacitive probe named “WP1”.
4.3. Validation of Combined Model
Using the intrinsic impedance and excitation models developed in Section 4.1 and Section 4.2.1 respectively, a model for the WEC was constructed in the common radiation-diffraction formulation according to the diagram in Figure 2. In particular, the radiation and excitation parts have been modeled separately with completely different types of experiments (experiments 091 and 010 for the impedance and excitation models respectively). In this section the two models are combined to form a complete model for the wave-body interaction of the WEC, which is validated using an experiment where both waves and actuator force are applied to the buoy. It is worth noting that the experimental conditions used for validation are completely different from the experiments used for the modeling process.
The first step for the validation is to calculate the excitation force as in (3). Here, this is done using the surface elevation measured during experiments 109-117, and the frequency response function H obtained as described in Section 4.2. The excitation force is added to the input force and the frequency-domain model is given by
where is the parametric model for the intrinsic admittance. Time-domain simulations can easily be performed by converting from transfer function to state space form; this process is called realization and it is easily computed, in MATLAB for example, by the command ss included in the Control System toolbox, which returns a linear model in state space form, when the input is a transfer function. Cross validation results are shown in Figure 29, for both the Black box and Grey box models, where data from experiment 115 has been used for validation. In this case, the fit for the Black box model, according to the metric in (25), is 85%, whereas the fit for the Grey box model is 83%.
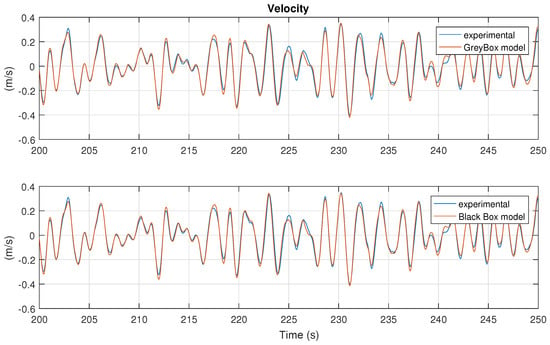
Figure 29.
Validation for Grey box and Black box models using experiment 115, where waves have a pink multisine spectrum and also the actuator’s force has a pink multisine spectrum.
4.4. WEC Model as Multiple-Input Single-Output System
Up to this point in our study, the WEC has been considered as composed of two blocks, one describing excitation effects and the second one describing the radiation effects. Each of the blocks have been identified (modeled) using different experimental configurations and data processing. This is in-line with the classical radiation/excitation approach most commonly used in WEC modeling. In this section, it is shown how the WEC can be modeled as a two-input system, using several executions of the same type of experiment, to obtain a global model of the device. It is also shown how the model obtained via this approach is equivalent to the classical radiation/excitation approach. In addition to the considerations discussed in Section 2.2, for the specific case of WECs, this MISO approach allows for at-sea SID of full scale devices, without the need for locked excitation tests.
According to Pintelon and Schoukens [6], it is possible to build a model for a two-input one-output system by running two experiments in which all the inputs are independent from each other. For the experiments described in this section, both inputs (actuator force and waves) have pink spectra. The phases of each input have been randomized (and are unique for each experiment).
Let be the frequency response matrix (FRM) for the frequency component k, the matrix of the inputs and the k-th frequency component and the matrix of the outputs. The system can then be described, for each frequency component, as
For the case considered in this section, the output matrix contains the k-th frequency component of the velocity for all the experiments:
where is the k-th frequency component of the velocity for the i-th experiment. Similarly, the input matrix is defined as
In this case the FRM, is a 1 by 2 complex matrix as
The estimation of the FRM G can then be carried out from
(31) as
It is clear that the estimation of G relies on the matrix not being singular for any k, hence the requirement for the input signals to be independent. A discussion on the techniques to build input signals for this type of experiments can be found in Pintelon and Schoukens [6], Section 2.7.2.
By comparing the definition of the matrix G in (31) and (5), it is possible to derive the equivalence between the blocks of the “classical” dual SISO model in Figure 2 and the blocks and composing the multiple input models described in this section. In particular, we can see that
Figure 30 shows the comparison between the components of the FRM G and the components of the dual SISO approach, showing good agreement over most of the frequency range.
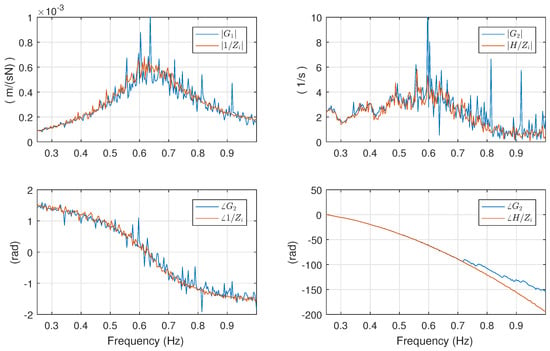
Figure 30.
FRFs of the 2-input, 1-output black-box model for the WEC. Here, the surface elevation is measured in inches and the force in kN.
5. WEC Modeling Using Pressure
A common area of interest in the modeling of WECs is the non-causal excitation model (see, e.g., [21]). When a time-domain model is produced for the excitation FRF (), a non-causal impulse response results. The true nature of the excitation phenomenon is indeed causal, but the choice of surface elevation as the input to the model results in this non-causal behavior. The incoming wave is the cause of both surface elevation and orbital fluid velocities. The orbital velocities of the wave (and the hydrodynamic pressures which they create) represent a better (more direct) input to the excitation model.
Based on this concept, it is possible to consider a modeling approach analogous to the case where surface elevation is the input (Figure 2), but where the inputs are the force exerted by the actuator and the pressure on the hull, as depicted in Figure 31. In this case, the block describes the dynamic between the pressure, p, measured at some point(s) on the hull of the device, and the excitation force , and is the usual intrinsic impedance. The block can be estimated in the same manner as for the excitation function H, as described in Section 4.2, that is by locking the device and estimating the function between the force and the pressure. The resulting FRF of is shown on the right-hand side Figure 32 in terms of its real and imaginary parts.
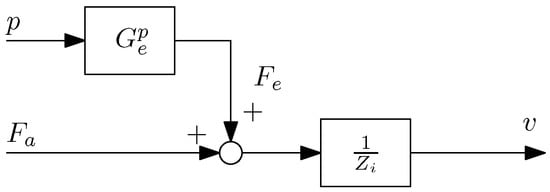
Figure 31.
Bock diagram of the two input one output structure (dual SISO).
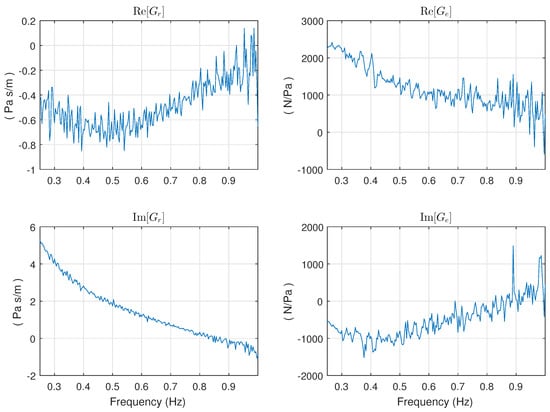
Figure 32.
FRFs of the radiation and excitation models using pressure (from experiments 089 and 010 respectively).
As discussed in Section 4, in a real experimental setup, a measurement of the pressure also includes effects due to radiation, thus a more appropriate block diagram is the one depicted in Figure 33. This diagram includes one additional block compared to the one in Figure 31, , which describes the dynamic between the velocity of the buoy and the pressure on the hull. This block can be estimated using the same experiments and similar data processing as used to estimate the intrinsic impedance . In particular, if we let be the discrete Fourier transform of the pressure and the discrete Fourier transform of the velocity, the function is
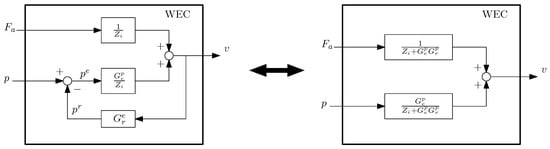
Figure 33.
Bock diagram of the MISO structure.
The left-hand side of Figure 32 shows the FRF of in terms of its real and imaginary parts. As one can see thus far, modeling of the WEC using pressure can follow a similar path as for surface elevation (dual SISO) discussed in Section 4; however, there is a fundamental difference. In Section 4 we have assumed that the contribution of radiation to the measured wave was negligible () because we have used signals from wave probes located at a large distance from the buoy. In this case, when using pressure, this assumption cannot be made because the pressure transducers are located directly on the hull of the device.
One of the objectives of this section is to validate the structure of the MISO models in Figure 33 using experimental data, against the classical dual SISO approach in Figure 31. A second objective of this section is to study the possibility to use pressure signals in order to predict the response of the WEC. Both objectives are of fundamental importance for the design of model based control systems and state estimators (e.g., Kalman filters).
In order to fulfill the first objective, that is to validate the models in the diagrams in Figure 33, the first step is to estimate a MISO model using the approach described in Section 4.4, where the inputs were force and elevation. The data has been collected using the same type of experiments described in Section 4.4, that is by forcing the motion of the buoy with both waves and force exerted by the actuator, and randomizing the phase at each experiment. In this case, the input matrix is
where is the k-th (complex) frequency component of the pressure recorded in the i-th experiment. The output matrix Y is identical to (32), and the estimated FRM for the system in Figure 33 is
The matrix is composed by two blocks as
By comparing the expression in (40) with the block diagram in Figure 33, the following equalities must be satisfied for the experimental validation of the models:
Figure 34 depicts the FRM of the MISO model and of the dual SISO model described by Figure 33. The data from experiments 010 and 082 has been used to calculate , and , whereas the FRM has been calculated using data from experiments 113 and 115. It can be noted that the FRM obtained from the MISO approach shows a higher level of noise; this is probably due to the internal feedback shown in Figure 33 which, as discussed in Section 2.2, makes the results more sensitive to noise. The noise could be reduced, for example, by performing more experiments with additional phase realizations for the input signals [6]. In addition, it should be noted that there seems to be a small offset between the imaginary parts of the two FRMs, which is probably due to nonlinearities. Overall, Figure 34 shows good agreement between the MISO and dual SISO models, which confirms (41) and (42), and thus the validity of the modeling approach. Additionally, the model structure in Figure 33 is confirmed by the results in Figure 35, which shows the Bode plot of a parametric MISO model and the FRM (in terms of magnitude and phase) of the dual SISO model. The high level of noise in both magnitude and phase for the transfer function from the pressure to the velocity (top and bottom plots on the right), at high frequency between 0.8 and 1 Hz, is due to the fact that magnitude of the signals is decreasing, thus the signal-to-noise ratio increases. This is not an issue because the magnitude of the transfer function is already very small (note that the y-scale is dB). Again, this comparison shows good agreement between the parametric model and experimental data.
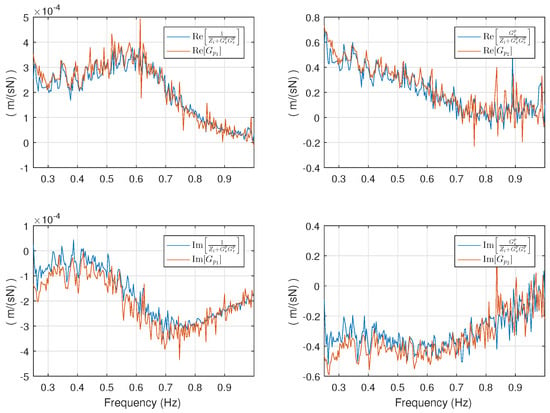
Figure 34.
FRFs of the MISO model and of the dual SISO model (shown in Figure 33).
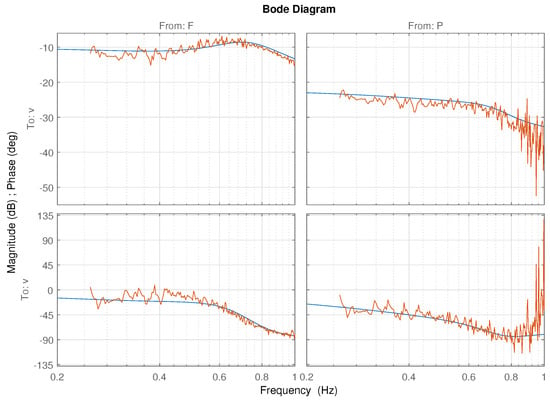
Figure 35.
Comparison of MISO parametric and dual SISO nonparametric models.
In the last part of this section, the focus is on the cross validation of the MISO parametric model. In this case, the parametric model has been identified using the MATLAB function n4sid, included in the System Identification toolbox; this function implements the subspace identification algorithm [5], which is a time-domain method that provides a parametric model of the system in state space form. The identification is carried out using data from experiment 105, in which both input signals are non-periodic. The force signal is a band-limited white noise and the waves have a Bretschneider spectrum with repeating period of 2 hours; however, the duration of the experiment is 30 minutes. Data from experiment 115 is used for validation; in this case, both inputs are pink multisines. Figure 36 shows a 50 s interval comparing the measured buoy’s velocity against the simulated velocity. In this case the fit, measured using the metric in (25), is 87%. We have found that the fit is generally good when using MISO models with pressure as an input. This shows a good potential for state estimation and model based control design.
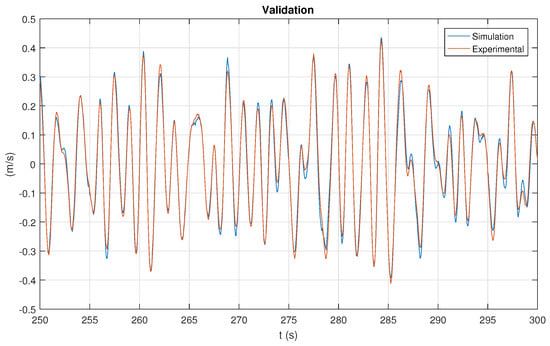
Figure 36.
Validation of the MISO model: comparison between measured and simulated velocity.
6. Discussion and Conclusions
A model-scale wave tank test was conducted to produce empirical models of a WEC in heave. This test was designed to investigate the usage of a more general set of SID techniques, which, while not yet widely used for wave tank testing, have been proven to be effective for many practical engineering systems. Thus, multi-input tests, utilizing periodic multisine input signals, were performed to provide data for SID. This novel approach, in comparison to the more common approach of performing distinct radiation and diffraction tests using monochromatic input signals, was shown to provide a number of advantages.
Using empirical data collected during testing, three separate models to predict the heave velocity of a WEC were constructed. A traditional radiation/diffraction model was formed from separate excitation and radiation models. Additionally, two types of MISO models were developed. These Black box models differ in their approach to including excitation effects: one model uses surface elevation while the other uses hull pressure. Of these three models, the Black box model utilizing hull pressure shows the best performance.
In addition to being more accurate, the pressure based model also shows promise since it may be more straightforward to implement in a full-scale system. While surface elevation based models require remote sensing and wave propagation modeling, the pressure based model can use local sensing (with relatively inexpensive sensors) and is inherently causal. The pressure measurement is also collocated with the device, which reduces some complexity introduced by compliant mooring systems.
A procedure has also been introduced to perform SID on a full-scale WEC deployed at sea. In the case of a full-scale WEC deployed in the open ocean, it is not possible to follow the procedures traditionally used in wave tank testing. The device cannot be locked in place and surface elevation measurements cannot be taken at the location of the device. In addition, one cannot “request” a certain frequency of monochromatic waves. Yet, it is certainly important that a model used to predict performance and employed in model-based control be as faithful to the full-scale device as possible. While model-scale testing can provide an initial estimate for the dynamics of a full-scale device, substantial differences may be introduced at full scale, due to, e.g., Reynolds scaling, a full-scale mooring system, etc. Additionally, drift in model parameters over the deployment lifetime of a WEC is likely; for example, bearing degradation can change the friction in a mechanical system and biofouling may increase both mass and viscous friction. Thus the ability to obtain an empirically based model of a full-scale WEC at sea will likely be essential to realizing performance gains at full-scale. The method suggested in this paper may fulfill this need.
The work summarized in this paper provides a number of insights into necessary future work. While local linear modeling has been shown here to provide good performance, nonlinear modeling of the WEC’s dynamics should also be considered. For the experiments considered here, mechanical friction appears to be the most influential nonlinear contribution. Additionally, work should also be done to extend the dynamic system to be studied beyond motion of the WEC; to include the full “wave-to-wire”’ system. Robust and reliable state estimators and observers need to be developed to provide access to challenging and/or inherently noisy states based on the models presented in this study.
Acknowledgments
This work was funded by the U.S. Department of Energy’s Water Power Technologies Office. Sandia National Laboratories is a multi-mission laboratory managed and operated by Sandia Corporation, a wholly owned subsidiary of Lockheed Martin Corporation, for the U.S. Department of Energy’s National Nuclear Security Administration under contract DE-AC04-94AL85000. The authors would like to thank Miguel Quintero and David Newborn of the Naval Surface Warfare Center, Carderock Division, for their support in executing wave tank testing.
Author Contributions
G.B. and R.G. wrote the paper; G.B. and D.P. performed the bulk of data processing and analysis; R.G., G.B. and D.W. performed the wave tank experiments.
Conflicts of Interest
The authors declare no conflict of interest. The founding sponsors had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, and in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| BEM | Boundary element method |
| FRF | Frequency response function |
| FRM | Frequency response matrix |
| FFT | Fast Fourier transform |
| LTI | Linear time invariant |
| IRF | Impulse response function |
| MASK | Maneuvering And Sea Keeping |
| MISO | Multiple input single-output |
| NRMSE | Normalized root mean square error |
| PTO | Power take-off |
| SID | System identification |
| SISO | Single input single output |
| WEC | Wave energy converter |
References
- Hals, J.; Falnes, J.; Moan, T. A Comparison of Selected Strategies for Adaptive Control of Wave Energy Converters. J. Offshore Mech. Arct. Eng. 2011, 133, 031101. [Google Scholar] [CrossRef]
- Wilson, D.; Bacelli, G.; Coe, R.G.; Bull, D.L.; Abdelkhalik, O.; Korde, U.A.; Robinett III, R.D. A Comparison of WEC Control Strategies; Technical Report SAND2016-4293; Sandia National Labs: Albuquerque, NM, USA, 2016. [Google Scholar]
- WAMIT. WAMIT User Manual, 7th ed.; Wave Analysis MIT (WAMIT): Chestnut Hill, MA, USA, 2012. [Google Scholar]
- Babarit, A.; Delhommeau, G. Theoretical and numerical aspects of the open source BEM solver NEMOH. In Proceedings of the 11th European Wave and Tidal Energy Conference (EWTEC2015), Nantes, France, 6–11 September 2015. [Google Scholar]
- Ljung, L. System Identification—Theory for the User; Prentice-Hall PTR: Upper Saddle River, NJ, USA, 1999. [Google Scholar]
- Pintelon, R.; Schoukens, J. System Identification: A Frequency Domain Approach; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Giorgi, S.; Davidson, J.; Ringwood, J.V. Identification of Wave Energy Device Models From Numerical Wave Tank Data Part 2: Data-Based Model Determination. IEEE Trans. Sustain. Energy 2016, 7, 1020–1027. [Google Scholar] [CrossRef]
- Davidson, J.; Giorgi, S.; Ringwood, J.V. Linear parametric hydrodynamic models for ocean wave energy converters identified from numerical wave tank experiments. Ocean Eng. 2015, 103, 31–39. [Google Scholar] [CrossRef]
- Cummins, W.E. The Impulse Response Function and Ship Motions; Technical Report DTNSDRC 1661; Department of the Navy, David Taylor Model Basin: Bethesda, MD, USA, 1962. [Google Scholar]
- Falnes, J. Ocean Waves and Oscillating Systems; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2002. [Google Scholar]
- Yu, Z.; Falnes, J. State-space modelling of a vertical cylinder in heave. Appl. Ocean Res. 1995, 17, 265–275. [Google Scholar] [CrossRef]
- Perez, T.; Fossen, T.I. Time- vs. Frequency-domain Identification of Parametric Radiation Force Models for Marine Structures at Zero Speed. Model. Identif. Control 2008, 29, 1–19. [Google Scholar] [CrossRef]
- Billings, S.A.; Lang, Z.Q. Truncation of nonlinear system expansions in the frequency domain. Int. J. Control 1997, 68, 1019–1042. [Google Scholar] [CrossRef]
- Schoukens, J.; Vaes, M.; Pintelon, R. Linear System Identification in a Nonlinear Setting: Nonparametric Analysis of the Nonlinear Distortions and Their Impact on the Best Linear Approximation. IEEE Control Syst. 2016, 36, 38–69. [Google Scholar] [CrossRef]
- Coe, R.G.; Bacelli, G.; Patterson, D.; Wilson, D.G. Advanced WEC Dynamics & Controls FY16 Testing Report; Technical Report SAND2016-10094; Sandia National Labs: Albuquerque, NM, USA, 2016.
- Brownell, W. Two New Hydromechanics Research Facilities at the David Taylor Model Basin; Technical Report 1690; Department Of The Navy, David Taylor Model Basin: Bethesda, MD, USA, 1962. [Google Scholar]
- Advanced WEC Dynamics and Controls, Test 1—Experimental Data Hosted on the “Marine and Hydrokinetic Data Repository”. U.S. DEPARTMENT OF ENERGY. Available online: https://mhkdr.openei.org/submissions/151 (accessed on 30 December 2016).
- Perez, T.; Fossen, T.I. A Matlab Toolbox for Parametric Identification of Radiation-Force Models of Ships and Offshore Structures. Model. Identif. Control A Nor. Res. Bull. 2009, 30, 1–15. [Google Scholar] [CrossRef]
- Ogata, K. Modern Control Engineering; Prentice Hall: Upper Saddle River, NJ, USA, 2002. [Google Scholar]
- Duclos, G.; Clement, A.; Chatry, G. Absorption of Outgoing Waves in a numerical wave tank using a self-adaptive boundary condition. In Proceedings of the 10th Int Offshore and Polar Engineering Conference ISOPE 2000, Seattle, WA, USA, 27 May–2 June 2000. [Google Scholar]
- Falnes, J. On non-causal impulse response functions related to propagating water waves. Appl. Ocean Res. 1995, 17, 379–389. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).