Digital-Control-Based Approximation of Optimal Wave Disturbances Attenuation for Nonlinear Offshore Platforms
Abstract
:1. Introduction
2. Problem Formulation
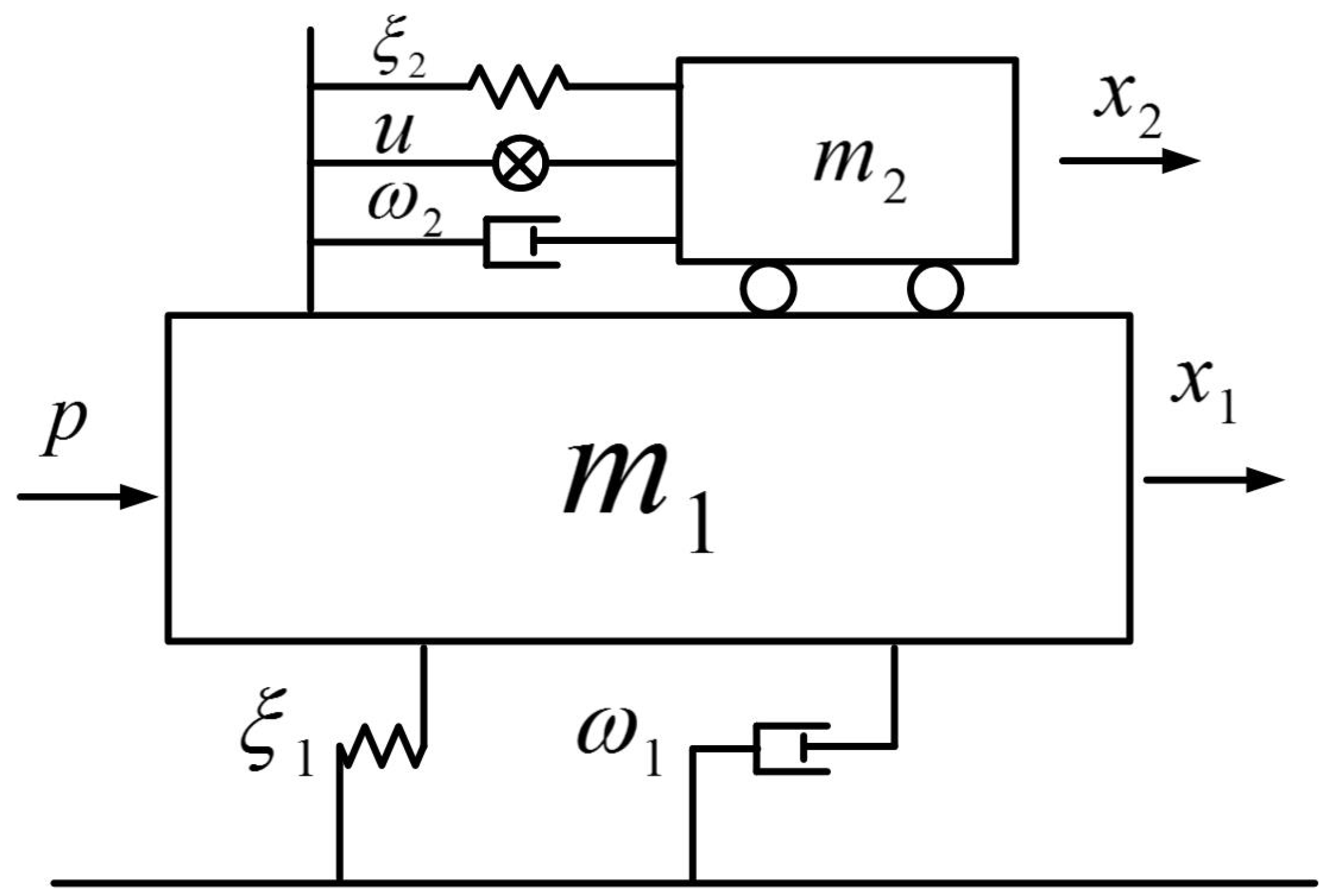
2.1. Jacket-Type Offshore Platform
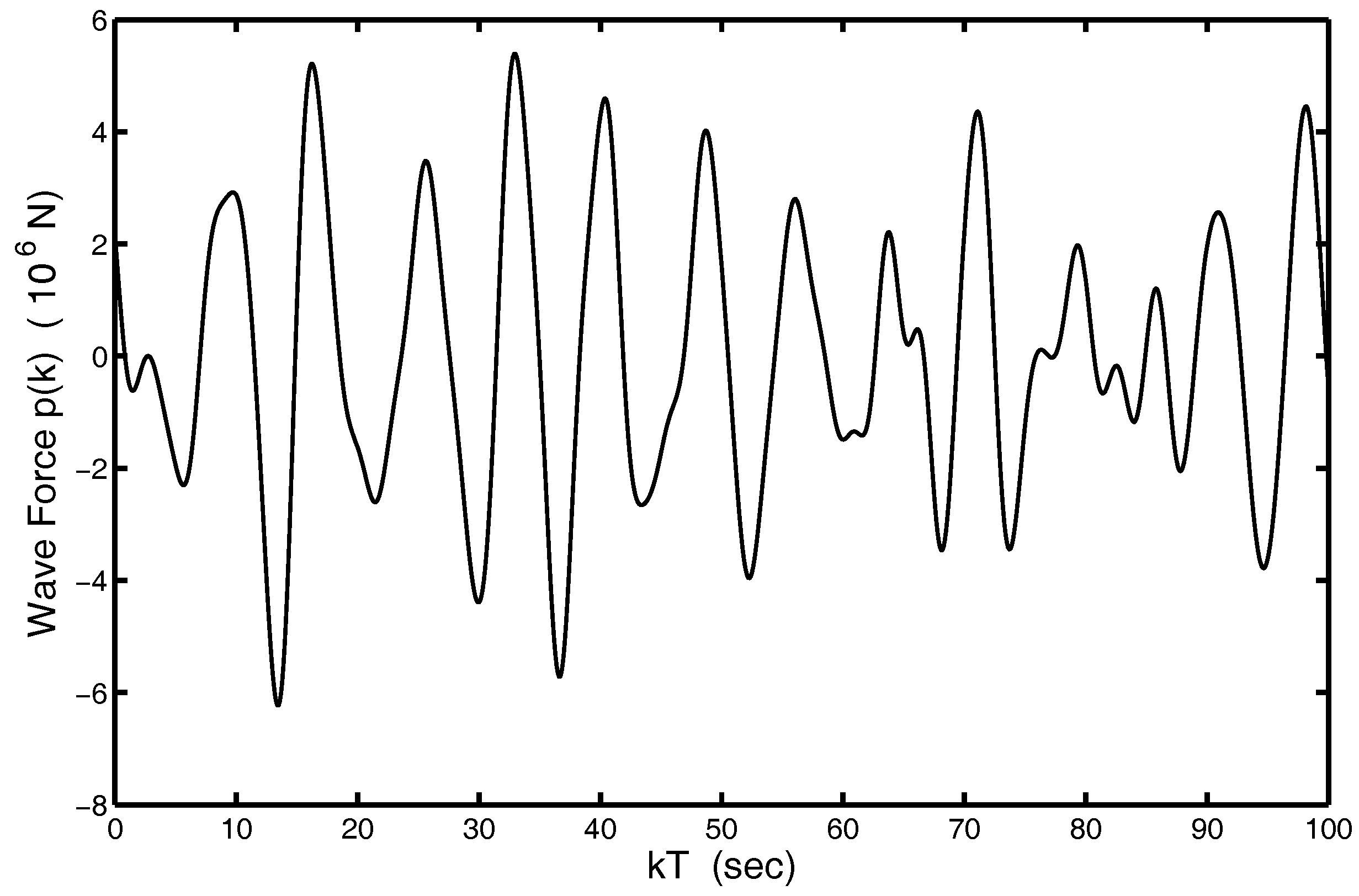
2.2. Irregular Wave Disturbances
2.3. Discrete Optimal Irregular Wave Disturbances Attenuation Problem
3. Main Results
3.1. Design of AOWDAC
3.2. The Feasibility of AOWDAC
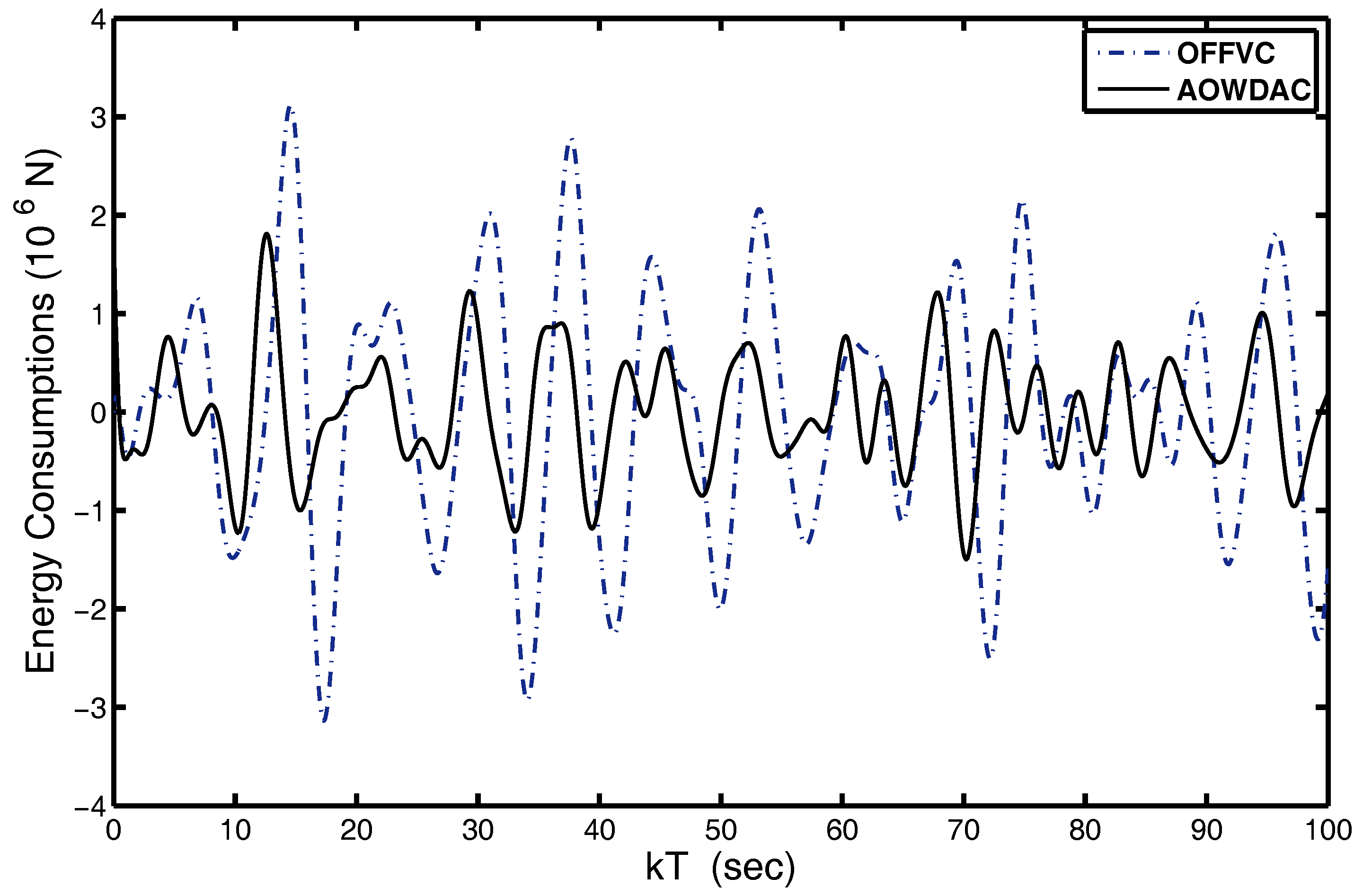
4. Simulation Results
4.1. Parameters of Wave Disturbance Attenuation Problem
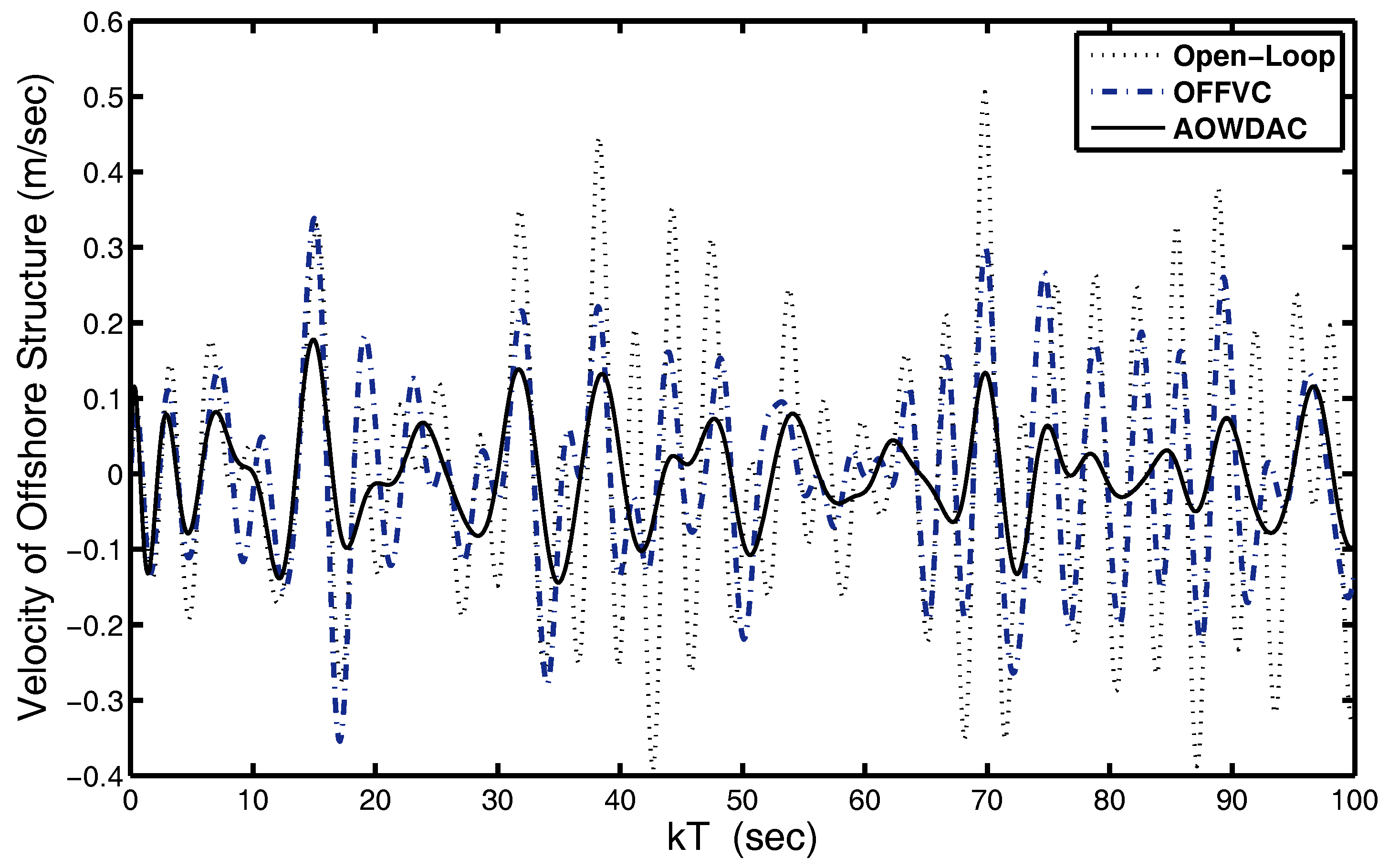
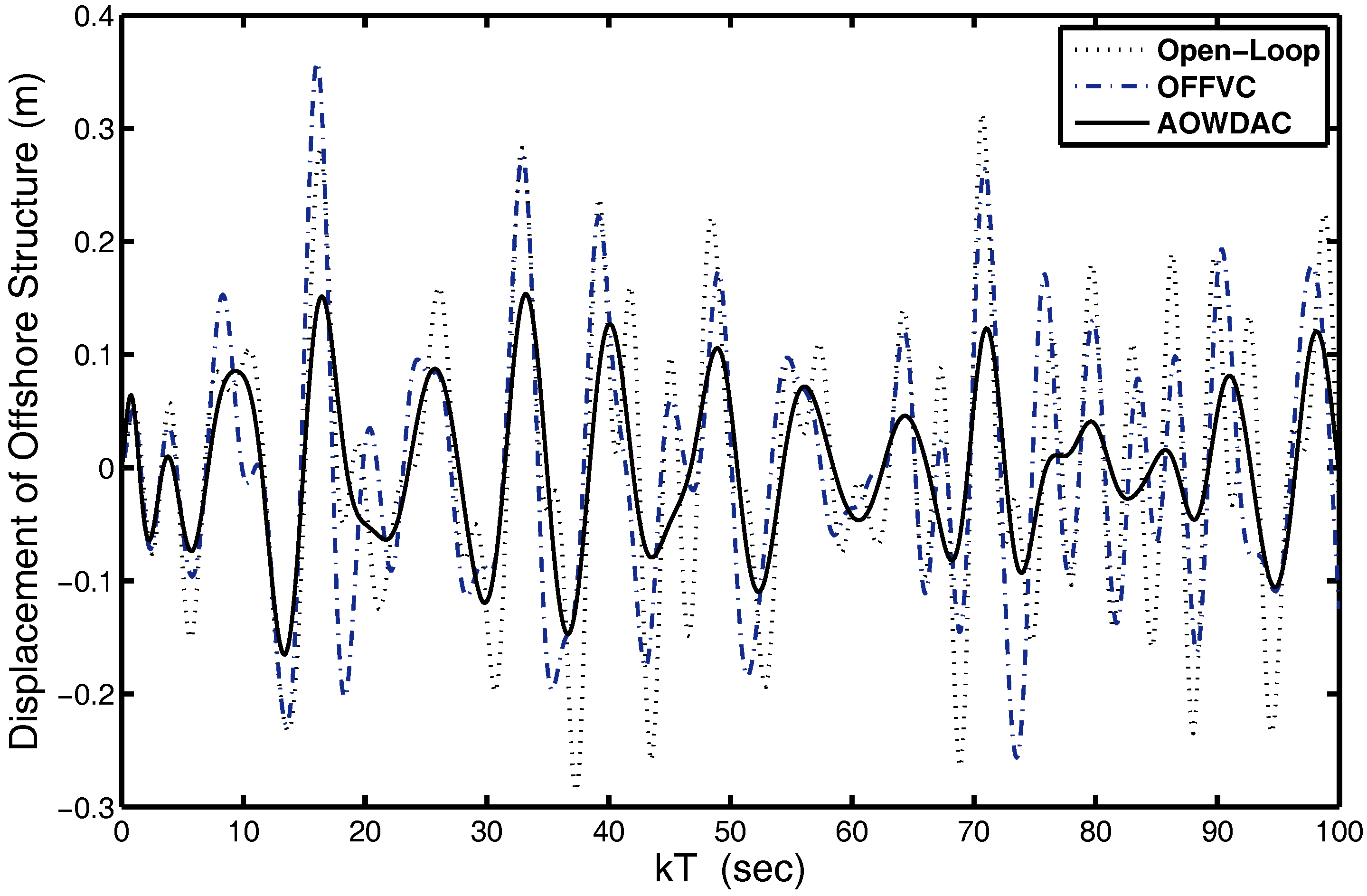
4.2. Analysis of Wave Disturbance Attenuation Abilities of Proposed AOWDAC
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Zhang, B.-L.; Han, Q.-L.; Zhang, X.-M. Recent advances in vibration control of offshore platforms. Nonlinear Dyn. 2017, 89, 755–771. [Google Scholar] [CrossRef]
- Yang, J.S. Hybrid active and passive control of a very large floating beam structure. Nonlinear Dyn. 2017, 87, 1835–1845. [Google Scholar] [CrossRef]
- Han, S.-Y.; Tang, G.-Y.; Chen, Y.-H.; Tang, X.-X.; Yang, X. Optimal vibration control for vehicle active suspension discrete-time systems with actuator time delay. Asian J. Control 2013, 15, 1579–1588. [Google Scholar] [CrossRef]
- Zhang, B.-L.; Han, Q.-L.; Zhang, X.-M. Robust non-fragile sampled-data control for offshore steel jacket platforms. Nonlinear Dyn. 2016, 83, 1939–1954. [Google Scholar] [CrossRef]
- Zhang, B.-L.; Ma, L.; Han, Q.-L. Sliding mode H∞ control for offshore steel jacket platforms subject to nonlinear self-excited wave force and external disturbance. Nonlinear Anal. Real World Appl. 2013, 14, 163–178. [Google Scholar] [CrossRef]
- Zhang, B.-L.; Huang, Z.-W.; Han, Q.-L. Delayed non-fragile H∞ control for offshore steel jacket platforms. J. Vib. Control 2015, 21, 959–974. [Google Scholar] [CrossRef]
- Wang, L.; Yang, B.; Chen, Y.; Zhang, X.; Orchard, J. Improving neural-network classifiers using nearest neighbor partitioning. IEEE Trans. Neural Netw. Learn. Syst. 2017, 28, 2255–2267. [Google Scholar] [CrossRef] [PubMed]
- Yu, Z.; Liu, Y.; Yu, X.; Pu, K.Q. Scalable distributed processing of K nearest neighbor queries over moving objects. IEEE Trans. Knowl. Data Eng. 2015, 27, 1383–1396. [Google Scholar] [CrossRef]
- Kandasamy, R.; Cui, F.; Townsend, N. A review of vibration control methods for marine offshore structures. Ocean Eng. 2016, 127, 279–297. [Google Scholar] [CrossRef]
- Faltinsen, O.M. Sea Loads on Ships and Offshore Structures; Cambridge University Press: Cambridge, UK, 1990. [Google Scholar]
- Kandasamy, R.; Cui, F.; Townsend, N. A systematic study of the lowest order small slope approximation for a Pierson–Moskowitz spectrum. IEEE Geosci. Remote Sens. Lett. 2011, 8, 158–162. [Google Scholar]
- Annalisa, C.; Constance, M.S. Characterizing JONSWAP rogue waves and their statistics via inverse spectral data. Wave Motion 2017, 71, 5–17. [Google Scholar]
- Cho, H.-Y.; Kweon, H.-M.; Jeong, W.-M.; Kim, S.-I. A study on the optimal equation of the continuous wave spectrum. Int. J. Nav. Archit. Ocean Eng. 2015, 7, 1056–1063. [Google Scholar] [CrossRef]
- Zhang, B.-L.; Liu, Y.-J.; Han, Q.-L.; Tang, G.-Y. Optimal tracking control with feedforward compensation for offshore jacket platforms with active mass damper mechanisms. J. Vib. Control 2016, 22, 695–709. [Google Scholar] [CrossRef]
- Zhang, B.-L.; Han, Q.-L. Network-based modelling and active control for offshore steel jacket platform with TMD mechanisms. J. Sound Vib. 2014, 333, 6796–6814. [Google Scholar] [CrossRef]
- Zhang, B.-L.; Han, Q.-L.; Zhang, X.-M. Event-triggered H∞ reliable control for offshore structures in network environments. J. Sound Vib. 2016, 368, 1–21. [Google Scholar] [CrossRef]
- Yang, J.S. Robust mixed H2/H ∞ active control for offshore steel jacket platform. Nonlinear Dyn. 2014, 2, 1503–1514. [Google Scholar] [CrossRef]
- Zhang, B.-L.; Han, Q.-L.; Zhang, X.-M.; Yu, X. Sliding mode control with mixed current and delayed states for offshore steel jacket platforms. IEEE Trans. Control Syst. Technol. 2014, 22, 1769–1783. [Google Scholar] [CrossRef]
- Nourisola, H.; Ahmadi, B. Robust adaptive sliding mode control based on wavelet kernel principal component for offshore steel jacket platforms subject to nonlinear wave-induced force. J. Vib. Control 2016, 22, 3299–3311. [Google Scholar] [CrossRef]
- Han, S.-Y.; Chen, Y.-H.; Tang, G.-Y. Sensor fault and delay tolerant control for networked control systems subject to external disturbances. Sensors 2017, 17, 700. [Google Scholar] [CrossRef] [PubMed]
- Han, S.Y.; Zhang, C.-H.; Tang, G.-Y. Approximation optimal vibration for networked nonlinear vehicle active suspension with actuator time delay. Asian J. Control 2017, 19, 983–995. [Google Scholar] [CrossRef]
- Han, S.-Y.; Chen, Y.-H.; Tang, G.-Y. Fault diagnosis and fault-tolerant tracking control for discrete-time systems with faults and delays in actuator and measurement. J. Frankl. Inst. 2017, 354, 4719–4738. [Google Scholar] [CrossRef]
- Han, S.Y.; Wang, D.; Chen, Y.H.; Tang, G.Y.; Yang, X.X. Optimal tracking control for discrete-time systems with multiple input delays under sinusoidal disturbances. Int. J. Control Autom. Syst. 2015, 13, 292–301. [Google Scholar] [CrossRef]
- Goebel, M.; Raitums, U. Constrained control of a nonlinear two point boundary value problem, I. J. Glob. Optim. 1994, 4, 367–395. [Google Scholar] [CrossRef]
- Chanane, B. Optimal control of nonlinear systems: A recursive approach. Comput. Math. Appl. 1998, 35, 29–33. [Google Scholar] [CrossRef]
- Beard, R.W.; Saridis, G.N.; Wen, J.T. Galerkin approximation of the generalized Hamilton-Jacobi-Bellman equation. Automatica 1997, 33, 2159–2177. [Google Scholar] [CrossRef]
- Tang, G.-Y.; Gao, D.-X. Approximation design of optimal controllers for nonlienar systems with sinusoidal disturbances. Nonlinear Anal. Theory Methods Appl. 2007, 66, 403–414. [Google Scholar] [CrossRef]
- Ma, H.; Tang, G.-Y.; Zhao, Y.-D. Feedforward and feedback optimal control for offshore structures subjected to irregular wave forces. Ocean Eng. 2006, 33, 1105–1117. [Google Scholar] [CrossRef]
| Name of Parameter | Variable | Value | Unit |
|---|---|---|---|
| Mass of AMD | 11,855 | ||
| Nature frequency of AMD | rad/s | ||
| Structure damping ratio of AMD | % | ||
| First modal mass of offshore structure | 2,371,100 | kg | |
| Nature frequency | rad/s | ||
| Structure damping ratio | 4 | % | |
| Shape function of first mode | / | ||
| Equivalent characteristic diameter of legs | m | ||
| Nonlinear parameter | 1,500,534 | / | |
| Nonlinear parameter | 2,371,100 | / | |
| Nonlinear parameter | 2,382,955 | / |
| Name of Parameter | Variable | Value | Unit |
|---|---|---|---|
| Water depth | d | m | |
| Drag coefficient | / | ||
| Inertial coefficient | / | ||
| Density of ocean fluid | / |
| Iteration Number | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| Performance index J |
| Control Scheme | Displacement (m) | Velocity (m/s) | N |
|---|---|---|---|
| Open-Loop | |||
| Optimal feedback and feedfoward vibration controller (36) | |||
| Approximation of optimal wave disturbances attenuation controller (33) | 0.1127 | 0.0910 | 1.6182 |
| Control Scheme | Displacement (m) | Velocity (m/s) | N |
|---|---|---|---|
| Open-Loop | |||
| Optimal feedback and feedfoward vibration controller (36) | |||
| Approximation of optimal wave disturbances attenuation controller (33) | 0.0451 | 0.0437 | 0.5884 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhong, X.-F.; Sun, Y.-H.; Han, S.-Y.; Zhou, J.; Wang, D. Digital-Control-Based Approximation of Optimal Wave Disturbances Attenuation for Nonlinear Offshore Platforms. Energies 2017, 10, 1997. https://doi.org/10.3390/en10121997
Zhong X-F, Sun Y-H, Han S-Y, Zhou J, Wang D. Digital-Control-Based Approximation of Optimal Wave Disturbances Attenuation for Nonlinear Offshore Platforms. Energies. 2017; 10(12):1997. https://doi.org/10.3390/en10121997
Chicago/Turabian StyleZhong, Xiao-Fang, Yu-Hong Sun, Shi-Yuan Han, Jin Zhou, and Dong Wang. 2017. "Digital-Control-Based Approximation of Optimal Wave Disturbances Attenuation for Nonlinear Offshore Platforms" Energies 10, no. 12: 1997. https://doi.org/10.3390/en10121997
APA StyleZhong, X.-F., Sun, Y.-H., Han, S.-Y., Zhou, J., & Wang, D. (2017). Digital-Control-Based Approximation of Optimal Wave Disturbances Attenuation for Nonlinear Offshore Platforms. Energies, 10(12), 1997. https://doi.org/10.3390/en10121997




