Abstract
Accurate estimation of the state of charge (SOC) of batteries is crucial in a battery management system. Many studies on battery SOC estimation have been investigated recently. Temperature is an important factor that affects the SOC estimation accuracy while it is still not adequately addressed at present. This paper proposes a SOC estimator based on a new temperature-compensated model with extended Kalman Filter (EKF). The open circuit voltage (OCV), capacity, and resistance and capacitance (RC) parameters in the estimator are temperature dependent so that the estimator can maintain high accuracy at various temperatures. The estimation accuracy decreases when applied in high current continuous discharge, because the equivalent polarization resistance decreases as the discharge current increases. Therefore, a polarization resistance correction coefficient is proposed to tackle this problem. The estimator also demonstrates a good performance in dynamic operating conditions. However, the equivalent circuit model shows huge uncertainty in the low SOC region, so measurement noise variation is proposed to improve the estimation accuracy there.
1. Introduction
Lithium-ion batteries are widely applied in electric vehicles (EV). Accurate estimation of battery state of charge (SOC) is the prerequisite for EV to optimize energy, safety, and battery balance management. Precise battery SOC estimation faces a lot of challenges, such as low measurement accuracy, strong nonlinear behavior of batteries, complex operating conditions, and battery aging.
There are a variety of methods to estimate SOC, such as coulomb counting, open circuit voltage (OCV)-based method, machine learning method, and model-based method [,]. Coulomb counting is widely applied in the industry due to its simplicity and convenience. However, the performance is highly reliant on the precision of current sensors and the accurate estimation of the initial SOC []. In addition, coulomb counting is unable to eliminate the accumulation of measurement errors thus regular calibration is needed. The OCV-based method makes use of the monotonous SOC-OCV relation. However, it is not suitable for online estimation because long rest time is required to measure the true OCV. Machine learning approaches, including artificial neural networks [,] and support vector machines [,], generally apply a set of data to train the model. However, this kind of method is reliant on the reliability of the training data. It is very difficult to collect sufficient data to cover the entire loading conditions. The model-based filtering estimation approach is widely applied due to its close-loop nature and concerning various uncertainties []. Plett [,,] is the first to apply EKF in SOC estimation using different battery models. In order to enhance the algorithm ability dealing with nonlinear battery behavior, many other advanced filters have been adopted, such as the unscented Kalman filter (UKF) [,], central difference Kalman filter (CDKF) [,,], adaptive extended Kalman Filter(EKF) [,], adaptive UKF [], particle filter (PF) [], and H infinity filter []. The advanced filters require high computing power, but result in a rather moderate improvement as compared to the general EKF [].
For model-based approaches, the accuracy of SOC estimation is directly related to the accuracy of the battery model. Battery performance is strongly influenced by the temperature and current rate. Therefore, an accuracy model should take these factors into consideration. Xing et al. [] proposed a model in which the OCV is adjusted based on ambient temperature. Their model is simple and behaves poorly in dynamic conditions. The model is improved by a calibrated constant, which may be not applicable in a working condition significantly different from the calibrated case. Liu et al. [] also proposed a simple temperature-compensated model. The internal resistance is temperature dependent with 3 order polynomial and the OCV is temperature dependent with a linear function. However, cell capacity in their model is not temperature dependent. He et al. [] proposed a battery model to include the impacts of different discharge rates and temperatures. They only consider the capacity dependence on temperature and discharge rate, whereas the OCV is not dealt with. Hu et al. [] established a model in which the OCV, RC parameters are both temperature and SOC dependent. All of the parameters in the temperature range 10–35 °C are fitted with analytic functions. However, the temperature range is narrow and to fit the analytic functions is troublesome. Tian et al. [] proposed a model in which the internal resistance is dependent on SOC and current rate, while the capacity is dependent on temperature and current rate. The temperature effect on internal resistance is neglected in their paper. Dey et al. [] developed a nonlinear adaptive observer based on a coupled electrochemical–thermal model. The SOC can be obtained by online identification. However, the convergence is poor when the load current is zero, and the model is only locally identifiable that calls for accurate initial values. They [] later proposed a sliding mode observer, including temperature effects for online state estimation. They supposed some parameters are constant and did not study the influence of temperature on the parameters. Tanim et al. [] used an enhanced SPM (single particle model) considering the temperature effects as the basis for a Luenberger observer in SOC estimation. The model is complex and the model parameters are assumed to be known. It may be difficult to identify model parameters in practice. So far, the variation of model parameters with temperature and current rate is seldom addressed in the literature. The different influences of ambient temperature and battery temperature on the performance of the battery have not been discussed. Model parameter variation induced by load current variation is generally neglected. Model Parameter variation induced by complex working conditions needs further research to improve the model performance. Some researchers applied online parameter estimator to determine the battery parameters. The general approach is to apply EKF [,] or recursive least squares (RLS) [,] to identify the parameters online. However, the battery model might not be completely observable when the load current is constant []. Therefore, the parameter database is still required.
In this paper, A SOC estimator based on a new temperature-compensated model with EFK is put forward. A correction scheme for the temperature dependence of OCV, capacity and RC parameters in the estimator is established. Two types of corrected temperature is recognized-ambient temperature and battery temperature, considering that the battery temperature will be much higher than the ambient temperature in some cases. To further improve the model accuracy, parameter variation in different discharge currents has also been compensated. In addition, variable measurement noise is proposed to improve the estimation accuracy in low SOC region.
The remainder of this paper is organized as follows. Section 2 introduces the experiment setup and test procedure. Section 3 presents the battery model and model parameter identification results. After that, the EKF-based SOC estimator is introduced in Section 4. The validation and improvement of the estimator are elaborated in Section 5, followed by the conclusion in Section 6.
2. Experiments
The experiment setup is shown in Figure 1. It consists of (1) a graphite/LiNixCoyMnzO2cell with a nominal voltage 3.6 V and nominal capacity 2.5 Ah; (2) a thermal chamber with temperature control deviation less than 1 °C; (3) a battery test system (Neware CT-4008, manufactured in Shenzhen, China, voltage measure range 0.025–5 V, current measure range 0.1–30 A. The measurement deviations of the current and voltage sensors are within 0.1%); (4) a PC installed Neware software for battery load control and data acquisition (the voltage, current, and surface temperature of the cell are measured).
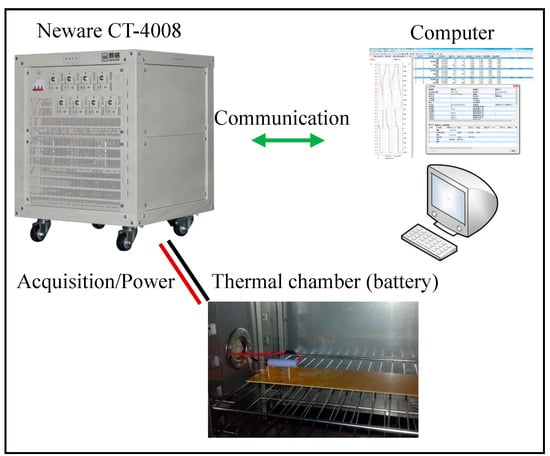
Figure 1.
Schematic of the battery test bench.
2.1. SOC-OCV Test
OCV is very important for SOC estimation. It is a function of cell SOC and temperature. There are two methods to measure the OCV, namely coulomb titration and voltage relaxation []. The former discharges and charges the cell with the same low current while measuring the terminal voltage. The OCV is defined as the average value of the charge and the discharge terminal voltage. The latter determines the SOC-OCV curve by resting the battery for a suitable period after charging or discharging under specific SOC intervals. Figure 2 shows the OCV measured by voltage relaxation and the battery terminal voltage by discharging and charging the battery with 1/25 C rate (OCV is got by discharge voltage relaxation. For this battery, there are little differences between OCV by discharge voltage relaxation and charge voltage relaxation). It can be seen that discharging and charging terminal voltage is not well symmetrical about the OCV, especially in low the SOC region. Therefore, OCV measured by voltage relaxation is chosen. The measure step of the OCV is as follows. First, the cell is charged with 0.8 A (about 1/3 C) until the voltage reaches 4.12 V at the room temperature, followed by a constant voltage charge until the current reaches 1/30 C (SOC is regarded as 1). After that, the thermal chamber is set to the tested temperature (0, 12.5, 25, or 45 °C), resting the cell for 2 h and measuring the OCV under SOC 1. Then, the cell is discharged with 0.8 A until the discharged ampere-hour reaches 0.2 Ah, measuring the cell OCV after it gets stable (in this paper when dV/dt is less than 1 mV/h, OCV is considered to be stable). Repeat this step to get the OCVs under other SOCs. At the last test point, the terminal voltage reaches 2.5 V and then measure the stable OCV.
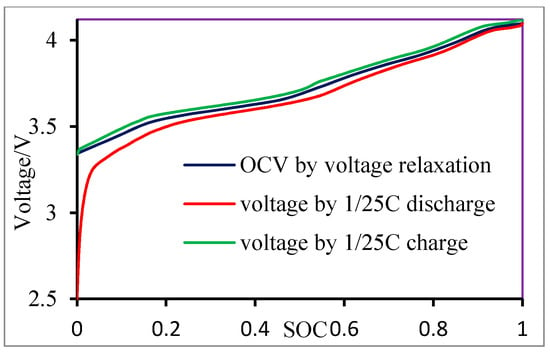
Figure 2.
OCV by voltage relaxation and terminal voltage by 1/25 C charge and discharge.
2.2. Model Identification Test
The battery is discharged with a constant current during the OCV test. The terminal voltage response can be used for electrical model parameter identification. Since the OCV test is in 0, 12.5, 25, and 45 °C, the RC parameters at these temperatures can be obtained. The SOC estimator also contains the cell nominal capacity, so the nominal capacity under the aforementioned four temperatures is measured. The way of measuring the nominal capacity under a certain temperature is as follows. First, the cell is full charged as the same procedure in the OCV test. Then the thermal chamber is set to the tested temperature. After 2 h, the cell is believed to reach equilibrium under the temperature. The cell is discharged with a 1/3 C rate until the terminal voltage reaches cutoff voltage of 2.5 V while the nominal capacity can be decided.
2.3. Model Validation Test
The cell is discharged with 1 C, 2 C rate under the tested temperature to test the estimator accuracy under other discharge rate. In order to validate the estimator under other temperature and dynamic load, the dynamic stress test (DST) test cycle is conducted at 20 °C from 100% SOC to cell terminal voltage reaching cutoff voltage. DST is designed by US Advanced Battery Consortium (USABC) to simulate a variable power discharge regime that represents the expected demands of an EV battery. The current profile of DST is shown in Figure 3. The positive current responds to discharging while the negative denotes charging.
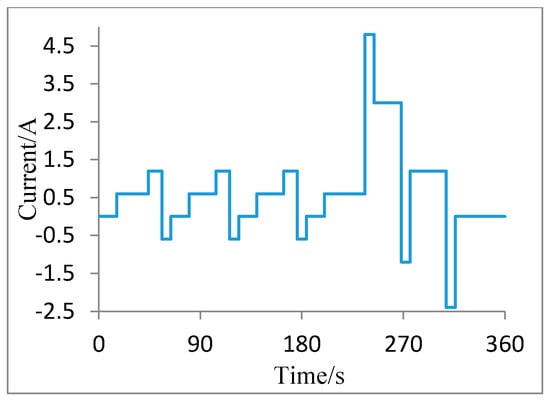
Figure 3.
Current prolife of DST.
3. Battery Modeling and Identification
3.1. Battery Model
Two aspects should be considered while choosing a model: firstly, it can reflect the characteristics of the battery precisely; secondly, the model is computationally efficient and easy to implement in the industry. Hu et al. [] compared several equivalent circuit models, verifying that the Thevenin model can achieve good results in simulation accuracy and convenience. Therefore, the Thevenin model is chosen in this paper. The schematic of this model is presented in Figure 4. The electrical behavior of the model is described by Equation (1).
where is the OCV, is the ohmic resistance, is the equivalent polarization resistance, is the equivalent capacitance, is the terminal voltage, is the polarization voltage, and is the load current.
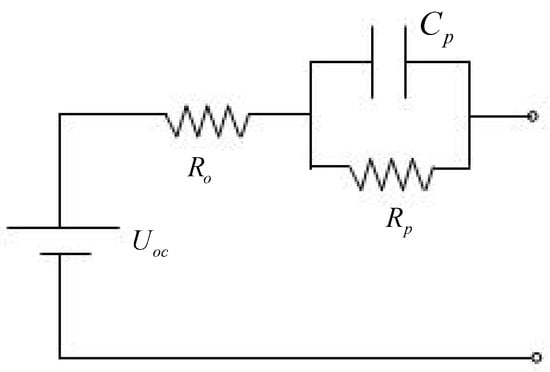
Figure 4.
Schematic of the Thevenin model.
3.2. Model Parameters Identification
Considering the SOC estimator, the following parameters should be determined: , (nominal capacity), , , and . is interpolated from the SOC-OCV table. The SOC-OCV curves under the test temperatures are shown in Figure 5. It should be mentioned that the total discharge capacity in the OCV test is a little higher than that of 1/3 C continuous discharge, usually about 1% higher than the latter. The deviation becomes more significant at a low temperature (shown in Table 1). This phenomenon is neglected to make the SOC vary from 0 to 1 in Figure 5. The OCV at different temperatures varies little under high SOC region. However, the differences are significant in the low SOC region, because the cell discharges much less of an amount of electricity at low temperature and there are remarkable differences of Li concentration in the electrodes. The minimum of dOCV/dSOC, for example in 25 °C is about 4 mV/0.01 SOC in SOC between 0.3 and 0.4. A small OCV error there may lead to large error in SOC estimation. The OCV in the estimator is obtained by 2D linear interpretation. However, the OCV is interpreted by ambient temperature rather than the battery temperature. It is more calculation efficient and should not cause large deviation.
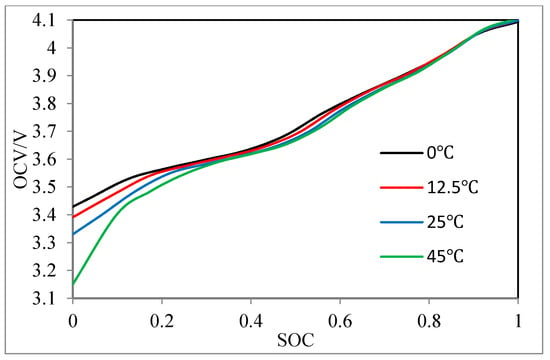
Figure 5.
SOC-OCV at different temperatures.

Table 1.
Capacity of 1/3 C intermittent and continuous discharge.
A second order polynomial is applied to reconstruct the nominal capacity at the temperature range of 0–45 °C. The fitting result is shown in Figure 6. It can be seen that the test data meets the second order curve very well. The fitting formula is shown in Equation (2). The cell nominal capacity is interpolated from the ambient temperature T∞, because capacity interpolated from battery temperature will cause a large error. For example, the cell is discharged with 2 C rate at 0 °C from SOC 1 to the cut-off voltage. Cell temperature reaches 15 °C when the discharged ampere-hour reaches 1.5 Ah. If the capacity is inferred from battery temperature by Equation (2), it will be around 2.4 Ah. However, the experiment result is 2.173 Ah. Therefore, it can be concluded that the battery capacity won’t change significantly induced by the rapid rising of the temperature during large discharge rate at low temperature. The diffusion in the battery is slow so that the effect of temperature on the battery takes a long time to appear. Therefore, predicting the battery capacity from the ambient temperature is more reasonable.
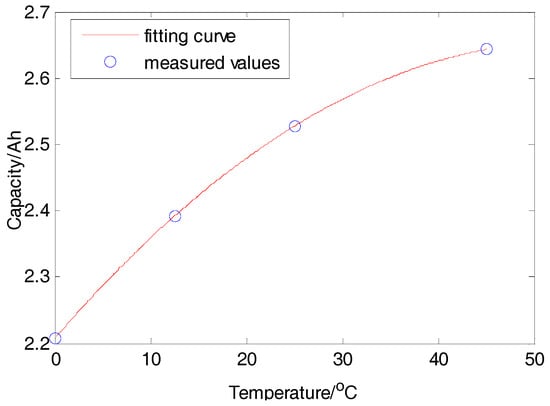
Figure 6.
Fitting result of capacity in 0–45 °C.
For the Thevenin model, the terminal voltage of the battery can be expressed by Equation (3). Since we have got the data by constant discharge during the OCV test, the RC parameters of the model can be identified by curve fitting. in Equation (3) cannot stay constant during discharge. One way is to obtain the instant by interpolation from the SOC-OCV curve, and the SOC is calculated purely from coulomb counting. Here, we apply a different way in which is modeled with − kILt (when the battery is discharged in a narrow SOC region, the linear hypothesis of is valid). Where the is the OCV just before the discharge which can be measured, is a constant considering the OCV decline caused by discharge. Therefore, Equation (3) is changed into Equation (4), and the latter can be directly fitted to identify the , and ( is the time constant).
It is found that the fitting result to some extent is dependent on the sampling time. When the sampling time is too short, the transient process of the cell may not fully exhibit. When the sampling time is too long, the linear OCV hypothesis may be invalid. The sampling time of 500 s is chosen. However, the RC parameters cannot stay constant for such a long time in a low SOC region (SOC < 0.15). Therefore, sampling time 200 s is chosen there. The parameters identified in the low SOC region are unreliable, so we have adjusted the parameters according to 1/3 C continuously discharged experiment. For RC values at SOC 0, linear interpolation combined with calibration is used to determine them. The final , , and are shown in Figure 7, Figure 8 and Figure 9, respectively. It can be seen that is stable when SOC is greater than 0.2. When SOC is near 0, increases rapidly. increases with temperature and it varies more quickly at a low temperature. When compared with , increases much more significantly in low SOC region. fluctuates more strongly than in SOC region of 0.2–1. There is no general rule for the variation of with SOC and temperature. The RC parameters are instant linear 2D interpolation of SOC and battery temperature to consider the battery performance variation caused by the battery temperature variation.
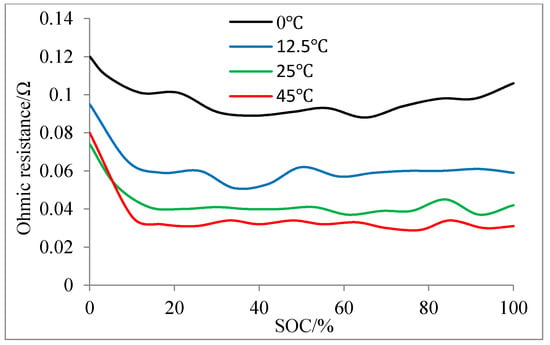
Figure 7.
Ohmic resistance at different temperatures, state of charge (SOCs).
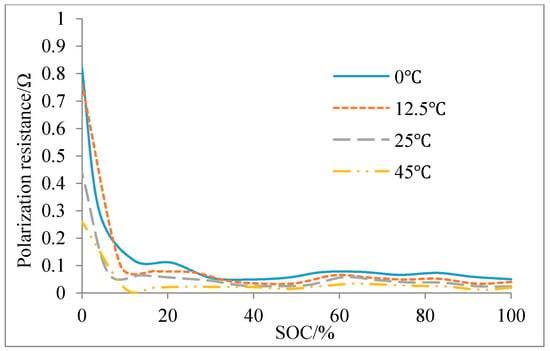
Figure 8.
Polarization resistance at different temperatures, SOCs.
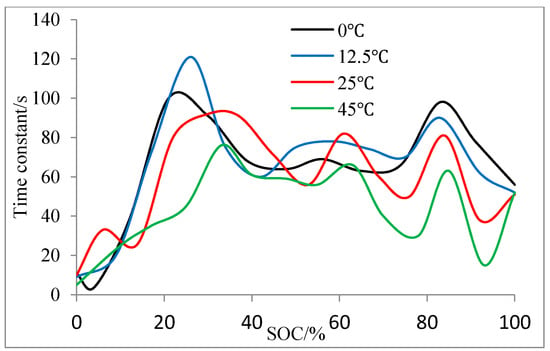
Figure 9.
Time constant at different temperatures, SOCs.
4. EKF-Based SOC Estimation Approach
4.1. SOC Definition
SOC is generally defined as the ratio of the remaining capacity to the nominal capacity of the cell [], given by:
where is the SOC at the kth sample time, is the initial SOC. is obtained from Equation (2).
The discretization of Equation (5) is
where is the sampling interval.
4.2. EKF Algorithm
EKF is a widely employed state estimation method for nonlinear dynamical systems. The general formation of the battery model is
where is the state vector, is the output vector, is the input vector, is plant matrix, is the input matrix, is the nonlinear output function, is assumed to be Gaussian white noise with zero mean, and covariance , is assumed to be Gaussian white noise with zero mean and covariance .
The process of EKF is shown as follows:
- (1)
- InitializationAssign the initial state estimate , error covariance , and .
- (2)
- Prediction
- (2)
- Correction
where is the output matrix.
4.3. SOC Estimation with EKF
Transform Equation (1) to a discrete system:
Then the state vector , output vector and input vector are defined as follows:
The , , , are defined as follows. Applying these matrices and function to Equations (8) and (9), the EKF based SOC estimator can be determined.
5. Validation and Improvement of the Estimator
5.1. Constant Discharge Validation
First, the estimator is validated under constant discharge at different temperatures. The constant current condition is very simple. Many researchers [,,,,,] validated their SOC algorithm in dynamic conditions rather than constant current conditions. However, we find that the model-based SOC estimator usually produces large errors in constant current conditions. The reason is that the model parameters identified based on some conditions may differ greatly from a constant current condition. The SOC estimation error during continuous constant current discharge cannot be corrected properly, thus the error may increase continuously. Therefore, it is necessary to verify the performance of the algorithm in constant current conditions.
At 25 °C, from cell fully charged to empty, the estimation results under 1/3 C, 1 C, and 2 C continuously discharge are shown in Figure 10, Figure 11 and Figure 12, respectively (the true SOC is calculated from the measured data using coulomb counting). The maximum absolute error (MAE) is below 3% under 1/3 C and 1 C discharge. However, when the cell is discharged with 2 C, the MAE is above 7%. The increasing error is caused by the battery nonlinear polarization. The polarization of the cell is divided into resistor polarization, concentration polarization, and activation polarization, and the latter two are the main sources of polarization nonlinearity. Experiment results manifest that the internal resistance decreases as the discharge current increases. It has also been tested that the polarization resistance is much more sensitive to discharge current than the ohmic resistance. Therefore, the polarization resistance is reduced by multiplying a coefficient during 2 C discharge, and the estimation result is shown in Figure 13. The MAE is within 3.5%. Further reduction of the error is hindered by the uncertainty of the parameters in low SOC region. Usually this kind of equivalent circuit model cannot maintain high accuracy in a low SOC region because of battery strong nonlinear behavior there. Many researchers avoid applying the algorithm to this case, considering that batteries on electric vehicles are usually forbidden to operate in SOC lower than 0.2. However, high accuracy in lower SOC may be necessary to optimize the management of the battery.
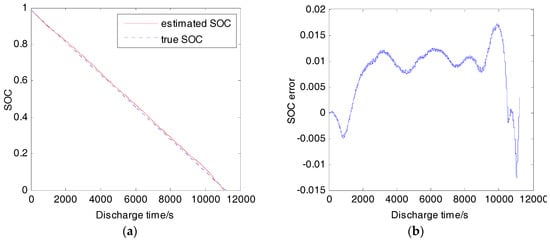
Figure 10.
SOC estimation result (25 °C, 1/3 C): (a) Estimated SOC and true SOC; (b) SOC estimation error.
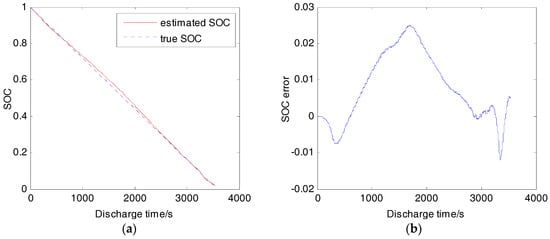
Figure 11.
SOC estimation result (25 °C, 1 C): (a) Estimated SOC and true SOC; (b) SOC estimation error.
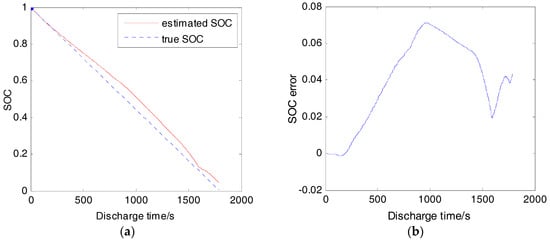
Figure 12.
SOC estimation result (25 °C, 2 C): (a) Estimated SOC and true SOC; (b) SOC estimation error.
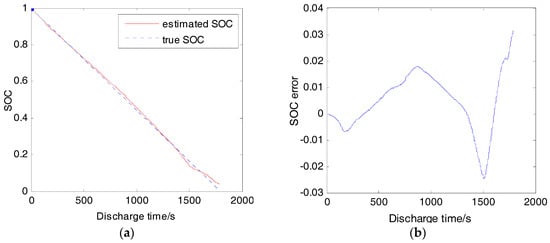
Figure 13.
SOC estimation result (25 °C, 2 C, resistance correction): (a) Estimated SOC and true SOC; (b) SOC estimation error.
The same tendency is found under constant discharge at other temperatures. The estimator can realize high accuracy under low current. However, when the current increases, the accuracy decreases. A polarization resistance correction efficient is introduced to improve the accuracy at high discharge current. The coefficient at the calibrated temperatures and currents is shown in Table 2. The value of the coefficient at other temperature and current can be obtained by two-dimensional (2D) interpolation. From Table 2, it can be seen that when the discharge current is below 1 C rate, no correction is introduced, except at 0 °C. The correction is introduced at all temperatures under 2 C discharge. The MAE under 2 C discharge with or without the correction is shown in Table 3. It can be concluded that the MAE is remarkably reduced by correction. The MAE is relative large under 12.5 °C, because of the model uncertainty at low SOC region. The problem can be fixed by variable measure noise variation which will be discussed latter.

Table 2.
Correction coefficient at the calibrated temperatures.

Table 3.
MAE with or without correction under 2 C discharge.
5.2. DST Validation
The estimation result under DST cycle at 20 °C is shown in Figure 14. Firstly the polarization resistance correction coefficient is not introduced. The MAE is about 5%. The accuracy is low in low SOC region. However, after multiplying the coefficient shown in Table 3, the result does not get better. It may be caused by: (1) The current in DST profile is lower than 1 C most of the time, so that the model is only corrected in a short time. (2) A relative high measure noise is set and the correction speed is low (process noise covariance Q is [0.1 0; 0 0.002], measurement noise covariance R is 0.5). (3) The cell nonlinear behavior in low SOC region is strong so that the correction proposed above is invalid. (4) The correction is obtained by calibration from constant current discharge tests, and it may be invalid in the dynamic current condition of the DST cycle.
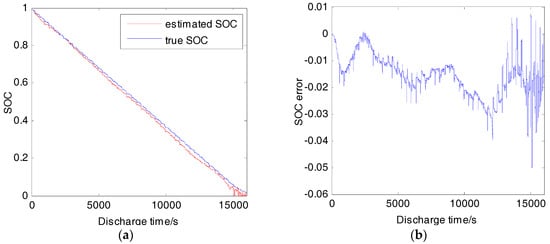
Figure 14.
SOC estimation result (DST, 20 °C): (a) Estimated SOC and true SOC; (b) SOC estimation error.
Considering that the cell model is unreliable in low SOC region, it is suggested that the measurement noise variation technology proposed by Lee et al. [] should be applied. The measurement noise covariance, R, has a strong influence on the Kalman gain. When R is large, the estimation mainly depends on the process model, otherwise the estimation mainly depending on the measurement model. We adjust the R in SOC lower than 0.2 by changing the original value 0.5 into 40 (this value acquired by trial and error). The result is shown in Figure 15. The MAE is below 4%. The measurement noise variation is a simple way to improve the estimation accuracy. However, if the measurement noise is too strong, a prompt correction of the initial SOC error will not be achieved. Therefore, it is preferred to set a different noise parameter in different SOC region to maximize the estimation accuracy.
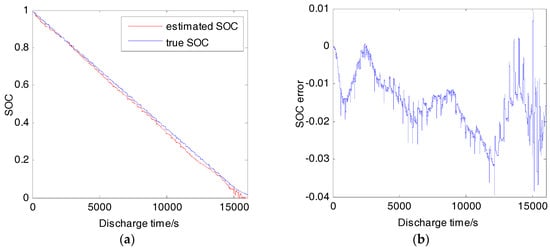
Figure 15.
SOC estimation result (DST, 20 °C, measurement noise adjustment): (a) Estimated SOC and true SOC; (b) SOC estimation error.
6. Conclusions
This paper proposes a SOC estimator based on a new temperature-compensated model with EKF, in which the capacity and OCV are adjusted by ambient temperature, while the RC parameters are adjusted by battery temperature. It can be used for SOC estimation in temperature range of 0–45 °C. Constant current discharge tests indicate that the estimation error is below 3% at low load current. However, its accuracy decreases when applied in high current discharge. It is found that the equivalent polarization resistance decreases as the discharge current increases. Therefore, a polarization resistance correction coefficient is introduced and the accuracy of the estimator is improved. The estimator also demonstrates good performance in dynamic load conditions. Nevertheless, the performance of the estimator is unable to be improved by the proposed polarization resistance correction. It seems that the correct scheme of battery long-term behavior and the short-term behavior should be differentiated. The model shows huge uncertainty in low SOC region. By increasing the measurement noise there, the estimation accuracy is improved. However, if the measurement noise is too strong, a prompt correction of the initial SOC error won’t be achieved. Therefore, it is preferred to set a different noise parameter in a different SOC region to maximize the estimation accuracy.
Acknowledgments
This work was supported by the key projects for new energy vehicles, national key research and development plan of China, under Grants 2016YFB0100305.
Author Contributions
Cheng Deng designed the algorithm and conducted the battery experiments. He wrote the main parts of the manuscript. Shichun Yang checked the results and the whole manuscript. Yulong Zhang conducted the battery experiment and did some data analysis. Yongling He helped develop the Matlab code of the algorithm.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Xing, Y.J.; He, W.; Pecht, M.; Tsui, K.L. State of charge estimation of lithium-ion batteries using the open-circuit voltage at various ambient temperatures. Appl. Energy 2014, 113, 106–115. [Google Scholar] [CrossRef]
- Waag, W.; Fleischer, C.; Sauer, D.U. Critical review of the methods for monitoring of lithium-ion batteries in electric and hybrid vehicles. J. Power Sources 2014, 258, 321–339. [Google Scholar] [CrossRef]
- Ng, K.S.; Moo, C.-S.; Chen, Y.-P.; Hsieh, Y.-C. Enhanced coulomb counting method for estimating state-of-charge and state-of-health of lithium-ion batteries. Appl. Energy 2009, 86, 1506–1511. [Google Scholar] [CrossRef]
- Kang, L.; Zhao, X.; Ma, J. A new neural network model for the state-of-charge estimation in the battery degradation process. Appl. Energy 2014, 121, 20–27. [Google Scholar] [CrossRef]
- Sheikhan, M.; Pardis, R.; Gharavian, D. State of charge neural computational models for high energy density batteries in electric vehicles. Neural Comput. Appl. 2013, 22, 1171–1180. [Google Scholar] [CrossRef]
- Antón, J.C.Á.; Nieto, P.J.G.; Viejo, C.B.; Vilán, J.A.V. Support vector machines used to estimate the battery state of charge. IEEE Trans. Power Electron. 2013, 28, 5919–5926. [Google Scholar] [CrossRef]
- Andre, D.; Appel, C.; Soczka-Guth, T.; Sauer, D.U. Advanced mathematical methods of SOC and SOH estimation for lithium-ion batteries. J. Power Sources 2013, 224, 20–27. [Google Scholar] [CrossRef]
- Plett, G.L. Extended Kalman filtering for battery management systems of LiPB-based HEV battery packs—Part 1. Background. J. Power Sources 2004, 134, 252–261. [Google Scholar] [CrossRef]
- Plett, G.L. Extended Kalman filtering for battery management systems of LiPB-based HEV battery packs—Part 2. Modeling and identification. J. Power Sources 2004, 134, 262–276. [Google Scholar] [CrossRef]
- Plett, G.L. Extended Kalman filtering for battery management systems of LiPB-based HEV battery packs—Part 3. State and parameter estimation. J. Power Sources 2004, 134, 277–292. [Google Scholar] [CrossRef]
- He, Z.; Gao, M.; Wang, C.; Wang, L.; Liu, Y. Adaptive state of charge estimation for li-ion batteries based on an unscented Kalman filter with an enhanced battery model. Energies 2013, 6, 4134–4151. [Google Scholar] [CrossRef]
- He, Y.; Liu, X.T.; Zhang, C.B.; Chen, Z.H. A new model for state-of-charge (SOC) estimation for high-power li-ion batteries. Appl. Energy 2013, 101, 808–814. [Google Scholar] [CrossRef]
- Plett, G.L. Sigma-point Kalman filtering for battery management systems of LiPB-based HEV battery packs—Part 1: Introduction and state estimation. J. Power Sources 2006, 161, 1356–1368. [Google Scholar] [CrossRef]
- Plett, G.L. Sigma-point Kalman filtering for battery management systems of LiPB-based HEV battery packs—Part 2: Simultaneous state and parameter estimation. J. Power Sources 2006, 161, 1369–1384. [Google Scholar] [CrossRef]
- He, H.W.; Zhang, Y.Z.; Xiong, R.; Wang, C. A novel Gaussian model based battery state estimation approach: State-of-energy. Appl. Energy 2015, 151, 41–48. [Google Scholar] [CrossRef]
- Sepasi, S.; Roose, L.; Matsuura, M. Extended kalman filter with a fuzzy method for accurate battery pack state of charge estimation. Energies 2015, 8, 5217–5233. [Google Scholar] [CrossRef]
- Sepasi, S.; Ghorbani, R.; Liaw, B.Y. A novel on-board state-of-charge estimation method for aged Li-ion batteries based on model adaptive extended kalman filter. J. Power Sources 2014, 245, 337–344. [Google Scholar] [CrossRef]
- He, H.; Xiong, R.; Peng, J. Real-time estimation of battery state-of-charge with unscented Kalman filter and RTOS μCOS-II platform. Appl. Energy 2016, 162, 1410–1418. [Google Scholar] [CrossRef]
- Tulsyan, A.; Tsai, Y.; Gopaluni, R.B.; Braatz, R.D. State-of-charge estimation in lithium-ion batteries: A particle filter approach. J. Power Sources 2016, 331, 208–223. [Google Scholar] [CrossRef]
- Zhang, Y.; Xiong, R.; He, H.; Shen, W. Lithium-ion battery pack state of charge and state of energy estimation algorithms using a hardware-in-the-loop validation. IEEE Trans. Power Electron. 2017, 32, 4421–4431. [Google Scholar] [CrossRef]
- Liu, X.; Chen, Z.; Zhang, C.; Wu, J. A novel temperature-compensated model for power Li-ion batteries with dual-particle-filter state of charge estimation. Appl. Energy 2014, 123, 263–272. [Google Scholar] [CrossRef]
- Hu, X.; Li, S.; Peng, H.; Sun, F. Robustness analysis of state-of-charge estimation methods for two types of Li-ion batteries. J. Power Sources 2012, 217, 209–219. [Google Scholar] [CrossRef]
- Tian, Y.; Xia, B.; Sun, W.; Xu, Z.; Zheng, W. A modified model based state of charge estimation of power lithium-ion batteries using unscented Kalman filter. J. Power Sources 2014, 270, 619–626. [Google Scholar] [CrossRef]
- Dey, S.; Ayalew, B.; Pisu, P. Nonlinear adaptive observer for a lithium-ion battery cell based on coupled electrochemical-thermal model. J. Dyn. Syst. Meas. Control 2015, 137, 111005. [Google Scholar] [CrossRef]
- Dey, S.; Mohon, S.; Pisu, P.; Ayalew, B.; Onori, S. Online state and parameter estimation of battery-double layer capacitor hybrid energy storage system. In Proceedings of the 2015 IEEE 54th Annual Conference on Decision and Control, Osaka, Japan, 15–18 December 2015. [Google Scholar]
- Tanim, T.R.; Rahn, C.D.; Wang, C.Y. State of charge estimation of a lithium ion cell based on a temperature dependent and electrolyte enhanced single particle model. Energy 2015, 80, 731–739. [Google Scholar] [CrossRef]
- Feng, F.; Lu, R.; Wei, G.; Zhu, C.; Sciubba, E. Online estimation of model parameters and state of charge of LiFePO4 batteries using a novel open-circuit voltage at various ambient temperatures. Energies 2015, 8, 2950–2976. [Google Scholar] [CrossRef]
- Verbrugge, M.; Tate, E. Adaptive state of charge algorithm for nickel metal hydride batteries including hysteresis phenomena. J. Power Sources 2004, 126, 236–249. [Google Scholar] [CrossRef]
- He, H.; Zhang, X.; Xiong, R.; Xu, Y.; Guo, H. Online model-based estimation of state-of-charge and open-circuit voltage of lithium-ion batteries in electric vehicles. Energy 2012, 39, 310–318. [Google Scholar] [CrossRef]
- Hu, X.; Li, S.; Peng, H. A comparative study of equivalent circuit models for li-ion batteries. J. Power Sources 2012, 198, 359–367. [Google Scholar] [CrossRef]
- Xiong, R.; Gong, X.; Mi, C.C.; Sun, F. A robust state-of-charge estimator for multiple types of lithium-ion batteries using adaptive extended Kalman filter. J. Power Sources 2013, 243, 805–816. [Google Scholar] [CrossRef]
- Xiong, R.; Sun, F.; Gong, X.; Gao, C. A data-driven based adaptive state of charge estimator of lithium-ion polymer battery used in electric vehicles. Appl. Energy 2014, 113, 1421–1433. [Google Scholar] [CrossRef]
- Lee, J.; Nam, O.; Cho, B.H. Li-ion battery SOC estimation method based on the reduced order extended Kalman filtering. J. Power Sources 2007, 174, 9–15. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).