Network Analysis of the Shanghai Stock Exchange Based on Partial Mutual Information

Abstract

Analyzing social systems, particularly financial markets, using a complex network approach has become one of the most popular fields within econophysics. A similar trend is currently appearing within the econometrics and finance communities, as well. In this study, we present a state-of-the-art method for analyzing the structure and risk within stock markets, treating them as complex networks using model-free, nonlinear dependency measures based on information theory. This study is the first network analysis of the stock market in Shanghai using a nonlinear network methodology. Further, it is often assumed that markets outside the United States and Western Europe are inherently riskier. We find that the Chinese stock market is not structurally risky, contradicting this popular opinion. We use partial mutual information to create filtered networks representing the Shanghai stock exchange, comparing them to networks based on Pearson’s correlation. Consequently, we discuss the structure and characteristics of both the presented methods and the Shanghai stock exchange. This paper provides an insight into the cutting edge methodology designed for analyzing complex financial networks, as well as analyzing the structure of the market in Shanghai and, as such, is of interest to both researchers and financial analysts.

1. Introduction

Due to human involvement, financial markets constitute complex adaptive systems. As economics does not have a theory fully explaining their behavior, the field is left with an assumption of the prices moving randomly, which is also known as the efficient-market hypothesis [1,2]. Within this paradigm, the evolution of stock prices can only be explained by random processes. It is then natural to ask whether these random processes are uncorrelated or whether they are in fact correlated and based on some common underlying causes. Studies looking into the interdependencies between financial instruments answer this very question.

The field of econophysics is perhaps best known for its treatment of financial markets as complex systems. Network theory plays an important role in such treatments, and it is most often used for the above-mentioned study of interdependencies between financial instruments. Usually, a correlation-based network is created, which quantifies the interrelations between the studied set of financial instruments. Such analysis uncovers the basic structure of the studied market, but can be also used for practical applications, such as portfolio optimization [3]. There have been many studies investigating stock markets on daily [4,5,6,7,8,9] and intraday [10,11,12] scales, as well as market indices [13,14,15,16,17,18,19,20] and foreign exchange markets [21]. These studies show that markets are structured according to sectors of economic activity for stock markets and geographical locations for market indices and foreign exchange markets. This result is important, as it cannot be reproduced by simulating a virtual market [22]. A limitation of this approach is connected with the researchers’ insistence on using Pearson’s correlation coefficient, which describes the system fully only if the system is behaving strictly linearly and, additionally, if an assumption of multivariate normal distribution holds true. This is the most used approach, even though it goes against the assumption of the complexity of those systems [23,24] and the solid evidence of the nonlinearity of financial markets with regards to stock returns [25,26,27,28,29], market index returns [30,31,32,33,34] and currency exchange rate changes [25,35,36,37,38]. This has recently been addressed by exchanging Pearson’s correlation coefficient with a more general (model-free [39]) measure of mutual information, which allows the study to account for nonlinearity and not rely on the assumption of multivariate normality [40,41].

In this paper, we address the above-mentioned issue by using network analysis of financial markets based on mutual information, as well as partial mutual information. Partial mutual information is a generalization of partial correlation, which is sensitive to nonlinear dependencies (but not sensitive to outliers), for which Pearson’s correlation and partial correlation cannot account. Partial mutual information allows us to refine the structural analysis of the market with Pearson’s correlation by adding nonlinearity and controlling for the mediating influence of third instruments and the stock market (through the index). However, partial mutual information may also be used to bring the analysis closer to market dynamics and causal relationships, similarly to the analysis performed with partial correlation in [42,43]. The latter will not be presented in this study, however.

We note that in order to include nonlinear dependencies, one could exchange Pearson’s correlation with Spearman’s rank correlation. There is a problem with such an approach, however. Spearman’s rank correlation considers only a limited class of association patterns (monotonically increasing functions), while mutual information does not have such constraints. For this reason, we prefer to use the information-theoretic approach. To justify this choice, we have performed the analysis using Spearman’s rank correlation, and it gives results very similar to Pearson’s correlation (the correlation between dependency measures for all studied pairs of stocks from both methods is around 0.95, much higher than between Pearson’s rho and mutual information, as presented in Figure 3). However, in cases where analysts would rather avoid the discretisation step (and consequently, the information-theoretic approach), we would advise against using Pearson’s correlation and in favor of using Spearman’s rank correlation or biweight mid-correlation, as these are better justified theoretically with regards to sensitivity to nonlinear behavior and outliers and also appeared to give marginally better results in the presence of noise or outliers in the comparisons that we have performed in our other studies.

Despite a growing interest and body of literature on this topic, there is still relatively little research produced within the econometrics community that analyzes complex financial networks using the above-mentioned tools. Most of the related articles are published within econophysics or general science journals. This is particularly surprising, as financial practitioners are quite commonly using tools based on such methodology (e.g. www.fna.fi). Despite interdependencies within financial markets being an area of interest in finance for decades now [6], the usage of complex networks in such inquiries is relatively new in the financial literature. Tse et al. first presented such complex networks to the financial research community in their paper analyzing U.S. stocks in 2010 [44]. Tumminello et al. presented a review of hierarchical networks for financial markets in the same year [45]. The econometrics literature largely ignores networks illustrating the market complexity based on historical data, but rather concentrates on more traditional economic issues, such as games on networks [46]. As such, this paper is an opportunity to present the cutting-edge version of the mentioned methodology to the econometrics community.

Further, an analysis of financial markets accounting for nonlinearity has yet to be applied to the Shanghai stock exchange. Due to the size and rate of growth of this market, such an analysis is of obvious importance to financial analysts. There have only been a handful of papers that have touched upon the basics of this methodology, but which have not been devoted solely to this topic. It has either been featured in a recent review of econophysics [47] or within a research devoted to the usage of random matrix theory [48]. The former is applied, but does not deal with financial networks in detail, whereas the latter is the only article dealing with financial networks in Chinese journals on interdisciplinary physics. This paper does not contain a detailed study of the Chinese stock market, however. Another study looks at the Chinese market from the network perspective, but is more interested in the network topology, rather than the market itself [49]. Yet another study published in Europhysics Letters uses random matrix theory to derive the subsector structure of American and Chinese markets and analyzes the differences between them, again with very little market insight [50]. Yet another study in the same journal merely notes that the cross-correlation structure of the Chinese market is less dependent on economic sectors in comparison with the other markets [51]. One can also find studies that use time series, which are too short to avoid statistical noise or to gain an insightful picture of the market [52], studies interested in networks based on geographical features, rather than price movements [53] or studies interested in the robustness of the networks rather than their economic significance [54]. The last study notes that the Chinese market is more resilient than other markets, a claim we also investigate in this study in detail. Our earlier studies [55] concentrated on industry indices and, additionally, using Pearson’s linear correlation coefficient, did not account for nonlinear relationships between the studied time series. It is of the utmost importance to note that none of these studies consider nonlinear relationships, which is puzzling, as noted above. Thus, we believe that there is a need for a paper that presents a cutting edge methodology for creating financial networks, together with a detailed analysis of the stock exchange in Shanghai. Such an analysis will be of interest to both researchers and market practitioners. Within this study, we also partially test the popular belief that markets outside the United States and Western Europe are inherently more risky.

This paper is structured as follows: in Section 2, we present the proposed methodology. In Section 3, we show the results obtained for the Shanghai Stock Exchange. In Section 4, we discuss these results. In Section 5, we conclude our study and propose further research.

2. Methods

The topological structure of networks modeling financial markets is most often based on Pearson’s correlation coefficients between time series describing logarithmic price changes (we use logarithmic returns, because prices are not stationary). These need to be calculated for all pairs in the studied set of financial instruments. The Pearson’s correlation coefficient is defined as [56]:

$${\rho }_{X,Y}=\frac{E\left(XY\right)-E\left(X\right)E\left(Y\right)}{\sqrt{(E\left(X^2\right)-E{\left(X\right)}^2)(E\left(Y^2\right)-E{\left(Y\right)}^2)}}$$

(1)

where X and Y are time series describing log price changes for two financial instruments under consideration. ρ is not a metric, and it may be easier to use one to determine a network’s topology and the geometry of the resulting plots. Thus, the below metric is most often used for this purpose [4]:

$$\delta (X,Y)=\sqrt{2(1-{\rho }_{X,Y})}.$$

(2)

This form guarantees that $\delta (X,Y)$ is a Euclidean metric and that it conforms to the three axioms: positivity, symmetry and triangle inequality.

Pearson’s correlation coefficients only describe the system fully if the interdependencies are strictly linear. As this is not the case in financial markets, we extend the similarity measure to account for nonlinear dependencies. We propose to use mutual information for this purpose. Mutual information is a term derivative to Shannon’s entropy [57], which is a measure of the uncertainty of a random variable. Mutual information, in Shannon’s sense, can be defined for two discrete random variables, X and Y, as:

$$I(X,Y)=\sum _{y\in Y}\sum _{x\in X}p(x,y)log\frac{p(x,y)}{p\left(x\right)p\left(y\right)}$$

(3)

where $p(x,y)$ is the joint probability distribution function of X and Y and $p\left(x\right)$ and $p\left(y\right)$ are the marginal probability distributions. For continuous variables, the definition is analogous using probability density functions. Equivalently, using entropy, mutual information is defined as:

$$I(X,Y)=H\left(X\right)+H\left(Y\right)-H(X,Y)$$

(4)

where $H\left(X\right)$ is Shannon’s entropy, which is a measure of the uncertainty of a random variable X defined as:

$$H\left(X\right)=-\sum _{i}p\left(x_i\right)logp\left(x_i\right)$$

(5)

summed over all possible outcomes $\left\{x_i\right\}$ with respective probabilities of $p\left(x_i\right)$. $H(X,Y)$ is the joint entropy associated with both variables, and is defined analogously to $H\left(X\right)$, but using joint probabilities. Mutual information, as defined above, measures information shared between the two variables, taking into account both linear and nonlinear dependencies. As a result, using it to describe dependencies on financial markets seems natural. Mutual information is non-negative and $I(X,X)=H\left(X\right)$. It is also worth noting that such an approach is inherently model-free [39].

Additionally, partial mutual information $I(X,Y|Z)$ denotes the part of mutual information $I(X,Y)$ that is not in Z and is defined as [58]:

$$I(X,Y|Z)=H(X,Z)+H(Y,Z)-H(Z)-H(X,Y,Z)$$

(6)

Partial mutual information is symmetric, so that $I(X,Y|Z)=I(Y,X\left|Z\right)$ and $0 \le I(X,Y|Z)$. Mutual information and partial mutual information are only equal to 0 when X and Y are strictly independent.

We have defined mutual information and partial mutual information in terms of Shannon’s entropy. Therefore, for practical purposes, we need an estimator of such entropy. There is a large number of estimators, and a discussion of these can be found in the literature [59,60,61,62,63]. In this paper, we use the Schurmann–Grassberger estimator of the entropy of a Dirichlet probability distribution, which is thought to be a good choice for most applications [64]. The Schurmann–Grassberger estimator is a Bayesian parametric procedure that assumes samples distributed following a Dirichlet distribution:

$$\widehat{H}\left(X\right)=\frac{1}{m+\left|\chi \right|N}\sum _{x\in \chi }(\#(x)+N)\left(\psi \right(m+\left|\chi \right|N+1)-\psi (\#\left(x\right)+N+1\left)\right)$$

(7)

where $\#\left(x\right)$ is the number of data points having value x, $\left|\chi \right|$ is the number of bins from the discretisation step, m is the sample size, and $\psi \left(z\right)=\mathrm{d} ln \Gamma \left(z\right)/\mathrm{d}z$ is the digamma function. The Schurmann–Grassberger estimator assumes $N=1/\left|\chi \right|$ as the prior [65]. Here, we note that the choice of this estimator (and consequently, also the Dirichlet prior) is irrelevant to our analysis, as the correlation between results obtained with Schurmann–Grassberger estimator and empirical estimator (entropy of the empirical probability distribution) is over 0.999999, while the same for Schurmann–Grassberger estimator and Miller–Madow asymptotic bias corrected empirical estimator is over 0.99999. We use the Schurmann–Grassberger estimator, as it is a popular choice in information theory. However, the results are robust with regards to this choice.

Using the Schurmann–Grassberger estimator, we are able to find mutual information, but then it needs to be converted to a Euclidean metric, as has been presented for correlation coefficients above. We present metrics based on mutual information and partial mutual information, both of which are used in this study. Metrics based on mutual information are known in the literature [66,67]. The quantity:

$$d(X,Y)=H(X,Y)-I(X,Y)$$

(8)

satisfies the mentioned axioms [67]. For partial mutual information, we want to base the distance on the smallest partial mutual information when controlling for all other stocks and the index of the studied exchange. We may define it in the following manner:

$$D(X,Y)=\left\{\begin{array}{cc}H(X,Y)-{min}_{Z\ne X,Y}I(X,Y|Z)\hfill & \text{if}X\ne Y\hfill \\ 0\hfill & \text{if}X=Y\hfill \end{array}\right.$$

(9)

which ensures that this is a Euclidean metric.

We have a method for estimating the topological structure of hierarchical networks modeling financial markets based on Pearson’s correlation, Shannon’s mutual information and partial mutual information. We need to briefly discuss methods for producing such networks in order to complete the presentation. Based on a matrix filled with the described pairwise metrics, we can now define methods for constructing hierarchical networks used for studying financial markets. Such methods filter the less important information out of the characteristic vector describing the system and allow for easier analysis of the most important information within the system. These methods are well known, and we only briefly define them here. In particular, we define methods used for creating minimally-spanning trees (MST) and planar maximally-filtered graphs (PMFG). The distance matrix $𝒟$ containing $\delta (X,Y)$, $d(X,Y)$ or $D(X,Y)$ for all studied pairs is defined above. From $𝒟$, we create an ordered list $𝒮$, in which the distances are listed in ascending order.

The minimally-spanning tree (MST) is created by using the ordered list $𝒮$, and starting from the pair with the lowest distance D, an edge is added to the graph between elements X and Y if and only if the graph obtained this way is still a forest or a tree [68]. After all appropriate links are added, such a graph is always reduced to a tree [45,68]. This method is known as Kruskal’s algorithm.

Less constrained graphs can also be constructed, where the genus is fixed: $g=k$. Such graphs are created similarly: from the ordered list $𝒮$, starting from the pair with the largest similarity measure, we add an edge between that pair if and only if the resulting graph can still be embedded on a surface of genus $g\le k$. Such a graph is less topologically restrictive than MST and always contains the relevant MST, as well as additional loops and cliques [68]. Then, if $g=0$, the resulting graph is planar [69]. Such a graph is the simplest extension of the MST and is called the planar maximally-filtered graph (PMFG). Each element in such a graph has to participate in at least one clique of three elements; thus, such a graph can be considered a topological triangulation of the sphere [68]. Larger cliques are not allowed, however [69,70].

The minimally-spanning tree presents only the most relevant dependencies in the studied system, thus making the analysis of large systems relatively easy, which is important in the analysis of financial markets. When a less restrictive structure is needed, the natural candidate is the planar maximally-filtered graph. Thus, we use both those structures, but it is worth noting that other structures have also been proposed [45].

Minimally-spanning trees and planar maximally-filtered graphs can be used to effectively reduce the complexity of financial dependencies and to understand the dynamics of financial markets. Tools for analyzing correlation-based networks are used by many investment funds, particularly to easily understand the changing structure (commonly based on economic sectors and subsectors) of the financial markets and to enhance the risk management of investment portfolios (baskets of stocks within the same cluster in the networks are inherently more risky). Such networks based on changes in stock prices commonly display a scale-free degree distribution. As such, this suggests that the variations in stock prices are strongly influenced by a relatively small number of stocks. Such networks provide an easy way to obtain information about these stocks and are particularly useful in managing risk associated with investment portfolios. Such networks can also help inquire into the existence and nature of common economic factors that drive the time evolution of stock prices [4]. Below, we create such networks for the market in China and analyze its structural properties.

3. Experimental Results

To apply networks based on correlation, mutual information and partial mutual information in the reality of the Shanghai Stock Exchange, so as to find their properties and the characteristics of the market itself, we have obtained daily log returns for 158 stocks belonging to the Shanghai Stock Exchange, as well as the index of this market (SSE Composite Index). The data on prices cover 1288 days between the 5 January 2009 and the 30 April 2014 and have been obtained from the Yahoo! Finance database. The choice of this particular period is motivated by two ways. First, we want to comment on the current state of the market in Shanghai, and thus, we take the data after the turmoil of the worldwide crisis of 2008. Second, we want the data to be sufficiently long, as mutual information does not work well for very short time series, but we also want the data not to be very long, so as not to lose economic homogeneity. The time series describing daily closing prices are transformed in the standard way for analyzing price movements, which is so that the data points are the log ratios between consecutive daily closing prices: $r_t=ln(p_t/p_{t-1})$, and those data points are, for the purpose of the mutual information estimator, discretized into four distinct states through the common procedure of binning into quantiles. The choice of the number of bins, as well as the discussion of the whole procedure can be found in [71]; here, we only note that the results are robust with regards to the choice of the number of quantiles. Additionally, the 158 stocks are divided into 10 sectors and 34 subsectors according to Bloomberg. Bloomberg has also provided the latest earnings per share ratios for all studied stocks.

On this basis, we have created six networks. For each of the above-introduced distances, $\delta (X,Y)$, $d(X,Y)$ and $D(X,Y)$, we have created a minimally-spanning tree and a planar maximally-filtered graph. All of those networks are undirected, weighed graphs, where nodes denote stocks and links denote closeness between them (in terms of correlation or (partial) mutual information). The nodes (the stocks) are assigned an economic sector and subsector according to Bloomberg’s classification, which does not affect the topology, and is only used later to compare how well the presented methods recreate sector structure from price changes alone, which is one of the main results of the general methodology [22]. Thus, we are able to comment on the different characteristics of these and, in particular, show that using partial mutual information is beneficial to the analysis, especially against the most commonly-used methodology based on Pearson’s correlation coefficient. A minimally-spanning tree based on partial mutual information is presented in Figure 1, and a planar maximally-filtered graph based on the same distance is presented in Figure 2. The most important stocks (in terms of node degree) are labeled with their tickers. These are as follows: 601588, Beijing North Star Co Ltd; 601168, Western Mining Co Ltd; and 601898, China Coal Energy Co Ltd.

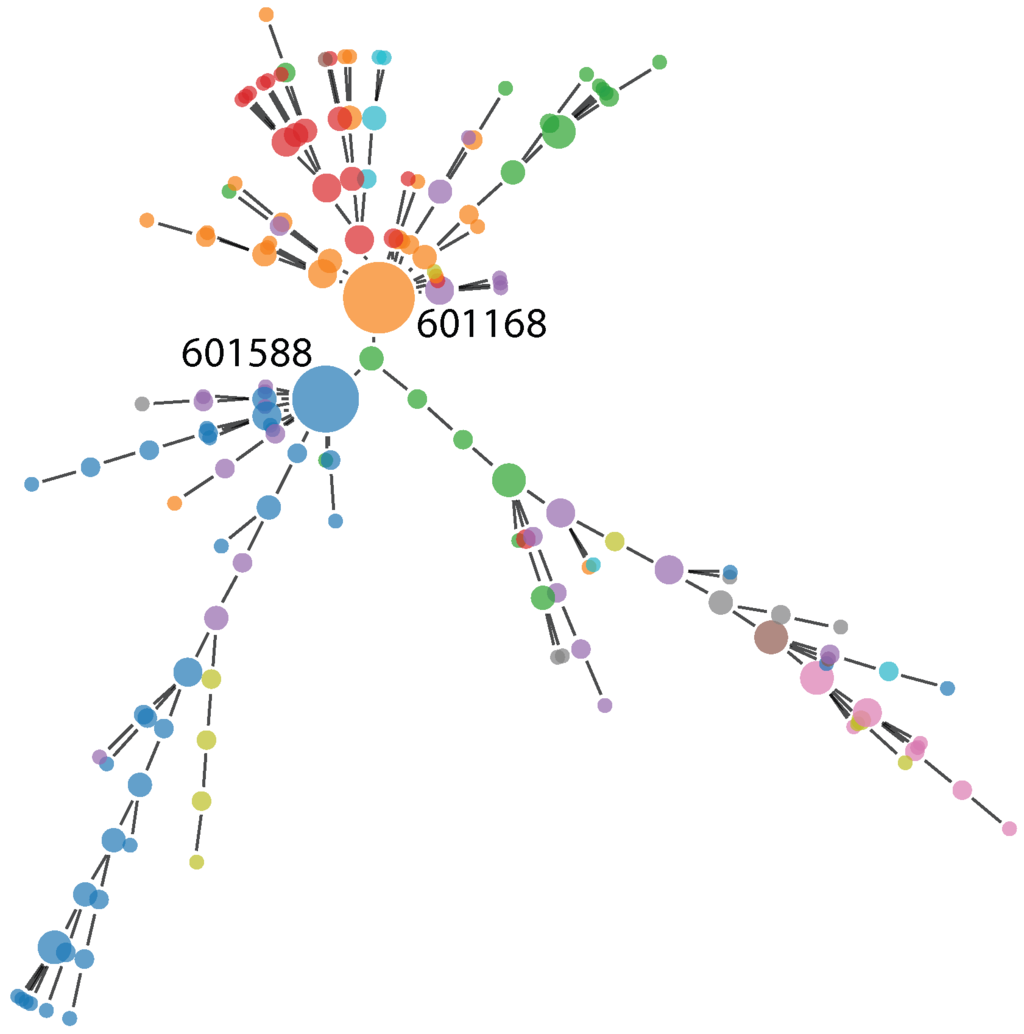
Figure 1. Minimally-spanning tree for the Shanghai Stock Exchange based on partial mutual information between studied stocks. Stocks with the highest node degrees have been named with their ticker symbols. The size of the nodes is proportional to their node degree.

Figure 1. Minimally-spanning tree for the Shanghai Stock Exchange based on partial mutual information between studied stocks. Stocks with the highest node degrees have been named with their ticker symbols. The size of the nodes is proportional to their node degree.

Figure 2. Planar maximally-filtered graph for the Shanghai Stock Exchange based on partial mutual information between studied stocks. Stocks with the highest node degrees have been named with their ticker symbols. The size of the nodes is proportional to their node degree.

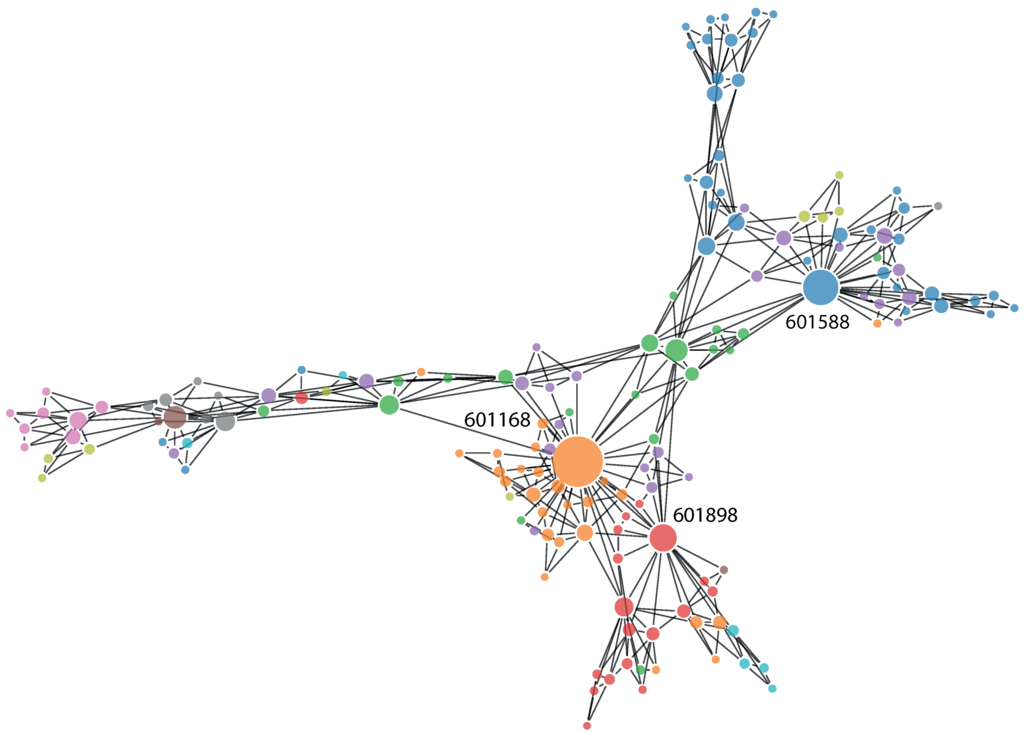
Figure 2. Planar maximally-filtered graph for the Shanghai Stock Exchange based on partial mutual information between studied stocks. Stocks with the highest node degrees have been named with their ticker symbols. The size of the nodes is proportional to their node degree.

Before commenting on the structure of the market in Shanghai, we discuss the advantages of using partial mutual information in creating financial networks, as compared to using Pearson’s correlation coefficient. First, we show that the two approaches do in fact give different results, before looking into whether we can say that one of them gives better results. To illustrate that there are differences between the three methods, we have calculated Pearson’s correlation coefficients between distances associated with the three used dependency measures (δ based on Pearson’s correlation (Corr), d based on mutual information (MI) and D based on partial mutual information (PMI)) for all pairs of stocks within the studied set ($\left(\genfrac{}{}{0pt}{}{158}{2}\right)=12,403$), which we have presented in Figure 3.

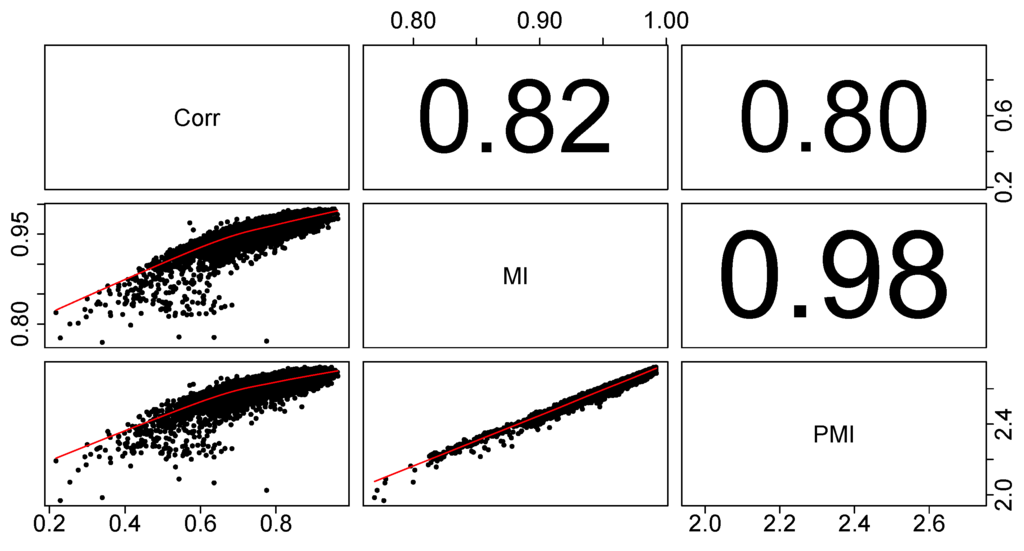
Figure 3. Pearson’s correlation coefficients between distances associated with the three used dependency measures (δ based on Pearson’s correlation (Corr), d based on mutual information (MI) and D based on partial mutual information (PMI)) for all pairs of stocks within the studied set. It is clear that using partial mutual information changes the analysis very slightly with regards to mutual information, but both give significantly different results from the analysis using Pearson’s correlation coefficients.

Figure 3. Pearson’s correlation coefficients between distances associated with the three used dependency measures (δ based on Pearson’s correlation (Corr), d based on mutual information (MI) and D based on partial mutual information (PMI)) for all pairs of stocks within the studied set. It is clear that using partial mutual information changes the analysis very slightly with regards to mutual information, but both give significantly different results from the analysis using Pearson’s correlation coefficients.

As mentioned above, both MST and PMFG show the strongest relations between assets, which create clusters based mostly on the economic sectors. This information is important, as it cannot be reproduced by simulating a virtual market [22]. Note that all nodes in the networks we have created are attributed as belonging to a specific economic sector (according to Bloomberg). As such, we may analyze how strongly the filtered graphs (MST, PMFG) are based on economic sectors. For this purpose, we calculate the ratio between the number of links between the stocks belonging to the same economic sector (according to Bloomberg) and the number of all links in the created networks. If a network were only to consist of links between stocks (nodes) belonging to the same economic sector, this ratio would be equal to 100% (in practice, this would require only one sector, as there must be (at least an indirect) link between all nodes within MST and PMFG).

Calculating the percentage of intra-sector links within the created networks allows us to see which of these networks reproduces the sector structure of the Shanghai Stock exchange from the price changes in the most accurate manner. The results are presented in Table 1. We note that it is very hard to probe the statistical significance of these results (a sample of one, as we only create one network based on each dependency measure and topology; there is not enough data to create multiple networks and test it this way), and as such, we base our conclusions mostly on the agreement between these results and results obtained in other studies, which cover different markets and analyze different years; see the discussion below. Nonetheless, we have performed a bootstrap analysis by shuffling the rows of the matrix containing log returns repeatedly without replacement in order to create a large number of surrogated time series of returns. After each shuffling, we calculate the correlation and mutual information between the original and shuffled log returns, create minimally-spanning trees on this basis and calculate the percentage of intra-sector links within these to observe how likely the results are due to pure chance. We applied this procedure a thousand times and have obtained a distribution of the percentage of intra-sector links within the networks based on surrogate data (close to being Gaussian) with a mean of 12.85% and a standard deviation of around 4% for correlation-based networks and an average of 4.18% with a standard deviation of around 1% for mutual information-based networks. These findings further increase our confidence in the results presented in Table 1. First, the obtained intra-sector link ratios are already stunningly significant at over 11 standard deviations above the mean for correlation-based networks and even more for mutual information-based networks. Second, as mentioned above, the ratio of intra-sector links is lower for networks based on mutual information than correlation (for surrogate data); thus, being the opposite for the original data makes us believe that this is due to the economic structure being unveiled by mutual information, rather than statistical noise.

Table 1. Percentage of links between instruments belonging to the same economic sector in all links within the studied networks. As a reference, the same is shown for an unrestricted network or a full graph. Both mutual information (d) and partial mutual information (D) reproduce the sector structure from price changes slightly more accurately than Pearson’s correlation coefficient (δ), which is in agreement with similar studies of other markets. MST, minimally-spanning tree; PMFG, maximally-filtered graph.

Distance	MST	PMFG
δ	64.97%	53.85%
d	66.24%	56.84%
D	66.88%	58.12%
None	13.96%	13.96%

Table 1. Percentage of links between instruments belonging to the same economic sector in all links within the studied networks. As a reference, the same is shown for an unrestricted network or a full graph. Both mutual information (d) and partial mutual information (D) reproduce the sector structure from price changes slightly more accurately than Pearson’s correlation coefficient (δ), which is in agreement with similar studies of other markets. MST, minimally-spanning tree; PMFG, maximally-filtered graph.

Distance	MST	PMFG
δ	64.97%	53.85%
d	66.24%	56.84%
D	66.88%	58.12%
None	13.96%	13.96%

One of the most important characteristics describing a network is the distribution of node degrees. Thus, we have plotted degree distributions for all created networks on a log-log scale, as presented in Figure 4. This allows us to see whether these are in fact scale-free networks or whether they follow a different distribution. We expect the distribution of node degrees to have fat tails, due to preferential attachment. The results (p-values) of the Kolmogorov–Smirnov test for the power law are as follows: 0.04120614 for Pearson’s correlation-based MST, 0.02516791 for Pearson’s correlation-based PMFG, 0.09684842 for mutual information-based MST, 0.07434126 for mutual information-based PMFG, 0.08852421 for partial mutual information-based MST and 0.06827215 for partial mutual information-based PMFG. As can be seen, while the networks based on the information-theoretic approach are not strictly following power law distributions (at 5% level of significance we would reject the null hypothesis of the two distributions being equal in the mutual information-based networks), they are nonetheless strongly fat-tailed, which shows that the presented information-theoretic methodology does not fail to produce networks with preferential attachment. Further, the results (p-values) of the Kolmogorov–Smirnov test for log-normal distribution are as follows: 0.01961782 for Pearson’s correlation-based MST, 0.01572181 for Pearson’s correlation-based PMFG, 0.02234679 for mutual information-based MST, 0.02875467 for mutual information-based PMFG, 0.01768697 for partial mutual information-based MST and 0.02850081 for partial mutual information-based PMFG. In all these cases we would not be able to reject the null hypothesis stating that the distributions are identical. The tests have been performed using the poweRlaw package in R.

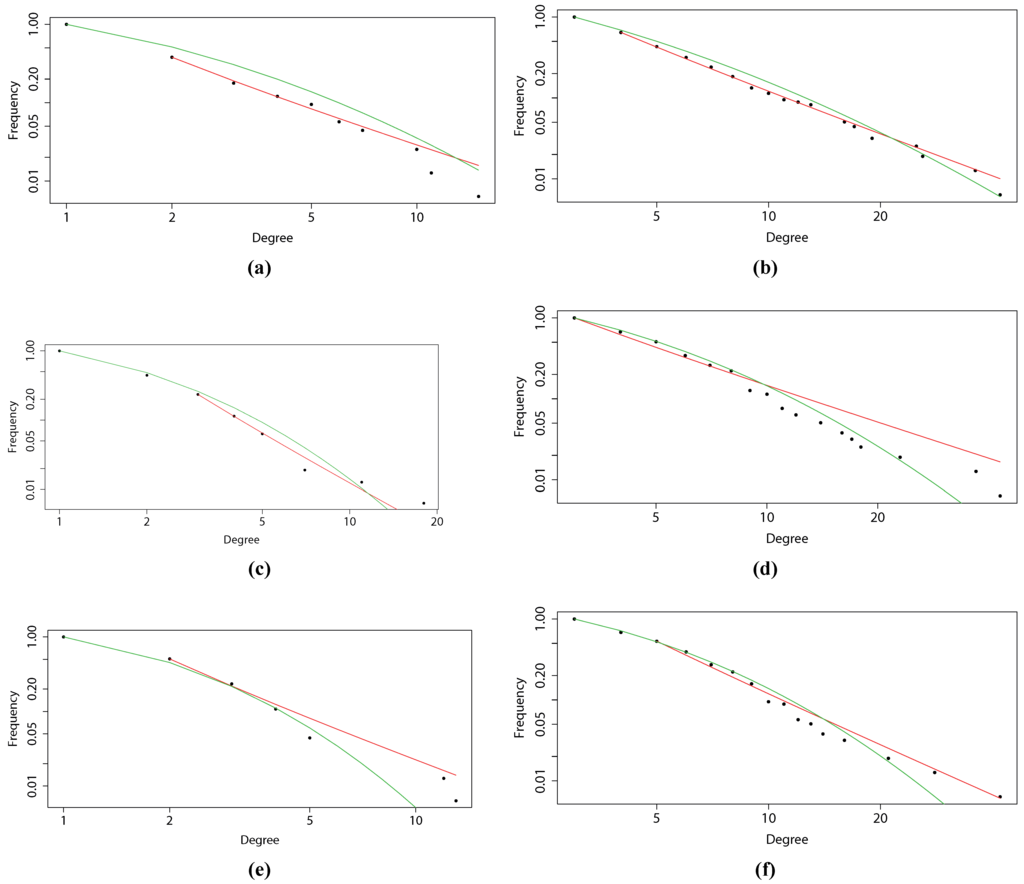
Figure 4. Degree distributions (with fitted power law and log-normal distribution) for: (a) a minimally-spanning tree based on correlation; (b) a planar maximally-filtered graph based on correlation; (c) MST based on mutual information; (d) PMFG based on MI; (e) MST based on partial mutual information; and (f) PMFG based on PMI.

Figure 4. Degree distributions (with fitted power law and log-normal distribution) for: (a) a minimally-spanning tree based on correlation; (b) a planar maximally-filtered graph based on correlation; (c) MST based on mutual information; (d) PMFG based on MI; (e) MST based on partial mutual information; and (f) PMFG based on PMI.

Finally, we look into how stocks with various levels of importance in the studied networks (in terms of node degree) behave economically in terms of earnings per share ratio. There is a negative correlation between node degree within the network presented in Figure 1 and the earnings per share (EPS) ratio for all studied companies, with a magnitude of around −0.1. Further, the two hubs in the networks (nodes with the largest degrees: 13 and 12) have modest EPS ratios, while all the outliers (both negative and positive) in terms of EPS are characterized by low degrees (five or less) within the studied networks. Additionally, in Table 2, we have presented the sum of the degrees for stocks in all studied sectors, the average degree for a stock in all studied sectors and the average EPS ratio in all studied sectors in MST and PMFG based on partial mutual information.

Table 2. The sum of node degrees for stocks belonging to the studied economic sectors in MST (1) and PMFG (3) based on partial mutual information, the average node degree for stocks belonging to the studied sectors in MST (2) and PMFG (4) based on partial mutual information and the average earnings per share (EPS) ratio for stocks belonging to the studied sectors (5). There is a negative correlation between the EPS ratio in a sector and the sector’s average importance in the network.

Sector	(1)	(2)	(3)	(4)	(5)
Communications	7	2.33	22	7.33	0.29
Consumer Discretionary	46	1.92	136	5.67	0.58
Consumer Staples	14	1.56	37	4.11	2.17
Energy	37	2.06	117	6.50	0.49
Financials	80	2.11	228	6.00	0.92
Healthcare	17	2.13	47	5.88	0.54
Industrials	38	2.00	113	5.95	0.15
Materials	55	2.12	171	6.58	0.33
Technology	10	1.43	39	5.57	0.53
Utilities	10	1.67	26	4.33	0.46

Table 2. The sum of node degrees for stocks belonging to the studied economic sectors in MST (1) and PMFG (3) based on partial mutual information, the average node degree for stocks belonging to the studied sectors in MST (2) and PMFG (4) based on partial mutual information and the average earnings per share (EPS) ratio for stocks belonging to the studied sectors (5). There is a negative correlation between the EPS ratio in a sector and the sector’s average importance in the network.

Sector	(1)	(2)	(3)	(4)	(5)
Communications	7	2.33	22	7.33	0.29
Consumer Discretionary	46	1.92	136	5.67	0.58
Consumer Staples	14	1.56	37	4.11	2.17
Energy	37	2.06	117	6.50	0.49
Financials	80	2.11	228	6.00	0.92
Healthcare	17	2.13	47	5.88	0.54
Industrials	38	2.00	113	5.95	0.15
Materials	55	2.12	171	6.58	0.33
Technology	10	1.43	39	5.57	0.53
Utilities	10	1.67	26	4.33	0.46

4. Discussion

First, we comment on the differences between networks created using the three mentioned distances ($\delta (X,Y)$, $d(X,Y)$, $D(X,Y)$) in the context of finding the accuracy of the created networks. The more general nature of mutual information over Pearson’s correlation together with the obvious nonlinearity of the behavior of financial markets hints that mutual information should be better suited for analyzing stock markets. This is confirmed for other markets in the studies mentioned above [40,41]. Nonetheless, since there is no theory of financial markets, we are not able to directly state that our method is representing the market in a more accurate manner than the standard method based on Pearson’s correlations. In other words, there is no benchmark, as we do not know what the network structure of the market really looks like (if we knew, the presented methodology would be pointless). We may observe some characteristics of these networks and comment on their differences, however, providing an indirect answer to this question. As we can see in Figure 3, there is quite a large (around 20%) difference between the distances based on correlation and (partial) mutual information. We would not expect a higher difference, as the most important dependencies on the market are captured by the correlations. We only want to enhance this methodology by involving nonlinear dependencies. We also see that the difference between distances based on mutual information and partial mutual information are small, thus controlling for a mediating influence is of secondary importance.

We also expect our method to recreate the sector structure of the Shanghai Stock Exchange from prices. This is an important feature of asset networks, as has been explained above. In Table 1, we see that all three methods give substantially higher percentages of intra-sector links than the full graph. Nonetheless, similarly to studies on other markets [40], mutual information also performs better in this study. Partial mutual information also slightly improves the analysis in this respect as compared to mutual information. Nonetheless, it is very hard to find the statistical significance of these results, but the consistency of the results pointing in favor of the information-theoretic approach in this and similar studies gives certain weight to our argument.

We also note that this result contradicts the results of one of the studies in the literature review [51], where the authors have found that “since the Chinese stock market is an emerging market, the companies are not operated strictly with the registered business.” Our results suggest that the sector structure, as reconstructed from price changes, is not different from the structure of mature markets, such as the United States and Europe. We also note that while we believe a method that recreates this structure in the best way can be seen as superior, there can be situations where we do not necessarily want this to be the case. For instance, in certain cases, we may prefer a method that uncovers a more surprising relationship for stocks belonging to different sectors, but having other things in common, such as shared ownership. It is difficult to judge a method based on such criteria, however, since the amount of relationships we could be looking for is virtually limitless, and it could therefore be used to justify any choice, while in our measurement, the standard is clear.

Finally, we take a look at the degree distributions presented in Figure 4, which may further shed light on the question of the accuracy of the networks. It appears that the distribution depends quite strongly on the structure of the graph. While MST seems to have the degrees distributed in a manner closer to log-normal distribution than PMFG, the latter is characterized by degree distributions closer to the power law. While many researchers strive to obtain the power law in such analyses, we believe the fat tails of a log-normal distribution are sufficient (and can in fact be better justified as the multiplication of various market complexities). We observe that the above-presented Kolmogorov–Smirnov test results for a log-normal distribution are sufficiently good to conclude that networks created using information-theoretic approach are characterized by fat-tailed degree distributions. We are therefore inclined to say that by using partial mutual information, we obtain financial networks that describe the financial markets more precisely, accounting for nonlinear dependencies, enhancing the reconstruction of the sector structure and not losing the (nearly) scale-free property. Therefore, we propose not to use the most popular correlation-based methodology, as there is no significant gain (in computational complexity or results) from the simplified procedure over the methodology presented in this paper.

Finally, we discuss the picture of the Shanghai Stock Exchange resulting from the partial mutual information network analysis presented above. The stocks dominating the market in Shanghai are not concentrated in one or two sectors, which is usually a sign of the good health of the market [72]. Here, by health, we mean the vulnerability to shocks originating within economic sectors. In this sense, a more diverse market (network) is better, spreading the risk more evenly. In fact, in the presented PMFG, within the ten stocks with the highest node degrees, we find two representatives of the energy, financial and industrial sectors, with four other sectors represented, as well. By far the highest node degree equal to 42 belongs to Western Mining Co Ltd, representing the materials sector. Second place belongs to Beijing North Star Co Ltd, representing the financial sector with 28, while third place belongs to China Coal Energy Co Ltd, representing the energy sector with 21 connections. This corroborates our earlier study, which showed that there is no single sector controlling the Chinese financial network, but that there is a number of sectors that are influential [55].

Despite this diversity within the most influential stocks on the Shanghai Stock Exchange, they have one thing in common: they are all very stable companies, with reasonable earnings per share ratios between 0.1657 and 0.284. As can be seen in Figure 2, these three stocks lead large clusters of stocks from their respective sectors. As mentioned above, the companies with large node degrees (top two stocks with degrees of 13 and 12; the other stocks have degrees equal or less than five) in MST are characterized by reasonable EPS ratio, while companies with low degrees vary greatly in their EPS ratios, hinting that the market is healthy, as in following only well-established companies (and not unstable companies, which may have very good results in the short term, but which could destabilize the market in the long term). This is by no means a fully precise statement, as the market is highly complex, and we can observe a lot of variation; however, the trend is visible. In fact, there is a negative correlation between the average node degree in a sector and the average EPS in a sector of −0.46 for MST and −0.63 for PMFG. This once again hints that companies with temporarily bloated financial results do not tend to be highly influential on the stock exchange in Shanghai. Finally, we comment on the sector structure presented in Table 2. The financial sector is the strongest in terms of the total number of connections related to their stocks within the studied networks. This is largely due to the number of stocks representing this sector, however. In terms of average degree for a stock belonging to a given sector, the picture is a lot more equal. On average, the communication sector is the most influential one. It is closely followed by the healthcare and material sectors. Within the PMFG, consumer staples make up the least influential sector on average, while within MST, this title is given, surprisingly, to the technology sector. It is interesting that the financial market is not dominating the Shanghai Stock Exchange, as is the case in most other financial markets. The picture painted by this analysis of the sectors of the Shanghai Stock Exchange leaves an impression of a healthy and diversified market. This gives partial evidence against the popular belief that the markets outside New York, London and Western Europe are inherently riskier. The Shanghai Stock Exchange appears better suited to withstand shocks than what follows from the countless studies of the NYSE based on network methodology, particularly due to lesser concentration on one economic sector.

5. Conclusions

In this paper, we have presented a methodology of creating financial networks based on partial mutual information. This is different from the most common methodology based on correlation, both in allowing nonlinear interdependencies in the analysis and in accounting for the mediating influence of third parties in pairwise dependencies within financial markets. We have applied this methodology to the Shanghai Stock Exchange and found that this methodology does indeed present a better picture of the market, particularly reconstructing the sector structure of the market more precisely, while retaining the (almost) scale-free property of the networks. Finally, we have commented on the resulting picture of the Shanghai Stock Exchange. We have found that the market is quite diversified and mature, even compared with more established markets. Further research should look into other stock exchanges in China and the region. Studies should also try to enhance the methodology to present the structure of markets in an even more clear and precise manner.