Optimal Investment and Consumption Problem with Stochastic Environments and Delay

Abstract

This paper examines an optimal investment–consumption problem in a setting where the financial environment is influenced by both stochastic factors and delayed effects. The investor, endowed with Constant Relative Risk Aversion (CRRA) preferences, allocates wealth between a risk-free asset and a single risky asset. The short rate follows a Vas$\check{\mathrm{i}}$ček-type term structure model, while the risky asset price dynamics are driven by a delayed Heston specification whose variance process evolves according to a Cox–Ingersoll–Ross (CIR) diffusion. Delayed dependence in the wealth dynamics is incorporated through two auxiliary variables that summarize past wealth trajectories, enabling us to recast the naturally infinite-dimensional delay problem into a finite-dimensional Markovian framework. Using Bellman’s dynamic programming principle, we derive the associated Hamilton–Jacobi–Bellman (HJB) partial differential equation and demonstrate that it generalizes the classical Merton formulation to simultaneously accommodate delay, stochastic interest rates, stochastic volatility, and consumption. Under CRRA utility, we obtain closed-form expressions for the value function and the optimal feedback controls. Numerical illustrations highlight how delay and market parameters impact optimal portfolio allocation and consumption policies.

1. Introduction

The continuous-time portfolio selection and consumption framework of Merton (1969, 1971) established stochastic control as a central methodology in mathematical finance. In the Merton setting, an investor with intertemporal preferences chooses dynamic portfolio and consumption strategies to maximize expected utility over time. The canonical model, however, relies on a relatively simple Markovian structure in which decisions depend solely on current state variables, such as current wealth and asset prices.

Over the past decades, many extensions have introduced richer sources of risk and incompleteness. Examples include stochastic interest rates, stochastic volatility, incomplete markets, transaction costs, and constraints. Nevertheless, a large portion of the literature preserves the Markovian assumption and does not incorporate explicit dependence on historical paths of the wealth or price processes. In practice, however, economic and financial systems often exhibit memory: policy decisions are implemented with delay, investors respond gradually to accumulated performance, and macroeconomic shocks propagate over time with persistence.

In parallel, there is strong empirical evidence that both interest rates and volatility fluctuate stochastically and exhibit mean-reverting behavior. Models such as Vas$\check{\mathrm{i}}$ček-type short-rate processes for interest rates and CIR-type dynamics for volatility have become standard tools in term-structure modeling and option pricing. Combining such stochastic factors with intertemporal portfolio choice leads to more realistic, but also more complex, optimization problems.

The aim of this paper is to develop and analyze a portfolio optimization and consumption model that simultaneously accounts for (i) stochastic interest rates; (ii) stochastic volatility in the risky asset; and (iii) delay effects in the wealth dynamics.

We consider a CRRA investor trading continuously in a financial market consisting of one risk-free asset and one risky security. The short rate follows a Vas$\check{\mathrm{i}}$ček model, while the risky asset price is driven by a Heston-type stochastic volatility process, whose variance follows a CIR diffusion. The decision to model the short rate as aVas$\check{\mathrm{i}}$ček process is based on its analytically tractable nature, which led to closed-form solutions for the HJB equations. Furthermore, the Vas$\check{\mathrm{i}}$ček model captures the essential mean-reverting behaviour of interest rates while keeping the process linear and Gaussian, which simplifies both the dynamic programming and numerical analysis. Alternatively, the Cox–Ingersoll–Ross (CIR) process could also be adopted, but its square-root diffusion term introduces additional nonlinearities that make it difficult to obtain closed-form solutions. For this reason, the Vas$\check{\mathrm{i}}$ček specification is adopted here as a balance between realism and tractability.

Delay is introduced through two auxiliary wealth-dependent variables: a smoothed average of historical wealth, denoted by $\mathcal{Y}\left(t\right)$, and a pointwise delayed wealth term, denoted by $\mathcal{Z}\left(t\right)$. These quantities are designed so that the resulting state process remains finite-dimensional, despite the presence of memory. The wealth process is governed by a stochastic delay differential equation (SDDE) in which both the current and delayed wealth components determine the drift. Direct analysis of SDDEs typically leads to infinite-dimensional state spaces. Here, by choosing the delay variables appropriately and imposing a structural condition linking model parameters, we obtain an equivalent representation in a finite-dimensional Markovian state space. This allows us to use the dynamic programming principle and derive the associated Hamilton–Jacobi–Bellman (HJB) equation.

Our contribution is twofold. First, at the modeling level, we propose a unified continuous-time investment–consumption problem that incorporates delay, stochastic interest rates, and stochastic volatility in a consistent and tractable framework. Second, at the analytical level, we derive explicit expressions for the value function and the optimal controls under CRRA preferences, relying on transformations that reduce the HJB PDE to a solvable form. We also highlight how the delay terms interact with the stochastic factors and discuss their impact on optimal strategies.

The remainder of the paper is organized as follows. Section 2 reviews the related literature on portfolio optimization with delay and stochastic factors. Section 3 presents the financial market, the wealth dynamics with delay, and the investor’s optimization problem. Section 4 develops the HJB equation, the associated transformations, and the derivation of the value function. Section 5 provides numerical illustrations and simulations examining the role of delay and parameter changes. Section 6 concludes and discusses possible extensions.

2. Related Literature

Merton’s classical contributions Merton (1969, 1971) form the benchmark for continuous-time portfolio and consumption optimization. Subsequent research has extended this framework along several dimensions. One important direction introduces delay into the dynamics. For example, Chunxiang and Shao (2017) study a portfolio optimization problem with delay in which the risky asset follows a CIR process, but consumption is not considered. L. Elsanosi and Larssen (2001) examine an optimal consumption problem under partial observation in a delayed stochastic system; in their setting, wealth evolves according to a stochastic delay differential equation, and they obtain closed-form expressions for policies and value functions under suitable specifications.

Other works explore delayed dependence in wealth or control systems using dynamic programming and maximum principle techniques. M. H. Chang et al. (2011) investigate an investment–consumption model with bounded memory, whereas Larssen (2002) develops dynamic programming methods for systems with delay and noise. I. Elsanosi et al. (2000) and M. H. Chang et al. (2008) derive stochastic maximum principles and explicit solutions for certain classes of control problems with delay. Functional Itô calculus and related tools have been applied to delayed portfolio problems by Pang and Hussain (2015, 2016), who work with bounded memory and infinite horizon formulations. Further contributions by Federico (2011); Federico et al. (2010) study delay in the context of state constraints and pension fund models, respectively. Memory effects in control problems have also been analyzed in advertising and economics; see, for instance, Gozzi and Marinelli (2006) and Gozzi et al. (2009).

Another branch of the literature focuses on stochastic interest rates and stochastic volatility in portfolio problems. H. Chang et al. (2013) consider optimal investment and consumption in a setting where the short rate follows a Ho–Lee model. Korn and Kraft (2002) and Li and Wu (2009) analyze models in which both the short rate and volatility are stochastic. Kraft (2005) obtains an explicit solution for optimal portfolios under the Heston stochastic volatility model and power utility, while J. Liu (2007) studies portfolio selection in general stochastic environments with diffusion-driven factors. Related contributions by Zariphopoulou (1999, 2001), Fleming and Hernández-Hernández (2003), and Fouque et al. (2000) examine optimal investment under unhedgeable or stochastic volatility risk and develop asymptotic and PDE-based solution methods. Z. Liu et al. (2024) investigated the optimal investment strategy for a defined contribution pension plan under stochastic salary dynamics and a Value-at-Risk constraint within a stochastic volatility framework. This study extended the classical Merton models to real stochastic environments. Bei et al. (2024) analysed an optimal reinsurance investment problem under stochastic volatility and stochastic interest rates, demonstrating how joint financial and insurance risks can be optimally managed within a unified stochastic control setting. Ma et al. (2023) considered optimal consumption and investment under the 4/2-CIR stochastic hybrid model, which generalizes the widely used Heston and 3/2 models. Results showed that richer volatility dynamics significantly affect optimal strategies. Cheng and Escobar-Anel (2023) consider robust portfolio choice and consumption under the 3/2 and 4/2 stochastic volatility models, addressing realistic model uncertainty and robustness, which is a key issue in financial decision-making.

The present paper lies at the intersection of these strands. To the best of our knowledge, there are comparatively few studies that integrate delay, stochastic interest rates, stochastic volatility, and consumption in a single continuous-time Markovian framework that admits explicit solutions. Our work contributes to filling this gap by formulating such a model, deriving the corresponding HJB equation, and obtaining closed-form expressions for the value function and optimal feedback controls in a delayed Heston–Vas$\check{\mathrm{i}}$ček environment.

3. Problem Formulation

We consider a continuous-time financial market defined on the interval $\left[0, T\right]$, where $T>0$ denotes the terminal time. The underlying probability space $(\Omega , \mathbb{F}, \mathcal{F}, \mathbb{P})$ is assumed to be complete, and the filtration ${\left({\mathcal{F}}_t\right)}_{0\le t\le T}$ satisfies the usual hypotheses of right-continuity and $\mathbb{P}$-completeness.

3.1. The Financial Market Model

The investor trades in two securities: a risk-free asset and a single risky asset. The risk-free asset may be interpreted as a money market account or a discount bond, and the risky asset as a stock or stock index. To incorporate memory, we introduce two delay variables driven by the wealth process $\mathcal{X}\left(t\right)$:

$$\begin{array}{c}\hfill \mathcal{Y}\left(t\right)={\int }_{-h}^0{e}^{-\lambda s}\mathcal{X}(t+s)ds,\end{array}$$

(1)

and

$$\begin{array}{c}\hfill \mathcal{Z}\left(t\right)=\mathcal{X}(t-h),\forall t\in [0,T],\end{array}$$

(2)

where $\lambda >0$ is the decay rate of the memory kernel (recent wealth has a greater influence) and $h>0$ denotes the delay horizon. The variable $\mathcal{Y}\left(t\right)$ summarizes a weighted history of wealth over $[t-h,t]$, while $\mathcal{Z}\left(t\right)$ captures a single lagged realization of wealth.

Working with delay variables of the form (1) and (2) allows us to incorporate memory effects in a way that is still compatible with a finite-dimensional Markovian representation. If we were instead to treat the full past trajectory $\left\{\mathcal{X}\right(s):s\in [t-h,t\left]\right\}$ as part of the state, the problem would naturally become infinite-dimensional, typically precluding an explicit solution. Consequently, our focus is on formulations in which the wealth dynamics depend on the delayed processes $\mathcal{Y}\left(t\right)$ and $\mathcal{Z}\left(t\right)$, but not directly on the entire path.

Let $\mathcal{B}\left(t\right)$ denote the value of the risk-free asset at time t. Its dynamics are given by

$$\begin{array}{c}\left\{\begin{array}{c}d\mathcal{B}\left(t\right)=r\left(t\right)\mathcal{B}\left(t\right)dt,\hfill \\ \mathcal{B}\left(0\right)=1,\hfill \end{array}\right.\end{array}$$

(3)

where $r\left(t\right)$ is the short rate, modeled by a Vas$\check{\mathrm{i}}$ček-type process:

$$\begin{array}{c}\left\{\begin{array}{c}dr\left(t\right)={\theta }_0\left(t\right)dt+{\sigma }_{0}d{W}^r\left(t\right),\hfill \\ r\left(0\right)=r_0>0.\hfill \end{array}\right.\end{array}$$

(4)

Here ${\theta }_0\left(t\right)$ represents the instantaneous mean drift of the short rate, ${\sigma }_0>0$ is a constant volatility parameter, and $W^r\left(t\right)$ is a one-dimensional standard Brownian motion. We assume that the drift can be written in mean-reverting form as ${\theta }_0\left(t\right)=\gamma \left[\beta -r\left(t\right)\right]$, with constants $\gamma ,\beta \in \mathbb{R}$.

Let $\mathcal{S}\left(t\right)$ denote the price of the risky asset. Its dynamics are specified by a delayed Heston-type model:

$$\begin{array}{c}\left\{\begin{array}{c}d\mathcal{S}\left(t\right)=\left[\mathcal{S}\left(t\right)\left(r\left(t\right)+k\eta \left(t\right)\right)+{\mu }_1\mathcal{Y}\left(t\right)+{\mu }_2\mathcal{Z}\left(t\right)\right]dt+{\sigma }_1\sqrt{\eta \left(t\right)}\mathcal{S}\left(t\right)d{W}^{\mathcal{S}}\left(t\right),\hfill \\ \mathcal{S}\left(0\right)=s_0>0,\hfill \end{array}\right.\end{array}$$

(5)

where $\eta \left(t\right)$ is the stochastic variance process, ${\mu }_1,{\mu }_2\in \mathbb{R}$ are constants scaling the impact of the delay variables, and $W^{\mathcal{S}}\left(t\right)$ is a one-dimensional Brownian motion. The term $k>0$ governs the excess return from exposure to volatility, while ${\sigma }_1>0$ determines the sensitivity of the risky asset to shocks in $\eta \left(t\right)$.

The variance process $\eta \left(t\right)$ follows a CIR diffusion:

$$\begin{array}{c}\left\{\begin{array}{c}d\eta \left(t\right)=\left[{\theta }_2-b\eta \left(t\right)\right]dt+{\sigma }_2\sqrt{\eta \left(t\right)}d{W}^{\eta }\left(t\right),\hfill \\ \eta \left(0\right)={\eta }_0>0,\hfill \end{array}\right.\end{array}$$

(6)

where ${\theta }_2>0$, $b>0$, and ${\sigma }_2>0$ are constants. The process $W^{\eta }\left(t\right)$ is a one-dimensional Brownian motion, possibly correlated with $W^{\mathcal{S}}\left(t\right)$, and we impose $\eta \left(t\right)\ge 0$ for all $t\ge 0$. The Brownian motions $(W^r,W^{\mathcal{S}},W^{\eta })$ are defined on the same filtered probability space with correlation coefficient $\rho$ between $W^{\mathcal{S}}$ and $W^{\eta }$ such that

$$\begin{array}{c}\hfill d{W}^{\mathcal{S}}\left(t\right)d{W}^{\eta }\left(t\right)=\rho dt,\rho \in [-1,1].\end{array}$$

(7)

3.2. The Wealth Model

Let $\mathcal{X}\left(t\right)$ denote the investor’s total wealth at time t. The investor consumes at an instantaneous rate $\mathcal{C}\left(t\right)$ and $\mathcal{K}\left(t\right)$ represents the amount invested in the risky security, with the remainder allocated to the risk-free security. To keep notation simple, we do not explicitly track the amount in the risk-free asset, writing $\mathcal{L}\left(t\right)$ only when needed to emphasize the allocation. Trading occurs continuously in time, and the strategy is assumed to be self-financing.

Under these assumptions, the wealth dynamics (in the additive $\mu$-terms case) satisfy

$$\begin{array}{cc}\hfill d\mathcal{X}\left(t\right)& =\left[r\left(t\right)\mathcal{X}\left(t\right)+\mathcal{K}\left(t\right)\mathcal{S}\left(t\right)k\eta \left(t\right)+\mathcal{K}\left(t\right)\left({\mu }_1\mathcal{Y}\left(t\right)+{\mu }_2\mathcal{Z}\left(t\right)\right)-\mathcal{C}\left(t\right)\right]dt\hfill \\ \hfill & +\mathcal{K}\left(t\right)\mathcal{S}\left(t\right){\sigma }_1\sqrt{\eta \left(t\right)}d{W}^{\mathcal{S}}\left(t\right),\hfill \end{array}$$

(8)

for $t\in [0,T]$, with initial history

$$\mathcal{X}\left(s\right)=\phi \left(s\right),s\in [-h, 0],\phi \in C\left(\right[-h, 0\left]\right).$$

The delay processes are given by

$$\mathcal{Y}\left(t\right)={\int }_{-h}^0{e}^{-\lambda s}\mathcal{X}(t+s)ds,\mathcal{Z}\left(t\right)=\mathcal{X}(t-h),t\in [0, T].$$

3.3. The Optimization Criterion

We now define admissible controls and the investor’s optimization objective.

Definition 1.

A control pair $\mathcal{V}=\left(\mathcal{K}\right(t), \mathcal{C}(t\left)\right)$ is called admissible if it satisfies:

(i) 

$\mathcal{K}\left(t\right)$ and $\mathcal{C}\left(t\right)$ are progressively ${\mathcal{F}}_t$-measurable, and

$${\int }_0^T{\left[\mathcal{K}\left(t\right)\right]}^{2}dt<\infty ,{\int }_0^T\mathcal{C}\left(t\right)dt<\infty ,\mathit{for}\mathit{all}T>0.$$

(ii) 

$\mathcal{C}\left(t\right)>0$ for all t, and $\mathcal{K}\left(t\right)$ is admissible as a portfolio weight.

(iii) 

The stochastic integral is square-integrable:

$$\mathbb{E}\left[{\int }_0^T{\left(\mathcal{K}\left(t\right){\sigma }_1\sqrt{\eta \left(t\right)}\right)}^{2}dt\right]<\infty .$$

(iv) 

There exists a constant $\xi >0$ such that

$$\left|\mathcal{K}\right(t\left)\right|\le \xi \left|\mathcal{X}\right(t)+\mathcal{Y}(t\left)\right|,\left|\mathcal{C}\right(t\left)\right|\le \xi \left|\mathcal{X}\right(t)+\mathcal{Y}(t\left)\right|,$$

for all $t\in [0, T]$.

(v) 

For each admissible pair $\left(\mathcal{K}\right(t), \mathcal{C}(t\left)\right)$, the wealth SDDE (8) admits a unique pathwise solution.

The investor’s preferences are modeled by a CRRA utility specification. Let $U_1\left(\mathcal{C}\left(t\right)\right)$ and $U_2\left(\mathcal{X}\left(T\right)\right)$ denote the utility from consumption and terminal wealth, respectively. We assume $U(·)$ is twice continuously differentiable, strictly increasing, and strictly concave; that is, $U^{\prime }(·)>0$ and $U^{″}(·)<0$. The subjective discount factor is $e^{-\lambda t}$, and the constant $\varphi \in (0,1)$ determines the relative weight assigned to intermediate consumption versus terminal wealth. Expectations are taken under the physical measure $\mathbb{P}$.

The investor’s goal is to allocate initial wealth $x_0$ between the risk-free and risky assets and to choose a consumption path so as to maximize expected discounted utility of consumption and terminal wealth. The optimization problem is

$$\begin{array}{c}\hfill \underset{\left(\mathcal{K}\right(t),\mathcal{C}(t\left)\right)\in \mathcal{A}}{max}\mathbb{E}\left[{\int }_0^T\varphi e^{-\lambda t}{U}_1\left(\mathcal{C}\left(t\right)\right)dt+(1-\varphi )e^{-\lambda T}{U}_2\left(\mathcal{X}\left(T\right)\right)\right],\end{array}$$

(9)

subject to the wealth and factor dynamics:

$$\begin{array}{c}\left\{\begin{array}{c}d\mathcal{X}\left(t\right)=\left[r\left(t\right)\mathcal{X}\left(t\right)+\mathcal{K}\left(t\right)\mathcal{S}\left(t\right)k\eta \left(t\right)+\mathcal{K}\left(t\right)\left({\mu }_1\mathcal{Y}\left(t\right)+{\mu }_2\mathcal{Z}\left(t\right)\right)-\mathcal{C}\left(t\right)\right]dt\hfill \\ +\mathcal{K}\left(t\right)\mathcal{S}\left(t\right){\sigma }_1\sqrt{\eta \left(t\right)}d{W}^{\mathcal{S}}\left(t\right),\hfill \\ \mathcal{X}\left(s\right)=\phi \left(s\right),-h\le s\le 0,\phi \in C\left(\right[-h,0\left]\right),h>0,\hfill \\ \mathcal{Y}\left(t\right)={\int }_{-h}^0{e}^{-\lambda s}\mathcal{X}(t+s)ds,\hfill \\ \mathcal{Z}\left(t\right)=\mathcal{X}(t-h),\hfill \end{array}\right.\end{array}$$

(10)

$$\begin{array}{c}\left\{\begin{array}{c}dr\left(t\right)={\theta }_0\left(t\right)dt+{\sigma }_{0}d{W}^r\left(t\right),\hfill \\ r\left(0\right)=r_0>0,\hfill \end{array}\right.\end{array}$$

(11)

and

$$\begin{array}{c}\left\{\begin{array}{c}d\eta \left(t\right)=\left({\theta }_2-b\eta \left(t\right)\right)dt+{\sigma }_2\sqrt{\eta \left(t\right)}d{W}^{\eta }\left(t\right),\hfill \\ \eta \left(0\right)={\eta }_0>0.\hfill \end{array}\right.\end{array}$$

(12)

Definition 2.

The value function associated with the control problem is defined by

$$\begin{array}{c}\hfill V(t,r,\eta ,x,y)=\underset{\left(\mathcal{K}\right(t),\mathcal{C}(t\left)\right)\in \mathcal{A}}{sup}\mathbb{E}\left[{\int }_t^T\varphi e^{-\lambda (s-t)}{U}_1\left(\mathcal{C}\left(s\right)\right)ds+(1-\varphi )e^{-\lambda (T-t)}{U}_2(\mathcal{X}\left(T\right),\mathcal{Y}\left(T\right))\right],\end{array}$$

(13)

where $U_1(·)$ and $U_2(·)$ satisfy the usual CRRA conditions $U^{\prime }(·)>0$ and $U^{″}(·)<0$, and λ and ϕ denote the discount rate and the relative weight on consumption, respectively.

4. The Hamilton–Jacobi–Bellman PDE

The optimal control problem described above can be analyzed via dynamic programming. In particular, Bellman’s principle of optimality leads to a Hamilton–Jacobi–Bellman (HJB) equation for the value function. The structure of the HJB equation reflects both the diffusion terms and the delay variables, which enter through the state $(x,y)$ and the relation between $\mathcal{Y}\left(t\right)$ and $\mathcal{Z}\left(t\right)$.

Using the delayed Itô formula presented in Appendix A (Lemma A1), the HJB PDE associated with the value function (13) is given by the nonlinear second-order equation

$$\begin{array}{cc}\hfill \underset{\{\mathcal{K},\mathcal{C}(t\left)\right\}\in \mathcal{A}}{sup}& [V_t-\lambda V+\left[xr+k\eta \left(t\right)\mathcal{K}\left(t\right)+{\mu }_{1}y+{\mu }_{2}z-\mathcal{C}\left(t\right)\right]V_x+{\displaystyle \frac{1}{2}}{\mathcal{K}}^2\left(t\right){\sigma }_1^2\eta \left(t\right)V_{xx}\hfill \\ \hfill & +{\theta }_0\left(t\right)V_r+{\displaystyle \frac{1}{2}}{\sigma }_0^2{V}_{rr}+({\theta }_2-b\eta \left(t\right))V_{\eta }+{\displaystyle \frac{1}{2}}{\sigma }_2^2\eta \left(t\right)V_{\eta \eta }+\mathcal{K}\left(t\right){\sigma }_1{\sigma }_2\eta \left(t\right)\rho V_{x\eta }\hfill \\ \hfill & +(x-\lambda y-e^{-\lambda h}z)V_y+e^{-\lambda t}\varphi U_1\left(\mathcal{C}\left(t\right)\right)]=0,\hfill \end{array}$$

(14)

where subscripts denote partial derivatives of V.

Remark 1.

Note that despite the value function in (13) being expressed as $V(t,r,\eta ,x,y)$, the delayed variable $\mathcal{Z}\left(t\right)$ appears in the HJB equation via the dynamics of $\mathcal{Y}\left(t\right)$, implying its appearance in (14) reflects this indirect influence. However, the subsequent structural restriction removes explicit dependence on z, so that the value function depends only on $(t,r,\eta ,x,y)$. Furthermore, $-\lambda V$ and $e^{-\lambda t}$ in the HJB equation should not be treated as a duplication. $-\lambda V$ is obtained by differentiating the exponential discount factor in the value function (13), while the explicit factor $e^{-\lambda t}$ ensures temporal weighting of instantaneous utility. Thus, the two terms are mathematically consistent.

The first-order conditions for optimality, obtained by differentiating the Hamiltonian with respect to $\mathcal{K}$ and $\mathcal{C}$, yield the candidate optimal controls

$$\begin{array}{c}\hfill {\mathcal{K}}^{*}={\displaystyle \frac{-k}{{\sigma }_1^2}}·{\displaystyle \frac{V_x}{V_{xx}}}-{\displaystyle \frac{{\sigma }_2\rho }{{\sigma }_1}}·{\displaystyle \frac{V_{x\eta }}{V_{xx}}}\end{array}$$

(15)

and

$$\begin{array}{c}\hfill U_1^{\prime }\left({\mathcal{C}}^{*}\right)={\displaystyle \frac{V_x}{\varphi e^{-\lambda t}}},\end{array}$$

(16)

where $U_1^{\prime }$ is strictly decreasing and therefore invertible.

Substituting (15) and (16) into the HJB Equation (14) leads, after simplification, to

$$\begin{array}{cc}\hfill V_t& -\lambda V+\left[rx+\left({\displaystyle \frac{-k}{{\sigma }_1^2}}{\displaystyle \frac{V_x}{V_{xx}}}-{\displaystyle \frac{{\sigma }_2\rho }{{\sigma }_1}}{\displaystyle \frac{V_{x\eta }}{V_{xx}}}\right)k\eta +{\mu }_{1}y+{\mu }_{2}z-{\mathcal{C}}^{*}\right]V_x\hfill \\ \hfill & +{\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{-k}{{\sigma }_1^2}}{\displaystyle \frac{V_x}{V_{xx}}}-{\displaystyle \frac{{\sigma }_2\rho }{{\sigma }_1}}{\displaystyle \frac{V_{x\eta }}{V_{xx}}}\right)}^2{\sigma }_1^2\eta V_{xx}+{\theta }_0{V}_r+{\displaystyle \frac{1}{2}}{\sigma }_0^2{V}_{rr}\hfill \\ \hfill & +({\theta }_2-b\eta )V_{\eta }+{\displaystyle \frac{1}{2}}{\sigma }_2^2\eta \left(t\right)V_{\eta \eta }+\left({\displaystyle \frac{-k}{{\sigma }_1^2}}{\displaystyle \frac{V_x}{V_{xx}}}-{\displaystyle \frac{{\sigma }_2\rho }{{\sigma }_1}}{\displaystyle \frac{V_{x\eta }}{V_{xx}}}\right){\sigma }_1{\sigma }_2\rho \eta V_{x\eta }\hfill \\ \hfill & +(x-\lambda y-e^{-\lambda h}z)V_y+\varphi U_1\left({\mathcal{C}}^{*}\right)=0,\hfill \end{array}$$

(17)

with terminal condition

$$\begin{array}{c}\hfill V(T,r,\eta ,x,y)={\displaystyle \frac{x^{\delta }}{\delta }}.\end{array}$$

(18)

Rearranging terms, we obtain the more compact representation

$$\begin{array}{cc}\hfill V_t& +rx{V}_x+({\mu }_{1}y+{\mu }_{2}z-{\mathcal{C}}^{*})V_x-{\displaystyle \frac{1}{2}}{\displaystyle \frac{k^2\eta V_x^2}{{\sigma }_1^2{V}_{xx}}}-{\displaystyle \frac{1}{2}}{\displaystyle \frac{{\sigma }_2^2{\rho }^2\eta V_{x\eta }^2}{V_{xx}}}+{\theta }_0{V}_r\hfill \\ \hfill & +{\displaystyle \frac{1}{2}}{\sigma }_0^2{V}_{rr}+({\theta }_2-b\eta )V_{\eta }+{\displaystyle \frac{1}{2}}{\sigma }_2^2\eta \left(t\right)V_{\eta \eta }-{\displaystyle \frac{k{\sigma }_2\rho \eta }{{\sigma }_1}}{\displaystyle \frac{V_x{V}_{x\eta }}{V_{xx}}}+(x-\lambda y-e^{-\lambda h}z)V_y\hfill \\ \hfill & +\varphi U_1\left({\mathcal{C}}^{*}\right)=0,\hfill \end{array}$$

(19)

subject to

$$\begin{array}{c}\hfill V(T,r,\eta ,x,y)={\displaystyle \frac{x^{\delta }}{\delta }}.\end{array}$$

(20)

In the following section, we exploit CRRA preferences to transform and solve the HJB Equation (19).

4.1. Optimal Policies and the Value Function

We assume the investor’s preferences are represented by a CRRA (power) utility function.

4.2. Power Utility Function

Definition 3.

The power utility specification is

$$\begin{array}{c}\left\{\begin{array}{c}{U}_1\left(x\right)=U_2\left(x\right)={\displaystyle \frac{x^{\delta }}{\delta }},\hfill \\ \delta <1,\delta \ne 0,\hfill \end{array}\right.\end{array}$$

(21)

where δ is the risk-aversion parameter.

Remark 2.

To obtain an explicit solution for the HJB PDE (19) in a finite-dimensional setting, we require that the value function be independent of z. This motivates an appropriate change of variables and a structural condition on the parameters.

To eliminate dependence on z, we set

$$\begin{array}{c}\hfill u=x+{\mu }_2{e}^{-\lambda h}y.\end{array}$$

(22)

This transformation absorbs the delayed term into a combined state variable u, thereby simplifying the PDE. We also postulate a separable form for the value function:

$$\begin{array}{c}\left\{\begin{array}{c}V(t,r,\eta ,x,y)=e^{-\lambda t}{\displaystyle \frac{u^{\delta }}{\delta }}g(t,r,\eta ),\hfill \\ g(T,r,\eta )=1-\varphi .\hfill \end{array}\right.\end{array}$$

(23)

The unknown function $g(t,r,\eta )$ encodes the effect of the stochastic factors $(r,\eta )$ and time t.

The relevant derivatives of V are

$$\begin{array}{c}\left\{\begin{array}{c}{V}_t=-\lambda e^{-\lambda t}{\displaystyle \frac{u^{\delta }}{\delta }}g+e^{-\lambda t}{\displaystyle \frac{u^{\delta }}{\delta }}{g}_t,\hfill \\ V_x=e^{-\lambda t}{u}^{\delta -1}g,\hfill \\ V_y={\mu }_2{e}^{-\lambda h}{e}^{-\lambda t}{u}^{\delta -1}g,\hfill \\ V_{xx}=e^{-\lambda t}(\delta -1)u^{\delta -2}g,\hfill \\ V_r=e^{-\lambda t}{\displaystyle \frac{u^{\delta }}{\delta }}{g}_r,\hfill \\ V_{rr}=e^{-\lambda t}{\displaystyle \frac{u^{\delta }}{\delta }}{g}_{rr},\hfill \\ V_{\eta }=e^{-\lambda t}{\displaystyle \frac{u^{\delta }}{\delta }}{g}_{\eta },\hfill \\ V_{\eta \eta }=e^{-\lambda t}{\displaystyle \frac{u^{\delta }}{\delta }}{g}_{\eta \eta },\hfill \\ V_{x\eta }=e^{-\lambda t}{u}^{\delta -1}{g}_{\eta }.\hfill \end{array}\right.\end{array}$$

(24)

Under CRRA preferences, the optimal consumption control implied by (16) takes the form

$$\begin{array}{c}\hfill {\mathcal{C}}^{*}={\varphi }^{{\displaystyle \frac{-1}{\delta -1}}}u{g}^{{\displaystyle \frac{1}{\delta -1}}}.\end{array}$$

(25)

Substituting (24) and (25) into (19) yields an equation for g:

$$\begin{array}{cc}\hfill & -\lambda \left[e^{-\lambda t}{\displaystyle \frac{u^{\delta }}{\delta }}\right]g+\left[e^{-\lambda t}{\displaystyle \frac{u^{\delta }}{\delta }}\right]g_t+\left((r+{\mu }_2{e}^{\lambda h})x+({\mu }_1-\lambda {\mu }_2{e}^{\lambda h})y\right)\left[e^{-\lambda t}{u}^{\delta -1}\right]g\hfill \\ \hfill & -\left({\displaystyle \frac{1}{2}}{\displaystyle \frac{k^2\eta }{{\sigma }_1^2}}{\displaystyle \frac{\delta }{\delta -1}}\right)\left[e^{-\lambda t}{\displaystyle \frac{u^{\delta }}{\delta }}\right]g-{\displaystyle \frac{1}{2}}{\displaystyle \frac{{\sigma }_2^2{\rho }^2\eta \left(t\right)\delta }{(\delta -1)}}{\displaystyle \frac{g_{\eta }{g}_{\eta }}{g}}\left[e^{-\lambda t}{\displaystyle \frac{u^{\delta }}{\delta }}\right]+\left[e^{-\lambda t}{\displaystyle \frac{u^{\delta }}{\delta }}\right]{\theta }_0{g}_r\hfill \\ \hfill & +\left[e^{-\lambda t}{\displaystyle \frac{u^{\delta }}{\delta }}\right]{\displaystyle \frac{1}{2}}{\sigma }_0^2{g}_{rr}+\left[e^{-\lambda t}{\displaystyle \frac{u^{\delta }}{\delta }}\right]({\theta }_2-b\eta \left(t\right))g_{\eta }+\left[e^{-\lambda t}{\displaystyle \frac{u^{\delta }}{\delta }}\right]{\displaystyle \frac{1}{2}}{\sigma }_2^2\eta \left(t\right)g_{\eta \eta }\hfill \\ \hfill & -\left[e^{-\lambda t}{\displaystyle \frac{u^{\delta }}{\delta }}\right]{\displaystyle \frac{k{\sigma }_2\rho \eta \left(t\right)}{{\sigma }_1}}{\displaystyle \frac{\delta g_{\eta }}{\delta -1}}+\left[e^{-\lambda t}{\displaystyle \frac{u^{\delta }}{\delta }}\right](-{\varphi }^{{\displaystyle \frac{-1}{\delta -1}}}{g}^{{\displaystyle \frac{1}{\delta -1}}})\left(\delta g\right)+\left[e^{-\lambda t}{\displaystyle \frac{u^{\delta }}{\delta }}\right]{\varphi }^{{\displaystyle \frac{-1}{\delta -1}}}{g}^{{\displaystyle \frac{\delta }{\delta -1}}}\hfill \\ \hfill & =0.\hfill \end{array}$$

(26)

To ensure that the reduced problem remains finite-dimensional, we impose the parameter restriction

$$\begin{array}{c}\hfill {\mu }_1-\lambda {\mu }_2{e}^{\lambda h}=(r+{\mu }_2{e}^{\lambda h}){\mu }_2{e}^{\lambda h}.\end{array}$$

(27)

Remark 3.

Condition (27) guarantees that the HJB Equation (19) can be solved in a finite-dimensional state space by removing explicit dependence on the lagged variable z. It is a modeling restriction rather than an identity that should hold for every possible realization of $r\left(t\right)$. It is imposed at the level of model parameters (the mean or long-run value of $r\left(t\right)$) to make the problem analytically tractable while preserving the qualitative behavior of the model. This is a key modeling assumption that permits the delay structure to be summarized by the transformed state variable u.

Under (27), Equation (26) simplifies to

$$\begin{array}{cc}\hfill e^{-\lambda t}{\displaystyle \frac{u^{\delta }}{\delta }}[& g_t+\left(\delta (r+{\mu }_2{e}^{\lambda h})-\lambda -{\displaystyle \frac{1}{2}}{\displaystyle \frac{k^2\eta \left(t\right)}{{\sigma }_1^2}}{\displaystyle \frac{\delta }{\delta -1}}\right)g-{\displaystyle \frac{1}{2}}{\displaystyle \frac{{\sigma }_2^2{\rho }^2\eta \left(t\right)\delta }{(\delta -1)}}{\displaystyle \frac{g_{\eta }{g}_{\eta }}{g}}+{\theta }_0{g}_r\hfill \\ \hfill & +{\displaystyle \frac{1}{2}}{\sigma }_0^2{g}_{rr}+{\displaystyle \frac{1}{2}}{\sigma }_2^2\eta \left(t\right)g_{\eta \eta }+\left({\theta }_2-b\eta \left(t\right)-{\displaystyle \frac{k{\sigma }_2\rho \eta \left(t\right)}{{\sigma }_1}}{\displaystyle \frac{\delta }{\delta -1}}\right)g_{\eta }+(1-\delta ){\varphi }^{{\displaystyle \frac{-1}{\delta -1}}}{g}^{{\displaystyle \frac{\delta }{\delta -1}}}]\hfill \\ \hfill & =0.\hfill \end{array}$$

(28)

Dropping the common factor $e^{-\lambda t}{u}^{\delta }/\delta$, we obtain

$$\begin{array}{cc}\hfill g_t& +\left(\delta (r+{\mu }_2{e}^{\lambda h})-\lambda -{\displaystyle \frac{1}{2}}{\displaystyle \frac{k^2\eta \left(t\right)}{{\sigma }_1^2}}{\displaystyle \frac{\delta }{\delta -1}}\right)g-{\displaystyle \frac{1}{2}}{\displaystyle \frac{{\sigma }_2^2{\rho }^2\eta \left(t\right)\delta }{(\delta -1)}}{\displaystyle \frac{g_{\eta }{g}_{\eta }}{g}}+{\theta }_0{g}_r\hfill \\ \hfill & +{\displaystyle \frac{1}{2}}{\sigma }_0^2{g}_{rr}+{\displaystyle \frac{1}{2}}{\sigma }_2^2\eta \left(t\right)g_{\eta \eta }+\left({\theta }_2-b\eta \left(t\right)-{\displaystyle \frac{k{\sigma }_2\rho \eta \left(t\right)}{{\sigma }_1}}{\displaystyle \frac{\delta }{\delta -1}}\right)g_{\eta }+(1-\delta ){\varphi }^{{\displaystyle \frac{-1}{\delta -1}}}{g}^{{\displaystyle \frac{\delta }{\delta -1}}}\hfill \\ \hfill & =0.\hfill \end{array}$$

(29)

To further simplify, we introduce the transformation

$$\begin{array}{c}\left\{\begin{array}{c}g(t,r,\eta )=f{(t,r,\eta )}^{1-\delta },\hfill \\ f(T,r,\eta )={(1-\varphi )}^{{\displaystyle \frac{1}{\delta -1}}}.\hfill \end{array}\right.\end{array}$$

(30)

The derivatives of g in terms of f are

$$\begin{array}{c}\left\{\begin{array}{c}{g}_t=(1-\delta )f^{-\delta }{f}_t,\hfill \\ g_r=(1-\delta )f^{-\delta }{f}_r,\hfill \\ g_{rr}=(1-\delta )(-\delta )f^{-\delta -1}{f}_r^2+(1-\delta )f^{-\delta }{f}_{rr},\hfill \\ g_{\eta }=(1-\delta )f^{-\delta }{f}_{\eta },\hfill \\ g_{\eta \eta }=(1-\delta )(-\delta )f^{-\delta -1}{f}_{\eta }^2+(1-\delta )f^{-\delta }{f}_{\eta \eta }.\hfill \end{array}\right.\end{array}$$

(31)

Substituting (31) into (29) and simplifying, we arrive at the PDE

$$\begin{array}{cc}\hfill f_t& +\left({\displaystyle \frac{\delta (r+{\mu }_2{e}^{\lambda h})-\lambda }{(1-\delta )}}+{\displaystyle \frac{1}{2}}{\displaystyle \frac{k^2\eta \left(t\right)}{{\sigma }_1^2}}{\displaystyle \frac{\delta }{{(\delta -1)}^2}}\right)f+{\displaystyle \frac{1}{2}}{\sigma }_2^2\eta \left(t\right)\left(\delta \right)[{\rho }^2-1]f^{-1}{f}_{\eta }^2\hfill \\ \hfill & +{\theta }_0{f}_r+{\displaystyle \frac{1}{2}}{\sigma }_0^2{f}_{rr}-{\displaystyle \frac{1}{2}}{\sigma }_0^2\delta {\displaystyle \frac{f_r^2}{f}}+{\displaystyle \frac{1}{2}}{\sigma }_2^2\eta \left(t\right)f_{\eta \eta }+\left({\theta }_2-b\eta \left(t\right)-{\displaystyle \frac{k{\sigma }_2\rho \eta }{{\sigma }_1}}{\displaystyle \frac{\delta }{\delta -1}}\right)f_{\eta }+{\varphi }^{{\displaystyle \frac{1}{1-\delta }}}\hfill \\ \hfill & =0.\hfill \end{array}$$

(32)

Remark 4.

The constant term ${\varphi }^{{\displaystyle \frac{1}{1-\delta }}}$ in (32) complicates a direct solution. Following the approach in J. Liu (2007), we relate (32) to an auxiliary PDE for a modified function $\widehat{f}$, which admits a more tractable representation. This transformation is described in Appendix B.

Appendix B (Lemma A2) shows that Equation (32) is equivalent, under an appropriate integral representation, to the PDE

$$\begin{array}{cc}\hfill {\widehat{f}}_t& +\left({\displaystyle \frac{\delta (r+{\mu }_2{e}^{\lambda h})-\lambda }{(1-\delta )}}+{\displaystyle \frac{1}{2}}{\displaystyle \frac{k^2\eta }{{\sigma }_1^2}}{\displaystyle \frac{\delta }{{(\delta -1)}^2}}\right)\widehat{f}+{\displaystyle \frac{1}{2}}{\sigma }_2^2\eta \left(t\right)\left(\delta \right)\left({\rho }^2-1\right){\widehat{f}}^{-1}{\widehat{f}}_{\eta }^2+{\theta }_0{\widehat{f}}_r+{\displaystyle \frac{1}{2}}{\sigma }_0^2{\widehat{f}}_{rr}\hfill \\ \hfill & -{\displaystyle \frac{1}{2}}{\sigma }_0^2\delta {\displaystyle \frac{{\widehat{f}}_r^2}{\widehat{f}}}+{\displaystyle \frac{1}{2}}{\sigma }_2^2\eta {\widehat{f}}_{\eta \eta }+\left({\theta }_2-b\eta \left(t\right)-{\displaystyle \frac{2k{\sigma }_2\rho \eta }{{\sigma }_1}}{\displaystyle \frac{\delta }{\delta -1}}\right){\widehat{f}}_{\eta }\hfill \\ \hfill & =0,\hfill \end{array}$$

(33)

with boundary condition $\widehat{f}(T,r,\eta )=1$.

5. Numerical Examples

In this section, we provide numerical illustrations of the optimal investment and consumption strategies and examine how they respond to changes in the delay term and other parameters.

5.1. Effects of Delay $\mathcal{Y}$ on Optimal Investment ${\mathcal{K}}^{*}$ and Consumption ${\mathcal{C}}^{*}\left(t\right)$

We first investigate how the delay variable $\mathcal{Y}$ influences the optimal portfolio weight ${\mathcal{K}}^{*}$ and the optimal consumption ${\mathcal{C}}^{*}$. From the explicit formulas for the feedback controls, one obtains

$$\begin{array}{c}\hfill {\displaystyle \frac{\partial {\mathcal{K}}^{*}}{\partial \mathcal{Y}}}=\left({\displaystyle \frac{k}{{\sigma }_1^2(1-\delta )}}+{\displaystyle \frac{{\sigma }_2\rho }{{\sigma }_1}}·{\displaystyle \frac{f_{\eta }}{f}}\right)\left({\mu }_2{e}^{\lambda h}\right),\end{array}$$

(34)

and hence

$$\left\{\begin{array}{cc}{\displaystyle \frac{\partial {\mathcal{K}}^{*}}{\partial \mathcal{Y}}}=0\hfill & \mathrm{i}\mathrm{f} {\mu }_2=0,\hfill \\ {\displaystyle \frac{\partial {\mathcal{K}}^{*}}{\partial \mathcal{Y}}}>0\hfill & \mathrm{i}\mathrm{f} {\mu }_2>0,\hfill \\ {\displaystyle \frac{\partial {\mathcal{K}}^{*}}{\partial \mathcal{Y}}}<0\hfill & \mathrm{i}\mathrm{f} {\mu }_2<0.\hfill \end{array}\right.$$

Similarly, for the consumption control,

$$\begin{array}{c}\hfill {\displaystyle \frac{\partial {\mathcal{C}}^{*}}{\partial \mathcal{Y}}}={\varphi }^{{\displaystyle \frac{1}{1-\delta }}}\left({\mu }_2{e}^{\lambda h}\right)f^{-1},\end{array}$$

(35)

so that

$$\left\{\begin{array}{cc}{\displaystyle \frac{\partial {\mathcal{C}}^{*}}{\partial \mathcal{Y}}}=0\hfill & \mathrm{i}\mathrm{f} {\mu }_2=0,\hfill \\ {\displaystyle \frac{\partial {\mathcal{C}}^{*}}{\partial \mathcal{Y}}}>0\hfill & \mathrm{i}\mathrm{f} {\mu }_2>0,\hfill \\ {\displaystyle \frac{\partial {\mathcal{C}}^{*}}{\partial \mathcal{Y}}}<0\hfill & \mathrm{i}\mathrm{f} {\mu }_2<0.\hfill \end{array}\right.$$

In summary,

(i)

When ${\mu }_2=0$, neither the optimal portfolio weight ${\mathcal{K}}^{*}$ nor the optimal consumption ${\mathcal{C}}^{*}\left(t\right)$ depends on the delay variable $\mathcal{Y}$. In this case, the investor behaves as if there were no delay.

(ii)

When ${\mu }_2>0$, both ${\mathcal{K}}^{*}$ and ${\mathcal{C}}^{*}\left(t\right)$ increase with $\mathcal{Y}$. Intuitively, a higher history of wealth performance makes the investor more willing to expand the risky position and to consume more.

(iii)

When ${\mu }_2<0$, the delay variable $\mathcal{Y}$ has an adverse effect: larger historical wealth (in the sense captured by $\mathcal{Y}$) leads to a reduction in both the risky allocation and consumption.

5.2. Simulations

We now perform simulations to illustrate how various parameters influence the optimal portfolio strategy. Throughout the numerical experiments, the parameters are chosen as follows:

$$t=0:0.05:1,h=1,k=0.6,{\sigma }_0=0.2,a=0.8,b=0.9,\delta =-1,$$

$${\sigma }_1=1.2,\eta =0.6,\lambda =0.5,{\theta }_0=0.25,{\theta }_2=0.26,\varphi =1,{\sigma }_2=1.1.$$

Figure 1, Figure 2, Figure 3 and Figure 4 display the relationships between wealth, optimal portfolio weights, and optimal consumption under different model configurations, including correlation coefficients $\rho =1$ and $\rho =-1$. The results indicate that an improvement in historical wealth performance generally leads to a higher optimal allocation to the risky asset, consistent with greater risk-taking when the investor has “good history” in terms of accumulated wealth. This pattern is robust across the sign of ${\mu }_2$ and across the considered parameter values.

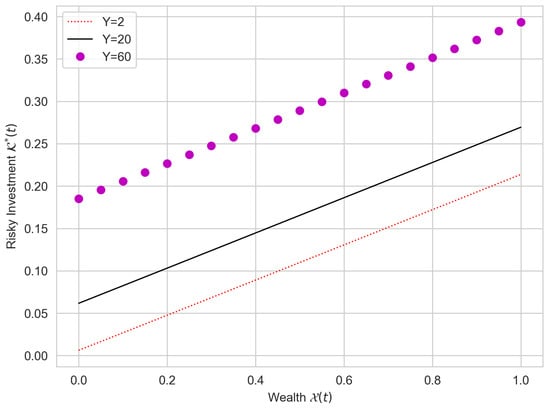
Figure 1. Optimal risky investment ${\mathcal{K}}^{*}\left(t\right)$ versus wealth $\mathcal{X}\left(t\right)$ for $\rho =1$ under a positive delay contribution.

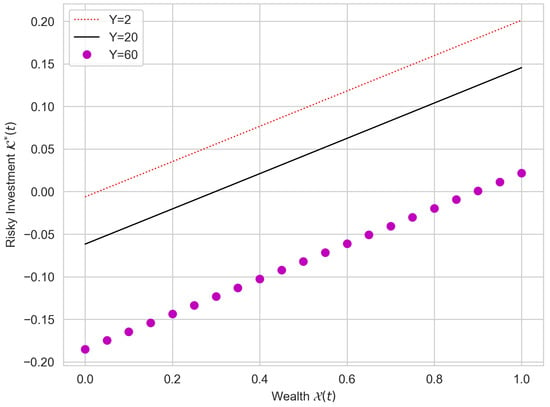
Figure 2. Optimal risky investment ${\mathcal{K}}^{*}\left(t\right)$ versus wealth $\mathcal{X}\left(t\right)$ for $\rho =1$ under a negative delay contribution.

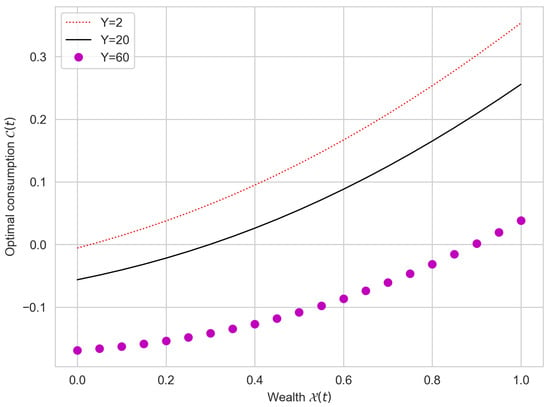
Figure 3. Optimal consumption $\mathcal{C}\left(t\right)$ versus wealth $\mathcal{X}\left(t\right)$ for $\rho =1$ under a negative delay contribution.

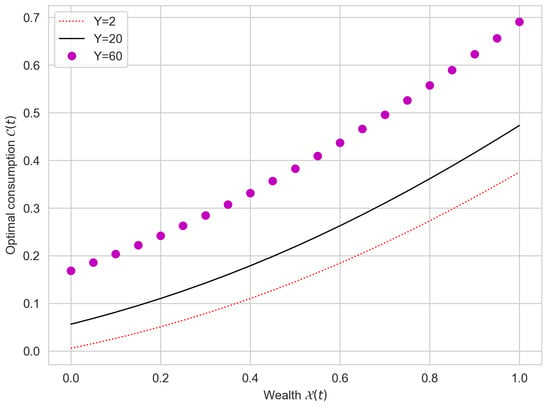
Figure 4. Optimal consumption $\mathcal{C}\left(t\right)$ versus wealth $\mathcal{X}\left(t\right)$ for $\rho =-1$ under a positive delay contribution.

The correlation parameter $\rho \in \{-1,1\}$ plays a central role in shaping the behavior of the optimal strategy. When $\rho =1$, shocks to the asset price and variance are perfectly positively correlated, reinforcing volatility shocks and affecting the optimal hedge component in ${\mathcal{K}}^{*}$. Conversely, when $\rho =-1$, the negative correlation dampens certain risk components, leading to different portfolio responses. Overall, the simulations illustrate how the interaction of delay, stochastic volatility, and correlation can materially alter the investor’s optimal policies.

6. Conclusions

This paper extends the classical Merton framework by studying an optimal investment–consumption problem in a financial market with stochastic interest rates, stochastic volatility, and delay in the wealth dynamics. The short rate evolves according to a Vas$\check{\mathrm{i}}$ček model, while the risky asset is driven by a delayed Heston specification with CIR variance. Memory effects are captured through delay variables that depend on past wealth, and the problem is formulated in such a way that the state space remains finite-dimensional.

Using Bellman’s dynamic programming principle, we derive the HJB equation associated with the optimization problem and obtain an explicit solution under CRRA preferences. The resulting value function and optimal feedback controls are characterized in closed form, subject to a mild structural condition that eliminates explicit dependence on the lag variable z. The analysis highlights how historical wealth performance, encoded through the delay terms, influences both portfolio choice and consumption, and how these effects interact with the stochastic interest rate and volatility dynamics.

Our numerical experiments show that higher historical wealth performance tends to increase both the optimal investment in the risky asset and the consumption rate, especially when the parameter ${\mu }_2$ is positive. The correlation between asset returns and volatility plays a key role in determining the sensitivity of the optimal strategies to shocks in the variance process.

Several extensions of this work are possible. For example, one could consider extending the model to include a jump in the dynamics of risky assets. Furthermore, multiple risky assets with correlated returns and volatility factors incorporate transaction costs or portfolio constraints, or explore alternative specifications of delay in the asset price dynamics considered. Such generalizations would likely lead to more complex HJB equations but could provide further insights into optimal portfolio behavior in realistic, memory-dependent financial markets.