Abstract
This study adopts a three-factor approach to the affine term structure models, aiming to analyse South African (SA) government bond yields across various maturities. The primary objective is to evaluate whether these models offer robust pricing capabilities—being both admissible and flexible—while capturing the conditional correlations and volatilities of yield factors specific to SA bond yields. For a model to be considered admissible, it must also demonstrate economic identification and maximal flexibility. We thus investigate the short-, medium-, and long-term dynamics of bond yields concurrently. Model estimation involves deriving joint conditional densities through the inversion of the Fourier transform applied to the characteristic function of the state variables. This enables the use of maximum likelihood estimation as an efficient method. We assume that the market prices of risk are proportional to the volatilities of the state variables. The analysis reveals negative correlations between factors. Among the models tested, the model outperforms the model in terms of fit, both in sample and out of sample.
1. Introduction
The yield curve continues to be a useful tool for financial market participants as a guide to levels of interest rates and their economic expectations. Synonymously, it is referred to as the term structure of interest rates, a representation of the yields plotted against a cross-section of unexpired maturities. Bonds and yields are used as a relative pricing benchmark for other financial instruments. Traders of various fixed income securities such as credit default swaps, loans, and related derivatives, among others, rely on the yield curve to price their trades. The yield is a discount rate at which cash flow of fixed income securities is equated to the present value of an instrument at a point in time. The yield is dependent on short-term interest rates, which in our SA context is a short rate such as a repo set by the Monetary Policy Committee of the SA Reserve Bank.
The yield is linked to a combination of either observable and unobservable (latent) factors, which may be either macroeconomic such as inflation, gross domestic product, yield curve factors, or the three statistical factors level, slope, and curvature as per the empirical evidence by Diebold et al. (2005). They evaluate methods of constructing yield curve factors and their loadings such as principal component analysis, the dynamic Nelson–Siegel model, and affine term structure models (ATSMs). The yield curve factors in particular refer to the instantaneous or short rate of interest changes and their volatility.
Our study, which motivates the choice for ATSMs, seeks to address the cross-sectional yield dynamics with special attention to conditional volatility and correlation in a multi-factor setting. This would enable us to study several active SA Treasury bonds of different maturities simultaneously. Moreover, these dynamics have a critical impact on the pricing of bond options, risk management (hedging), and measurements such as calculations of value at risk. Stochastic volatility models of (Christiansen & Lund, 2002; Collin-Dufresne et al., 2009; Dai & Singleton, 2000), among others, consider the interest rate volatility to be a latent factor from which many properties of the yield may be observed.
A recent study by Shu et al. (2018) models the SA government bond yield using the interpolation method of Nelson–Siegel. Their report cites a remarkable statement that the SA bond market is considered to be a leader within the emerging markets and also ranked the highest in terms of liquidity. In addition, our review of the BIS quarter 4 of 2023 statistics highlights an amount of USD billion of debt securities issued by the SA central government in all markets at all original maturities denominated in domestic currency at nominal value; see BIS (n.d.) “http://www.bis.org/statistics/”. Whereas the Nelson–Siegel method produced good-fitting results in their study, our aim is to exploit the econometric modelling capabilities within ATSMs to model the SA bond yields. ATSMs provide a tractable and flexible framework to describe this dynamic behaviour of the entire term structure of interest rates by modelling the evolution of short-term and long-term rates simultaneously. They are known to have certain mathematical properties that make them analytically tractable. In particular, they can accommodate stochastic volatility, jumps, and correlation among risk factors that drive asset returns. Affine representations of state variables in the DAPMs are popular because they lead to computationally tractable pricing relations and moment equations that can be used in estimation; see Singleton (2006).
The traditional practice of capturing the bond yield movement over time together with some macroeconomic variables has been conducted by using methods such as the vector autoregression. However, there are limitations when it comes to the treatment of certain aspects of the bond and yield. First, a bond is an asset, and the same bond with several different maturities may be traded at the same time. Second, there is a risk of holding long-dated bonds for a short term as the investors may require compensation for such risk. There is an expectation that long-term yields represent a risk-adjusted average of a cross-section of short-term yields plus a risk premium in the absence of arbitrage. Third, the yields are not normally distributed, thus making it difficult to compute the expected values of future short rates. ATSMs provide a solution for this problem; see Piazzesi (2010).
ATSMs commence with the presumption that the instantaneous short rate is an affine function of an dimensional state vector Y, , and that followed Gaussian and square root diffusions, respectively. Affine models were extended by Duffie and Kan (1996) into consistent and arbitrage-free multi-factor models of the term structure of interest rates in which yields at selected fixed maturities follow a parametric multivariate Markov diffusion process with “stochastic volatility”. Dai and Singleton (2000) explore the structural differences and relative goodness of fit of the ATSMs. In particular, they consider a trade-off between the following modelling issues. First, the economic representation of both short- and long-term dynamics of the state variable when studied simultaneously. Second, the computational burden of estimation and curve fitting. This trade-off is formalized by their classification of the factor affine family into non-nested subfamilies of models. Their special attention to three-factor ATSMs suggests, based on theoretical considerations and empirical evidence, that some subfamilies of ATSMs are better suited than others to explain historical interest rate behaviour. One example is the case where the conditional probability density of yields in closed form is non-existent, rendering the maximum likelihood of no use. To circumvent this, a feasible choice should come from estimation methods such as Fourier-based, generalised methods of moments (GMM), Markov chain Monte Carlo (MCMC), and simulated methods of moments (SMM), among others. It is known that the conditional likelihood function of the latent state vector may not be known, and as a result, Dai and Singleton (2000) follow the SMM of Gallant and Tauchen (1996).
The remainder of this paper is structured as follows: Section 2 captures the review of the relevant literature. Section 3 describes the ATSMs. Section 4 defines a canonical representation of the ATSM and restrictions that are imposed on the parameters. Section 5 provides an overview and describes the three-factor ATSMs. Section 6 reviews briefly the characteristic function-based estimation methods for the ATSMs. Section 7, Section 8, Section 9 and Section 10 discuss data collection, scenario determination, model implementation, and analysis of the results. In Section 11, we conclude.
2. Literature Review
This paper explores the behaviour of the SA interest rates in terms of historical time series and a cross-section of yields across a maturity spectrum. Inspired by the seminal work of Dai and Singleton (2000), we proceed by implementing their model and its maximal counterpart. Among three options of models tested on US Treasury swaps, their was found to perform better than other models, followed by their . Initially, they consider a comprehensive framework for the specification, analysis, and classification of ATSMs. They provide a complete characterisation of admissible and identified ATSMs from which it is required that sufficient general conditions exist; see Duffie et al. (2003), who describe the regular affine process. They also characterise the sufficient general conditions that must be met for a process to be affine; see Piazzesi (2010); Singleton (2006), among others.
ATSMs are among popular models in the vast literature on interest rate term structure and bond pricing. Few examples are the early generation consisting of a single-factor Gaussian of Vasicek (1977) and a square root process by Cox et al. (1980), extended by Langetieg (1980) into a multi-factor. The next generation are the correlated mixture affine models of Dai and Singleton (2000); Duffie and Kan (1996), among others. The reason for their popularity is the ability to accommodate stochastic volatility, jumps, and correlations among factors driving the asset returns and lead to computationally tractable closed-form prices, as well as estimation through moment equations; see Singleton (2006). Among research problems addressed using ATSMs is the description and treatment of the co-movement of short- and long-term bond yields. An affine process Y is defined as one in which a conditional mean and variance are affine functions of Y. The process is further defined and characterised by Duffie et al. (2003) as a regular affine process, a class of time-homogeneous Markov processes. They consider a state space , for integers and , from which the logarithm of a characteristic function of a transitional probability of such a process is affine with respect to the initial state . Singleton (2006) conveniently formalises it in terms of their exponential affine Fourier (for continuous time) and Laplace (for discrete time) transforms. The affine relationship is defined by coefficients which are solved by a family of ordinary differential equations (ODEs). These ODEs are the essence of the tractability of regular affine processes. Duffie and Kan (1996) apply the ODEs as time-dependent drivers of the solution to a zero-coupon bond, provided the parameters are admissible. An inverted form of these zero-coupon bonds gives rise to a yield as a state variable. They also exploit the idea of a yield-only analysis without including additional economic variables as latent factors.
Realdon (2021) presents discrete-time ATSMs with squared Gaussian shocks (SGSs). The addition of SGSs guarantees the presence of non-negative conditions for the factors under parameter restrictions. SGSs also have the effect that the market price of risk can alter both the drift and diffusion, unlike in the case of continuous-time models where only drift is altered. It exempts the model from the Feller condition. The introduction of the second-order conditional Escher transform allows the flexible risk premia which can alter even the conditional correlation of factors and yields. Evidence from US yields shows that SGSs tend to perform better than popular autoregressive gamma models (AGs). There were no specific limitations reported about the SGSs in their paper.
There are extensions beyond the popular three-factor ATSMs. A paper by Jang et al. (2021) investigates time-varying risk premia in Korean government bonds using a five-factor ATSM. Their model exhibits a nearly perfect fit for yields and estimates the expected bond returns with precision. Their results show that the fifth factor is dominant in explaining time variation in expected returns across maturities and the rigour of high-order factors in ATSMs. Regression results indicate both negative and positive coefficients, suggesting both mean reversion and signs of momentum trading, respectively. There are some inconclusive reasons for momentum trading not addressed by their investigation.
Dai et al. (2006); Darolles et al. (2001) are among several authors who have approached the application of ATSMs in discrete time, although they are known to have less popularity compared to their continuous-time counterparts. Earlier models exhibited a tendency of having perfectly correlated returns of bonds of all maturities, which is an unrealistic behaviour and unsuitable for hedging; see Aït-Sahalia and Kimmel (2016). Several authors extended these one-factor Markov representations of a short rate by introducing a range of multi-factor models with the long-run mean and the stochastic volatility of that are affine functions of , for which Dai and Singleton (2000) explores several specifications. Balduzzi et al. (1996) endorse a parsimonious representation of the yield curve matching the time series and cross-sectional variation in bond yields through three-factor models. They develop a simple estimation approach by exploiting the exponential affine structure of these models; see also Chen (1996) on the stochastic mean and stochastic volatility and three-factor model of the term structure of interest rates and its applications in derivatives pricing and risk management.
A specification of an ATSM should be “admissible” and therefore lead to well-defined bond prices. The admissibility property is completely characterised by Duffie et al. (2003) in the “canonical” state space with a non-negative diagonal matrix. However, this property has a problem of imposing parameter restrictions on the affine process to ensure that it is well defined. One typical scenario is the restriction of parameters to ensure that the conditional variance of a state variable remains non-negative. The requirements for admissibility become more complex as the number of state variables determining conditional variances increases; see Singleton (2006). The admissibility condition ensures that the process does not exit the domain . A family of models with a domain are a common admissible family of models, where M factors evolve in a positive state space while evolve in an unrestricted space; see Tebaldi and Veronesi (2016). Dai and Singleton (2000) verify this easily through admissible factor ATSMs that are uniquely classified into non-nested subfamilies.
Admissible models should also be canonical, meaning that they are economically identified and maximally flexible; see Singleton (2006). As a result, the benchmark ATSM models should have a canonical representation and also satisfy the non-negative and non-explosive solution of Ikeda and Watanabe (2014). Their drift should satisfy a Lipschitz condition, and the diffusion should satisfy the uniqueness condition of Yamada and Watanabe (1971); see Piazzesi (2010). These conditions have an effect of restricting the correlation structure of the affine diffusions. Exploiting the Gaussian and square root form of diffusions, there still appears to be non-satisfaction of the regularity conditions of non-explosive growth and uniqueness, giving rise to the need for a Feller condition1 see Piazzesi (2010). A multi-dimensional extension of a Feller condition was implemented by Duffie and Kan (1996), which was found to handle the general correlated affine diffusions. The condition ensures that only positive factors enter the volatility . This involves restrictions on the state variables that prevent the instantaneous conditional variances from becoming negative. This condition is sufficient for the existence of a unique solution to the affine SDE according to Duffie et al. (2003).
For each of the subfamilies, there exists a maximal model that is econometrically plausible for all other models within this subfamily. They describe further the maximal models in relation to the classification and highlight an interaction within the family of ATSMs between the dependence of the conditional variance of each on and the admissible structure of the correlation matrix for Y. A key advantage of maximal models is that of overcoming the overidentifying restrictions that are imposed on yield curve dynamics; see Dai and Singleton (2000). The admissibility property is also confirmed by the no-arbitrage solution for a zero-coupon bond following Duffie and Kan (1996).
Dai and Singleton (2000)’s specification applied the continuous-time approach to the ATSMs, which is popular in the majority of the empirical literature. They explore the structural differences and relative goodness of fits of ATSMs. They refer to a trade-off between flexibility in modelling the conditional correlations and volatilities of the risk factors. They classify a family of factor affines into non-nested subfamilies of models. From their three-factor ATSMs, empirical analysis suggests that some subfamilies of ATSMs are better suited than others to explain historical interest rate behaviour.
Several authors assess the impact of the market price of risk on the yield curve estimation and bond pricing. Whereas Dai and Singleton (2000) only focus on the completely affine form, (Cheridito et al., 2010; Duarte, 2004; Duffee, 2002) study various forms of risk premia. A recent paper by Christensen and Steenkamp (2025) introduced a novel DTSM that identifies, from a panel of data of the same legal entity, liquidity and credit risk premia. The model was implemented to estimate the liquidity and credit risk premia embedded in the SA government bond prices. They recommend the model for other emerging market entities and corporate bond markets of advanced economies.
The focus of this research is to implement the specifications of Dai and Singleton (2000) to test the pricing of zero-coupon bonds and forecast the yield curve dynamics when using the SA bond yield. It also attempts to extract the latent factors from the yield itself, without any consideration for other economic factors; see Duffie and Kan (1996). ATSMs are proven to dominate both theoretical and empirical frameworks in term structure modelling; see Piazzesi (2010). A link between the cross-sectional and time series properties is made consistent by the ATSMs. The evolution of unobserved factors from the risk-neutral dynamics of the yield is proved to have both the drift and the diffusion coefficients as affine functions of such factors by the ATSMs; see Piazzesi (2010). Several methods of estimation are available and require mostly the knowledge of the joint conditional density of yields. In this study, we follow the estimation method of Fourier inversion for the characteristic function of a state variable, which is assumed to lead to a conditional density. This method leads to a closed-form solution where the maximum likelihood is an efficient estimator.
3. Model Establishment
We discuss the model in the context of the admissibility of ATSMs. In the absence of arbitrage opportunities, a zero-coupon bond that matures at time T is priced as
where
- is the price of a bond at time t maturing at time .
- t is the current or initial time at which the bond is evaluated.
- is the maturity date, at which the bond pays its face value.
- s is a continuous-time variable at which the interest rate process evolves.2
- denotes the conditional expectation under the risk-neutral measure Q given the information available at time t.
To obtain an factor ATSM, it is assumed that an instantaneous short rate is an affine function of a vector of N unobservable state variables , written as
where and .
Another assumption is that follows an affine diffusion:
and represent the reversion rate and central tendency (long-term mean) parameters under a risk-neutral measure, respectively. is an dimensional independent Brownian motion under the risk-neutral measure Q and and are matrices, which may be asymmetric or non-diagonal. is a diagonal matrix with the diagonal elements written as
where and . The parameter can be interpreted as an intercept, which represents the base or long-run level of the variance for the component. represents the sensitivity of the variance for the component to the state vector . Together, and ensure that the conditional variance is always positive. The non-negativity in (4) is the core requirement for admissibility in this framework.
The drifts in (3) and conditional variances in (4) are both affine in . Duffie and Kan (1996) had the following time-dependent solution to the price of a zero-coupon bond, provided that parameters are admissible:
and the related yield is computed as
where and are coefficients whose solution satisfies the following ODEs (Ricatti equations):
A solution to these ODEs is found through numerical integration, starting from the initial conditions =. Risk-neutral dynamics of the short rate in (2) through to (4) determine this specification of the ODEs.
To use the closed-form representation of (1) in the empirical study of ATSMs, it is required that the distributions of and under actual physical measure P be known. To this end, a market price of risk is introduced as
where is an vector of constants. The process under physical measure P, therefore, also has an affine form3:
Note that a superscript Q has been removed. is an dimensional vector of independent Brownian motion under P, , and . comprises in its row, and is an vector with as its element.
Dai and Singleton (2000) acknowledge that their main purpose of (9) is to preserve the affine structure of under . They do not pursue the impact of the market price of risk on the forecast but only focus on the correlation and volatility dynamics of the state variables. The square root process is followed here to ensure non-negativity to the price of risk. Their form is referred to as “completely affine”, which is found to have limitations as far as pricing of risk is concerned. As a result, some authors extended the completely affine form of market price of risk to address various factors that impact the price of risk itself; see (Cheridito et al., 2007; Duarte, 2004; Duffee, 2002), among others. Our approach focusses on the econometric representation of state variables, which we assume to incorporate a detailed market price of risk. In spite of this, we follow in the footsteps of Dai and Singleton (2000), where the main focus was to address the specification problems considering both correlation and volatility on the cross-section of yield data. Our workings would not focus on analysing the market price of risk but rather leave it to future research which might incorporate other forms suitable for the SA yield curve. We also support the idea of extending a detailed market price of risk to the emerging markets to respond to factors such as volatility, liquidity, and bond credit risk; see the recent report by Christensen and Steenkamp (2025). Their report addresses a joint modelling of liquidity and credit risk for the SA bond market, where they recommend their model or a similar approach for emerging markets and corporate bonds.
4. A Canonical Representation of ATSMs
According to Dai and Singleton (2000), a general specification for (10) may not always lead to positive conditional variances over a range of Y, given an arbitrary set of parameters . However, admissibility requires that parameters restrict in (10) to be strictly positive for all i, where denotes the matrix of coefficients on Y in .
From (4), there is a special case where there is no admissibility problem when , for all i, since the instantaneous conditional variances are all constant. Outside the special case, it is necessary to impose constraints on the drift parameters and and diffusion coefficients and . The requirements for admissibility become more restrictive as the number of state variables determining increases.
They consider a case where there are M state variables driving the instantaneous conditional variance of the vector Y, such that . They further propose a set of benchmark models as the most flexible econometrically identified affine DTSM on the state space ; see also (Duffie et al. (2003)). It is only when the admissibility conditions are met that a canonical representation may be defined.
Definition 1.
For each M, is partitioned as , where is and is and V and D represent the volatility sources and the dependent factor, respectively. The canonical representation of the benchmark model is defined as a special case of (3) with
for , and is either lower or upper triangular for .
The canonical representation of is the mean reversion matrix, with diagonal terms expected to pull the mean level to non-negativity, thus influencing positive variances. Its off-diagonal terms, on the other hand, reflect how different state variables influence each other, indicating potential dependencies or interactions that could affect the overall system behaviour. The matrix therefore captures both the stabilising effects of the mean reversion rates and the dynamic interplay between different state variables. In the three-factor analysis, this trade-off between non-negative variance and correlations requires special attention. It also has an impact on the choice of M, the number of state variables entering volatility, and the interactions among factors:
The following parameter restrictions are imposed:
Dai and Singleton (2000) define a subfamily of affine DTSM as nested special cases of the canonical model or its invariant transformation, where . Equivalent affine models are obtained under invariant transformations that preserve admissibility and identification and leave the observable quantities like short rate unchanged. Details on invariant transformation are discussed in Appendix A of Dai and Singleton (2000).
The following issues are further noted from Dai and Singleton (2000):
The assumed structure of ensures that for the canonical representation. To verify that M resides in , instantaneous conditional correlations among are zero, whereas the instantaneous correlations among are determined by parameters because . Admissibility is established provided (20) holds and that the conditional covariance matrix of Y depends only on . Zero restrictions in the upper right block of and the constraints in (18) and (19) ensure that is positive. Stationarity is also assured by ensuring that all the eigenvalues of are strictly positive; see also Appendix B in Dai and Singleton (2000).
In addition to an admissible canonical representation, in which the minimal known sufficient conditions for admissibility were imposed, minimal normalisations for econometric identification are imposed to derive a “maximal” model in . A more unique class of maximal , referred to as the equivalence class of the model, is obtained by invariant transformation of the canonical representation; see Appendix A in Dai and Singleton (2000).
Dai and Singleton (2000) further point out that the canonical representation of models may not always be a practical way for analysing state variables in ATSMs. Often, the existing literature opted for parameterising ATSMs with the riskless rate r as a state variable, resulting in “affine in r” (Ar) representation. This can be rewritten as an “affine in Y” , where can be expressed as an unobserved state vector . As a result, a thorough specification analysis for factor ATSMs necessitates evaluating non-nested, maximal models and ensuring that a thorough understanding of the model’s structure and implications is obtained.
5. The Three-Factor ATSMs
Three-factor models are used to describe the historical behaviour of the term structure of interest rates. Traditionally, these factors are unobserved (latent) and can only be defined statistically using techniques such as principal component analysis to convey economic meaning. Popular yield curve fitting approaches such as the dynamic Nelson–Siegel model apply the principal component analysis (PCA) loadings to fit a yield curve; see Diebold et al. (2005). These approaches appear to fit and forecast well but lack the theoretical rigour to enforce some no-arbitrage restrictions. Contrary to the yield curve fitting approaches, the empirical approaches to the factor models such as the ATSMs are worth pursuing. They consider the maximal parameterisation through which, in general, the economic identification of factors can be revealed. Balduzzi et al. (1996) is among the early works that are based on enforcing the no-arbitrage restrictions by implementing the three-factor models. They constructed a simple affine model with short-term interest rate, mean rate, and volatility as three factors, which are easy to estimate. They further conclude that the short rate plays an important role in yield curve modelling, following their observation that it could not be dominated by any other factor across all maturities.
Dai and Singleton (2000) explore various forms of the canonical ATSMs and their maximal counterparts, as influenced by the number conditional volatility and correlation of factors. Fixing these factors into gives rise to their three-factor models, which posit mainly the representation of the short rate itself, its mean rate, and volatility as the three-factors. Analysis and comparisons are made of the Gaussian versus the square root diffusion forms of the models, even though the latter appears to be preferred as it imposes the non-negative variance restrictions.
Three-factor models were derived from the notation , where M is the number of state variables that enter volatility according to Dai and Singleton (2000). Emphasis has been put on the trade-off between conditional volatility and correlation as a focus for the analysis of the term structure of interest rates. As previously discussed, Duffie and Kan (1996) introduced a multi-dimensional Feller condition. It ensures that negative state factors do not enter the volatility by restricting correlations; see also Piazzesi (2010). We have also previously discussed, in a similar context, the role of the mean reversion rate matrix , its non-negative diagonal terms restrictions, and interactions among state variables through its off-diagonal terms.
A number M of the factors that drive the process which enters a volatility becomes the main argument for the choice of an model, depending on the purpose of the study. Andersen and Benzoni (2005) point out that more volatility factors result in less flexibility in allowing risk premium and correlation structure. As a result, they are in favour of a one conditional volatility factor model such as the by Dai and Singleton (2000). Bikbov and Chernov (2004) also favour the with and for the same purpose of allowing flexibility for risk premium and correlation. Their focus is to impose restrictions on the parameters of such that the volatility factor disappears from the bond pricing equation. In our approach, we analyse the admissibility of parameters and cross-equation restrictions that result from interactions among the factors . As previously discussed, the mean reversion rate matrix has elements with either negative or positive magnitudes playing a role in ensuring that factors are pulled from entering the variance only for non-negative values; otherwise, non-negative correlations are the result. This is also applicable in the case of a three-factor model.
In this study, we focus on the and models and their maximal counterparts and to determine both the fit and estimation when applied to the SA bond yield curve.
5.1.
These models are characterised by one factor Y as a source of conditional volatility. As a result, gives rise to the model form of . From the original Balduzzi et al. (1996) BDFS model, the , according to the notation of Dai and Singleton (2000), is specified as
where .
The state variables , , and are the stochastic volatility for , central tendency or long-run mean of , and short rate processes, respectively. The volatility affects the short rate through its volatility factor . The coefficient represents the rate at which the short rate reverts to the central tendency. The stochastic volatility also enters , and it is also instantaneously correlated with , as noted in the last term .
The maximal model is best suited for interpreting the parameter restrictions. As a result, Dai and Singleton (2000) prefer the following model in (23) as a maximal , which is affine in r. They determine their by relaxing the parameters and in order to accommodate a non-zero correlation between the short rate and central tendency. All the other parameters inside the square boxes are set to zero to impose significant restrictions on the dynamics of interest rates and their volatility:
where serves as stochastic volatility for but also enters the drift of and is correlated to , as noted in the term ; is the central tendency of r; and is the rate at which the short rate reverts to its central tendency. Appendix E in Dai and Singleton (2000) describes the transformation framework from which a test for admissibility and canonical representations in can be achieved.
5.2.
These models are characterised by two factors of Y as a source of conditional volatility. As a result, gives rise to the model form of . The Chen (1996) model is a member of this sub-class of models, and it is represented as
, , and are independent Brownian motions. The follows a square root diffusion, unlike in the case of the BDFS model. Other parameters , , and are the same as in the above models. These lead us to the convenient maximal model for , which is represented as
Dai and Singleton (2000) relax the restrictions on , , and , while other parameters within a square box are restricted to zero.
6. Estimation for Affine Models
Several estimation strategies such as the maximum likelihood, generalised method of moments, simulated method of moments, Markov chain Monte Carlo, and the characteristic function-based method are discussed by many authors; see Singleton (2001), Singleton (2006), and Piazzesi (2010). We mention three among a possible list of issues to consider when selecting an estimation strategy for the affine models. First, an infinite set of moment conditions can cause a stochastic singularity problem, which leads to constraints for the GMM. This results from cross-sectional yield data with many maturities. Second, a choice between the inclusion or non-inclusion of a measurement error in a representation that links the observed yield with a state variable. Third, maximum likelihood efficiency is dependent on the conditional density of the state variable, which is not always known; see Carrasco et al. (2007).
In contrast to the maximum likelihood estimation, which requires that the density functions must be computed, CCF-based methods are straight forward. They depend on the knowledge of the functional form of the CCF for variables that are observed from affine diffusions. CCFs are the foundation for computationally tractable and asymptotically efficient estimators of the parameters of affine diffusions and asset pricing models representing the affine state variables; see Singleton (2001).
It is generally known that the conditional density function f of has a solution up to an inverse Fourier transform of :
The characteristic function for given :
From Proposition 1 of Duffie et al. (2000), it can be shown that under suitable regulations, (5) is the conditional characteristic function of , with and derived from the solution of (7) and (8) for . Therefore, the conditional characteristic function becomes
The log-likelihood form for (27) becomes
By conjecturing the parameters and computing the Fourier inversion, maximum likelihood can be obtained by maximising (30) to obtain a maximum likelihood estimator by the characteristic function (ML-CCF); see Singleton (2006).
Singleton (2006) considers densities of individual columns for . A selector vector is assigned an entry of one and zero elsewhere. The density f of given the entire is the inverse Fourier transform of :
The estimation of (31) is based on one-dimensional N instead of dimensional integrations.
Alternatively, the general method of moments (GMM) using a characteristic function is achieved by the residual:
For an arbitrary instrument , the estimator becomes
The GMM approach is a better alternative to a multi-dimensional Fourier inversion. However, as a grid of becomes finer, correlations among moments become increasingly large, leading to a singular distance matrix; see Singleton (2006).
For an affine DTSM, a link between a set of N-dimensional yields of several maturities , it follows from (6) that ; where follows an affine diffusion, A is an vector, and B is an matrix. Vector is a set of parameters linking to the affine representation under the risk-neutral measure .
A solution to the latent variable can be solved, provided is invertible, as
By the standard change-of-variable analysis, the conditional density function of under P becomes
If the conditional density function of a state vector is known, it is easy to continue with the estimation of parameters . For special cases of continuous-time Gaussian and independent square root processes, is known as long as the choice of the market price of risk is chosen to suit an affine process under P; see Singleton (2006) and the references therein.
For the continuous-time affine models in the family , the unknown can be computed from the CCF. It is easy to express the CCF of in terms of the CCF of since is nonsingular and both and can generate the same information set; see Singleton (2006).
For an affine diffusion, it can be shown that the CCF of is
The Fourier inversion becomes
Fourier transforms are more suitable for low-dimension problems as they become numerically burdensome as N increases. The burden could be avoided by selecting a method of moments, though at the expense of econometric efficiency; see Singleton (2006).
From (34), it is clear that the measurement errors in the yields were excluded. As a result, can be inverted to compute the state vector , with Kalman filtering becoming very useful; see Piazzesi (2010) and the references therein. Kalman filtering provides the best solution for extracting nonlinear state vectors from the affine diffusions. We do not discuss the Kalman filter and its different forms in this paper, even though we apply it to filter out the state vector . There are many sources for a detailed discussion on the Kalman filter; see Hirsa (2013).
7. Data Collection
A sample of weekly yields for active SA government Treasury bonds over the periods October 2013 to September 2024 with maturities of 3 months and 5, 10, 12, 20, 25, and 30 years were retrieved from the Thomson Reuters database. Our in-sample and out-sample data were based on the periods October 2013 to Sep 2023 and October 2023 to September 2023, respectively. The out-sample will be best-suited for forecasting and validation. A summary of descriptive statistics for yields across maturities is presented in Table 1. Mean values range between 6.6% and 10.4%, exhibiting an upward slope which is also convex in shape. A recent study by Shu et al. (2018) reported a similar behaviour for the average yields. The highest weekly standard deviation of 1.3% is observed for the 3-month maturity, which is typical in the short end of the yield curve, suggesting that yields may react quickly to changes in monetary policy or market sentiment. It is followed by a drop to 0.7% and 0.6% for the 5-year and 10-year maturities, respectively. The 20-year maturity exhibits a rise in weekly standard deviation to 0.9%, remaining constant towards the long end. This suggests variation and higher volatility in the short end, followed by relative stability for the long end of the yield curve.

Table 1.
Statistical summary of in-sample yields for the SA Treasury bond by maturity caption. Data were retrieved from Thomson Reuters.
Table 2 presents the correlations across maturities of yields. The short end of the yield curve is characterised by weak correlations. The 3-month and 5-year terms exhibit negative correlations with their long-end counterparts. This may suggest a difference and diversity in dynamics between the short and long end of the yield curve. It is also possibly among reasons for the negative correlation that the high liquidity in the SA bond market has a portion of foreign investors who are favoured by falling currency exchange rates. The SA bond is also found to have long maturities when compared to its emerging market counterparts; see Christensen and Steenkamp (2025). Other possibilities pertaining to positive correlations towards the long end should be associated with lower volatility and large portions of pension fund portfolios investing in the same bonds with similar maturities but less trading activity. From the 10-year maturity, higher correlations ranging from 0.612 to 0.999 are observed, suggesting stability as the yield curve approaches its long end.

Table 2.
Correlation matrix of in-sample yields across maturities. Data were retrieved from Thomson Reuters.
Figure 1 presents the first three principal components (PCs) of the yields over maturities. They are explained by the variance of about 99.70%, which is close but slightly above the 98% empirical finding according to Litterman et al. (1991); see also Diebold et al. (2005); Piazzesi (2010). The first PC represents a key rate shift or level change in rates. It is the result of volatility causing rates of all maturities to fluctuate by almost the same amount. The observation is that the short end is associated with high volatility and increasing rates. At mid-term around 10-year maturity, they reach a peak, followed by stability as they approach the long end of the yield curve. The second PC represents a slope, which exhibits a downward slope but with its highest level in the short end, which might be associated with rate increases and volatility, followed by a drop in rates in the mid-term region and stable but falling rates towards the long end. Volatility forces a fall in rates in the short end followed by a drop towards the mid-term, and the 10-year maturity, thereafter, stabilises towards the long end. Both the slope and curvature exhibit the downward and convex slope in the same direction, suggesting a stylised fact of high volatility in the short end and low towards the long end.
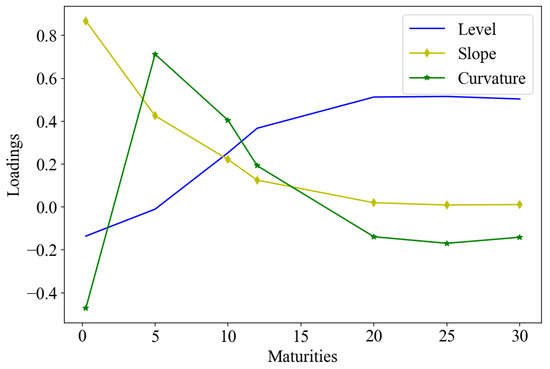
Figure 1.
Loadings of the first three principal components of the yields over maturities. Data were retrieved from Thomson Reuters.
The behaviour of PCs is also associated with the correlations as discussed earlier, where the short end is associated with weak correlations whereas in the long end of the yield curve, strong correlations are observed. These patterns are suitable for trading in swaps and correlation-based hedging strategies. Our focus being the ATSMs, we believe that these PCs are somehow closely related to the latent factors derived by the solution of coefficients and in (6). The three-factor models with three labels short rate, volatility, and central tendency should exhibit nearly a similar pattern to PCs; see Piazzesi (2010).
Figure 2 presents a time series of three principal components level, slope, and curvature, as derived from the observed yields. They are compared to the Kalman filtered time series of state vectors, namely factor 1, factor 2, and factor 3. Both time series are plotted against the observation period of October 2013 to Sep 2023. Both plots have similar patterns with factors on the right hand exhibiting smoother shapes than the principal components on the left. The analysis is extended to conducting a regression between the Kalman-filtered factors (the dependent variable) and principal components (PCs), with results presented in Table 3. We note a high cumulative variance (94.3%), suggesting that the first few PCs explain the yield variance. Intercept coefficients are close to zero for all the PCs, suggesting less impact in explaining the behaviour of movements relative to the PCs. A sharp jump from 84.1% to 95.8% is a confirmation that the first few PCs captured most of the information in the yields data, with the later components contributing progressively less. The standard errors also vary across rows, with some being quite small, which indicates that the estimates of the corresponding coefficients are relatively precise. It can be concluded that the level, slope, and curvature display similar characteristics to the factors from an affine model, therefore confirming the empirical findings by Litterman et al. (1991).
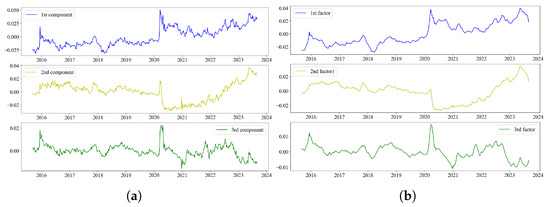
Figure 2.
(a) Time series of the first principal components of observed yields . (b) Time series of the latent factors as extracted from the affine diffusion using (34) and the Kalman filtering. Data were retrieved from Thomson Reuters.

Table 3.
Regression analysis between the three factors from the affine model against the three principal components. Factors are labelled , , and and principal components level, slope, and curvature are labelled , , and , respectively.
Figure 3 presents a selection of observed yields from the SA Treasury bonds plotted against maturities of up to 30 years. A spread between 5 and 20 years is also plotted and expected to represent a slope. Crossovers are observed among individual plots from time to time, indicative of either positive or negative (inverted) yield curves. Initial unobserved inputs to the three-factor simulation of are set to the initial values of the first three principal components. The length of a full matrix of yields comprising 418 weekly observations and seven maturities is based on the maturity column with a minimum length. No gaps in the data were discovered; otherwise, the omissions would be filled by applying an average of any preceding two values. We apply the first vector of the yield matrix as an initial input value together with the initially guessed parameters to simulate the state variables from (10). These are further used as inputs to the solution of ODE (7) and (8) from which coefficients and are obtained. Thereafter, a model-based set of zero-coupon bonds and zero yields are obtained from (6). The selection is also guided by the observations from the PCA, suggesting that our selection is a proxy for level, slope, and curvature, taking into consideration the PCA features for the short end, mid-term, and long end.
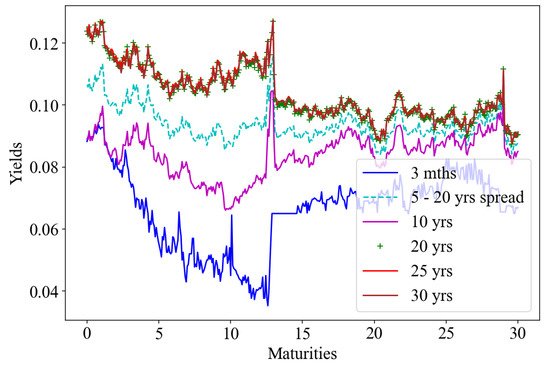
Figure 3.
Three–month and five-, ten-, twenty-, and thirty-year observed yields are plotted together with the spread between five- and twenty-year yields, against maturities. The 5–20–year spread is indicative of a slope while there are overlaps between one line and others, suggesting either positive or inverted yields. Data were retrieved from Thomson Reuters.
8. Scenario Determination
Our objective is to fit the ATSMs using the SA bond yield curve to extract the latent factors by way of zero yields. From these zero yields, we pursue a three-factor approach to model specifications in the following scenarios:
- Evaluate the performance of model and its maximal counterpart from the in sample. Ensure that parameters are admissible and that models meet the canonical form in sample.
- Evaluate the performance of model and its maximal counterpart from the in sample. Ensure that parameters are admissible and that models meet the canonical form in sample.
- Estimate both models and their counterparts out sample and evaluate their performance.
Further, we draw more insight from optimisation results and statistical analysis. In all the scenarios, we assume the market price of risk is completely affine and of the form .
9. Model Implementation
Three-Factor Models
The first three principal components are selected as proxies to the required three factors. Their initial values are inputs to both the and and their maximal counterparts. To calibrate the three-factor parameters, we select the 3-month, 10-year, and 20-year observed yields. The solution to SDE is initialised by the initial state vector and parameters to obtain , , and . The market price of risk associated with each of these factors is also computed by derived equations, following a transformation process; see Appendix E in Dai and Singleton (2000).
The three-factor models are further calibrated using the ML-CCF, which is an efficient estimator for the log-likelihood function. The calibration process identifies optimal parameters and the maximum of the log-likelihood function. In addition, the scores of likelihood functions are used to identify the market price of risk parameters; see (Carrasco et al., 2007; Singleton, 2001). The same assumptions of completely affine prices of risk are made regarding the market price of risk. Individual parameters , , and are assumed to be easy to identify in the case where time-varying volatility exists. The scores of the likelihood function are also applicable to identify the market price of risk as the parameters , , and are expected to be non-constant nor collinear. From the invariant transformations, Dai and Singleton (2000) derive the equations to compute these parameters in Appendix E.
10. Analysis of Results
10.1. Fitting the Yield Curve from the Instantaneous Rate
The main output from the three-factor models is the instantaneous rate from (22) and (25) for and , respectively. The process also applies to their maximal counterparts. From the short rate , we bootstrap zero-coupon bond prices using a discount function (1), which are thereafter inverted using (6) to obtain the model-implied yields. The performance analysis is based on the root mean square error (RMSE) and the residual , written as
where and are simulated yields and observed yields at time i for maturity t, respectively:
where K= number of observations and N is the number of maturities. A pairwise analysis between models is conducted using the above metrics.
10.2. In-Sample Analysis
10.2.1. and Models
In-sample data were applied to implement both models through SDEs, from which variables , , and for stochastic volatility, central tendency, and short rate, respectively, were produced. The market price of risk parameters , , and is also obtained from the results of these SDE according to the formulation from Appendix E in Dai and Singleton (2000). A linear combination of these variables results in a short rate that is fitted according to the affine function (22). The process is followed by the implementation of optimisation techniques from which an efficient maximum likelihood and parameters estimates are obtained.
Table 4 presents the estimation results for both the model and its maximal counterpart . The estimation results are based on the Fourier inversion of the characteristic function ML-CCF of the factor from (30). Variables , , and were simulated from (23), where initial guess parameters and the initial vector of factors for , at time t, were inputs. According to Dai and Singleton (2000), the BDFS model is a special case of (23) with the parameters in square brackets restricted to zero. However, in their specification, parameters and are relaxed and can be assumed to take any other non-zero value.

Table 4.
The estimators reported here are based on the log-likelihood computed from the Fourier inversion of the characteristic function of yields. Computation is based on variables , , and of both the model-based and observed yields. Parameters in the first column are the same as those used in (23), second column are initial guesses, while the third and fourth columns are calibrated from the models and , respectively. Bold and underlined figures in the second column refer to initial parameter values which are restricted to zero in terms of the model assumptions.
The Nelder–Mead algorithm was used as it does not require a computation of gradients or second derivatives. This is despite its significant limitation that it cannot directly produce standard errors for the parameter estimates due to its inability to compute the Hessian matrix. To evaluate model goodness of fit and performance, we relied on the chi-squared () statistics. Both AIC and BIC indicate how model complexity was penalised, taking into account both fit and the number of parameters.
AIC and BIC are both lower for compared to , indicating to be slightly better at balancing model complexity while it also has slightly more parameters. However, differences between AIC and BIC values such as −1557.54 vs. −1615.92 for AIC and −1460.68 vs. −1519.07 for BIC are quite small, suggesting that the models might be very similar in performance. Nonetheless, seems to be marginally better. The model with a lower of 16.38, which is the , appears to have a better fit than the with a of 24.98.
Parameters , , , and are restricted to zero for the model, whereas they are relaxed for the maximal model . In addition, some negative correlations were introduced for and . A small movement in after calibration from zero to 0.035 for is exhibited. This suggests that the model incorporated a weak positive relationship between short rate and volatility, which could reflect realistic market dynamics, though the effect is not large enough to dominate the model’s outcomes.
For model , there is no change in from −0.094 to −0.094 after calibration, which is interpreted as an almost unchanged relationship between the volatility of the central tendency and short rate r. For , a change to 0.089 reflects a slightly weak inverse relationship between the volatility of and r. is therefore slightly less sensitive to the impact of central tendency volatility on short rate volatility.
In the case of , for , there was no change after calibration from −3.420, suggesting no increase in the negative relationship between the volatility of the short rate r and the central tendency . For , a change from −3.420 to −3.770 indicates a significant increase in the negative correlation between the volatility of r and . In summary, exhibits a weaker relationship with volatilities, while in the case of , a slightly stronger negative correlation between short rate and central tendency is observed.
10.2.2. and Models
Table 5 presents the results of parameter estimation for both models and . The second column lists the initial guesses of parameters4. The third and fourth columns report the estimates of parameters that result from the optimisation.

Table 5.
The estimators reported here are based on the log-likelihood computed from the Fourier inversion of the characteristic function of yields. Computation is based on moment labels , , and of both the model-based and observed yields. Parameters in the first column are the same as those used in (26), second column is initial guesses, while the third and fourth columns are calibrated from the models and , respectively. Bold and underlined figures in the second column refer to initial parameter values, which are restricted to zero in terms of the model assumptions.
Both AIC and BIC are almost the same, suggesting that either one of them is worth a selection from a model complexity perspective. However, individual differences of −1750.42 vs. −1721.53 for AIC and −1645.50 vs. −1616.61 for BIC suggest model to be slightly better at balancing model complexity while it also has slightly lower parameters. Marginally, the differences are too small, implying both models to be balancing the parameter and model complexity in the same manner. statistics of 4.83 and 5.15 for models and suggest a slightly better fit for the data in . The same applies to the p-values of one for each model, which may suggest a good fit, except for the issue of possible overfitting.
Parameter under model moves from −33.900 to −33.962, which suggests a stronger mean reversion, which may lead to lower stochastic volatility and a more stable behaviour of the short rate. For model , it moves to −12.400, indicative of weaker mean reversion, higher stochastic volatility, and more variability in the short rate. For , exhibits a movement from −35.300 to −35.071 (a difference of 0.229). This suggests an increase in the negative relationship between short rate and volatility and an increase in volatility. A large negative value of −273.996 in for is observed, and this implies that even a small change in the short rate would have a large effect on volatility.
The covariance parameters in exhibit a move from −182.000 to −182.301, which is a modest increase in the negative relationship between the short rate r and volatility . This implies a slight increase in negative correlation between the r and . For , a change from −182.000 to −133.003 indicates a significant increase in the negative correlation between the r and . It is apparent that exhibits a slight increase in relationship with volatilities, while in the case of , a slight increase in negative correlation between r and is observed.
Table 6 reports the model performance in terms of both the RMSE and mean residuals. A pairwise analysis between model and is accomplished by comparing the RMSE, t-statistic, and p-value for each model in the upper panel. The same analysis is carried out for the mean residual , where and are residuals for models and , respectively. The same variables can be applied to models and , whose values are located on the right-hand side of the table.

Table 6.
The table contains a pairwise analysis between models and and their maximal counterparts. In the top panel, in-sample RMSE for each maturity. In the lower panel, mean errors are reported for each maturity. They are both accompanied by the t-statistics and p-values at each maturity level.
Model exhibits a lesser RMSE than within the short end of the yield curve, up to the region just over 10-year maturity. For the MAE model, is below , although with a marginally small difference. This pattern is confirmed by Figure 4a,c. Statistically, most differences are not significant except for the 10-year maturity with a p-value of 0.012, which is less than 0.05. In general, this suggests that there is no strong evidence that the models differ consistently in their performance in terms of the RMSE. In the case of mean error , four instances exhibit a negative direction, implying lesser errors for model . Overall, also does not prove a significant difference between the models despite four instances found to have p-values less than 0.05.
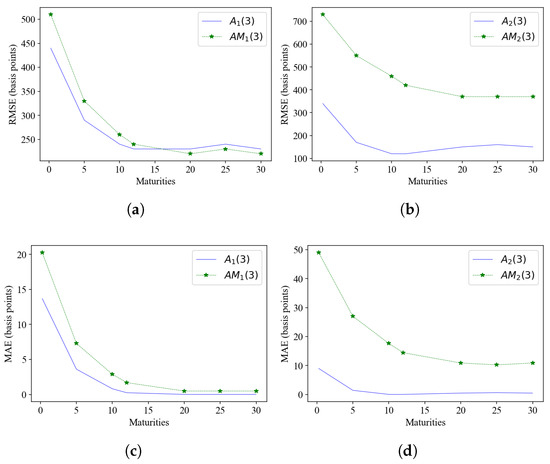
Figure 4.
In-sample models and are plotted versus their maximal counterparts. The top panel plots RMSE against maturities while the bottom panel plots the MAE against maturities. (a) RMSE for model vs. . (b) RMSE for model vs. . (c) MAE for model vs. . (d) MAE for model vs. .
Model exhibits lesser errors than , both in terms of the RMSE and MAE. The plots in Figure 4b,d confirm the observation. There are significant differences between the models and at 0.25, 5, and 10 maturities with p-values of 0.012, 0.001, and 0.012. For other maturities, p-values of 0.154, 0.345, 0.993, and 0.665 provide evidence for no significance due to higher p-values. Therefore, despite few instances of significance that were observed, in general, the evidence does not consistently show significant differences across all maturities. In the case of mean errors, has p-values far less than 0.05, which confirms that models are significantly different. The plots are in favour of the differences in models, particularly favouring model versus its maximal counterpart, both in terms of the RMSE and MAE.
Finally, we compare models and to determine the best performing in terms of the RMSE using a pairwise analysis. The results are reported in Table 7, where model displays a lower RMSE when compared to . Statistically, three instances show evidence for significance, but the majority show strong support for no differences in the models. The decision on model performance is in favour of .

Table 7.
In-sample pairwise analysis between models and as a refinement to the tests performed comprehensively against their maximal counterparts.
10.3. Instantaneous Short Rate
Figure 5 plots the model-implied instantaneous rate against maturities. Both and are in blue and magenta, respectively. The plots are based on estimated parameters fitted to the models. and its maximal counterpart are plotted against maturities in Figure 6.
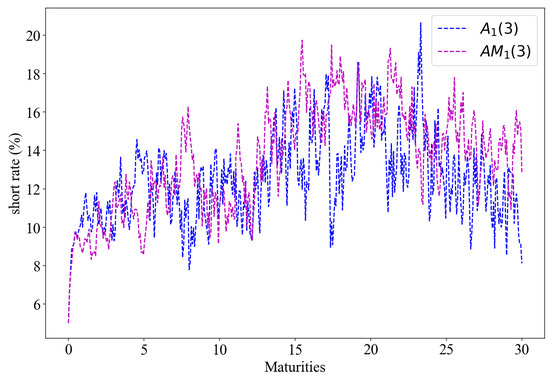
Figure 5.
Model-implied instantaneous rate in percentages is plotted against maturities. and appear in blue and magenta colours, respectively. Data were retrieved from Thomson Reuters.
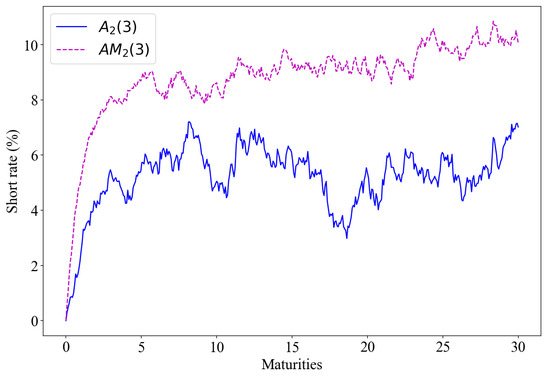
Figure 6.
Model-implied instantaneous rate in percentages is plotted against maturities. and appear in blue and magenta colours, respectively. Data were retrieved from Thomson Reuters.
The model-implied instantaneous short rate functions from (22) and (25) are made up of a linear combination of factors mapped to , , and and representing volatility, central tendency, and short rate, respectively. They exhibit an average of 11.9% and 8.1% short rates for and , respectively. The and models exhibit higher volatility than the and models. As the instantaneous rate evolves, the mean reversion persists throughout the process. Both subfamilies of models suggest that positive but stable economic growth is forecasted, except for a higher volatility, as reflected in the and plot.
10.4. Out-Sample Analysis
Table 8 presents the results of the RMSE and mean error to determine both the goodness of fit and model performance. The RMSE figures show smaller errors for when compared to . Statistically, p-values show strong evidence of no differences in the models. and , on the other hand, display a mixture of the RMSE, where early sections of one model have a lower RMSE and a higher RMSE, and in the other section, vice versa. The statistical results display strong significance differences between the models and with all p-values far below 0.05.

Table 8.
The table contains a pairwise analysis between models and and their maximal counterparts. In the top panel, out-sample RMSE for each maturity. In the lower panel, mean errors are reported for each maturity. They are both accompanied by the t-statistics and p-values at each maturity level.
For mean error analysis, tends to be slightly more consistent with a mix of positive and negative , but shows a slightly better performance in pairs where the differences are statistically significant. As a result, may be considered to have a slightly better performance in those instances. Model and show different patterns, with performing slightly better than its non-maximal counterparts, but with strong evidence for significance.
In Table 9, a final pairwise comparison between models and is reported. The results confirm that model outperforms when measured in terms of the RMSE.

Table 9.
Out-sample pairwise analysis between models and as a refinement to the tests performed comprehensively against their maximal counterparts.
11. Conclusions
The specific contribution of this study lies in its rigorous application and evaluation of three-factor ATSMs in the context of South African government bond yields, an area that remains underexplored in emerging markets. While ATSMs have been widely studied in developed economies, their effectiveness in pricing bonds within an emerging market like South Africa—where market dynamics are influenced by liquidity constraints, exchange rate volatility, and political risk—has not been extensively tested. This study fills that gap by assessing whether these models provide an admissible and flexible framework for capturing the term structure of interest rates in South Africa.
A key contribution is the methodological approach employed to estimate model parameters. Using Fourier transform inversion to derive joint conditional densities and applying maximum likelihood estimation, this work enhances the computational efficiency of term structure modelling. It also examines the interaction among key yield curve factors (stochastic volatility, central tendency, and the short rate) while demonstrating that negative correlations exist between these factors in the South African bond market. This empirical insight is valuable for researchers and practitioners seeking to understand yield dynamics in an emerging market setting.
This study provides an important model comparison, showing that the model outperforms the model in both in-sample and out-of-sample performance. Using various model selection criteria, including AIC, BIC, and statistics, it demonstrates that while both models fit the data well, exhibits slightly better predictive power—a meaningful finding for policymakers, financial institutions, and investors who rely on accurate yield curve modelling for interest rate forecasting and risk management.
The discussion concerning the inability of three-factor ATSMs to fully capture latent volatility also contributes to the literature. Identification of the potential benefits of unspanned stochastic volatility models lays the groundwork for future studies to explore improved modelling techniques that may be more effective in capturing hidden risks and addressing bond market discontinuities.
This work extends the application of ATSMs to an emerging market, introduces an efficient estimation technique, provides novel empirical insights into yield factor interactions, and offers a robust model comparison that can inform both academia and industry. Its discussion of the challenges and limitations of current models, along with a clear direction for future research, makes it a valuable contribution to the literature on fixed-income modelling and the emerging market finance.
Author Contributions
Conceptualization, M.M. and G.v.V.; methodology, G.v.V.; software, M.M.; validation, M.M. and G.v.V.; formal analysis, M.M. and G.V; investigation, M.M. and G.v.V.; resources, M.M. and G.V; data curation, M.M. and G.V; writing—original draft preparation, M.M.; writing—review and editing, G.v.V.; visualization, M.M.; supervision, G.v.V.; project administration, G.v.V. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data that support the findings of this study are available from the authors upon reasonable request.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ATSM | Affine term structure models |
| AIC | Akaike information criterion |
| BIC | Bayesian information criterion |
| BDFS | Balduzzi P, Das SR, Foresi S |
| DTSM | Dynamic term structure models |
| GMM | Generalised method of moments |
| MCMC | Markov chain Monte Carlo |
| ML-CCF | Maximum likelihood estimator by conditional characteristic function |
| ODE | Ordinary differential equation |
| PCA | Principal component analysis |
| RMSE | Root mean square error |
| SMM | Simulated method of moments |
| SDE | Stochastic differential equation |
| USV | Unspanned stochastic volatility |
Notes
| 1 | A; condition is met when ; where represents the mean reversion speed, and the mean reversion rate. It ensures that the drift is sufficiently large to guarantee a positive variance. |
| 2 | The state variable Y is a Markov process, therefore the future state at time s depends only on the current state at time t and not on the history before time t. Y satisfies the Markov property; see definition 5.1 in Singleton (2006). |
| 3 | Continuous-time SDE are better treated in discrete form using methods such as the Euler approach. A discretised version also ensures a positive truncation for the variance; We approximate as ; where is the approximation of at time ; is a standard normal variable. Several authors discuss these discretisation schemes; see (Hirsa, 2013, p. 229) and (Rouah, 2013, p. 177). |
| 4 | The parameters we used as initial guesses are based on the estimates according to Dai and Singleton (2000). We find these parameters to be the best starting point as they have empirically been tested to result in convergence. The same approach was also applied in the case of our and models. |
References
- Aït-Sahalia, Y., & Kimmel, R. L. (2016). The econometrics of fixed-income markets. In Handbook of fixed-income securities (pp. 265–281). McGraw Hill. [Google Scholar]
- Andersen, T. G., & Benzoni, L. (2005). Can bonds hedge volatility risk in the us treasury market? a specification test for affine term structure models (Tech. Rep.). Working Paper. Kellogg School of Management, Northwestern University. [Google Scholar]
- Balduzzi, P., Das, S. R., & Foresi, S. (1996). A simple approach three-factor affine term structure models. Available online: https://www.researchgate.net/profile/Rangarajan-Sundaram/publication/247906542_A_Simple_Approach_to_Three-Factor_Affine_Term_Structure_Models/links/5730ac1b08aed286ca0db95d/A-Simple-Approach-to-Three-Factor-Affine-Term-Structure-Models.pdf (accessed on 13 March 2025).
- Bikbov, R., & Chernov, M. (2004). Term structure and volatility: Lessons from the Eurodollar markets. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=562454 (accessed on 13 March 2025).
- BIS. (n.d.). Available online: http://www.bis.org/statistics/ (accessed on 23 September 2024).
- Carrasco, M., Chernov, M., Florens, J.-P., & Ghysels, E. (2007). Efficient estimation of jump diffusions and general dynamic models with a continuum of moment conditions. Journal of Econometrics, 140(2), 529–573. [Google Scholar] [CrossRef]
- Chen, L. (1996). Stochastic mean and stochastic volatility: A three-factor model of the term structure of interest rates and its applications in derivatives pricing and risk management. Blackwell Publishers. [Google Scholar]
- Cheridito, P., Filipović, D., & Kimmel, R. L. (2007). Market price of risk specifications for affine models: Theory and evidence. Journal of Financial Economics, 83(1), 123–170. [Google Scholar] [CrossRef]
- Cheridito, P., Filipović, D., & Kimmel, R. L. (2010). A note on the Dai–Singleton canonical representation of affine term structure models. Mathematical Finance: An International Journal of Mathematics, Statistics and Financial Economics, 20(3), 509–519. [Google Scholar] [CrossRef]
- Christensen, J. H., & Steenkamp, D. (2025). Joint estimation of liquidity and credit risk premia in bond prices with an application. South African Reserve Bank Working Paper Series WP/25/01. Available online: https://www.resbank.co.za/content/dam/sarb/publications/working-papers/2025/joint-estimation-of-liquidity-and-credit-risk-premia-in-bond-prices-with-an-application.pdf (accessed on 13 March 2025).
- Christiansen, C., & Lund, J. (2002). Revisiting the shape of the yield curve: The effect of interest rate volatility. Available online: https://pure.au.dk/portal/files/34302281/D02_3.pdf (accessed on 13 March 2025).
- Collin-Dufresne, P., Goldstein, R. S., & Jones, C. S. (2009). Can interest rate volatility be extracted from the cross section of bond yields? Journal of Financial Economics, 94(1), 47–66. [Google Scholar] [CrossRef]
- Cox, J. C., Ingersoll, J. E., & Ross, S. A. (1980). An analysis of variable rate loan contracts. The Journal of Finance, 35(2), 389–403. [Google Scholar] [CrossRef]
- Dai, Q., Le, A., & Singleton, K. J. (2006). Discrete-time dynamic term structure models with generalized market prices of risk. Available online: https://archive.nyu.edu/handle/2451/26367 (accessed on 13 March 2025).
- Dai, Q., & Singleton, K. J. (2000). Specification analysis of affine term structure models. The Journal of Finance, 55(5), 1943–1978. [Google Scholar] [CrossRef]
- Darolles, S., Gourieroux, C., & Jasiak, J. (2001). Compound autoregressive processes. Unpublished working paper. CREST. [Google Scholar]
- Diebold, F. X., Piazzesi, M., & Rudebusch, G. D. (2005). Modeling bond yields in finance and macroeconomics. American Economic Review, 95(2), 415–420. [Google Scholar] [CrossRef]
- Duarte, J. (2004). Evaluating an alternative risk preference in affine term structure models. The Review of Financial Studies, 17(2), 379–404. [Google Scholar] [CrossRef]
- Duffee, G. R. (2002). Term premia and interest rate forecasts in affine models. The Journal of Finance, 57(1), 405–443. [Google Scholar] [CrossRef]
- Duffie, D., Filipović, D., & Schachermayer, W. (2003). Affine processes and applications in finance. The Annals of Applied Probability, 13(3), 984–1053. [Google Scholar] [CrossRef]
- Duffie, D., & Kan, R. (1996). A yield-factor model of interest rates. Mathematical Finance, 6(4), 379–406. [Google Scholar] [CrossRef]
- Duffie, D., Pan, J., & Singleton, K. (2000). Transform analysis and asset pricing for affine jump-diffusions. Econometrica, 68(6), 1343–1376. [Google Scholar] [CrossRef]
- Gallant, A. R., & Tauchen, G. (1996). Which moments to match? Econometric Theory, 12(4), 657–681. [Google Scholar] [CrossRef]
- Hirsa, A. (2013). Computational methods in finance. CRC Press. [Google Scholar]
- Ikeda, N., & Watanabe, S. (2014). Stochastic differential equations and diffusion processes. Elsevier. [Google Scholar]
- Jang, G.-Y., Kang, H.-G., & Lee, D.-J. (2021). An Extension of the Five-factor Affine Term Structure Model: Predicting Future Bond Returns. Asia-Pacific Journal of Financial Studies, 50(6), 659–689. [Google Scholar] [CrossRef]
- Langetieg, T. C. (1980). A multivariate model of the term structure. The Journal of Finance, 35(1), 71–97. [Google Scholar]
- Litterman, R. B., Scheinkman, J., & Weiss, L. (1991). Volatility and the yield curve. The Journal of Fixed Income, 1(1), 49–53. [Google Scholar] [CrossRef]
- Piazzesi, M. (2010). Affine term structure models. In Handbook of financial econometrics: Tools and techniques (pp. 691–766). Elsevier. [Google Scholar]
- Realdon, M. (2021). Discrete time affine term structure models with squared Gaussian shocks (DTATSM-SGS). Quantitative Finance, 21(8), 1365–1386. [Google Scholar] [CrossRef]
- Rouah, F. D. (2013). The heston model and its extensions in matlab and c. John Wiley & Sons. [Google Scholar]
- Shu, H.-C., Chang, J.-H., & Lo, T.-Y. (2018). Forecasting the term structure of South African government bond yields. Emerging Markets Finance and Trade, 54(1), 41–53. [Google Scholar] [CrossRef]
- Singleton, K. J. (2001). Estimation of affine asset pricing models using the empirical characteristic function. Journal of Econometrics, 102(1), 111–141. [Google Scholar] [CrossRef]
- Singleton, K. J. (2006). Empirical dynamic asset pricing: Model specification and econometric assessment. Princeton University Press. [Google Scholar]
- Tebaldi, C., & Veronesi, P. (2016). Risk-neutral pricing: Monte carlo simulations. In Handbook of fixed-income securities (pp. 435–468). McGraw-Hill Education. [Google Scholar]
- Vasicek, O. (1977). An equilibrium characterization of the term structure. Journal of Financial Economics, 5(2), 177–188. [Google Scholar] [CrossRef]
- Yamada, T., & Watanabe, S. (1971). On the uniqueness of solutions of stochastic differential equations. Journal of Mathematics of Kyoto University, 11(1), 155–167. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).