Abstract
This study evaluates the performance of United States (US) and European Exchange Traded Funds (ETFs) using the non-oriented version of the base point-slack-based measure (BP-SBM) Data Envelopment Analysis (DEA) model, which allows for handling negative data that can arise in some of the metrics traditionally used in this type of analysis. Our findings show that US efficient ETFs are considered benchmarks more often than European efficient ETFs. Nonetheless, it was possible to conclude that European inefficient ETFs were generally less inefficient than US ETFs. Our findings also show that ETFs’ efficiency (particularly for US ETFs) in the short run is more related to risk than to profitability factors. This implies that as the time horizon lengthens, the importance of profitability factors for the ETFs’ financial performance grows.
1. Introduction
ETFs are open-end investment funds that aim to replicate the return and risk of their reference index (Gastineau 2001; Neves et al. 2019; Tsolas 2022). Since the early 1990s, the popularity of ETFs has been continuously growing. ETFs offer diversification benefits and indirect access to overseas equities that are otherwise inaccessible or hard to acquire due to their low fees, transparency, liquidity, and tax efficiency (Dragomirescu-Gaina et al. 2021; Bowes and Ausloos 2021; Tsolas 2022; Henriques et al. 2022). Most of the research concerning ETFs has been devoted to examining their performance (e.g., Roll 1978; Golany and Roll 1989; Gouveia et al. 2018; Poterba and Shoven 2002; Kostovetsky 2003; Zopounidis et al. 2010; Hill et al. 2015; Neves et al. 2019; Navratil et al. 2021; Henriques et al. 2022). The performance assessment of these funds is generally carried out according to risk-adjusted measures (Admati and Ross 1985; Blitz and Huij 2012; Osterhoff and Kaserer 2016; Lettau and Pelger 2020; Lobato et al. 2021). The Sharpe ratio (Sharpe 1966) and Jensen’s Alpha (Jensen 1968) are the indicators mostly used to measure the performance of ETFs (Tsolas 2022; Henriques et al. 2022). However, besides the criticism inherent to their isolated use, i.e., the need to find benchmarks and the significance of market timing (Tsolas 2022; Henriques et al. 2022), there is also the challenge of combining them into a single metric (Murthi et al. 1997; Henriques et al. 2022; Tsolas 2022).
This article aims to explore the different risk-adjusted performance measures used in assessing ETFs. To this end, the BP-SBM DEA model (Tone et al. 2019) is used to address the difficulties associated with the consideration of negative values that usually arise in this type of analysis and to combine into a single score the multiplicity of metrics available in the assessment of ETFs’ performance.
In this context, the DEA approach originally proposed by Charnes et al. (1978) can be particularly useful (Basso and Funari 2001, 2007, 2014, 2016; Proença et al. 2023). DEA is a mathematical programming methodology that allows assessing the efficiency of a set of units called Decision-Making Units (DMUs), in our case the ETFs under evaluation, whose performance is characterized by multiple inputs (risk indicators) and outputs (profitability indicators). With this methodology, DMUs are classified as efficient or inefficient according to a single efficiency score. Additionally, DEA enables finding the benchmarks of inefficient DMUs, providing managers with valuable information regarding the best practices to be followed. Furthermore, the DEA methodology has been accepted and used to measure the performance of ETFs because it allows for the elimination of limitations associated with traditional performance measures (Murthi et al. 1997; Galagedera and Silvapulle 2002; Choi and Min 2017; Kiymaz 2019).
In fact, Murthi et al. (1997) highlighted the advantages offered by this tool in the assessment of portfolio performance. First, this methodology does not require any theoretical reference model (e.g., CAPM or APT). The efficiency of each fund (DMU) is measured against a set of efficient funds within the same category. Second, it allows simultaneously considering both risk (inputs) and profit measures (outputs), resulting in a single performance assessment score.
In this framework, the literature devoted to the use of DEA in the performance assessment of ETFs can be grouped into three main branches. The first considers the single use of DEA models. In this vein, Chu et al. (2010) used a range directional measure (RDM) (Portela et al. 2004) to evaluate the performance of IShare World exchange-traded funds (ETFs), including major countries in Asia Pacific, Europe, North America, and some emerging markets, from 2006 to 2009. The inputs considered in their study were downside risk, and expense ratio, and the outputs were monthly return and upside deviation. Prasanna (2012) employed the Charnes, Cooper, and Rhodes (CCR) DEA model (Charnes et al. 1978) to evaluate the performance of 82 ETFs floated and traded on the Indian stock market. They considered as inputs the standard deviation, maximum drawdown, and monthly downside deviation. The profitable month’s percentage and the compounded monthly return were used as outputs. Acharya et al. (2015) assessed five gold ETFs versus four index ETFs during 2009–2013 with the CCR and Banker, Charnes, and Cooper (BCC) DEA model (Banker et al. 1984). The standard deviation and maximum drawdown have been used as inputs, whereas market value, annual return, and the Sharpe ratio have been used as outputs.
Choi and Min (2017) analyzed the efficiency of the KOSPI 200 index, the eight ETFs that follow it, and the 200 stocks that make up the index. The RDM was used to measure the efficiency of the ETFs. The standard deviation and systematic risk were used as inputs, and the return of these funds was considered an output. Isakov (2019) assessed the performance of ETFs on the Xetra platform (Germany) through the CCR model. The expense ratio and downside risk-return were used as inputs, and the upper deviation was used as an output.
The second uses two-stage DEA assessments intending to identify performance-related factors. After obtaining the efficiency scores from the first stage, regression models are used to find the reasons behind inefficiency. In this context, Tsolas and Charles (2015) employed a two-step technique to evaluate natural resources ETFs, integrating the generalized proportional distance function (Kerstens and Van de Woestyne 2011) with a censored Tobit model. Tsolas and Charles (2015) used a two-stage process for evaluating the performance of “green ETFs” using the range-adjusted measure (RAM-BCC) DEA model, Tobit censored, ordinary least squares (OLS), and boot-strapped-truncated regression. The performance was measured by considering as inputs the price cash flow (P/CF) and price book (P/B) and as outputs the Sharpe ratio and Jensen’s Alpha.
The third combines DEA with other techniques. In this context, Tsolas (2019) assessed the efficiency of ten “utility ETFs” through grey relational analysis, the BCC model, and the additive model. The factors considered were the P/E ratio and expense ratio as inputs and the Sharpe ratio as output. Henriques et al. (2022) evaluated the performance of 60 ETFs in the energy sector from 2014 to 2018. The Weighted Russell Directional Distance DEA model was combined with a multiobjective interval portfolio model to measure the performance of these ETFs. Beta, standard deviation, and Jensen’s Alpha were used to measure risk (inputs), while the Sharpe index, mean annual return, and trailing total return were used to measure profitability (outputs). Later, Tsolas (2022) also used the superefficient RAM DEA model to assess the performance of utility ETFs.
Although the advantages associated with the use of the DEA methodology to assess ETFs’ performance have been well documented, it can be established that the available scientific literature is not very prolific (Gregoriou 2006; Gregoriou and Henry 2015). Overall, only a few studies (e.g., Tsolas and Charles 2015; Choi and Min 2017; Tsolas 2022) have dealt with negative data. Additionally, from the literature review conducted, it can be concluded that most of the studies used DEA models that are radial (unrealistically considering proportionate changes of either the inputs or the outputs) or oriented (either fixing the outputs or the inputs) models. As a result, unlike the CCR and BCC models, we employ the SBM model (Tone 2001), which offers a more comprehensive analysis of efficiency. The SBM model is non-radial (i.e., inputs and outputs are allowed to have non-proportional changes) and non-oriented in its analysis of efficiency (i.e., inputs and outputs can change simultaneously). In the SBM model, all possible improvements in inputs or outputs are fully considered in the objective function. This is a key feature of the SBM model, as it ensures that all opportunities for improving efficiency are thoroughly analyzed and considered. The main feature of the SBM model is that it leaves no input or output slack unaccounted for, i.e., all possible improvements are exhausted and properly considered in the objective function.
All in all, this work aims at contributing to the existing literature by further exploring the use of DEA in the evaluation of ETFs’ performance. Another novelty introduced by this study is the selection of ETFs in pairs, following the same reference index, with one member of the pair domiciled in the US and the other in Europe (Graham et al. 2020).
This work is structured as follows: in the next section, a description of the DEA methodology used is given. In Section 2, the main premises regarding the data collected for assessing the performance of the funds under scrutiny are given. Section 3 delivers the main results obtained and their corresponding analyses. Finally, the main conclusions of this work and future developments are established.
2. Methodology
In this work, we use the non-oriented version of the DEA model proposed by Tone (2001), called Slack-Based Measure (SBM), which is a non-radial DEA model.
This model provides a more comprehensive efficiency assessment tool because, since it is non-radial and non-oriented, it considers that the inefficiency linked to the use of a specific input by a DMU is not necessarily related to the inefficiency regarding the use of another input by the same DMU; also, it contemplates the fact that a DMU may produce distinct outputs at the same time, but with a different production capacity, and hence the production efficiency for different outputs may also be distinct.
Consider the set of DMUs , where X = [xij, i = 1, 2, …, m, j = 1, 2, …, n] is the (m × n) matrix of inputs, Y = [yrj, r = 1, 2, …, s, j = 1, 2, …, n] is the matrix of outputs (s × n), and the rows of these matrices corresponding to the inputs and outputs of DMUo are given by and , respectively, with T denoting the transpose of a vector. The SBM model is given by (Tone 2001):
In problem (1) it is assumed that the matrices of inputs and outputs have non-negative elements, i.e., X ≥ 0 and Y ≥ 0. Furthermore, it is also possible to conclude that an increase in each element of or , ceteris paribus, will decrease the value of the objective function of the problem (1). Therefore, it can be concluded that 0 < ρ < 1.
The value of ρ in (1) can also be written as follows:
In terms of interpretation, the ratio assesses the rate of reduction of input i and therefore, assesses the average percentage reduction of inputs. Similarly, the ratio evaluates the rate of increase of output r and is the average percentage increase in outputs. Therefore, ρ can be seen as the ratio of average inefficiencies of inputs and outputs. To consider variable returns to scale, it is only necessary to add the constraint to model (1). So, problem (1) can be converted into problem (3), by using a positive scalar variable t:
Then, problem (3) becomes:
The optimal solution corresponds to:
Definition 1.
A DMUo is SBM-Efficient if . This condition is equivalent to = 0 and = 0.
Definition 2.
The set of efficient reference units for the SBM-inefficient DMUo is obtained by considering the indices of the DMUs associated with .
Consider the reference set of the SBM-inefficient DMUo as follows:
The point of the efficient frontier that can be seen as a reference DMU for the SBM-inefficient DMUo is:
One of the limitations of the original model proposed by Tone (2001) is that it does not allow the treatment of negative factors. To overcome this problem, Tone et al. (2019) have recently proposed the BP-SBM DEA model, which transforms negative factors into positive factors by considering “reference points”.
In this context, Sharp et al. (2007) proposed an SBM DEA model similar to the one suggested by Tone et al. (2019). The first model uses the scheme suggested by Portela et al. (2004) to accept negative data. Nevertheless, although the Sharp et al. (2007) model, unlike the BP-SBM DEA model, has the property of translation invariance, it can only be run under the VRS assumption in order to obtain an efficiency score within [0, 1]. Furthermore, the efficiency scores obtained by this model are very sensitive to the maximum output values and the minimum input values, whereas these extreme values have only small effects on the efficiency scores computed with the BP-SBM DEA model because only inputs and outputs with negative values are translated into positive values. Finally, the first DEA model cannot prevent division by zero in the objective function.
Definition 3.
The reference points are the minimum values of inputs and outputs.
The minimum value of the input , is:
The proposed transformation is carried out as follows:
Therefore, if , it is not necessary to change input i since it is positive for all DMUs. If , i.e., if one or more DMUs do not use this input, then a very small perturbation, , should be considered instead. If , i.e., if one or more DMUs have negative input , this input is converted into an amount large enough to make it strictly positive for all DMUs. To ensure that the use of this input is strictly positive, another term for disturbance, , is considered. It should be noted that both and are positive numbers.
Similarly, the minimum value of output , , is obtained as follows:
and the proposed transformation is then:
Finally, the transformed factors correspond to:
3. Data and Assumptions
The sample of this study consists of 38 ETFs1 ordered in pairs, each pair following the same index, domiciled in the US (19 funds), and Europe (14 funds from Ireland and five funds from Luxembourg). The indicators collected for each ETF were Jensen’s Alpha, the Sharpe ratio, the trailing total return for evaluating their performance, and Beta and standard deviation2 to account for their risk. The time horizon of the study is between 2014 and 2018 and refers to one year (2018), three years (2016–2018), and five years (2014–2018).
Table A1 in the Appendix A presents the data for the DMUs evaluated, specifically their acronyms, names, countries of origin, benchmarks, release dates, and legal structure.
The regions chosen for this study were the US and Europe (Ireland and Luxembourg), because these represent the largest ETF world markets.
According to the Irish fund3, around 968 fund managers from more than 53 countries have assets managed in Ireland. Ireland offers managers access to the European Union (EU) market passport, the Undertaking for Collective Investment in Transferable Securities (UCITS), and Alternative Investment Funds (AIFs). Ireland leads in this fast-growing sector and is the center of excellence for supporting ETFs all over Europe. The ETFs domiciled in Ireland correspond to more than half of the European ETF market.
In addition, as claimed by the Association of the Luxembourg Funds Industry (ALFI)4, Luxembourg is the second-largest center of ETFs in Europe, with funds distributed across 70 countries.
Finally, the three largest US fund providers (which are BlackRock, Vanguard, and State Street) represent more than 70% of the global ETF market.
Inputs and outputs were selected according to the factors generally considered in the literature. Thus, we have selected as inputs the Beta and standard deviation, and as outputs, we have considered Jensen’s Alpha, the Sharpe ratio, and the total trailing return.
Beta is a market risk indicator that measures the sensitivity of an ETF to a portfolio of assets representing the market (benchmark) and is calculated as the covariance between the return of the ETF and the benchmark index, divided by the variance of the return of the benchmark index. A Beta greater than one means that the ETF is high-risk, as its profitability shows higher volatility than the market.
In turn, the standard deviation represents the total risk of a fund and measures the volatility of a fund over a period. In this case, a high standard deviation means that the fund is very volatile.
The Sharpe ratio measures the excess return of an ETF compared to a risk-free asset per unit of total risk. The higher the value of this indicator, the better the risk/return ratio of the ETF, i.e., the better the historical performance adjusted to the risk of the ETF.
Regarding Jensen’s Alpha, this indicator is a risk-adjusted measure that measures the excess return of an ETF above its expected return determined by the CAPM. The higher the value of this indicator, the higher the performance of the ETF.
Finally, the trailing total return indicates the return that could be obtained from an ETF in a specific period.
Table 1 presents the four models that will be used to measure the performance of investments in ETFs after adjusting for their risk. These models differ only in the factors to be considered as outputs.

Table 1.
DEA models.
Table A2 and Table A3 in the Appendix A provide information on the risk and performance indicators, respectively, for each ETF considered in the analysis.
4. Results
In this section, we present and discuss the results obtained for the four models considered in the periods of one, three, and five years, respectively.
4.1. Results for the Complete Set of ETFs
The results for DEA Model 1 (M1) show that, in general, domiciled US ETFs are used more often as benchmarks (see Table A4 in the Appendix A). For one year, five efficient ETFs were obtained, three of which were domiciled in Ireland (CPXJ, CUKS, and IEMS) and two in the US (EWA, EWM) (see Table A4 in the Appendix A). The ETFs based in the US were more often used as a benchmark (EWA, 32 times; EWM, twice)—see Table A4 in the Appendix A. Among the efficient ETFs based in Ireland, the CPXJ served as a reference only once (see Table A4 in the Appendix A). No combination of ETFs that track the same index was efficient. For the period of three years, six efficient ETFs were obtained, four of which are based in the US (IVV, URTH, EWA, and EWM) and two of which are based in Ireland (CSPX and SSAC)—see Table A4 in the Appendix A. The ETFs URTH, SSAC, and EWA are used as references 31 times, six times, and three times, respectively (see Table A4 in the Appendix A). In this case, there are two ETFs (IVV and CSPX) that track the same index but do not serve as a benchmark. Finally, the 5-year period includes three efficient ETFs, two of which are domiciled in Ireland (CSPX and SSAC) and one in the US (SCJ) (see Table A4 in the Appendix A). The ETF SCJ was used as a benchmark 34 times (having a lower sensitivity to the market movement and a higher Jensen’s Alpha), followed by the ETFs CSPX (five times) and SSAC (two times)—see Table A4 in the Appendix A. Nevertheless, it should be noted that inefficient ETFs domiciled in the US show, in general, greater variability in terms of inefficiency than the corresponding pair in Europe (the scores of efficiency of EU ETFs ranged between 0.31 and 0.91, 0.16 and 0.77, and 0.36 and 0.85, for one-, three- and five-year periods, respectively, whereas those for US ETFs ranged between 0.19 and 0.73, 0.04 and 0.92, and 0 and 0.81, for one year, three years, and five years, respectively).
Table A5 in the Appendix A presents the analysis of the descriptive statistics related to the efficient and inefficient ETFs for M1 for the three periods under analysis. It is possible to verify that the average values of the risk factors associated with efficient ETFs are maintained as the time horizon increases, always being below the unit (the opposite situation occurs for inefficient ETFs). On the other hand, in a three-year time horizon, there is a very significant reduction in the average values of the outputs associated with these same funds.
From the analysis of Figure 1a–l, it can be seen that in M1, the efficiency scores of efficient ETFs do not seem to be related to their volatility with the market, regardless of the period of analysis considered.
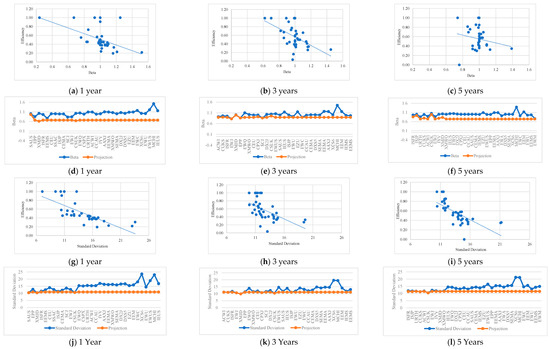
Figure 1.
Efficiency scores vs. inputs and projections (ETFs are ordered in decreasing order of efficiency) for the different time horizons–M1.
In the case of inefficient ETFs, there seems to be an evident correlation between efficiency levels and Beta. This result is particularly corroborated for one year (see the projections associated with this factor in Figure 1d).
Regarding the standard deviation, efficient ETFs present, in general, average values that are more or less uniform, varying approximately between 7 and 13. For inefficient ETFs, these values vary between 10 and 24, showing higher volatility (see Table A5 in the Appendix A). Then again, this situation has been particularly evident for one year (see projections associated with this factor in Figure 1j).
Concerning the model’s outputs depicted in Figure 2a–l (Jensen’s Alpha and trailing total return), efficiency is much more correlated to the profitability measures over five years (see Table A6 in the Appendix A), meaning that the investor exceeds his or her profitability expectations in relation to the value he or she previously estimated.
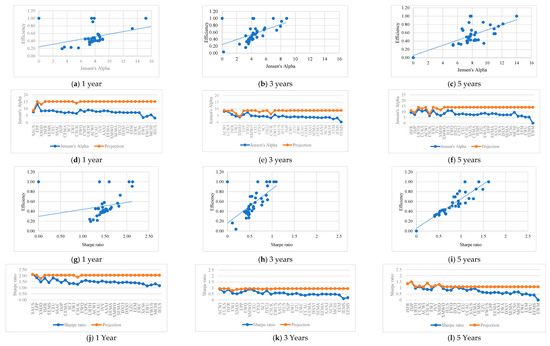
Figure 2.
Efficiency scores vs. outputs and projections (ETFs are ordered in decreasing order of efficiency) for the different time horizons–M1.
Finally, it is possible to conclude that in order to compensate for the higher levels of risk recorded over the period of one year (see Figure 1d,j), the necessary adjustments to the levels of return are always greater for this time horizon (see the projections associated with Jensen’s Alpha in Figure 2d).
The results for DEA Model 2 (M2) also illustrate that ETFs domiciled in the US were more often used as a reference for best practices (see Table A7 in the Appendix A). Then again, at 1 year, the US ETF EWA is viewed as a benchmark 32 times, and at 3 years, the US ETF URTH is considered 31 times as a benchmark (see Table A7 in the Appendix A). At 5 years, the US ETF SCJ has been used 32 times as a benchmark (see Table A7 in the Appendix A). Inefficient European ETFs, on the other hand, show once again, in general, a lower variability of inefficiency than inefficient US ETFs (the scores of efficiency of EU ETFs ranged between 0.33 and 0.83, 0.27 and 0.78, and 0.36 and 0.84, for one-, three- and five-year periods, respectively, whereas those for US ETFs ranged between 0.19 and 0.76, 0.04 and 0.92, and 0 and 0.90, for one year, three years, and five years, respectively).
Table A8 in the Appendix A presents the analysis of the descriptive statistics relating to the efficient and inefficient ETFs of M2 for the three periods under analysis. From the analysis of Table A8 and Figure 3a–l and Figure 4a–l, it is possible to conclude that the results obtained do not differ much from those of the previous model. It should be noted that M2 uses the trailing total return as an alternative variable to the Sharpe ratio, with this variable being responsible for two more efficient ETFs during the five-year period than the previous model (see Table A7 in the Appendix A), suggesting that risk-free measures of performance lead to less conservative results.
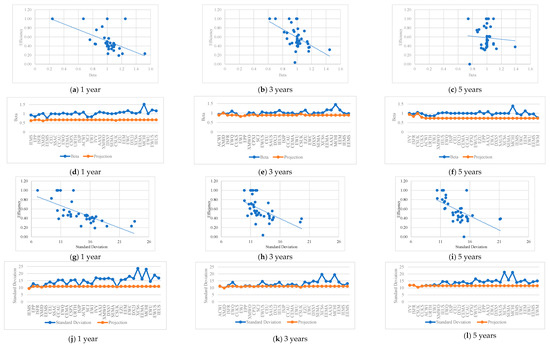
Figure 3.
Efficiency scores vs. inputs and projections (ETFs are ordered in decreasing order of efficiency) for the different time horizons–M2.
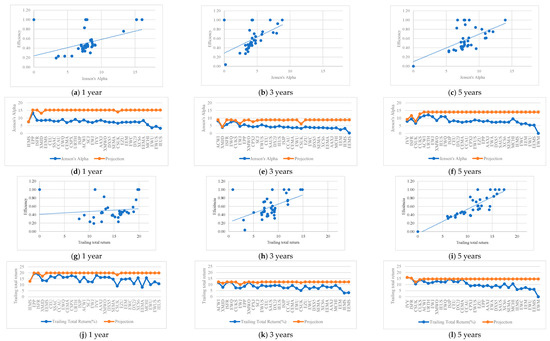
Figure 4.
Efficiency scores vs. outputs and projections (ETFs are ordered in decreasing order of efficiency) for the different time horizons–M2.
Table A9, in the Appendix A, provides the efficiency scores attained by ETFs according to Model 3 (M3) for the periods of one, three and five years, respectively, considering beta and standard deviation as inputs and the Sharpe ratio and the trailing total return as outputs.
For the period of one year, there are two efficient ETFs based in the US (EWA and EWM) and three in Ireland (CPXJ, SAUS, and IEMS)—see Table A9 in the Appendix A. The ETF EWA was used as benchmark 32 times, while the EWM was used twice—see Table A9 in the Appendix A. Even though efficient European ETFs outnumbered US ETFs for the first time, the former were never used as benchmarks (see Table A9 in the Appendix A).
For the three years, there were four efficient ETFs based in the US (IVV, URTH, EWA, and EWM) and two in Ireland (CSPX and SSAC). The ETFs IVV and CSPX are highlighted here because they serve as references for best practices 18 and 14 times, respectively. This pair of ETFs achieved the highest output values, demonstrating the importance of the Sharpe ratio’s contribution to efficiency (see Table A3 in the Appendix A).
Finally, for the five-year period, two efficient ETFs based in the US (EEMA and SCJ), two in Ireland (CSPX and SSAC), and one in Luxembourg (XMJD) were obtained. In this case, we will see for the first time that an ETF based in Europe—the CSPX in Ireland—serves as a reference 32 times, having presented the highest value for the Sharpe ratio. When it comes to the US, the ETF SCJ stands out, serving as a reference ten times.
When contrasting the results obtained for DEA M3 with the previous models, it was observed that the European ETFs obtained higher levels of performance with the indicators used. For the period of five years, this latter model also differed from the others, with an ETF domiciled in Ireland becoming a benchmark. In regards to inefficient ETFs, the volatility of inefficiency is, generally, lower in European ETFs (the scores of efficiency of EU ETFs ranged between 0.4 and 0.75, 0.14 and 0.86, and 0.33 and 0.90, for one-, three- and five-year periods, respectively, whereas those for US ETFs ranged between 0.33 and 0.77, 0.19 and 0.91, and 0 and 0.88, for one year, three years, and five years, respectively). According to Table A10 in the Appendix A and Figure 5a–l and Figure 6a–l, the results suggest that the risk factors of inefficient ETFs practically show no need for adjustments at this level for the three- and five-year periods, in contrast to what happens for one year. In the case of using the Sharpe ratio as a risk-adjusted performance indicator, the opposite situation is verified. This result highlights the trade-off traditionally studied in the literature between risk and return (Henriques and Neves 2019). Finally, it is important to note that the choice of indicators can influence the efficiency levels of ETFs, suggesting that the investor or manager must take a leading role in the choice of the factors to be used.
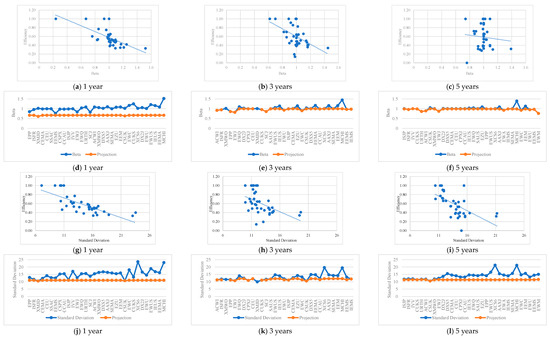
Figure 5.
Efficiency scores vs. inputs and projections (ETFs are ordered in decreasing order of efficiency) for the different time horizons–M3.
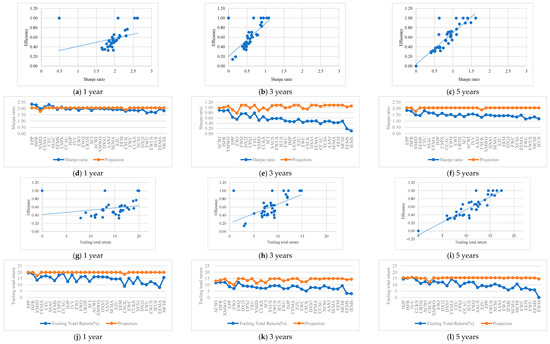
Figure 6.
Efficiency scores vs. outputs and projections (ETFs are ordered in decreasing order of efficiency) for the different time horizons–M3.
Table A11, in the Appendix A, shows the efficiency scores obtained from Model 4 (M4) over one, three, and five years, with all factors considered simultaneously.
According to M4, there are four efficient ETFs based in Ireland (CPXJ, SAUS, CUKS, and IEMS) and two in the US (EWA and EWM) for the one-year period—see Table A11 in the Appendix A. However, only the US-based ETF EWA has been used as a reference 31 times (see Table A11 in the Appendix A), corroborating the results of Chu et al. (2010).
During the three-year period, four efficient ETFs from the US (IVV, URTH, EWA, and EWM) and two from Ireland (CSPX and SSAC) were obtained, with the existence of a pair of efficient ETFs (IVV and CSPX) never being considered as a reference (see Table A11 in the Appendix A). The ETF URTH stood out, serving as a reference 31 times. SSAC ranked first among European ETFs, serving as a reference six times.
Over a five-year period, there were two efficient ETFs based in the US (EEMA and SCJ), two in Ireland (CSPX and SSAC), and one in Luxembourg (KXMJD)—see Table A11 in the Appendix A. The SSAC and XMJD served as references twice, the CSPX served as references three times, and the SCJ served as references 32 times, demonstrating once more the best positioning of efficient US-based ETFs.
After analyzing Table A12 in the Appendix A and Figure 7a–l and Figure 8a–r, it is possible to conclude that, as in the previous model, the risk factors of ETFs are less susceptible to undergo adjustments to make these funds efficient for the periods of three and five years, registering the opposite situation for one year. Regarding the risk-adjusted performance factors, the trade-off between risk and return is again evident.
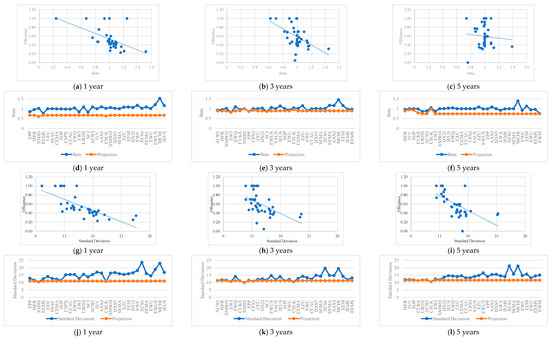
Figure 7.
Efficiency scores vs. inputs and projections (ETFs are ordered in decreasing order of efficiency) for the different time horizons–M4.
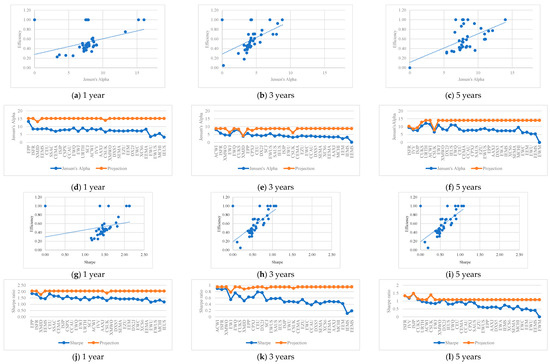
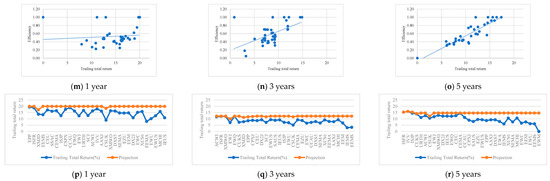
Figure 8.
Efficiency scores vs. outputs and projections (ETFs are ordered in decreasing order of efficiency) for the different time horizons–M4.
From the analysis of the different models for one year, the influence of inputs on the efficiency measure obtained far exceeds that of outputs. We discovered a more balanced situation over the three-year period, with inputs having a slightly greater influence than outputs on M1 and M2, except for the Sharpe ratio on M1, and outputs having a greater influence on M3 and M4, except for Jensen’s Alpha on M4. With the exception of Jensen’s Alpha, which has a lower influence than the standard deviation over the five years, the influence of outputs on the obtained measure of efficiency is much greater than that of inputs. In summary, short-term efficiency is more related to risk factors, and with the expansion of the time horizon, the efficiency of funds becomes increasingly related to return factors.
4.2. Results by Region
In addition to the study carried out for the different models regarding the periods considered, an analogous empirical study by region was also performed, with the sample being divided into US (19) and European (18) ETFs (Table 2).

Table 2.
Summary table of efficient ETFs from the global sample and by region.
The results obtained corroborate the conclusions previously established regarding US ETFs.
Table A13 and Table A14 in the Appendix A show the descriptive statistics of the efficient and inefficient ETFs for each region for the periods of one, three, and five years for M1.
Regardless of the period considered, European inefficient ETFs always presented a lower magnitude of average inefficiency compared to US ETFs (the scores of efficiency of EU ETFs ranged between 0.52 and 0.98, 0.19 and 0.89, and 0.40 and 0.92, for one-, three- and five-year periods, respectively, whereas those for US ETFs ranged between 0.19 and 0.73, 0.04 and 0.92, and 0 and 0.81, for one year, three years, and five years, respectively)—see Table A13 and Table A14. On the other hand, efficient US ETFs presented, on average, less risk, while efficient European ETFs showed, on average, greater performance.
For the one-year period in the US, the risk indicators (Beta and standard deviation) had a significant correlation with efficiency in the four models (see Table A15 in the Appendix A). Furthermore, these results suggest that efficiency is more related to short-term risk factors. On the European side, the results obtained indicate a situation of greater balance concerning the factors that are correlated with the efficiency of this type of fund (see Table A15 in the Appendix A).
In turn, for the three years in the US sample, the results are similar to those obtained in the previous period. Concerning Europe, risk factors are less correlated with efficiency when compared to profitability factors (see Table A15 in the Appendix A).
Finally, for the five years in the US, risk indicators had a lower correlation with efficiency when compared to profitability indicators. In Europe, the standard deviation and the Sharpe ratio showed a higher correlation with efficiency for these funds (see Table A15 in the Appendix A).
These results suggest that the US ETFs follow the trend observed in the global sample, i.e., they show a greater correlation of efficiency with risk in the short term and a greater correlation with profitability as the time horizon expands. However, this trend has not been confirmed for European ETFs.
5. Conclusions
ETFs are the future of the fund industry, and several characteristics contribute to their popularity: transparency, ease of access, tax efficiency, and low cost, among others. Traditionally, their performance is assessed by risk-adjusted profitability indicators, namely the Sharpe ratio and Jensen’s Alpha. However, these measures have limitations, as they do not incorporate some of the factors seen as essential for assessing the performance of portfolios of assets: Jensen’s Alpha is sensitive to the choice of benchmark and market timing, and the Sharpe ratio can be manipulated by individuals to present their best side (i.e., in theory, if the three-year Sharpe ratio of a portfolio is not appealing, the fund manager could calculate the ratio for a 5-year period considering that the portfolio had a good performance in the past). On the other hand, the isolated consideration of these indicators does not allow the investor to take into account the multiple factors underlying the decision-making process. To overcome this issue, in this study, a non-parametric technique that considers multiple assessment factors was used. Traditionally, the literature on ETFs has fundamentally referred to the performance of the ETFs in comparison with their benchmark index or with the performance of other types of funds, mainly mutual funds (Ippolito 1989). In this study, some originality was sought, and the DEA methodology was used to evaluate the efficiency of ETFs domiciled in the US and Europe (Ireland and Luxembourg). These ETFs were selected in pairs, following the same reference index, with one member of the pair domiciled in the US and the other in Europe. The sample included 38 ETFs (19 in the US, 14 in Ireland, and five in Luxembourg), and the time horizon considered was from 2014 to 2018, with data for one year (2018), three years (2018–2016), and five years (2018–2014), respectively. Four models were used, whose inputs are the Beta and standard deviation and whose outputs are the Sharpe ratio, Jensen’s Alpha, and the total trailing return. First, the models for the complete sample were obtained, and then the sample was separated by regions. Efficient US ETFs were viewed more often as a reference for best practices than efficient European ETFs. For inefficient ETFs, those from Europe showed, in general, less variability in terms of inefficiency than those from the US. Overall, for one year, efficiency depended more on risk factors than on profitability, and as the time horizon increased, efficiency became more related to profitability factors. This trend was also seen in the sample of ETFs from the US. However, these findings were not corroborated in the case of Europe. The results also showed that efficiency levels are related to the risk-adjusted performance factors used, thus highlighting the need to reflect the preferences of investors/managers in the choice of the factors to be used in this assessment.
Similarly to other empirical studies (e.g., Tsolas and Charles 2015; Choi 1995; Choi and Min 2017), it was found that the DEA methodology complements traditional performance measures, providing investors with a broader perspective of ETFs’ performance since it allows the contemplation of several risk-adjusted-performance assessment factors simultaneously.
This work presents relevant theoretical and practical implications, which it is important to highlight. On the one hand, academics and researchers may find this article a good foundation for further work as we identified a gap in the literature when studying ETFS on a comparative basis between the US and Europe using an innovative methodology. On the other hand, both fund managers, potential investors, and civil society can understand what contributes to the performance and risk levels of this type of diversified funds, in different periods. At a time when interest rates are rising given the high inflation rates and weak returns on bank investments, this investment alternative can translate into an increasingly attractive reality for long term investors. While in the US this type of product is already truly used to diversify portfolios, in Europe it is a reality that is still recent but that is here to stay given the increasingly adverse macroeconomic environment in terms of banking dependence in these countries and the increasing weaknesses of long-term investments in banking.
As a future study, it would be interesting to analyze the efficiency of ETFs from different regions and see if their domiciliation has any impact on efficiency, using, for example, portfolio models and considering new periods, including bear markets such as the war in Ukraine.
Author Contributions
Methodology, C.O.H. and J.A.C.; Software, C.O.H.; Formal analysis, M.E.N., J.A.C. and E.S.V.; Investigation, C.O.H. and J.A.C.; Resources, M.E.N.; Data curation, C.O.H., M.E.N. and J.A.C.; Writing—original draft, J.A.C.; Writing—review & editing, C.O.H. and E.S.V.; Visualization, M.E.N.; Supervision, E.S.V. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by national funds, through the FCT—Portuguese Foundation for Science and Technology under the project UIDB/04011/2020. This work has also been funded by the Portuguese Foundation for Science and Technology funds through Projects UID/MULTI/00308/2020 and UIDB/05037/2020.
Data Availability Statement
Data is contained within the article.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
Data on DMUs.
Table A1.
Data on DMUs.
| DMU | ETF | Home | Index Followed | Launch | Legal Structure |
|---|---|---|---|---|---|
| IVV | iShares core S&P 500 ETF | US | S&P 500 | 15/05/2000 | ETF |
| CSPX | iShares Core S&P 500 UCITS ETF | Ireland | S&P 500 | 19/05/2010 | UCITS ETF |
| EWU | iShares MSCI United Kingdom ETF | US | MSCI United Kingdom | 12/03/1996 | ETF |
| CSUK | iShares MSCI United Kingdom UCITS ETF | Ireland | MSCI United Kingdom | 12/01/2010 | UCITS ETF |
| EWQ | iShares MSCI France ETF | US | MSCI France | 12/03/1996 | ETF |
| ISFR | iShares MSCI France UCITS ETF | Ireland | MSCI France | 05/09/2014 | UCITS ETF |
| URTH | iShares MSCI World EFT | US | MSCI World | 10/01/2012 | ETF |
| XMWO | XTRACKERS MSCI World UCITS ETF 1C | Ireland | MSCI World | 22/07/2014 | UCITS ETF |
| EWJ | iShares MSCI Japan ETF | US | MSCI Japan | 12/03/1996 | ETF |
| XMJD | Xtrackers MSCI Japan UCITS ETF 1C | Luxembourg | MSCI Japan | 09/01/2007 | UCITS ETF |
| EEMA | iShares MSCI Emergent Market Asia ETF | US | MSCI Emergent Market Asia | 08/02/2012 | ETF |
| CEMA | iShares MSCI Emergent Asia UCITS ETF | Ireland | MSCI Emergent Market Asia | 06/08/2010 | UCITS ETF |
| MCHI | iShares MSCI China ETF | US | MSCI China | 29/03/2011 | ETF |
| XCS6 | Xtrackers MSCI China UCITS ETF 1C | Luxembourg | MSCI China | 24/06/2010 | UCITS ETF |
| EWC | iShares MSCI Canada ETF | US | MSCI Custom Capped Canada | 12/03/1996 | ETF |
| CCAU | iShares MSCI Canada UCITS ETF | Ireland | MSCI Canada | 12/01/2010 | UCITS ETF |
| EEM | iShares MSCI Emerging Markets ETF | US | MSCI Emerging Markets Index (SM) | 07/04/2003 | ETF |
| SEMA | iShares MSCI EM UCITS ETF USD (Acc) | Ireland | MSCI Emerging Markets Index (SM) | 25/09/2009 | UCITS ETF |
| EZU | iShares MSCI EMU ETF | US | MSCI MEU | 25/07/2000 | ETF |
| CEU | iShares MSCI EMU UCITS ETF | Ireland | MSCI MEU | 12/01/2010 | UCITS ETF |
| EPP | iShares MSCI Pacific ex Japan ETF | US | MSCI Pacific ex-Japan Index | 25/10/2001 | ETF |
| CPXJ | iShares Core MSCI Pacific ex-Japan UCITS ETF | Ireland | MSCI Pacific ex-Japan Index | 12/01/2010 | UCITS ETF |
| EWA | iShares MSCI Australia ETF | US | MSCI Australia Index | 12/03/1996 | ETF |
| SAUS | iShares MSCI Australia UCITS ETF | Ireland | MSCI Australia Index | 22/01/2010 | UCITS ETF |
| ACWI | iShares MSCI ACWI ETF | US | MSCI ACWI Index | 26/03/2008 | ETF |
| SSAC | iShares MSCI ACWI UCITS ETF | Ireland | MSCI ACWI Index | 21/10/2011 | UCITS ETF |
| SCJ | iShares MSCI Japan Small-Cap ETF | US | MSCI Japan Small Cap Index | 20/12/2007 | ETF |
| ISJP | iShares MSCI Japan Small Cap UCITS ETF | Ireland | MSCI Japan Small Cap Index | 09/05/2008 | UCITS ETF |
| EWUS | iShares MSCI United Kingdom Small-Cap ETF | US | MSCI United Kingdom Small Cap Index | 25/01/2012 | ETF |
| CUKS | iShares MSCI UK Small Cap UCITS ETF | Ireland | MSCI United Kingdom Small Cap Index | 01/07/2009 | UCITS ETF |
| EWM | iShares MSCI Malaysia ETF | US | MSCI Malaysia Index | 12/03/1996 | ETF |
| LG6 | Xtrackers MSCI Malaysia UCITS ETF 1C | Luxembourg | MSCI Malaysia TRN INDEX | 24/06/2010 | UCITS ETF |
| EEMS | iShares MSCI Emerging Markets Small-Cap ETF | US | MSCI Emerging Markets Small Cap Index | 16/08/2011 | ETF |
| IEMS | iShares MSCI EM Small Cap UCITS ETF | Ireland | MSCI Emerging Markets Small Cap Index | 06/03/2009 | UCITS ETF |
| IEUS | iShares MSCI Europe Small-Cap ETF | US | MSCI Europe Small Cap Index | 12/11/2007 | ETF |
| DX2J | Xtrackers MSCI Europe Small Cap UCITS ETF 1C | Luxembourg | MSCI Europe Small Cap Index | 17/01/2008 | UCITS ETF |
| AAXJ | iShares MSCI All Country Asia ex Japan ETF | US | MSCI AC Asia ex Japan Index | 13/08/2008 | ETF |
| DXS5 | Xtrackers MSCI AC Asia ex Japan Swap UCITS ETF 1C | Luxembourg | MSCI AC Asia ex Japan Index | 20/01/2009 | UCITS ETF |

Table A2.
Input-related data.
Table A2.
Input-related data.
| Inputs | Beta | Standard Deviation (%) | ||||
|---|---|---|---|---|---|---|
| DMU | 1 Year | 3 Years | 5 Years | 1 Year | 3 Years | 5 Years |
| IVV | 1 | 1 | 1 | 17 | 12.07 | 11.92 |
| CSPX | 0.98 | 0.99 | 0.99 | 15.17 | 11.4 | 11.29 |
| EWU | 1.01 | 0.93 | 0.95 | 14.46 | 12.01 | 13.14 |
| CSUK | 1.02 | 1.04 | 1.05 | 10.66 | 10.48 | 10.47 |
| EWQ | 1.04 | 1.1 | 1.04 | 15.38 | 14 | 14.37 |
| ISFR | 0.96 | 0.95 | 0.96 | 11.53 | 11.76 | 11.91 |
| URTH | 1.09 | 0.89 | 0.86 | 15.54 | 11.21 | 11.65 |
| XMWO | 1.06 | 1.02 | 1 | 16.28 | 11.54 | 11.81 |
| EWJ | 0.84 | 0.82 | 0.87 | 12.72 | 10.7 | 12.3 |
| XMJD | 1.02 | 1.01 | 1.02 | 10.44 | 9.94 | 11.53 |
| EEMA | 1.09 | 1.17 | 1.09 | 16.13 | 14.76 | 15.46 |
| CEMA | 0.99 | 1.01 | 1 | 12.22 | 12.72 | 14.49 |
| MCHI | 1.52 | 1.45 | 1.39 | 23.04 | 19.44 | 21.12 |
| XCS6 | 1.02 | 1.01 | 1 | 23.57 | 19.66 | 21.24 |
| EWC | 1.17 | 0.9 | 0.92 | 18.04 | 13.28 | 14.68 |
| CCAU | 0.98 | 0.99 | 1 | 15.38 | 12.19 | 13.1 |
| EEM | 1.09 | 1.16 | 1.13 | 15.91 | 14.18 | 15.65 |
| SEMA | 1 | 1 | 1 | 15.9 | 14.21 | 15.65 |
| EZU | 1.08 | 1.15 | 1.09 | 15.42 | 14.2 | 14.74 |
| CEU | 1 | 1 | 1 | 14.04 | 12.04 | 13.98 |
| EPP | 0.85 | 0.86 | 0.99 | 12.88 | 11.47 | 14.02 |
| CPXJ | 1 | 1 | 1 | 10.34 | 10.88 | 13.17 |
| EWA | 0.67 | 0.7 | 0.92 | 10.97 | 10.98 | 14.5 |
| SAUS | 1 | 1 | 1 | 10.52 | 11.82 | 14.08 |
| ACWI | 1.09 | 0.92 | 0.89 | 15.37 | 11.28 | 11.74 |
| SSAC | 1 | 1 | 1 | 12.7 | 9.92 | 10.43 |
| SCJ | 0.83 | 0.86 | 0.74 | 13.69 | 11.65 | 11.53 |
| ISJP | 0.99 | 1 | 1 | 11.42 | 11.14 | 11.72 |
| EWUS | 1.21 | 1.06 | 0.99 | 18.86 | 14.67 | 16.46 |
| CUKS | 1.25 | 0.96 | 0.99 | 13.17 | 11.1 | 11.32 |
| EWM | 0.24 | 0.62 | 0.76 | 7.07 | 11.84 | 15.01 |
| EEMS | 0.76 | 0.97 | 0.97 | 12.48 | 13.09 | 14.4 |
| IEMS | 0.93 | 0.98 | 0.99 | 9.42 | 11.86 | 13.93 |
| IEUS | 1.16 | 1.14 | 1.03 | 16.81 | 14 | 14.58 |
| DX2J | 106 | 1.03 | 1.01 | 16.56 | 12.4 | 13.61 |
| AAXJ | 1.1 | 1.16 | 1.09 | 16.35 | 14.67 | 15.4 |
| DXS5 | 1.02 | 1.01 | 1 | 16.7 | 14.89 | 15.48 |
| Average | 1.00 | 1.00 | 0.99 | 14.44 | 12.69 | 13.83 |
| Minimum | 0.24 | 0.62 | 0.74 | 7.07 | 9.92 | 10.43 |
| Maximum | 1.52 | 1.45 | 1.39 | 23.57 | 19.66 | 21.24 |
Source: Financial Times.

Table A3.
Output-related data.
Table A3.
Output-related data.
| Outputs | Jensen’s Alpha | Sharpe Ratio | Trailing Total Return (%) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| DMU | 1 Year | 3 Years | 5 Years | 1 Years | 3 Years | 5 Years | 1 Year | 3 Years | 5 Years |
| IVV | −0.03 | −0.03 | −0.04 | 0.74 | 1.08 | 0.83 | 14.29 | 14.87 | 10.73 |
| CSPX | −0.05 | −0.07 | −0.09 | 0.8 | 1.03 | 1.27 | 13.92 | 14.5 | 10.37 |
| EWU | −4.39 | −0.54 | −2.52 | 0.34 | 0.48 | 0.06 | 6.48 | 6.93 | 0.97 |
| CSUK | −1.44 | −1.13 | −1.32 | 0.47 | 0.47 | 0.52 | 5.35 | 5.06 | 5.35 |
| EWQ | 1.03 | 3.1 | 3 | 0.7 | 0.75 | 0.46 | 12.62 | 11.88 | 6.85 |
| ISFR | 0.52 | 1.49 | 1.54 | 0.97 | 0.86 | 0.99 | 15.16 | 11.93 | 10.1 |
| URTH | 1.06 | 4.47 | 4.2 | 0.72 | 0.94 | 0.62 | 13.07 | 12.16 | 5.85 |
| XMWO | −0.34 | 0.42 | 0.52 | 0.68 | 0.89 | 0.59 | 12.75 | 11.95 | 7.61 |
| EWJ | −0.96 | 0.21 | 3.02 | 0.54 | 0.54 | 0.49 | 8.76 | 7.05 | 6.54 |
| XMJD | 0.37 | −0.49 | −1.2 | 0.67 | 0.5 | 0.93 | 10.08 | 7.75 | 11.18 |
| EEMA | 0.34 | −0.88 | 0.58 | 0.65 | 0.48 | 0.28 | 4.32 | 7.93 | 12.16 |
| CEMA | −1.02 | −0.75 | −0.69 | 0.82 | 0.45 | 0.6 | 12.79 | 9.22 | 9.18 |
| MCHI | −2.39 | −0.74 | 1.63 | 0.51 | 0.47 | 0.31 | 12.21 | 9.27 | 5.44 |
| XCS6 | −0.8 | −0.67 | −0.6 | 0.5 | 0.46 | 0.3 | 12.19 | 9.19 | 5.36 |
| EWC | −0.78 | −0.5 | −1.78 | 0.56 | 0.42 | 0.1 | 11.53 | 6.61 | 1.42 |
| CCAU | −0.08 | −0.22 | −0.22 | 0.64 | 0.37 | 0.45 | 15.28 | 7.21 | 5.9 |
| EEM | −0.7 | −1.97 | −1.47 | 0.6 | 0.41 | 0.16 | 11.12 | 6.74 | 2.34 |
| SEMA | −0.73 | −0.64 | −0.58 | 0.59 | 0.41 | 0.16 | 11.06 | 6.69 | 2.34 |
| EZU | −0.83 | −0.12 | 0.43 | 0.6 | 0.54 | 0.29 | 10.94 | 8.69 | 4.29 |
| CEU | 0.65 | 0.4 | 0.37 | 1 | 0.78 | 0.59 | 13.43 | 8.58 | 7.25 |
| EPP | 5.27 | 1.37 | −0.17 | 1.03 | 0.62 | 0.23 | 15.78 | 8.5 | 3.41 |
| CPXJ | −0.15 | −0.11 | −0.13 | 1.31 | 0.61 | 0.63 | 16.1 | 8.83 | 3.7 |
| EWA | 7.19 | 2.65 | −0.56 | 1.23 | 0.67 | 0.18 | 16.29 | 8.81 | 2.69 |
| SAUS | −0.35 | −0.31 | −0.35 | 1.3 | 0.57 | 0.53 | 16.35 | 8.85 | 2.71 |
| ACWI | 0.67 | 3.78 | 3.61 | 0.7 | 0.89 | 0.57 | 12.68 | 11.63 | 7.31 |
| SSAC | −0.14 | −0.14 | −0.21 | 0.83 | 0.87 | 1.05 | 12.42 | 11.17 | 6.85 |
| SCJ | −0.52 | 0.19 | 6.06 | 0.53 | 0.51 | 0.74 | 8.99 | 7.21 | 9.4 |
| ISJP | −0.35 | −0.36 | −0.38 | 0.63 | 0.46 | 1.14 | 8.92 | 7.22 | 9.32 |
| EWUS | −3.45 | 1.22 | 0.88 | 0.42 | 0.57 | 0.26 | 8.84 | 9.36 | 4.1 |
| CUKS | 8 | 3.62 | 2.5 | 0.56 | 0.64 | 0.75 | 7.51 | 7.31 | 8.67 |
| EWM | −8.02 | −4.34 | −7.92 | −0.82 | −0.01 | −0.35 | −3.65 | 0.85 | −5.24 |
| EEMS | 0.56 | −4.15 | −2.53 | 0.62 | 0.18 | 0.06 | 9.65 | 3.27 | 0.87 |
| IEMS | −0.53 | −1.12 | −0.46 | 0.78 | 0.1 | 0.39 | 9.32 | 3 | 0.74 |
| IEUS | −4.72 | 0.41 | 3.16 | 0.36 | 0.58 | 0.46 | 7.27 | 9.19 | 6.94 |
| DX2J | −0.46 | −0.19 | −0.14 | 0.62 | 0.76 | 0.75 | 7.24 | 9.28 | 6.93 |
| AAXJ | 0.55 | −1 | 0.31 | 0.66 | 0.47 | 0.27 | 12.47 | 7.74 | 4.06 |
| DXS5 | −0.75 | −0.63 | −0.67 | 0.65 | 0.47 | 0.27 | 12.59 | 7.85 | 4.06 |
| Average | −0.21 | 0.06 | 0.21 | 0.66 | 0.58 | 0.48 | 10.98 | 8.49 | 5.61 |
| Minimum | −8.02 | −4.34 | −7.92 | −0.82 | −0.01 | −0.35 | −3.65 | 0.85 | −5.24 |
| Maximum | 8 | 4.47 | 6.06 | 1.31 | 1.08 | 1.27 | 16.35 | 14.87 | 12.16 |

Table A4.
Efficiency scores and benchmarks computed with model M1.
Table A4.
Efficiency scores and benchmarks computed with model M1.
| DMU | 1 Year | 3 Years | 5 Years | Number of Times as Benchmark (1 Year) | Number of Times as Benchmark (3 Years) | Number of Times as Benchmark (5 Years) | Home |
|---|---|---|---|---|---|---|---|
| IVV | 0.41 | 1.00 | 0.66 | US | |||
| CSPX | 0.44 | 1.00 | 1.00 | 5 | Ireland | ||
| EWU | 0.24 | 0.44 | 0.32 | US | |||
| CSUK | 0.45 | 0.50 | 0.69 | Ireland | |||
| EWQ | 0.45 | 0.66 | 0.58 | US | |||
| ISFR | 0.56 | 0.73 | 0.85 | Ireland | |||
| URTH | 0.44 | 1.00 | 0.81 | 31 | US | ||
| XMWO | 0.39 | 0.63 | 0.61 | Ireland | |||
| EWJ | 0.45 | 0.70 | 0.69 | US | |||
| XMJD | 0.58 | 0.70 | 0.66 | Luxembourg | |||
| EEMA | 0.40 | 0.34 | 0.42 | US | |||
| CEMA | 0.46 | 0.39 | 0.50 | Ireland | |||
| MCHI | 0.22 | 0.27 | 0.35 | US | |||
| XCS6 | 0.31 | 0.33 | 0.36 | Luxembourg | |||
| EWC | 0.33 | 0.41 | 0.34 | US | |||
| CCAU | 0.42 | 0.39 | 0.51 | Ireland | |||
| EEM | 0.37 | 0.26 | 0.32 | US | |||
| SEMA | 0.38 | 0.36 | 0.37 | Ireland | |||
| EZU | 0.37 | 0.41 | 0.43 | US | |||
| CEU | 0.50 | 0.60 | 0.55 | Ireland | |||
| EPP | 0.73 | 0.67 | 0.43 | US | |||
| CPXJ | 1.00 | 0.58 | 0.56 | 1 | Ireland | ||
| EWA | 1.00 | 1.00 | 0.40 | 32 | 3 | US | |
| SAUS | 0.91 | 0.48 | 0.51 | Ireland | |||
| ACWI | 0.43 | 0.92 | 0.76 | US | |||
| SSAC | 0.48 | 1.00 | 1.00 | 6 | 2 | Ireland | |
| SCJ | 0.45 | 0.54 | 1.00 | 34 | US | ||
| ISJP | 0.48 | 0.46 | 0.85 | Ireland | |||
| EWUS | 0.23 | 0.50 | 0.43 | US | |||
| CUKS | 1.00 | 0.77 | 0.79 | Ireland | |||
| EWM | 1.00 | 1.00 | 0.00 | 2 | US | ||
| EEMS | 0.55 | 0.04 | 0.30 | US | |||
| IEMS | 1.00 | 0.16 | 0.47 | Ireland | |||
| IEUS | 0.19 | 0.46 | 0.58 | US | |||
| DX2J | 0.38 | 0.53 | 0.57 | Luxembourg | |||
| AAXJ | 0.41 | 0.33 | 0.41 | US | |||
| DXS5 | 0.38 | 0.38 | 0.40 | Luxembourg |

Table A5.
Descriptive statistics of efficient and inefficient DMUs in model M1.
Table A5.
Descriptive statistics of efficient and inefficient DMUs in model M1.
| Model DEA 1 | 1 Year | 3 Years | 5 Years | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | Stand. Deviation | Minimum | Maximum | Mean | Stand. Deviation | Minimum | Maximum | Mean | Stand. Deviation | Minimum | Maximum | |
| Efficient DMUs | ||||||||||||
| Beta | 0.82 | 0.38 | 0.24 | 1.25 | 0.87 | 0.17 | 0.62 | 1.00 | 0.91 | 0.15 | 0.74 | 1.00 |
| Standard deviation | 10.19 | 2.23 | 7.07 | 13.17 | 11.24 | 0.76 | 9.92 | 12.07 | 11.08 | 0.58 | 10.43 | 11.53 |
| Alpha | 9.33 | 6.56 | 0.01 | 16.03 | 4.77 | 2.99 | 0.00 | 8.81 | 9.85 | 3.59 | 7.72 | 13.99 |
| Sharpe | 1.43 | 0.86 | 0.00 | 2.13 | 0.77 | 0.41 | 0.00 | 1.09 | 1.37 | 0.27 | 1.09 | 1.62 |
| Efficiency | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 |
| Inefficient DMUs | ||||||||||||
| Beta | 1.03 | 0.13 | 0.76 | 1.52 | 1.02 | 0.12 | 0.82 | 1.45 | 1.00 | 0.10 | 0.76 | 1.39 |
| Standard deviation | 15.10 | 3.10 | 10.44 | 23.57 | 12.97 | 2.26 | 9.94 | 19.66 | 14.08 | 2.36 | 10.47 | 21.24 |
| Alpha | 7.58 | 1.73 | 3.31 | 13.30 | 4.33 | 1.55 | 0.19 | 8.12 | 7.99 | 2.19 | 0.01 | 12.13 |
| Sharpe | 1.49 | 0.20 | 1.16 | 2.12 | 0.55 | 0.18 | 0.11 | 0.90 | 0.79 | 0.30 | 0.00 | 1.49 |
| Efficiency | 0.43 | 0.14 | 0.19 | 0.91 | 0.48 | 0.19 | 0.04 | 0.92 | 0.51 | 0.19 | 0.00 | 0.85 |

Table A6.
Correlation of the efficiency scores with inputs and outputs for each model.
Table A6.
Correlation of the efficiency scores with inputs and outputs for each model.
| (a) Correlation with Efficiency (M1) | ||||
| Input/output | 1 year | 3 years | 5 years | Bigger |
| Beta | −0.52 | −0.53 | −0.19 | 3 years |
| Standard Deviation | −0.74 | −0.55 | −0.70 | 1 year |
| Jensen’s Alpha | 0.40 | 0.50 | 0.64 | 5 years |
| Sharpe ratio | 0.20 | 0.64 | 0.91 | 5 years |
| (b) Correlation with efficiency (M2) | ||||
| Input/output | 1 year | 3 years | 5 years | Bigger |
| Beta | −0.51 | −0.52 | −0.07 | 3 years |
| Standard Deviation | −0.70 | −0.53 | −0.60 | 1 year |
| Jensen’s Alpha | 0.41 | 0.51 | 0.56 | 5 years |
| Trailing total return | 0.11 | 0.51 | 0.86 | 5 years |
| (c) Correlation with efficiency (M3) | ||||
| Input/output | 1 year | 3 years | 5 years | Maior |
| Beta | −0.64 | −0.51 | −0.09 | 1 year |
| Standard Deviation | −0.75 | −0.51 | −0.61 | 1 year |
| Sharpe ratio | 0.29 | 0.69 | 0.86 | 5 years |
| Trailing total return | 0.22 | 0.56 | 0.89 | 5 years |
| (d) Correlation with efficiency (M4) | ||||
| Input/output | 1 year | 3 years | 5 years | Maior |
| Beta | −0.51 | −0.51 | −0.08 | 1 year |
| Standard Deviation | −0.73 | −0.52 | −0.63 | 1 year |
| Jensen’s Alpha | 0.39 | 0.50 | 0.55 | 5 years |
| Sharpe ratio | 0.23 | 0.66 | 0.86 | 5 years |
| Trailing total return | 0.09 | 0.54 | 0.89 | 5 years |

Table A7.
Efficiency scores and benchmarks computed with model M2.
Table A7.
Efficiency scores and benchmarks computed with model M2.
| DMU | 1 Year | 3 Years | 5 Years | Number of Times as Benchmark (1 Year) | Number of Times as Benchmark (3 Years) | Number of Times as Benchmark (5 Years) | Home |
|---|---|---|---|---|---|---|---|
| IVV | 0.44 | 1.00 | 0.90 | US | |||
| CSPX | 0.46 | 1.00 | 1.00 | Ireland | |||
| EWU | 0.23 | 0.46 | 0.34 | US | |||
| CSUK | 0.39 | 0.45 | 0.83 | Ireland | |||
| EWQ | 0.47 | 0.73 | 0.61 | US | |||
| ISFR | 0.58 | 0.75 | 0.84 | Ireland | |||
| URTH | 0.46 | 1.00 | 0.75 | 31 | US | ||
| XMWO | 0.41 | 0.64 | 0.61 | Ireland | |||
| EWJ | 0.44 | 0.70 | 0.71 | US | |||
| XMJD | 0.57 | 0.78 | 1.00 | 2 | Luxembourg | ||
| EEMA | 0.30 | 0.37 | 1.00 | 2 | US | ||
| CEMA | 0.47 | 0.47 | 0.52 | Ireland | |||
| MCHI | 0.23 | 0.32 | 0.38 | US | |||
| XCS6 | 0.33 | 0.39 | 0.39 | Luxembourg | |||
| EWC | 0.35 | 0.44 | 0.36 | US | |||
| CCAU | 0.47 | 0.48 | 0.52 | Ireland | |||
| EEM | 0.38 | 0.28 | 0.34 | US | |||
| SEMA | 0.40 | 0.40 | 0.39 | Ireland | |||
| EZU | 0.38 | 0.45 | 0.46 | US | |||
| CEU | 0.50 | 0.56 | 0.55 | Ireland | |||
| EPP | 0.76 | 0.69 | 0.45 | US | |||
| CPXJ | 1.00 | 0.61 | 0.47 | 1 | Ireland | ||
| EWA | 1.00 | 1.00 | 0.43 | 32 | 3 | US | |
| SAUS | 1.00 | 0.52 | 0.42 | Ireland | |||
| ACWI | 0.45 | 0.92 | 0.76 | US | |||
| SSAC | 0.48 | 1.00 | 1.00 | 6 | 2 | Ireland | |
| SCJ | 0.45 | 0.56 | 1.00 | 32 | US | ||
| ISJP | 0.46 | 0.50 | 0.60 | Ireland | |||
| EWUS | 0.23 | 0.56 | 0.46 | US | |||
| CUKS | 1.00 | 0.71 | 0.80 | Ireland | |||
| EWM | 1.00 | 1.00 | 0.00 | 3 | US | ||
| EEMS | 0.54 | 0.04 | 0.31 | US | |||
| IEMS | 0.83 | 0.27 | 0.36 | Ireland | |||
| IEUS | 0.19 | 0.50 | 0.61 | US | |||
| DX2J | 0.34 | 0.52 | 0.53 | Luxembourg | |||
| AAXJ | 0.43 | 0.36 | 0.44 | US | |||
| DXS5 | 0.40 | 0.42 | 0.42 | Luxembourg |

Table A8.
Descriptive statistics of efficient and inefficient DMUs in model M2.
Table A8.
Descriptive statistics of efficient and inefficient DMUs in model M2.
| Model DEA 2 | 1 Year | 3 Years | 5 Years | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | Stand. Deviation | Minimum | Maximum | Mean | Stand. Deviation | Minimum | Maximum | Mean | Stand. Deviation | Minimum | Maximum | |
| Efficient DMUs | ||||||||||||
| Beta | 0.83 | 0.39 | 0.24 | 1.25 | 0.87 | 0.17 | 0.62 | 1.00 | 0.97 | 0.13 | 0.74 | 1.09 |
| Standard deviation | 10.41 | 2.19 | 7.07 | 13.17 | 11.24 | 0.76 | 9.92 | 12.07 | 12.05 | 1.96 | 10.43 | 15.46 |
| Alfa | 9.36 | 6.54 | 0.01 | 16.03 | 4.77 | 2.99 | 0.00 | 8.81 | 8.96 | 2.88 | 6.73 | 13.99 |
| TTR | 14.17 | 8.78 | 0.00 | 20.00 | 10.39 | 5.18 | 0.85 | 14.87 | 15.24 | 2.03 | 12.10 | 17.41 |
| Efficiency | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 |
| Inefficient DMUS | ||||||||||||
| Beta | 1.03 | 0.13 | 0.76 | 1.52 | 1.02 | 0.12 | 0.82 | 1.45 | 1.00 | 0.10 | 0.76 | 1.39 |
| Standard deviation | 15.06 | 3.16 | 9.42 | 23.57 | 12.97 | 2.26 | 9.94 | 19.66 | 14.11 | 2.38 | 10.47 | 21.24 |
| Alfa | 7.58 | 1.73 | 3.31 | 13.30 | 4.33 | 1.55 | 0.19 | 8.12 | 8.01 | 2.25 | 0.01 | 12.13 |
| TTR | 14.70 | 2.89 | 7.97 | 19.43 | 8.13 | 2.13 | 3.00 | 11.95 | 10.18 | 3.32 | 0.01 | 15.98 |
| Efficiency | 0.43 | 0.13 | 0.19 | 0.83 | 0.51 | 0.18 | 0.04 | 0.92 | 0.52 | 0.19 | 0.00 | 0.90 |

Table A9.
Efficiency scores and benchmarks computed with model M3.
Table A9.
Efficiency scores and benchmarks computed with model M3.
| DMU | 1 Year | 3 Years | 5 Years | Number of Times as Benchmark (1 Year) | Number of Times as Benchmark (3 Years) | Number of Times as Benchmark (5 Years) | Home |
|---|---|---|---|---|---|---|---|
| IVV | 0.54 | 1.00 | 0.88 | 18 | US | ||
| CSPX | 0.59 | 1.00 | 1.00 | 14 | 32 | Ireland | |
| EWU | 0.38 | 0.50 | 0.30 | US | |||
| CSUK | 0.46 | 0.44 | 0.70 | Ireland | |||
| EWQ | 0.53 | 0.66 | 0.53 | US | |||
| ISFR | 0.75 | 0.86 | 0.90 | Ireland | |||
| URTH | 0.52 | 1.00 | 0.72 | 10 | US | ||
| XMWO | 0.51 | 0.83 | 0.66 | Ireland | |||
| EWJ | 0.53 | 0.70 | 0.66 | US | |||
| XMJD | 0.65 | 0.63 | 1.00 | 1 | Luxembourg | ||
| EEMA | 0.33 | 0.41 | 1.00 | US | |||
| CEMA | 0.64 | 0.49 | 0.63 | Ireland | |||
| MCHI | 0.33 | 0.34 | 0.32 | US | |||
| XCS6 | 0.40 | 0.41 | 0.38 | Luxembourg | |||
| EWC | 0.42 | 0.45 | 0.32 | US | |||
| CCAU | 0.57 | 0.41 | 0.54 | Ireland | |||
| EEM | 0.47 | 0.36 | 0.31 | US | |||
| SEMA | 0.48 | 0.38 | 0.33 | Ireland | |||
| EZU | 0.47 | 0.47 | 0.40 | US | |||
| CEU | 0.63 | 0.64 | 0.60 | Ireland | |||
| EPP | 0.77 | 0.70 | 0.39 | US | |||
| CPXJ | 1.00 | 0.64 | 0.54 | Ireland | |||
| EWA | 1.00 | 1.00 | 0.38 | 32 | 3 | US | |
| SAUS | 1.00 | 0.57 | 0.47 | Ireland | |||
| ACWI | 0.52 | 0.91 | 0.72 | US | |||
| SSAC | 0.62 | 1.00 | 1.00 | 6 | 1 | Ireland | |
| SCJ | 0.52 | 0.58 | 1.00 | 10 | US | ||
| ISJP | 0.55 | 0.49 | 0.90 | Ireland | |||
| EWUS | 0.35 | 0.51 | 0.39 | US | |||
| CUKS | 0.42 | 0.60 | 0.77 | Ireland | |||
| EWM | 1.00 | 1.00 | 0.00 | 2 | US | ||
| EEMS | 0.60 | 0.19 | 0.28 | US | |||
| IEMS | 1.00 | 0.14 | 0.38 | Ireland | |||
| IEUS | 0.35 | 0.50 | 0.53 | US | |||
| DX2J | 0.40 | 0.64 | 0.66 | Luxembourg | |||
| AAXJ | 0.49 | 0.40 | 0.38 | US | |||
| DXS5 | 0.50 | 0.43 | 0.66 | Luxembourg |

Table A10.
Descriptive statistics of efficient and inefficient DMUs in model M3.
Table A10.
Descriptive statistics of efficient and inefficient DMUs in model M3.
| Model DEA 3 | 1 Year | 3 Years | 5 Years | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | Stand. Deviation | Minimum | Maximum | Mean | Stand. Deviation | Minimum | Maximum | Mean | Stand. Deviation | Minimum | Maximum | |
| Efficient DMUs | ||||||||||||
| Beta | 0.77 | 0.32 | 0.24 | 1.00 | 0.87 | 0.17 | 0.62 | 1.00 | 0.97 | 0.13 | 0.74 | 1.09 |
| Standard deviation | 9.66 | 1.56 | 7.07 | 10.97 | 11.24 | 0.76 | 9.92 | 12.07 | 12.05 | 1.96 | 10.43 | 15.46 |
| Alfa | 2.07 | 0.91 | 0.49 | 2.62 | 0.77 | 0.41 | 0.00 | 1.09 | 1.20 | 0.37 | 0.63 | 1.62 |
| TTR | 14.54 | 8.66 | 0.00 | 20.00 | 10.39 | 5.18 | 0.85 | 14.87 | 15.24 | 2.03 | 12.10 | 17.41 |
| Efficiency | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 |
| Inefficient DMUs | ||||||||||||
| Beta | 1.04 | 0.14 | 0.76 | 1.52 | 1.02 | 0.12 | 0.82 | 1.45 | 1.00 | 0.10 | 0.76 | 1.39 |
| Standard deviation | 15.18 | 3.01 | 10.44 | 23.57 | 12.97 | 2.26 | 9.94 | 19.66 | 14.11 | 2.38 | 10.47 | 21.24 |
| Alfa | 1.96 | 0.16 | 1.65 | 2.34 | 0.55 | 0.18 | 0.11 | 0.90 | 0.78 | 0.30 | 0.00 | 1.49 |
| TTR | 14.64 | 2.94 | 7.97 | 19.43 | 8.13 | 2.13 | 3.00 | 11.95 | 10.18 | 3.32 | 0.01 | 15.98 |
| Efficiency | 0.51 | 0.11 | 0.33 | 0.77 | 0.53 | 0.18 | 0.14 | 0.91 | 0.52 | 0.21 | 0.00 | 0.90 |

Table A11.
Efficiency levels and benchmarks computed with model M4.
Table A11.
Efficiency levels and benchmarks computed with model M4.
| DMU | 1 Year | 3 Years | 5 Years | Number of Times as Benchmark (1 Year) | Number of Times as Benchmark (3 Years) | Number of Times as Benchmark (5 Years) | Home |
|---|---|---|---|---|---|---|---|
| IVV | 0.46 | 1.00 | 0.92 | US | |||
| CSPX | 0.49 | 1.00 | 1.00 | 3 | Ireland | ||
| EWU | 0.27 | 0.47 | 0.33 | US | |||
| CSUK | 0.43 | 0.47 | 0.74 | Ireland | |||
| EWQ | 0.48 | 0.70 | 0.59 | US | |||
| ISFR | 0.62 | 0.78 | 0.92 | Ireland | |||
| URTH | 0.47 | 1.00 | 0.77 | 31 | US | ||
| XMWO | 0.43 | 0.71 | 0.65 | Ireland | |||
| EWJ | 0.47 | 0.70 | 0.70 | US | |||
| XMJD | 0.60 | 0.70 | 1.00 | 2 | Luxembourg | ||
| EEMA | 0.34 | 0.38 | 1.00 | US | |||
| CEMA | 0.51 | 0.45 | 0.56 | Ireland | |||
| MCHI | 0.25 | 0.31 | 0.36 | US | |||
| XCS6 | 0.34 | 0.38 | 0.39 | Luxembourg | |||
| EWC | 0.36 | 0.43 | 0.35 | US | |||
| CCAU | 0.48 | 0.43 | 0.54 | Ireland | |||
| EEM | 0.40 | 0.30 | 0.33 | US | |||
| SEMA | 0.42 | 0.39 | 0.37 | Ireland | |||
| EZU | 0.41 | 0.45 | 0.45 | US | |||
| CEU | 0.54 | 0.61 | 0.58 | Ireland | |||
| EPP | 0.75 | 0.69 | 0.44 | US | |||
| CPXJ | 1.00 | 0.62 | 0.53 | Ireland | |||
| EWA | 1.00 | 1.00 | 0.41 | 31 | 3 | US | |
| SAUS | 1.00 | 0.53 | 0.47 | Ireland | |||
| ACWI | 0.46 | 0.92 | 0.76 | US | |||
| SSAC | 0.52 | 1.00 | 1.00 | 6 | 2 | Ireland | |
| SCJ | 0.47 | 0.56 | 1.00 | 32 | US | ||
| ISJP | 0.49 | 0.49 | 0.86 | Ireland | |||
| EWUS | 0.26 | 0.53 | 0.44 | US | |||
| CUKS | 1.00 | 0.70 | 0.82 | Ireland | |||
| EWM | 1.00 | 1.00 | 0.00 | 2 | US | ||
| EEMS | 0.56 | 0.05 | 0.31 | US | |||
| IEMS | 1.00 | 0.18 | 0.41 | Ireland | |||
| IEUS | 0.23 | 0.50 | 0.59 | US | |||
| DX2J | 0.37 | 0.57 | 0.60 | Luxembourg | |||
| AAXJ | 0.44 | 0.37 | 0.43 | US | |||
| DXS5 | 0.42 | 0.42 | 0.42 | Luxembourg |

Table A12.
Descriptive statistics of efficient and inefficient DMUs in model M4.
Table A12.
Descriptive statistics of efficient and inefficient DMUs in model M4.
| Model DEA 4 | 1 Year | 3 Years | 5 Years | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | Stand. Deviation | Minimum | Maximum | Mean | Stand. Deviation | Minimum | Maximum | Mean | Stand. Deviation | Minimum | Maximum | |
| Efficient DMUs | ||||||||||||
| Beta | 0.85 | 0.35 | 0.24 | 1.25 | 0.87 | 0.17 | 0.62 | 1.00 | 0.97 | 0.13 | 0.74 | 1.09 |
| Standard deviation | 10.25 | 2.00 | 7.07 | 13.17 | 11.24 | 0.76 | 9.92 | 12.07 | 12.05 | 1.96 | 10.43 | 15.46 |
| Alfa | 9.05 | 5.90 | 0.01 | 16.03 | 4.77 | 2.99 | 0.00 | 8.81 | 8.96 | 2.88 | 6.73 | 13.99 |
| TTR | 1.55 | 0.82 | 0.00 | 2.13 | 0.77 | 0.41 | 0.00 | 1.09 | 1.20 | 0.37 | 0.63 | 1.62 |
| Efficiency | 13.97 | 7.87 | 0.00 | 20.00 | 10.39 | 5.18 | 0.85 | 14.87 | 15.24 | 2.03 | 12.10 | 17.41 |
| Inefficient DMUs | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 |
| Beta | ||||||||||||
| Standard deviation | 1.03 | 0.13 | 0.76 | 1.52 | 1.02 | 0.12 | 0.82 | 1.45 | 1.00 | 0.10 | 0.76 | 1.39 |
| Alfa | 15.25 | 3.04 | 10.44 | 23.57 | 12.90 | 2.27 | 9.94 | 19.66 | 14.11 | 2.38 | 10.47 | 21.24 |
| TTR | 7.58 | 1.76 | 3.31 | 13.30 | 4.36 | 1.57 | 0.19 | 8.12 | 8.01 | 2.25 | 0.01 | 12.13 |
| Efficiency | 1.47 | 0.17 | 1.16 | 1.85 | 0.55 | 0.18 | 0.11 | 0.90 | 0.78 | 0.30 | 0.00 | 1.49 |
| DMU efficient | 14.76 | 2.92 | 7.97 | 19.43 | 8.14 | 2.17 | 3.00 | 11.95 | 10.18 | 3.32 | 0.01 | 15.98 |
| Beta | 0.44 | 0.11 | 0.23 | 0.75 | 0.51 | 0.18 | 0.05 | 0.92 | 0.53 | 0.21 | 0.00 | 0.92 |

Table A13.
Descriptive statistics of efficient and inefficient DMUs (US. M1).
Table A13.
Descriptive statistics of efficient and inefficient DMUs (US. M1).
| Model DEA 1US | 1 Year | 3 Years | 5 Years | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | Stand. Deviation | Minimum | Maximum | Mean | Stand. Deviation | Minimum | Maximum | Mean | Stand. Deviation | Minimum | Maximum | |
| Efficient DMUs | ||||||||||||
| Beta | 0.46 | 0.30 | 0.24 | 0.67 | 0.81 | 0.15 | 0.62 | 1.00 | 0.87 | 0.18 | 0.74 | 1.00 |
| Standard deviation | 9.02 | 2.76 | 7.07 | 10.97 | 11.36 | 0.58 | 10.70 | 12.07 | 11.73 | 0.28 | 11.53 | 11.92 |
| Alfa | 7.61 | 10.76 | 0.01 | 15.22 | 4.94 | 3.32 | 0.00 | 8.81 | 10.94 | 4.31 | 7.89 | 13.99 |
| TTR | 1.03 | 1.45 | 0.00 | 2.05 | 0.65 | 0.42 | 0.00 | 1.09 | 1.14 | 0.06 | 1.09 | 1.18 |
| Efficiency | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 |
| Inefficient DMUs | ||||||||||||
| Beta | 1.05 | 0.18 | 0.76 | 1.52 | 1.06 | 0.16 | 0.86 | 1.45 | 1.00 | 0.14 | 0.76 | 1.39 |
| Standard deviation | 15.89 | 2.57 | 12.48 | 23.04 | 13.76 | 2.06 | 11.28 | 19.44 | 14.66 | 2.14 | 11.65 | 21.12 |
| Alfa | 7.48 | 2.35 | 3.31 | 13.30 | 4.36 | 1.99 | 0.19 | 8.12 | 8.16 | 2.99 | 0.01 | 12.13 |
| TTR | 1.43 | 0.16 | 1.16 | 1.85 | 0.54 | 0.16 | 0.19 | 0.90 | 0.61 | 0.23 | 0.00 | 0.97 |
| Efficiency | 0.39 | 0.13 | 0.19 | 0.73 | 0.45 | 0.21 | 0.04 | 0.92 | 0.45 | 0.19 | 0.00 | 0.81 |

Table A14.
Descriptive statistics of efficient and inefficient DMUs (EUR. M1).
Table A14.
Descriptive statistics of efficient and inefficient DMUs (EUR. M1).
| Model DEA 1EUR | 1 Year | 3 Years | 5 Years | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | Stand. Deviation | Minimum | Maximum | Mean | Stand. Deviation | Minimum | Maximum | Mean | Stand. Deviation | Minimum | Maximum | |
| Efficient DMUs | ||||||||||||
| Beta | 1.04 | 0.15 | 0.93 | 1.25 | 0.98 | 0.02 | 0.95 | 1.00 | 0.99 | 0.02 | 0.96 | 1.00 |
| Standard deviation | 11.12 | 1.62 | 9.42 | 13.17 | 11.05 | 0.80 | 9.92 | 11.76 | 11.24 | 0.61 | 10.43 | 11.91 |
| Alfa | 9.99 | 4.05 | 7.50 | 16.03 | 5.57 | 1.77 | 4.20 | 7.96 | 8.86 | 1.31 | 7.72 | 10.43 |
| TTR | 1.73 | 0.32 | 1.38 | 2.13 | 0.86 | 0.16 | 0.65 | 1.04 | 1.37 | 0.21 | 1.10 | 1.62 |
| Efficiency | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 |
| Inefficient DMUS | ||||||||||||
| Beta | 1.01 | 0.03 | 0.98 | 1.06 | 1.01 | 0.02 | 0.98 | 1.04 | 1.01 | 0.01 | 0.99 | 1.05 |
| Standard deviation | 14.40 | 3.54 | 10.44 | 23.57 | 12.56 | 2.44 | 9.94 | 19.66 | 13.88 | 2.60 | 10.47 | 21.24 |
| Alfa | 7.64 | 0.54 | 6.59 | 8.68 | 3.93 | 0.47 | 3.21 | 4.76 | 7.51 | 0.51 | 6.61 | 8.45 |
| TTR | 1.55 | 0.22 | 1.29 | 2.12 | 0.53 | 0.20 | 0.11 | 0.90 | 0.91 | 0.26 | 0.51 | 1.49 |
| Efficiency | 0.73 | 0.12 | 0.52 | 0.98 | 0.58 | 0.17 | 0.19 | 0.89 | 0.64 | 0.14 | 0.40 | 0.92 |

Table A15.
Correlation of the efficiency scores with inputs and outputs for each model by region (US and Europe).
Table A15.
Correlation of the efficiency scores with inputs and outputs for each model by region (US and Europe).
| Correlation with Efficiency US (M1) | Correlation with Efficiency Europe (M1) | ||||||||
| Input/output | 1 year | 3 years | 5 years | Bigger | Input/output | 1 year | 3 years | 5 years | Bigger |
| Beta | −0.86 | −0.66 | −0.25 | 1 year | Beta | 0.02 | −0.31 | −0.25 | 3 years |
| Standard deviation | −0.82 | −0.67 | −0.62 | 1 year | Standard deviation | −0.77 | −0.46 | −0.77 | 5 years |
| Jensen’s Alfa | 0.34 | 0.50 | 0.80 | 5 years | Jensen’s Alfa | 0.45 | 0.69 | 0.53 | 3 years |
| Sharpe ratio | −0.09 | 0.48 | 0.97 | 5 years | Sharpe ratio | 0.66 | 0.91 | 0.92 | 5 years |
| Correlation with efficiency US (M2) | Correlation with efficiency Europe (M2) | ||||||||
| Input/output | 1 year | 3 years | 5 years | Bigger | Input/output | 1 year | 3 years | 5 years | Bigger |
| Beta | −0.83 | −0.63 | −0.11 | 1 year | Beta | −0.02 | −0.40 | −0.06 | 3 years |
| Standard deviation | −0.80 | −0.64 | −0.48 | 1 year | Standard deviation | −0.61 | −0.45 | −0.73 | 5 years |
| Jensen’s Alfa | 0.35 | 0.52 | 0.75 | 5 years | Jensen’s Alfa | 0.44 | 0.69 | 0.40 | 3 years |
| Trailing total return | −0.03 | 0.36 | 0.95 | 5 years | Trailing total return | 0.47 | 0.77 | 0.86 | 5 years |
| Correlation with efficiency US (M3) | Correlation with efficiency Europe (M3) | ||||||||
| Input/output | 1 year | 3 years | 5 years | Bigger | Input/output | 1 year | 3 years | 5 years | Bigger |
| Beta | −0.86 | −0.67 | −0.13 | 1 year | Beta | −0.60 | −0.36 | −0.09 | 1 year |
| Standard deviation | −0.82 | −0.69 | −0.50 | 1 year | Standard deviation | −0.59 | −0.40 | −0.72 | 5 years |
| Jensen’s Alfa | −0.10 | 0.47 | 0.87 | 5 years | Jensen’s Alfa | 0.83 | 0.89 | 0.94 | 5 years |
| Trailing total return | −0.03 | 0.31 | 0.94 | 5 years | Trailing total return | 0.66 | 0.77 | 0.84 | 5 years |
| Correlation with efficiency US (M4) | Correlation with efficiency Europe (M4) | ||||||||
| Input/output | 1 year | 3 years | 5 years | Bigger | Input/output | 1 year | 3 years | 5 years | Bigger |
| Beta | −0.85 | −0.64 | −0.13 | 1 year | Beta | −0.01 | −0.31 | −0.12 | 3 years |
| Standard deviation | −0.82 | −0.65 | −0.50 | 1 year | Standard deviation | −0.67 | −0.42 | −0.75 | 5 years |
| Jensen’s Alfa | 0.34 | 0.51 | 0.74 | 5 years | Jensen’s Alfa | 0.45 | 0.69 | 0.42 | 3 years |
| Sharpe ratio | −0.08 | 0.49 | 0.87 | 5 years | Sharpe ratio | 0.70 | 0.91 | 0.91 | 3 and 5 years |
| Trailing total return | −0.05 | 0.35 | 0.94 | 5 years | Trailing total return | 0.39 | 0.78 | 0.84 | 5 years |
Notes
| 1 | ETF LG6, which is domiciled in Luxembourg, is excluded from the analysis due to a lack of data for the period under analysis. |
| 2 | These measures will be further explained in Section 3. |
| 3 | Irish funds are the abbreviation for Irish Funds Industry Association, which is an association that aims to support, complement, and develop the funds industry in Ireland. |
| 4 | ALFI represents the face and voice of asset management in Luxembourg and the investment fund community. |
References
- Acharya, Satya Ranjan, Amit Kumar Dwivedi, and Bhumika Darshak Panchal. 2015. Application od Data Envelopment analysis on Indian Gold ETFs. International Journal of Business Continuity and Risk Management 6: 147–61. [Google Scholar] [CrossRef]
- Admati, Anat R., and Stephen A. Ross. 1985. Measuring Investment Performance in a Rational Expectations Equilibrium Model. The Journal of Business 53: 1–26. [Google Scholar] [CrossRef]
- Banker, Rajiv D., Abraham Charnes, and William Wager Cooper. 1984. Some models for estimating technical and scale inefficiencies in data envelopment analysis. Management Science 30: 1078–92. [Google Scholar] [CrossRef]
- Basso, Antonella, and Stefania Funari. 2001. A data envelopment analysis approach to measure mutual fund performance. European Journal of Operational Research 135: 477–92. [Google Scholar] [CrossRef]
- Basso, Antonella, and Stefania Funari. 2007. DEA models for ethical and non ethical mutual funds with negative data. Mathematics and Methods in Economics Finance 2: 21–40. [Google Scholar]
- Basso, Antonella, and Stefania Funari. 2014. Constant and variable returns to scale DEA models for socially responsible investment funds. European Journal of Operational Research 235: 775–83. [Google Scholar] [CrossRef]
- Basso, Antonella, and Stefania Funari. 2016. DEA performance assessment of mutual funds. In Data Envelopment Analysis. Boston: Springer, pp. 229–87. [Google Scholar] [CrossRef]
- Blitz, David, and Joop Huij. 2012. Evaluating the performance of global emerging markets equity exchange-traded funds. Emerging Markets Review 13: 149–58. [Google Scholar] [CrossRef]
- Bowes, Jordan, and Marcel Ausloos. 2021. Financial Risk and Better Returns through smart beta exchange-traded funds? Journal of Risk and Financial Management 14: 283. [Google Scholar] [CrossRef]
- Charnes, Abraham, William W. Cooper, and Edwardo Rhodes. 1978. Measuring the efficiency of decision making units. European Journal of Operational Research 2: 429–44. [Google Scholar] [CrossRef]
- Choi, Hyung-Suk, and Daiki Min. 2017. Efficiency of well-diversified portfolios: Evidence from data envelopment analysis. Omega 73: 104–13. [Google Scholar] [CrossRef]
- Choi, Yoon K. 1995. The sensitivity in tests of the efficiency of a portfolio and portfolio performance measurement. Quarterly Review of Economics and Finance 35: 187–206. [Google Scholar] [CrossRef]
- Chu, Jacky, Frank Chen, and Philip Leung. 2010. ETF performance measurement-Data envelopment analysis. Paper present at 2010 7th International Conference on Service Systems and Service Management, Proceedings of ICSSSM’, Tokyo, Japan, June 28–30, vol. 10, pp. 173–78. [Google Scholar] [CrossRef]
- Dragomirescu-Gaina, Catalin, Emilios Galariotis, and Dionisis Philippas. 2021. Chasing the ‘green bandwagon’ in times of uncertainty. Energy Policy 151: 112190. [Google Scholar] [CrossRef]
- Galagedera, Don UA, and Param Silvapulle. 2002. Australian mutual fund performance appraisal using data envelopment analysis. Managerial Finance 28: 60–73. [Google Scholar] [CrossRef]
- Gastineau, Gary L. 2001. Exchange-Traded Funds. The Journal of Portfolio Management 27: 88–96. [Google Scholar] [CrossRef]
- Golany, Boaz, and Yaakov Roll. 1989. An application procedure for DEA. Omega 17: 237–50. [Google Scholar] [CrossRef]
- Gouveia, Maria, Elisabete Duarte Neves, Luís Cândido Dias, and Carlos Henggeler Antunes. 2018. Performance evaluation of Portuguese mutual fund portfolios using the value-based DEA method. Journal of the Operational Research Society 69: 1628–39. [Google Scholar] [CrossRef]
- Graham, J. Edward, Carlos Lassala, and Belén Ribeiro Navarrete. 2020. Influences on mutual fund performance: Comparing US and Europe using qualitative comparative analysis. Economic research-Ekonomska istraživanja 33: 3049–70. [Google Scholar] [CrossRef]
- Gregoriou, Greg N. 2006. Optimisation of the largest US mutual funds using data envelopment analysis. Journal of Asset Management 6: 445–55. [Google Scholar] [CrossRef]
- Gregoriou, Greg N., and Stephen C. Henry. 2015. Undesirable outputs in commodities trading advisers: A data envelopment analysis approach. Journal of Wealth Management 17: 85–92. [Google Scholar] [CrossRef]
- Henriques, Carla Oliveira, and Maria Elisabete Duarte Neves. 2019. A multiobjective interval portfolio framework for supporting investor’s preferences under different risk assumptions. Journal of the Operational Research Society 70: 1639–61. [Google Scholar] [CrossRef]
- Henriques, Carla Oliveira, Maria Elisabete Neves, Licínio Castelão, and Duc Khuong Nguyen. 2022. Assessing the performance of exchange traded funds in the energy sector: A hybrid DEA multiobjective linear programming approach. Annals of Operations Research 313: 341–66. [Google Scholar] [CrossRef] [PubMed]
- Hill, Joanne M., Dave Nadig, and Matt Hougan. 2015. A Comprehensive Guide to Exchange-Traded Funds (ETFs). Charlottesville: CFA Institute Research Foundation. [Google Scholar] [CrossRef]
- Ippolito, Richard A. 1989. Efficiency with costly information: A study of mutual fund performance, 1965–1984. The Quarterly Journal of Economics 104: 1–23. [Google Scholar] [CrossRef]
- Isakov, Vsevolod. 2019. Performance Appraisal of Exchange-Traded Funds using Clustering and Data Envelopment analysis (Xetra, Germany). Master’s thesis, LUT School of Business and Management, Lappeenranta, Finland. [Google Scholar]
- Jensen, Michael C. 1968. The Performance of Mutual Funds in the Period 1945–1964. The Journal of Finance 23: 389–416. [Google Scholar] [CrossRef]
- Kerstens, Kristiaan, and Ignace Van de Woestyne. 2011. Negative data in DEA: A simple proportional distance function approach. Journal of the Operational Research Society 62: 1413–19. [Google Scholar] [CrossRef]
- Kiymaz, Halil. 2019. Factors influencing SRI fund performance. Journal of Capital Markets Studies 3: 68–81. [Google Scholar] [CrossRef]
- Kostovetsky, Leonard. 2003. Index mutual funds and exchange-traded funds. Journal of Portfolio Management 29: 80–92. [Google Scholar] [CrossRef]
- Lettau, Martin, and Markus Pelger. 2020. Factors that fit the time series and cross-section of stock returns. The Review of Financial Studies 33: 2274–325. [Google Scholar] [CrossRef]
- Lobato, Manuel, Javier Rodríguez, and Herminio Romero. 2021. A volatility-match approach to measure performance: The case of socially responsible exchange-traded funds (ETFs). The Journal of Risk Finance 22: 34–43. [Google Scholar] [CrossRef]
- Murthi, B. P. S., Yoon K. Choi, and Preyas Desai. 1997. Efficiency of mutual funds and portfolio performance measurement: A non-parametric approach. European Journal of Operational Research 98: 408–18. [Google Scholar] [CrossRef]
- Navratil, Robert, Stephen Taylor, and Jan Vecer. 2021. On equity market inefficiency during the COVID-19 pandemic. International Review of Financial Analysis 77: 101820. [Google Scholar] [CrossRef]
- Neves, Maria Elisabete Duarte, Carla Manuela Fernandes, and Pedro Coimbra Martins. 2019. Are ETFs good vehicles for diversification? New evidence for critical investment periods. Borsa Istanbul Review 19: 149–57. [Google Scholar] [CrossRef]
- Osterhoff, Friedrich, and Christoph Kaserer. 2016. Determinants of tracking error in German ETFs–the role of market liquidity. Managerial Finance 42: 417–37. [Google Scholar] [CrossRef]
- Portela, Silva, Emmanuel Thanassoulis, and Gary Simpson. 2004. Negative data in DEA: A directional distance approach applied to bank branches. Journal of the Operational Research Society 55: 1111–21. [Google Scholar] [CrossRef]
- Poterba, James M., and John B. Shoven. 2002. Exchange-traded Funds: A New Investment Option for Taxable Investors. American Economic Review 92: 422–27. [Google Scholar] [CrossRef]
- Prasanna, P. Krishna. 2012. Performance of Exchange-Traded Funds in India. International Journal of Business and Management 7: 122. [Google Scholar] [CrossRef]
- Proença, C., E. Neves, M. Gouveia, and M. Madaleno. 2023. Technological, healthcare and consumer: Influence of COVID-19. Operational Research, unpublished. [Google Scholar]
- Roll, Richard. 1978. Ambiguity when performance is measured by the securities market line. The Journal of Finance 33: 1051–69. [Google Scholar] [CrossRef]
- Sharp, John A., Wang Meng, and Wei Liu. 2007. A modified slacks-based measure model for data envelopment analysis with “natural” negative outputs and inputs. Journal of the Operational Research Society 58: 1672–77. [Google Scholar] [CrossRef]
- Sharpe, William F. 1966. Mutual Fund Performance, Part 2: Supplement on Security Prices. The Journal of Business 39: 119–38. [Google Scholar] [CrossRef]
- Tone, Kaoru. 2001. Slacks-Based measure of efficiency. European Journal of Operational Research 130: 498–509. [Google Scholar] [CrossRef]
- Tone, Kaoru, Tsung-Sheng Chang, and Chen-Hui Wu. 2019. Handling negative data in slacks-based measure data envelopment analysis models. European Journal of Operational Research 282: 926–35. [Google Scholar] [CrossRef]
- Tsolas, Ioannis E. 2019. Utility exchange traded fund performance evaluation. A comparative approach using grey relational analysis and data envelopment analysis Modelling. International Journal of Financial Studies 7: 67. [Google Scholar] [CrossRef]
- Tsolas, Ioannis E. 2022. Performance Evaluation of Utility Exchange-Traded Funds: A Super-Efficiency Approach. Journal of Risk and Financial Management 15: 318. [Google Scholar] [CrossRef]
- Tsolas, Ioannis E., and Vincent Charles. 2015. Green exchange-traded fund performance appraisal using slacks-based DEA models. Operational Research 15: 51–77. [Google Scholar] [CrossRef]
- Zopounidis, Constantin, Michael Doumpos, and Panos M. Pardalos, eds. 2010. Handbook of Financial Engineering. Berlin: Springer Science & Business Media, vol. 18. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).