Exchange Rate Forecasting with Advanced Machine Learning Methods

Abstract

Historically, exchange rate forecasting models have exhibited poor out-of-sample performances and were inferior to the random walk model. Monthly panel data from 1973 to 2014 for ten currency pairs of OECD countries are used to make out-of sample forecasts with artificial neural networks and XGBoost models. Most approaches show significant and substantial predictive power in directional forecasts. Moreover, the evidence suggests that information regarding prediction timing is a key component in the forecasting performance.

1. Introduction

A long-standing conundrum in macroeconomic theory is the inability to predict exchange rate movements with economic fundamentals. Several exchange rate forecasting models have been derived from assumptions that are nowadays an essential part of the economics curriculum. The uncovered interest parity (UIP), for example, is based on the empirically confirmed covered interest parity and the assumption of risk neutrality, both of which are widely accepted (Neely and Sarno 2002). However, while many exchange rate forecasting models are well founded from a theoretical point of view, their empirical applications have exhibited poor forecasting performances. In most cases, a simple random walk (RW) prediction outperforms the well thought through models. Arguably the most prominent exchange rate forecasting models are the aforementioned UIP model, the purchase power parity (PPP) model and the monetary model (MM). They are based on economic theories derived from different assumptions. For decades, little to no significant influence of the fundamentals used in these models on exchange rate movements has been found in the short term, although the theoretical explanations seem reasonable. The fact that no relationship between fundamentals and exchange rate movements could be demonstrated with the help of the aforementioned economic models does not mean that no relationship exists per se. As Amat et al. (2018) point out, a critical constraining factor of these models is their functional form. The forecasting equations consist of simple linear combinations of the fundamentals. This way, potential nonlinearites are neglected. The reason for the strict linear form are the theoretical derivations of the models. The fundamentals could have a significant and substantial effect on the movement of exchange rates if a nonlinear model equation was used. The authors of Amat et al. (2018) use simple machine learning (ML) methods with economic fundamentals to test if this leads to better forecasting results compared to ordinary least squares (OLS) estimates. Although their ridge regression and exponentially weighted average models improve the performance compared to the OLS estimates, they could not always beat the RW prediction.

Building on the research of Amat et al. (2018), I argue that the use of more complex ML models could lead to a better forecasting performance because they are better suited for capturing potential nonlinearities. The question I address with this examination is simple:

Q:

Do fundamentals from the PPP, UIP or MM model have forecasting power with regard to exchange rate movements, regardless of the functional form of the estimation equation?

The flexibility of ANN and XGBoost models should allow one to approximate a function which exploits the information in the economic fundamentals. Thus, if the fundamentals have predictive power, this should be evident by a higher predictive performance relative to the RW benchmark. The research question can be further specified by the following two specific questions:

Q₁:

Can complex ML methods with economic fundaments beat the RW predictions in forecasting exchange rate differentials?

Q₂:

Can complex ML methods with economic fundaments beat the RW predictions in forecasting exchange rate movement directions?

Here, the complex ML methods are XGBoost and ANN models, and economic fundamentals are derived from the PPP, UIP and MM theories. I show that neither ML model is able to convincingly outperform the RW forecast of exchange rate differentials, and when they do, the effect is comparatively small and statistical significance is almost always lacking. In predicting the direction of the exchange rate movements, on the other hand, both ML methods outperform the RW forecasts in almost all cases with varying levels of statistical significance. Moreover, ANNs provide better forecasting results than the XGBoost models. Additionally, the advantage of the ML models over the RW model disappears completely when time dummies are excluded from the features in the training phase. This suggests that the information driving the models’ directional forecast for the exchange rate is not derived from the fundamentals alone, but depends largely on the prediction timing, which is defined by the time dummy variables. This argument is supported by the good performance of a separate ANN model that predicts the direction of exchange rate movement using only time dummies as explanatory variables. However, models trained with fundamental variables still perform slightly better, suggesting that fundamentals may still have predictive power but are dependent on prediction timing.

This paper is structured as follows: In Section 2, I discuss the related literature. Section 3 follows with the description of the methodology, including the classic PPP, UIP and MM models, which the economic fundamentals included in the empirical part of this study stem from as well as the applied ML methods ANN and XGBoost. In Section 4, I describe the dataset. Section 5 continues with the description of the results, followed by a brief discussion of the implications. Finally, the conclusions are drawn.

2. Related Literature

Classic economic exchange rate forecasting models are based on the PPP, UIP and MM theories and have been the subject of numerous studies. The most famous of these studies was conducted by Meese and Rogoff (1983), who tested various specifications of the monetary model. They included both sticky as well as flexible-price approaches in the form of the Drenkel–Bilson, the Dornbusch–Frenkel and the Hopper–Morton monetary models (Meese and Rogoff 1983). They included different country pairs and varied the considered forecasting horizon from one to twelve months. Despite the different approaches, their models failed to outperform the RW benchmark in forecasting exchange rates. The authors of Vitek (2005) repeated this approach with a larger dataset at a later time and confirmed these findings. In recent years, the literature has found conflicting evidence on the predictability of exchange rates using MM fundamentals. In a study by Mark (1995), a model based on MM fundamentals was able to beat the RW benchmark in forecasting exchange rate differentials over a long time horizon. On the other hand, Engel et al. (2017) found that their monetary model using Taylor-rule fundamentals cannot consistently beat the RW benchmark in the short run in out-of-sample (OOS) forecasts, even though the coefficients of fundamentals in their OLS regression are statistically significant. Regarding the significance of UIP fundamentals in exchange rate forecasting, they conducted an examination of the effect of these fundamentals including inflation. They found that the coefficients of inflation were in many cases highly significant when predicting exchange rate differentials. However, the interest rate differential, which is supposed to be the explanatory factor for exchange rates changes according to the classical UIP theory, is not statistical significance in most cases (Engel et al. 2017). Regarding the PPP model, Edison and Klovland (1987) examined the short-term forecastability of exchange rate differentials. They used a time series from 1874 to 1971 for the country pair Norway and United Kingdom. They found no evidence for an effect of PPP fundamentals on the exchange rate differentials (Edison and Klovland 1987). In Dal Bianco et al. (2012), the authors find a good in-sample fit of their fundamental-based econometric models with an $R^2$ of $0.8$ using short-term weekly and monthly data. However, in OOS comparisons, their model is inferior to the RW model. In addition to using various sets of fundamentals, researchers also use various machine learning models to improve their predictions. The authors of Plakandaras et al. (2015) apply a wide range of machine learning models and model combinations to forecast exchange rate movements, ranging from ARIMA models to support vector machines and ANNs. They outperform the RW in OOS exchange rate prediction, taking into account a variety of variables, from commodity and equity prices to interest rates and GDP. However, they do not focus on a specific economic theory, as their objective is to achieve the best OOS performance possible (Plakandaras et al. 2015). In Amat et al. (2018), the authors use the exponentially weighted average strategy (EWA) with discount factors and ridge regression to forecast the exchange rate differentials as well as the direction of exchange rate movements. They incorporate fundamentals from the classic economic PPP, MM and UIP models. They compare the OOS forecasts of their models with OLS and RW benchmark models. They tested their results for statistical significance using the Diebold–Mariano (DM) statistics and p-values. In some cases, they narrowly beat the RW model; often the difference is less than one percent of the RMSE for different country pairs. Their directional forecasts show that the EWA model performs best, but the OLS regression can also correctly predict the direction of exchange rate movement over 50 percent of the time for most currency pairs (Amat et al. 2018).

The authors of Bajari et al. (2015) compare common machine learning models with classical econometric models for demand forecasting. They use linear and logistic regressions as econometric models, which they compare with random forests and support vector machines, as well as other machine learning models. Using Monte Carlo simulations, they show that model combination with linear regression improves OOS predictive power. Using real demand forecasting data, they show that ML models consistently provide better OOS predictions than their econometric counterparts, demonstrating why machine learning models should be considered in traditionally econometric settings.

A more complex machine learning model for economic forecasting is used by Qureshi et al. (2020). They use a two-stage XGBoost model for their Canadian GDP forecasts. In the first stage, they select variables based on the significance of their XGBoost model and in the second stage, they make predictions using a separate XGBoost model trained on the selected variables. Their results show that XGBoost models can lead to good predictive performance for monthly growth rate forecasts, as shown by the OOS forecasting performance (Qureshi et al. 2020).

3. Methodology

The fundamentals used in this research come from the UIP, PPP, and MM theories. In addition, I include the “all fundamentals” (AF) approach, which is the combined set of fundamentals from all three models. The descriptions of the models are by no means exhaustive and are instead intended to give an idea of where the linear form of the forecasting equations of classical models comes from and how the fundamentals are selected.

3.1. Uncovered Interest Rate Parity (UIP) Model

The UIP exchange rate forecasting model is based on the UIP condition. The UIP is derived from the covered interest rate parity (CIP) and the assumption of risk neutrality. The CIP states that investors cannot exploit differences in interest rates of two countries by using forward contracts and is expressed by Equation (1) below.

$$\frac{F_t}{S_t}=\frac{1+r_d}{1+r_f}$$

(1)

where $F_t$ is the price of a forward contract on the exchange rage $S_{t+1}$ at time t + 1. $S_t$ is the exchange rate at time t, denoted in units of the domestic country’s currency. $r_d$ and $r_f$ are the interest rates of the domestic and the foreign countries, respectively, on comparable assets with equal maturity. Transforming Equation (2) by applying the natural logarithm and assuming small values for $r_d$ and $r_f$, yields the following equation (Equation (2)):

$$f_t-s_t=r_{d,t}-r_{f,t}$$

(2)

where the forward rate is defined by $f_t=log\left(F_t\right)$ and the spot rate is defined by $s_t=log\left(S_t\right)$.

The forward rate $f_t$ can be represented as a composition of the investors, expectation of the spot rate and the risk associated with holding a domestic asset relative to the risk associated with holding a foreign asset, expressed by the risk premium ${\rho }_t$. Hence, the forward rate $f_t$ can be described by Equation (3):

$$f_t=s_t^e+{\rho }_t$$

(3)

Combining Equations (2) and (3) yields Equation (4), which relates the change in the expected spot rate $\Delta s_t^e$ to the difference in interest rates in t ($r_{d,t}-r_{f,t}$) and the risk premium ${\rho }_t$:

$$\Delta s_t^e=(r_{d,t}-r_{f,t})-{\rho }_t$$

(4)

When risk neutrality of the investor is assumed, the risk premium is neutralized (${\rho }_t=0$), leading to the UIP, described by Equation (5):

$$\Delta s_t^e=r_{d,t}-r_{f,t}$$

(5)

Therefore, the difference in interest rates between the associated countries is assumed to explain the change in the exchange rate of their currencies. Hence, the explanatory variables considered for the later models are the current period interest rates of both countries for comparable assets with the same maturity (Meredith and Chinn 1998).

3.2. Purchasing Power Parity (PPP) Model

An alternative way of explaining the exchange rate movement lies in the PPP theory. According to the PPP theory, goods are internationally tradable substitutes. Neglecting complex trading behavior, e.g., due to differences in preferences and tastes, PPP theory assumes the homogeneity of goods and allows them to be easily tradable between countries. The purchasing power parity is defined by the following equation (Equation (6)):

$$p_{d,t}=p_{f,t}+s_t$$

(6)

where $p_{d,t}$ and $p_{f,t}$ are the natural logarithms of the price levels in the domestic and the foreign country, respectively. Due to the no-arbitrage condition on the goods markets assumed in PPP theory, the expected exchange rate in $t+1$ is given by Equation (7):

$$E\left[s_{t+1}\right]=p_{d,t}-p_{f,t}$$

(7)

Therefore, the only variables to consider when forecasting exchange rate movements are the price levels of the respective countries, often reported as the consumer price index (CPI) (Juselius 1995).

3.3. Monetary Model (MM)

Regarding the MM model, there are several variants that distinguish, for example, between rigid and flexible prices, such as the Dornbusch–Frankel model (rigid prices) and the Frenkel–Bilson model (flexible prices) (Meese and Rogoff 1983).This examination follows the forecasting approach of Amat et al. (2018), which is based on the Frenkel–Bilson flexible price model. They model the relationship between income and money supply as the following linear equation, Equation (8):

$$s_t={\alpha }_0+{\alpha }_1(m_{d,t}-m_{f,t})-{\alpha }_2(y_{d,t}-y_{f,t})$$

(8)

where $m_{d,t}$ and $m_{f,t}$ denote the log levels of the money supply of the domestic and foreign countries, respectively, while $y_{d,t}$ and $y_{f,t}$ represent their log incomes. To estimate exchange rate differences, the difference between two consecutive periods leads to Equation (9):

$$\Delta s_t={\beta }_1\Delta m_{d,t}-{\beta }_2\Delta m_{f,t}-{\beta }_3\Delta y_{d,t}+{\beta }_4\Delta y_{f,t}$$

(9)

where $\Delta$ indicates that the connected variable is the time differential between the specified period and the previous period of the associated variable (i.e., $\Delta x=x_t-x_{t-1}$) (Amat et al. 2018).

3.4. Artificial Neural Networks (ANN)

All of the classical macroeconomic forecasting models described so far assume a linear relationship between fundamentals and exchange rate differentials or directions of movement. The reason for assuming linearity in these models stems from the theoretical derivations of the models. However, the restriction to a linear form may be a hindrance if the actual functional form is nonlinear. Multilayer perceptrons are known to be universal approximators. According to the universal approximation theorem, a multilayer perceptron model can approximate any continuous function between two Euclidean spaces. The reason for the flexibility of ANNs is the high complexity of the model due to the high number of parameters as well as the use of activation functions, which are responsible for the nonlinear characteristic of the approximation (Hornik 1991). A detailed and extensive explanation of the functionality of neural networks can be found in Goodfellow et al. (2016). In my study, I use a multilayer perceptron with two hidden layers. The first hidden layer consists of 1000 artificial neurons, the second of 500. The model equation of this network is shown in Equation (10) below. Let ${\mathit{x}}_{\mathit{t}}$ denote the vector of inputs to the network at time t. The vector consists of the values of the p economic fundamentals at time t. For the regression models, the prediction $\widehat{\Delta y_{t+1}}$ (where $\Delta y_{t+1}=y_{t+1}-y_t$) of the model at time t is calculated as follows:

$$\widehat{\Delta y_{t+1}}={\mathit{w}}_{\mathbf{3}}^{\mathbf{\prime }}{\varphi }_{hidde{n}_2}({\mathit{w}}_{\mathbf{2}}^{\mathbf{\prime }}{\varphi }_{hidde{n}_1}({\mathit{w}}_{\mathbf{1}}^{\mathbf{\prime }}{\mathit{x}}_{\mathit{t}}+b_1)+b_2)+b_3$$

(10)

while for the classification models, the predicted probability $\widehat{P(z_{t+1}=1|{\mathit{x}}_{\mathit{t}})}$ of the model at time t is calculated as follows:

$$\widehat{P(z_{t+1}=1|{\mathit{x}}_{\mathit{t}})}={\varphi }_{output}({\mathit{w}}_{\mathbf{3}}^{\mathbf{\prime }}{\varphi }_{hidde{n}_2}({\mathit{w}}_{\mathbf{2}}^{\mathbf{\prime }}{\varphi }_{hidde{n}_1}({\mathit{w}}_{\mathbf{1}}^{\mathbf{\prime }}{\mathit{x}}_{\mathit{t}}+b_1)+b_2)+b_3)$$

(11)

where ${\varphi }_{hidde{n}_1}$,${\varphi }_{hidde{n}_2}$ and ${\varphi }_{output}$ are the activation functions of the first, the second hidden layers, as well as the output layer, respectively. The prediction $\widehat{\Delta y_{t+1}}$ is the predicted exchange rate differential. The prediction $\widehat{P(z_{t+1}=1|{\mathit{x}}_{\mathit{t}})}$ is the predicted probability of the exchange rate differential to be positive. $z_{t+1}$ is a binary response variable, that is defined as follows

$$z_{t+1}=\left\{\begin{array}{cc}1\hfill & \mathrm{if}\Delta y_{t+1}>o\hfill \\ 0\hfill & \mathrm{else}\hfill \end{array}\right.\forall y\in \{y_1,\dots ,y_n\}$$

(12)

${\mathit{w}}_{\mathbf{1}}$, ${\mathit{w}}_{\mathbf{2}}$ and ${\mathit{w}}_{\mathbf{1}}$ are differently sized weight matrices of the first and the second hidden layer, as well as the output layer. $b_1$, $b_2$ and $b_3$ denote scalar bias terms, that are added in the first and second hidden layers, as well as the output layer. For the activation functions ${\varphi }_{hidde{n}_1}$ and ${\varphi }_{hidde{n}_2}$ I chose the relu function, as stated in Equation (14) below.

$$relu\left(x\right)=max\{0,x\}$$

(13)

For the binary classification MLP models, which predict the direction of change of exchange rate movements, a sigmoid activation function, presented in Equation (14), is used for as the activation function of the ouput neuron ${\varphi }_{output}$. For the later regressions, no activation function ${\varphi }_{output}$ is applied.

$$sigmoid\left(x\right)=\frac{1}{1-e^{-x}}$$

(14)

The MLP model is fit to a training dataset, consisting of 75 % of the considered data. As the objective function for regression, I chose the sum of squared residuals (SSR) loss function.

$$Los{s}_{SSR}\left(x\right)=\sum _{t=1}^T(\widehat{\Delta y_t}-\Delta y_t{)}^2$$

(15)

For classification, I implemented the binary cross-entropy (BCE) function as the loss function.

$$Los{s}_{BCE}\left(x\right)=-\frac{1}{n}\sum _{t=1}^T{z}_t·log(\widehat{P(z_{t+1}=1|{\mathit{x}}_{\mathit{t}})})+(1-z_t)·log(1-\widehat{P(z_{t+1}=1|{\mathit{x}}_{\mathit{t}}\left)\right)}$$

(16)

The loss function is minimized using the backpropagation algorithm. The backpropagation algorithm calculates the gradients of the loss function in respect to the weights in the network $\frac{\partial loss}{\partial {\mathit{w}}_{\mathit{h}}}$ for each layer $h\in \{1,2,3\}$ and update the weights. Backpropagation uses the chain rule to compute the gradients and the gradient descent algorithm to apply the necessary weight changes to the network. Gradient descent decreases the gradients according to the learning rate before subtracting them from the weight matrices in the networks, as shown in Equation (17) below (Goodfellow et al. 2016).

$${\mathit{w}}_{\mathit{h},\mathit{t}+\mathbf{1}}={\mathit{w}}_{\mathit{h},\mathit{t}}-\alpha \frac{\partial loss}{\partial {\mathit{w}}_{\mathit{h},\mathit{t}}}$$

(17)

Here, $\alpha$ denotes the learning rate. I chose the value for $\alpha$, which produces the greatest reduction in loss. Further, I did not use the exact version of the gradient descent algorithm described above, but the more advanced optimization algorithm Adam, which extends the gradient descent algorithms using momentum terms, as described by Kingma and Ba (2015). I use mini-batch training, which updates the weights after every mini-batch (Goodfellow et al. 2016). Once the training set is iterated through, an epoch is completed. I set the maximum epoch size to 1000. This number of epochs was, however, never reached, as I implemented Earlystopping as a callback. Earlystopping interrupts the training process, whenever a predefined improvement criterion is no longer fullfilled. In my examition, Earlystopping interrupted the training of a model, whenever the validation error did not improve by a margin of 0.0001 over the last 100 epochs. Setting this margin is a delicate process, as setting it too high can lead to underfitting, i.e., the model does not fit the training data closely enough and therefore loses potential predictive power. On the other hand, setting it to low might result in unnecessary long traninig time without improvement (Yao et al. 2007). To further prevent overfitting, I implement the regularization method dropout. Dropout prevents co-adaptation, the over-adjustment of the model to the idiosyncrasies of the training dataset, by eliminating neurons during the training process (Srivastava et al. 2014). I apply dropout to both hidden layers with a respective probability of p = 0.5 for each node to be left out at each pass during the training.

3.5. EXtreme Gradient Boosting (XGboost)

XGBoost stands for eXtreme Gradient Boosting and is a package developed by Chen and Guestrin (2016) for easy application and tuning of gradient boosting with regularization methods on linear models and CART models (classification and regression trees). For my empirical studies, I use classification and regression trees as weak learners for the XGBoost models. XGBoost, as well as other gradient boosting methods, have provided state-of-the-art results in a variety of domains for both classification and regression problems. In general, gradient boosting is an ensemble method that combines the weighted predictions of multiple weak learners, in this case tree models, into a superior prediction model. In the training process, the XGBoost model is built by sequentially fitting weak learners to bootstrap samples. However, instead of fitting them to the target variable, the goal is to reduce the pseudo-residuals of the previously fitted weak learners model. Therefore, the weak learners are sequentially fitted to the residuals of the previously fitted weak learners. By adding up the predictions of the weak learners, the prediction error is minimized. Once, the error can not be effectively reduced by additional weak learners, the final additive model takes the form of Equation (18) for regression and Equation (19) for classification (Chen and Guestrin 2016).

$$\widehat{\Delta y_{t+1}}=\sum _{k=1}^K{f}_k^r\left({\mathit{x}}_{\mathit{t}}\right)$$

(18)

$$\widehat{P(z_{t+1}=1|{\mathit{x}}_{\mathit{t}})}=\sum _{k=1}^K{f}_k^c\left({\mathit{x}}_{\mathit{t}}\right)$$

(19)

where $f_k^r$ and $f_k^c$ denote regression and classification tree models, respectively, and K is the number of weak learners contained in the final model. Like the MLP model, the additive model is also fitted by minimizing a predefined loss function. Unlike before, the loss function includes a penalty term for regularization, as shown by Equation (20) for regression and (21) for classification.

$$Los{s}_r(\widehat{\Delta y_{t+1}},\Delta y_{t+1})=\sum _{t=1}^T\kappa (\widehat{\Delta y_{t+1}},\Delta y_{t+1})+\sum _{k=1}^K\Omega \left(f_k\right)$$

(20)

$$Los{s}_c(\widehat{P(z_{t+1}=1|{\mathit{x}}_{\mathit{t}})},z_{t+1})=\sum _{t=1}^T\kappa (\widehat{P(z_{t+1}=1|{\mathit{x}}_{\mathit{t}})},z_{t+1})+\sum _{k=1}^K\Omega \left(f_k\right)$$

(21)

For the loss functions the penalty term is specified in Equation (22).

$$\Omega \left(f_k\right)=\gamma M+\frac{1}{2}\lambda {\parallel w\parallel }^2$$

(22)

Here, M denotes the number of leaves in a CART weak learner and $\parallel w{\parallel }^2$ denotes the $L^2$-norm of the weights w attached with each leave in a tree. Since M and w define the complexity of a tree, the term $\Omega \left(f_k\right)$ penalizes both the complexity of the tree and unnecessarily large weights in the loss function. A detailed explanation can be found in Chen and Guestrin (2016).

4. Data

The dataset consists of fundamentals and exchange rates from 1973–2014 for 10 different country pairs. The fundamentals for this examination stem from the aforementioned UIP, PPP and MM theories as well as an AF approach. Exchange rates are expressed relative to the USD dollar and recorded at the end of the month. The dataset is provided by Amat et al. (2018) and is available at their website, which I kindly refer to for more information about the dataset. The data were originally sourced from Datastream, the OECD, and the Federal Reserve’s website (Amat et al. 2020).

When training complex machine learning models, it is necessary to provide the algorithm with many observations in order to achieve an acceptable level of adaptation without overfitting. For this reason, I chose to train the algorithms using the combined data of all currencies, but to make the OOS forecasts for each currency pair separately. All variables are being scaled with maximum absolute scaling. To distinguish between countries, I encoded the IDs of the currency pairs with dummy variables. Also included are time dummies for months and years.

For every country pair, the dataset is split into a training set (in-sample) containing the first 67% of the available periods and a validation set (out-of-sample) consisting of the remaining 33% of the periods.

With this approach, I pursue the objective set by Amat et al. (2018). The goal is not to provide the most accurate forecasts of the exchange rate differentials or movement directions. Rather, the aim is to examine whether fundamentals from the aforementioned economic models have predictive power regarding the exchange rate differentials or movement directions.

5. Results

The hyperparameters for ANN as well as XBoost models are chosen sequentially according to the associated reduction in OOS loss. The results of the examinations are recorded in Table 1, Table 2, Table 3, Table 4 and Table 5. Each table contains the metrics obtained from the OOS predictions, i.e., Diebold–Mariano (DM) statistics, DM p-values and Theil ratios for the regressions as well as DM statistics, DM p-values, and error rates for the classification, for each of the 10 currency pairs, once with and once without time dummies.

Table 1. One-month-ahead forecasting of exchange rate differentials with fundamentals using XGBoost.

XGBoost—Regression—With Time Dummies
	All fundamentals			MM fundamentals			PPP fundamentals			UIP fundamentals
Currency pair	DM	p-value	Theil Ratio	DM	p-value	Theil Ratio	DM	p-value	Theil Ratio	DM	p-value	Theil Ratio
PTE/USD	2.8188	0.005 ***	1.037	−0.2974	0.7663	0.9966	−1.4645	0.1436	0.9888	−0.0099	0.9921	0.9999
AUD/USD	0.3755	0.7074	1.0027	0.86	0.39	1.0066	−0.4406	0.6596	0.997	0.5876	0.5569	1.0039
CAN/USD	0.3755	0.7074	1.0027	0.86	0.39	1.0066	−0.4406	0.6596	0.997	0.5876	0.5569	1.0039
CHF/USD	0.3755	0.7074	1.0027	0.86	0.39	1.0066	−0.4406	0.6596	0.997	0.5876	0.5569	1.0039
DEM/USD	2.0298	0.0427 **	1.0144	0.3154	0.7526	1.0025	1.7917	0.0735 *	1.0114	0.7116	0.4769	1.0045
DNK/USD	0.3176	0.7509	1.0024	0.3046	0.7607	1.0025	0.6475	0.5175	1.0036	−0.3226	0.7471	0.9981
FRF/USD	5.4862	0.0000 ***	1.0465	2.7878	0.0054 *	1.0292	1.9342	0.0534 *	1.0139	2.5725	0.0103 ***	1.0247
ITL/USD	2.0298	0.0427 **	1.0144	0.3154	0.7526	1.0025	1.7917	0.0735 *	1.0114	0.7116	0.4769	1.0045
JPY/USD	0.3755	0.7074	1.0027	0.86	0.39	1.0066	−0.4406	0.6596	0.997	0.5876	0.5569	1.0039
SEK/USD	0.3755	0.7074	1.0027	0.86	0.39	1.0066	−0.4406	0.6596	0.997	0.5876	0.5569	1.0039
XGBoost—Regression—No Time Dummies
	All fundamentals			MM fundamentals			PPP fundamentals			UIP fundamentals
Currency pair	DM	p-value	Theil Ratio	DM	p-value	Theil Ratio	DM	p-value	Theil Ratio	DM	p-value	Theil Ratio
PTE/USD	2.8006	0.0053 **	1.0503	1.7965	0.0729 *	1.0194	1.7516	0.0804 *	1.0218	1.3372	0.1817	1.0216
AUD/USD	0.5369	0.5914	1.005	2.0364	0.042 **	1.0162	2.231	0.0259 **	1.018	1.5522	0.1209	1.0092
CAN/USD	0.5369	0.5914	1.005	2.0364	0.042 **	1.0162	2.231	0.0259 **	1.018	1.5522	0.1209	1.0092
CHF/USD	0.5369	0.5914	1.005	2.0364	0.042 **	1.0162	2.231	0.0259 **	1.018	1.5522	0.1209	1.0092
DEM/USD	2.7782	0.0056 *	1.027	1.7247	0.0849 **	1.013	2.3919	0.017 **	1.0234	0.8883	0.3746	1.0059
DNK/USD	1.6858	0.0922 *	1.0198	3.3895	0.0007 ***	1.0262	3.2347	0.0013 ***	1.0233	1.9187	0.0553	1.0131
FRF/USD	2.7165	0.0067 *	1.0342	2.0077	0.045 **	1.0209	3.4899	0.0005 ***	1.0451	0.5599	0.5757	1.0053
ITL/USD	2.7782	0.0056 *	1.027	1.7247	0.0849 *	1.013	2.3919	0.017 **	1.0234	0.8883	0.3746	1.0059
JPY/USD	0.5369	0.5914	1.005	2.0364	0.042 **	1.0162	2.231	0.0259 **	1.018	1.5522	0.1209	1.0092
SEK/USD	0.5369	0.5914	1.005	2.0364	0.042 **	1.0162	2.231	0.0259 **	1.018	1.5522	0.1209	1.0092

For every currency pair, a separate XGBoost model is estimated to regress exchange rate differentials on every set of fundamentals from the PPP, UIP and the MM theories as well as the combined AF approach. Out-of-sample Diebold–Mariano statistics and p-values are calculated for differences in RMSE between the estimated models and the random walk benchmark. Statistical significance is marked by *, ** or *** for the 10, 5, or 1 percentage level, respectively. The data range from March 1973 to December 2014. A Theil ratio above one indicates that the OOS RMSE of the XGBoost model is smaller than the one of the random walk.

Table 2. One-month-ahead forecasting of exchange rate differentials with fundamentals using ANN.

ANN—Regression—With Time Dummies
	All fundamentals			MM fundamentals			PPP fundamentals			UIP fundamentals
Currency pair	DM	p-value	Theil Ratio	DM	p-value	Theil Ratio	DM	p-value	Theil Ratio	DM	p-value	Theil Ratio
PTE/USD	2.0587	0.04 **	1.0472	2.3238	0.0205 **	1.0663	2.3042	0.0216 **	1.0507	1.905	0.0573 *	1.0378
AUD/USD	−0.4744	0.6353	0.995	0.3059	0.7598	1.0023	−1.2247	0.221	0.9966	−0.3437	0.7312	0.9984
CAN/USD	−1.5079	0.1319	0.9887	−0.8013	0.4231	0.998	−1.1149	0.2652	0.9931	0.2258	0.8214	1.0033
CHF/USD	−0.6049	0.5454	1.0074	−0.3143	0.7533	1.0031	−0.6113	0.5411	0.995	−0.5662	0.5714	0.9974
DEM/USD	4.544	0.0000 ***	1.0469	4.1126	0.0000 ***	1.0447	5.3071	0.0000 ***	1.0435	3.783	0.0002 ***	1.027
DNK/USD	−1.3697	0.1711	0.9945	−0.1012	0.9194	1.0107	−0.2069	0.8361	1.0101	0.5283	0.5974	1.0122
FRF/USD	5.895	0.0000 ***	1.1146	6.4874	0.0000 ***	1.0893	4.816	0.0000 ***	1.0641	5.0974	0.0000 ***	1.0781
ITL/USD	4.9056	0.0000 ***	1.0452	4.6223	0.0000 ***	1.0659	5.0842	0.0000 ***	1.0547	4.112	0.0000 ***	1.0385
JPY/USD	1.4623	0.144	1.0208	−1.3256	0.1853	0.9942	−1.4138	0.1577	0.9963	−0.3669	0.7138	1.0038
SEK/USD	−1.1639	0.2448	0.9982	−0.9254	0.355	0.9967	0.0905	0.9279	1.0082	0.1046	0.9167	1.0017
ANN—Regression—No Time Dummies
	All fundamentals			MM fundamentals			PPP fundamentals			UIP fundamentals
Currency pair	DM	p-value	Theil Ratio	DM	p-value	Theil Ratio	DM	p-value	Theil Ratio	DM	p-value	Theil Ratio
PTE/USD	2.8867	0.004 ***	1.0027	0.2556	0.7983	0.9958	0.7651	0.4445	0.9969	−0.2006	0.8411	0.9947
AUD/USD	1.529	0.1266	1.0026	1.3829	0.167	0.9988	1.0547	0.2918	0.9976	1.1906	0.2341	0.9984
CAN/USD	0.1696	0.8654	0.9989	1.5529	0.1208	0.9994	2.0126	0.0444 **	1.0009	2.6056	0.0093 ***	1.0043
CHF/USD	1.7308	0.0838	1.002	2.3972	0.0167 **	1.0029	2.6225	0.0089 ***	1.0026	2.484	0.0132 **	1.0021
DEM/USD	−1.434	0.1519	1.0001	−2.4894	0.013 **	0.995	−1.1249	0.2609	1.0028	−1.4956	0.1351	0.9967
DNK/USD	0.0051	0.9959	0.9977	0.498	0.6186	0.9972	2.7943	0.0053 ***	1.0046	2.1206	0.0342 **	1.0005
FRF/USD	−1.3868	0.1659	0.9982	−1.3869	0.1659	0.9957	−1.1267	0.2602	0.9985	−1.5057	0.1325	0.9978
ITL/USD	−1.4885	0.137	0.9972	−1.7542	0.0797	0.9959	−1.2554	0.2096	0.9977	−1.7742	0.0763 *	0.9977
JPY/USD	1.4867	0.1374	1.001	1.8733	0.0613	1.0002	1.3946	0.1634	0.9988	2.7358	0.0063 ***	1.0027
SEK/USD	2.2396	0.0253 **	1.0039	3.186	0.0015 **	1.0079	1.8933	0.0586 *	0.9995	1.7569	0.0792 *	1.0001

For every currency pair, a separate MLP model is estimated to regress exchange rate differentials on every set of fundamentals from the PPP, UIP and the MM theories as well as the combined AF approach. Out-of-sample Diebold–Mariano statistics (DM) and p-values are calculated for differences in RMSE between the estimated models and the random walk benchmark. Statistical significance is marked by *, ** or *** for the 10, 5, or 1 percentage level, respectively. The data range from March 1973 to December 2014. A Theil ratio above one indicates that the OOS RMSE of the XGBoost model is smaller than the one of the random walk.

Table 3. One-month-ahead forecasting of exchange rate direction with fundamentals using XGBoost.

XGBoost—Classification—With Time Dummies
	All fundamentals			MM fundamentals			PPP fundamentals			UIP fundamentals
Currency pair	DM	p-value	CE	DM	p-value	CE	DM	p-value	CE	DM	p-value	CE
PTE/USD	−2.4682	0.0139 **	0.4497	−1.5584	0.1197	0.4681	−1.5584	0.1197	0.4681	−1.1472	0.2517	0.4765
AUD/USD	−0.6406	0.5219	0.4897	−1.2821	0.2001	0.4795	−1.2821	0.2001	0.4795	−0.2562	0.7978	0.4959
CAN/USD	−0.6406	0.5219	0.4897	−1.2821	0.2001	0.4795	−1.2821	0.2001	0.4795	−0.2562	0.7978	0.4959
CHF/USD	−0.6406	0.5219	0.4897	−1.2821	0.2001	0.4795	−1.2821	0.2001	0.4795	−0.2562	0.7978	0.4959
DEM/USD	−1.2293	0.2192	0.4801	−1.0998	0.2717	0.4822	−1.4887	0.1369	0.4759	−1.0998	0.2717	0.4822
DNK/USD	−1.2657	0.206	0.4789	−0.9322	0.3515	0.4845	−1.3324	0.1831	0.4778	−0.9989	0.3181	0.4834
FRF/USD	−0.6915	0.4894	0.488	−0.6223	0.5339	0.4892	−0.8299	0.4068	0.4856	−1.1762	0.2399	0.4797
ITL/USD	−1.2293	0.2192	0.4801	−1.0998	0.2717	0.4822	−1.4887	0.1369	0.4759	−1.0998	0.2717	0.4822
JPY/USD	−0.6406	0.5219	0.4897	−1.2821	0.2001	0.4795	−1.2821	0.2001	0.4795	−0.2562	0.7978	0.4959
SEK/USD	−0.6406	0.5219	0.4897	−1.2821	0.2001	0.4795	−1.2821	0.2001	0.4795	−0.2562	0.7978	0.4959
XGBoost—Classification- No Time Dummies
	All fundamentals			MM fundamentals			PPP fundamentals			UIP fundamentals
Currency pair	DM	p-value	CE	DM	p-value	CE	DM	p-value	CE	DM	p-value	CE
PTE/USD	−0.0819	0.9348	0.4983	−3.981	0.0001 ***	0.4195	−3.981	0.0001 ***	0.4195	−0.737	0.4614	0.4849
AUD/USD	−0.2562	0.7978	0.4959	0.1922	0.8477	0.5031	−0.3203	0.7488	0.4949	−1.4106	0.1587	0.4774
CAN/USD	−0.2562	0.7978	0.4959	0.1922	0.8477	0.5031	−0.3203	0.7488	0.4949	−1.4106	0.1587	0.4774
CHF/USD	−0.2562	0.7978	0.4959	0.1922	0.8477	0.5031	−0.3203	0.7488	0.4949	−1.4106	0.1587	0.4774
DEM/USD	−1.4887	0.1369	0.4759	−1.4238	0.1548	0.477	−1.4238	0.1548	0.477	−0.3233	0.7466	0.4948
DNK/USD	−0.5991	0.5492	0.49	0.1331	0.8941	0.5022	−1.0656	0.2869	0.4823	−0.7323	0.4642	0.4878
FRF/USD	−1.1762	0.2399	0.4797	−1.94	0.0527 *	0.4665	−1.94	0.0527 *	0.4665	0.6915	0.4894	0.512
ITL/USD	−1.4887	0.1369	0.4759	−1.4238	0.1548	0.477	−1.4238	0.1548	0.477	−0.3233	0.7466	0.4948
JPY/USD	−0.2562	0.7978	0.4959	0.1922	0.8477	0.5031	−0.3203	0.7488	0.4949	−1.4106	0.1587	0.4774
SEK/USD	−0.2562	0.7978	0.4959	0.1922	0.8477	0.5031	−0.3203	0.7488	0.4949	−1.4106	0.1587	0.4774

For every currency pair, a separate XGBoost model is estimated to forecast exchange rate movement direction for every set of fundamentals from the PPP, UIP and the MM theories as well as the combined AF approach. Out-of-sample Diebold–Mariano statistics and p-values are calculated for differences in classification error rate (CE) between the estimated models and the random walk benchmark. Statistical significance is marked by *, ** or *** for the 10, 5, or 1 percentage level, respectively. The data range from March 1973 to December 2014. A CE below 0.5 indicates that the estimated model outperforms the random walk benchmark.

Table 4. One-month-ahead forecasting of exchange rate direction with fundamentals using ANN.

ANN—Classification—With Time Dummies
	All fundamentals			MM fundamentals			PPP fundamentals			UIP fundamentals
Currency pair	DM	p-value	CE	DM	p-value	CE	DM	p-value	CE	DM	p-value	CE
PTE/USD	−1.8057	0.0715 *	0.4631	−0.819	0.4131	0.4832	−1.3116	0.1902	0.4732	−2.7179	0.0068 ***	0.4446
AUD/USD	−3.0245	0.0026 ***	0.4517	−3.0895	0.0021 ***	0.4507	−2.8298	0.0048 ***	0.4548	−3.1545	0.0017 ***	0.4497
CAN/USD	−4.5968	0.0000 ***	0.4271	−4.4646	0.0000 ***	0.4292	−3.3498	0.0008 ***	0.4466	−3.2847	0.0011 ***	0.4476
CHF/USD	−4.0694	0.0001 ***	0.4353	−3.9381	0.0001 ***	0.4374	−2.0541	0.0402 **	0.4671	−3.1545	0.0017 ***	0.4497
DEM/USD	0.1293	0.8971	0.5021	−1.1645	0.2445	0.4812	−1.1645	0.2445	0.4812	−0.3879	0.6982	0.4937
DNK/USD	−3.6881	0.0002 ***	0.439	−3.8243	0.0001 ***	0.4368	−2.5381	0.0113 **	0.4579	−3.2129	0.0014 ***	0.4468
FRF/USD	−1.1069	0.2687	0.4809	0.6223	0.5339	0.5108	0.4148	0.6784	0.5072	−0.2765	0.7822	0.4952
ITL/USD	0.0647	0.9485	0.501	0.194	0.8463	0.5031	0.0647	0.9485	0.501	−1.2293	0.2192	0.4801
JPY/USD	−4.5306	0.0000 ***	0.4281	−3.2196	0.0013 ***	0.4487	−3.9381	0.0001 ***	0.4374	−4.1351	0.0000 ***	0.4343
SEK/USD	−1.7964	0.0727 *	0.4713	−3.0895	0.0021 ***	0.4507	−3.2196	0.0013 ***	0.4487	−2.7002	0.007 ***	0.4569
ANN—Classification—No Time Dummies
	All fundamentals			MM fundamentals			PPP fundamentals			UIP fundamentals
Currency pair	DM	p-value	CE	DM	p-value	CE	DM	p-value	CE	DM	p-value	CE
PTE/USD	0.6551	0.5127	0.5134	0.1637	0.87	0.5034	0.0819	0.9348	0.5017	0.5731	0.5668	0.5117
AUD/USD	1.9896	0.0469 **	0.5318	1.9896	0.0469 **	0.5318	1.3463	0.1785	0.5216	2.1831	0.0293 **	0.5349
CAN/USD	1.6677	0.0957 *	0.5267	1.732	0.0836 *	0.5277	1.732	0.0836 *	0.5277	2.3122	0.021 **	0.537
CHF/USD	1.732	0.0836 *	0.5277	1.6034	0.1092	0.5257	2.3122	0.021 **	0.537	2.3122	0.021 **	0.537
DEM/USD	0.0000 ***	1.0	0.50	−0.6466	0.518	0.4895	−0.6466	0.518	0.4895	−0.0647	0.9485	0.499
DNK/USD	1.5996	0.11	0.5266	1.7333	0.0834 *	0.5288	2.4037	0.0164 **	0.5399	2.875	0.0041 ***	0.5477
FRF/USD	−0.3457	0.7297	0.494	−1.5924	0.1117	0.4725	−0.1383	0.8901	0.4976	−0.2765	0.7822	0.4952
ITL/USD	−0.0647	0.9485	0.499	−1.6834	0.0926 *	0.4728	−0.1293	0.8971	0.4979	−0.0647	0.9485	0.499
JPY/USD	1.732	0.0836 *	0.5277	1.8608	0.0631 *	0.5298	2.3122	0.021 **	0.537	1.9252	0.0545 *	0.5308
SEK/USD	1.9896	0.0469 **	0.5318	1.732	0.0836 *	0.5277	2.1186	0.0344 **	0.5339	1.9896	0.0469 **	0.5318

For every currency pair, a separate MLP model is estimated to forecast exchange rate movement direction for every set of fundamentals from the PPP, UIP and the MM theories as well as the combined AF approach. Out-of-sample Diebold–Mariano statistics and p-values are calculated for differences in classification error rate (CE) between the estimated models and the random walk benchmark. Statistical significance is marked by *, ** or *** for the 10, 5, or 1 percentage level, respectively. The data range from March 1973 to December 2014. A CE below 0.5 indicates that the estimated model outperforms the random walk benchmark.

Table 5. One-month-ahead forecasting of exchange rate differentials/direction without fundamentals using ANN/XGBoost.

	XGBoost Regression			XGBoost Classification
Currency pair	DM	p-value	Theil Ratio	DM	p-value	CE
PTE/USD	−0.664	0.5069	0.9939	−2.4682	0.0139 **	0.5503
AUD/USD	0.5155	0.6063	1.0032	−1.0254	0.3054	0.5164
CAN/USD	0.5155	0.6063	1.0032	−1.0254	0.3054	0.5164
CHF/USD	0.5155	0.6063	1.0032	−1.0254	0.3054	0.5164
DEM/USD	1.1951	0.2323	1.0062	−1.0998	0.2717	0.5178
DNK/USD	0.9425	0.3462	1.006	−1.7333	0.0834 *	0.5288
FRF/USD	1.4999	0.134	1.0099	−1.1762	0.2399	0.5203
ITL/USD	1.1951	0.2323	1.0062	−1.0998	0.2717	0.5178
JPY/USD	0.5155	0.6063	1.0032	−1.0254	0.3054	0.5164
SEK/USD	0.5155	0.6063	1.0032	−1.0254	0.3054	0.5164
	ANN Regression			ANN Classification
Currency pair	DM	p-value	Theil Ratio	DM	p-value	CE
PTE/USD	1.6533	0.0988 *	1.0365	0.0000	1.0000	0.5000
AUD/USD	0.7242	0.4691	1.0174	−3.5455	0.0004 ***	0.4435
CAN/USD	0.2173	0.828	1.0104	−2.1831	0.0293 **	0.4651
CHF/USD	0.8895	0.3739	1.0139	−3.2196	0.0013 **	0.4487
DEM/USD	4.0828	0.0000 ***	1.0302	0.0000	1.0000	0.5000
DNK/USD	1.2517	0.211	1.0219	−2.4037	0.0164 **	0.4601
FRF/USD	5.234	0.0000 ***	1.0734	0.0691	0.9449	0.5012
ITL/USD	4.3449	0.0000 ***	1.0398	−0.1293	0.8971	0.4979
JPY/USD	−0.4738	0.6357	1.0067	−3.415	0.0007 ***	0.4456
SEK/USD	−0.3102	0.7565	1.0019	−3.7416	0.0002 ***	0.4405

For every currency pair, a separate XGBoost ANN model is estimated to forecast exchange rate differentials, movement directions, only using time dummies as features. Out-of-sample Diebold–Mariano statistics and p-values are calculated for differences in RMSE/CE between the estimated models and the random walk benchmark. Statistical significance is marked by *, ** or *** for the 10, 5, or 1 percentage level, respectively. The data range from March 1973 to December 2014. A classification error rate (CE) below 0.5, a Theil ration below one, indicates that the estimated model outperforms the random walk benchmark.

Table 1 contains the results for regressions with all sets of fundamentals using XGBoost. It is noticeable that in no case is the Theil ratio below 1, indicating that all the associated models predict the OOS exchange rate differences worse than the RW predictions. Moreover, in many cases the RW prediction is significantly better than the associated XGBoost model. This is the case when the Theil ratio is above 1 and the DM test and p-value simultaneously suggest statistical significance.This is particularly evident for the model variants that do not contain time dummies. Here, the p-values for most countries and for all sets of fundamental suggest statistical significance at least at the 10 percent level, sometimes even at the 1 percent level. Using the XGBoost algorithm, I can find no evidence that economic fundamentals improve the prediction of exchange rate differentials.

Alternatively, Table 2 shows the results for regressions using ANNs with all sets of fundamentals, once including and once excluding time dummies. Unlike the comparable results using XGBoost in Table 1, the Theil ratios are now closer to one. In about half of all cases they are even slightly below one. However, the difference is always very small and in most cases not statistically significant. There is no significant difference between the predictions generated by different sets of economic fundamentals and between the approaches that include time dummies or omit them. Although it appears that the ANNs are better fitted to the data than the XGBoost models, as indicated by the lower Theil ratios, this does not lead to significantly better predictions. Thus, it does not lead to the significance necessary to infer an overall effect of fundamentals on exchange rate differentials. Therefore, there is no evidence to support the claim that economic fundamentals have predictive power on exchange rate differentials.

Table 3 contains the results for the classifications with all sets of fundamentals, once with and once without time dummies, using XGBoost for classification to classify the direction of the exchange rate movement. In contrast to the results of the regression models of Table 1 and Table 2, the results for the classification yield some predictive power. In almost all cases, the error rate of each XGBoost model is lower than the RW error rate, i.e., less than 0.5, which means that the XGBoost model predicts the correct direction in more than 50 percent of the cases. However, the only cases where the models’ predictions differ significantly from the RW prediction are for the PTE/USD and FRF/USD currency pairs. However, this is true for all sets of fundamentals that include time dummies. Moreover, when comparing the models with time dummies to the models without time dummies, we observe an increase in the error rates as well as in the p-values for the models without time dummies. Thus, prediction timing seems to be important for classification, which is interesting since in most cases the original economic models do not consider prediction timing as a determining factor, but level differences between countries.

The results for the classifications using ANNs are shown in Table 4. For all sets of fundamentals, the error rates are much lower than for the RW benchmark. For most models that include time dummies, the results are statistically significant. Between these models, the differences in error rates and statistical significance are small. The low classification errors, as well as the presence of statistical significance in many cases, suggest the predictive power of fundamentals in terms of the exchange rate direction. However, the classification errors are much higher when the time dummies are excluded, and statistical significance disappears. This shows that the time dummies contain significant information for the predictions.

Based on these observations, I tested a new approach, in which I included only the time dummies as features. The goal was to investigate whether the time dummies alone could be responsible for the forecastability of exchange rate movement directions. Table 5 contains the results of this experiment. It can be observed that the error rates of the ANN models are in most cases smaller than the RW error rates and the difference is highly statistically significant. This raises the question of the role of fundamentals and their contribution to the predictive performance in the classification models of Table 3 and Table 4. In Figure 1, I compare the error rates of the fundamentals-based ANN models from Table 4, including time dummies, with the error rates of the ANN models only using time dummies as features from Table 5. It can be seen that the error rates from the predictions of the ANN models from Table 5, called “Only TD”, are not strictly lower than those from the ANN models in Table 4, “AF”, “PPP”, “UIP”, and “MM”. e.g., in the majority of cases, “MM” yields lower error rates than "Only TD". Furthermore, Figure 2 shows, in how many cases a certain level of statistical significance was reached by the models from Table 4 compared to the “Only TD” model of Table 5. It can be observed that “Only TD” displays statistical significance in six cases (for six country pairs) of which it reached three times the significance at the one percent level and three times at the five percent level. This is arguably worse than, for example, the “MM” model of Table 4, which reaches statistical significance at the one percent level in six cases. From this, I conclude that the good performance of the classifying ANN models from Table 4 cannot be attributed to the prediction timing alone, but fundamentals have contributed to the forecasting performance as well. However, the amount of the contribution of the fundamentals to the forecasting performance is unclear. There might be complex interactions between time dummies and fundamentals that are responsible for the forecasting performance of Table 4.

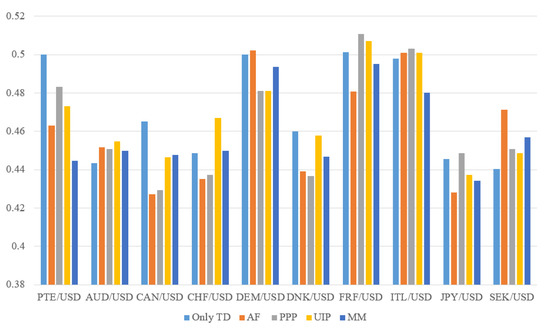
Figure 1. Error rates—every set of fundamentals vs. only TD.

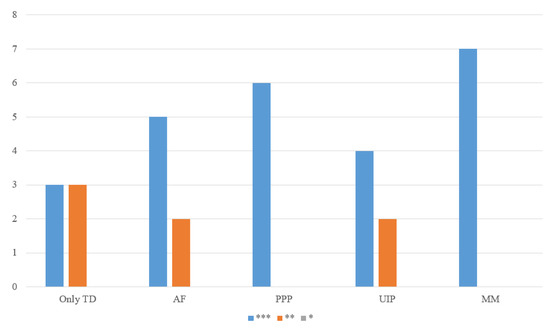
Figure 2. Level of significance—every set of fundamentals vs. only TD.

6. Discussion

According to Alvarez et al. (2007), if fundamentals do not have a significant effect on exchange rate movements, monetary policy would not affect the exchange rate, since stimulating fundamentals would not lead to changes in exchange rates, but only to risk premia. The results from the ANN classification models of Table 4 suggest that fundamentals have forecasting power for exchange rates. However, as Table 5 shows, much of this is due to the time dummies. Therefore, the prediction timing is important. A possible explanation for these observations is that the fundamentals have some forecasting power for the exchange rate movement directions, but only in combination with the prediction timing. It is possible that there are complex interdependencies between time dummies and fundamental data. This fits well with the scapegoat theory of Bacchetta and Wincoop (2004). They argue that fundamental variables can be scapegoats in that the perceived importance of certain fundamentals by market participants, policymakers, and analysts change over time. Therefore, the weight they attach to individual fundamentals changes over time, leading to time-varying expectations as well as varying foreign exchange trading decisions. Therefore, the influence of macroeconomic fundamentals on exchange rates also changes similarly over time. This effect could be captured by complex interactions between the time dummies and the fundamentals, since the time dummies contain the information about the timing. This has implications for monetary policy because the temporary scapegoat effect distorts the relationship between fundamentals and exchange rates. As a result, policymakers cannot rely on past relationships between fundamentals and exchange rates because they might have changed. Moreover, changes in fundamentals might indicate that policy intervention is needed, but the scapegoat effect distorts the exchange rate, making it appear that policy intervention is not needed and that the exchange rate is independent of fluctuations in fundamentals. The empirical results of this paper strengthen the necessary conditions for the existence of the scapegoat effect, namely that the effect size of the influence of fundamentals on exchange rates depends on prediction timing.

7. Conclusions

In this paper, I examined the predictive power of macroeconomic fundamentals, when used in nonlinear machine learning models. I applied artificial neural networks (ANNs) in form of a multilayer perceptron model, as well as gradient boosted decision trees using XGBoost, to forecast exchange rates movements. I compared the OOS-RMSE for regression as well as the OOS classification error for the classification of individually trained models for each currency pair to the random walk benchmark. The fundamentals were derived from the PPP, UIP, and MM theories. I compared the significance of the differences in the predictive performance of the trained models with the random walk benchmark using the Diebold–Mariano test statistic and p-value. For the regression setting, i.e., the prediction of exchange rate differentials, I found no convincing evidence that fundamentals possess predictive power. For the classification setting, i.e., the prediction of exchange rate movement directions, the XGBoost models were able to outperform the random walk benchmark by a small margin, which was in some cases statistically significant. The ANN models were able to outperform the random walk benchmark by a larger margin, which was statistically significant at the 1 percent level in many cases. However, this was only the case when time dummies were included in the models. ANN regressions using only time dummies as explanatory variables showed good predictive performances and high levels of statistical significance in many cases as well. This called into question the role of fundamentals in the predictions of the well-performing models. However, a comparison of these results with the ANN models for classifications with fundamental data showed that the use of the MM fundamentals leads to better results in terms of statistical significance and error rates. Hence, the predictive performance cannot be attributed to the time dummies alone. One possible explanation for this is that complex interactions between time dummies and fundamentals could be the key to good directional forecasts for exchange rates. The relationship between time dummies and fundamental data needs to be explored in more detail in future studies.