A Multi-Constraint Co-Optimization LQG Frequency Steering Method for LEO Satellite Oscillators
Abstract
1. Introduction
2. System Basic Principle
2.1. System Clock State Modeling
2.2. Linear Quadratic Gaussian Control
2.2.1. Kalman Filter
2.2.2. Linear Quadratic Regulator (LQR)
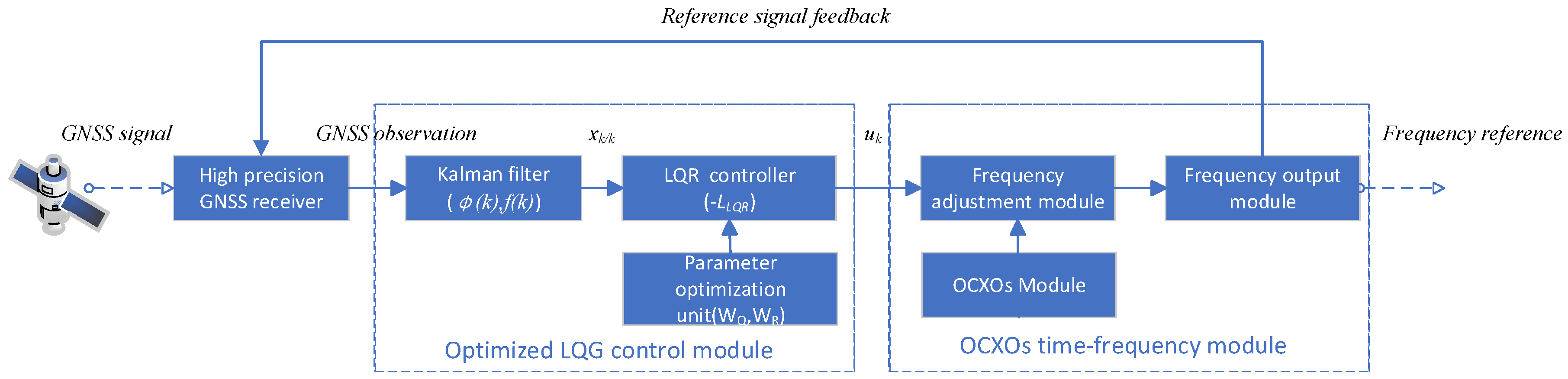
3. The LQG Closed-Loop Control Method Based on Multi-Constraint Optimization
3.1. Quantization Noise Analysis in Frequency Precision Steering
3.2. Multi-Source Error Propagation Modeling
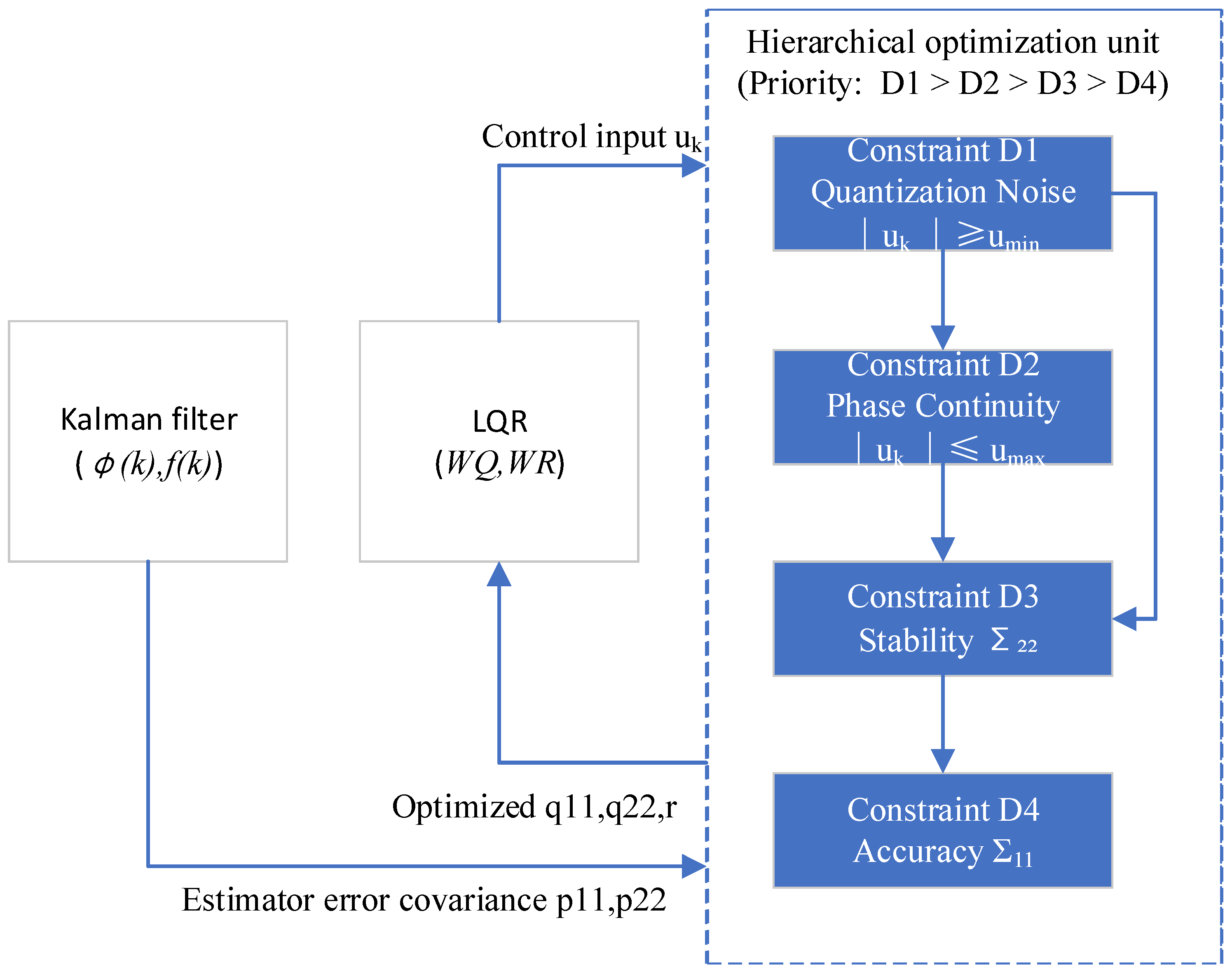
3.3. Hierarchical Constraint Framework for Frequency Precision Steering
3.3.1. Constraint D1 for Quantization Noise
3.3.2. Constraint D2 for Phase Continuity
3.3.3. Constraint D3 for Stability
3.3.4. Constraint D4 for Accuracy
3.3.5. Four-Dimensional Constraint Integrated (FDCI) Model Parameters
3.4. Priority-Driven Co-Optimization Algorithm Flow
3.4.1. Initialization
- Oscillator noise characterization
- 2.
- Adjustment range set
3.4.2. Iterative Optimization
- Stability constraint enforcement (D3)
- The frequency deviation weight q22 being increased by factor α;
- The control input weight r being decreased by factor β;
- This adjustment sequence is repeated until the stability constraint is satisfied.
- 2.
- Accuracy constraint enforcement (D4)
- The clock bias weight q11 being increased by factor γ;
- The control weight r being slightly incremented β_1 for control smoothing;
- 3.
- Adjustment step safeguarding
- is clamped to ;
- is decreased;
- r is increased;
- The stability optimization step is reinitiated.
- 4.
- Convergence verification
- Parameter variations < 0.1% over three consecutive iterations;
- Closed-loop pole magnitude λ < 0.95;
- 5.
- Command execution
- 6.
- System actuation
3.4.3. Process of the Parameter Optimization Algorithm
4. Experiment Validation
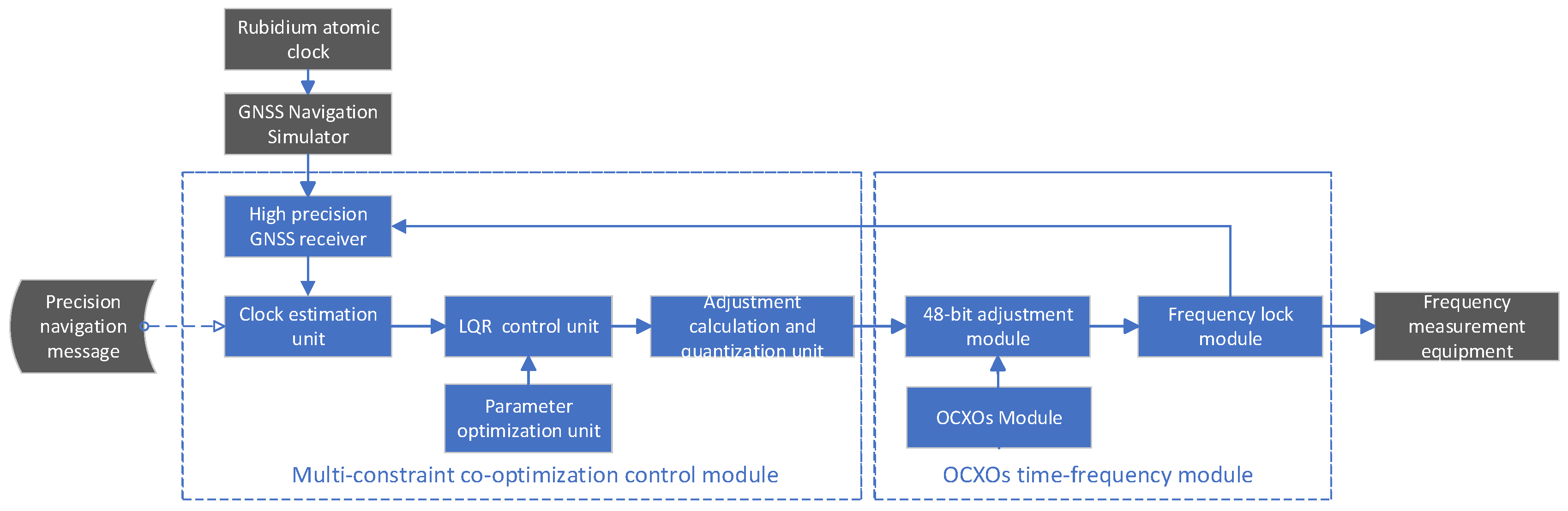
4.1. Architecture of the High-Precision Time–Frequency Control System
- GNSS Signal Simulation: A GNSS signal simulator generated navigation signals using precise ephemerides, satellite clock biases, and LEO precise orbital data.
- Clock Bias Measurement: A high-precision GNSS receiver acquired pseudorange and carrier phase observations at 1 Hz to determine local clock bias.
- State Estimation: A Kalman filter fused GNSS observations with injected orbit/clock data to estimate clock bias and frequency deviation . LEO orbital corrections were applied to enhance accuracy [38].
- Parameter Optimization: The control module optimized weight matrices and under multi-constraint conditions.
- Steering Trigger: Frequency adjustment was initiated when clock bias exceeded ±0.2 ns.
- Command Execution: The steering unit calculated , quantized it to (subject to ), and sent commands to the OCXO.
- Performance Evaluation: Output signals were monitored for 24 h to measure clock bias and frequency stability.
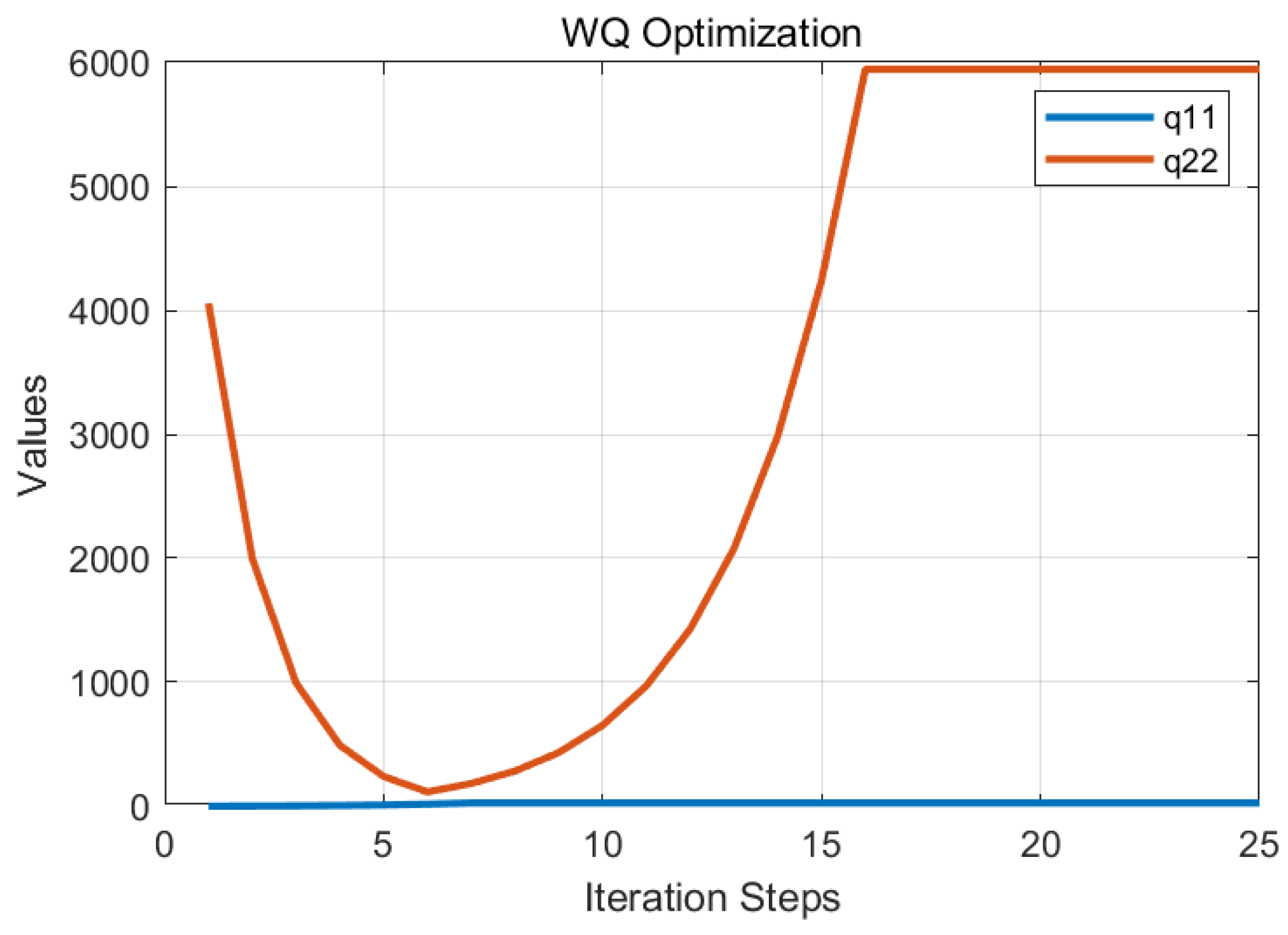
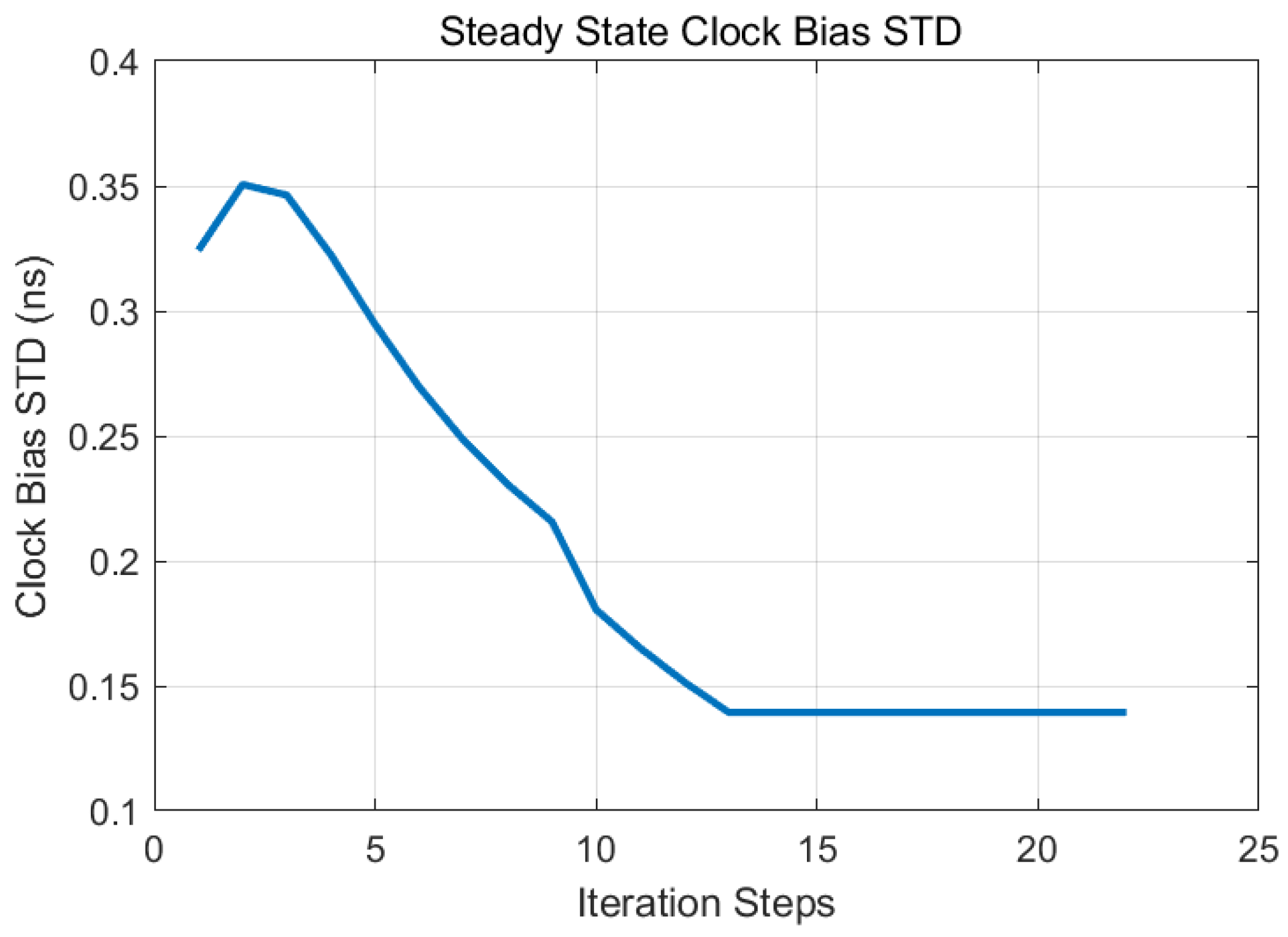
4.2. Results of LQG Parameter Optimization Under Multi-Constraint
- in was constrained within 1 × 10−1 to 1 × 103
- in was bounded between 1 × 101 and 1 × 104
- r was limited to the interval 1 × 103 to 1 × 1010.
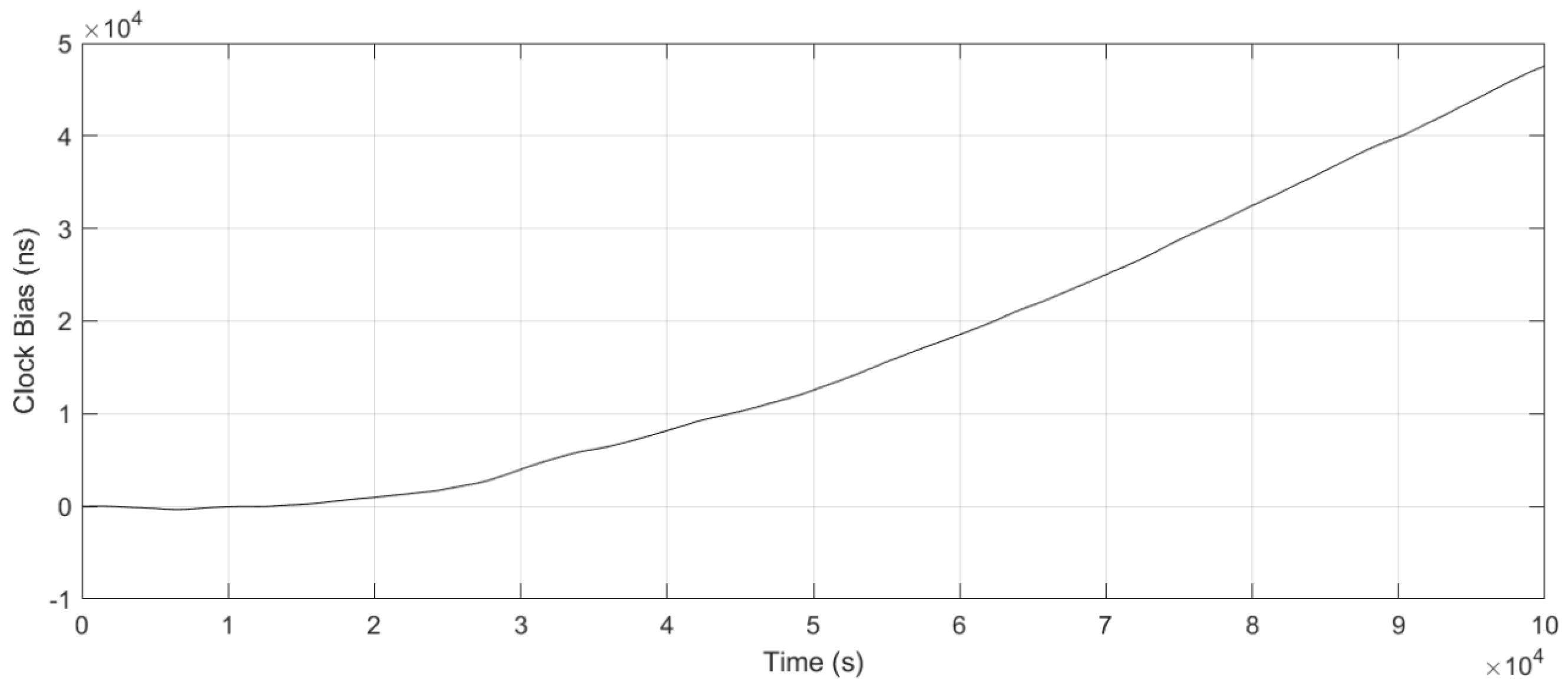
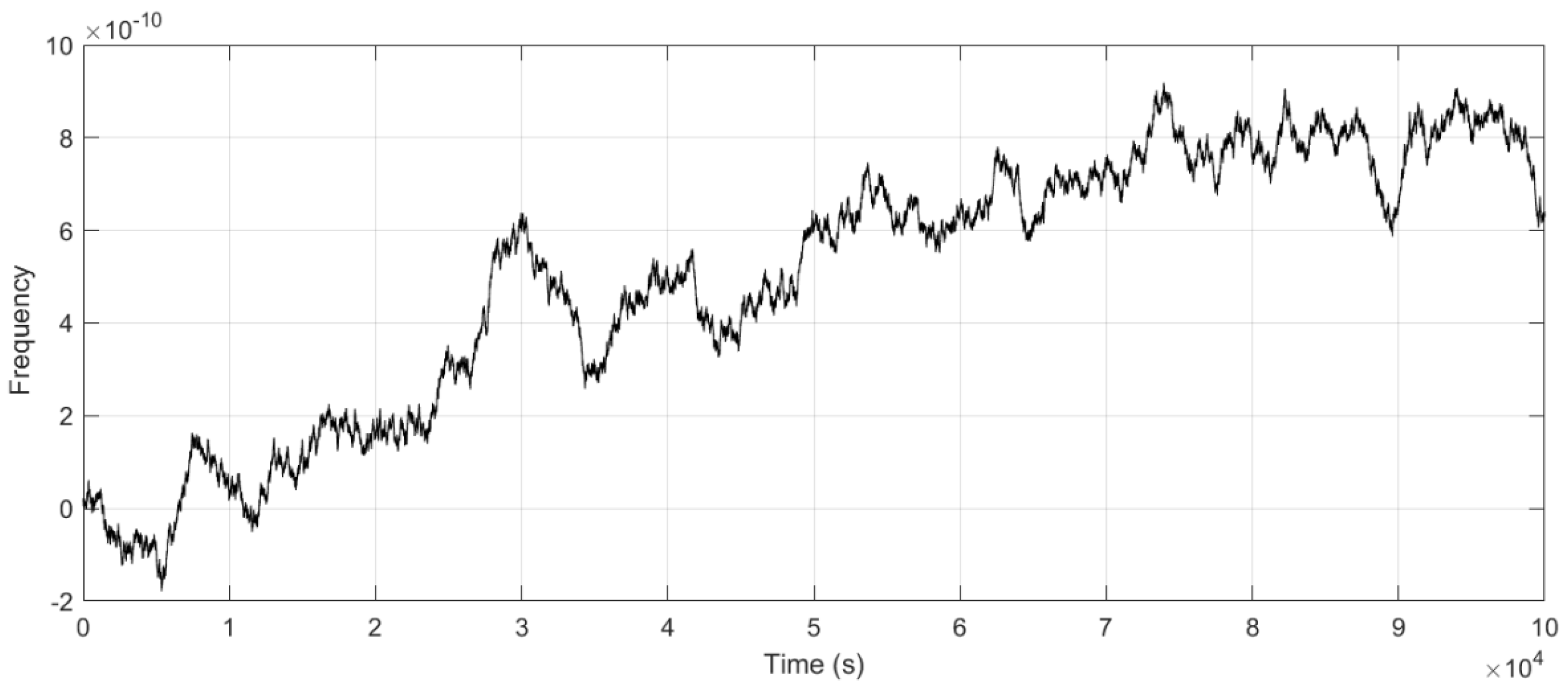
4.3. Frequency Adjustment Analysis
4.4. System Performance Under the Optimized LQG Control
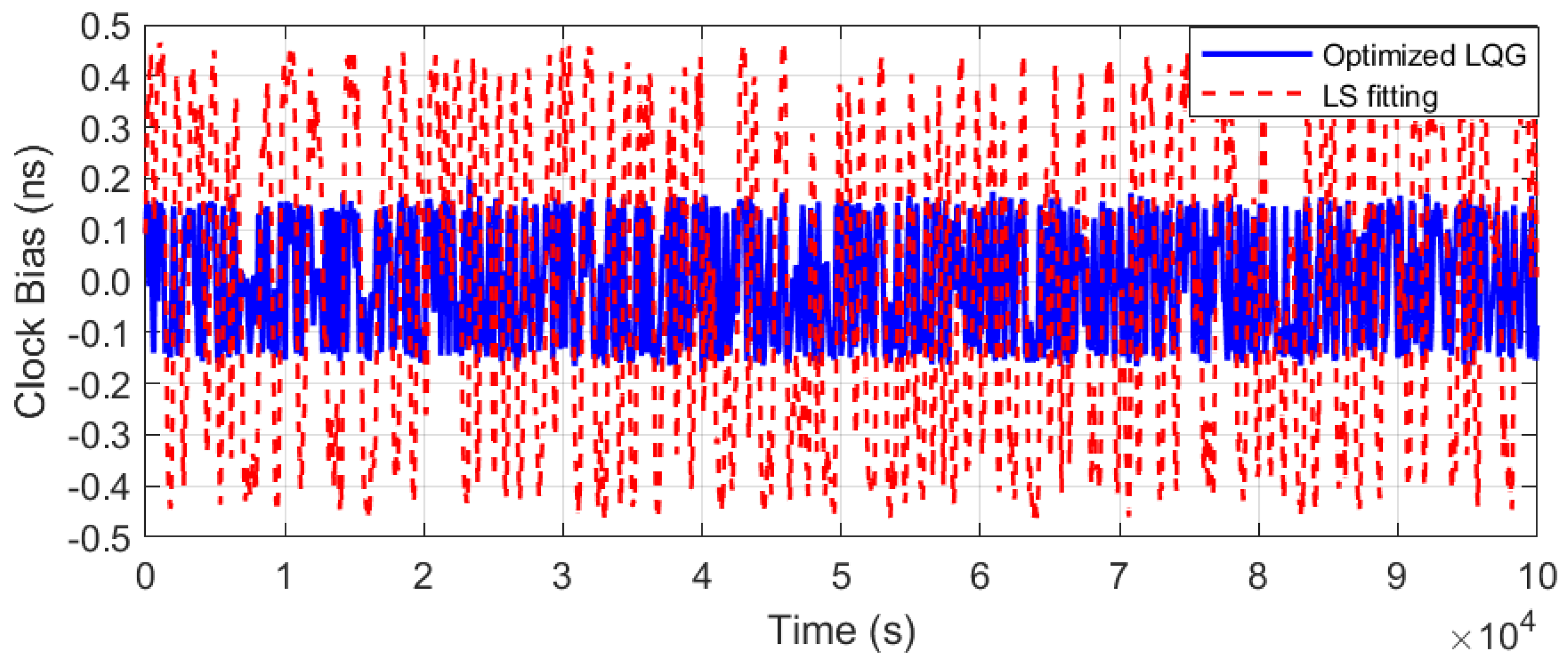
4.4.1. Measurement Results for Clock Bias Performance
4.4.2. Measurement Results for Frequency Deviation
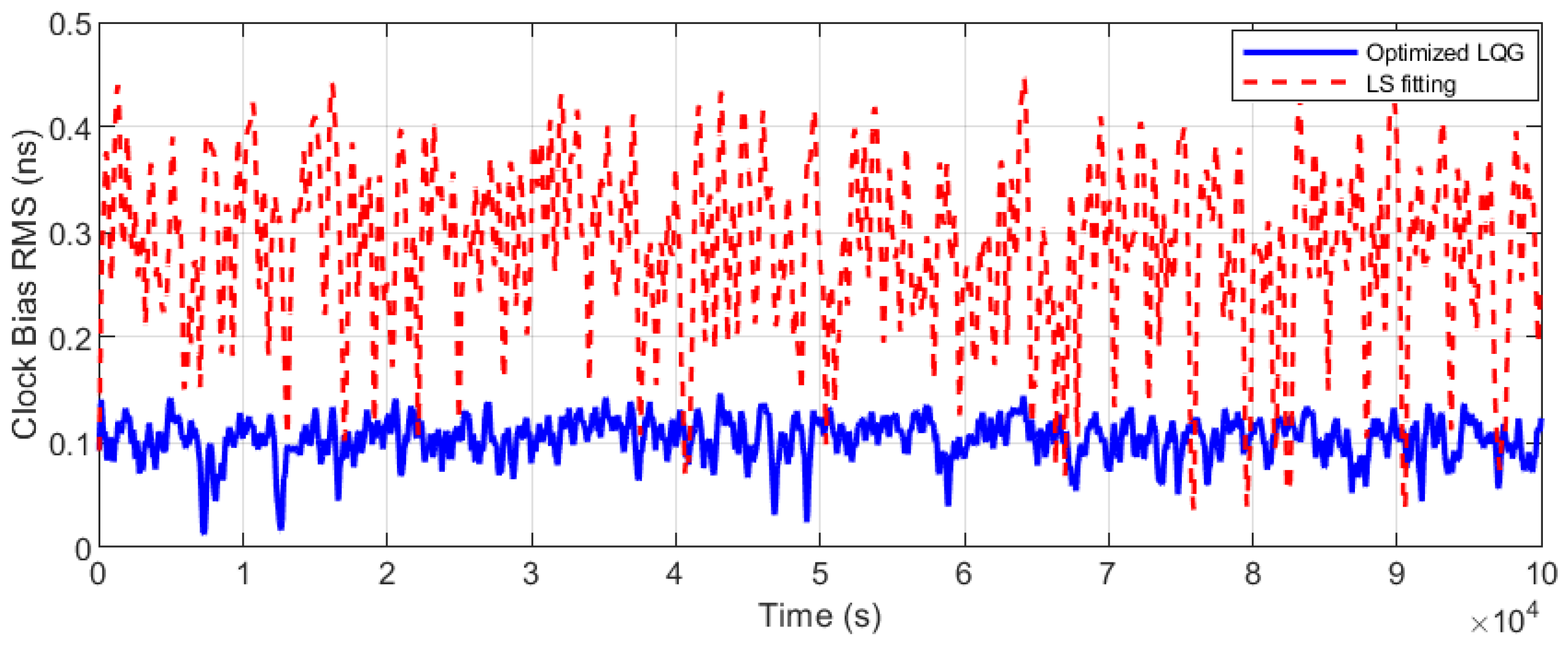
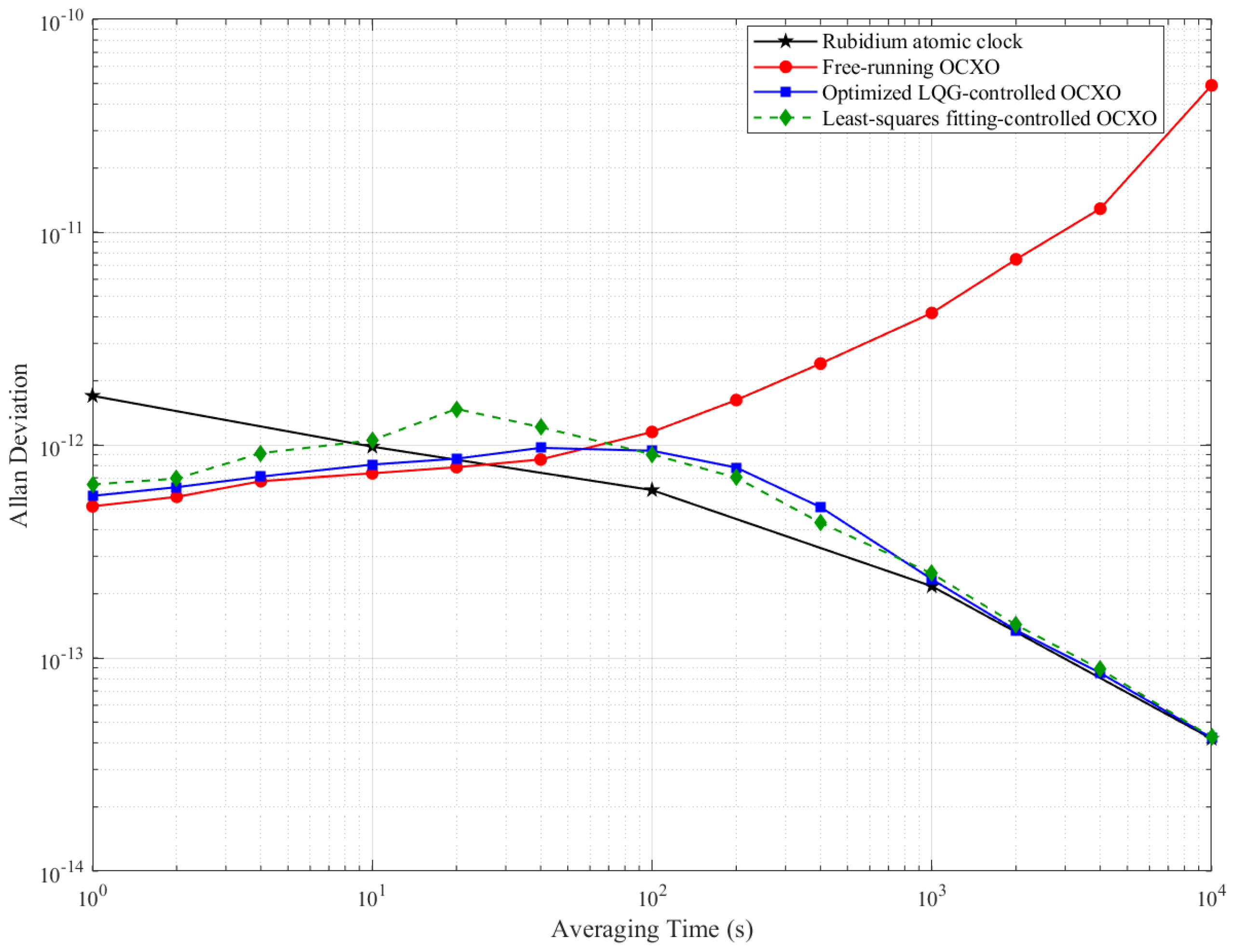
4.4.3. Measurement Results for Frequency Stability
4.4.4. Comprehensive Improvement Analysis for Performance Metrics
4.5. Environmental Robustness Validation of the Optimized LQG Control
4.5.1. Experimental Design
- Vacuum level: better than 6.5 × 10−3 Pa;
- Heat sink temperature: not exceeding 100 K;
- Temperature gradient range: from −20 °C to +45 °C at 10 °C intervals;
- Temperature stability requirement: ±1.5 °C;
- Dwell time per temperature point: 6 h;
- Random Vibration Test Conditions
- Frequency range: 20 Hz to 2000 Hz;
- Acceleration power spectral density (PSD): +3 dB/oct from 20 Hz to 100 Hz, 0.02 g2/Hz from 100 Hz to 1000 Hz, −6 dB/oct from 1000 Hz to 2000 Hz;
- Overall RMS level: 5.38 grms;
- Directional application: 2 min per axis (X, Y, Z);
- During the active excitation phase, vibration was applied in 10 cycles. Each cycle consisted of one 6 min vibration followed by a 2 min pause.
- Sinusoidal Vibration Test Conditions
- Frequency sweep range: 5 Hz to 100 Hz;
- Vibration amplitude: 3 mm (0 to peak) from 5 Hz to 12 Hz, 0.5 g from 12 Hz to 100 Hz.
- Sweep rate: 4 oct/min;
- Approximate sweep duration: 65 s;
- During the active excitation phase, vibration was applied in 15 cycles. Each cycle consisted of one frequency sweep (65 s) followed by a 4 min pause.
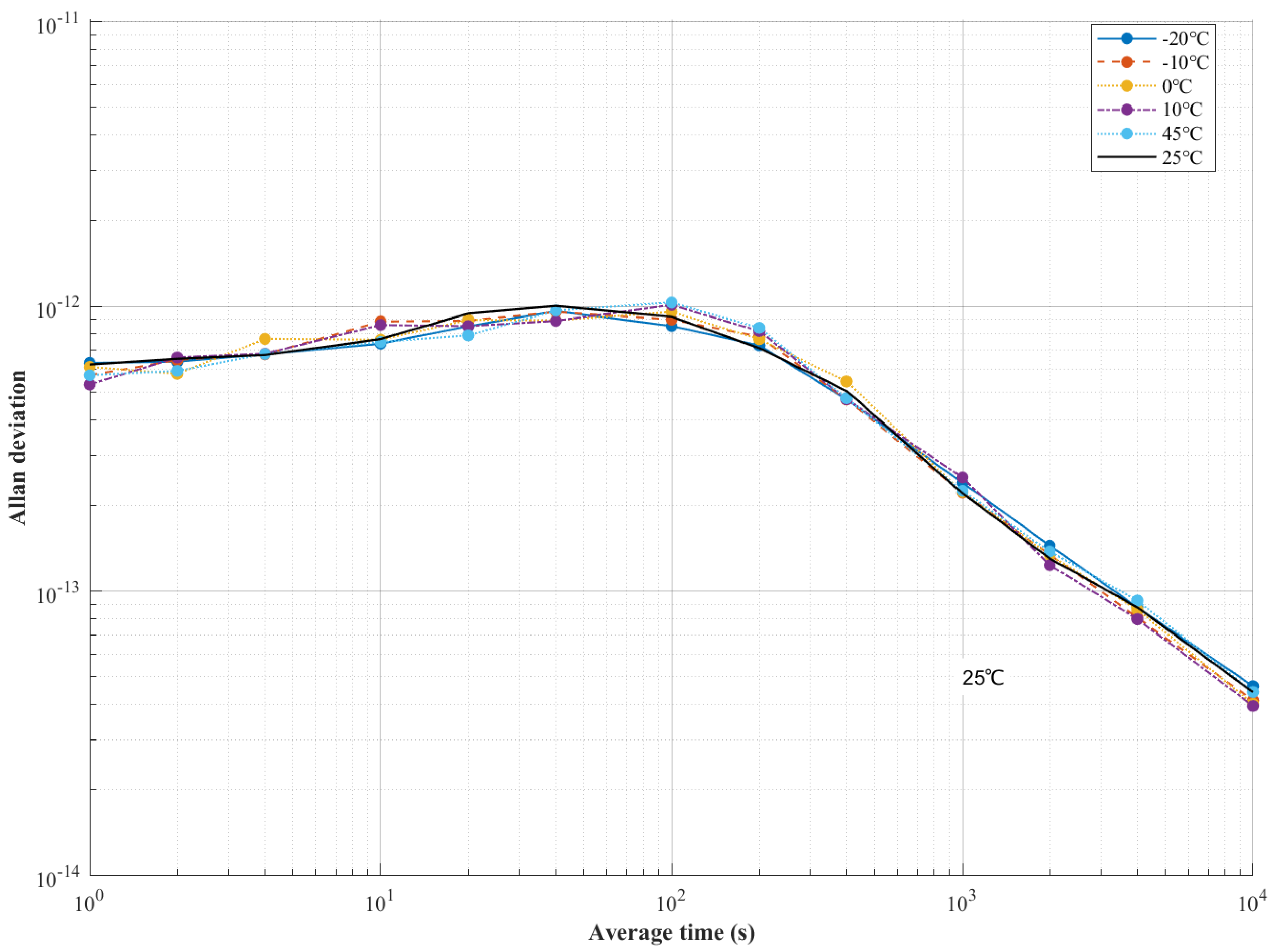
4.5.2. Thermal Impact Analysis
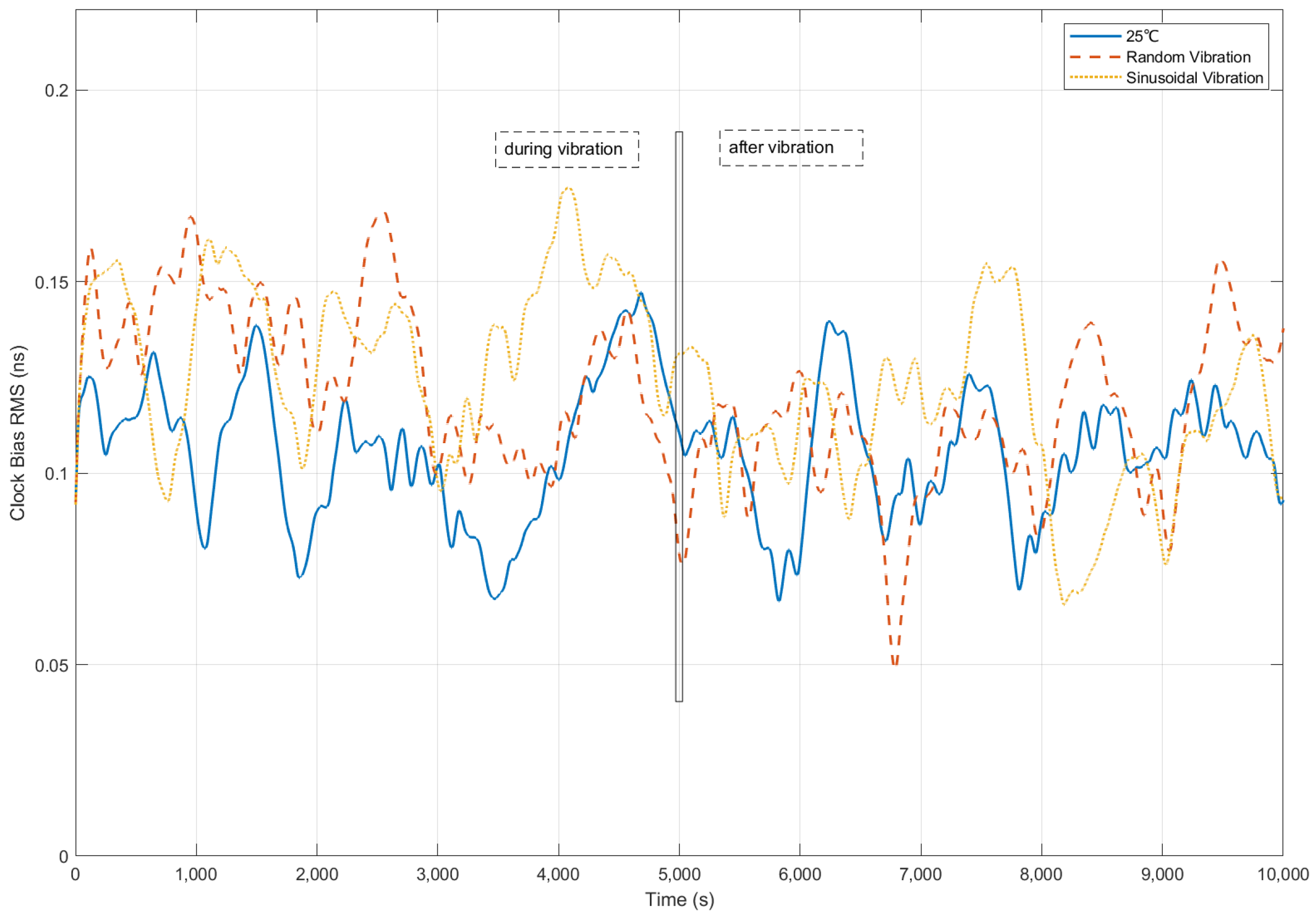
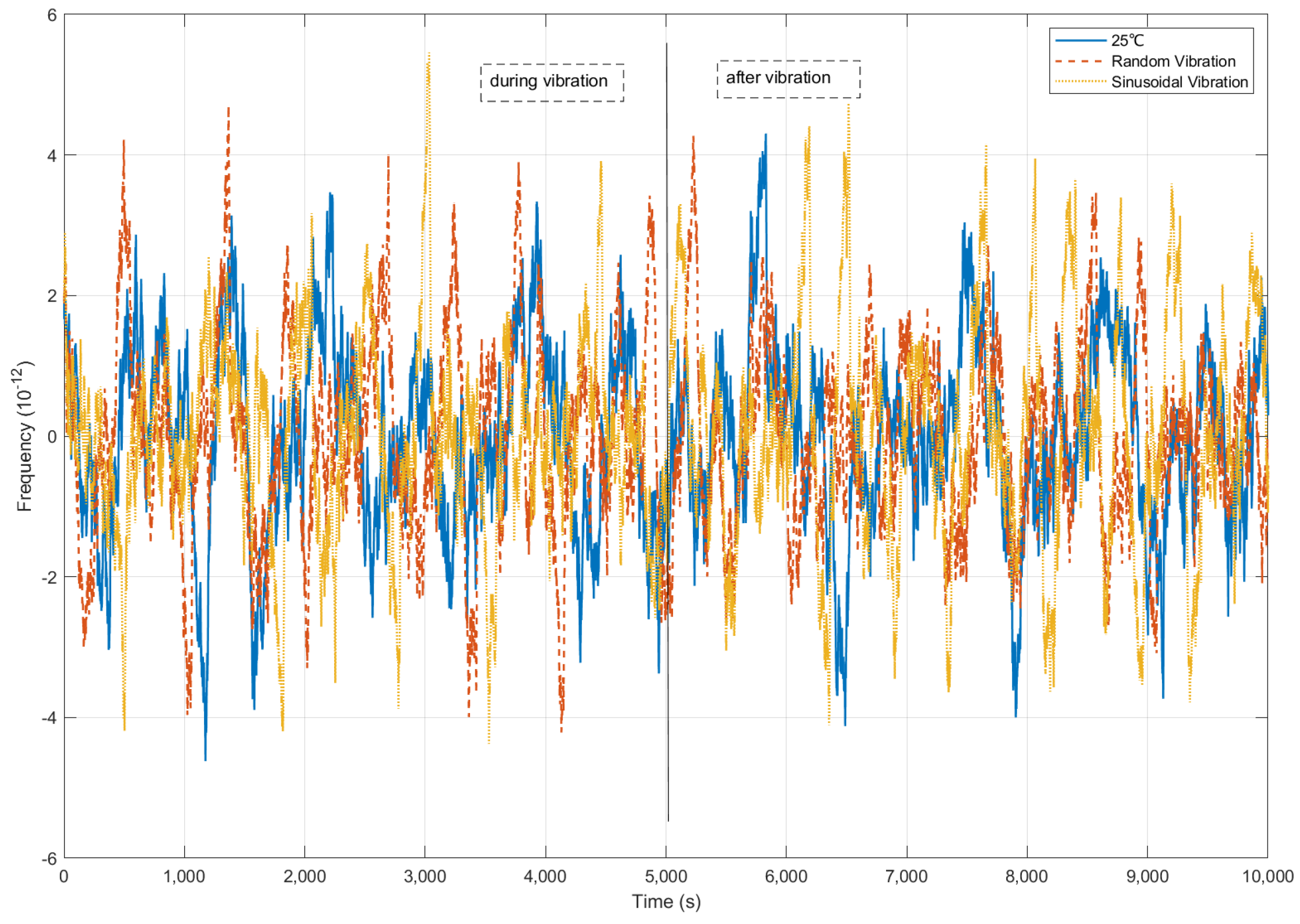
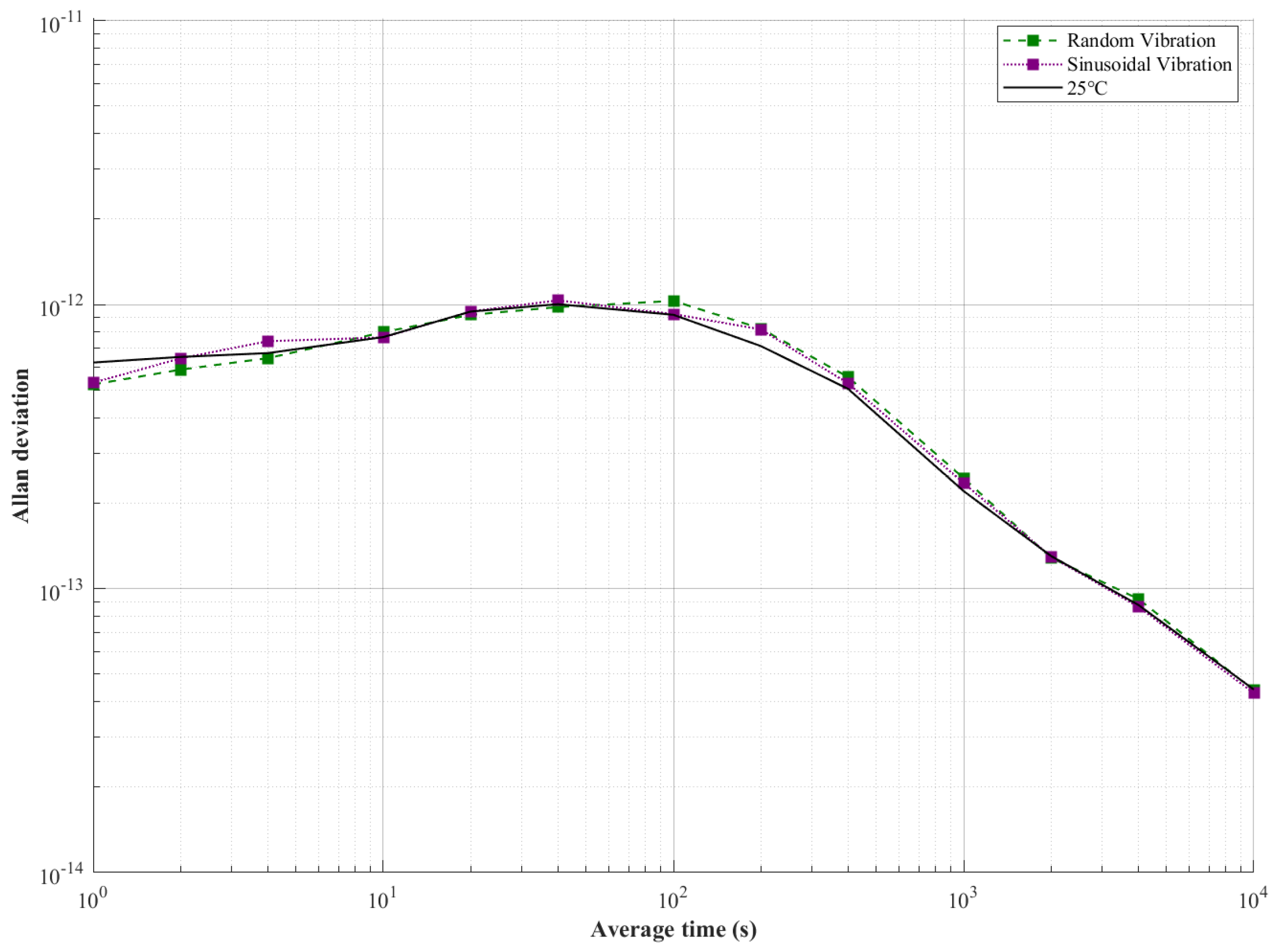
4.5.3. Vibration Impact Analysis
4.5.4. Comprehensive Analysis for Robustness Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| LEO | Low Earth Orbit |
| GNSS | Global Navigation Satellite System |
| OCXO | Oven-Controlled Crystal Oscillator |
| RT | Real Time |
| PPS | Pulse Per Second |
| LQR | Linear Quadratic Regulator |
| KF | Kalman Filter |
| LS | Least Squares |
| LQG | Linear Quadratic Gaussian |
| FDCI | Four Dimension Constraint Integrated |
| STS | Short-Term Stability |
| LTS | Long-Term Stability |
References
- Prol, F.S.; Ferre, R.M.; Saleem, Z.; Valisuo, P.; Pinell, C.; Lohan, E.S.; Elsanhoury, M.; Elmusrati, M.; Islam, S.; Celikbilek, K.; et al. Position, navigation, and timing (PNT) through low earth orbit (LEO) satellites: A survey on current status, challenges, and opportunities. IEEE Access 2022, 10, 83971–84002. [Google Scholar] [CrossRef]
- Wang, K.; El-Mowafy, A. LEO satellite clock analysis and prediction for positioning applications. Geo-Spat. Inf. Sci. 2022, 25, 14–33. [Google Scholar] [CrossRef]
- Yan, M.; Zhang, S.; Wei, T.; Yang, M.; Li, N. Development and application of simple GNSS disciplined module. Metrol. Sci. Technol. 2021, 65, 30–34. [Google Scholar]
- Miao, X.; Hu, C.; Qiao, Y. A Novel Two Variables PID Control Algorithm in Precision Clock Disciplining System. Electronics 2024, 13, 3820. [Google Scholar] [CrossRef]
- Kubczak, P.; Jessa, M.; Kasznia, M. Fast frequency and phase synchronization of high-stability oscillators with 1 PPS signal from satellite navigation systems. GPS Solut. 2025, 29, 52. [Google Scholar] [CrossRef]
- Zhang, K.; Zou, D.; Wang, P.; Jing, W. A new device for two-way time-frequency real-time synchronization. J. Internet Technol. 2023, 24, 1267–1275. [Google Scholar] [CrossRef]
- Wang, J.; Li, Z.; Peng, J.; Ma, M.; Yang, X. Research on secondary frequency standards control algorithm based on linear quadratic regulator. SPIE Proc. 2021, 13394, 133940M. [Google Scholar] [CrossRef]
- Guo, W.; Zuo, H.; Mao, F.; Chen, J.; Gong, X.; Gu, S.; Liu, J. On the satellite clock datum stability of RT-PPP product and its application in one-way timing and time synchronization. J. Geod. 2022, 96, 52. [Google Scholar] [CrossRef]
- Rønningen, O.P.; Danielsen, M. A novel PPP disciplined oscillator. In Proceedings of the 2019 Joint Conference of the IEEE International Frequency Control Symposium and European Frequency and Time Forum (EFTF/IFC), Orlando, FL, USA, 14–18 April 2019; pp. 1–4. [Google Scholar] [CrossRef]
- Liu, K.; Guan, X.; Ren, X.; Wu, J. Disciplining a Rubidium Atomic Clock Based on Adaptive Kalman Filter. Sensors 2024, 24, 4495. [Google Scholar] [CrossRef]
- Fan, D.-S.; Shi, S.-H.; Li, X.-H. An algorithm for the rubidium atomic clock control based on the Kalman filter. J. Astronaut. 2015, 36, 90. [Google Scholar]
- Chen, W.; Jing, Y.; Zhao, S.; Yan, L.; Liu, Q.; He, Z. A Distributed Collaborative Navigation Strategy Based on Adaptive Extended Kalman Filter Integrated Positioning and Model Predictive Control for Global Navigation Satellite System/Inertial Navigation System Dual-Robot. Remote Sens. 2025, 17, 721. [Google Scholar] [CrossRef]
- Liang, K.; Hao, S.; Yang, Z.; Wang, J. A Multi-Global Navigation Satellite System (GNSS) Time Transfer Method with Federated Kalman Filter (FKF). Sensors 2023, 23, 5328. [Google Scholar] [CrossRef]
- Li, X.; Li, Y.; Xiong, Y.; Wu, J.; Zheng, H.; Li, L. An efficient strategy for multi-GNSS real-time clock estimation based on the undifferenced method. GPS Solut. 2023, 27, 23. [Google Scholar] [CrossRef]
- Wang, X.; Yang, Y.; Wang, B.; Lin, Y.; Han, C. Resilient timekeeping algorithm with multi-observation fusion Kalman filter. Satell. Navig. 2023, 4, 25. [Google Scholar] [CrossRef]
- Sun, L.; Huang, W.; Gao, S.; Li, W.; Guo, X.; Yang, J. Joint timekeeping of navigation satellite constellation with inter-satellite links. Sensors 2020, 20, 670. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Yang, Y.; Hu, X.; Tang, C.; Guo, R.; Zhou, Z.; Xu, J.; Pan, J.; Su, M. BeiDou-3 broadcast clock estimation by integration of observations of regional tracking stations and inter-satellite links. GPS Solut. 2021, 25, 57. [Google Scholar] [CrossRef]
- Guo, W.; Zhu, M.; Tang, S.; Bian, X.; Zuo, H.; Liu, J. Linear quadratic Gaussian-based clock steering system for GNSS real-time precise point positioning timing receiver. GPS Solut. 2024, 28, 53. [Google Scholar] [CrossRef]
- Guan, X.; Wu, J.; Zhou, Z.; Xing, Y.; Li, Y.; Wu, H.; Zhao, A. Algorithm for taming rubidium atomic clocks based on longwave (Loran-C) timing signals. Remote Sens. 2025, 17, 1049. [Google Scholar] [CrossRef]
- Zhao, S.; Shmaliy, Y.S.; Ahn, C.K.; Liu, F. Self-tuning unbiased finite impulse response filtering algorithm for processes with unknown measurement noise covariance. IEEE Trans. Control Syst. Technol. 2021, 29, 1372–1379. [Google Scholar] [CrossRef]
- Dou, J.; Xu, B.; Dou, L. Robust GNSS positioning using unbiased finite impulse response filter. Remote Sens. 2023, 15, 4528. [Google Scholar] [CrossRef]
- Farina, M.; Galleani, L.; Tavella, P.; Bittanti, S. A control theory approach to clock steering techniques. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2010, 57, 2257–2270. [Google Scholar] [CrossRef]
- Wu, Y.; Yang, B.; Xiao, S.; Wang, M. Atomic clock models and frequency stability analyses. Geomat. Inf. Sci. Wuhan Univ. 2019, 44, 1226–1232. [Google Scholar]
- Zhao, L.; Li, N.; Li, H.; Wang, R.; Li, M. BDS satellite clock prediction considering periodic variations. Remote Sens. 2021, 13, 4058. [Google Scholar] [CrossRef]
- Chen, H.; Jiang, W.; Ge, M.; Wickert, J.; Schuh, H. Efficient high-rate satellite clock estimation for PPP ambiguity resolution using carrier-ranges. Sensors 2014, 14, 22300–22312. [Google Scholar] [CrossRef] [PubMed]
- Luo, Y.; Li, J.; Yu, C.; Xu, B.; Li, Y.; Hsu, L.-T.; El-Sheimy, N. Research on time-correlated errors using Allan variance in a Kalman filter for vector-tracking GNSS receivers. Remote Sens. 2019, 11, 1026. [Google Scholar] [CrossRef]
- Ferre-Pikal, E.S.; Vig, J.R.; Camparo, J.C.; Cutler, L.S.; Maleki, L.; Riley, W.J.; Stein, S.R.; Thomas, C.; Walls, F.L.; White, J.D. Draft revision of IEEE STD 1139-1988 standard definitions of physical quantities for fundamental, frequency and time metrology-random instabilities. In Proceedings of the International Frequency Control Symposium, Orlando, FL, USA, 30 May 1997; IEEE: New York, NY, USA, 1997; pp. 338–357. [Google Scholar]
- Riley, W.J.; Howe, D.A. Handbook of Frequency Stability Analysis; NIST Special Publication 1065; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2008. [CrossRef]
- Athans, M. The role and use of the stochastic Linear-Quadratic-Gaussian problem in control system design. IEEE Trans. Autom. Control 1971, 6, 529–552. [Google Scholar] [CrossRef]
- Yan, Y.; Kawaguchi, T.; Yano, Y.; Hanado, Y.; Ishizaki, T. Structured Kalman filter for time scale generation in atomic clock ensembles. IEEE Control Syst. Lett. 2024, 8, 187–192. [Google Scholar] [CrossRef]
- Zhao, S.; Dong, S.; Bai, S.; Gao, Z. Research on An Optimized Frequency Steering Algorithm. J. Electron. Inf. Technol. 2021, 43, 1457–1464. [Google Scholar] [CrossRef]
- Song, H.-J.; Dong, S.-W.; Wang, X.; Jiang, M.; Zhang, Y.; Guo, D.; Zhang, J.-H. Frequency control algorithm of domestic optically pumped small cesium clock based on optimal control theory. Acta Phys. Sin. 2024, 73, 060201. [Google Scholar] [CrossRef]
- Lan, J.; Zhao, D. Finding the LQR Weights to Ensure the Associated Riccati Equations Admit a Common Solution. IEEE Trans. Autom. Control. 2023, 68, 6393–6400. [Google Scholar] [CrossRef]
- Mishagin, K.G.; Lysenko, V.A.; Medvedev, S.Y. A practical approach to optimal control problem for atomic clocks. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2019, 67, 1080–1087. [Google Scholar] [CrossRef]
- Zhao, G.; Ban, Y.; Zhang, Z.; Shi, Y.; Liu, H. Phase Demodulation Strategy Based on Kalman Filter for Sinusoidal Encoders. IEEE Sens. J. 2023, 23, 10625–10632. [Google Scholar] [CrossRef]
- Venhoek, D. Estimating noise for clock-synchronizing Kalman filters. In Proceedings of the 2024 IEEE International Symposium on Precision Clock Synchronization for Measurement, Control, and Communication (ISPCS), Tokyo, Japan, 7–11 October 2024; IEEE: New York, NY, USA, 2024; pp. 1–7. [Google Scholar] [CrossRef]
- Falconi, L.; Ferrante, A.; Zorzi, M. Distributionally robust LQG control under distributed uncertainty. Automatica 2025, 174, 112128. [Google Scholar] [CrossRef]
- Wu, M.; Wang, K.; Wang, J.; Liu, J.; Chen, B.; Xie, W.; Zhang, Z.; Yang, X. Real-time LEO satellite clocks based on near-real-time clock determination with ultra-short-term prediction. Remote Sens. 2024, 16, 1326. [Google Scholar] [CrossRef]
- Diao, W.T.; Zhen, G.G.; Wang, D.D. Analysis of impact of crystal oscillator short stability on PPP accuracy of navigation enhancement system. J. Telem. Track. Command. 2023, 44, 32–39. [Google Scholar]







| Dimension | Symbol | Constraint Formulation | Physical Parameter |
|---|---|---|---|
| Quantization noise | D1 | *1 | Minimum step for micro-step |
| Phase continuity | D2 | Maximum step for frequency adjustment | |
| Long-term stability | D3 | , at least *2 | Allan deviation |
| Accuracy | D4 | *3 | Clock bias error (RMS) |
| Average Time (s) | Allan Deviation (Rubidium Clock) | Allan Deviation (Free-Running) | Allan Deviation (LS Fitting) | Allan Deviation (Optimized LQG) | Improvement Ratio1 (LS/Free) | Improvement Ratio2 (Optimize LQG/Free) |
|---|---|---|---|---|---|---|
| 1 | 1.72 × 10−12 | 5.15 × 10−13 | 6.51 × 10−13 | 5.76 × 10−13 | 1.2659 | 1.1195 |
| 2 | / | 5.70 × 10−13 | 6.94 × 10−13 | 6.33 × 10−13 | 1.2182 | 1.1100 |
| 4 | / | 6.75 × 10−13 | 9.14 × 10−13 | 7.09 × 10−13 | 1.3535 | 1.0504 |
| 10 | 9.86 × 10−13 | 7.35 × 10−13 | 1.05 × 10−12 | 8.08 × 10−13 | 1.4313 | 1.0993 |
| 20 | / | 7.85 × 10−13 | 1.48 × 10−12 | 8.61 × 10−13 | 1.8790 | 1.0968 |
| 40 | / | 8.54 × 10−13 | 1.21 × 10−12 | 9.68 × 10−13 | 1.4180 | 1.1335 |
| 100 | 6.13 × 10−13 | 1.15 × 10−12 | 9.02 × 10−13 | 9.38 × 10−13 | 0.7843 | 0.8157 |
| 200 | 1.62 × 10−12 | 7.01 × 10−13 | 7.82 × 10−13 | 0.4317 | 0.4815 | |
| 400 | 2.41 × 10−12 | 4.31 × 10−13 | 5.10 × 10−13 | 0.1788 | 0.2116 | |
| 1000 | 2.17 × 10−13 | 4.17 × 10−12 | 2.49 × 10−13 | 2.34 × 10−13 | 0.0597 | 0.0561 |
| 2000 | 7.45 × 10−12 | 1.43 × 10−13 | 1.35 × 10−13 | 0.0192 | 0.0181 | |
| 4000 | 1.29 × 10−11 | 8.85 × 10−14 | 8.50 × 10−14 | 0.0069 | 0.0066 | |
| 10,000 | 4.18 × 10−14 | 4.90 × 10−11 | 4.25 × 10−14 | 4.22 × 10−14 | 0.0009 | 0.0009 |
| Metric | Free-Running OCXO | LS Fitting | Optimized LQG | LQG vs. Free (LQG/Free) | LQG vs. LS (LQG/LS) |
|---|---|---|---|---|---|
| Clock Bias peak to peak (ns) | 930 | 0.9 | 0.3 | ↑ 99.97% | ↑ 66.67% |
| Clock Bias RMS (ns) | 420 | 0.46 | 0.14 | ↑ 99.89% | ↑ 69.56% |
| Frequency Deviation | 9.15 × 10−11 | 8.94 × 10−12 | 2.5 × 10−12 | ↑ 97.27% | ↑ 72.04% |
| Stability @10 s (ADEV) | 7.35 × 10−13 | 1.05 × 10−12 | 8.08 × 10−13 | ↓ 9.93% | ↑ 23.05% |
| Stability @100 s (ADEV) | 1.15 × 10−12 | 9.02 × 10−13 | 9.38 × 10−13 | ↑ 81.57% | ↓ 3.90% |
| Stability @1000 s (ADEV) | 4.17 × 10−12 | 2.49 × 10−13 | 2.34 × 10−13 | ↑ 94.39% | ↑ 6.02% |
| Stability @10,000 s (ADEV) | 4.90 × 10−11 | 4.25 × 10−14 | 4.22 × 10−14 | ↑ 99.91% | ↑ 0.71% |
| Condition | Clock Bias RMS (ns) | Frequency Deviation | Frequency Stability (ADEV τ = 1 s) | Frequency Stability (ADEV τ = 10 s) | Frequency Stability (ADEV τ = 100 s) | Frequency Stability (ADEV τ = 1000 s) | Frequency Stability (ADEV τ = 10,000 s) |
|---|---|---|---|---|---|---|---|
| Baseline (25 °C) | 0.14 | 4.3 × 10−12 | 6.25 × 10−13 | 7.68 × 10−13 | 9.2 × 10−13 | 2.2 × 10−13 | 4.41 × 10−14 |
| +45 °C | 0.19 (↓ 35%) | 5.42 × 10−12 (↓ 26%) | 5.72 × 10−13 (↑ 8%) | 7.5 × 10−13 (↑ 2%) | 1.03 × 10−12 (↓1 2%) | 2.25 × 10−13 (↓ 2%) | 4.42 × 10−14 (↓ 0.2%) |
| +10 °C | 0.17 (↓ 21%) | 5.48 × 10−12 (↓ 27%) | 5.31 × 10−13 (↑ 15%) | 8.61 × 10−13 (↓ 12%) | 1.01 × 10−12 (↓ 9%) | 2.51 × 10−13 (↓ 14%) | 4.24 × 10−14 (↑ 4%) |
| 0 °C | 0.16 (↓ 14%) | 5.52 × 10−12 (↓ 28%) | 6.13 × 10−13 (↑ 2%) | 7.64 × 10−13 (↑ 0.5%) | 9.57 × 10−13 (↓ 4%) | 2.22 × 10−13 (↓ 0.9%) | 4.01 × 10−14 (↑ 9%) |
| −10 °C | 0.16 (↓ 14%) | 4.63 × 10−12 (↓ 7%) | 5.73 × 10−13 (↑ 8%) | 8.85 × 10−13 (↓ 15%) | 8.99 × 10−13 (↑ 2%) | 2.21 × 10−13 (↓ 0.45%) | 4.13 × 10−14 (↑ 6%) |
| −20 °C | 0.18 (↓ 28%) | 5.36 × 10−12 (↓ 24%) | 6.32 × 10−13 (↑ 1%) | 7.4 × 10−13 (↑ 3.6%) | 8.53 × 10−13 (↑ 7%) | 2.4 × 10−13 (↓ 9%) | 4.63 × 10−14 (↓ 5%) |
| Random Vibration | 0.16 (↓ 12%) | 4.67 × 10−12 (↓ 8.6%) | 5.23 × 10−13 (↑ 16%) | 7.99 × 10−13 (↓ 4%) | 1.02 × 10−12 (↓ 10%) | 2.45 × 10−13 (↓ 11%) | 4.38 × 10−14 (↑ 0.6%) |
| Sinusoidal Vibration | 0.17 (↓ 21%) | 5.45 × 10−12 (↓ 26%) | 5.31 × 10−13 (↑ 15%) | 7.66 × 10−13 (↑ 0.3%) | 9.25 × 10−13 (↓ 0.5%) | 2.35 × 10−13 (↓ 7%) | 4.39 × 10−14 (↑ 0.6%) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, D.; Liao, W.; Liu, B.; Yu, Q. A Multi-Constraint Co-Optimization LQG Frequency Steering Method for LEO Satellite Oscillators. Sensors 2025, 25, 4733. https://doi.org/10.3390/s25154733
Wang D, Liao W, Liu B, Yu Q. A Multi-Constraint Co-Optimization LQG Frequency Steering Method for LEO Satellite Oscillators. Sensors. 2025; 25(15):4733. https://doi.org/10.3390/s25154733
Chicago/Turabian StyleWang, Dongdong, Wenhe Liao, Bin Liu, and Qianghua Yu. 2025. "A Multi-Constraint Co-Optimization LQG Frequency Steering Method for LEO Satellite Oscillators" Sensors 25, no. 15: 4733. https://doi.org/10.3390/s25154733
APA StyleWang, D., Liao, W., Liu, B., & Yu, Q. (2025). A Multi-Constraint Co-Optimization LQG Frequency Steering Method for LEO Satellite Oscillators. Sensors, 25(15), 4733. https://doi.org/10.3390/s25154733





