Practical and Compact Guided Mode Resonance Sensing System for Highly Sensitive Real-Time Detection
Abstract
1. Introduction
2. Design and Sensing Principle of GMR Sensor
3. Materials and Methods
3.1. Fabrication of Sensors
3.2. Optical Detection System
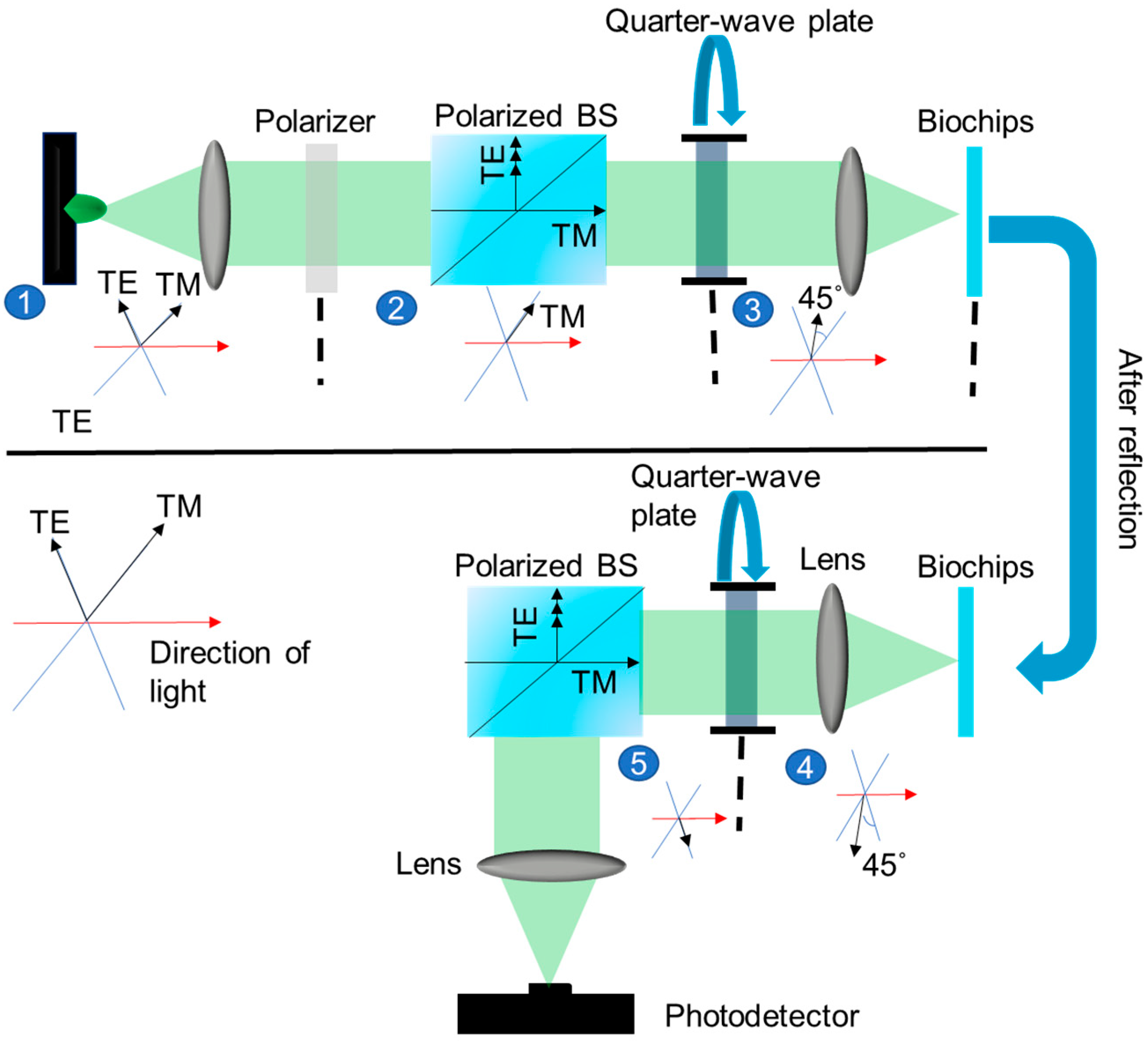
4. Results and Discussion
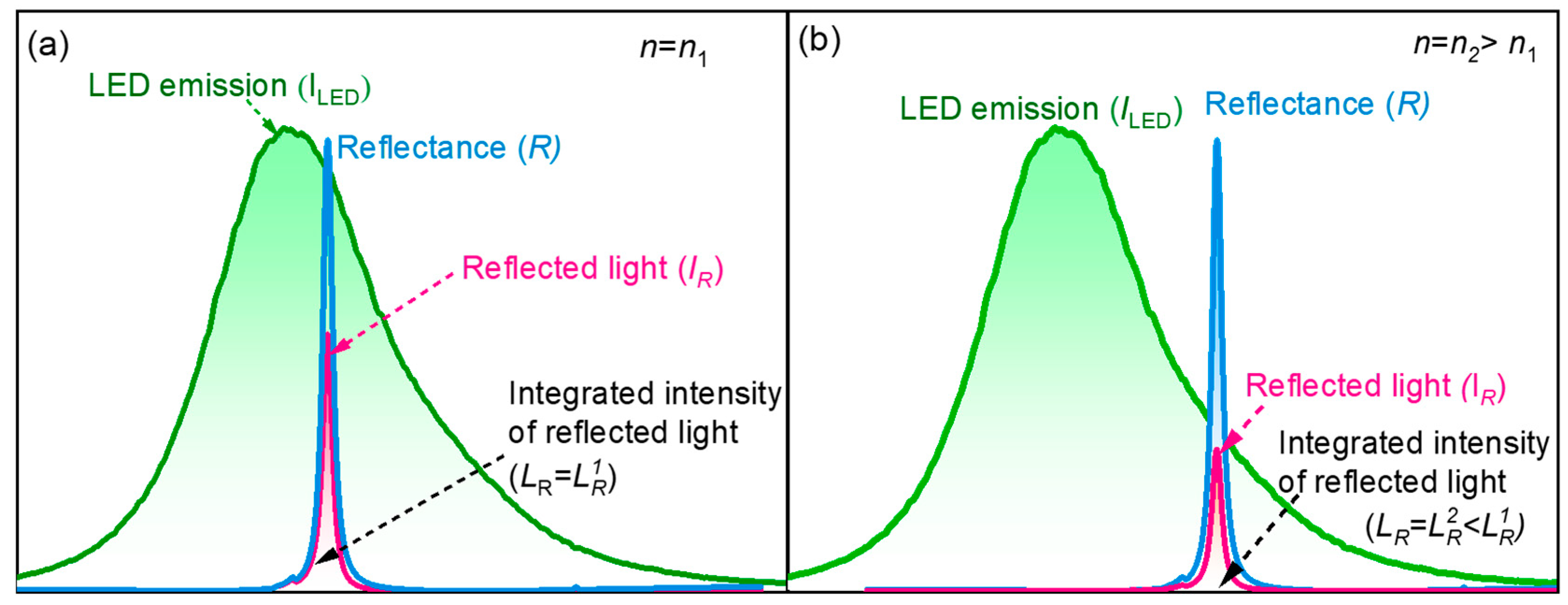
4.1. Simulation Results
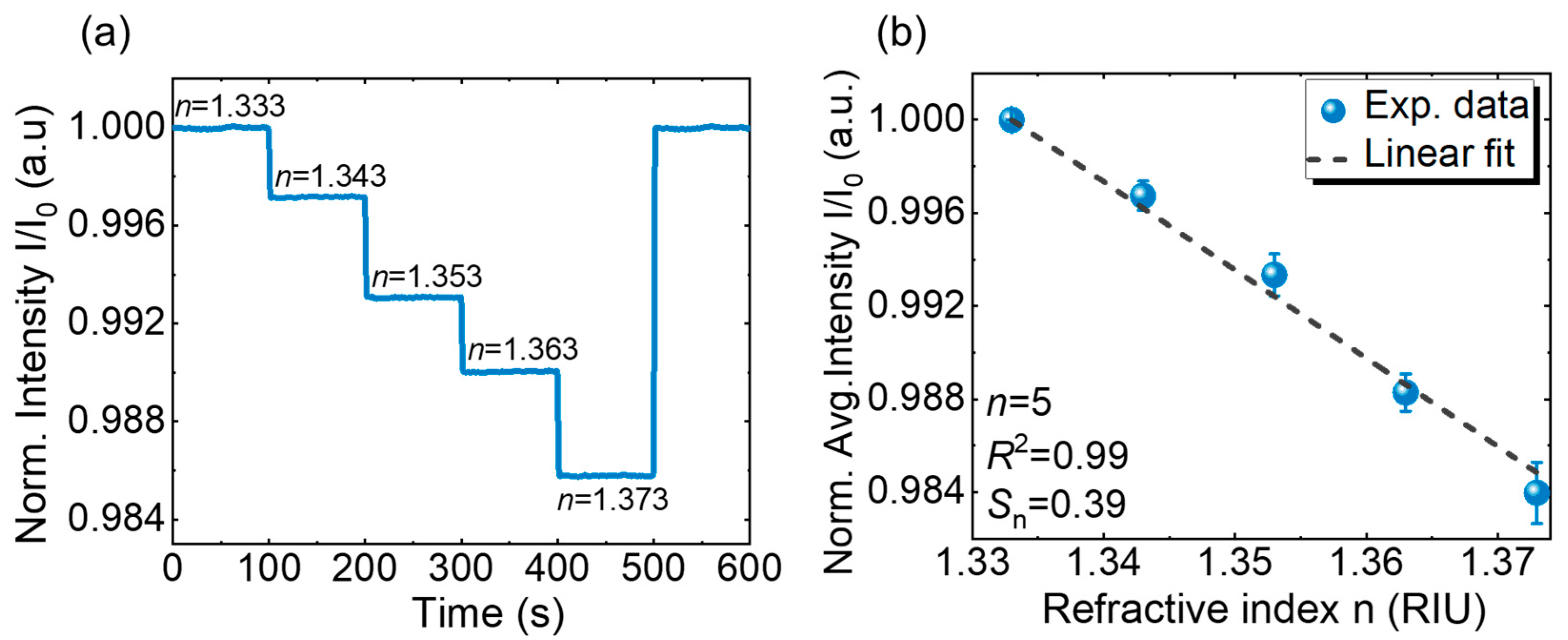
4.2. RI Sensing
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tsai, M.-Z.; Hsiung, C.-T.; Chen, Y.; Huang, C.-S.; Hsu, H.-Y.; Hsieh, P.-Y. Real-time CRP detection from whole blood using micropost-embedded microfluidic chip incorporated with label-free biosensor. Analyst 2018, 143, 503–510. [Google Scholar] [CrossRef] [PubMed]
- Lin, Y.-C.; Hsieh, W.-H.; Chau, L.-K.; Chang, G.-E. Intensity-detection-based guided-mode-resonance optofluidic biosensing system for rapid, low-cost, label-free detection. Sens. Actuators B 2017, 250, 659–666. [Google Scholar] [CrossRef]
- Liu, A.; Hofmann, W.H.; Bimberg, D.H. Integrated high-contrast-grating optical sensor using guided mode. IEEE J. Quantum Electron. 2014, 51, 1–8. [Google Scholar] [CrossRef]
- Roy, D.; Kwak, J.-W.; Maeng, W.J.; Kim, H.; Park, J.W. Dendron-modified polystyrene microtiter plate: Surface characterization with picoforce AFM and influence of spacing between immobilized amyloid beta proteins. Langmuir 2008, 24, 14296–14305. [Google Scholar] [CrossRef]
- Qi, Z.-M.; Matsuda, N.; Santos, J.H.; Takatsu, A.; Kato, K. Prism-coupled multimode waveguide refractometer. Opt. Lett. 2002, 27, 689–691. [Google Scholar] [CrossRef]
- Llobera, A.; Wilke, R.; Büttgenbach, S. Optimization of poly (dimethylsiloxane) hollow prisms for optical sensing. Lab Chip 2002, 5, 506–511. [Google Scholar] [CrossRef] [PubMed]
- Heideman, R.; Lambeck, P. Remote opto-chemical sensing with extreme sensitivity: Design, fabrication and performance of a pigtailed integrated optical phase-modulated Mach–Zehnder interferometer system. Sens. Actuators B 1999, 61, 100–127. [Google Scholar] [CrossRef]
- Crespi, A.; Gu, Y.; Ngamsom, B.; Hoekstra, H.J.W.M.; Dongre, C.; Pollnau, M.; Ramponi, R.; Vlekkert, H.H.v.D.; Watts, P.; Cerullo, G.; et al. Three-dimensional Mach-Zehnder interferometer in a microfluidic chip for spatially-resolved label-free detection. Lab Chip 2010, 10, 1167–1173. [Google Scholar] [CrossRef]
- Djinovic, Z.; Tomic, M.; Kocsis, A. Optofluidic Micromachined Platform for RefractiveIndex Measurement. Chemosensors 2022, 10, 197. [Google Scholar] [CrossRef]
- Mazumdar, S.D.; Barlen, B.; Kramer, T.; Keusgen, M. A rapid serological assay for prediction of Salmonella infection status in slaughter pigs using surface plasmon resonance. J. Microbiol. Methods 2008, 75, 545–550. [Google Scholar] [CrossRef]
- Hu, W.; Li, C.M.; Dong, H. Poly (pyrrole-co-pyrrole propylic acid) film and its application in label-free surface plasmon resonance immunosensors. Anal. Chim. Acta 2008, 630, 67–74. [Google Scholar] [CrossRef] [PubMed]
- Gobi, K.V.; Iwasaka, H.; Miura, N. Self-assembled PEG monolayer based SPR immunosensor for label-free detection of insulin. Biosens. Bioelectron. 2007, 22, 1382–1389. [Google Scholar] [CrossRef]
- Chien, W.-Y.; Khalid, M.Z.; Hoa, X.D.; Kirk, A.G. Monolithically integrated surface plasmon resonance sensor based on focusing diffractive optic element for optofluidic platforms. Sens. Actuators B 2009, 138, 441–445. [Google Scholar] [CrossRef]
- Jose, J.; Park, M.; Pyun, J.-C. E. coli outer membrane with autodisplayed Z-domain as a molecular recognition layer of SPR biosensor. Biosens. Bioelectron. 2010, 25, 1225–1228. [Google Scholar] [CrossRef]
- Vaisocherová, H.; Mrkvová, K.; Piliarik, M.; Jinoch, P.; Šteinbachová, M.; Homola, J. Surface plasmon resonance biosensor for direct detection of antibody against Epstein-Barr virus. Biosens. Bioelectron. 2007, 22, 1020–1026. [Google Scholar] [CrossRef]
- Malic, L.; Sandros, M.G.; Tabrizian, M. Designed biointerface using near-infrared quantum dots for ultrasensitive surface plasmon resonance imaging biosensors. Anal. Chem. 2011, 83, 5222–5229. [Google Scholar] [CrossRef] [PubMed]
- Fry, D.R.; Bobbitt, D.R. Hapten immobilization for antibody sensing using a dynamic modification protocol. Talanta 2001, 55, 1195–1203. [Google Scholar] [CrossRef] [PubMed]
- Hsu, W.-T.; Hsieh, W.-H.; Cheng, S.-F.; Jen, C.-P.; Wu, C.-C.; Li, C.-H.; Lee, C.-Y.; Li, W.-Y.; Chau, L.-K.; Chiang, C.-Y.; et al. Integration of fiber optic-particle plasmon resonance biosensor with microfluidic chip. Anal. Chim. Acta 2001, 697, 75–82. [Google Scholar] [CrossRef] [PubMed]
- Sai, V.; Kundu, T.; Deshmukh, C.; Titus, S.; Kumar, P.; Mukherji, S. Label-free fiber optic biosensor based on evanescent wave absorbance at 280 nm. Sens. Actuators B 2010, 143, 724–730. [Google Scholar] [CrossRef]
- Tazawa, H.; Kanie, T.; Katayama, M. Fiber-optic coupler based refractive index sensor and its application to biosensing. Appl. Phys. Lett. 2007, 91, 113901. [Google Scholar] [CrossRef]
- Chau, L.-K.; Lin, Y.-F.; Cheng, S.-F.; Lin, T.-J. Fiber-optic chemical and biochemical probes based on localized surface plasmon resonance. Sens. Actuators B 2006, 113, 100–105. [Google Scholar] [CrossRef]
- Block, I.D.; Chan, L.L.; Cunningham, B.T. Photonic crystal optical biosensor incorporating structured low-index porous dielectric. Sens. Actuators B 2006, 120, 187–193. [Google Scholar] [CrossRef]
- Surdo, S.; Merlo, S.; Carpignano, F.; Strambini, L.M.; Trono, C.; Giannetti, A.; Baldini, F.; Barillaro, G. Optofluidic microsystems with integrated vertical one-dimensional photonic crystals for chemical analysis. Lab Chip 2012, 12, 4403–4415. [Google Scholar] [CrossRef]
- Guider, R.; Gandolfi, D.; Chalyan, T.; Pasquardini, L.; Samusenko, A.; Pederzolli, C.; Pucker, G.; Pavesi, L. Sensitivity and limit of detection of biosensors based on ring resonators. Sens. Bio-Sens. Res. 2015, 6, 99–102. [Google Scholar] [CrossRef]
- Soria, S.; Berneschi, S.; Brenci, M.; Cosi, F.; Nunzi Conti, G.; Pelli, S.; Righini, G.C. Optical microspherical resonators for biomedical sensing. Sensors 2011, 11, 785–805. [Google Scholar] [CrossRef] [PubMed]
- Barshilia, D.; Chau, L.-K.; Chang, G.-E. Low-cost planar waveguide-based optofluidic sensor for real-time refractive index sensing. Opt. Express 2020, 28, 27337–27345. [Google Scholar] [CrossRef] [PubMed]
- Barshilia, D.; Komaram, A.C.; Chen, P.-C.; Chau, L.-K.; Chang, G.-E. Slab waveguide-based particle plasmon resonance optofluidic biosensor for rapid and label-free detection. Analyst 2022, 147, 4417–4425. [Google Scholar] [CrossRef]
- Barshilia, D.; Huang, J.-J.; Komaram, A.C.; Chen, Y.-C.; Chen, C.-D.; Syu, M.-Y.; Chao, W.-C.; Chau, L.-K.; Chang, G.-E. Ultrasensitive and rapid detection of procalcitonin via waveguide-enhanced nanogold-linked immunosorbent assay for early sepsis diagnosis. Nano Lett. 2024, 24, 2596–2602. [Google Scholar] [CrossRef]
- Ku, Y.-F.; Li, H.-Y.; Hsieh, W.-H.; Chau, L.-K.; Chang, G.-E. Enhanced sensitivity in injection-molded guided-mode-resonance sensors via low-index cavity layers. Opt. Express 2015, 23, 14850–14859. [Google Scholar] [CrossRef]
- Zeng, Z.; Liu, H.; Zhang, H.; Cheng, S.; Yi, Y.; Yi, Z.; Wang, J.; Zhang, J. Tunable ultra-sensitive four-band terahertz sensors based on Dirac semimetals. Phot. Nanostruct. Fund. App. 2025, 63, 101347. [Google Scholar] [CrossRef]
- Zeng, L.; Li, B.; Zhang, X. Plasmonic sensor based on multi fano resonance in inverse T shape structure for detection of CO2 concentration. IEEE Photonics J. 2023, 15, 1–5. [Google Scholar] [CrossRef]
- Orgovan, N.; Kovacs, B.; Farkas, E.; Szabó, B.; Zaytseva, N.; Fang, Y.; Horvath, R. Bulk and surface sensitivity of a resonant waveguide grating imager. Appl. Phys. Lett. 2014, 104, 083506. [Google Scholar] [CrossRef]
- Lin, S.-F.; Wang, C.-M.; Ding, T.-J.; Tsai, Y.-L.; Yang, T.-H.; Chen, W.-Y.; Chang, J.-Y. Sensitive metal layer assisted guided mode resonance biosensor with a spectrum inversed response and strong asymmetric resonance field distribution. Opt. Express 2012, 20, 14584–14595. [Google Scholar] [CrossRef] [PubMed]
- Fang, Y.; Ferrie, A.M.; Fontaine, N.H.; Mauro, J.; Balakrishnan, J. Resonant waveguide grating biosensor for living cell sensing. Biophys. J. 2006, 91, 1925–1940. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J. Polarization Optics; Dinglong Books Co., Ltd.: Taipei City, Taiwan, 2013. [Google Scholar]
- Yang, J.-M.; Yang, N.-Z.; Chen, C.-H.; Huang, C.-S. Gradient waveguide thickness guided-mode resonance biosensor. Sensors 2021, 21, 376. [Google Scholar] [CrossRef]
- Huang, L.; Jin, R.; Zhou, C.; Li, G.; Xu, L.; Overvig, A.; Deng, F.; Chen, X.; Lu, W.; Alù, A.; et al. Ultrahigh-Q guided mode resonances in an all-dielectric metasurface. Nat. Commun. 2023, 14, 3433. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Wang, B.; Guo, Z.; Wu, X. Guided mode resonance sensors with optimized figure of merit. Nanomaterials 2019, 9, 837. [Google Scholar] [CrossRef]
- Maleki, M.; Mehran, M. Guided-mode resonance sensors: Different schemes for different applications. J. Opt. Soc. Am. 2022, 39, 1634. [Google Scholar] [CrossRef]
- Pamanes, A.D.L.; Osuna, E.C.; Mago, D.L. Jones Matrix Characterization of Optical Elements via Evolutionary Algorithms. arXiv 2021, arXiv:2101.12293. [Google Scholar]
- Li, H.-Y.; Hsu, W.-C.; Liu, K.-C.; Chen, Y.-L.; Chau, L.-K.; Hsieh, S.; Hsieh, W.-H. A low cost: Label-free biosensor based on a novel double-sided grating waveguide coupler with sub-surface cavities. Sens. Actuators B Chem. 2015, 206, 371–380. [Google Scholar] [CrossRef]
- Viphavakit, C.; Patchoo, W.; Boonruang, S.; Themistos, C.; Komodromos, M.; Mohammed, W.S.; Rahman, B.M.A. Demonstration of polarization-independent surface plasmon resonance polymer waveguide for refractive index sensing. J. Light. Tech. 2017, 35, 3012–3019. [Google Scholar] [CrossRef][Green Version]
- Goyal, A.-K.; Dutta, H.-S.; Pal, S. Development of uniform porous one-dimensional photonic crystal-based sensor. Optik 2020, 223, 165597. [Google Scholar] [CrossRef]
- Liu, I.-C.; Chen, P.-C.; Chau, L.-K.; Chang, G.-E. Optofluidic refractive-index sensors employing bent waveguide structures for low-cost, rapid chemical and biomedical sensing. Opt. Exp. 2018, 26, 273–283. [Google Scholar] [CrossRef] [PubMed]
- Das, S.; Patnaik, A.; Singh, A.; Rao, V.R.; Kundu, T. A novel thiol-ene-epoxy polymer based Optical Waveguide for Refractometric Sensing. J. Light. Tech 2023, 42, 2178–2185. [Google Scholar] [CrossRef]
- Lin, S.-F.; Chang, F.-C.; Chen, Z.-H.; Wang, C.-M.; Yang, T.-H.; Chen, W.-Y.; Chang, J.-Y. A polarization control system for intensity-resolved guided mode resonance sensors. Sensors 2014, 14, 5198–5206. [Google Scholar] [CrossRef]
- Lapsley, M.I.; Chiang, I.-K.; Zheng, Y.B.; Ding, X.; Mao, X.; Huang, T.J. A single-layer, planar, optofluidic Mach–Zehnder interferometer for label-free detection. Lab Chip 2011, 11, 1795–1800. [Google Scholar] [CrossRef]
- Kan, T.; Tsujiuchi, N.; Iwase, E.; Matsumoto, K.; Shimoyama, I. Planar near-infrared surface plasmon resonance sensor with Si prism and grating coupler. Sens. Actuators B Chem. 2010, 144, 295–300. [Google Scholar] [CrossRef]




| Component Type | Representation of the Jones Moment Oscillation of the Component |
|---|---|
| Green light source | |
| Polarizer | |
| Polarizing beam splitter TM | |
| Quarter—wave plate 45° | |
| Chip reflection | |
| 1/4 Wave plate (quarter-wave plate-45°) reverse | |
| Polarizing beam splitter TE |
| Sensor Type | Fabrication Method | Resolution (RIU) | Cost | Ref. |
|---|---|---|---|---|
| Gold-coated SPR sensor | Contact lithography and nanoimprinting | Low | [42] | |
| PhC | PECVD | Low | [43] | |
| Bent waveguide | Spin coating and UV lithography | Low | [44] | |
| Functional polymer-based planar optical waveguide | Spin coating | High | [45] | |
| GMR sensor | Laser interference lithography | Low | [46] | |
| Interferometer | Soft lithography | Low | [47] | |
| Si prism and grating coupler | EB lithography | High | [48] | |
| GMR sensor | Injection molding and nanoimprinting. | Low | This work |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.-S.; Barshilia, D.; Hsieh, C.-J.; Li, H.-Y.; Hsieh, W.-H.; Chang, G.-E. Practical and Compact Guided Mode Resonance Sensing System for Highly Sensitive Real-Time Detection. Sensors 2025, 25, 4019. https://doi.org/10.3390/s25134019
Chen Y-S, Barshilia D, Hsieh C-J, Li H-Y, Hsieh W-H, Chang G-E. Practical and Compact Guided Mode Resonance Sensing System for Highly Sensitive Real-Time Detection. Sensors. 2025; 25(13):4019. https://doi.org/10.3390/s25134019
Chicago/Turabian StyleChen, Yen-Song, Devesh Barshilia, Chia-Jui Hsieh, Hsun-Yuan Li, Wen-Hsin Hsieh, and Guo-En Chang. 2025. "Practical and Compact Guided Mode Resonance Sensing System for Highly Sensitive Real-Time Detection" Sensors 25, no. 13: 4019. https://doi.org/10.3390/s25134019
APA StyleChen, Y.-S., Barshilia, D., Hsieh, C.-J., Li, H.-Y., Hsieh, W.-H., & Chang, G.-E. (2025). Practical and Compact Guided Mode Resonance Sensing System for Highly Sensitive Real-Time Detection. Sensors, 25(13), 4019. https://doi.org/10.3390/s25134019








