Abstract
The blockchain-enabled industrial Internet of Things (IIoT) faces security threats such as quantum computing attacks and privacy disclosure. Targeting these issues, in this study, we design a new lattice-based linkable ring signature (LRS) scheme, which is used to achieve privacy protection for the blockchain-enabled IIoT. Firstly, by using the trapdoor generation algorithm on the lattice and the rejection sampling lemma, we propose a new lattice-based LRS scheme with anti-quantum security and anonymity. Then, we introduce it into blockchain. Through the stealth address and key image technologies, we construct a privacy protection scheme for blockchain in the IIoT, and this LRS scheme protects identity privacy for users through anonymous blockchain. In addition, it also can resist the double spending attack with the linking user’s signature. Lastly, we provide a security analysis, and it is proven that our ring signature scheme satisfies correctness, anonymity, unforgeability and linkability. Compared with other similar schemes, the performance simulation indicates that our scheme’s public key and signature are shorter in size, and its computation overhead and time cost are lower. Consequently, our novel LRS scheme is more secure and practical, which provides privacy protection and anti-quantum security for the blockchain-enabled IIoT.
1. Introduction
Recently, the integration of blockchain and the industrial Internet of Things (IIoT) has emerged as a novel trend and area of research within industrial applications [1,2]. However, smart objects attached to the IIoT interact with humans and also process their private data [3,4]. Moreover, information is collected in large quantities and disclosed to the Internet without the consent of specific persons. In data storage, privacy disclosure stands out as one of the most serious threats within the IIoT [5,6].
In 2008, Nakamoto proposed blockchain for the first time [7]. However, with the in-depth study of blockchain, more and more people take a skeptical attitude towards blockchain’s anonymity in bitcoin trading [8,9,10,11]. In 2016, Zerocash was designed, which satisfies anonymity [12]. Saberhagen et al. designed the CryptoNote protocol [13]. Afterwards, Monero was proposed based on this CryptoNote protocol by using a ring signature to achieve anonymity. Thus, the ring signature was proposed [14]. Then, Liu et al. proposed a new kind of ring signature scheme, which was called the linkable ring signature (LRS) [15]. In LRS, not only does the signer’s identity in a ring signature remain anonymous but two ring signatures that are signed by the same signer can also be linked [16]. Considering its advantages, the LRS scheme is suitable in many different practical applications, such as e-voting, e-money, supply chains, and healthcare [17,18,19]. However, it still faces a problem, which cannot be ignored in Monero and Zerocash [20]. More specifically, in 2018, Fedorov clearly pointed out the security risks of quantum computing in blockchain [21].
Fortunately, lattice-based cryptography has been proven to have anti-quantum security [22]. Afterwards, Ajtai provided an innovative algorithm for constructing random short lattices [23,24]. Gentry et al. put forward a trapdoor function to construct a cryptographic algorithm [25]. Subsequently, some lattice-based signature schemes were proposed based on the bonsai tree algorithm [26]. In 2010, Agrawal et al. proposed an efficient lattice basis delegation algorithm [27]. By using this algorithm, Wang proposed an identity-based ring signature scheme [28]. Lyubashevsky provided the rejection sampling lemma for constructing lattice-based signatures without using the hash-and-sign methodology. This signature scheme is provably secure based on the worst-case hardness of the -SIVP problem [29]. Then, a new ring signature scheme on lattice was proposed, and its security was proven under the random oracle model [30].
Facing quantum computing attacks and privacy disclosure issues in blockchain-enabled IIoT, we propose a new LRS scheme and introduce it into blockchain to design a new post-quantum blockchain (PQB) with privacy protection for IIoT.
The rest of this study is organized as follows. In Section 2, some definitions and lemmas of the lattice theories are presented. In Section 3, we propose a secure LRS scheme based on lattice. A security proof is presented in Section 4. In Section 5, this LRS scheme is introduced into blockchain; we construct a privacy protection scheme for blockchain in IIoT and present a performance analysis and efficiency comparison of our scheme with other schemes. In Section 6, conclusions are provided.
2. Preliminaries
2.1. Lattice and Hard Problem
In the following, denotes the real number set, and denotes the positive integer set. Therefore, we use to stand for the m-dimensional Euclidean vector space. In general, . and denote lattice in the following content, vector in the space , and .
Definition 1.
(Lattice): Suppose that there are n linearly independent vectors , so lattice L can be represented as follows.
Definition 2.
(Lattice shortest independent vector problem (SIVP)): Given an n-dimensional lattice L, output a set of n linearly independent vectors and
Definition 3.
(Lattice SIS problem): Suppose that we have a real constant and a matrix where q is a prime. Find a non-zero vector such that and .
2.2. Trapdoor and Lemmas
Lemma 1
[25]. Select a matrix where prime number q > 2, B is a basis of , the Gaussian parameter . Thus, for any vector , there exists a probabilistic polynomial time (PPT) algorithm , which can output a vector from a distribution that is close to .
Lemma 2
[25]. For any prime and any , there exists a PPT algorithm , which can output a matrix and a full-rank basis of . And the distribution of A is statistically close to uniform over , such that and .
Lemma 3
[27]. For a matrix , the m-dimensional lattice , the Gaussian parameter , input a basis T of the lattice , and it has the nonsingular matrix , . By running the PPT algorithm , a basis of can be obtained and with overwhelming probability .
Lemma 4. Rejection sampling
[29]. Suppose that V is a subset and each element v has norm less than t, , and is a probability distribution. Thus, there is a constant such that output distribution statistical distance of the following two algorithms is less than .
Algorithm A: , , output (x,v) with the probability .
Algorithm B: , , output (x,v) with the probability .
The probability that algorithm A outputs something is at least .
2.3. Related Work
Some related works from recent years of the blockchain-based LRS schemes and privacy-preserving blockchain mechanisms for IIoT are given in this section. In 2018, Wang et al. proposed a lattice-based ring signature scheme without trapdoors [31]. Gao et al. presented a new ring signature scheme from lattice in 2019 [32]. Through experiments under the same parameters, we find that this scheme’s signature size is large, which leads to its low efficiency. In 2021, Le et al. presented an identity-based LRS (IdLRS) in both integer lattice and ideal lattice settings [33]. Subsequently, Tang et al. constructed a new identity-based LRS scheme over NTRU lattice by employing the technologies of trapdoor generation and rejection sampling [34]. In 2022, Cao et al. proposed a new LRS scheme with lattice [35]. In this scheme, ring members’ public keys and the real signer’s private key are both used as the input of a hash function to obtain the output instead of the vector obeying the discrete Gaussian distribution selected in other schemes. In 2023, Cao et al. proposed an efficient LRS based on ideal lattice [36]. Subsequently, in 2024, Zhang et al. designed a lattice-based LRS scheme to provide accurate signature traceability mechanisms for transactions in the blockchain-enabled system [37]. It can protect the system by resisting the quantum attack. Then, Duan et al. presented a novel ring confidential transactions protocol by introducing the linkable threshold ring signature (LTRS) [38]. Afterwards, Xie et al. proposed a linkable, k-times traceable and revocable ring signature (Lk-TRS), which is used to construct a blockchain anonymous transaction system in 2025 [39].
The above method innovatively integrates and utilizes the security features of lattice-based cryptography and LRS, fully leveraging the excellent performance of lattice-based cryptography in resisting quantum computing attacks and the unique advantages of LRS in safeguarding user privacy, thereby achieving significant improvements in both the privacy protection and quantum security of blockchain-enabled IIoT. Unfortunately, in the above LRS schemes, both the amount of signature computation and the size of the signature will increase linearly with the number of ring members. This leads to overall low efficiency and insufficient practicality of the LRS scheme, especially in applications with a large number of users and transactions such as blockchain.
3. Lattice-Based LRS Scheme
3.1. Formal Definition
Suppose that the number of users in the ring is k, and represents all users in the ring.
Definition 4.
(Linkable ring signature): The linkable ring signature scheme is usually composed of five PPT algorithms as follows.
Setup (): Select a security parameter n. This Setup algorithm outputs public parameters PP and the master key Mk.
KeyGen: Input public parameters, the KeyGen algorithm can output the secret key pair (pk, sk) and a corresponding public key I. So, we can obtain a public key set .
Ringsign : Input public key set R of the ring, the signer’s key pair and the message . Run the Ringsign algorithm to output signature e of message M.
Ringverify (e, R, M): Input the public key set R, message M and ring signature e; if the signature e is reasonable, the Ringverify algorithm accepts or refuses.
Link : Take a set and two signatures and . Output “linked” or “independent”.
3.2. Security Model
Generally speaking, the linkable ring signature scheme should satisfy three important security properties, namely anonymity, unforgeability and linkability.
Anonymity. The anonymity is defined by a game between adversary with a challenger as follows.
KeyGen (n). Input a security parameter n, challenger runs KeyGen algorithm to output a private key sk and a public key pk for each game participant, and there are k participants, . So, challenger obtains the public and private key pairs set .
Queries. Set the public key set . Suppose adversary selects a participant I with his public key . Challenger uses participant I’s public and private key pair and runs Ringsign algorithm to output the signature ; then, he returns to adversary .
Challenge. Adversary submits a message , ring and two other participants . The challenger chooses a bit and runs Ringsign algorithm to output signature , then returns to adversary .
Verify. If adversary outputs a guess and , adversary wins this game.
In this game, suppose that the probability of opponent a winning the game is , and the advantage of adversary is . If for every probabilistic polynomial-time adversary , the advantage is negligible, the ring signature scheme is anonymous.
Unforgeability. Unforgeability is defined by using the game between an adversary with a challenger as follows.
Setup. The challenger runs Setup(n) algorithm to generate public parameters PP and MK, and sends PP to the adversary . Then, adversary issues k queries on identity .
Queries. Set the public key set . Suppose adversary selects a participant I with his public key . Challenger uses participant I’s public and private key pair . Adversary submits a ring , private key and message msg. The challenger runs Ringsign algorithm to output signature , then returns to adversary .
Forgery. The adversary outputs , wins this game if:
- (1)
- Verify = accept.
- (2)
- Adversary does not have the private key of the user in .
- (3)
- is not submitted to sign query.
Linkability. For two different messages and , the signer can obtain two different signatures and . There exists a PPT algorithm which verifies the probability of the same signer is not negligible. On the contrary, if the two different signatures and are signed by different signers, the PPT algorithm verifies that the probability of the same signer is negligible. Thus, the signature scheme is linkable.
3.3. Details of Our Scheme
Here, a security parameter , a prime , , and is a collision-resistant hash function. . Suppose that there are k users in the ring . Our linkable ring signature scheme contains the five PPT algorithms as follows.
Setup
: Select and input the security parameter .
- (1)
- Based on Lemma 2, sender runs and obtain a random matrix and a corresponding short basis . is sender’s master key .
- (2)
- For each user , the hash function takes as input ID, outputs and message . Thus, the public parameter .
KeyGen
: For each member, select each ID and input the Gaussian parameter , MK, and PP.
Based on Lemma 3, sender runs and obtains his private key . Thus, is a basis of , and his public key .
RingSign : Generate a signature by the following steps.
- (1)
- Randomly select a vector , compute .
- (2)
- Set and , select , then select vectors .
- (3)
- (4)
- Compute .
- (5)
- Let , if , . If , .
- (6)
- Output the ring signature .
Verify : Verifier can verify the correctness of this signature as follows.
- (1)
- For each and , verify .
- (2)
- Verify .
If the above conditions are satisfied, the verifier runs the following Link algorithm. Otherwise, this signature e will be rejected.
Link (I,e): There is a set I that these values are stored in, verifier checks if has been used in past signatures.
For two signatures and , if , return 1 (linked) to indicate these two signatures are signed by the same user. If not, return 0 (unlinked).
Correctness. Suppose that there is a set l, and , such that
Such that . Therefore, this linkable ring signature scheme satisfies correctness.
4. Security Analysis
4.1. Anonymity
Theorem 1.
Our proposed ring signature scheme satisfies anonymity.
Proof.
Suppose that there is an adversary attacking this proposed ring signature scheme based on the anonymity’s definition. □
KeyGen. At first, challenger selects k users to obtain an ID set . Then, for each user ID, input a security parameter n; challenger runs algorithm and generates a uniformly random matrix with a corresponding short basis . At last, challenger runs to obtain the private key . Similarly, a corresponding public key is . There are k participants , and challenger can obtain the public–private key pairs set .
Queries. Challenger answers the hash queries, private key queries and signing queries of adversary . Suppose adversary selects a participant with his ID. Challenger returns this ID’s public and private key pair and runs Ringsign algorithm to output signature , then returns this signature to adversary .
Challenge. Adversary submits a message , ring and two other participants . The challenger chooses a bit and runs Ringsign algorithm to output signature , then he returns this signature to adversary .
Guess. Adversary outputs a guess and verify .
For the signature, if , . If , . According to Lemma 4, is not distinguishable from Gauss distribution . Similarly, is also not distinguishable from . We can see that, because these two signatures, e and , have the same distribution of the domain, they are computationally indistinguishable.
In summary, under the simulated environment, the adversary in this anonymity game advantage is negligible in guessing the right identity.
4.2. Unforgeability
Theorem 2.
Under the lattice SIS problem assumption, the proposed linkable ring signature scheme is existentially unforgeable.
Proof.
Suppose that A is regarded as a PPT adversary. A is able to successfully attack this proposed scheme and forge a new signature. We use to denote the probability of success. Then, A is a subroutine, which can solve the lattice short integer solution problem via non-negligible probability. Thus, a PPT algorithm T is constructed, which is realized through interaction with the adversary A as follows. □
Setup. The challenger selects a user set and a user . And runs the Setup algorithm to obtain PP and MK, and sends PP to . Then, issues queries on identity .
KeyGen. For , challenger does as follow.
- (1)
- According to Lemma 2, challenger uses to obtain a random matrix with a corresponding short basis . is sender’s master key .
- (2)
- For each user , the hash function outputs . For message . obtains the public parameter . Then, transmits PP and U to .
- (3)
- Run to generate a secret key which is a basis of . Correspondingly, .
Queries. Challenger answers the following hash queries, private key queries and signing queries from adversary .
- (1)
- Hash queries. Adversary chooses a user’s . Challenger checks the list . If adversary submitted this query before, it will return the same result. Otherwise, Challenger runs the algorithm , returns to adversary and stores it in .
- (2)
- Private key queries. Adversary selects a user from U. Challenger checks the list and finds (). Then, challenger runs to return his private key to adversary and store it in .
- (3)
- Signing queries. Adversary submits a message M, a ring and . Challenger runs Ringsign algorithm to output ring signature , then return to adversary .
Forgery. Adversary submits a message , a ring , a user , adversary can forge a signature . wins the game if:
- (i)
- Verify is accepted.
- (ii)
- Adversary does not have the private key of the user in .
- (iii)
- is not submitted to the signing query.
According to our signature scheme, it is shown that if is a legal signature of ring , we have
Because challenger can use private key queries to obtain the private key of , is also a legal signature of ring , so we have
Through the analysis of Equations (3) and (4), we have
So, ; then, we have
Let , so , such that
Consequently, it means that the result is a non-zero solution to the lattice SIS problem.
At last, according to the preimage min-entropy property, the probability of the non-zero solution is not less than . The probability that adversary successfully forges a legal signature is , and . Therefore, the non-zero solution to the lattice problem with a negligible probability .
As shown in the calculation and analysis, the probability that adversary forges a legal and valid signature is negligible. Under the lattice SIS problem assumption, the proposed linkable ring signature scheme satisfies unforgeability. Thus, the proof of this theorem is completed.
4.3. Linkability
Theorem 3.
The proposed ring signature scheme is linkable. Formally, adversary cannot produce valid signatures with key images for any .
Proof.
Suppose that, for the sake of contradiction, adversary A can generate valid signatures. Since the secret key set , there is at least one which does not belong to the set I. Without a loss of generality, considering this event happened in , which is a valid signature, we have . Because does not belong to the set I, its secret key does not belong to secret key set S. Therefore, for and it contradicts previous assumptions, in which adversary A can generate valid signatures. Consequently, our ring signature scheme is linkable. □
5. LRS-Based Blockchain for IIoT
5.1. Stealth Address
As described in CryptoNote, the stealth address technology is used in all transactions to provide privacy protection for the receiver. For instance, Alice and Bob have a transaction to make. In this transaction, Alice needs to pay her cryptocurrency to Bob. At first, Alice generates a one-time address for Bob and publishes it as a broadcast in the distributed network. Subsequently, Bob has to check each transaction by using his private key to identify which transaction belongs to him. Subsequently, he recovers this secret key corresponding to the destination address.
Through using a stealth address, the connection of a blockchain transaction’s output with the recipient’s wallet address is broken. More specifically, the actual destination address of a transaction is hidden with the stealth address in CryptoNote. For the sake of protecting the privacy of receivers in blockchain, we also produce stealth addresses as follows, which will be used as the verifying and signing key pairs in the PQB with privacy protection based on lattice.
5.2. Blockchain with Privacy Protection
According to the framework of CryptoNote, in this subsection, we introduce our LRS scheme into blockchain to design a secure PQB scheme with privacy protection for IIoT. Suppose that Alice wants to transfer her cryptocurrency to Bob from her address of a secret key pair . As shown in Figure 1, we describe our scheme through the implementation of a transaction as follows.
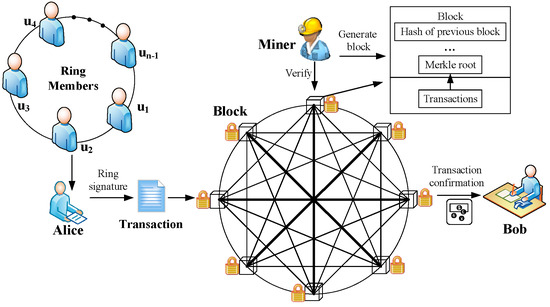
Figure 1.
Transaction in PQB with privacy protection.
Key generation. Alice and Bob run the KeyGen algorithm to obtain her/his secret key pairs and , respectively. It should be noted that Alice’s secret key pair address has been used for receiving the cryptocurrency in the last transaction.
Key image. Bob randomly selects a string . Then, he calculates and sends this hash value to Alice. Then, Alice calculates and key image .
Transaction generation. Alice specifies n−1 foreign outputs with the same amount as her outputs and mixes all of these foreign outputs without other people’s participation. All previous transactions with outputs are added to the hash function. Then, this hash value h is signed by running the Ringsign algorithm, which generates a ring signature . Afterwards, as shown in Figure 2, she inputs these outputs, Y, key image X, ring signature e and generates a new transaction tx.
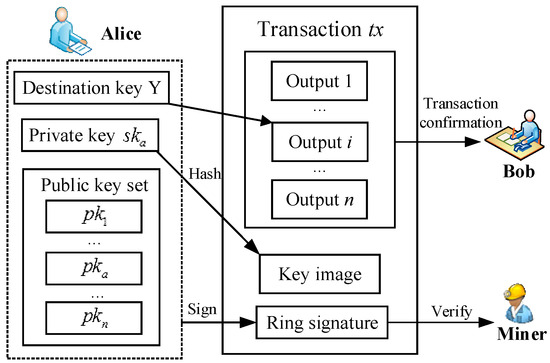
Figure 2.
LRS with privacy protection transactions for blockchain.
Transaction verification. By running the Link algorithm, the miner nodes verify whether the cryptocurrency in the transaction has been consumed to prevent a double spending attack. Subsequently, miner nodes run the Verify algorithm to verify whether the signature of this transaction is correct. If it is correct, this transaction will be encapsulated in a new block. Otherwise, this transaction will be discarded.
Transaction confirmation. Bob checks this transaction. Afterwards, he extracts the destination key from this transaction and calculates . If , this transaction is the one which Alice sends to Bob. Thus, Bob accepts this transaction, and he records with and in his wallet. When he wants to spend this coin with the destination address , he can use the corresponding one-time key pair to generate a new transaction as in the above steps.
Different from traditional blockchain, for each ring signature , it can be checked by using the public key set in our proposed scheme instead of a unique public key. Before the owner uses the same key pair to generate a second signature, the identity of the signer cannot be distinguished from other users in the public key set. More specifically, by using our LRS scheme in PQB for IIoT, the signer’s identity in a ring signature remains anonymous, and two ring signatures, which are signed by the same signer, can be linked. Therefore, this new PQB not only protects the user’s privacy information but also resists the double spending attack. Additionally, as discussed above, the LRS scheme used in PQB satisfies unforgeability. With these above security advantages, the proposed PQB scheme enhances data security for IIoT.
5.3. Security and Comparison
As previously highlighted, the lattice-based cryptography algorithm represents a unique mathematical structural model. It has been rigorously demonstrated to possess robust resistance against quantum computing attacks, positioning it as an indispensable component in the future landscape of information security. Consequently, in line with the aforementioned considerations, we opted to employ lattice-based cryptography as the foundational framework for constructing our linkable ring signature scheme. In this study, our linkable ring signature scheme’s security mainly depends on the intractability of the SIS problem from lattice-based cryptography. And the lattice SIS problem in an average case can be reduced to the SIVP in the worst case, which is often used to construct signature schemes for resisting quantum computing attacks [40]. Therefore, our scheme has anti-quantum security.
Furthermore, lattice-based cryptography algorithms are matrix and vector operations, and the computation cost largely determines the cryptography algorithm’s efficiency, especially the public key size and signature size. In this subsection, it is assumed that the parameters (n, m, q, k) are the same in our scheme and other related lattice-based ring signature schemes. The detailed comparison results are shown in Table 1. Compared with other schemes, the results show that our public key size and signature size are shorter than those in Refs. [32,33,34,35]. Therefore, our scheme is efficient, with lower computation costs.

Table 1.
Comparison of computation costs.
Meanwhile, Ttg, Tbd, Teb, Terb, Trb, Tsp, Tgsp, Tmul are set to represent the average consumption time of the following algorithms, TrapGen, BasisDel, ExtBasis, ExtRandBasis, RandBasis, SamplePre, GenSamplePre and vector multiplication, respectively. Then, the master key generation time, user key generation time and signature generation time in these above ring signature schemes are compared, respectively, and the time cost comparison results are shown in Table 2. Among them, our ring signature scheme only uses the TrapGen algorithm once in the master key generation, and the user key generation adopts the BasisDel algorithm times. Using the rejection sampling lemma, the main steps of generating a ring signature adopt simple vector multiplication. Through this comprehensive comparison, it shows that in the transaction signature process, our scheme’s time cost is less than that in other schemes.

Table 2.
Comparison of time costs.
Furthermore, based on the parameters of 80-bit and 192-bit security levels in Ref. [41], and in combination with the parameter requirements of the scheme in our study, the parameters used in the experimental testing are set as follows. We consider two security level of 80-bit and 192-bit, and the parameters polynomial degree n and modulus q are set as n = 256; q = 210, m = 3853 and n = 512; q = 210, m = 7706, respectively. Other reasonable parameters include g = 256, k = 10, . Under two security levels of 80-bit and 192-bit, the public key size, signature size and private key of our proposed scheme and those in Refs. [32,33,34,35] are compared. The simulation results are shown in Figure 3, where (a) and (b) represent the 80-bit security level and 192-bit security level, respectively. As shown in Figure 3, the public key size and signature size of the transaction in our scheme are 362.42 KB and 14.11 KB for 80-bit security, 1444.87 KB and 28.22 KB for 192-bit security. Under the same security levels, our scheme achieves a significant reduction in public key size and signature size compared to Refs. [32,33,35]. In terms of the generated private key size, since the private key sizes in Refs. [32,35] are 4m2logq, according to the parameter settings of 80-bit and 192-bit security levels, it is obvious that their sizes are much larger than other schemes. Ref. [33]’s generated private key sizes at 80-bit and 192-bit security levels are 458.74 KB and 1834.97 KB, respectively. Ref. [34]’s private key sizes are 0.38 KB and 0.76 KB at 80-bit and 192-bit security levels, respectively. And our scheme’s private key sizes are 0.09 KB for 80-bit security and 0.19 KB for 192-bits security, which are significantly smaller than those in other schemes. After comprehensive comparisons, our LRS scheme for blockchain has lower computational overhead, reduces storage costs, and achieves higher efficiency.

Figure 3.
(a) Comparison with 80-bit security; (b) comparison with 192-bit security [32,33,34,35].
6. Conclusions
This study contributes to privacy protection in the process of optimizing user privacy data sharing in blockchain-enabled IIoT. We design an LRS scheme with anti-quantum security and anonymity. This scheme is based on the lattice problem and has superior security. At the same time, the characteristics of LRS can better hide the personal privacy in blockchain. In particular, by combining the stealth address and key image technologies, this scheme is introduced into the construction of blockchain-enabled IIoT, which can support secure data sharing and ensure that data are not tampered with. Meanwhile, the combination of LRS and blockchain-enabled IIoT can effectively enhance the privacy and security of users. Then, it is proved that the LRS scheme in our construction satisfies the security requirements of correctness, unforgeability, anonymity, and linkability. The comparison of key sizes shows that the proposed LRS scheme is efficient and reduces data space overhead. Performance comparisons indicate that our scheme is more practical for IIoT. Our work provides new solutions to the privacy leakage problem of data sharing in the current IIoT system and promotes the application of blockchain in IIoT. In the field of the data sharing of IIoT, there are still several highly promising research directions that urgently need to be explored, especially identity authentication technology, refined data access control mechanisms, and efficient data retrieval strategies. These cutting-edge topics will constitute the content of our future research work.
Author Contributions
Conceptualization, F.G. and Y.G.; methodology, F.G., J.J. and Y.G.; formal analysis, F.G. and Y.G.; writing—original draft preparation, F.G. and Y.G.; writing—review and editing, Y.G., X.C. (Xueting Chen), X.C. (Xiubo Chen) and Z.J.; F.G. and Y.G. contributed equally to this work and should be considered joint first authors. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by the National Natural Science Foundation of China (62172005, 72293583, 72293580, 62176240), the Fundamental Research Funds for the Central Universities (CUC24QT04), the Research and Development of Digital System and Application Platform for Art Archives (HG22031), the National Key Research and Development Program in China (2022YFC3302103-01), the Strategic Research Program of Science and Technology Commission of the Ministry of Education of China (JYB2022-01).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Acknowledgments
The authors extend their appreciation to the State Key Laboratory of Media Convergence and Communication in the Communication University of China for funding this research work through Fundamental Research Funds for the Central Universities.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Gao, Y.; Feng, W.; He, L.; Dong, M. Novel and Efficient Rainbow Signature Scheme Based on Circulant and Toeplitz Matrices for Intelligent IoT. IEEE Internet Things J. 2025, 99, 1. [Google Scholar] [CrossRef]
- Wang, J.; Chen, J.; Ren, Y.; Sharma, P.K.; Alfarraj, O.; Tolba, A. Data security storage mechanism based on blockchain industrial Internet of Things. Comput. Ind. Eng. 2022, 164, 107903. [Google Scholar] [CrossRef]
- Cai, X.; Geng, S.; Zhang, J.; Wu, D.; Cui, Y.; Yhang, W.; Chen, J. A Sharding scheme-based many-objective optimization algorithm for enhancing security in Blockchain-enabled industrial internet of things. IEEE Trans. Ind. Inform. 2021, 17, 7650–7658. [Google Scholar] [CrossRef]
- Lin, W.; Zhang, X.; Qi, L.; Li, W.; Li, S.; Sheng, V.S.; Nepal, S. Location-aware service recommendations with privacy-preservation in the Internet of Things. IEEE Trans. Comput. Soc. Syst. 2020, 8, 227–235. [Google Scholar] [CrossRef]
- Li, C.; Dong, M.; Li, J.; Xu, G.; Chen, X.; Ota, K. Healthchain: Secure EMRs management and trading in distributed healthcare service system. IEEE Internet Things J. 2020, 8, 7192–7202. [Google Scholar] [CrossRef]
- Das, A.K.; Wazid, M.; Kumar, N.; Vasilakos, A.V.; Rodrigues, J.J. Biometrics-based privacy-preserving user authentication scheme for cloud-based industrial Internet of Things deployment. IEEE Internet Things J. 2018, 5, 4900–4913. [Google Scholar] [CrossRef]
- Nakamoto, S. Bitcoin: A Peer-to-Peer Electronic Cash System. 2008. Available online: https://bitcoin.org/bitcoin.pdf (accessed on 1 December 2022).
- Reid, F.; Harrigan, M. An analysis of anonymity in the bitcoin system. In Security and Privacy in Social Networks; Springer: New York, NY, USA, 2013; pp. 197–223. [Google Scholar]
- Ober, M.; Katzenbeisser, S.; Hamacher, K. Structure and anonymity of the bitcoin transaction graph. Future Internet 2013, 5, 237–250. [Google Scholar] [CrossRef]
- Wijaya, D.A.; Liu, J.K.; Steinfeld, R.; Sun, S.F.; Huang, X. Anonymizing bitcoin transaction. In Proceedings of the 12th International Conference on Information Security Practice and Experience, Zhangjiajie, China, 16–18 November 2016. [Google Scholar]
- Koshy, P.; Koshy, D.; McDaniel, P. An analysis of anonymity in bitcoin using p2p network traffic. In Proceedings of the International Conference on Financial Cryptography and Data Security, Christ Church, Barbados, 3–7 March 2014. [Google Scholar]
- Sasson, E.B.; Chiesa, A.; Garman, C.; Green, M.; Miers, I.; Tromer, E.; Virza, M. Zerocash: Decentralized anonymous payments from bitcoin. In Proceedings of the2014 IEEE Symposium on Security and Privacy, San Jose, CA, USA, 18–21 May 2014. [Google Scholar]
- Van Saberhagen, N. CryptoNote v 2.0. 2013. Available online: https://bytecoin.org/old/whitepaper.pdf (accessed on 1 December 2021).
- Rivest, R.L.; Shamir, A.; Tauman, Y. How to leak a secret. In Proceedings of the International Conference on the Theory and Application of Cryptology and Information Security, Gold Coast, Australia, 9–13 December 2001. [Google Scholar]
- Liu, J.K.; Wei, V.K.; Wong, D.S. Linkable spontaneous anonymous group signature for ad hoc groups. In Proceedings of the Australasian Conference on Information Security and Privacy, Sydney, Australia, 13–15 July 2004. [Google Scholar]
- Liu, J.K.; Au, M.H.; Susilo, W.; Zhou, J. Linkable ring signature with unconditional anonymity. IEEE Trans. Knowl. Data Eng. 2013, 26, 157–165. [Google Scholar] [CrossRef]
- Kshetri, N.; Voas, J. Blockchain-enabled e-voting. IEEE Softw. 2018, 35, 95–99. [Google Scholar] [CrossRef]
- Kouhizadeh, M.; Saberi, S.; Sarkis, J. Blockchain technology and the sustainable supply chain: Theoretically exploring adoption barriers. Int. J. Prod. Econ. 2021, 231, 107831. [Google Scholar] [CrossRef]
- Shi, S.; He, D.; Li, L.; Kumar, N.; Khan, M.K.; Choo, K.K.R. Applications of blockchain in ensuring the security and privacy of electronic health record systems: A survey. Comput. Secur. 2020, 97, 101966. [Google Scholar] [CrossRef]
- Biryukov, A.; Tikhomirov, S. Security and privacy of mobile wallet users in Bitcoin, Dash, Monero, and Zcash. Pervasive Mob. Comput. 2019, 59, 101030. [Google Scholar] [CrossRef]
- Fedorov, A.K.; Kiktenko, E.O.; Lvovsky, A.I. Quantum computers put blockchain security at risk. Nature 2018, 563, 465–467. [Google Scholar] [CrossRef]
- Lauter, K. Postquantum opportunities: Lattices, homomorphic encryption, and supersingular isogeny graphs. IEEE Secur. Priv. 2017, 15, 22–27. [Google Scholar] [CrossRef]
- Ajtai, M. Generating hard instances of lattice problems. In Proceedings of the Twenty-Eighth Annual ACM Symposium on Theory of Computing (STOC ’96), Philadelphia, PA, USA, 22–24 May 1996. [Google Scholar]
- Ajtai, M. Generating hard instances of the short basis problem. In Proceedings of the International Colloquium on Automata, Languages, and Programming, Prague, Czech Republic, 11–15 July 1999. [Google Scholar]
- Gentry, C.; Peikert, C.; Vaikuntanathan, V. Trapdoors for hard lattices and new cryptographic constructions. In Proceedings of the Fortieth Annual ACM Symposium on Theory of Computing (STOC ’08), Victoria, BC, Canada, 17–20 May 2008. [Google Scholar]
- Li, C.Y.; Chen, X.B.; Chen, Y.L.; Hou, Y.Y.; Li, J. A new lattice-based signature scheme in post-quantum blockchain network. IEEE Access 2018, 7, 2026–2033. [Google Scholar] [CrossRef]
- Agrawal, S.; Boneh, D.; Boyen, X. Lattice basis delegation in fixed dimension and shorter-ciphertext hierarchical IBE. In Proceedings of the Annual Cryptology Conference, Santa Barbara, CA, USA, 15–19 August 2010. [Google Scholar]
- Wang, J.; Sun, B. Ring signature schemes from lattice basis delegation. In Proceedings of the International Conference on Information and Communications Security, Beijing, China, 23–26 November 2011. [Google Scholar]
- Lyubashevsky, V. Lattice signatures without trapdoors. In Proceedings of the Annual International Conference on the Theory and Applications of Cryptographic Techniques, Cambridge, UK, 15–19 April 2012. [Google Scholar]
- Li, Y.; Tian, M.; Huang, L. An identity-based ring signature scheme from lattice. J. Chin. Comput. Syst. 2013, 34, 1768–1771. [Google Scholar]
- Wang, S.; Zhao, R.; Zhang, Y. Lattice-based ring signature scheme under the random oracle model. Int. J. High Perform. Comput. Netw. 2018, 11, 332–341. [Google Scholar] [CrossRef]
- Gao, W.; Hu, Y.; Wang, B.; Chen, J.; Wang, X. Efficient ring signature scheme without random oracle from lattices. Chin. J. Electron. 2019, 28, 266–272. [Google Scholar] [CrossRef]
- Le, H.Q.; Vo, B.; Duong, D.H. Identity-based linkable ring signatures from lattices. IEEE Access 2021, 9, 84739–84755. [Google Scholar] [CrossRef]
- Tang, Y.; Xia, F.; Ye, Q.; Wang, M.-Z.; Mu, R.; Zhang, X. Identity-Based Linkable Ring Signature on NTRU Lattice. Secur. Commun. Netw. 2021, 1, 9992414. [Google Scholar] [CrossRef]
- Cao, C.; You, L.; Hu, G. A New Formal-Based Identity-Based Linkable Signature Scheme. J. Cryptologic Res. 2022, 9, 969–981. [Google Scholar]
- Cao, C.; You, L.; Hu, G. A Novel Linkable Ring Signature on Ideal Lattices. Entropy 2023, 25, 237. [Google Scholar] [CrossRef]
- Zhang, Y.; Tang, Y.; Li, C.; Dong, M.; Huang, M.; Yhang, H.; Ota, K. Privacy-Preserving for Blockchain-Enabled Cold-Chain Logistics System with IoV and Linkable Ring Signature. IEEE Trans. Veh. Technol. 2024, 73, 12585–12596. [Google Scholar] [CrossRef]
- Duan, J.; Zheng, S.; Wang, W.; Wang, L.; Hu, X.; Gu, L. Concise RingCT Protocol Based on Linkable Threshold Ring Signature. IEEE Trans. Dependable Secur. Comput. 2024, 21, 5014–5028. [Google Scholar] [CrossRef]
- Xie, J.; Zhou, J.; Cao, Z.; Dong, X.; Choo, K.-K.R. Linkable, k-Times Traceable, and Revocable Ring Signature for Fine-Grained Accountability in Blockchain Transactions. IEEE Internet Things J. 2025, 12, 4349–4361. [Google Scholar] [CrossRef]
- Gao, Y.L.; Chen, X.B.; Chen, Y.L.; Sun, Y.; Niu, X.X.; Yang, Y.X. A secure cryptocurrency scheme based on post-quantum blockchain. IEEE Access 2018, 6, 27205–27213. [Google Scholar] [CrossRef]
- Li, C.; Dong, M.; Li, J.; Xu, G.; Chen, X.B.; Liu, W.; Ota, K. Efficient Medical Big Data Management with Keyword-Searchable Encryption in Healthchain. IEEE Syst. J. 2022, 16, 5521–5532. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).