Switchable THz Bi-Functional Device for Absorption and Dual-Band Linear-to-Circular Polarization Conversion Based on Vanadium Dioxide–Graphene
Abstract
1. Introduction
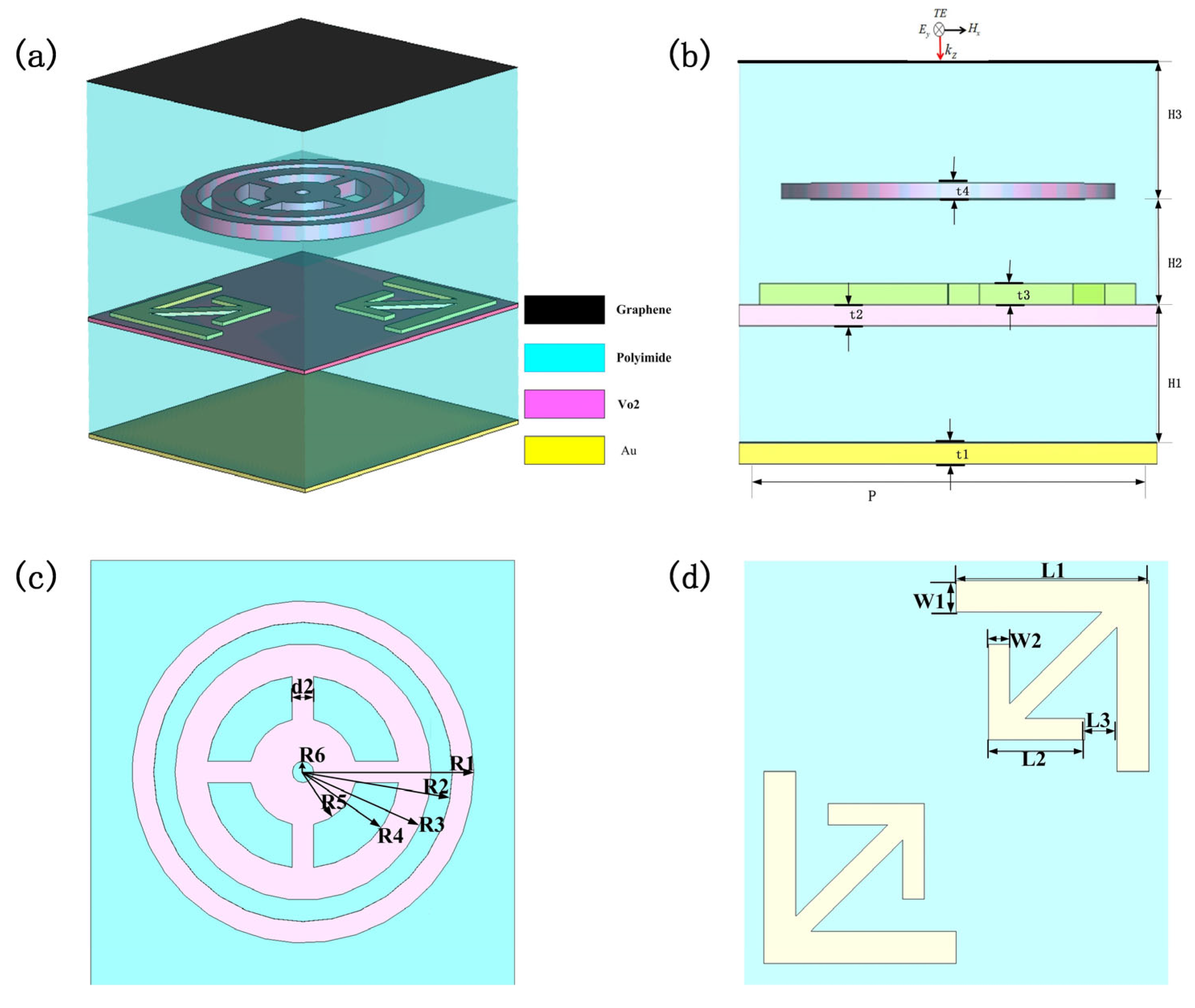
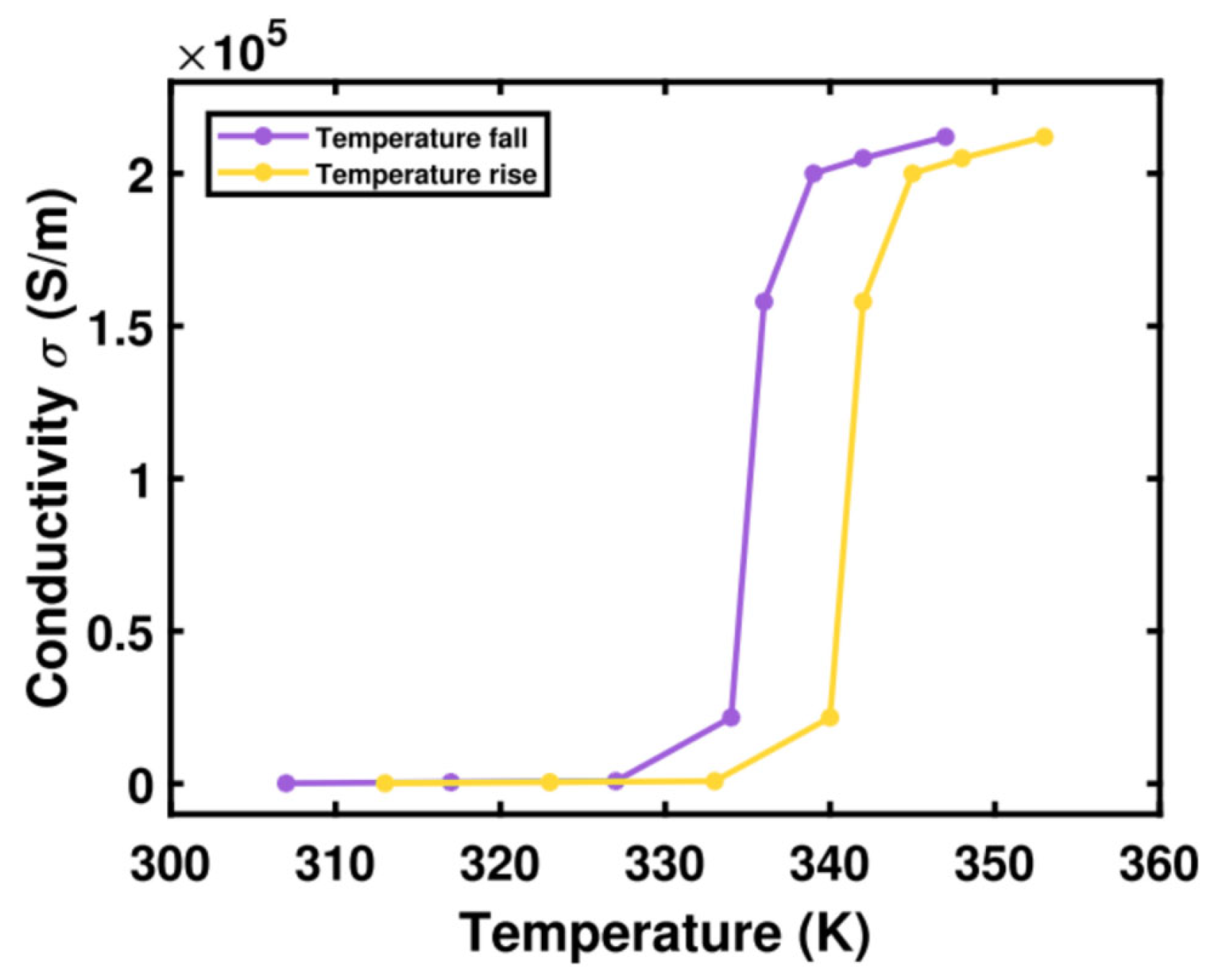
2. Theory and Method
3. Results and Discussion
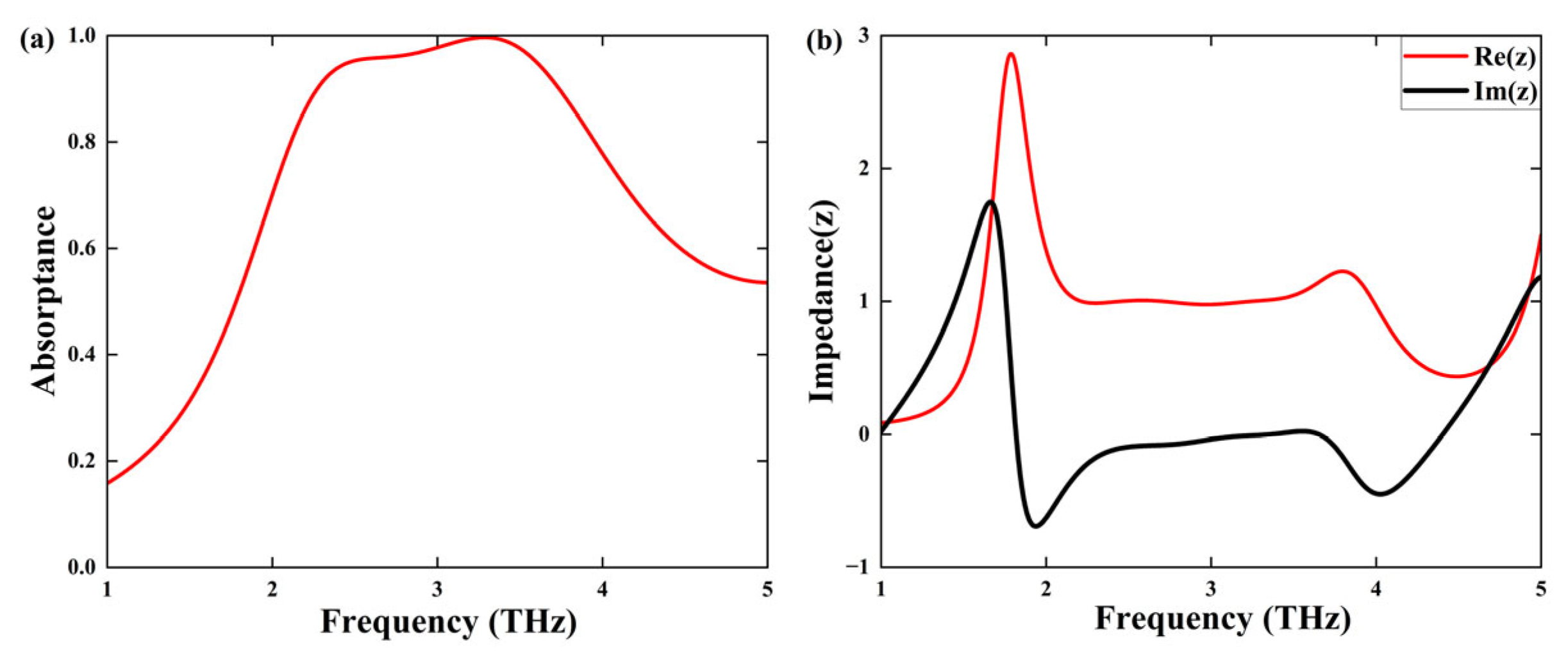
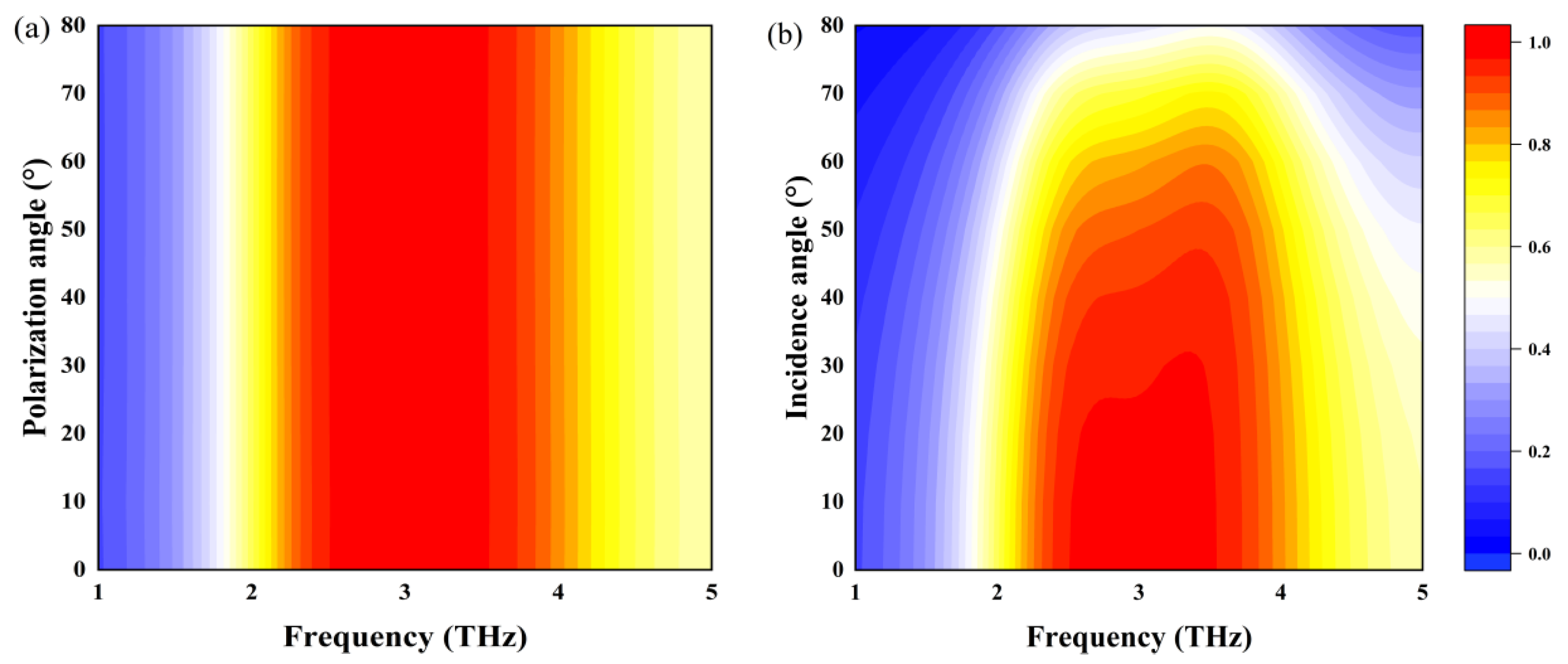
3.1. Broadband Absorber
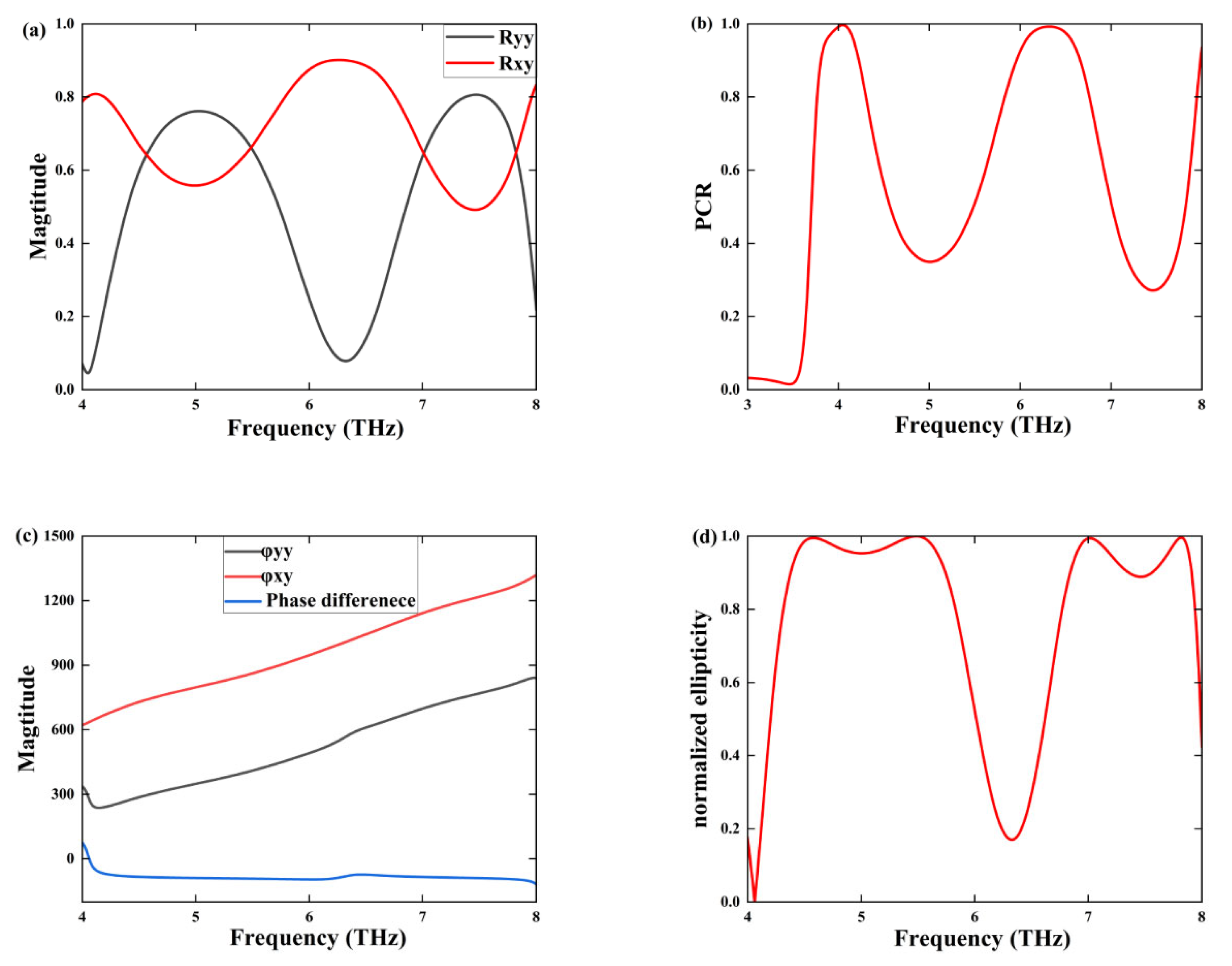
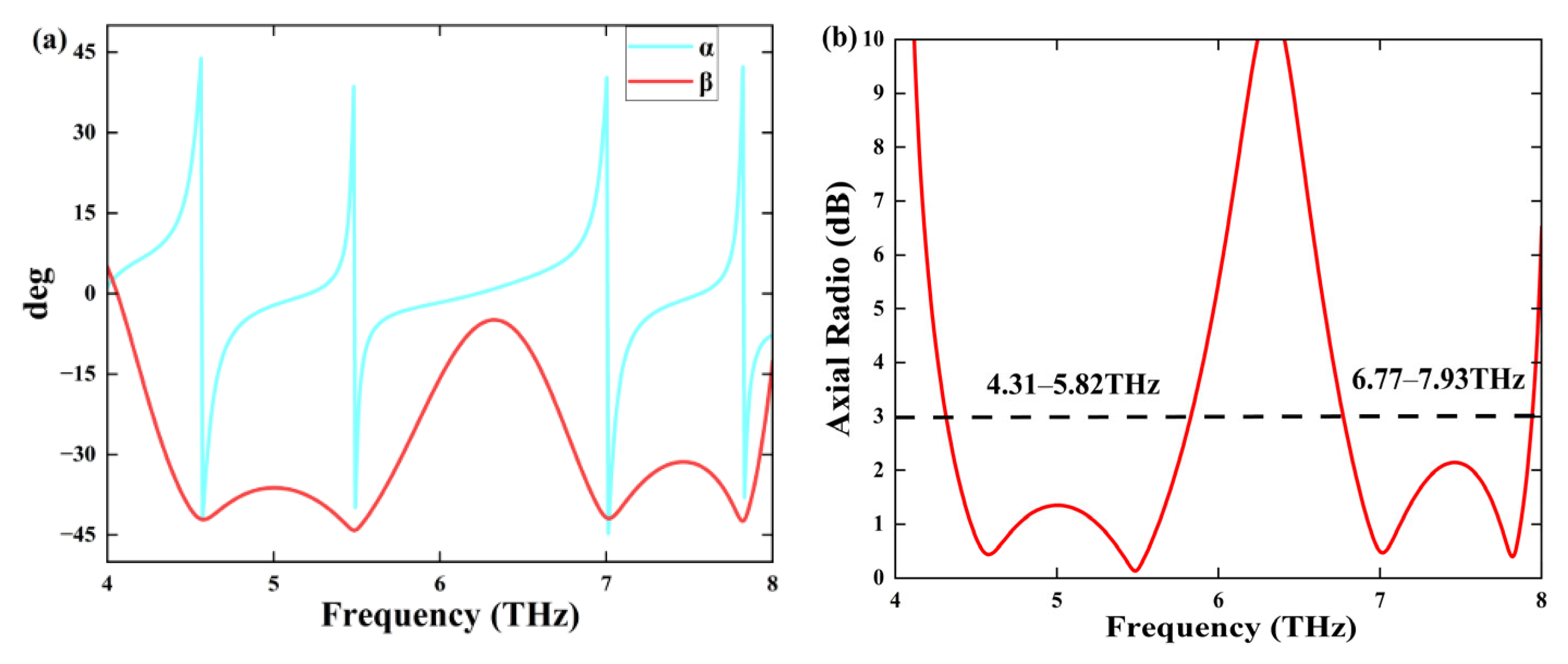
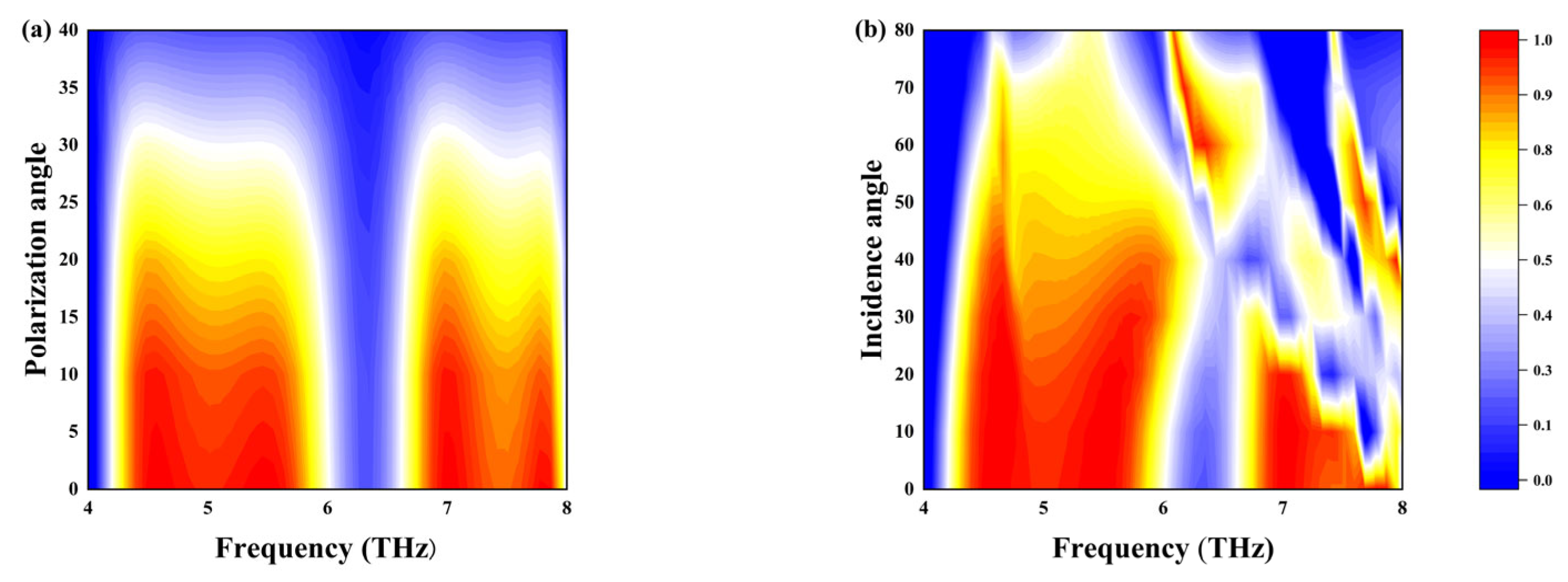
3.2. Linear-to-Circular Polarization Converter
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sreekanth, K.V.; ElKabbash, M.; Alapan, Y.; Rashed, A.R.; Gurkan, U.A.; Strangi, G. A multiband perfect absorber based on hyperbolic metamaterials. Sci. Rep. 2016, 6, 26272. [Google Scholar] [CrossRef] [PubMed]
- Sun, S.; Yang, K.; Wang, C.; Juan, T.; Chen, W.; Liao, C.; He, Q.; Xiao, S.; Kung, W.; Guo, G. High-efficiency broadband anomalous reflection by gradient meta-surfaces. Nano Lett. 2012, 12, 6223–6229. [Google Scholar] [CrossRef] [PubMed]
- Padilla, W.J.; Basov, D.N.; Smith, D.R. Negative refractive index metamaterials. Mater. Today 2006, 9, 28–35. [Google Scholar] [CrossRef]
- Zheng, B.; Xiong, X.; Tang, J.; Zhang, R. Intelligent reflecting surface-aided electromagnetic stealth against radar detection. IEEE Trans. Signal Process. 2024, 72, 3438–3452. [Google Scholar] [CrossRef]
- Tyc, T.; Zhang, X. Perfect lenses in focus. Nature 2011, 480, 42–43. [Google Scholar] [CrossRef]
- Xu, Y.; Fu, Y.; Xu, L.; Chen, H. Conjugate metamaterials and the perfect lens. arXiv 2015, arXiv:1510.08638. [Google Scholar]
- Park, J.; Kim, S.J.; Landreman, P.; Brongersma, M.L. An over-coupled phase-change metasurface for efficient reflection phase modulation. Adv. Opt. Mater. 2020, 8, 2000745. [Google Scholar] [CrossRef]
- Pu, M.; Wang, M.; Hu, C.; Huang, C.; Zhao, Z.; Wang, Y.; Luo, X. Engineering heavily doped silicon for broadband absorber in the terahertz regime. Opt. Express 2012, 20, 25513–25519. [Google Scholar]
- Cao, T.; Wang, R.; Simpson, R.E.; Li, J. Photonic Ge-Sb-Te phase change metamaterials and their applications. Prog. Quantum Electron. 2020, 74, 100299. [Google Scholar] [CrossRef]
- Guo, L.; Ma, X.; Chang, Z.; Xu, C.; Liao, J.; Zhang, R. Tunable and temperature-dependent GST-based metamaterial absorber for switching and sensing applications. J. Mater. Res. Technol. 2021, 14, 772–779. [Google Scholar]
- Tao, W.; Wu, Y.; Zhao, F.; Li, C.; Fang, B.; Jing, X.; Yu, M. Research progress in metamaterials and metasurfaces based on the phase change material Ge2Sb2Te5. Opt. Laser Technol. 2024, 177, 111064. [Google Scholar] [CrossRef]
- Chen, B.; Brink, G.H.T.; Palasantzas, G.; Kooi, B.J. Size-dependent and tunable crystallization of GeSbTe phase-change nanoparticles. Sci. Rep. 2016, 6, 39546. [Google Scholar] [CrossRef] [PubMed]
- Dash, S.; Psomas, C.; Patnaik, A.; Krikidis, I. An ultra-wideband orthogonal-beam directional graphene-based antenna for THz wireless systems. Sci. Rep. 2022, 12, 22145. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Li, Z.; Xing, F. Review of polarization optical devices based on graphene materials. Int. J. Mol. Sci. 2020, 21, 1608. [Google Scholar] [CrossRef]
- Guo, G.; Zhang, X.; Niu, L.; Wu, T.; Chen, X.; Xu, Q.; Han, J.; Zhang, W. Programmable graphene metasurface for terahertz propagation control based on electromagnetically induced transparency. Carbon 2023, 208, 345–354. [Google Scholar] [CrossRef]
- Zhang, Y.; Feng, Y.; Zhao, J. Graphene-enabled active metamaterial for dynamical manipulation of terahertz reflection/transmission/absorption. Phys. Lett. A 2020, 384, 126840. [Google Scholar] [CrossRef]
- Yuan, X.; Chen, J.; Wu, J.; Yan, X.; Zhang, Y.; Zhang, X. Graphene-based tunable linear and linear-to-circular polarization converters in the THz band. Results Phys. 2022, 37, 105571. [Google Scholar] [CrossRef]
- Song, Z.; Zhang, B. Controlling wideband absorption and electromagnetically induced transparency via a phase change material. Europhys. Lett. 2020, 129, 57003. [Google Scholar] [CrossRef]
- Lian, X.; Ma, M.; Tian, J.; Yang, R. Study on a bifunctional switchable metasurface with perfect absorption and polarization conversion based on VO2 and grapheme in THz region. Diam. Relat. Mater. 2023, 136, 110060. [Google Scholar] [CrossRef]
- Song, Z.; Zhang, J. Achieving broadband absorption and polarization conversion with a vanadium dioxide metasurface in the same terahertz frequencies. Opt. Express 2020, 28, 12487–12497. [Google Scholar] [CrossRef]
- Niu, J.; Yao, Q.; Mo, W.; Li, C.; Zhu, A. Switchable bi-functional metamaterial based on vanadium dioxide for broadband absorption and broadband polarization in terahertz band. Opt. Commun. 2023, 527, 128953. [Google Scholar] [CrossRef]
- Zhang, M.; Song, Z. Terahertz bifunctional absorber based on a graphene-spacer-vanadium dioxide-spacer-metal configuration. Opt. Express 2020, 28, 11780–11788. [Google Scholar] [CrossRef] [PubMed]
- Liu, M.; Plum, E.; Li, H.; Li, S.; Xu, Q.; Zhang, X.; Zhang, C.; Zou, C.; Jin, B.; Han, J.; et al. Temperature-Controlled Optical Activity and Negative Refractive Index. Adv. Funct. Mater. 2021, 31, 2010249. [Google Scholar] [CrossRef]
- Chen, B.; Wang, X.; Li, C.; Wang, Z.; Guo, H.; Wu, J.; Fan, K.; Zhang, Z.; Wu, P. Electrically addressable integrated intelligent terahertz metasurface. Sci. Adv. 2022, 41, 1126–1296. [Google Scholar] [CrossRef]
- Wang, X.; Ma, C.; Xiao, L.; Xiao, B. Dual-band dynamically tunable absorbers based on graphene and double vanadium dioxide metamaterials. J. Opt. 2024, 53, 596–604. [Google Scholar] [CrossRef]
- Zhu, Y.; Huang, Z.; Su, J.; Tang, B. Actively tunable and switchable terahertz metamaterials with multi-band perfect absorption and polarization conversion. Phys. Chem. Chem. Phys. 2024, 26, 11649–11656. [Google Scholar] [CrossRef]
- Bakhtiari, B.; Oraizi, H.; Taravati, S. Dual-functional terahertz tunable polarization conversion by graphene-VO2 metasurfaces. In Proceedings of the 2021 15th European Conference on Antennas and Propagation (EuCAP), Dusseldorf, Germany, 22–26 March 2021; Volume 10, pp. 1–4. [Google Scholar]
- Li, D.; He, S.; Su, L.; Du, H.; Tian, Y.; Gao, Z.; Xie, B.; Huang, G. Switchable and tunable terahertz metamaterial absorber based on graphene and vanadium dioxide. Opt. Mater. 2024, 147, 114655. [Google Scholar] [CrossRef]
- Zhang, H.; He, X.; Zhang, D.; Zhang, H. Multitasking device with switchable and tailored functions of ultrabroadband absorption and polarization conversion. Opt. Express 2022, 30, 23341–23358. [Google Scholar] [CrossRef]
- Barkabian, M.; Sharifi, N.; Granpayeh, N. Multifunctional high-efficiency reflective polarization converter based on an ultra-thin graphene metasurface in the THz band. Opt. Express 2021, 29, 20160–20174. [Google Scholar] [CrossRef]
- Wang, X.; Xiao, Z.; Zheng, Q. Switchable and tunable broadband terahertz absorption, linear polarization conversion and linear to circular polarization based on graphene-vanadium dioxide metamaterials. Opt. Mater. 2024, 150, 115238. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, K.; Chen, B.; Guo, L.; Kong, W. Switchable multi-functional broadband polarization converter in terahertz band. Opt. Express 2022, 30, 41969–41979. [Google Scholar] [CrossRef] [PubMed]
- Matsui, H.; Ho, Y.L.; Kanki, T.; Tanaka, H.; Delaunay, J.J.; Tabata, H. Mid-infrared plasmonic resonances in 2D VO2 nanosquare arrays. Adv. Opt. Mater. 2015, 3, 1759–1767. [Google Scholar] [CrossRef]
- Barzegar-Parizi, S.; Ebrahimi, A.; Ghorbani, K. Two bits dual-band switchable terahertz absorber enabled by composite graphene and vanadium dioxide metamaterials. Sci. Rep. 2024, 14, 5818. [Google Scholar] [CrossRef]
- Barzegar-Parizi, S.; Khavasi, A. Designing dual-band absorbers by graphene/metallic metasurfaces. IEEE J. Quantum Electron. 2019, 55, 1–8. [Google Scholar] [CrossRef]
- Li, W.; Xu, F.; Cheng, S.; Yang, W.; Liu, B.; Liu, M.; Yi, Z.; Tang, B.; Chen, J.; Sun, T. Six-band rotationally symmetric tunable absorption film based on AlCuFe quasicrystals. Opt. Laser Technol. 2024, 169, 110186. [Google Scholar] [CrossRef]
- Smith, D.R.; Schultz, S.; Markoš, P.; Soukoulis, C. Determination of effective permittivity and permeability of metamaterials from reflection and transmission coefficients. Phys. Rev. B 2002, 65, 195104. [Google Scholar] [CrossRef]
- Chen, F.; Cheng, Y.; Luo, H. A broadband tunable terahertz metamaterial absorber based on single-layer complementary gammadion-shaped graphene. Materials 2020, 13, 860. [Google Scholar] [CrossRef]
- Cong, L.; Cao, W.; Zhang, X.; Tian, Z.; Gu, J.; Singh, R.; Han, J.; Zhang, W. A perfect metamaterial polarization rotator. Appl. Phys. Lett. 2013, 103, 171107. [Google Scholar] [CrossRef]
- Huang, C.; Ma, X.; Pu, M.; Yi, G.; Wang, Y.; Luo, X. Dual-band 90° polarization rotator using twisted split ring resonators array. Opt. Commun. 2013, 291, 345–348. [Google Scholar] [CrossRef]

| Ref. | Tunable Material | Absorption | Polarization Conversion | ||
|---|---|---|---|---|---|
| Absorption (THz) | Bandwidth (THz) | PC (THz) | Bandwidth (THz) | ||
| [20] | VO2 | 0.52–1.20 (>90%) | 0.68 | 0.42–1.04 | 0.62 |
| [29] | VO2 | 0.68–1.60 (>90%) | 0.92 | 0.82–1.60 | 0.78 |
| [17] | Graphene | NO | NO | 2.89–3.34 | 2.89–3.34 |
| 3.34–3.59 | 3.34–3.59 | ||||
| [30] | Graphene | NO | NO | 0.60–0.67 | 0.07 |
| 0.72–0.97 | 0.27 | ||||
| [31] | Graphene and VO2 | 1.38–3.16 (>90%) | 1.78 | 3.76–4.01 | 0.25 |
| [32] | Graphene and VO2 | NO | NO | 1.57–2.74 | 1.17 |
| 1.13–1.59 | 0.46 | ||||
| This work | Graphene and VO2 | 2.28–3.73 (>90%) | 1.45 | 4.31–5.82 | 1.51 |
| 6.77–7.93 | 1.16 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Xie, H.; Liu, R.; Dong, J. Switchable THz Bi-Functional Device for Absorption and Dual-Band Linear-to-Circular Polarization Conversion Based on Vanadium Dioxide–Graphene. Sensors 2025, 25, 3644. https://doi.org/10.3390/s25123644
Wang Y, Xie H, Liu R, Dong J. Switchable THz Bi-Functional Device for Absorption and Dual-Band Linear-to-Circular Polarization Conversion Based on Vanadium Dioxide–Graphene. Sensors. 2025; 25(12):3644. https://doi.org/10.3390/s25123644
Chicago/Turabian StyleWang, Yiqu, Haohan Xie, Rong Liu, and Jun Dong. 2025. "Switchable THz Bi-Functional Device for Absorption and Dual-Band Linear-to-Circular Polarization Conversion Based on Vanadium Dioxide–Graphene" Sensors 25, no. 12: 3644. https://doi.org/10.3390/s25123644
APA StyleWang, Y., Xie, H., Liu, R., & Dong, J. (2025). Switchable THz Bi-Functional Device for Absorption and Dual-Band Linear-to-Circular Polarization Conversion Based on Vanadium Dioxide–Graphene. Sensors, 25(12), 3644. https://doi.org/10.3390/s25123644






