Abstract
Arterial stiffness is a major condition related to many cardiovascular diseases. Traditional approaches in the assessment of arterial stiffness supported by machine learning techniques are limited to the pulse wave velocity (PWV) estimation based on pressure signals from the peripheral arteries. Nevertheless, arterial stiffness can be assessed based on the pressure–strain relationship by analyzing its hysteresis loop. In this work, the capacity of deep learning models based on generative adversarial networks (GANs) to transfer pressure signals from the peripheral arterial region to pressure and area signals located in the central arterial region is explored. The studied signals are from a public and validated virtual database. Compared to other works in which the assessment of arterial stiffness was performed via PWV, in the present work the pressure–strain hysteresis loop is reconstructed and evaluated in terms of classical machine learning metrics and clinical parameters. Least-square GAN (LSGAN) and Wasserstein GAN with gradient penalty (WGAN-GP) adversarial losses are compared, yielding better results with LSGAN. LSGAN mean ± standard deviation of error for pressure and area pulse waveforms are 0.8 ± 0.4 mmHg and 0.1 ± 0.1 cm2, respectively. Regarding the pressure–strain elastic modulus, it is achieved a mean absolute percentage error of 6.5 ± 5.1%. GAN-based deep learning models can recover the pressure–strain loop of central arteries while observing pressure signals from peripheral arteries.
1. Introduction
1.1. Arterial Stiffness
Cardiovascular (CV) disease remains the leading cause of death around the world [1]. Early detection is currently one of the main strategies to mitigate occurrence and damage caused by CV disease events. In this sense, increased arterial stiffness is considered a major CV risk factor, jointly with aging, hypertension, smoking, and diabetes, among others, due to its impact on the viscoelastic properties of the arterial wall (mainly in large arteries such as the aortic, carotid, and femoral) [2]. While the elastic function of vascular mechanics is performed by collagen and elastin fibers, the viscous behavior is related to the vascular smooth muscle cells [3]. The viscoelastic dynamics can be addressed through the pressure–strain relationship, in which the delay of the arterial deformation against the pressure produces a hysteresis loop [4]. From a biomechanical perspective, the pressure-diameter (P-D) relationship provides valuable information in terms of the elastic and viscous properties of the arterial wall. In particular, the elastic module (E) is usually obtained from the diastolic phase, whereas the viscous module is estimated from the P-D loop enclosed area [4]. Unfortunately, in vivo measurements of aortic dynamics along this pathway are difficult to obtain due to their invasiveness and the requirement for specialized equipment and trained operators.
1.2. Arterial Stiffness and Machine Learning
In recent years, advances in machine learning (ML) have offered different models and algorithms that can be adapted to CV healthcare. In this context, ML model tasks are divided into parameter estimation and subject risk stratification. For instance, systolic blood pressure (SBP) and diastolic blood pressure (DBP) value estimation constitutes a typical approach of the use of both classic ML and deep learning models. In certain cases, classic ML models such as support vector machine (SVM) and fully-connected neural network (NN) implement a feature extraction step in their pipeline. On the contrary, deep learning models have the capacity to generate their own features, meaning that the feature extraction step is not required. Nevertheless, deep learning models require a greater amount of samples to produce better generalization compared to classic ML models. This condition is probably the reason why there seems to be a gap in the use of in vivo datasets jointly with deep learning models. According to the literature, researchers in the CV signal field have focused on a feature-based approach with classic ML, using peripheral blood pressure (BP) or photoplethysmography (PPG) signals rather than deep learning techniques. In Alty et al. [5], several PPG features were extracted and used as the input of a SVM model in order to estimate PWV, a surrogate of regional arterial stiffness. Similarly, in Tavallali et al. [6], features were extracted from the uncalibrated carotid pulse wave (PW) and clinical information was used to train a NN and estimate PWV. In particular, and focusing on the same objective, in Jin et al. [7] both classic ML and deep learning models were compared using in vivo radial PWs.
1.3. Virtual Databases in Research
Deep learning models are usually trained using synthetic datasets [8], as the acquisition of real samples, even when possible, turns to out be difficult, expensive, and/or time-consuming. In this context, 1D modeling of arterial PWs, such as that specified in Charlton et al. [9] and Xiao et al. [10], allows the limitations of deep learning samples to be overcome. Furthermore, different profiles or “virtual subjects” are generated by modifying the more representative CV properties, allowing consolidation of a useful database. These simulations can be used then to (1) complement clinical studies [11]; (2) examine methods [12]; or (3) explore the capacity of ML models to explain the relationship between PWs and the underlying CV parameters. In keeping with this approach, Willemet et al. [11] proposed that the occurrence of reflected waves in the late diastole phase affects the foot-to-foot PWV algorithm, causing inaccuracies in PWV estimation. With respect to point (2), Alastruey [12] compared methods for estimating PWV and concluded that those relying on P-D loops were closer to the theoretical values. Finally, regarding ML capacity, several works have proposed estimating CV parameters using a features-based approaches, generally with peripheral arterial information. Bikia et al. [13] used classic ML models to estimate aortic systolic BP, cardiac output, and end-systolic elastance from cuff SBP and DBP, heart rate, and PWV. Ipar et al. [14] investigated a similar approach, extracting features such as systemic vascular resistance from radial and carotid signals. Xiao et al. [15] estimated the stroke volume based on features using only radial signals. Jin et al. [7] examined different signal-to-noise ratios and their impact in terms of percentage error by estimating the PWV from radial pressure PW.
By virtue of the above, it is clear that the research approaches in the literature are consistent with the use of pressure signals from peripheral arteries in estimating parameters related to the properties of the central arteries. Nevertheless, to the best of our knowledge, aortic dynamics have not been addressed in terms of the P-D relationship in a way that is non-invasive using deep learning approaches. This rest of this work is structured as follows. In Section 2, the information obtained from public databases is detailed along with the framework for P-D loop evaluation, the deep learning model, the metrics used to evaluate the results, and the definitions of the different hyperparameter settings used in the experiments. In Section 3, the experimental results of the trained models are reported. In Section 4, the results are discussed and similarities and differences in relation to other works are pointed out. Lastly, in Section 5, a brief conclusion of the present work is summarized.
2. Methodology
2.1. Dataset
The dataset used in this work corresponds to the one in Charlton et al. [9]. It is composed of 3837 simulated PWs with different cardiac, vascular, arterial, vascular bed, and blood properties. The simulated PWs’ hemodynamic characteristics exhibit tendencies that are in accordance with those in the literature in terms of both values and morphology [9]. The magnitudes provided by this dataset are pressure (mmHg), luminal area (m2) and flow velocity (m/s), corresponding to different sites of the arterial tree. Furthermore, because the arterial wall viscosity property is considered in the database [9], the hysteresis phenomenon between pressure and strain can be evaluated, as shown in Figure 1.
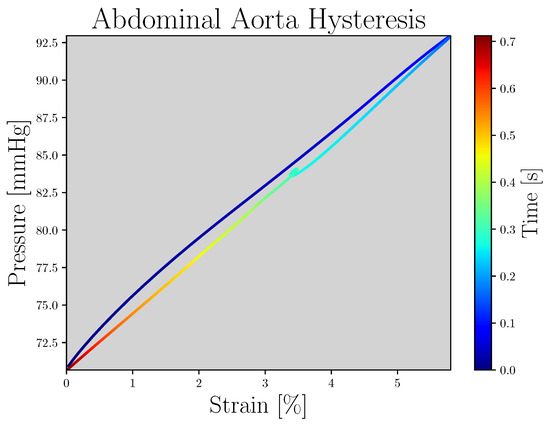
Figure 1.
Abdominal aorta pressure–strain hysteresis loop; the color of the line refers to the time.
For the present study, the pressure from the radial and brachial artery (PBra-Rad) signals correspond to the X domain (the blue and green lines in Figure 2) and the aortic abdominal pressure and area (P-AAbdo) signals correspond to the Y domain (the red lines in Figure 2). Although PWs are noiseless, a pre-processing stage is performed to prepare the model’s input. First, the area magnitude is converted to cm2. Second, because PWs have different durations, the time-window is fixed to the maximum PW duration across the database; shorter pulses are repeated until time-windows are fulfilled, considering a stationary situation. Third, a MinMax [−1, 1] normalization is performed for both pressure and area magnitude. Finally, PWs are resampled from 500 Hz to 256 Hz, which is done for two reasons: (1) to reduce computational cost, and (2) because 256 Hz is a common sampling frequency used in commercial devices (SphygmoCor®XCEL, AtCor Medical, Sydney, Australia).
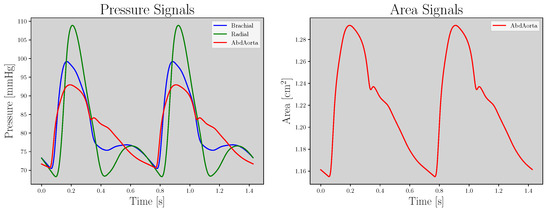
Figure 2.
Left: Brachial, radial and abdominal aorta pressure signals (blue, green, and red lines, respectively). Right: Abdominal aorta area signal.
2.2. Pressure–Strain Elastic Modulus
From a biomechanical point of view, arterial stiffness is defined in terms of E:
where refers to the arterial strain and to the axial stress, defined as
where h is the h, P refers to the inner BP, and R is the arterial radius. Nevertheless, because h is not directly defined in the dataset, a simplification of Equation (1) that only regards P and , called EP- [16], is considered as the measurement of arterial stiffness:
As detailed in the next section, the proposed model estimates the magnitudes of both pressure and area. Then, in Section 2.4, after the P-D loops are constituted from estimations, EP- is observed as an evaluation parameter.
2.3. CycleGAN Model
GANs are a type of generative deep learning models composed of a discriminator (D) and a generator (G). The generator tries to generate samples similar to a given domain in such a way that the discriminator cannot differentiate between real and fake samples. On the contrary, the discriminator tries to recognize real samples from created by the generator. GANs are trained by defining the Adversarial Loss (), which is a function that measures the distance between two probabilistic distributions.
The CycleGAN [17] architecture has been proposed to learn mapping functions between two domains, X and Y, using GANs. Although it was originally proposed for unpaired image-to-image translation, in this work the X and Y samples are paired, as mentioned before, and correspond to the PBra-Rad and P-AAbdo signals, respectively.
2.3.1. General Architecture
As shown in Figure 3, the mapping functions are and , given training samples and . Two adversarial discriminators and are incorporated, where the goal of is to discriminate signals from X and . Similarly, aims to distinguish signals from Y and . In addition to , a Cycle-Consistency Loss () function is added to force learnable mapping functions to recover their originals inputs.
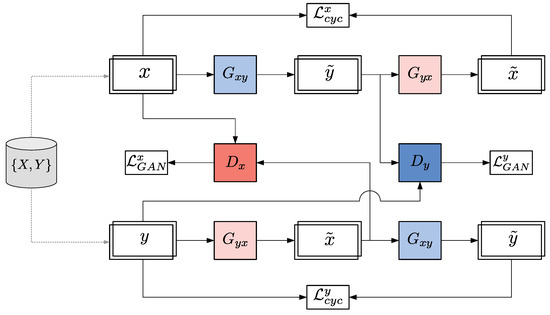
Figure 3.
CycleGAN architecture and its training connection flow.
The full objective function contains two terms [17],
we expand and in detail in Section 2.3.3; moreover, is a scalar that helps to scale the losses.
2.3.2. Architecture of Generators and Discriminators
In the present work, the generators and are two stacked gated recurrent unit (GRU) layers followed by a linear projection with two out features and ending with a activation function. Discriminators and are five stacked layers of convolutional
neural networks (CNNs) (kernel, stride, and padding having sizes of 5, 2, and 1, respectively) with a normalization layer and LeakyReLU ( 0.2) activation function in each layer. At each layer of discriminator, the number of output features is doubled; finally, one last layer of linear projection with one output feature ending with an activation function is added. Depending on the selected , the normalization and last activation layers change; details are provided in Section 2.3.4. Figure 4 shows the structures of G and D.
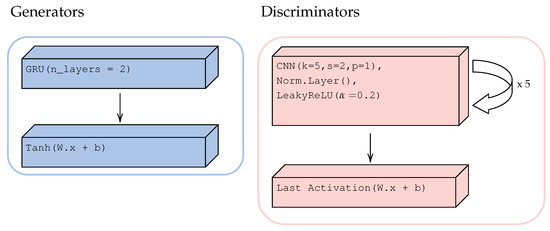
Figure 4.
Generator and discriminator components.
2.3.3. Loss Functions
To measure , two different metrics have been implemented:
- LSGAN [18]
- WGAN-GP [19]
- where LSGAN and WGAN-GP measure the Pearson divergence and the Wasserstein distance, respectively. For the sake of simplicity, only the case where (the second term in Equation (5)) is written, because is defined analogously by replacing the X with the Y domain and vice versa. The objective for considering LSGAN is defined as follows:
When WGAN-GP is considered, the objective for is as follows [18]:
where is a scalar hyperparameter defined as 10, (given ) and ∇ is the differential operator. The third term in Equation (7) is a regularization term that penalizes the gradient during training in order to achieve the constraint that discriminators must be 1-Lipschitz functions [19].
Finally, the objective of , the second term of Equation (4), is
2.3.4. Hyperparameters and Experimental Settings
All experiments were performed in tge Google Collaboratory environment. The training and test set proportions were 85% and 15%, respectively, from the total virtual subjects mentioned in Section 2.1. The CycleGAN parameters were updated using the Adam optimizer [20], the learning rate (LR) value was , and the batch size was equal to 96. All the hyperparameters are shown in Table 1. In particular, the number of discriminators per generator updates () was only considered for the WGAN-GP case [21], while for the LSGAN case it was always 1. The normalization layers and last activation function for LSGAN were batch-normalization and sigmoid function, respectively, while for WGAN-GP they were instance-normalization and linear function, respectively. Models were trained for 1750 epochs.

Table 1.
Grid search of hyperparameters. refers to the adversarial loss function. and refer to the feature size of the generator’s GRU units and the first layer output’s discriminators. refers to the number of discriminators per generator updates (only for WGAN-GP; for LSGAN it is always 1).
2.4. Evaluation
After the training was finished, the only relevant part of the CycleGAN interesting for clinical purpose was . Recalling that the signals were within the MinMax ranges defined in Section 2.1, the predictions were returned to the original scale. Furthermore, evaluation was performed only across the first completed pulse presented in both the test and estimated signals. Two scopes were considered. The first was a typical ML metric, using the root-mean squared error (RMSE) for both pressure and area prediction:
where N, T, z, and refer to the number of samples, pulse duration, ground truth pulse, and estimated pulse, respectively.
Second, in order to evaluate the elastic properties of the predictions, EP- was calculated for both the ground truth and estimated pulses. The strain was derived from the area PW, then EP- is computed as the slope of a simple linear regression:
After calculating each , mean error (ME) and mean absolute percentage error (MAPE) were evaluated regarding EP- as follows:
To account for the possible differences in duration between the estimated and true pulses, the shorter one was used. Finally, the minimum and maximum values for pressure and diameter were extracted to perform a Bland–Altman analysis.
3. Results
The statistical results for the test set are shown in Table 2 for the best hyperparameter combination of each . The means ± standard deviation of error during evaluations for the best LSGAN and WGAN-GP were 0.8 ± 0.4 mmHg and 1.7 ± 0.8 mmHg, respectively. For area evaluations, the results were 0.1 ± 0.1 cm2 and 0.2 ± 0.2 cm2, respectively. Figure 5 compares the true and predicted samples.

Table 2.
Mean ± standard deviation of error for Brachial–Radial to Aortic Abdominal case on the test set.
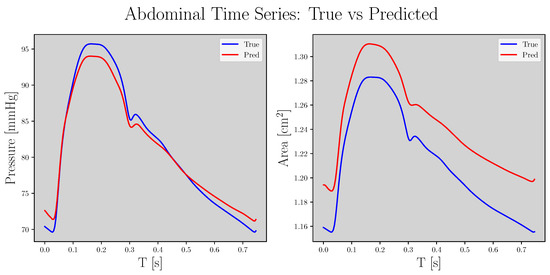
Figure 5.
Comparison between true and predicted signals for pressure (left) and area (right); blue and red correspond to the true and predicted signals, respectively.
Concerning EP-, the ME for the best LSGAN and WGAN-GP results were 13.1 ± 56.5 mmHg/% and 70.6 ± 216.0 mmHg/%, respectively. Finally, according to MAPE, the LSGAN and WGAN-GP results were 6.5 ± 5.1% and 28.6 ± 19.3%, respectively. Figure 6 shows a hysteresis comparison for the same signals in Figure 5, where the black dotted line represents the and parameters from Equation (10).
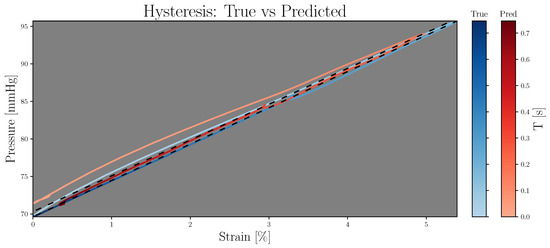
Figure 6.
Comparison between true (blue) and predicted (red) hysteresis cycles. Line brightness refers to time; the black dashed lines refer to and from Equation (10).
The esults in Table 3 corresponding to the training set are presented to demonstrate that the error does not suffer from overfitting.

Table 3.
Mean ± standard deviation of error for Brachial–Radial to Aortic Abdominal case on training set.
In particular, the Bland–Altman plots (Figure 7) for the SBP and DBP values for the LSGAN best model (Table 2, experiment A) express a mean difference of 0.81 and 0.27 mmHg, respectively. It is worth repeating that the SBP and DBP values are the maximum and minumum values of the pressure signal, respectively. Limits of agreement (LOA) are [, ] mmHg for SBP, while the LOA for DBP are [, ] mmHg. Concerning the maximum and minimum values of the diameter, the Bland–Altman plots show a mean difference of 0.013 and 0.017 cm, respectively. limits of agreement LOA for the maximum diameter are [, ] cm, while LOA for the minimum diameter are [, ] cm.
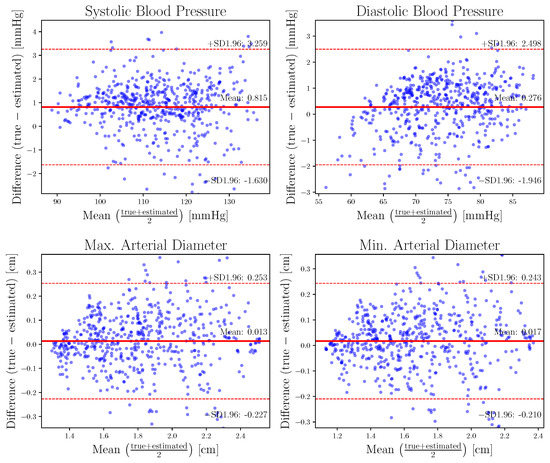
Figure 7.
Bland–Altman plots showing the difference between the maximum and minimum values of pressure (top) and diameter (bottom) for true and estimated signals; the plots were obtained for the best LSGAN model.
4. Discussion
In this paper, a new methodology based on a deep learning technique (CycleGAN) is proposed to estimate pressure vs. strain dynamics. While the majority of the literature considers the estimation of PWV using the feature extraction approaches, in this paper two peripheral pressure PWs are considered to estimate central pressure and area PWs. Consequently, a wider approach to the aortic dynamics is achieved in terms of the P-D relationship. According to the literature [16,22], after these two PW are estimated both the ground truth and estimated hysteresis loop can be constructed and evaluated through assessment of each EP-. It is worth noting that the obtained P-D loops correspond to an aortic site where the real measurement would, while highly invasive, be very useful regarding the potential information that could extracted [23,24].
Regarding the LSGAN model, and considering that it was not particularly trained to estimate calibration values, visual inspection of the Bland–Altman plots in Figure 7 does not suggest any heteroscedasticity. In relation to systematic bias, DBP seems to be slightly overestimated as values increase. It is observed that estimation of pressure PW values shows a lower relative error compared to area estimation. It is hypothesized that calibration similarities between PBra-Rad and PAbdo reduce the learning difficulty and offer bounds on the estimated PW. For example, systolic PBra-Rad values are always greater than PAbdo, and the model can easily learn this, while the shape of the PW remains as a challenging task. On the contrary, the calibration of the area PW values has no reference points from the pressure values, meaning that the learning task increases in complexity. In particular, for the pressure PW, in comparison with previous works [25,26,27] it is apparent that the error as presented in Table 2 is lower. It should be noted, however, that these previous works were obtained from real subjects, which is a more challenging task.
It is worth mentioning that a similar model was used in Brophy et al. [28], where domain transformation was performed from finger PPG to peripheral BP and signals were taken from subjects in intensive care units. In Brophy et al. [28], evaluation was performed only with respect to the mean BP and trained with a single , while in the present approach two were explored, a generator returned both pressure and area values, and the evaluation was performed across all the PWs and their inter-relationship (P-D loop).
Although the best hyperparameter results were obtained with LSGAN, it is noteworthy that WGAN-GP results are less sensitive to hyperparameter search and more stable in terms of training. Increasing the number of epochs could produce better results; however, considering our resource capacity, 1750 epochs seems to offer a fair comparison between . In Appendix A, Table A1 and Table A2, the complete results of the grid search and their corresponding hyperparameters as proposed in Table 1 are reported. Finally, to ensure collaborate with the community and for ease of reproducibility, our code is publicly available (please see Supplementary Materials section)
In order to validate the proposed methodology and open new lines of research, in vivo P-D measurements such as those detailed in [29,30] should be performed. It is noteworthy that the virtual subjects considered in this study were simulated assuming a healthy condition. In addition, the impact of the surrounding tissue on the mechanical behavior of the arteries was not taken into account [31]. Lastly, as a future line of work, it would be interesting to evaluate model performance considering subjects with particular CV diseases.
5. Conclusions
The ability of GAN-based deep learning models to transfer pressure signals from the peripheral artery regions to pressure and area signals in the central arterial region is analyzed in this paper. Unlike previous studies that used PWV to quantify arterial stiffness, the present study reconstructs and evaluates the pressure–strain hysteresis loop. When adversarial losses from LSGAN and WGAN-GP are compared, LSGAN provides more accurate results.
Supplementary Materials
Source codes are available at https://github.com/AguirreNicolas/ABPCycleGAN.
Author Contributions
Conceptualization, N.A., E.G.-M. and L.J.C., methodology and software, N.A.; validation, E.I.; funding acquisition, E.G.-M. and R.L.A.; Supervision, E.G.-M. and L.J.C.; writing—original draft preparation, N.A.; writing—review and editing, E.G.-M. and L.J.C.; project administration, R.L.A. All authors have read and agreed to the published version of the manuscript.
Funding
This work was partially funded by the Universidad Tecnológica Nacional (Grant: ICUTIBA7647 and ICTCABA8443 R&D projects) and by the ML-Cardyn project, co-funded by the European Union. The authors would like to thank Europe for its commitment in Champagne-Ardenne with the European Regional Development Fund (FEDER).
Data Availability Statement
The database is publicly available at https://doi.org/10.5281/zenodo.3275625.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study, in the collection, analysis, or interpretation of data, in the writing of the manuscript, or in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| BP | blood pressure |
| CNN | convolutional neural network |
| CV | cardiovascular |
| CVD | cardiovascular disease |
| DBP | diastolic blood pressure |
| E | elastic module |
| EP- | pressure–strain elastic modulus |
| GAN | generative adversarial network |
| GRU | gated recurrent unit |
| LOA | limit of agreement |
| LR | learning rate |
| LSGAN | least-square GAN |
| MAPE | mean absolute percentage error |
| ME | mean error |
| ML | machine learning |
| NN | neural network |
| P-D | pressure–diameter |
| PPG | photoplethysmography |
| PW | pulse wave |
| PWV | pulse wave velocity |
| RMSE | root mean squared error |
| SBP | systolic blood pressure |
| SVM | support vector machine |
| WGAN-GP | Wasserstein GAN with gradient penalty |
Appendix A

Table A1.
Experiments and their hyperparameters.
Table A1.
Experiments and their hyperparameters.
| Experiment | |||||
|---|---|---|---|---|---|
| LSGAN | 128 | 8 | 1 | 5 | A |
| WGAN-GP | 64 | 6 | 15 | 25 | B |
| LSGAN | 64 | 6 | 1 | 15 | C |
| 64 | 6 | 1 | 25 | D | |
| 64 | 6 | 1 | 5 | E | |
| WGAN-GP | 128 | 8 | 15 | 5 | F |
| 64 | 6 | 10 | 5 | G | |
| 64 | 6 | 15 | 15 | H | |
| 64 | 6 | 15 | 5 | I | |
| 64 | 6 | 50 | 15 | J | |
| 64 | 6 | 50 | 25 | K |

Table A2.
Detailed Brachial–Radial to Aortic Abdominal results.
Table A2.
Detailed Brachial–Radial to Aortic Abdominal results.
| Experiment | Pressure [mmHg] | Area [cm2] | [mmHg/%] | ||
|---|---|---|---|---|---|
| RMSE | RMSE | ME | MAPE | ||
| LSGAN | A | 0.8 ± 0.4 | 0.1 ± 0.1 | 13.1 ± 56.5 | 6.5 ± 5.1 |
| WGAN-GP | B | 1.7 ± 0.8 | 0.2 ± 0.2 | 70.6 ± 216.0 | 28.6 ± 19.3 |
| LSGAN | C | 4.4 ± 1.2 | 0.2 ± 0.1 | 229.3 ± 304.6 | 45.0 ± 25.7 |
| D | 27.1 ± 6.3 | 0.2 ± 0.1 | 654.2 ± 265.4 | 137.5 ± 14.6 | |
| E | 5.8 ± 3.3 | 0.3 ± 0.2 | 18.0 ± 137.7 | 17.3 ± 13.1 | |
| WGAN-GP | F | 2.7 ± 1.7 | 0.4 ± 0.2 | 3.1 ± 349.1 | 59.7 ± 54.4 |
| G | 3.8 ± 1.8 | 0.2 ± 0.1 | 84.3 ± 201.0 | 28.7 ± 19.5 | |
| H | 1.5 ± 0.7 | 0.4 ± 0.3 | 104.8 ± 222.3 | 28.7 ± 22.7 | |
| I | 3.4 ± 2.1 | 0.3 ± 0.2 | 10.9 ± 273.3 | 39.3 ± 31.9 | |
| J | 1.6 ± 0.7 | 0.4 ± 0.2 | 12.7 ± 300.1 | 48.2 ± 47.0 | |
| K | 2.0 ± 0.8 | 0.2 ± 0.2 | 68.4 ± 242.7 | 32.9 ± 23.6 | |
References
- World Health Organization. Cardiovascular Diseases (CVDs). 2021. Available online: https://www.who.int/news-room/fact-sheets/detail/cardiovascular-diseases-(cvds) (accessed on 19 May 2022).
- Salvi, P. Pulse Waves: How Vascular Hemodynamics Affects Blood Pressure, 2nd ed.; Springer International Publishing: Cham, Switzerland, 2017. [Google Scholar] [CrossRef]
- Armentano, R.L.; Barra, J.G.; Levenson, J.; Simon, A.; Pichel, R.H. Arterial Wall Mechanics in Conscious Dogs. Circ. Res. 1995, 76, 468–478. [Google Scholar] [CrossRef] [PubMed]
- Cymberknop, L.J.; Gabaldon Castillo, F.; Armentano, R.L. Beat to Beat Modulation of Arterial Pulse Wave Velocity Induced by Vascular Smooth Muscle Tone. In Proceedings of the 2019 41st Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Berlin, Germany, 23–27 July 2019; Volume 2019, pp. 5030–5033. [Google Scholar] [CrossRef]
- Alty, S.R.; Angarita-Jaimes, N.; Millasseau, S.C.; Chowienczyk, P.J. Predicting Arterial Stiffness From the Digital Volume Pulse Waveform. IEEE Trans. Biomed. Eng. 2007, 54, 2268–2275. [Google Scholar] [CrossRef] [PubMed]
- Tavallali, P.; Razavi, M.; Pahlevan, N.M. Artificial Intelligence Estimation of Carotid-Femoral Pulse Wave Velocity Using Carotid Waveform. Sci. Rep. 2018, 8, 1014. [Google Scholar] [CrossRef] [PubMed]
- Jin, W.; Chowienczyk, P.; Alastruey, J. Estimating Pulse Wave Velocity from the Radial Pressure Wave Using Machine Learning Algorithms. PLoS ONE 2021, 16, e0245026. [Google Scholar] [CrossRef]
- Mildenhall, B.; Srinivasan, P.P.; Tancik, M.; Barron, J.T.; Ramamoorthi, R.; Ng, R. NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis. arXiv 2020, arXiv:cs/2003.08934. [Google Scholar] [CrossRef]
- Charlton, P.H.; Mariscal Harana, J.; Vennin, S.; Li, Y.; Chowienczyk, P.; Alastruey, J. Modeling Arterial Pulse Waves in Healthy Aging: A Database for in Silico Evaluation of Hemodynamics and Pulse Wave Indexes. Am. J. Physiol.-Heart Circ. Physiol. 2019, 317, H1062–H1085. [Google Scholar] [CrossRef]
- Xiao, H.; Tan, I.; Butlin, M.; Li, D.; Avolio, A.P. Arterial Viscoelasticity: Role in the Dependency of Pulse Wave Velocity on Heart Rate in Conduit Arteries. Am. J. Physiol.-Heart Circ. Physiol. 2017, 312, H1185–H1194. [Google Scholar] [CrossRef]
- Willemet, M.; Vennin, S.; Alastruey, J. Computational Assessment of Hemodynamics-Based Diagnostic Tools Using a Database of Virtual Subjects: Application to Three Case Studies. J. Biomech. 2016, 49, 3908–3914. [Google Scholar] [CrossRef]
- Alastruey, J. Numerical Assessment of Time-Domain Methods for the Estimation of Local Arterial Pulse Wave Speed. J. Biomech. 2011, 44, 885–891. [Google Scholar] [CrossRef]
- Bikia, V.; Papaioannou, T.G.; Pagoulatou, S.; Rovas, G.; Oikonomou, E.; Siasos, G.; Tousoulis, D.; Stergiopulos, N. Noninvasive Estimation of Aortic Hemodynamics and Cardiac Contractility Using Machine Learning. Sci. Rep. 2020, 10, 15015. [Google Scholar] [CrossRef]
- Ipar, E.; Aguirre, N.A.; Cymberknop, L.J.; Armentano, R.L. Blood Pressure Morphology as a Fingerprint of Cardiovascular Health: A Machine Learning Based Approach. In Proceedings of the Applied Informatics; Florez, H., Pollo-Cattaneo, M.F., Eds.; Communications in Computer and Information Science; Springer International Publishing: Cham, Switzerland, 2021; pp. 253–265. [Google Scholar] [CrossRef]
- Xiao, H.; Liu, D.; Avolio, A.P.; Chen, K.; Li, D.; Hu, B.; Butlin, M. Estimation of Cardiac Stroke Volume from Radial Pulse Waveform by Artificial Neural Network. Comput. Methods Programs Biomed. 2022, 218, 106738. [Google Scholar] [CrossRef]
- Armentano, R.L.; Cymberknop, L.J.; Legnani, W.; Pessana, F.M.; Craiem, D.; Graf, S.; Barra, J.G. Arterial Pressure Fractality Is Highly Dependent on Wave Reflection. In Proceedings of the 2013 35th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Osaka, Japan, 3–7 July 2013; pp. 1960–1963. [Google Scholar] [CrossRef]
- Zhu, J.Y.; Park, T.; Isola, P.; Efros, A.A. Unpaired Image-to-Image Translation Using Cycle-Consistent Adversarial Networks. arXiv 2020, arXiv:1703.10593. [Google Scholar]
- Mao, X.; Li, Q.; Xie, H.; Lau, R.Y.K.; Wang, Z.; Smolley, S.P. Least Squares Generative Adversarial Networks. arXiv 2017, arXiv:1611.04076. [Google Scholar]
- Gulrajani, I.; Ahmed, F.; Arjovsky, M.; Dumoulin, V.; Courville, A. Improved Training of Wasserstein GANs. arXiv 2017, arXiv:1704.00028. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2017, arXiv:1412.6980. [Google Scholar]
- Arjovsky, M.; Chintala, S.; Bottou, L. Wasserstein GAN. arXiv 2017, arXiv:1701.07875. [Google Scholar]
- Stefanadis, C.; Stratos, C.; Vlachopoulos, C.; Marakas, S.; Boudoulas, H.; Kallikazaros, I.; Tsiamis, E.; Toutouzas, K.; Sioros, L.; Toutouzas, P. Pressure-Diameter Relation of the Human Aorta. Circulation 1995, 92, 2210–2219. [Google Scholar] [CrossRef]
- McEniery Carmel, M.; Yasmin, N.; McDonnell, B.; Munnery, M.; Wallace Sharon, M.; Rowe Chloe, V.; Cockcroft John, R.; Wilkinson Ian, B. Central Pressure: Variability and Impact of Cardiovascular Risk Factors. Hypertension 2008, 51, 1476–1482. [Google Scholar] [CrossRef]
- Agabiti-Rosei, E.; Mancia, G.; O’Rourke Michael, F.; Roman Mary, J.; Safar Michel, E.; Smulyan, H.; Wang, J.-G.; Wilkinson Ian, B.; Williams, B.; Vlachopoulos, C. Central Blood Pressure Measurements and Antihypertensive Therapy. Hypertension 2007, 50, 154–160. [Google Scholar] [CrossRef]
- Sadrawi, M.; Lin, Y.T.; Lin, C.H.; Mathunjwa, B.; Fan, S.Z.; Abbod, M.F.; Shieh, J.S. Genetic Deep Convolutional Autoencoder Applied for Generative Continuous Arterial Blood Pressure via Photoplethysmography. Sensors 2020, 20, 3829. [Google Scholar] [CrossRef]
- Sideris, C.; Kalantarian, H.; Nemati, E.; Sarrafzadeh, M. Building Continuous Arterial Blood Pressure Prediction Models Using Recurrent Networks. In Proceedings of the 2016 IEEE International Conference on Smart Computing (SMARTCOMP), St. Louis, MO, USA, 18–20 May 2016; pp. 1–5. [Google Scholar] [CrossRef]
- Aguirre, N.; Grall-Maës, E.; Cymberknop, L.J.; Armentano, R.L. Blood Pressure Morphology Assessment from Photoplethysmogram and Demographic Information Using Deep Learning with Attention Mechanism. Sensors 2021, 21, 2167. [Google Scholar] [CrossRef] [PubMed]
- Brophy, E.; De Vos, M.; Boylan, G.; Ward, T. Estimation of Continuous Blood Pressure from PPG via a Federated Learning Approach. arXiv 2021, arXiv:2102.12245. [Google Scholar] [CrossRef]
- Armentano, R.L.; Cymberknop, L.J. Quantitative Vascular Evaluation: From Laboratory Experiments to Point-of-Care Patient (Clinical Approach). Curr. Hypertens. Rev. 2018, 14, 86–94. [Google Scholar] [CrossRef]
- Armentano, R.L.; Cymberknop, L.J. Quantitative Vascular Evaluation: From Laboratory Experiments to Point-of-Care Patient (Experimental Approach). Curr. Hypertens. Rev. 2018, 14, 76–85. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Dang, C.; Garcia, M.; Gregersen, H.; Kassab, G.S. Surrounding Tissues Affect the Passive Mechanics of the Vessel Wall: Theory and Experiment. Am. J. Physiol.-Heart Circ. Physiol. 2007, 293, H3290–H3300. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).