A LiDAR SLAM-Assisted Fusion Positioning Method for USVs
Abstract
1. Introduction
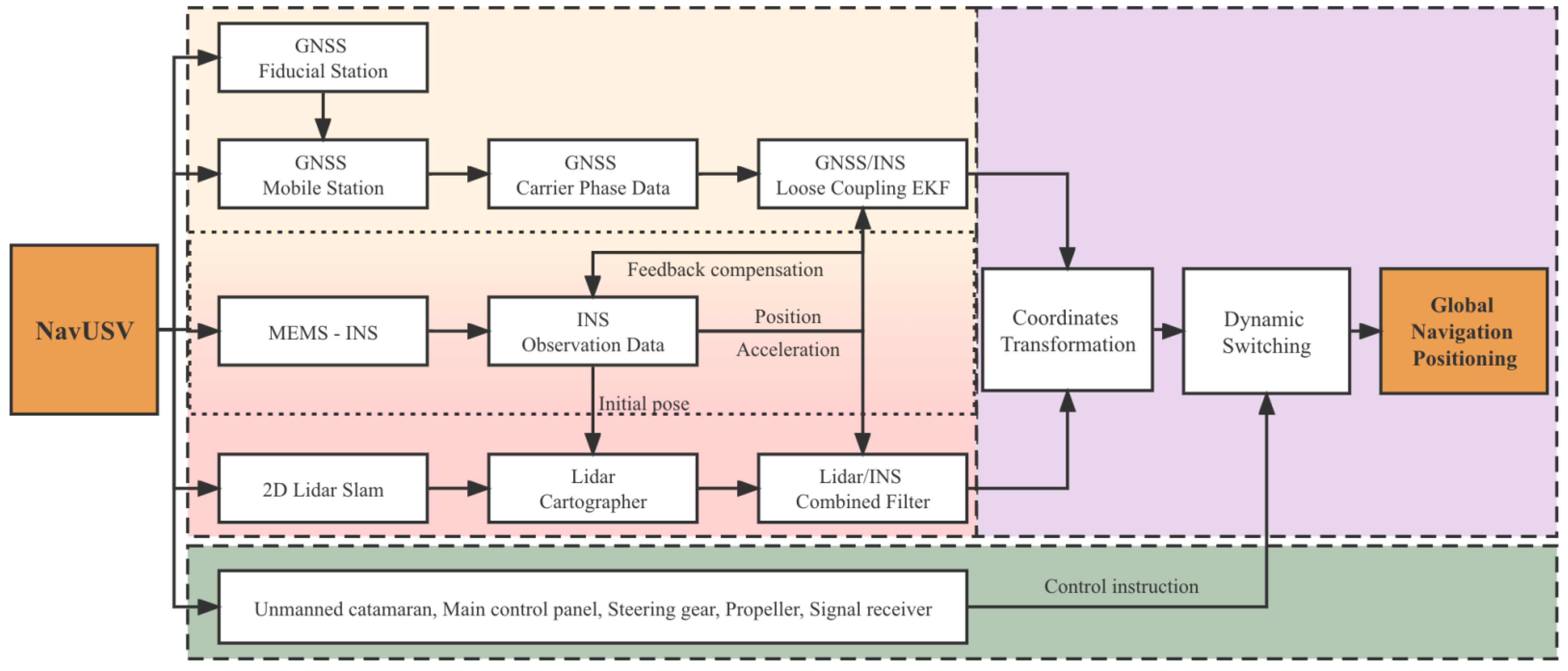
2. Method Description
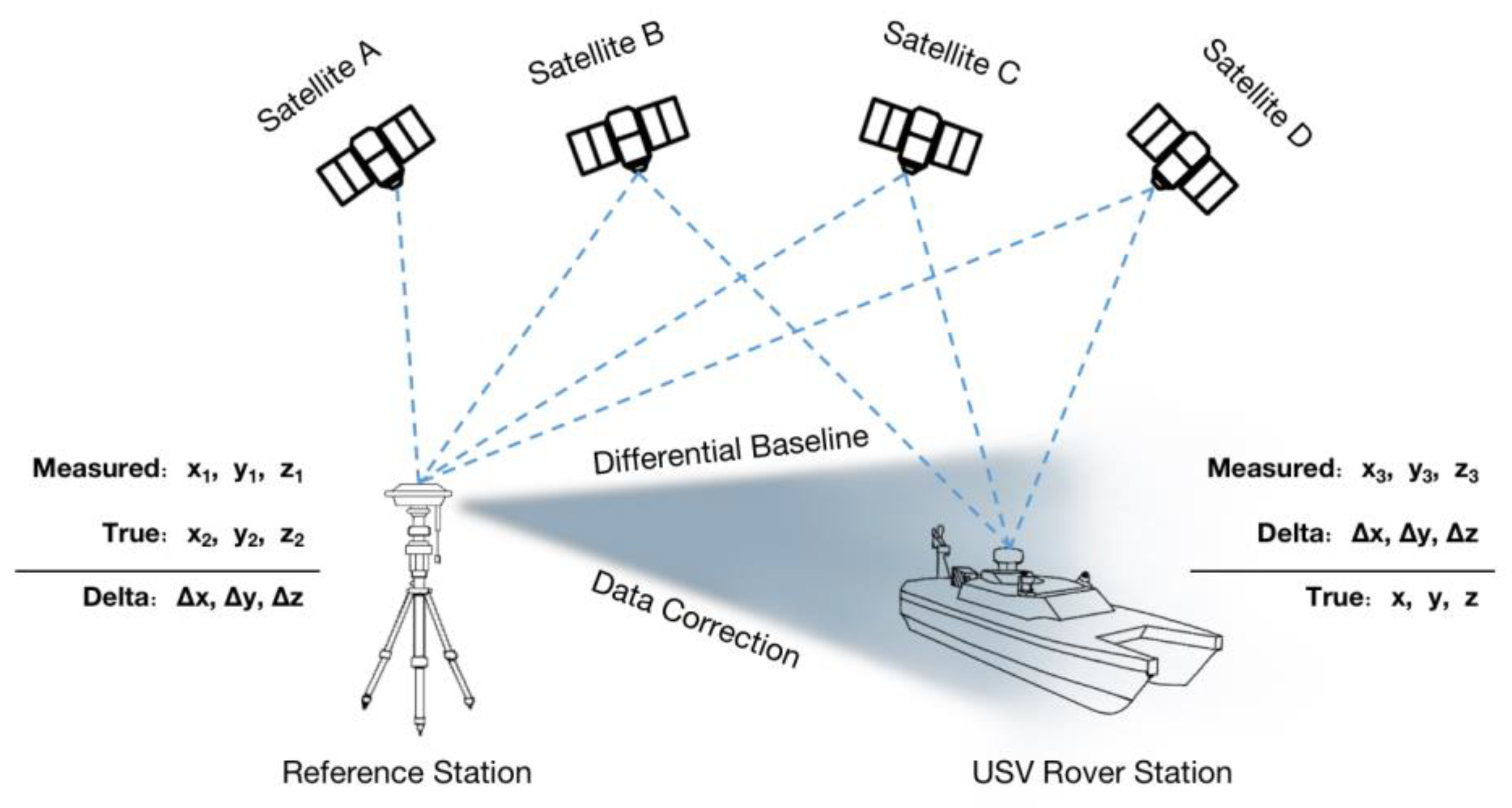
2.1. GNSS/INS Loosely-Coupled Integrated System
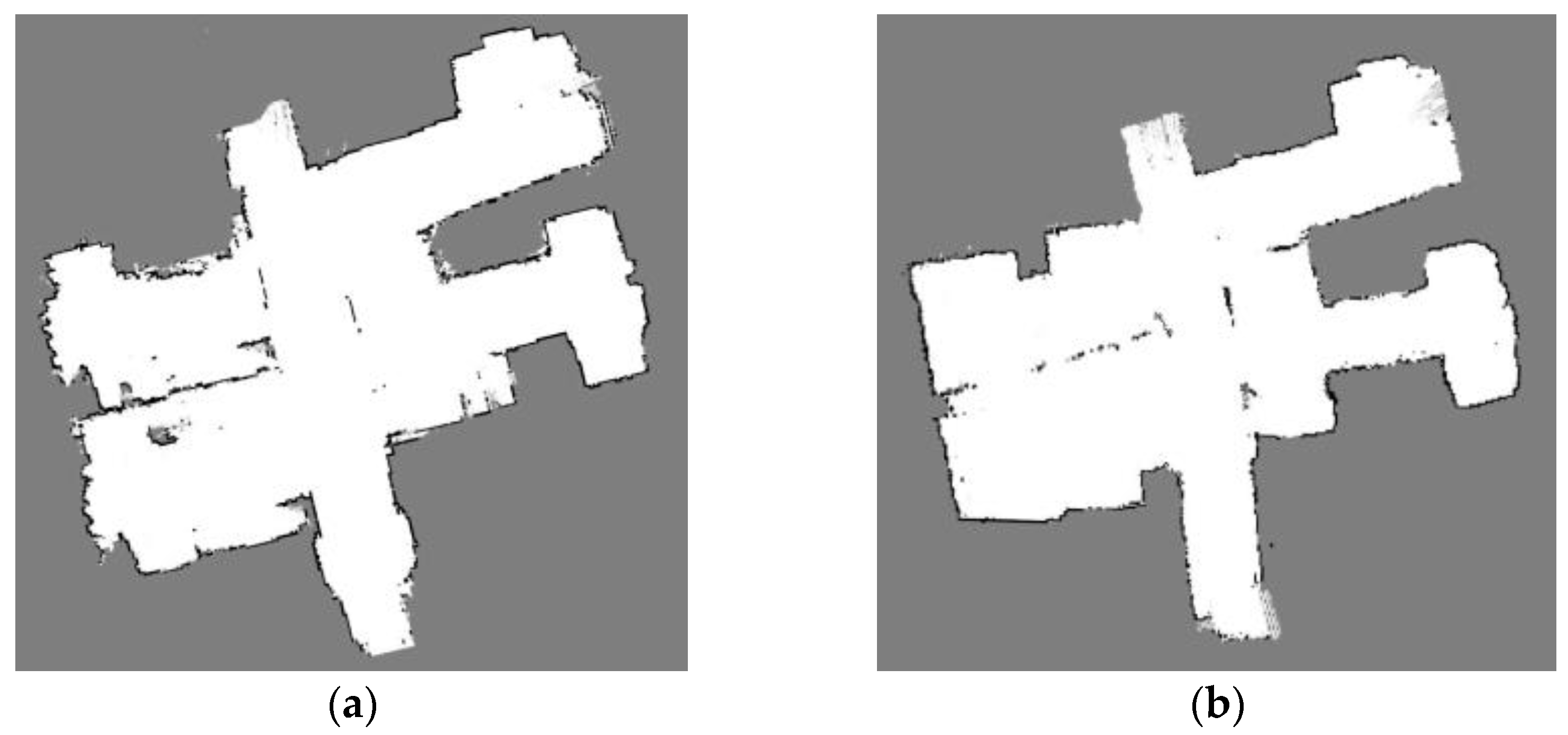
2.2. D LiDAR-SLAM/INS Integrated System during GNSS Outages
2.3. Multi-Source Information Fusion Positioning
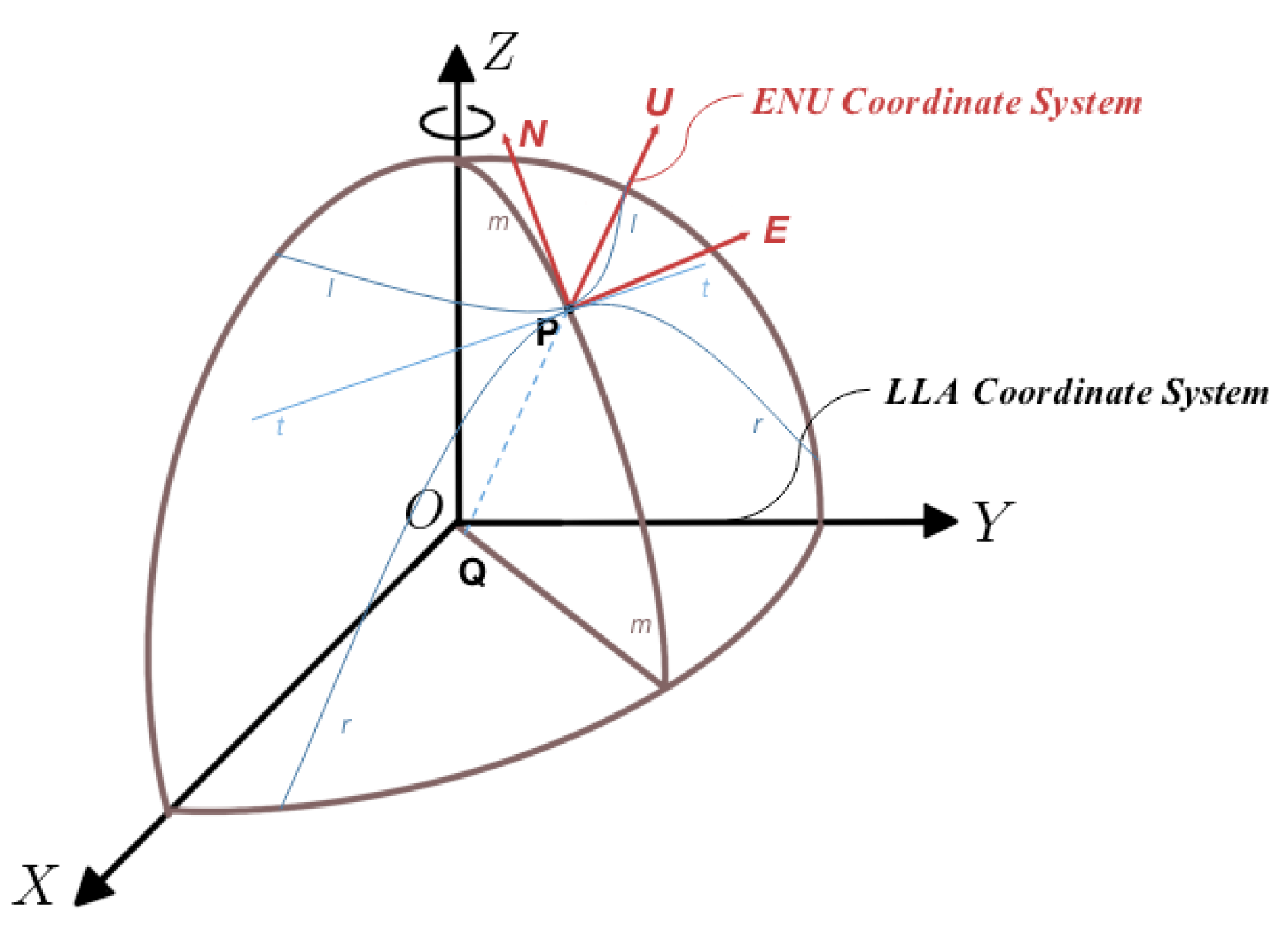
2.3.1. Coordinate System Transformation
2.3.2. Dynamic Sensor Switching Framework
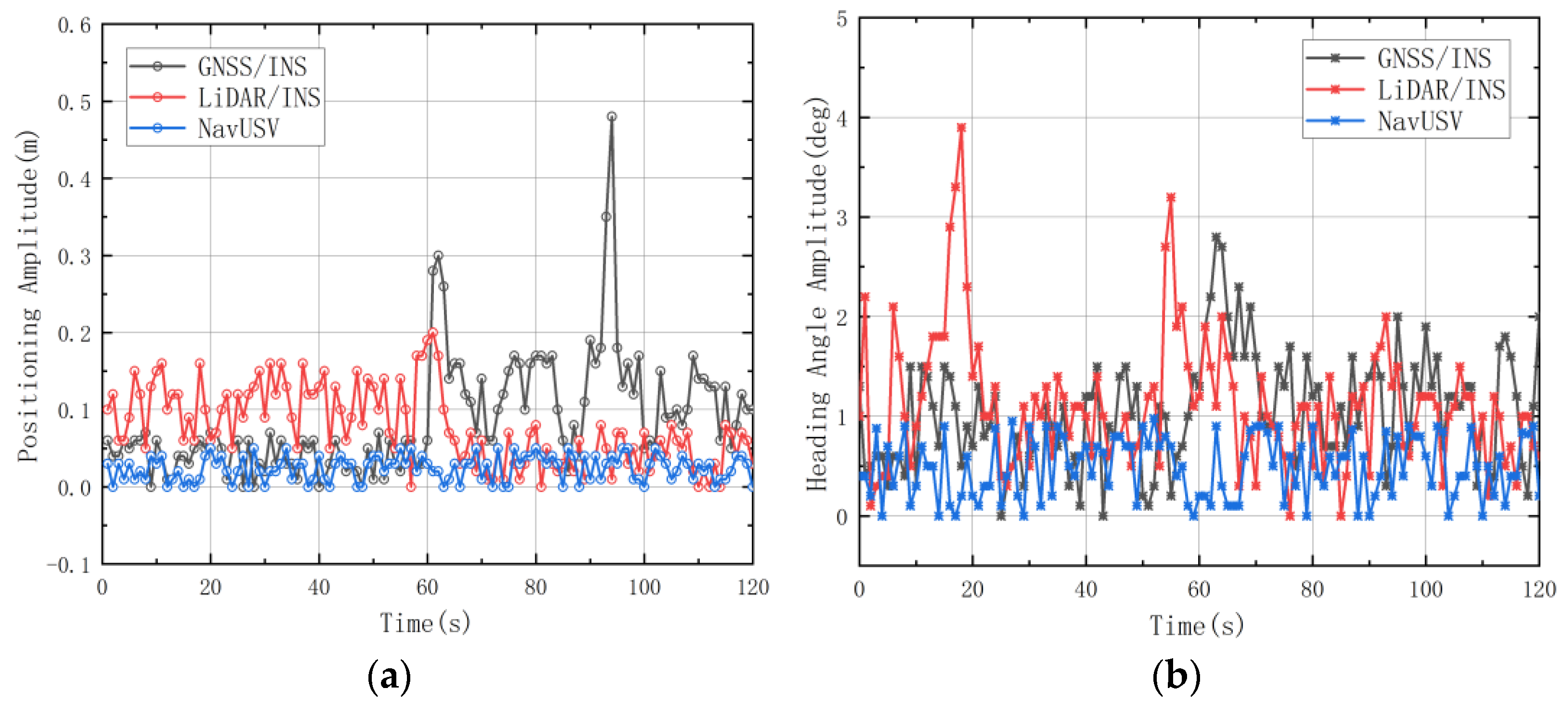
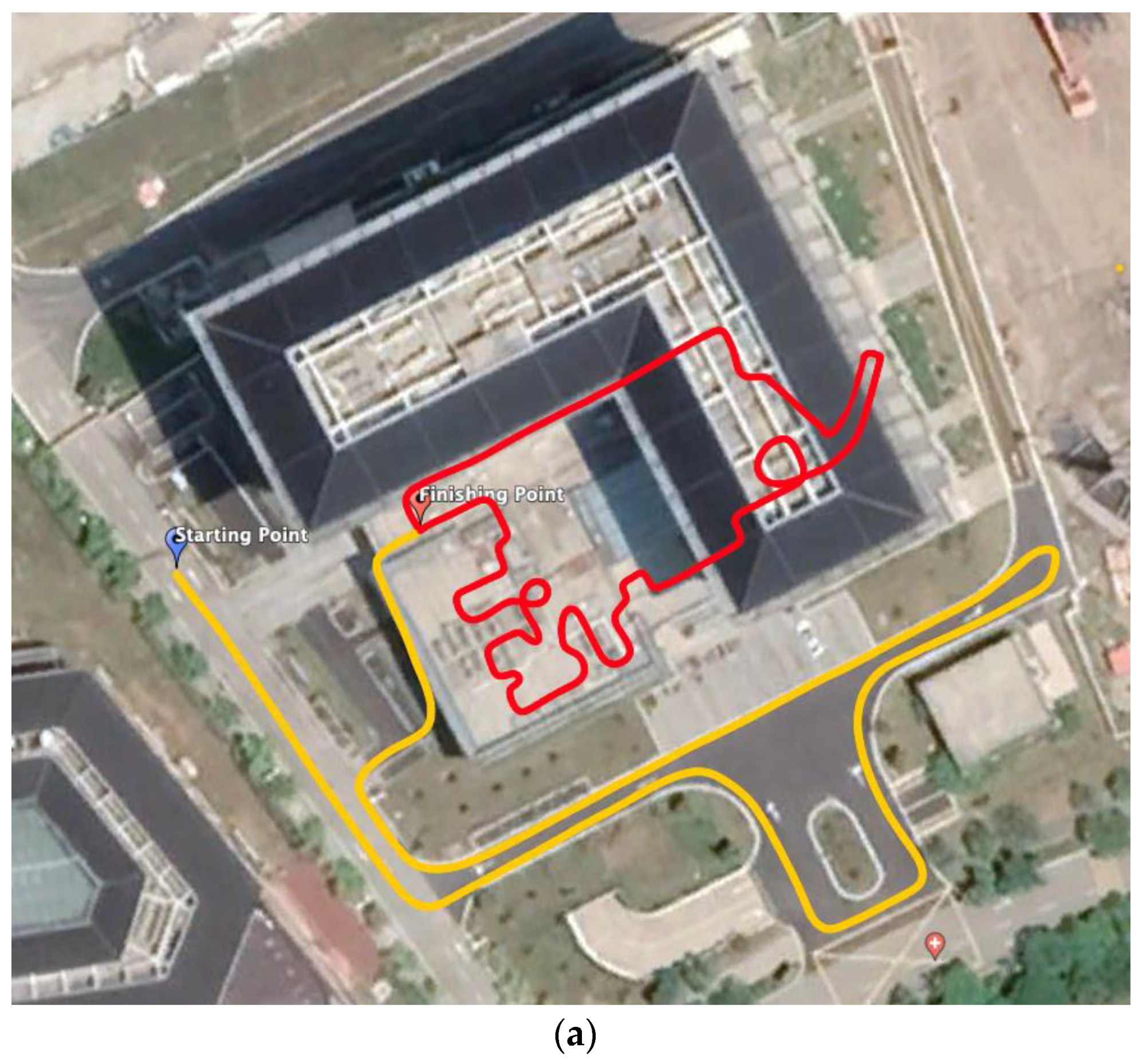
3. NavUSV-Based USV Positioning Experiments
3.1. USV Hardware Platform
3.2. Sailing Test
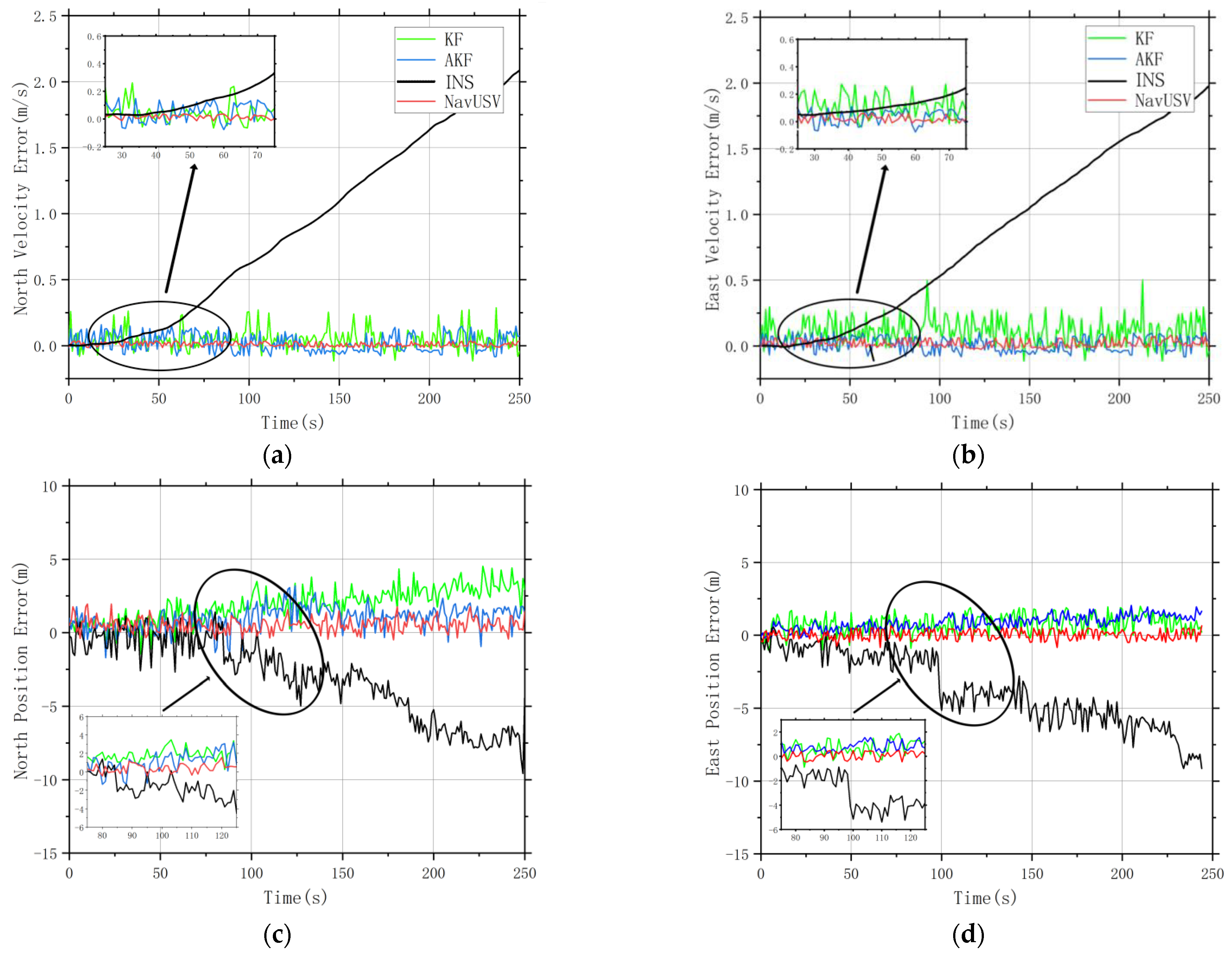
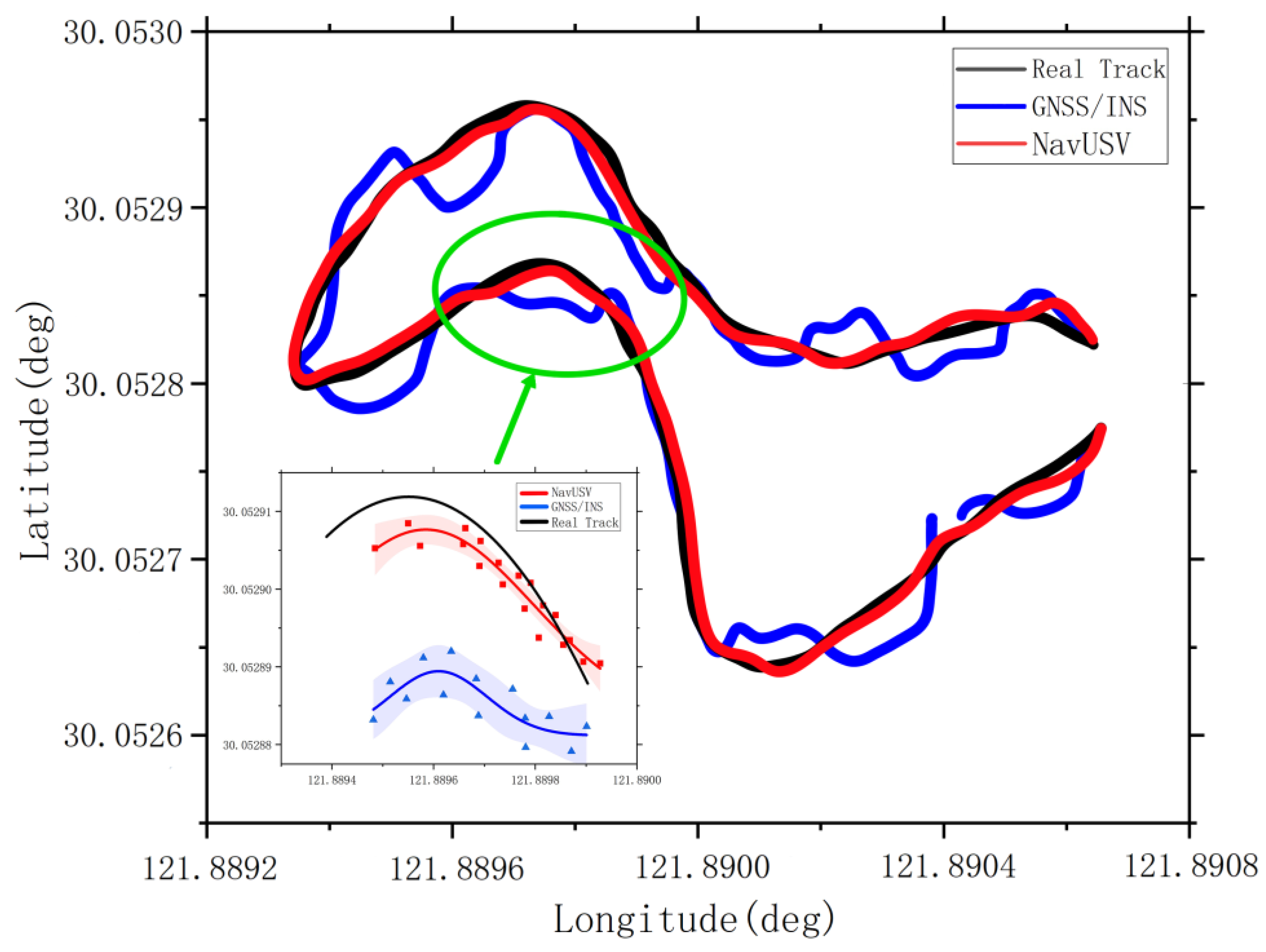
4. Results and Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wynn, R.B.; Huvenne, V.A.; Le Bas, T.P.; Murton, B.J.; Connelly, D.P.; Bett, B.J.; Ruhl, H.A.; Morris, K.J.; Peakall, J.; Parsons, D.R. Autonomous Underwater Vehicles (AUVs): Their past, present and future contributions to the advancement of marine geoscience. Mar. Geol. 2014, 352, 451–468. [Google Scholar] [CrossRef]
- Xu, Y.; Xiao, K. Advances in intelligent marine robot technology. J. Autom. 2007, 33, 518–521. [Google Scholar]
- Wang, W. Research on Remote Control System of Unmanned Monitoring Ship. Ph.D. Thesis, Zhejiang University, Hangzhou, China, 2014. [Google Scholar]
- Meng, X. Research on Path Planning Algorithm for Unmanned Ship. Ph.D. Thesis, Tianjin University of Technology, Tianjin, China, 2017. [Google Scholar]
- Bo, F.; Li, L.; Jiuhong, B. GPS/INS/speed log integrated navigation system based on MAKF and priori velocity information. In Proceedings of the 2013 IEEE International Conference on Information and Automation (ICIA), Yingchuan, China, 26–28 August 2013; pp. 54–58. [Google Scholar]
- Grewal, M.S.; Weill, L.R.; Andrews, A.P. Global Positioning Systems, Inertial Navigation, and Integration; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Ziebold, R.; Medina, D.; Romanovas, M.; Lass, C.; Gewies, S. Performance characterization of GNSS/IMU/DVL integration under real maritime jamming conditions. Sensors 2018, 18, 2954. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y. Research and Realization of Simulation Algorithm for Strapdown Inertial Navigation System. Ph.D. Thesis, Dalian University of Technology, Dalian, China, 2005. [Google Scholar]
- Tang, J.; Chen, Y.; Niu, X.; Wang, L.; Chen, L.; Liu, J.; Shi, C.; Hyyppä, J. LiDAR scan matching aided inertial navigation system in GNSS-denied environments. Sensors 2015, 15, 16710–16728. [Google Scholar] [CrossRef] [PubMed]
- Kumar, G.A.; Patil, A.K.; Patil, R.; Park, S.S.; Chai, Y.H. A LiDAR and IMU integrated indoor navigation system for UAVs and its application in real-time pipeline classification. Sensors 2017, 17, 1268. [Google Scholar] [CrossRef] [PubMed]
- Qian, C.; Liu, H.; Tang, J.; Chen, Y.; Kaartinen, H.; Kukko, A.; Zhu, L.; Liang, X.; Chen, L.; Hyyppä, J. An integrated GNSS/INS/LiDAR-SLAM positioning method for highly accurate forest stem mapping. Remote Sens. 2016, 9, 3. [Google Scholar] [CrossRef]
- Hess, W.; Kohler, D.; Rapp, H.; Andor, D. Real-time loop closure in 2D LiDAR SLAM. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 1271–1278. [Google Scholar]
- Yao, Y.; Xu, X.; Zhu, C.; Chan, C.-Y. A hybrid fusion algorithm for GPS/INS integration during GPS outages. Measurement 2017, 103, 42–51. [Google Scholar] [CrossRef]
- Li, Z.; Wang, R.; Gao, J.; Wang, J. An approach to improve the positioning performance of GPS/INS/UWB integrated system with two-step filter. Remote Sens. 2017, 10, 19. [Google Scholar] [CrossRef]
- Jiang, C.; Zhang, S.-B.; Zhang, Q.-Z. Adaptive estimation of multiple fading factors for GPS/INS integrated navigation systems. Sensors 2017, 17, 1254. [Google Scholar] [CrossRef] [PubMed]
- Zhong, M.; Guo, J.; Zhou, D. Adaptive in-flight alignment of INS/GPS systems for aerial mapping. IEEE Trans. Aerosp. Electron. Syst. 2017, 54, 1184–1196. [Google Scholar] [CrossRef]
- Kim, Y.; An, J.; Lee, J. Robust navigational system for a transporter using GPS/INS fusion. IEEE Trans. Ind. Electron. 2017, 65, 3346–3354. [Google Scholar] [CrossRef]
- Ren, G.; Ai, C.; Xu, Q.; Wang, Z.; Wang, Z.; Geng, D. Research on Indoor and Outdoor Navigation Technology Based on the Combination of Differential GNSS and LiDAR SLAM. In Proceedings of the 2020 IEEE International Conference on Real-time Computing and Robotics (RCAR), Asahikawa, Hokkaido, Japan, 28–29 September 2020; pp. 134–139. [Google Scholar]
- Feng, K.; Li, J.; Zhang, X.; Zhang, X.; Shen, C.; Cao, H.; Yang, Y.; Liu, J. An improved strong tracking cubature Kalman filter for GPS/INS integrated navigation systems. Sensors 2018, 18, 1919. [Google Scholar] [CrossRef] [PubMed]
- Meng, Q.; Hsu, L.T. Resilient Interactive Sensor-Independent-Update Fusion Navigation Method. IEEE Trans. Intell. Transp. Syst. 2022, 23, 16433–16447. [Google Scholar] [CrossRef]
- Bijjahalli, S.; Lim, Y.; Ramasamy, S.; Sabatini, R. An adaptive sensor-switching framework for urban UAS navigation. In Proceedings of the AIAA/IEEE Digital Avionics Systems Conference, St. Petersburg, FL, USA, 17–21 September 2017; pp. 16–21. [Google Scholar]
- Park, G.; Lee, B.; Sung, S. Integrated Pose Estimation Using 2D LiDAR and INS Based on Hybrid Scan Matching. Sensors 2021, 21, 5670. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Fan, X.; Lv, C.; Wu, J.; Li, L.; Ding, D. An innovative information fusion method with adaptive Kalman filter for integrated INS/GPS navigation of autonomous vehicles. Mech. Syst. Signal Process. 2018, 100, 605–616. [Google Scholar] [CrossRef]
- Chang, L.; Niu, X.; Liu, T.; Tang, J.; Qian, C. GNSS/INS/LiDAR-SLAM integrated navigation system based on graph optimization. Remote Sens. 2019, 11, 1009. [Google Scholar] [CrossRef]
- Zhao, S.; Farrell, J.A. 2D LIDAR aided INS for vehicle positioning in urban environments. In Proceedings of the 2013 IEEE International Conference on Control Applications (CCA), Dubrovnik, Croatia, 3–5 October 2013; pp. 376–381. [Google Scholar]
- Hening, S.; Ippolito, C.A.; Krishnakumar, K.S.; Stepanyan, V.; Teodorescu, M. 3D LiDAR SLAM integration with GPS/INS for UAVs in urban GPS-degraded environments. In Proceedings of the AIAA Information Systems-AIAA Infotech@ Aerospace, Grapevine, TX, USA, 9–13 January 2017; p. 0448. [Google Scholar]
- Kohlbrecher, S.; Von Stryk, O.; Meyer, J.; Klingauf, U. A flexible and scalable SLAM system with full 3D motion estimation. In Proceedings of the 2011 IEEE International Symposium on Safety, Security, and Rescue Robotics, Kyoto, Japan, 1–5 November 2011; pp. 155–160. [Google Scholar]




| INS Parameter | Parameter Value |
|---|---|
| Update Rate | 200 Hz |
| Gyro Range | ±2000°/s |
| Gyro RMS Noise | 0.05°/s |
| Accelerometer Range | ±16 g |
| Accelerometer RMS Noise | 0.75~1 mg |
| Index Content | Value |
|---|---|
| Measuring Distance | 40 m |
| Sampling Frequency | 9200 Hz |
| Mapping Resolution | 0.05 m |
| Maximum Inclination Angle | ±3° |
| Algorithm | Target | East Position | North Position | East Velocity | North Velocity | Horizontal Error |
|---|---|---|---|---|---|---|
| /m | /m | /(m/s) | /(m/s) | /m | ||
| KF | RMSE | 1.0223 | 1.2892 | 0.1473 | 0.0886 | 1.4362 |
| SD | 1.1678 | 2.4039 | 0.7210 | 0.7011 | 1.6373 | |
| MAX | 1.9876 | 3.1923 | 0.4969 | 0.2877 | 3.4387 | |
| ε | - | - | - | - | 0.1243 | |
| AKF | RMSE | 0.9915 | 0.9203 | 0.0569 | 0.0727 | 1.2249 |
| SD | 0.8543 | 1.6094 | 0.2534 | 0.4314 | 1.0761 | |
| MAX | 2.0592 | 4.5312 | 0.1098 | 0.1599 | 3.7086 | |
| ε | - | - | - | - | 0.0968 | |
| NavUSV | RMSE | 0.3380 | 0.7241 | 0.0331 | 0.0188 | 0.9462 |
| SD | 0.5819 | 0.3067 | 0.1738 | 0.1374 | 0.9019 | |
| MAX | 0.6584 | 1.9537 | 0.0821 | 0.0359 | 2.2197 | |
| ε | - | - | - | - | 0.0822 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, W.; Yang, Z.; Yang, C.; Li, X. A LiDAR SLAM-Assisted Fusion Positioning Method for USVs. Sensors 2023, 23, 1558. https://doi.org/10.3390/s23031558
Shen W, Yang Z, Yang C, Li X. A LiDAR SLAM-Assisted Fusion Positioning Method for USVs. Sensors. 2023; 23(3):1558. https://doi.org/10.3390/s23031558
Chicago/Turabian StyleShen, Wei, Zhisong Yang, Chaoyu Yang, and Xin Li. 2023. "A LiDAR SLAM-Assisted Fusion Positioning Method for USVs" Sensors 23, no. 3: 1558. https://doi.org/10.3390/s23031558
APA StyleShen, W., Yang, Z., Yang, C., & Li, X. (2023). A LiDAR SLAM-Assisted Fusion Positioning Method for USVs. Sensors, 23(3), 1558. https://doi.org/10.3390/s23031558







