Pelican Optimization Algorithm: A Novel Nature-Inspired Algorithm for Engineering Applications
Abstract
:1. Introduction
1.1. Motivation
1.2. Research Gap
1.3. Contribiution
1.4. Paper Organization
2. Background
3. Pelican Optimization Algorithm
3.1. Inspiration and Behavior of Pelican during Hunting
3.2. Mathematical Model of the Proposed POA
- (i)
- Moving towards prey (exploration phase).
- (ii)
- Winging on the water surface (exploitation phase).
3.2.1. Phase 1: Moving towards Prey (Exploration Phase)
3.2.2. Phase 2: Winging on the Water Surface (Exploitation Phase)
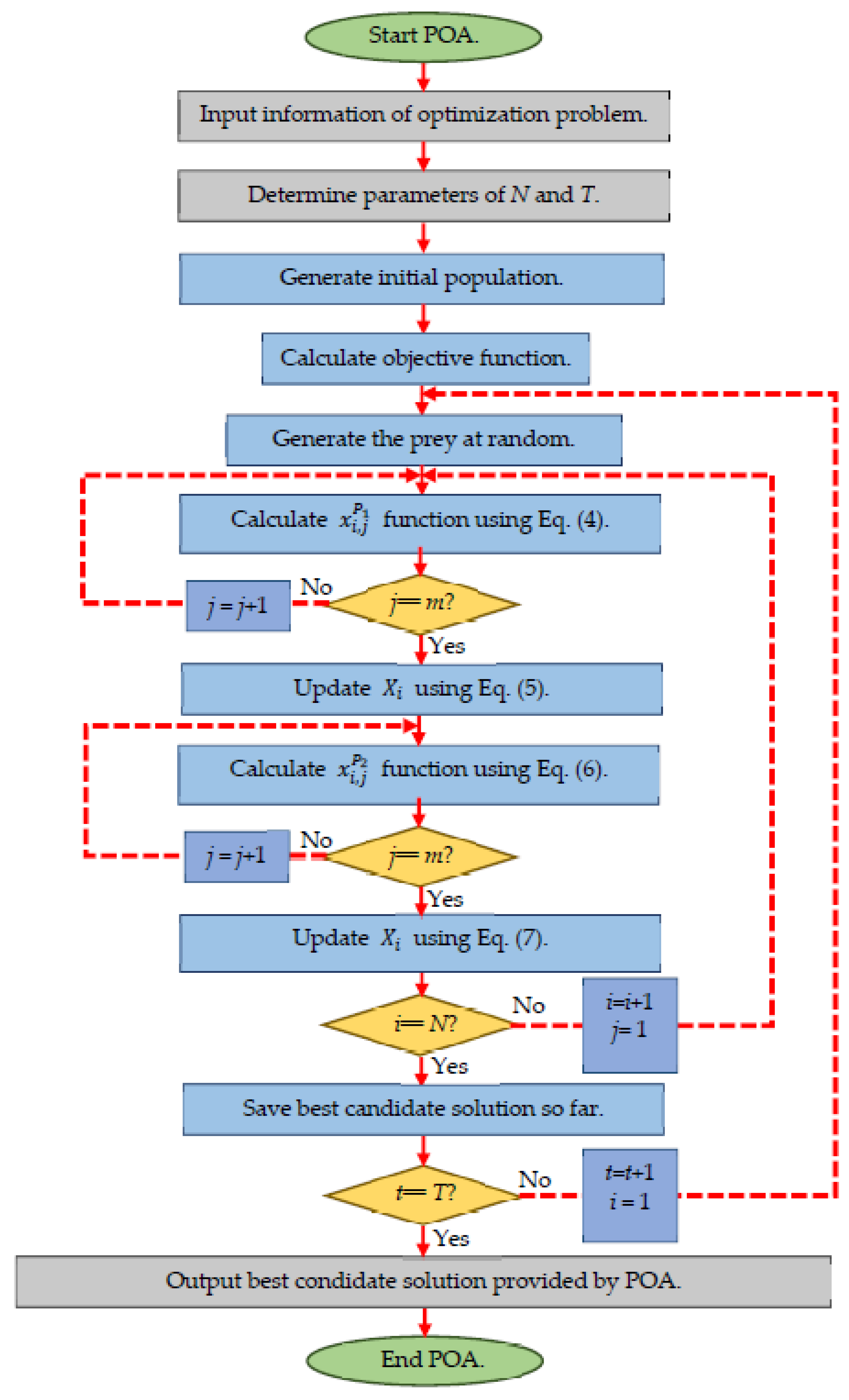
3.2.3. Steps Repetition, Pseudo-Code, and Flowchart of the Proposed POA
| Algorithm 1. Pseudo-code of POA. | ||||
| Start POA. | ||||
| 1. | Input the optimization problem information. | |||
| 2. | Determine the POA population size (N) and the number of iterations (T). | |||
| 3. | Initialization of the position of pelicans and calculate the objective function. | |||
| 4. | For t = 1:T | |||
| 5. | Generate the position of the prey at random. | |||
| 6. | For I = 1:N | |||
| 7. | Phase 1: Moving towards prey (exploration phase). | |||
| 8. | For j = 1:m | |||
| 9. | Calculate new status of the jth dimension using Equation (4). | |||
| 10. | End. | |||
| 11. | Update the ith population member using Equation (5). | |||
| 12. | Phase 2: Winging on the water surface (exploitation phase). | |||
| 13. | For j = 1:m. | |||
| 14. | Calculate new status of the jth dimension using Equation (6). | |||
| 15. | End. | |||
| 16. | Update the ith population member using Equation (7). | |||
| 17. | End. | |||
| 18. | Update best candidate solution. | |||
| 19. | End. | |||
| 20. | Output best candidate solution obtained by POA. | |||
| End POA. | ||||
3.3. Computational Complexity of the Proposed POA
4. Simulation Studies and Results
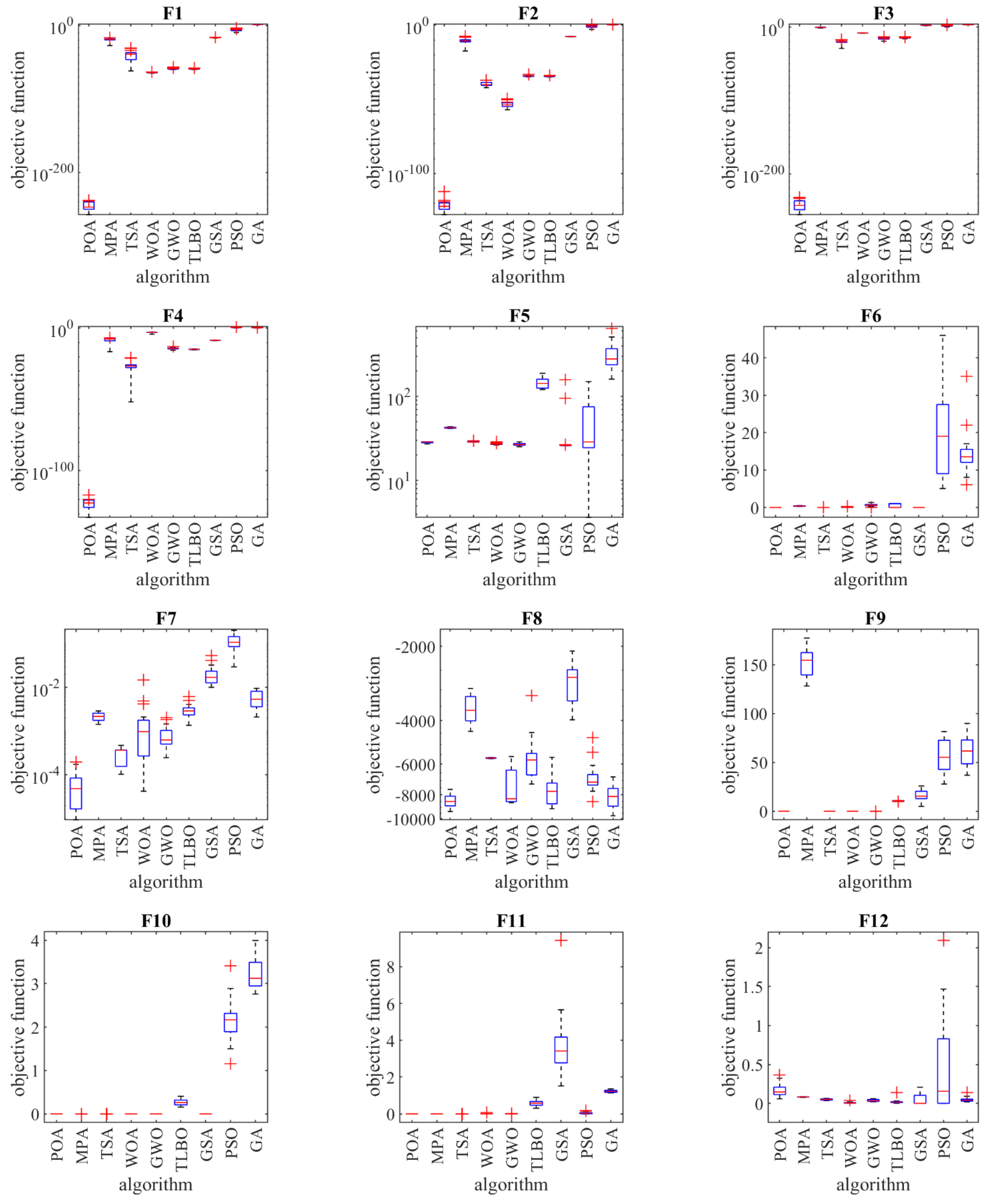
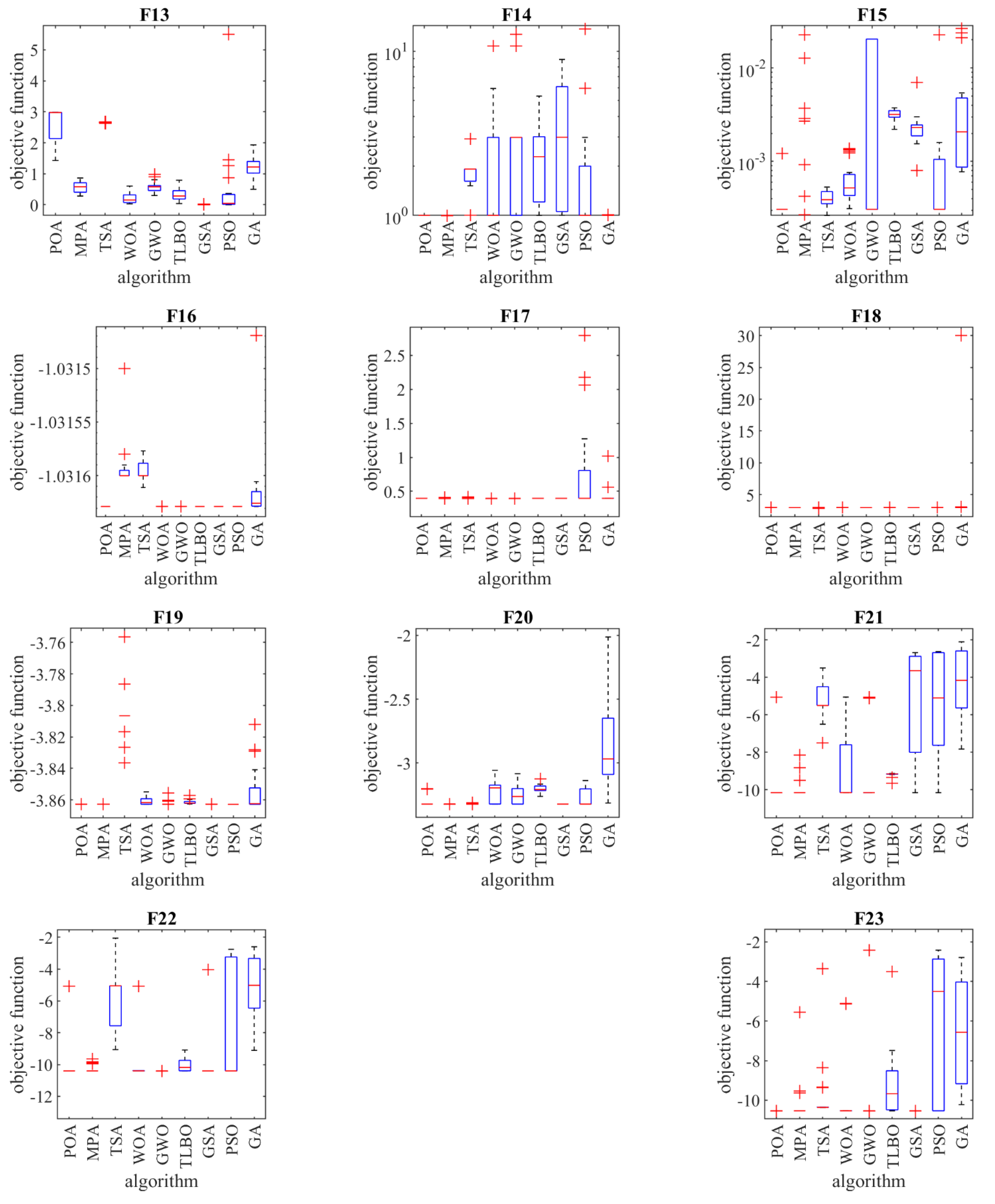
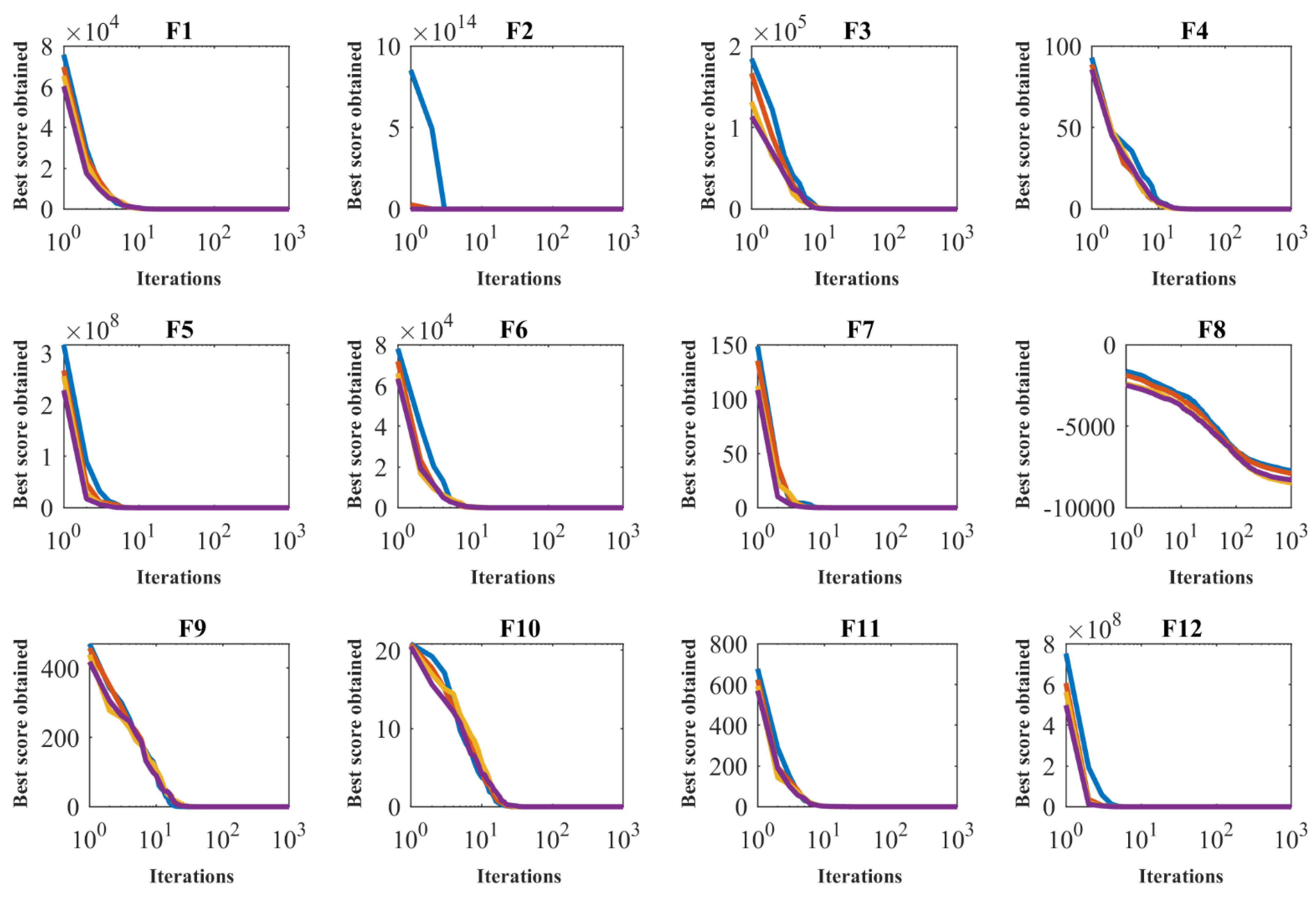
4.1. Evaluation of Unimodal Functions
4.2. Evaluation of High-Dimensional Multimodal Functions
4.3. Evaluation of Fixed-Dimensional Multimodal Functions
4.4. Statistical Analysis
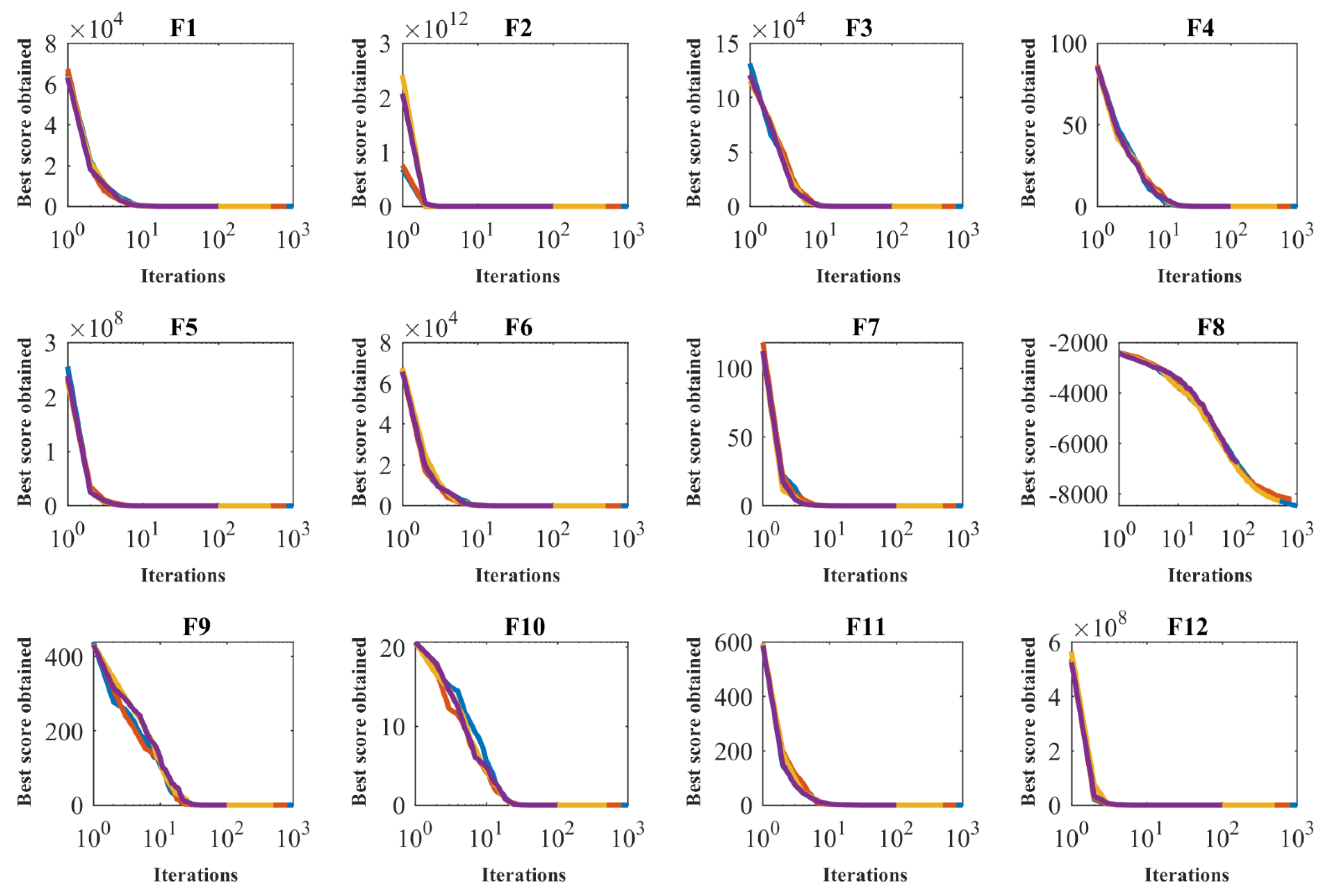
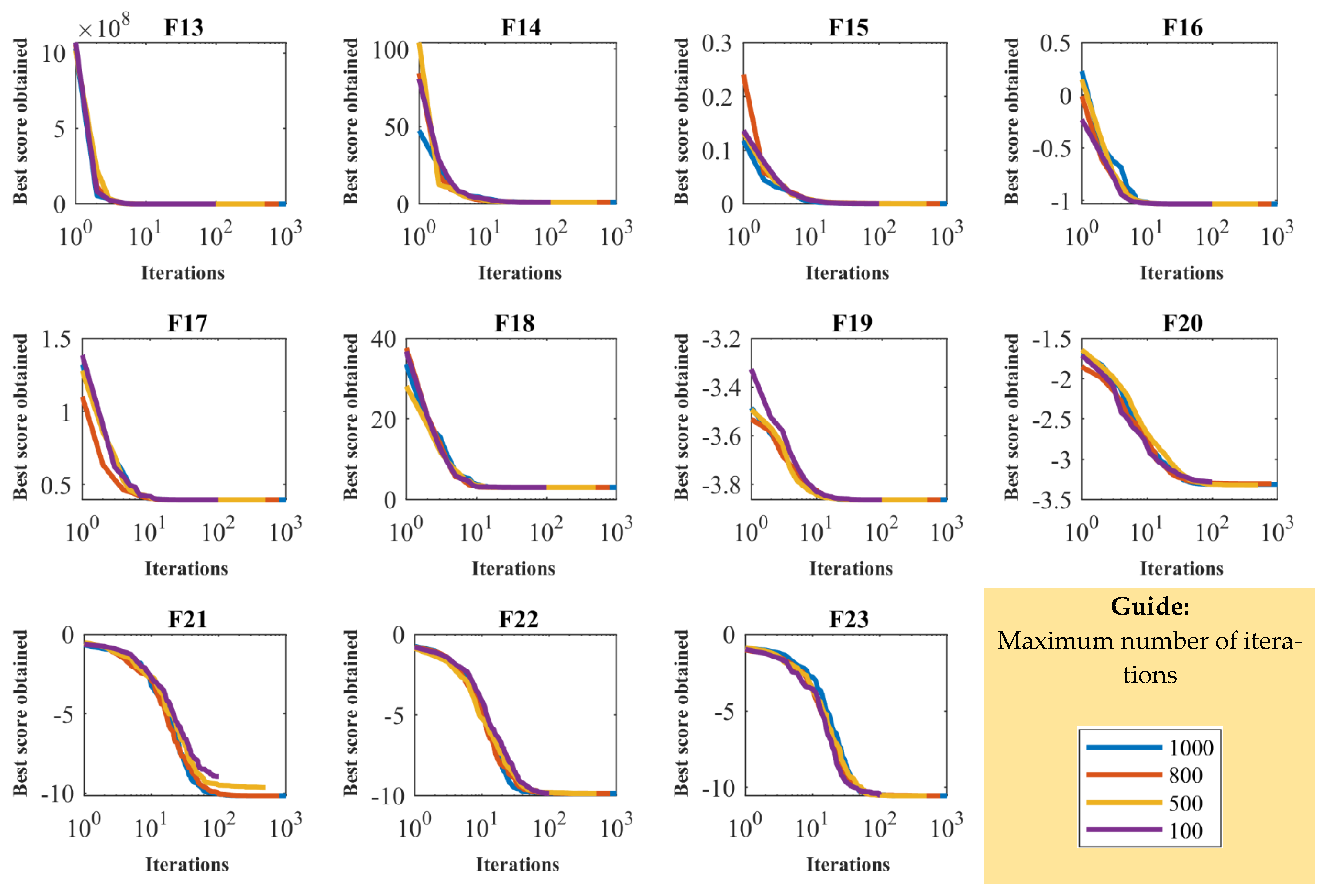
4.5. Sensitivity Analysis
5. Discussion
6. POA for Real-World Applications
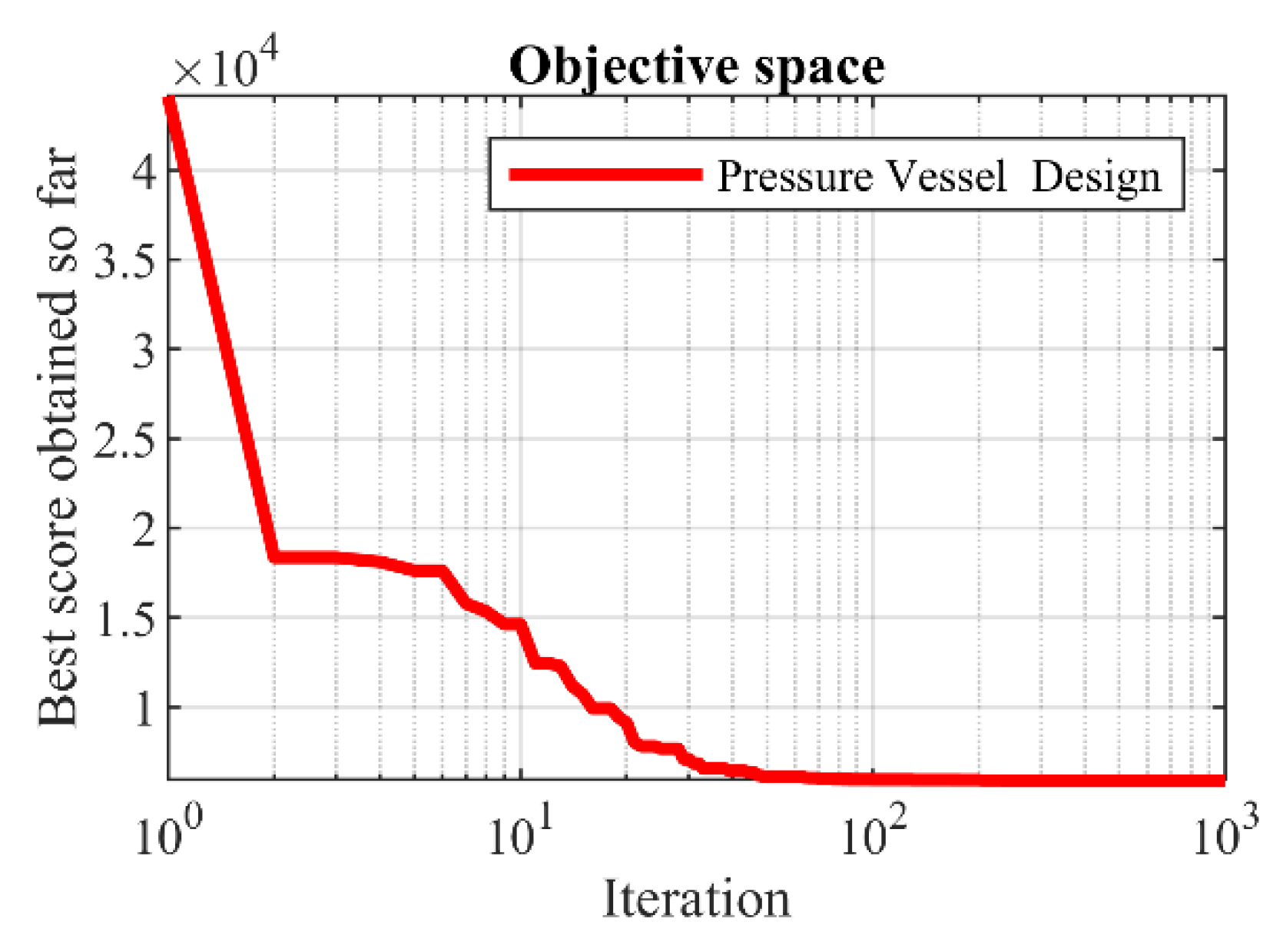
6.1. Pressure Vessel Design

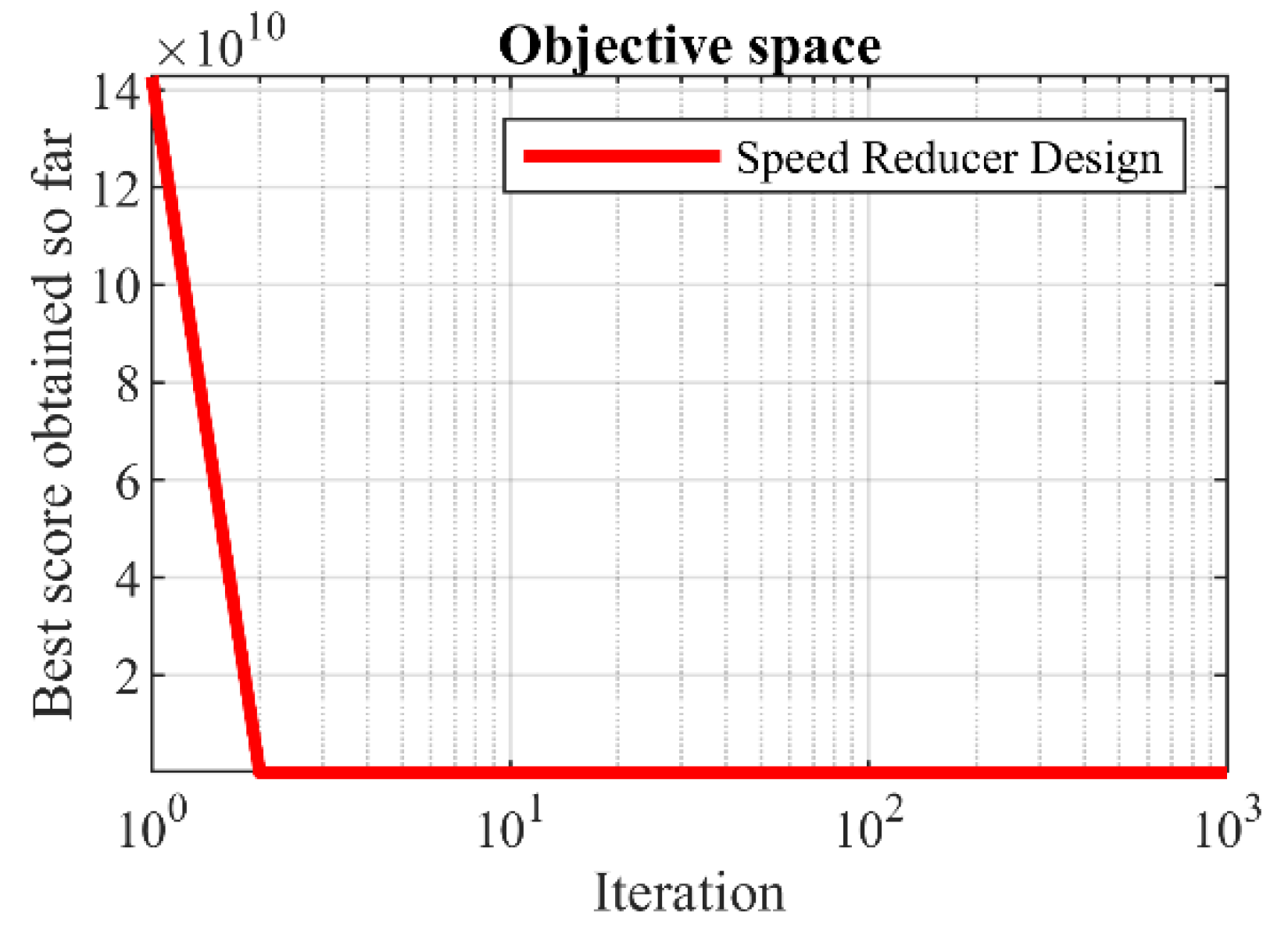
6.2. Speed Reducer Design Problem

6.3. Welded Beam Design

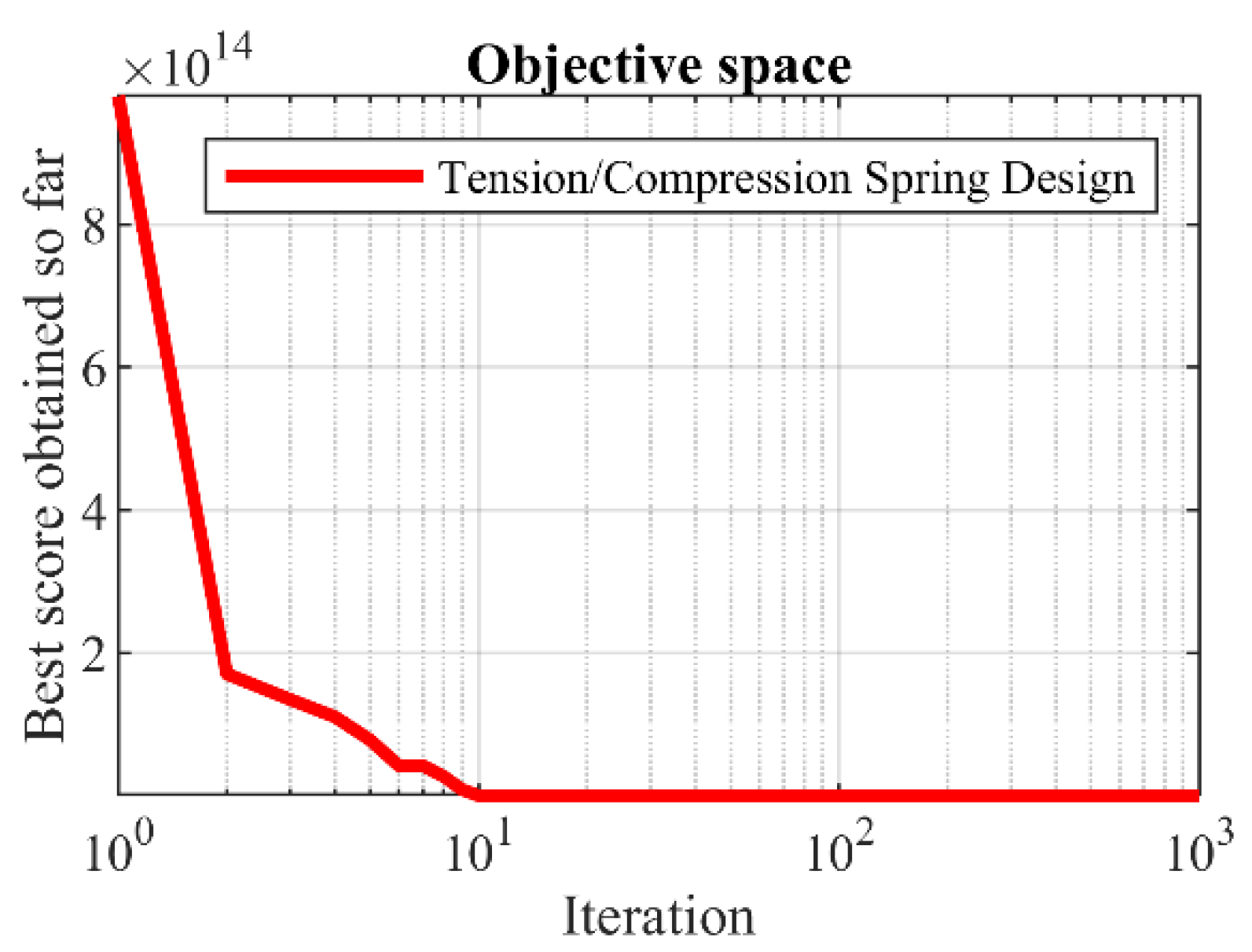
6.4. Tension/Compression Spring Design Problem

6.5. The POA’s Applicability in Image Processing and Sensor Networks
7. Conclusions and Future Works
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Objective Function | Range | Dimensions | |
|---|---|---|---|
| 30 | 0 | ||
| 30 | 0 | ||
| 30 | 0 | ||
| 30 | 0 | ||
| 30 | 0 | ||
| 30 | 0 | ||
| 30 | 0 |
| Objective Function | Range | Dimensions | Fmin |
|---|---|---|---|
| 30 | −12,569 | ||
| 30 | 0 | ||
| 30 | 0 | ||
| 30 | 0 | ||
| where | 30 | 0 | |
| 30 | 0 |
| Objective Function | Range | Dimensions | Fmin |
|---|---|---|---|
| 2 | 0.998 | ||
| 4 | 0.00030 | ||
| 2 | −1.0316 | ||
| [-5, 10] [0, 15] | 2 | 0.398 | |
| 2 | 3 | ||
| 3 | −3.86 | ||
| 6 | −3.22 | ||
| 4 | −10.1532 | ||
| 4 | −10.4029 | ||
| 4 | −10.5364 |
References
- Farshi, T.R. Battle royale optimization algorithm. Neural Comput. Appl. 2021, 33, 1139–1157. [Google Scholar] [CrossRef]
- Ray, T.; Liew, K.-M. Society and civilization: An optimization algorithm based on the simulation of social behavior. IEEE Trans. Evol. Comput. 2003, 7, 386–396. [Google Scholar] [CrossRef]
- Francisco, M.; Revollar, S.; Vega, P.; Lamanna, R. A comparative study of deterministic and stochastic optimization methods for integrated design of processes. IFAC Proc. Vol. 2005, 38, 335–340. [Google Scholar] [CrossRef] [Green Version]
- Hashim, F.A.; Hussain, K.; Houssein, E.H.; Mabrouk, M.S.; Al-Atabany, W. Archimedes optimization algorithm: A new metaheuristic algorithm for solving optimization problems. Appl. Intell. 2021, 51, 1531–1551. [Google Scholar] [CrossRef]
- Abualigah, L.; Yousri, D.; Abd Elaziz, M.; Ewees, A.A.; Al-qaness, M.A.; Gandomi, A.H. Aquila Optimizer: A novel meta-heuristic optimization Algorithm. Comput. Ind. Eng. 2021, 157, 107250. [Google Scholar] [CrossRef]
- Iba, K. Reactive power optimization by genetic algorithm. IEEE Trans. Power Syst. 1994, 9, 685–692. [Google Scholar] [CrossRef]
- Geetha, K.; Anitha, V.; Elhoseny, M.; Kathiresan, S.; Shamsolmoali, P.; Selim, M.M. An evolutionary lion optimization algorithm-based image compression technique for biomedical applications. Expert Syst. 2021, 38, e12508. [Google Scholar] [CrossRef]
- Yadav, R.K.; Mahapatra, R.P. Hybrid metaheuristic algorithm for optimal cluster head selection in wireless sensor network. Pervasive Mob. Comput. 2021, 79, 101504. [Google Scholar] [CrossRef]
- Cano Ortega, A.; Sánchez Sutil, F.J.; De la Casa Hernández, J. Power factor compensation using teaching learning based optimization and monitoring system by cloud data logger. Sensors 2019, 19, 2172. [Google Scholar] [CrossRef] [Green Version]
- Todorčević, V. Harmonic Quasiconformal Mappings and Hyperbolic Type Metrics; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Debnath, P.; Konwar, N.; Radenovic, S. Metric Fixed Point Theory: Applications in Science, Engineering and Behavioural Sciences; Springer: Berlin/Heidelberg, Germany, 2021. [Google Scholar]
- Wolpert, D.H.; Macready, W.G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef] [Green Version]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Rao, R.V.; Savsani, V.J.; Vakharia, D. Teaching–learning-based optimization: A novel method for constrained mechanical design optimization problems. Comput. Aided Des. 2011, 43, 303–315. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef] [Green Version]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Kaur, S.; Awasthi, L.K.; Sangal, A.L.; Dhiman, G. Tunicate Swarm Algorithm: A new bio-inspired based metaheuristic paradigm for global optimization. Eng. Appl. Artif. Intell. 2020, 90, 103541. [Google Scholar] [CrossRef]
- Faramarzi, A.; Heidarinejad, M.; Mirjalili, S.; Gandomi, A.H. Marine Predators Algorithm: A nature-inspired metaheuristic. Expert Syst. Appl. 2020, 152, 113377. [Google Scholar] [CrossRef]
- Goldberg, D.E.; Holland, J.H. Genetic Algorithms and Machine Learning. Mach. Learn. 1988, 3, 95–99. [Google Scholar] [CrossRef]
- De Castro, L.N.; Timmis, J.I. Artificial immune systems as a novel soft computing paradigm. Soft Comput. 2003, 7, 526–544. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef]
- Rashedi, E.; Nezamabadi-Pour, H.; Saryazdi, S. GSA: A gravitational search algorithm. Inf. Sci. 2009, 179, 2232–2248. [Google Scholar] [CrossRef]
- Dehghani, M.; Mardaneh, M.; Guerrero, J.M.; Malik, O.; Kumar, V. Football game based optimization: An application to solve energy commitment problem. Int. J. Intell. Eng. Syst 2020, 13, 514–523. [Google Scholar] [CrossRef]
- Kaveh, A.; Zolghadr, A. A novel meta-heuristic algorithm: Tug of war optimization. Iran Univ. Sci. Technol. 2016, 6, 469–492. [Google Scholar]
- Louchart, A.; Tourment, N.; Carrier, J. The earliest known pelican reveals 30 million years of evolutionary stasis in beak morphology. J. Ornithol. 2010, 152, 15–20. [Google Scholar] [CrossRef]
- Marchant, S. Handbook of Australian, New Zealand & Antarctic Birds: Australian Pelican to Ducks; Oxford University Press: Melbourne, Australia, 1990. [Google Scholar]
- Perrins, C.M.; Middleton, A.L. The Encyclopaedia of Birds; Guild Publishing: London, UK, 1985; pp. 53–54. [Google Scholar]
- Anderson, J.G. Foraging behavior of the American white pelican (Pelecanus erythrorhyncos) in western Nevada. Colonial Waterbirds 1991, 14, 166–172. [Google Scholar] [CrossRef]
- Wilcoxon, F. Individual comparisons by ranking methods. In Breakthroughs in Statistics; Springer: New York, NY, USA, 1992; pp. 196–202. [Google Scholar]
- Kannan, B.; Kramer, S.N. An augmented Lagrange multiplier based method for mixed integer discrete continuous optimization and its applications to mechanical design. J. Mech. Des. 1994, 116, 405–411. [Google Scholar] [CrossRef]
- Gandomi, A.H.; Yang, X.-S. Benchmark problems in structural optimization. In Computational Optimization, Methods and Algorithms; Springer: Berlin/Heidelberg, Germany, 2011; pp. 259–281. [Google Scholar]
- Mezura-Montes, E.; Coello, C.A.C. Useful Infeasible Solutions in Engineering Optimization with Evolutionary Algorithms. In Proceedings of the Mexican International Conference on Artificial Intelligence, Monterrey, Mexico, 14–18 November 2005; Springer: Berlin/Heidelberg, Germany, 2005; pp. 652–662. [Google Scholar]


| Algorithm | Parameter | Value |
|---|---|---|
| MPA | Binary vector | U = 0 or 1 |
| Random vector | ||
| Constant number | p = 0.5 | |
| Fish Aggregating Devices (FADs) | FADs = 0.2 | |
| TSA | c1, c2, c3 | random numbers lie in the interval [0, 1]. |
| Pmin | 1 | |
| Pmax | 4 | |
| WOA | l is a random number in [−1, 1]. | |
| Convergence parameter (a) | a: Linear reduction from 2 to 0. | |
| GWO | Convergence parameter (a) | a: Linear reduction from 2 to 0. |
| TLBO | random number | rand is a random number from interval [0, 1]. |
| TF: teaching factor | ||
| GSA | Alpha | 20 |
| G0 | 100 | |
| Rnorm | 2 | |
| Rnorm | 1 | |
| PSO | Velocity limit | 10% of dimension range |
| Topology | Fully connected | |
| Inertia weight | Linear reduction from 0.9 to 0.1 | |
| Cognitive and social constant | ||
| GA | Type | Real coded |
| Mutation | Gaussian (Probability = 0.05) | |
| Crossover | Whole arithmetic (Probability = 0.8) | |
| Selection | Roulette wheel (Proportionate) |
| GA | PSO | GSA | TLBO | GWO | WOA | TSA | MPA | POA | ||
|---|---|---|---|---|---|---|---|---|---|---|
| F1 | avg | 11.6208 | 4.1728 × 10−4 | 2.0259 × 10−16 | 3.8324 × 10−59 | 1.0896 × 10−57 | 5.37 × 10−62 | 5.7463 × 10−37 | 3.2612 × 10−20 | 2.87 × 10−258 |
| std | 2.6142 × 10−11 | 3.6142 × 10−21 | 6.9113 × 10−30 | 9.6318 × 10−72 | 5.1462 × 10−73 | 5.78 × 10−78 | 6.3279 × 10−20 | 1.5264 × 10−19 | 4.51 × 10−514 | |
| bsf | 5.593489 | 2 × 10−10 | 8.2 × 10−18 | 9.36 × 10−61 | 7.73 × 10−61 | 1.61 × 10−65 | 1.14 × 10−62 | 3.41 × 10−28 | 7.62 × 10−264 | |
| med | 11.04546 | 9.92 × 10−7 | 1.78 × 10−17 | 4.69 × 10−60 | 1.08 × 10−59 | 8.42 × 10−54 | 3.89 × 10−38 | 1.27 × 10−19 | 8.2 × 10−248 | |
| F2 | avg | 4.6942 | 0.3114 | 7.0605 × 10−7 | 4.6237 × 10−34 | 2.0509 × 10−33 | 2.51 × 10−55 | 4.5261 × 10−38 | 6.3214 × 10−11 | 1.43× 10−128 |
| std | 5.4318 × 10−14 | 4.4667 × 10−16 | 8.5637 × 10−23 | 9.3719 × 10−49 | 6.3195 × 10−29 | 5.60 × 10−58 | 2.6591 × 10−40 | 3.6249 × 10−11 | 2.90× 10−129 | |
| bsf | 1.591137 | 0.001741 | 1.59 × 10−8 | 1.32 × 10−35 | 1.55 × 10−35 | 3.42 × 10−63 | 8.26 × 10−43 | 4.25 × 10−18 | 2.61 × 10−131 | |
| med | 2.463873 | 0.130114 | 2.33 × 10−8 | 4.37 × 10−35 | 6.38 × 10−35 | 1.59 × 10−51 | 8.26 × 10−41 | 3.18 × 10−11 | 7.1 × 10−123 | |
| F3 | avg | 1361.2743 | 588.3012 | 280.6014 | 7.0772 × 10−14 | 4.7206 × 10−14 | 7.5621 × 10−9 | 5.6230 × 10−20 | 0.0819 | 1.88× 10−256 |
| std | 6.6096 × 10−12 | 9.7117 × 10−12 | 5.2497 × 10−12 | 8.9637 × 10−30 | 6.5225 × 10−28 | 1.02 × 10−18 | 7.0925 × 10−19 | 0.1370 | 5.16× 10−614 | |
| bsf | 1014.689 | 1.614937 | 81.91242 | 1.21 × 10−16 | 4.75 × 10−20 | 1.9738 × 10−11 | 7.29 × 10−30 | 0.032038 | 7.36 × 10−262 | |
| med | 1510.715 | 54.15445 | 291.4308 | 1.86 × 10−15 | 1.59 × 10−16 | 17085.2 | 9.81 × 10−21 | 0.378658 | 8.2 × 10−244 | |
| F4 | avg | 2.0396 | 4.3693 | 2.6319 × 10−8 | 8.9196 × 10−14 | 1.9925 × 10−13 | 0.0013 | 3.1162 × 10−22 | 6.3149 × 10−8 | 2.36× 10−133 |
| std | 4.3321× 10−14 | 4.2019 × 10−15 | 5.3017 × 10−23 | 1.7962 × 10−29 | 1.8305 × 10−28 | 0.0877 | 6.3129 × 10−21 | 2.3687 × 10−9 | 8.37× 10−134 | |
| bsf | 1.389849 | 1.60441 | 2.09 × 10−09 | 6.41 × 10−16 | 3.43 × 10−16 | 0.0001 | 1.87 × 10−52 | 3.42 × 10−17 | 6.08 × 10−138 | |
| med | 2.09854 | 3.260672 | 3.34 × 10−09 | 1.54 × 10−15 | 7.3 × 10−15 | 0.0010 | 3.13 × 10−27 | 3.03 × 10−08 | 2.8 × 10−123 | |
| F5 | avg | 308.4196 | 50.5412 | 36.01528 | 147.6214 | 27.1786 | 27.17543 | 28.8592 | 46.0408 | 27.1253 |
| std | 3.0412 × 10−12 | 1.8529 × 10−13 | 2.6091 × 10−13 | 6.3017 × 10−13 | 8.7029 × 10−14 | 0.393959 | 4.3219 × 10−3 | 0.4199 | 1.91× 10−15 | |
| bsf | 160.5013 | 3.647051 | 25.83811 | 120.7932 | 25.21201 | 26.43249 | 28.53831 | 41.58682 | 26.2052 | |
| med | 279.5174 | 28.69298 | 26.07475 | 142.8936 | 26.70874 | 26.93542 | 28.53913 | 42.49068 | 28.707 | |
| F6 | avg | 15.6231 | 20.2691 | 0 | 0.5531 | 0.6518 | 0.071527 | 5.7268 × 10−20 | 0.3894 | 0 |
| std | 7.3160 × 10−14 | 2.6314 | 0 | 3.1971 × 10−15 | 5.3096 × 10−16 | 0.006113 | 2.1163 × 10−24 | 0.2001 | 0 | |
| bsf | 6 | 5 | 0 | 0 | 1.57 × 10−05 | 0.014645 | 6.74 × 10−26 | 0.274582 | 0 | |
| med | 13.5 | 19 | 0 | 0 | 0.621487 | 0.029296 | 6.74 × 10−21 | 0.406648 | 0 | |
| F7 | avg | 8.6517 × 10−2 | 0.3218 | 0.0234 | 0.0011 | 0.0077 | 0.00103 | 8.2196 × 10−4 | 1.2561× 10−3 | 9.37× 10−6 |
| std | 8.9206 × 10−17 | 3.4333 × 10−16 | 7.1526 × 10−17 | 3.2610 × 10−18 | 7.2307 × 10−19 | 1.12 × 10−5 | 9.6304 × 10−5 | 9.6802× 10−3 | 8.03× 10−20 | |
| bsf | 0.002111 | 0.029593 | 0.01006 | 0.001362 | 0.000248 | 4.24 × 10−5 | 0.000104 | 0.001429 | 7.05 × 10−07 | |
| med | 0.005365 | 0.107872 | 0.016995 | 0.002912 | 0.000629 | 0.00215 | 0.000367 | 0.00218 | 4.86 × 10−05 | |
| GA | PSO | GSA | TLBO | GWO | WOA | TSA | MPA | POA | ||
|---|---|---|---|---|---|---|---|---|---|---|
| F8 | avg | −8210.3415 | −6899.9556 | −2854.5207 | −7410.8016 | −5903.3711 | −7239.1 | −5737.7822 | −3611.2271 | −9336.7304 |
| std | 833.5126 | 625.4286 | 2641576 | 513.4752 | 467.8216 | 261.0117 | 39.5203 | 811.1459 | 2.64× 10−12 | |
| bsf | −9717.68 | −8501.44 | −3969.23 | −9103.77 | −7227.05 | −7568.9 | −5706.3 | −4419.9 | −9850.21 | |
| med | −8117.66 | −7098.95 | −2671.33 | −7735.22 | −5774.63 | −7124.8 | −5669.63 | −3632.84 | −8505.55 | |
| F9 | avg | 62.1441 | 57.0503 | 16.5714 | 10.1379 | 8.1036 × 10−14 | 0 | 6.0311 × 10−3 | 139.9806 | 0 |
| std | 2.1637 × 10−13 | 6.0013 × 10−14 | 6.1972 × 10−14 | 4.9631 × 10−14 | 4.6537 × 10−29 | 0 | 5.6146 × 10−3 | 25.9024 | 0 | |
| bsf | 36.86623 | 27.85883 | 4.974795 | 9.873963 | 0 | 0 | 0.004776 | 128.2306 | 0 | |
| med | 61.67858 | 55.22468 | 15.42187 | 10.88657 | 0 | 0 | 0.005871 | 154.6214 | 0 | |
| F10 | avg | 3.8134 | 2.6304 | 3.5438 × 10−9 | 0.2691 | 8.6234 × 10−13 | 3.91 × 10−15 | 8.6247 × 10−13 | 8.6291 × 10−11 | 8.88× 10−16 |
| std | 6.8972 × 10−15 | 6.9631 × 10−15 | 2.7054 × 10−24 | 6.4129 × 10−14 | 5.6719 × 10−28 | 7.01 × 10−30 | 1.6240 × 10−12 | 5.3014 × 10−11 | 0 | |
| bsf | 2.757203 | 1.155151 | 2.64 × 10−09 | 0.156305 | 1.51 × 10−14 | 8.88 × 10−16 | 8.14 × 10−15 | 1.68 × 10−18 | 8.88 × 10−16 | |
| med | 3.120322 | 2.170083 | 3.64 × 10−09 | 0.261541 | 1.51 × 10−14 | 4.44 × 10−15 | 1.1 × 10−13 | 1.05 × 10−11 | 8.88 × 10−16 | |
| F11 | avg | 1.1973 | 0.0364 | 3.9123 | 0.5912 | 0.0013 | 2.03 × 10−4 | 5.3614 × 10−7 | 0 | 0 |
| std | 4.8521 × 10−15 | 2.6398 × 10−17 | 4.0306 × 10−14 | 6.2914 × 10−15 | 6.1294 × 10−17 | 1.82 × 10−17 | 6.3195 × 10−7 | 0 | 0 | |
| bsf | 1.140471 | 7.29 × 10−09 | 1.519288 | 0.310117 | 0 | 0 | 4.23 × 10−15 | 0 | 0 | |
| med | 1.227231 | 0.029473 | 3.424268 | 0.582026 | 0 | 0 | 8.77 × 10−07 | 0 | 0 | |
| F12 | avg | 0.0469 | 0.4792 | 0.0341 | 0.0219 | 0.0364 | 0.007728 | 0.0372 | 0.0815 | 0.0583 |
| std | 1.7456 × 10−14 | 9.3071 × 10−15 | 2.0918 × 10−16 | 2.6195 × 10−14 | 1.3604 × 10−13 | 8.07E-05 | 8.6391 × 10−2 | 0.0162 | 2.73 × 10−16 | |
| bsf | 0.018364 | 0.000145 | 5.57 × 10−20 | 0.002031 | 0.019294 | 0.001142 | 0.035428 | 0.077912 | 0.0452 | |
| med | 0.04179 | 0.1556 | 1.48 × 10−19 | 0.015181 | 0.032991 | 0.003887 | 0.050935 | 0.082108 | 0.1464 | |
| F13 | avg | 1.2106 | 0.5156 | 0.0017 | 0.3306 | 0.5561 | 0.193293 | 2.8041 | 0.4875 | 1.42866 |
| std | 3.5630 × 10−15 | 4.1427 × 10−16 | 1.9741 × 10−13 | 5.6084 × 10−15 | 5.6219 × 10−15 | 0.022767 | 3.9514 × 10−11 | 0.1041 | 2.83× 10−15 | |
| bsf | 0.49809 | 9.99 × 10−07 | 1.18 × 10−18 | 0.038266 | 0.297822 | 0.029662 | 2.63175 | 0.280295 | 1.428663 | |
| med | 1.218053 | 0.043997 | 2.14 × 10−18 | 0.282764 | 0.578323 | 0.146503 | 2.66175 | 0.579854 | 2.976773 | |
| GA | PSO | GSA | TLBO | GWO | WOA | TSA | MPA | POA | ||
|---|---|---|---|---|---|---|---|---|---|---|
| F14 | avg | 0.9969 | 2.3909 | 3.9505 | 2.4998 | 4.1140 | 1.106143 | 2.061 | 0.9980 | 0.9980 |
| std | 6.3124 × 10−14 | 8.0126 × 10−15 | 8.9631 × 10−15 | 6.3014 × 10−15 | 1.3679 × 10−14 | 0.48689 | 5.6213 × 10−7 | 1.9082 × 10−15 | 0 | |
| bsf | 0.998004 | 0.998004 | 0.999508 | 0.998391 | 0.998004 | 0.998004 | 0.9979 | 0.9980 | 0.9980 | |
| med | 0.998018 | 0.998004 | 2.986658 | 2.275231 | 2.982105 | 0.998004 | 1.912608 | 0.9980 | 0.9980 | |
| F15 | avg | 0.0042 | 0.0528 | 0.0027 | 0.0031 | 0.0059 | 0.000463 | 0.0005 | 0.0028 | 0.0003 |
| std | 1.6317 × 10−17 | 2.6159 × 10−18 | 3.6051 × 10−18 | 6.3195 × 10−16 | 3.0598 × 10−17 | 1.22 × 10−7 | 1.6230 × 10−5 | 1.2901 × 10−14 | 1.21× 10−19 | |
| bsf | 0.000775 | 0.000307 | 0.000805 | 0.002206 | 0.000307 | 0.000313 | 0.000264 | 0.00027 | 0.0003 | |
| med | 0.002074 | 0.000307 | 0.002311 | 0.003185 | 0.000308 | 0.000492 | 0.00039 | 0.0027 | 0.0003 | |
| F16 | avg | −1.0307 | −1.0312 | −1.0309 | −1.0310 | −1.0316 | −1.0316 | −1.0314 | −1.0315 | −1.0316 |
| std | 9.1449 × 10−15 | 3.2496 × 10−15 | 5.4162 × 10−15 | 1.3061 × 10−14 | 3.0816 × 10−15 | 2.38 × 10−20 | 6.0397 × 10−15 | 2.1679 × 10−15 | 1.93× 10−18 | |
| bsf | −1.0316 | −1.0316 | −1.0316 | −1.0316 | −1.0316 | −1.0316 | −1.03161 | −1.0316 | −1.03163 | |
| med | −1.0309 | −1.0311 | −1.0310 | −1.0308 | −1.0316 | −1.0316 | −1.0311 | −1.0312 | −1.03163 | |
| F17 | avg | 0.4401 | 0.7951 | 0.3980 | 0.3978 | 0.3981 | 0.39788 | 0.3987 | 0.3991 | 0.3978 |
| std | 1.4109 × 10−16 | 3.9801 × 10−5 | 1.0291 × 10−16 | 2.1021 × 10−15 | 6.0391 × 10−16 | 1.42 × 10−12 | 6.1472 × 10−15 | 5.9317 × 10−14 | 0 | |
| bsf | 0.3978 | 0.3978 | 0.3978 | 0.3978 | 0.3978 | 0.397887 | 0.3980 | 0.3982 | 0.3978 | |
| med | 0.4016 | 0.6521 | 0.3979 | 0.3978 | 0.3979 | 0.397887 | 0.3990 | 0.3977 | 0.3978 | |
| F18 | avg | 4.3601 | 3.0010 | 3.0016 | 3.0010 | 3.0009 | 3.000009 | 3 | 3.0013 | 3 |
| std | 2.6108 × 10−15 | 1.1041 × 10−14 | 3.7159 × 10−15 | 7.6013 × 10−14 | 5.0014 × 10−14 | 2.42 × 10−15 | 5.6148 × 10−14 | 2.3017 × 10−14 | 1.09× 10−16 | |
| bsf | 3.0002 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | |
| med | 3.7581 | 3.0005 | 3.0008 | 3.0006 | 3.0006 | 3.000001 | 3 | 3.0009 | 3 | |
| F19 | avg | −3.8519 | −3.8627 | −3.8627 | −3.8615 | −3.8617 | −3.86068 | −3.8205 | −3.8627 | −3.86278 |
| std | 3.6015 × 10−14 | 7.0114 × 10−14 | 5.3419 × 10−14 | 1.0314 × 10−14 | 9.6041 × 10−14 | 6.55 × 10−6 | 6.7514 × 10−14 | 2.6197 × 10−14 | 6.45× 10−16 | |
| bsf | −3.86278 | −3.8627 | −3.8627 | −3.8625 | −3.8627 | −3.86278 | −3.8366 | −3.8627 | −3.86278 | |
| med | −3.8413 | −3.8560 | −3.8627 | −3.8620 | −3.8612 | −3.86216 | −3.8066 | −3.8627 | −3.86278 | |
| F20 | avg | −2.8301 | −3.2626 | −3.0402 | −3.1927 | −3.2481 | −3.22298 | −3.3201 | −3.3195 | −3.3220 |
| std | 3.7124 × 10−15 | 3.4567 × 10−15 | 5.2179 × 10−13 | 5.3140 × 10−14 | 3.3017 × 10−14 | 0.008173 | 6.5203 × 10−14 | 9.8160 × 10−10 | 1.97× 10−16 | |
| bsf | −3.31342 | −3.322 | −3.322 | −3.26174 | −3.32199 | −3.32198 | −3.3212 | −3.3213 | −3.322 | |
| med | −2.96828 | −3.2160 | −2.9014 | −3.2076 | −3.26248 | −3.19935 | −3.3206 | −3.3211 | −3.322 | |
| F21 | avg | −4.2593 | −5.4236 | −5.2014 | −9.2049 | −9.6602 | −8.87635 | −5.1477 | −9.9561 | −10.1532 |
| std | 2.3631 × 10−8 | 6.3014 × 10−9 | 5.8961 × 10−8 | 3.8715 × 10−14 | 5.3391 × 10−14 | 5.123359 | 6.1974 × 10−12 | 8.7195 × 10−10 | 1.93× 10−16 | |
| bsf | −7.82781 | −8.0267 | −7.3506 | −9.6638 | −10.1532 | −10.1531 | −7.5020 | −10.1532 | −10.1532 | |
| med | −4.16238 | −5.10077 | −3.64802 | −9.1532 | −10.1526 | −10.1518 | −5.5020 | −10.1531 | −10.1532 | |
| F22 | avg | −5.1183 | −7.6351 | −9.0241 | −10.0399 | −10.4199 | −9.33732 | −5.0597 | −10.2859 | −10.4029 |
| std | 6.1697 × 10−14 | 5.0610 × 10−14 | 5.0231 × 10−11 | 6.7925 × 10−13 | 6.1496 × 10−14 | 4.752577 | 3.1673 × 10−14 | 7.3596 × 10−10 | 3.57× 10−16 | |
| bsf | −9.1106 | −10.4024 | −10.4026 | −10.4023 | −10.4021 | −10.4028 | −9.06249 | −10.4029 | −10.4029 | |
| med | −5.0296 | −10.4020 | −10.4017 | −10.1836 | −10.4015 | −10.4013 | −5.06249 | −10.4027 | −10.4029 | |
| F23 | avg | −6.5675 | −6.1653 | −8.9091 | −9.2916 | −10.1319 | −9.45231 | −10.3675 | −10.1409 | −10.5364 |
| std | 5.6014 × 10−14 | 5.3917 × 10−15 | 8.0051 × 10−14 | 5.2673 × 10−14 | 2.6912 × 10−15 | 9.47 × 10−9 | 2.9637 × 10−12 | 5.0981 × 10−10 | 3.97× 10−16 | |
| bsf | −10.2227 | −10.5364 | −10.5364 | −10.5340 | −10.5363 | −10.5363 | −10.3683 | −10.5364 | −10.5364 | |
| med | −6.5629 | −4.50554 | −10.5360 | −9.6717 | −10.5361 | −10.5349 | −10.3613 | −10.2159 | −10.5364 | |
| Functions Type | Compared Algorithms | |||||||
|---|---|---|---|---|---|---|---|---|
| POA and MPA | POA and TSA | POA and WOA | POA and GWO | POA and TLBO | POA and GSA | POA and PSO | POA and GA | |
| Unimodal | 0.0156 | 0.0156 | 0.0156 | 0.0156 | 0.0156 | 0.0312 | 0.0156 | 0.0156 |
| High-dimensional multimodal | 0.3125 | 0.2187 | 0.1562 | 0.8437 | 0.3125 | 0.3125 | 0.1562 | 0.1562 |
| Fixed-dimensional multimodal | 0.0195 | 0.0039 | 0.0078 | 0.0117 | 0.0058 | 0.0195 | 0.0039 | 0.0019 |
| Objective Function | Number of Population Members | |||
|---|---|---|---|---|
| 20 | 30 | 50 | 80 | |
| F1 | 9.3343 × 10−212 | 1.6451 × 10−235 | 2.87 × 10−258 | 7.3038 × 10−260 |
| F2 | 1.5489 × 10−98 | 2.303 × 10−119 | 1.42 × 10−128 | 2.0842 × 10−132 |
| F3 | 1.6656 × 10−206 | 9.9891 × 10−249 | 1.879 × 10−256 | 2.1553 × 10−259 |
| F4 | 6.0489 × 10−112 | 1.4332 × 10−127 | 2.36 × 10−133 | 3.6451 × 10−136 |
| F5 | 28.4440 | 27.1418 | 27.1253 | 25.4195 |
| F6 | 0 | 0 | 0 | 0 |
| F7 | 0.0001 | 8.8865 × 10−6 | 9.37 × 10−6 | 1.3305 × 10−6 |
| F8 | −7727.8678 | −8924.3072 | −9336.7304 | −9385.8725 |
| F9 | 0 | 0 | 0 | 0 |
| F10 | 8.88 × 10−16 | 8.88 × 10−16 | 8.88 × 10−16 | 8.88 × 10−16 |
| F11 | 0 | 0 | 0 | 0 |
| F12 | 0.2944 | 0.0369 | 0.0583 | 0.0142 |
| F13 | 2.9548 | 2.0214 | 1.4286 | 2.0471 |
| F14 | 1.6403 | 1.0120 | 0.9980 | 0.9980 |
| F15 | 0.0024 | 0.0003 | 0.0003 | 0.0003 |
| F16 | −1.0311 | −1.0314 | −1.0316 | −1.03163 |
| F17 | 0.3987 | 0.3983 | 0.3978 | 0.3978 |
| F18 | 3.0003 | 3.0001 | 3.0000 | 3.0000 |
| F19 | −3.8615 | −3.8625 | −3.8628 | −3.8628 |
| F20 | −3.3041 | −3.3120 | −3.322 | −3.322 |
| F21 | −7.3492 | −10.1529 | −10.1532 | −10.1532 |
| F22 | −8.0110 | −10.4023 | −10.4029 | −10.4029 |
| F23 | −8.6436 | −10.5357 | −10.5364 | −10.5364 |
| Objective Function | Maximum Number of Iterations | |||
|---|---|---|---|---|
| 100 | 500 | 800 | 1000 | |
| F1 | 2.7725 × 10−19 | 6.2604 × 10−115 | 4.3539 × 10−185 | 2.87 × 10−258 |
| F2 | 1.1541 × 10−9 | 3.5658 × 10−57 | 1.61505 × 10−94 | 1.42 × 10−128 |
| F3 | 2.1172 × 10−19 | 5.0884 × 10−117 | 6.461 × 10−180 | 1.879 × 10−256 |
| F4 | 5.9252 × 10−10 | 1.8962 × 10−56 | 3.1178 × 10−92 | 2.36 × 10−133 |
| F5 | 28.9350 | 28.5274 | 28.3259 | 27.1253 |
| F6 | 0 | 0 | 0 | 0 |
| F7 | 0.0007 | 0.0001 | 9.0872 × 10−5 | 9.37 × 10−6 |
| F8 | −6753.5658 | −8063.7455 | −8208.3044 | −9336.7304 |
| F9 | 0 | 0 | 0 | 0 |
| F10 | 1.1932 × 10−16 | 8.88 × 10−16 | 8.88 × 10−16 | 8.88 × 10−16 |
| F11 | 0 | 0 | 0 | 0 |
| F12 | 0.5768 | 0.2211 | 0.1673 | 0.0583 |
| F13 | 2.8999 | 2.7595 | 2.7286 | 1.4286 |
| F14 | 1.0012 | 0.9996 | 0.9980 | 0.9980 |
| F15 | 0.0013 | 0.0007 | 0.0004 | 0.0003 |
| F16 | −1.0310 | −1.0314 | −1.0316 | −1.03163 |
| F17 | 0.3983 | 0.3972 | 0.3978 | 0.3978 |
| F18 | 3.0172 | 3.0120 | 3.0001 | 3.0000 |
| F19 | −3.7928 | −3.8598 | −3.8628 | −3.8628 |
| F20 | −3.2810 | −3.3160 | −3.3041 | −3.322 |
| F21 | −9.8968 | −9.6433 | −9.8982 | −10.1532 |
| F22 | −10.4002 | −10.4018 | −10.4022 | −10.4029 |
| F23 | −10.5358 | −10.5361 | −10.5363 | −10.5364 |
| OF | R Value | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1 | |
| F1 | 4.84 × 10−244 | 2.87 × 10−258 | 7.98 × 10−246 | 3.79 × 10−244 | 6.25 × 10−240 | 6.31 × 10−235 | 2.32 × 10−231 | 4.98 × 10−227 | 6.44 × 10−224 | 1.04 × 10−221 |
| F2 | 1.50 × 10−126 | 1.42 × 10−128 | 2.72 × 10−125 | 7.70 × 10−125 | 2.01 × 10−123 | 3.85 × 10−122 | 1.89 × 10−121 | 2.56 × 10−120 | 4.69 × 10−119 | 6.50 × 10−115 |
| F3 | 6.84 × 10−256 | 1.879 × 10−256 | 3.92 × 10−251 | 4.90 × 10−248 | 1.83 × 10−244 | 4.39 × 10−241 | 8.56 × 10−236 | 2.83 × 10−236 | 8.20 × 10−235 | 1.96 × 10−234 |
| F4 | 3.50 × 10−126 | 2.36 × 10−133 | 8.99 × 10−120 | 1.96 × 10−123 | 1.90 × 10−126 | 2.60 × 10−122 | 4.96 × 10−115 | 4.04 × 10−112 | 1.40 × 10−112 | 6.74 × 10−110 |
| F5 | 27.5583 | 27.1253 | 27.5641 | 27.5912 | 27.8162 | 28.4294 | 28.5964 | 28.6237 | 28.6907 | 28.7015 |
| F6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| F7 | 3.43 × 10−5 | 9.37 × 10−6 | 4.86 × 10−5 | 7.62 × 10−5 | 4.31 × 10−5 | 2.06 × 10−4 | 2.71 × 10−4 | 4.63 × 10−4 | 3.66 × 10−4 | 5.70 × 10−4 |
| F8 | −8934.1836 | −9336.7304 | −8963.8127 | −8898.2760 | −8702.3872 | −8629.6948 | −8485.2713 | −8212.2289 | −8070.2688 | −7919.3914 |
| F9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| F10 | 8.88 × 10−16 | 8.88 × 10−16 | 8.88 × 10−16 | 8.88 × 10−16 | 8.88 × 10−16 | 8.88 × 10−16 | 8.88 × 10−16 | 8.88 × 10−16 | 8.88 × 10−16 | 8.88 × 10−16 |
| F11 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| F12 | 0.1542 | 0.0583 | 0.0629 | 0.0701 | 0.0821 | 0.08659 | 0.08826 | 0.09184 | 0.09633 | 0.097571 |
| F13 | 2.8516 | 1.4286 | 2.1295 | 2.5203 | 2.591 | 2.6314 | 2.4736 | 2.3871 | 2.7630 | 2.8532 |
| F14 | 0.9980 | 0.9980 | 0.9980 | 0.9980 | 0.9980 | 0.9980 | 0.9980 | 0.9980 | 0.9980 | 0.9980 |
| F15 | 0.0003 | 0.0003 | 0.0003 | 0.0003 | 0.0003 | 0.0003 | 0.0003 | 0.0003 | 0.0003 | 0.0003 |
| F16 | −1.03163 | −1.03163 | −1.03163 | −1.03163 | −1.03163 | −1.03163 | −1.03163 | −1.03163 | −1.03163 | −1.03163 |
| F17 | 0.3978 | 0.3978 | 0.3978 | 0.3978 | 0.3978 | 0.3978 | 0.3978 | 0.3978 | 0.3978 | 0.3978 |
| F18 | 3.0000 | 3.0000 | 3.0000 | 3.0000 | 3.0000 | 3.0000 | 3.0000 | 3.0000 | 3.0000 | 3.0000 |
| F19 | −3.8628 | −3.8628 | −3.8628 | −3.8628 | −3.8628 | −3.8628 | −3.8628 | −3.8628 | −3.8628 | −3.8628 |
| F20 | −3.322 | −3.322 | −3.322 | −3.3219 | −3.3218 | −3.3218 | −3.1984 | −3.1821 | −3.1167 | −3.0126 |
| F21 | −10.1532 | −10.1532 | −10.1531 | −10.1531 | −10.1529 | −10.1527 | −9.8965 | −9.9623 | −9.2196 | −9.1637 |
| F22 | −10.4029 | −10.4029 | −10.4027 | −10.4027 | −10.3827 | −10.3561 | −10.0032 | −9.7304 | −9.1931 | −9.0157 |
| F23 | −10.5364 | −10.5364 | −10.5363 | −10.5363 | −10.2195 | −10.0412 | −9.6318 | −9.2305 | −9.1027 | −10.0081 |
| Algorithm | Optimum Variables | Optimum Cost | |||
|---|---|---|---|---|---|
| Ts | Th | R | L | ||
| POA | 0.778035 | 0.384607 | 40.31261 | 199.9972 | 5883.0278 |
| MPA | 0.782101 | 0.386813 | 40.51662 | 200 | 5915.005 |
| TSA | 0.78293 | 0.386583 | 40.52943 | 200 | 5918.816 |
| WOA | 0.782856 | 0.386606 | 40.52252 | 200 | 5920.845 |
| GWO | 0.849948 | 0.420657 | 44.03535 | 157.1635 | 6041.572 |
| TLBO | 0.821665 | 0.420022 | 41.95814 | 184.4906 | 6168.059 |
| GSA | 1.091229 | 0.954362 | 49.59196 | 170.3348 | 11608.05 |
| PSO | 0.756124 | 0.401538 | 40.65478 | 198.9927 | 5919.78 |
| GA | 1.105021 | 0.911112 | 44.67868 | 180.5572 | 6582.773 |
| Algorithm | Best | Mean | Worst | Std. Dev. | Median |
|---|---|---|---|---|---|
| POA | 5883.0278 | 5887.082 | 5894.256 | 24.35317 | 5886.457 |
| MPA | 5915.005 | 5890.388 | 5895.267 | 2.894447 | 5889.171 |
| TSA | 5918.816 | 5894.47 | 5897.571 | 13.91696 | 5893.595 |
| WOA | 5920.845 | 6534.769 | 7398.285 | 534.3861 | 6419.322 |
| GWO | 6041.572 | 6480.544 | 7254.542 | 327.1705 | 6400.679 |
| TLBO | 6168.059 | 6329.924 | 6515.61 | 126.6723 | 6321.477 |
| GSA | 11608.05 | 6843.963 | 7162.87 | 5793.52 | 6841.052 |
| PSO | 5919.78 | 6267.137 | 7009.253 | 496.3761 | 6115.746 |
| GA | 6582.773 | 6647.309 | 8009.442 | 657.8518 | 7589.802 |
| Algorithm | Optimum Variables | Optimum Cost | ||||||
|---|---|---|---|---|---|---|---|---|
| b | m | p | l1 | l2 | d1 | d2 | ||
| POA | 3.5 | 0.7 | 17 | 7.3 | 7.8 | 3.350215 | 5.286683 | 2996.3482 |
| MPA | 3.503341 | 0.7 | 17 | 7.3 | 7.8 | 3.352946 | 5.291384 | 3000.05 |
| TSA | 3.508443 | 0.7 | 17 | 7.381059 | 7.815726 | 3.359526 | 5.289411 | 3002.789 |
| WOA | 3.501769 | 0.7 | 17 | 8.3 | 7.8 | 3.354088 | 5.289358 | 3007.266 |
| GWO | 3.510256 | 0.7 | 17 | 7.410236 | 7.816034 | 3.359752 | 5.28942 | 3004.429 |
| TLBO | 3.510509 | 0.7 | 17 | 7.3 | 7.8 | 3.462751 | 5.291858 | 3032.078 |
| GSA | 3.6018 | 0.7 | 17 | 8.3 | 7.8 | 3.371343 | 5.291869 | 3052.646 |
| PSO | 3.512008 | 0.7 | 17 | 8.35 | 7.8 | 3.363882 | 5.290367 | 3069.095 |
| GA | 3.521884 | 0.7 | 17 | 8.37 | 7.8 | 3.368653 | 5.291363 | 3030.517 |
| Algorithm | Best | Mean | Worst | Std. Dev. | Median |
|---|---|---|---|---|---|
| POA | 2996.3482 | 2999.88 | 3001.491 | 1.782335 | 2998.715 |
| MPA | 3000.05 | 3002.04 | 3006.292 | 1.933476 | 3001.586 |
| TSA | 3002.789 | 3008.25 | 3011.159 | 5.84261 | 3006.923 |
| WOA | 3007.266 | 3107.736 | 3213.743 | 79.70181 | 3107.736 |
| GWO | 3004.429 | 3031.264 | 3063.407 | 13.02901 | 3029.453 |
| TLBO | 3032.078 | 3068.37 | 3107.263 | 18.08866 | 3068.061 |
| GSA | 3052.646 | 3172.87 | 3366.564 | 92.64666 | 3159.277 |
| PSO | 3069.095 | 3189.072 | 3315.85 | 17.13229 | 3200.746 |
| GA | 3030.517 | 3297.965 | 3622.361 | 57.06912 | 3291.288 |
| Algorithm | Optimum Variables | Optimum Cost | |||
|---|---|---|---|---|---|
| h | l | T | b | ||
| POA | 0.205719 | 3.470104 | 9.038353 | 0.205722 | 1.725021 |
| MPA | 0.205604 | 3.475541 | 9.037606 | 0.205852 | 1.726006 |
| TSA | 0.205719 | 3.476098 | 9.038771 | 0.20627 | 1.72734 |
| WOA | 0.19745 | 3.315724 | 10.000 | 0.201435 | 1.820759 |
| GWO | 0.205652 | 3.472797 | 9.042739 | 0.20575 | 1.725817 |
| TLBO | 0.204736 | 3.536998 | 9.006091 | 0.210067 | 1.759525 |
| GSA | 0.147127 | 5.491842 | 10.000 | 0.217769 | 2.173293 |
| PSO | 0.164204 | 4.033348 | 10.000 | 0.223692 | 1.874346 |
| GA | 0.206528 | 3.636599 | 10.000 | 0.20329 | 1.836617 |
| Algorithm | Best | Mean | Worst | Std. Dev. | Median |
|---|---|---|---|---|---|
| POA | 1.724968 | 1.726504 | 1.728593 | 0.004328 | 1.725779 |
| MPA | 1.726006 | 1.727209 | 1.727445 | 0.000287 | 1.727168 |
| TSA | 1.72734 | 1.72851 | 1.728946 | 0.001158 | 1.728469 |
| WOA | 1.820759 | 2.232094 | 3.05067 | 0.324785 | 2.246459 |
| GWO | 1.725817 | 1.731064 | 1.743044 | 0.00487 | 1.728802 |
| TLBO | 1.759525 | 1.819111 | 1.874907 | 0.027565 | 1.821584 |
| GSA | 2.173293 | 2.546274 | 3.00606 | 0.256064 | 2.49711 |
| PSO | 1.874346 | 2.120935 | 2.321981 | 0.034848 | 2.098726 |
| GA | 1.836617 | 1.364618 | 2.036875 | 0.139597 | 1.937297 |
| Algorithm | Optimum Variables | Optimum Cost | ||
|---|---|---|---|---|
| d | D | p | ||
| POA | 0.051892 | 0.361608 | 11.00793 | 0.012666 |
| MPA | 0.051154 | 0.34382 | 12.09792 | 0.012677 |
| TSA | 0.050188 | 0.341609 | 12.0759 | 0.012681 |
| WOA | 0.05001 | 0.310476 | 15.003 | 0.013195 |
| GWO | 0.05001 | 0.316019 | 14.22908 | 0.012819 |
| TLBO | 0.05079 | 0.334846 | 12.72523 | 0.012712 |
| GSA | 0.05001 | 0.317375 | 14.23152 | 0.012876 |
| PSO | 0.05011 | 0.310173 | 14.0028 | 0.013039 |
| GA | 0.05026 | 0.316414 | 15.24265 | 0.012779 |
| Algorithm | Best | Mean | Worst | Std. Dev. | Median |
|---|---|---|---|---|---|
| POA | 0.012666 | 0.012688 | 0.012677 | 0.001022 | 0.012685 |
| MPA | 0.012677 | 0.012693 | 0.012724 | 0.005623 | 0.012696 |
| TSA | 0.012681 | 0.012706 | 0.01273 | 0.004157 | 0.012709 |
| WOA | 0.013195 | 0.014828 | 0.017875 | 0.002274 | 0.013202 |
| GWO | 0.012819 | 0.014474 | 0.017852 | 0.001623 | 0.014031 |
| TLBO | 0.012712 | 0.012849 | 0.013008 | 7.81E-05 | 0.012854 |
| GSA | 0.012876 | 0.013448 | 0.014222 | 0.000287 | 0.013377 |
| PSO | 0.013039 | 0.014046 | 0.016263 | 0.002074 | 0.013011 |
| GA | 0.012779 | 0.013079 | 0.015225 | 0.000375 | 0.012961 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Trojovský, P.; Dehghani, M. Pelican Optimization Algorithm: A Novel Nature-Inspired Algorithm for Engineering Applications. Sensors 2022, 22, 855. https://doi.org/10.3390/s22030855
Trojovský P, Dehghani M. Pelican Optimization Algorithm: A Novel Nature-Inspired Algorithm for Engineering Applications. Sensors. 2022; 22(3):855. https://doi.org/10.3390/s22030855
Chicago/Turabian StyleTrojovský, Pavel, and Mohammad Dehghani. 2022. "Pelican Optimization Algorithm: A Novel Nature-Inspired Algorithm for Engineering Applications" Sensors 22, no. 3: 855. https://doi.org/10.3390/s22030855
APA StyleTrojovský, P., & Dehghani, M. (2022). Pelican Optimization Algorithm: A Novel Nature-Inspired Algorithm for Engineering Applications. Sensors, 22(3), 855. https://doi.org/10.3390/s22030855







